Abstract
Since the taper ratio of most wings is not equal to 1, the beam-disk trailing edge deflection mechanism originally designed for the rectangular wing is not fully applicable to the non-equal chord wing. Moreover, it is not only expected that the wing shape can achieve excellent aerodynamic performance under different flight conditions, but one also needs to consider whether the flexible skin can achieve this deformation. This paper used the honeycomb composite structure with zero Poisson’s ratio as the flexible skin of the trailing edge for the variable camber wing, and designed the beam-disk trailing edge deflection mechanism for the non-equal chord wing. The aerodynamic configuration was optimized considering the deformation capability of the skin, and the multidisciplinary design and optimization method of the variable camber wing with non-equal chord was studied. The results show that the aerodynamic performances of the optimized non-equal chord wings were better than before under all given flight conditions. The flexible skin could withstand the strain caused by the maximum deflection of the trailing edge of the wing, and the weight of the wing structure was reduced by 47.1% compared with the initial design when the structural stiffness and strength were satisfied.
1. Introduction
The morphing wing can adjust its aerodynamic configuration smoothly and spontaneously under different flight conditions or flight environments, so that the aircraft can always obtain the optimal aerodynamic performance during the whole flight mission. The application of variant technology can extend the flight envelope, improve handling characteristics, reduce resistance, increase the range and reduce or eliminate the wing’s flutter. By dynamically adapting or optimizing the shape to various flight conditions, there are many unexplored opportunities beyond the current proof-of-concept demonstrations [1].
Because the variation in variable camber is relatively practicable, it has been widely studied. FlexSys and NASA replaced the Gulfstream III’s traditional aluminum alloy trailing edge flap with an adaptive compliant trailing edge [2]. German Aerospace developed two typical variable camber mechanisms for trailing edges: “finger” type [3] and “belt-rib” type [4,5]. Friswell et al. proposed a variable camber trailing edge design that mimics fish bone [6]. Guo et al. proposed the variable camber leading/trailing edge design of a curved beam matching curved disk [7,8]. Yokozeki et al. proposed a scheme for the variable camber trailing edge based on a corrugated structure [9,10,11]. Li et al. proposed a design of the variable camber leading edge based on a five-bar gear mechanism [12]. Zhang et al. proposed a variable camber wing with compliant leading and trailing edges that was designed using large displacement compliant mechanisms [13]. Balaji designed a multi-segment variable camber fixed wing for unmanned aerial vehicles, utilizing four rib segments with pneumatic actuators, and found that a basic linkage framework inserted inside the wing can achieve a camber change [14]. Zhao et al. investigated a novel double rib sheet structure for an adaptive variable camber wing [15,16]. Chen designed a flexible wing with variable camber at leading and trailing edges using large displacement compliant mechanisms [17]. At present, most studies on the morphing wing in the literature are based on the rectangular wing. However, aircraft mostly use non-equal chord wings nowadays. Since the taper ratio is not equal to 1, the original trailing edge deflection mechanism designed for the rectangular wing is not fully applicable to the non-equal chord wing.
Moreover, in the process of wing variation, it is necessary for the skin to have good in-plane deformation ability to achieve seamless wing deformation, as well as large out-of-plane stiffness to bear aerodynamic loads. The composite skin structure [18] based on a honeycomb structure and flexible surface layer is an effective solution. The honeycomb structure with zero Poisson’s ratio will not appear to be “saddle-shaped” or show “double-curved” warping [19,20] when subjected to bending; so, it is more suitable for 1D deformation schemes such as variable camber and variable chord.
In this paper, the honeycomb composite structure with zero Poisson’s ratio was adopted as the flexible skin of the trailing edge, and a deflection mechanism of the trailing edge for the non-equal chord wing based on the “curved beam–planar disk” trailing edge deflection mechanism designed for the rectangular wing was designed. Furthermore, the multidisciplinary optimization method was used to study the aerodynamic, material, structural and other aspects of the variable camber of the trailing edge of the non-equal chord wing.
2. Design of Trailing Edge Deflection Mechanism
We designed a trailing edge deflection mechanism for flexible skin driven by a curved beam and planar disk for the rectangular wing (Figure 1). The planar disk is fixed on the curved beam, the stringer is fixed on the skin, the planar disk can be connected with the stringer and the planar disk can slide along the wingspan. When the deflection mechanism rotates (a motor at the root of each curved beam drives the curved beam to rotate), it drives the skin deformation through the stringer, changes the camber and thickness of the trailing edge of the wing and forms the shape of the wing under different flight conditions. The curved beam is inserted into the wedge, and the wedge is surrounded by a number of “plates” similar to the wing ribs, which play the role of maintaining the shape of the rear edge of the wedge.
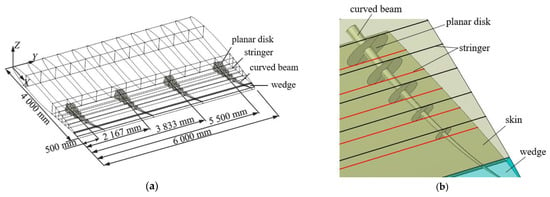
Figure 1.
Rectangular wing structure model: (a) whole model; (b) local model.
A two-cell wing structure of a small UAV is taken as an example in this paper. The inner segment is rectangular and the outer segment is trapezoidal. The plane shape of the semi-wing is shown in Figure 2. The proportional deflection of the wing root and wing tip is performed only on the trailing edge of the outer segment wing.
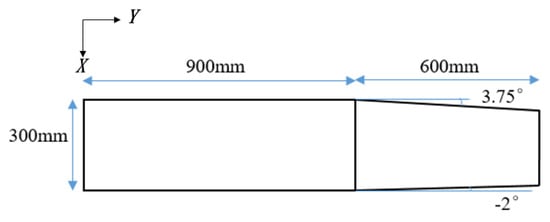
Figure 2.
Plane shape of the semi-wing.
If the existing trailing edge deflection mechanism is directly applied to the trailing edge of the outer wing in this paper, as shown in Figure 3, due to the trapezoidal ratio, the generated spanwise “plate” 1 and 2 will not be parallel to the rear spar, that is, during the rotation of the curved beam, the length of the curved beam inserted into the wedge part is constantly changing. Hence, the slot height of the spanwise “plate” 1 should change according to the diameter of the curved beam; it is not easy to implement. In addition, the end of the curved beam will be separated from the spanwise “plate” 2, so that the shape of the trailing edge wedge cannot be maintained.
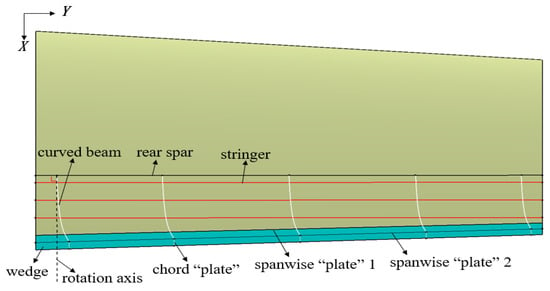
Figure 3.
The original method applied to the non-equal chord wing.
Therefore, based on the original mechanism, this paper improved the trailing edge deflection mechanism for the non-equal chord wing. This wing size was small, and the height of the wedge part was also narrow. In order to facilitate the subsequent actual production and processing, the spanwise “plate” 1 was removed, and the end of all of the curved beams shared the same spanwise “plate” 2. The rotation axis of the curved beam was perpendicular to the trailing edge of the outer segment wing, the stringer, and the spanwise “plate” 2 was parallel to the trailing edge, as shown in Figure 4. The curved beam was not inserted into the wedge, but only the ball at the tip of curved beam was inserted into the spanwise “plate” 2, as shown in Figure 4b. When the curved beam rotates, the wedge can be deflected. Due to the small part of the wedge in this paper, the appropriate materials were used to make it able to withstand the aerodynamic force to maintain the shape, and no other support structure was set inside the wedge.
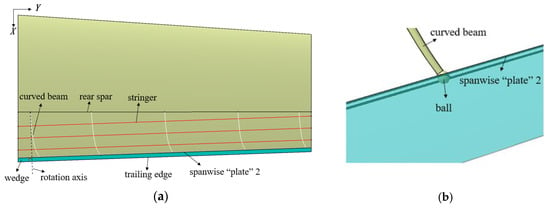
Figure 4.
Improved deflection mechanism: (a) top view; (b) the ball is inserted into the spanwise “plate” 2.
3. Multidisciplinary Optimization Framework for Non-Equal Chord Morphing Wing
In this paper, the design and optimization for aerodynamic and zero Poisson’s ratio honeycomb material and structure were carried out for this non-equal chord morphing wing. The main process was as follows (Figure 5):
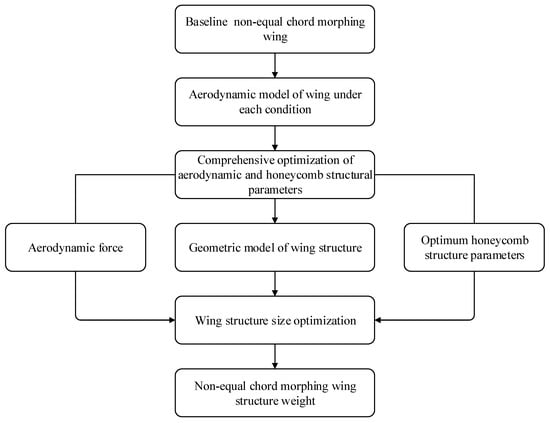
Figure 5.
Multidisciplinary optimization flowchart of non-equal chord morphing wing.
(1) According to the shape parameters of the non-equal chord wing, establish the initial aerodynamic model in each condition;
(2) Considering the deformation ability of honeycomb skin, complete airfoil optimization in each condition and honeycomb structure parameter optimization;
(3) According to the optimized wing shape and wing structure parameters, establish the wing structure geometric model;
(4) Extract the aerodynamic load and honeycomb structure parameter optimization results, and obtain the minimum weight of wing structure by the wing structure optimization.
4. Comprehensive Optimization of Aerodynamics and Honeycomb Structure Parameters
4.1. Aerodynamic Model of the Wing
We utilized the CST airfoil parameterization method [21], which can reflect the geometric parameters of airfoil and has good fitting ability, and is suitable for airfoil optimization. The CST method multiplies the classification function C(x) and the shape function S(x), plus the thickness of the trailing edge of the airfoil . This method is also known as the BPn method (where BP represents the Bernstein polynomial and n represents the order of the polynomial). The airfoil curve can be expressed as follows:
where , , k is the coefficient describing the proportion of generating airfoil, N1 and N2 are the parameters controlling the shape of airfoil and the coordinate of control points is , i = 0, 1, 2, …, n.
Four typical flight conditions were selected as aerodynamic optimization objects, as shown in Figure 6. Airfoil 1 was the NACA 2412 reference airfoil, and 66% of the chord length of the reference airfoil was taken as the trailing edge deflection point: k = 1, N1 = 0.5, N2 = 1 and n = 6. The thickness of the reference airfoil at the trailing edge control point was changed based on the CST method to generate trailing edge deflection airfoil 2, 3 and 4. The flight parameters and wing states under the four flight conditions are described in Table 1.
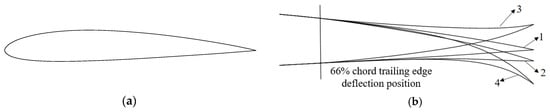
Figure 6.
Initial trailing edge shapes of the four airfoils: (a) NACA 2412 reference airfoil; (b) shape of trailing edge.

Table 1.
Introduction of four flight conditions.
In four flight conditions, its inner wing adopts airfoil 1.
The aerodynamic analysis and calculation of the wing shape under four flight conditions were carried out using Cart3D [22] and Friction [23]. Cart3D is a highly accurate non-viscous flow analysis software that solves compressible Euler equations based on the finite volume method and non-structurally adaptive Cartesian grids for aerodynamic and load distribution calculations during the conceptual design and preliminary design phase of aircraft. The computational mesh can be generated automatically by inputting the far field radius, max number of refinements and number of buffer cell layers. The Mach number, angle of attack, sideslip angle, reference point of torque, reference area and reference length should be inputted during aerodynamic calculation. The Friction program can calculate laminar and turbulent surface friction and shape drag and is suitable for the preliminary design of aircraft, and it uses standard flat plate skin friction formulas and form factors; the input requires geometric information and either the Mach and altitude combination or the Mach and Reynolds number at which the results are desired. In this paper, friction drag coefficient CDf and shape drag coefficient CDform were calculated using the Friction program (the entire flow was solved as turbulent flow in this paper), and induced drag coefficient CDi was calculated using Cart3D. In this paper, the lift–drag ratio K is given as follows:
4.2. Equivalent Parameters of Honeycomb Structure with Zero Poisson’s Ratio
The zero Poisson’s ratio honeycomb sandwich material was used as the flexible skin structure for the trailing edge of the wing with variable camber. The outer layer is silicone rubber material with good ductility, and the inner layer has an accordion honeycomb [24] structure made of duralumin alloy. As shown in Figure 7, the length of a single inclined beam in the X-direction is , the height in the Y-direction is , the wall thickness is , the angle between the inclined beam and the X axis is , the interval in the Y-direction is , the wall thickness of the vertical beam is and the depth of the whole honeycomb structure in the Z-direction is . Furthermore, is the height coefficient of the inclined beam, is the interval coefficient of the inclined beam, is the thickness coefficient of the inclined beam, is the relative thickness coefficient of the vertical beam and ; is the thickness coefficient of the vertical beam.
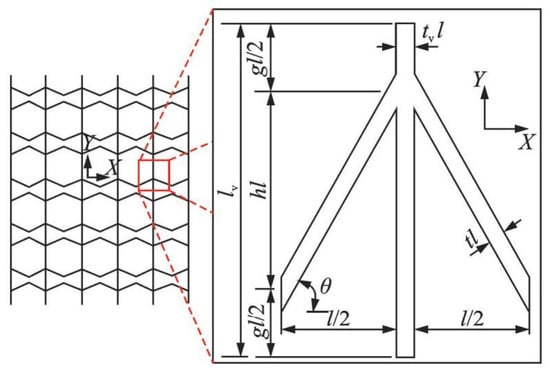
Figure 7.
Accordion honeycomb structure parameters [24].
Through the force analysis of the element structure, the equivalent elastic modulus in the X, Y and Z directions and the equivalent shear modulus in the X–Y, X–Z and Y–Z planes can be obtained using Castigliano’s theorem, the principle of minimum complementary energy and the principle of minimum potential energy:
where is the shear stress shape coefficient of the element section, and is 1.2 [25] in this paper. and are, respectively, the elastic modulus and Poisson’s ratio of the raw materials used in the honeycomb structure. Poisson’s ratio of the cell structure is 0.
When the accordion honeycomb structure is subjected to tension F in the X-direction, the X-direction displacement of the right end of the inclined beam can be obtained according to Castigliano’s second theorem:
Therefore, the equal strain of the inclined beam in the X direction is
According to the force of the inclined beam, the maximum positive strain of the material is
The bearing force of the material should meet the requirements of its allowable strain, namely
According to Equations (10)–(12), it can be obtained that
According to Equation (13), the relationship between the equivalent allowable strain of the accordion honeycomb structure and the allowable strain of the raw materials can be obtained:
The thickness of wing skin is thin, usually approximate to a thin plate structure, and the X-direction is the main tensile direction in the trailing edge of the variable camber skin surface; hence, the honeycomb structure equivalent allowable strain approximates as the allowable strain of flexible skin.
4.3. Comprehensive Optimization
As can be seen in Figure 6, the deflection angle of the trailing edge of the wing in the outer segment under condition D is the largest, and the deformation requirement on the trailing edge of the honeycomb skin is also the largest. The specific implementation process of the aerodynamic optimization of the wing trailing edge variable camber considering the deformation ability of the honeycomb skin is shown in Figure 8:
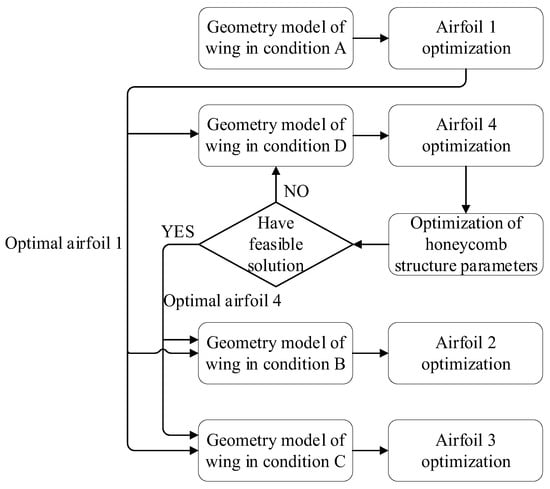
Figure 8.
Optimization flowchart.
The first step:
(1) Given the wing shape model under condition A, optimize airfoil 1;
(2) Transfer optimal airfoil 1 to conditions B, C and D for their respective inner segment wing modeling.
The second step:
(1) Given the wing shape model under condition D, optimize airfoil 4; when optimal airfoil 1 is deflected to optimal airfoil 4, the strain required to achieve the geometric deformation of optimal airfoil 4 is obtained according to the strain calculation formula.
(2) Optimize the honeycomb structure parameters, and determine whether the equivalent allowable strain of the honeycomb structure is greater than the strain in (1). If yes, transfer the optimal airfoil 4 to the conditions B and C, which are used as the constraint conditions for airfoils 2 and 3 optimization (see below for details). If not, reduce the deflection angle of airfoil 4 appropriately, and re-optimize the airfoil 4 and honeycomb structure parameters.
The third step:
(1) Given the wing shape model under conditions B and C, optimize airfoils 2 and 3.
Since the planar disk in the trailing edge deflection mechanism is fitted by the thickness of the airfoil at each flight state of the disk station, the influence of the thickness of the airfoil on the shape of the disk should be considered in order to ensure that a regular shape of the disk (as shown in Figure 9a) can be fitted after the optimization of the airfoil. As shown in Figure 10, an ellipse can be determined according to the thickness of optimal airfoils 1 and 4 at the disk station. The length of the upper and lower line segments of airfoils 2 and 3 at the disk station is , , and , the deflection angle of the line segment is and the length of the line segment at the ellipse is ; then, should be greater than or equal to 0, and the closer to 0 the better.
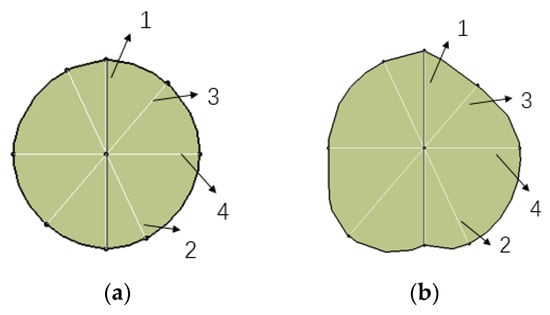
Figure 9.
Shape of planar disk: (a) regular plate; (b) irregular plate.
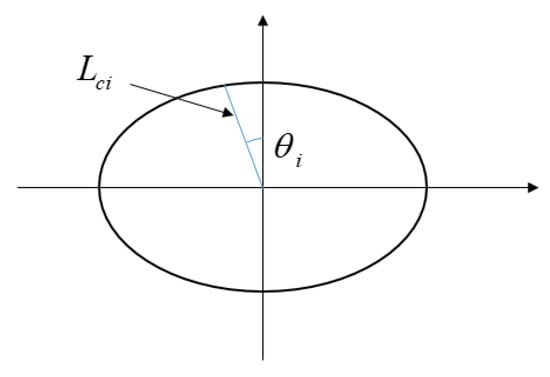
Figure 10.
Schematic diagram of the ellipse.
Honeycomb skin not only needs to have good in-plane deformation ability, but also needs to have large out-plane stiffness to withstand aerodynamic load and maintain the shape of the wing when it meets the strain requirements. In the optimization process of honeycomb structure parameters, in order to ensure the reasonable shape of the honeycomb structure (Figure 11), it can be obtained that according to geometric relations.
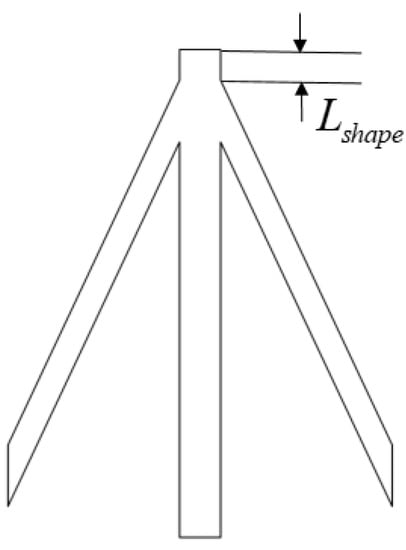
Figure 11.
Reasonable honeycomb structure shape.
The airfoil optimization problem under each condition is defined as follows:
- (1)
- Condition A
Maximize: lift–drag ratio K.
Find: Z-direction coordinates , , and at airfoil trailing edge control point 11/15 and 13/15 chord.
- (2)
- Condition D
Maximize: lift coefficient CL.
Find: Z-direction coordinates , , , , and at airfoil trailing edge control points 11/15, 13/15 and 14/15, and 1 chord.
- (3)
- Condition B
Maximize: lift–drag ratio K.
Find: Z-direction coordinates , , , , and at airfoil trailing edge control points 11/15, 13/15 and 14/15, and 1 chord.
Subject to: .
- (4)
- Condition C
Maximize: coefficient of rolling moment C1.
Find: Z-direction coordinates , , , , and at airfoil trailing edge control points 11/15, 13/15 and 14/15, and 1 chord.
Subject to: .
The optimization problem of honeycomb structure parameters is defined as follows:
Maximize: equivalent and maximum equivalent .
Find: honeycomb structural parameters , , and .
Subject to: the equivalent allowable strain of the honeycomb structure is greater than the strain generated by optimal airfoil 4 on the geometrical deformation, and is greater than 0.
5. Non-Equal Chord Wing Structure Model
5.1. Wing Structure Design
In this paper, a double spar wing was chosen, and the positions of the front and rear spar were 0.2 and 0.66 chord, respectively. The ribs were arranged along the airflow, and the spacing between two ribs was 150 mm. Five curved beams were set at the trailing edge of the wing of the outer segment, and the distance between each curved beam and the wing root of the outer segment is described in Table 2. Figure 12 shows the designed “curved beam–planar disk” model. Three stringers are arranged parallel to the trailing edge of the outer segment wing, and their chord stations are 0.7, 0.8 and 0.9 of the airfoil where the fifth curved beam is located. The chord position of the wedge is 0.97 of the airfoil where the fifth curved beam is located. The top view of the internal structure arrangement of the wing in condition A is shown in Figure 13.

Table 2.
Distance between the curved beam and the wing root of the outer segment.
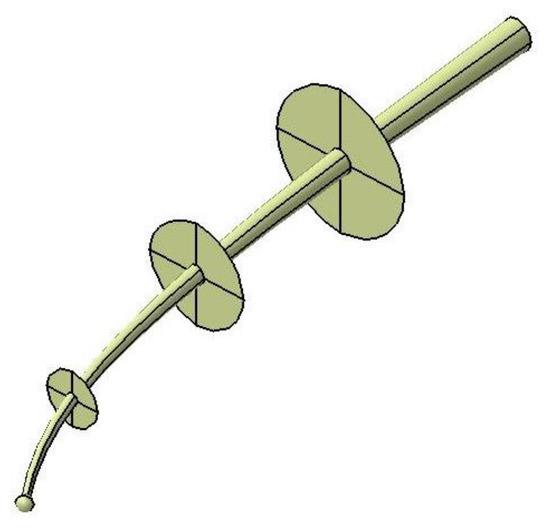
Figure 12.
Curved beam–planar disk.
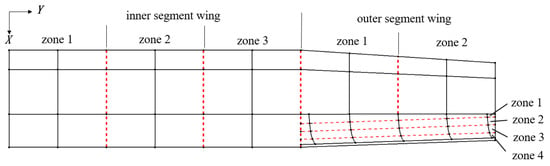
Figure 13.
Top view of internal wing structure arrangement.
The finite element mesh of the non-equal chord wing generated using HyperMesh [26] software is shown in Figure 14. The duralumin alloy is used for the rest of the wing structure except for the flexible skin on the trailing edge of the wing. The load on the wing involves both aerodynamic force and gravity. The boundary conditions are assumed to be that the front and rear spars are fixed at the wing root. In this paper, the safety factor of 1.5 was taken, two load factors of “+2.5 G” and “−1 G” were set for the wing structure under condition A (0.3 Ma cruise), and the static analysis was carried out using OptiStruct [27] solver.
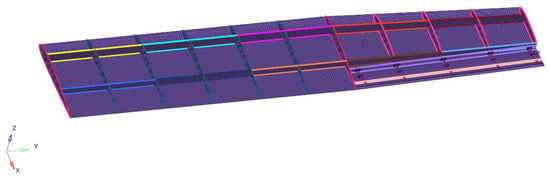
Figure 14.
Finite element mesh of the wing (with the upper skin hidden).
5.2. Definition of Structural Optimization Problems
As shown in Figure 12, the inner wing is divided into three zones, the front and middle parts of the outer wing are divided into two zones and the flexible skin on the trailing edge of the outer wing with three stringers is divided into four zones. Each curved beam is divided into four zones according to the position of the three planar disks on it. Now, the subscript ij is determined, where i represents the inner and outer segment wings (1 represents the inner segment and 2 represents the outer segment), and j represents the zone number. The optimization problem is defined as follows:
Minimize: weight of wing structure.
Find: the thickness of the upper and lower skin of each zone in the inner and outer segment wing, denoted as USij and LSij; the thickness of the front and rear spar web in each zone of the inner and outer segment wing, denoted as FSWij and BSWij; the cross-sectional area of the front and back spar rod in each zone of the inner and outer segment wing, denoted as FSRij and BSRij; the thickness of the common rib web of the inner and outer segment wing, denoted as RWi (i = 1~2); the cross-sectional area of the common rib rod of the inner and outer segment wing, denoted as RRi (i = 1~2); the thickness of the strengthened rib web of the inner segment wing, denoted as SRW1; the cross-sectional area of the strengthened rib rod of the inner segment wing, denoted as SRR1; the thickness of the upper and lower flexible skin of the trailing edge of the outer segment wing, denoted as UHSj and LHSj (j = 1~4); the thickness of the upper and lower skin and the chord and span of the wedge, denoted as JPUS, JPLS, JPX1, JPX2 and JPY; the cross-section radius of the circle beam in each section of each curved beam, denoted as CBmn (m = 1~5, n = 1~4); and the thickness of each planar disk on each curved beam, denoted as Pmn (m = 1~5, n = 1~3). There are a total of 84 design variables. Table 3 lists the value range of each design variable.

Table 3.
Value range of each design variable.
In addition to the above design variables used for optimization, the structural dimension parameters of the three stringers were taken as fixed parameters in this paper, and the cross-section shape of the stringers is shown in Figure 15. The dimension parameters of each stringer are presented in Table 4.
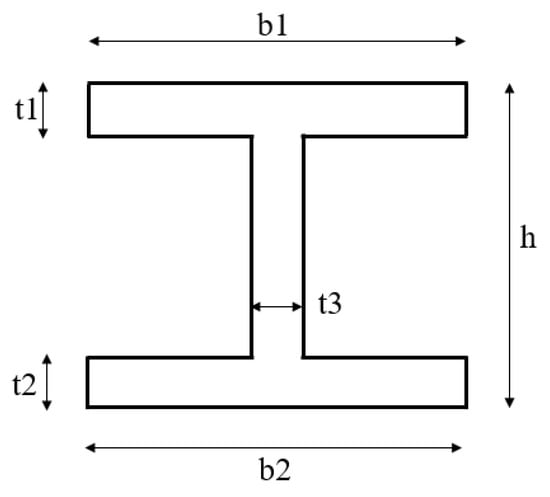
Figure 15.
I-section.

Table 4.
Dimension parameters of each stringer.
Subject to: The constraints are shown in Table 5. The upper limit of the flexible skin strain at the trailing edge of the outer segment wing is the equivalent allowable strain value of the honeycomb structure obtained after the optimization of the honeycomb structure parameters.

Table 5.
Constraints of structure optimization.
6. Results and Analysis of Multidisciplinary Optimization
The multidisciplinary optimization of the non-equal chord morphing wing was integrated using Isight software. The platform consists of two modules: the comprehensive optimization module of aerodynamic and honeycomb structure parameters, and the optimization module of wing structure size. The former mainly completes the establishment of morphing wing geometry and airfoil optimization considering the deformation ability of honeycomb skin. This part of optimization is completed by the optimization module of Isight [28] software. The latter mainly completes the establishment of the morphing wing structure model and the optimization of the morphing wing structure, which is completed by OptiStruct in HyperMesh. The optimization results are shown in Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12.

Table 6.
Optimization results of airfoil 1 under condition A.

Table 7.
Optimization results of airfoil 4 under condition D.

Table 8.
Optimization results of airfoil 2 under condition B.

Table 9.
Optimization results of airfoil 3 under condition C.

Table 10.
Optimization results of honeycomb structure parameters.

Table 11.
Optimization results of wing structure design variables.

Table 12.
Optimization results of wing structure performance index.
- (1)
- Aerodynamic optimization
Condition A: The sequential quadratic programming algorithm is adopted (set “max iterations” to 40). The optimization results are shown in Table 6.
Condition D: firstly, the multi-island genetic algorithm was used for global optimization (set “sub-population size” to 25, “number of islands” to 10 and “number of generations” to 10), and then the sequential quadratic programming algorithm was used to find the local optimal solution (set “max iterations” to 40). The optimization results are shown in Table 7.
Condition B: firstly, the multi-island genetic algorithm was used for global optimization (set “sub-population size” to 10, “number of islands” to 10 and “number of generations” to 5), and then the sequential quadratic programming algorithm was used to find the local optimal solution (set “max iterations” to 40). The optimization results are shown in Table 8.
Condition C: firstly, the multi-island genetic algorithm was used for global optimization (set “sub-population size” to 10, “number of islands” to 10 and “number of generations” to 5), and then the sequential quadratic programming algorithm was used to find the local optimal solution (set “max iterations” to 40). The optimization results are shown in Table 9.
As can be seen from the above results, after optimization, the target aerodynamic performance in each condition is improved. For condition B, the initial value of the lift–drag ratio is greater than the optimization result, because the initial value of the design variable does not consider the impact on the disk shape; this set of initial values does not meet the constraints on the disk geometry, that is, it does not meet .
- (2)
- Optimization of honeycomb structure parameters
Firstly, the multi-island genetic algorithm was used for global optimization, and then the sequential quadratic programming algorithm was used to find the local optimal solution. The optimization results are shown in Table 10. It can be seen that the X-direction elastic modulus of the accordion honeycomb structure decreases and the Z-direction elastic modulus increases, and the equivalent allowable strain also increases greatly.
- (3)
- Wing structure optimization
The method of feasible directions algorithm in OptiStruct was used for optimization, and the optimization results of the design variables of the morphing wing structure with the non-equal chord are shown in Table 11. Because the aerodynamic force decreases along the wingspan, the skin thickness becomes thinner along the span after optimization.
Table 12 shows the optimization results of structural performance of the non-equal chord morphing wing. The optimization results show that the structure of the non-equal chord morphing wing meets the corresponding constraints, and some of them are close to the constraint upper limit, indicating that the material utilization rate is higher. The structural weight of the non-equal chord morphing wing is 4.54134 kg before optimization, and becomes 2.40296 kg after optimization, decreasing by 47.1%. The structural weight reduction effect is very obvious. The energy required to rotate the curved beam from condition A to condition D is about 15 kJ.
The contours of the optimized non-equal chord morphing wing structure are shown in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25. As can be seen in the figures, under the load factor of “+2.5 G” in condition A (0.3 Ma cruise state), the stress at the wing root of the front and rear spar is very large because of the fixed support constraint set. The planar disk transmits the air force of the flexible skin to the curved beam, and the joint place between the planar disk and the curved beam is under large stress; hence, the center of the planar disk can be thickened later. In the place supported by a planar disk, the deformation of the trailing edge flexible skin is small, and in the part between the second and third planar disk, the strain is larger. Under condition D (take-off and landing condition), the overall structure of the wing is displaced and deformed along the Z-axis. The deformation state of the flexible skin on the trailing edge of the outer wing is roughly similar to the shape of the wing after aerodynamic optimization. Due to the large downward deflection angle of the trailing edge flexible skin, the strain near the third planar disk is also large, and the strain is greater closer to the wing root. When the flexible skin on the trailing edge is deflected downward, the curved beam and planar disk will be subjected to the reaction force of the flexible skin on the trailing edge. Therefore, the curved beam and planar disk will have positive displacement and deformation along the Z-axis. Where there is part of the planar disk at the connection point with the lower flexible skin, the stress is greater. The stress is large at the root of the curved beam and at the junction with the planar disk.

Figure 16.
Z-direction displacement (“+2.5 G” in condition A).

Figure 17.
Stress of aluminum wing structure (“+2.5 G” in condition A): (a) shell element; (b) rod element; (c) beam element; (d) planar disk.

Figure 18.
Strain of flexible skin (“+2.5 G” in condition A).

Figure 19.
Wing stability analysis (“+2.5 G” in condition A).
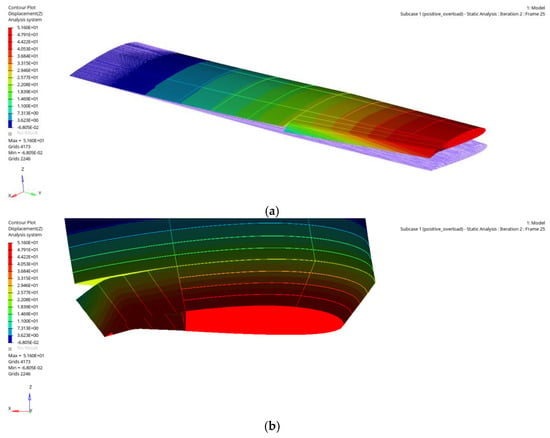
Figure 20.
Z-direction displacement (condition D): (a) global deformation; (b) deformation of flexible skin.

Figure 21.
Stress of aluminum wing structure (condition D): (a) shell element; (b) rod element; (c) beam element.

Figure 22.
Strain of flexible skin (condition D).

Figure 23.
Z-direction displacement of curved beam and planar disk (condition D).

Figure 24.
Stress of planar disk (condition D).

Figure 25.
Stress of curved beam (condition D).
In this paper, a small part of flexible skin on the trailing edge of the wing was selected under condition A to show its real elastic shape. The flexible skin was made of the zero Poisson’s ratio honeycomb sandwich material, the outer panel was made of silicone rubber material with a thickness of 0.1 mm and the inner layer had an accordion honeycomb structure with a thickness of 1.5 mm. The plane shape of the optimized accordion honeycomb unit is shown in Figure 26, and the real elastic shape is shown in Figure 27.
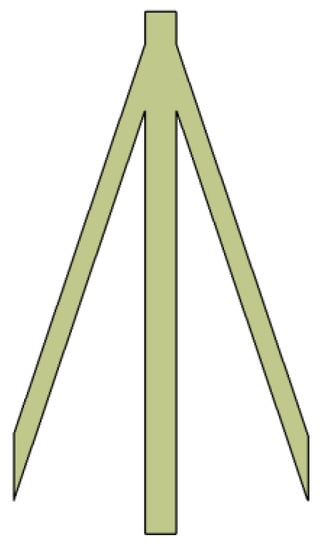
Figure 26.
The plane shape of the optimized accordion honeycomb unit.
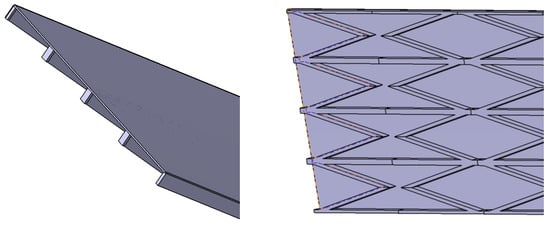
Figure 27.
The real elastic shape of the wing’s skin.
7. Conclusions
In this paper, the deflection mechanism of the non-equal chord variable camber wing was designed, and multidisciplinary design and optimization were carried out. The main conclusions are as follows:
(1) The original trailing edge deflection mechanism suitable for the rectangular wing was improved, and a trailing edge deflection mechanism suitable for the non-equal chord wing was designed. Combined with zero Poisson’s ratio honeycomb skin, it could realize the deflection of the non-equal chord wing trailing edge.
(2) The deformation ability of honeycomb skin was considered in the aerodynamic optimization, and the optimized airfoils not only had good aerodynamic performances, but also the deflection amplitude was within the range of the honeycomb skin strain. After the optimization of the honeycomb structure parameters, the out-of-plane stiffness increased and the in-plane stiffness decreased.
(3) After the optimization of the non-equal chord morphing wing structure, the structural weight was reduced by 47.1% when it satisfied the requirements. The weight reduction mainly came from the reduction in the thickness of the skin, spar web and rib web. Secondly, the radius of each curved beam and the thickness of the planar disk were also greatly reduced.
Author Contributions
Conceptualization, Y.W. and X.L.; data curation, X.L.; formal analysis, Y.W. and X.L.; investigation, X.L., T.W. and H.Y.; methodology, Y.W., X.L. and T.W.; resources, Y.W. and X.L.; software, Y.W. and X.L.; supervision, Y.W., X.L. and T.W.; validation, X.L. and T.W.; visualization, Y.W.; writing—original draft, Y.W., X.L., T.W. and H.Y.; writing—review and editing, Y.W., X.L., T.W. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project of the Natural Science Foundation of China, grant number 12032011.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, D.C.; Zhao, S.W.; Ronch, A.D.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Miller, E.J.; Lokos, W.A.; Cruz, J.; Crampton, G.; Craig, A. Approach for Structurally Clearing an Adaptive Compliant Trailing Edge Flap for Flight; Society of Flight Test Engineers International Annual Symposium; NASA: Washington, DC, USA, 2015.
- Monner, H.P. Realization of an optimized wing camber by using formvariable flap structures. Aerosp. Sci. Technol. 2001, 5, 445–455. [Google Scholar] [CrossRef]
- Campanile, L.F.; Sachau, D. The Belt-Rib Concept: A Structronic Approach to Variable Camber. J. Intell. Mater. Syst. Struct. 2000, 11, 215–224. [Google Scholar] [CrossRef]
- Campanile, L.F.; Seack, O.; Sachau, D. Belt-rib concept for variable-camber airfoils: Recent developments. Smart Struct. 2000, 3985, 110–120. [Google Scholar]
- Woods, B.K.; Bilgen, O.; Friswell, M.I. Wind tunnel testing of the fish bone active camber morphing concept. J. Intell. Mater. Syst. Struct. 2014, 25, 772–785. [Google Scholar] [CrossRef]
- Morishima, R.; Guo, S.J.; Ahmed, S. A Composite Wing with a Morphing Leading Edge. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Orlando, FL, USA, 12–15 April 2010; pp. 7865–7878. [Google Scholar]
- Li, D.C.; Guo, S.J.; Aburass, T.O.; Yang, D.; Xiang, J. Active control design for an unmanned air vehicle with a morphing wing. Aircr. Eng. Aerosp. Technol. 2016, 88, 168–177. [Google Scholar] [CrossRef]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development of Variable Camber Morphing Airfoil Using Corrugated Structure. J. Aircr. 2014, 51, 1023–1029. [Google Scholar] [CrossRef]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development and wind tunnel test of variable camber morphing wing. In Proceedings of the 22nd AIAA/ASME/AHS Adaptive Structures Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Takahashi, H.; Yokozeki, T.; Hirano, Y. Development of variable camber wing with morphing leading and trailing sections using corrugated structures. J. Intell. Mater. Syst. Struct. 2016, 27, 2827–2836. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ge, W.J.; Zhou, J.; Zhang, Y.; Zhao, D.; Wang, Z.; Dong, D. Design and experiment of concentrated flexibility-based variable camber morphing wing. Chin. J. Aeronaut. 2022, 35, 455–469. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Ge, W.J.; Zhang, Z.A.; Mo, X.; Zhang, Y. Design of compliant mechanism-based variable camber morphing wing with nonlinear large deformation. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419886740. [Google Scholar] [CrossRef]
- Balaji, S. Evaluation and Delineations of Multi Segment Variable Camber Fixed Wing for Unmanned Aerial Vehicles. Fluid Mech. Open Access 2018, 5, 186. [Google Scholar]
- Zhao, A.M.; Hui, Z.; Liu, D.S.; Liu, B.F. Structure design of an innovative adaptive variable camber wing. MATEC Web Conf. 2018, 151, 04003. [Google Scholar] [CrossRef]
- Zhao, A.M.; Hui, Z.; Hai, C.J.; Dong, S.W. Structural design and verification of an innovative whole adaptive variable camber wing. Aerosp. Sci. Technol. 2019, 89, 11–18. [Google Scholar] [CrossRef]
- Chen, T.G.; Jiang, J.; Zhang, Q.; Wang, H.L.; Zhang, X.Y. Experiments and modeling of variable camber guide vane embedded with shape memory alloy plate. Smart Mater. Struct. 2021, 30, 045012. [Google Scholar] [CrossRef]
- Olympio, K.; Gandhif, F. Flexible skins for morphing aircraft using cellular honeycomb cores. J. Intell. Mater. Syst. Struct. 2010, 21, 1719–1735. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Chiriam, G.; Ravirala, N.; Zied, K. The in-plane linear elastic constants and out-of plane bending of 3-coordinated ligament and cylinderligament honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Q.H.; Scarpa, F.; Liu, Y.; Leng, J. Bending and benchmark of zero Poisson’s ratio cellular structures. Compos. Struct. 2016, 152, 729–736. [Google Scholar] [CrossRef]
- Kulfan, B.M.; Bussoletti, J.E. “Fundamental” parametric geometry representations for aircraft component shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference 2006-6948, Portsmouth, VA, USA, 6–8 September 2006. [Google Scholar]
- Aftosmis, M.J.; Bbeger, M.J.; Melton, J.E. Robust and Efficient Cartesian Mesh Generation for Component-Based Geometry. AIAA J. 1998, 36, 925–960. [Google Scholar] [CrossRef]
- Cummings, R.M.; Mason, W.H.; Morton, S.A.; McDaniel, R. Applied Computational Aerodynamics: A Modern Engineering Approach; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Liu, W.; Li, H. Equivalent Moduli of Accordion Honeycomb with Zero Poisson’s Ratio. Chin. J. Solid Mech. 2018, 39, 100–112. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M.; Cusens, A.R. Mechanics of Materials; Van Nostrand Reinhold Company: New York, NY, USA, 1972. [Google Scholar]
- Yu, K.P.; Zhou, C.Y.; Tan, H.F. HyperMesh from Entry to Mastery; Science Press: Beijing, China, 2005. [Google Scholar]
- Sheng, J.H.; Xu, Y.D.; Han, J.; Jia, Z.Y. Size Optimization Design for Cantilever Structure of an Ammunition Supply Truck Based on Optistruct. In Proceedings of the 2019 4th International Conference on Automation, Control and Robotics Engineering, Shenzhen, China, 19–21 July 2019. [Google Scholar]
- Liu, L.L.; Jiang, W.; Liu, Z.W.; Yu, R.X.; Bian, T. Multi-objective optimization of shaftless rim-driven thruster based on ISIGHT. J. Phys. Conf. Ser. 2022, 2369, 012023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).