Exploring Delay Propagation Causality in Various Airport Networks with Attention-Weighted Recurrent Graph Convolution Method
Abstract
1. Introduction
- The proposed ARGC-Net can uncover both the spatial and temporal dependencies in delay time across different airports simultaneously, and the embedded attention mechanism can indicate the delay causality links between any two airports.
- The developed model shows great transferability when applied to different airport networks. Additionally, the delay propagation networks can be automatically built through testing from the identified attention scores.
- The delay propagation mechanism of three airport networks with various topological characteristics are compared based on the complex network theory.
- The airport delays are grouped into three states, and the delay state transition network is developed and compared in three different ATC areas.
2. Methodology
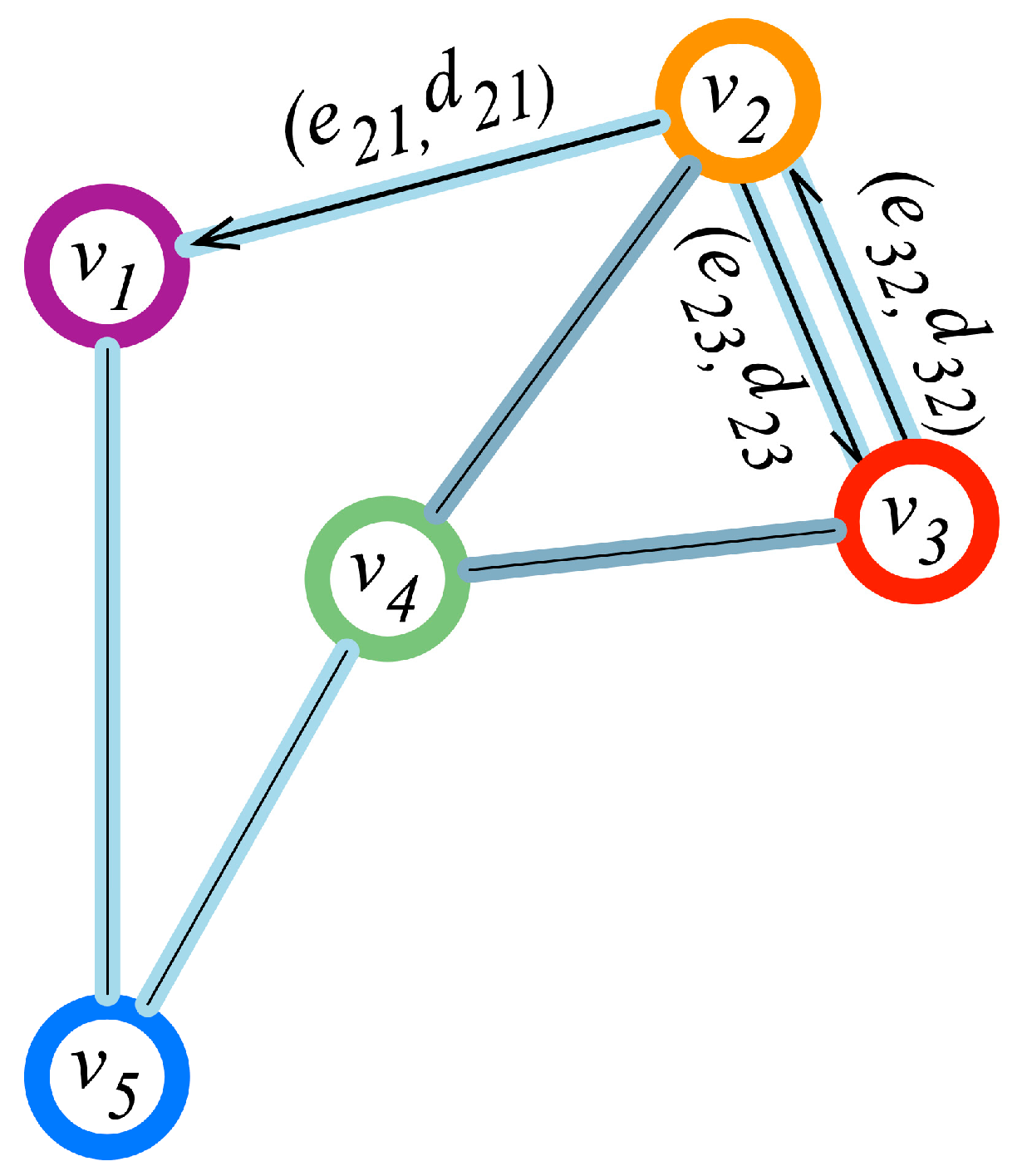
2.1. Problem Formulation
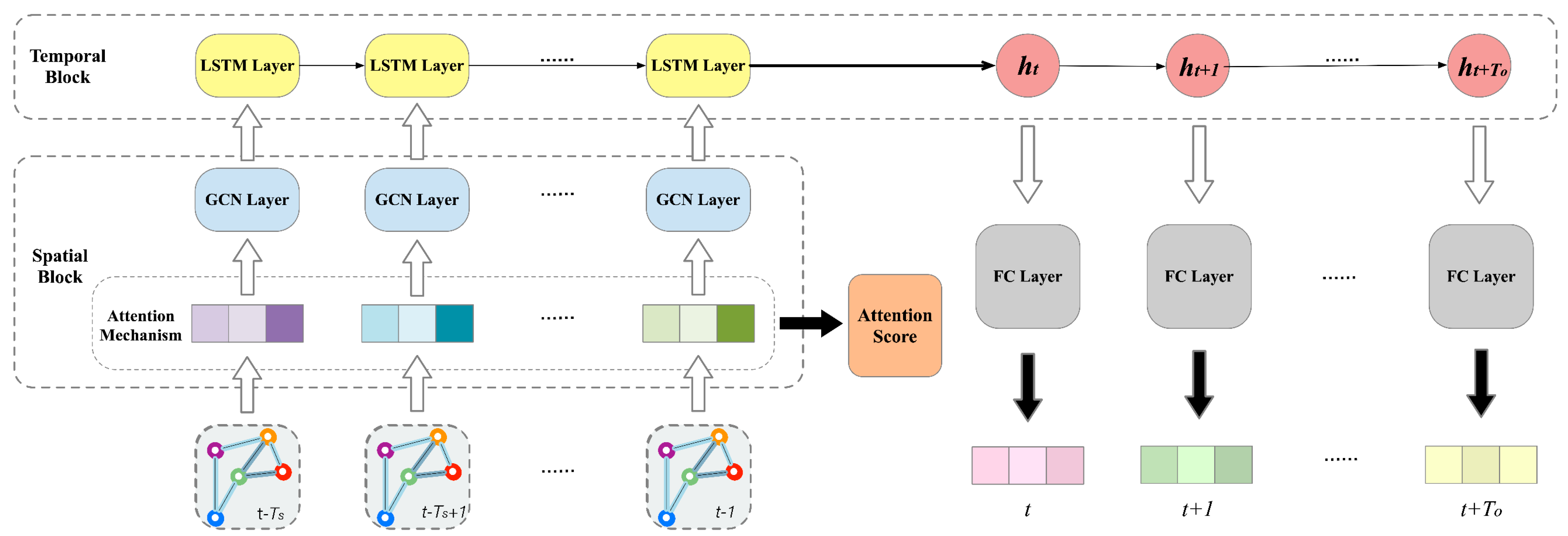
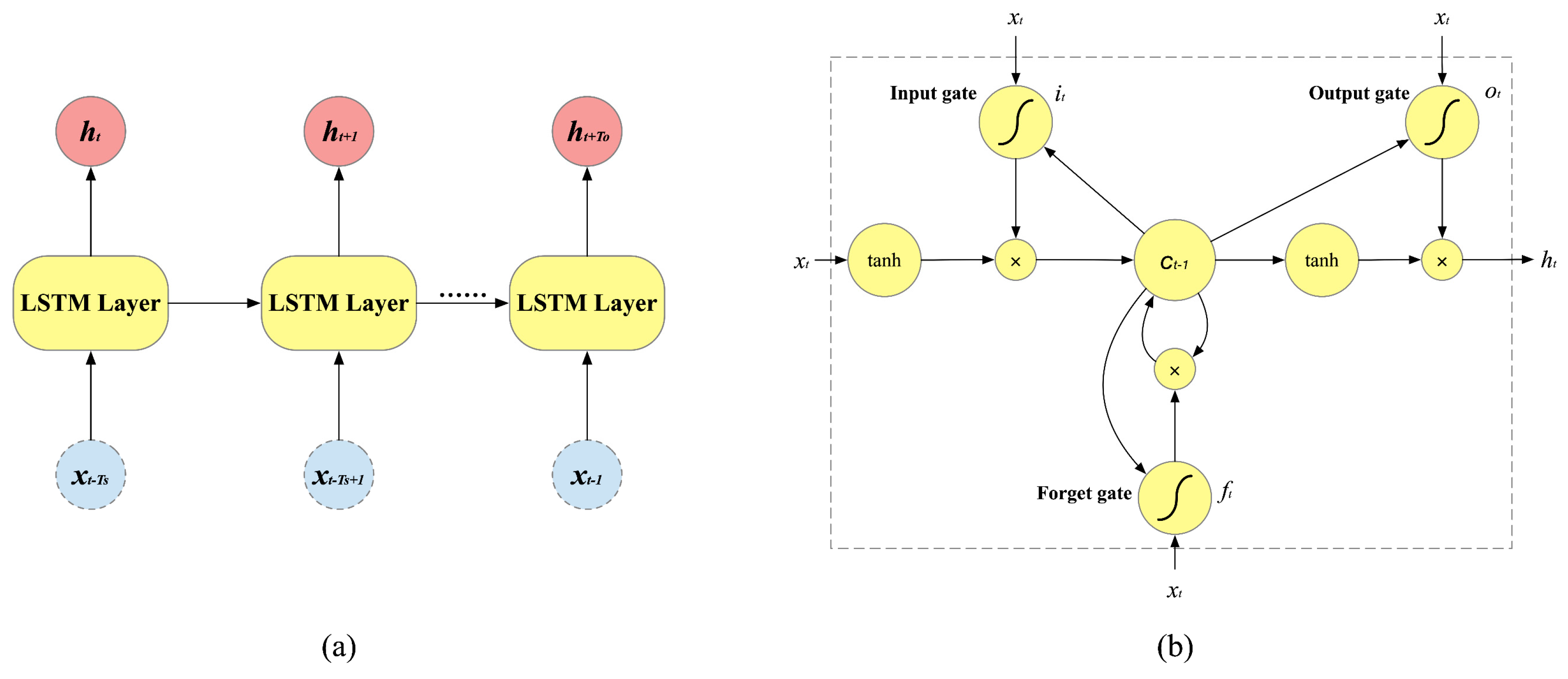
2.2. The Framework of Proposed ARGC Model
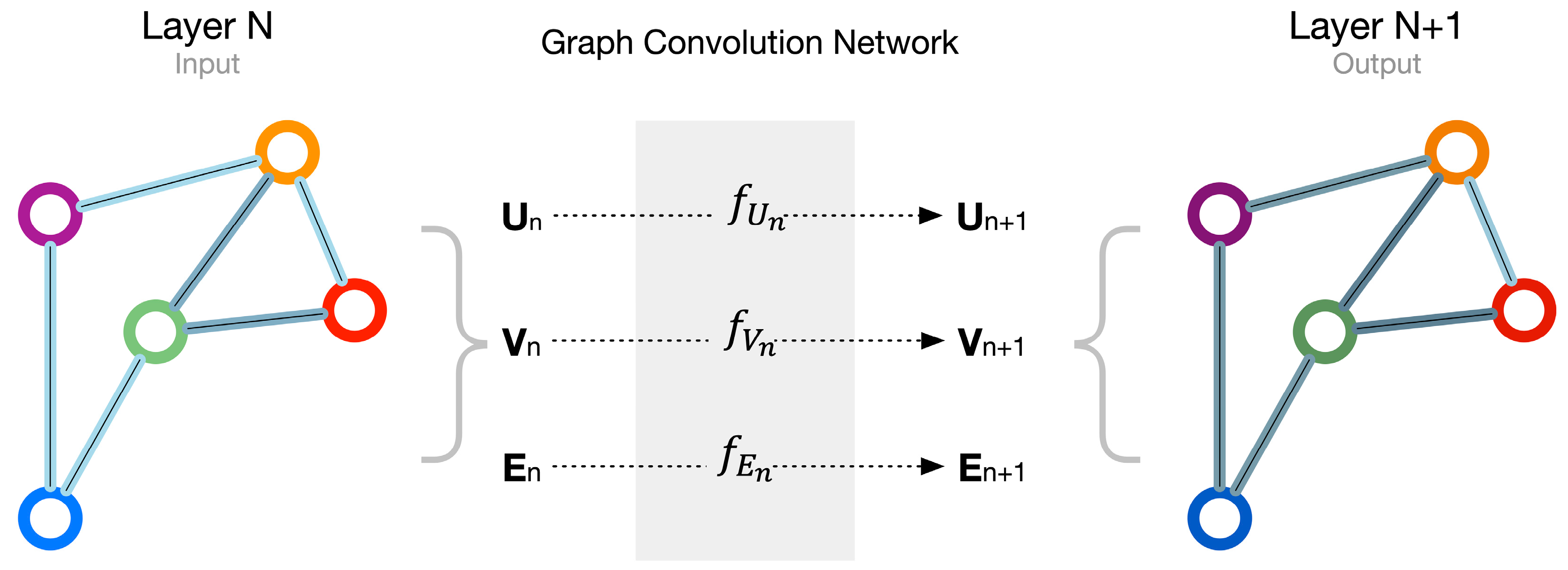
2.3. Graph Convolutional Network
2.4. Attention Mechanism
2.5. Long Short-Term Memory Neural Network
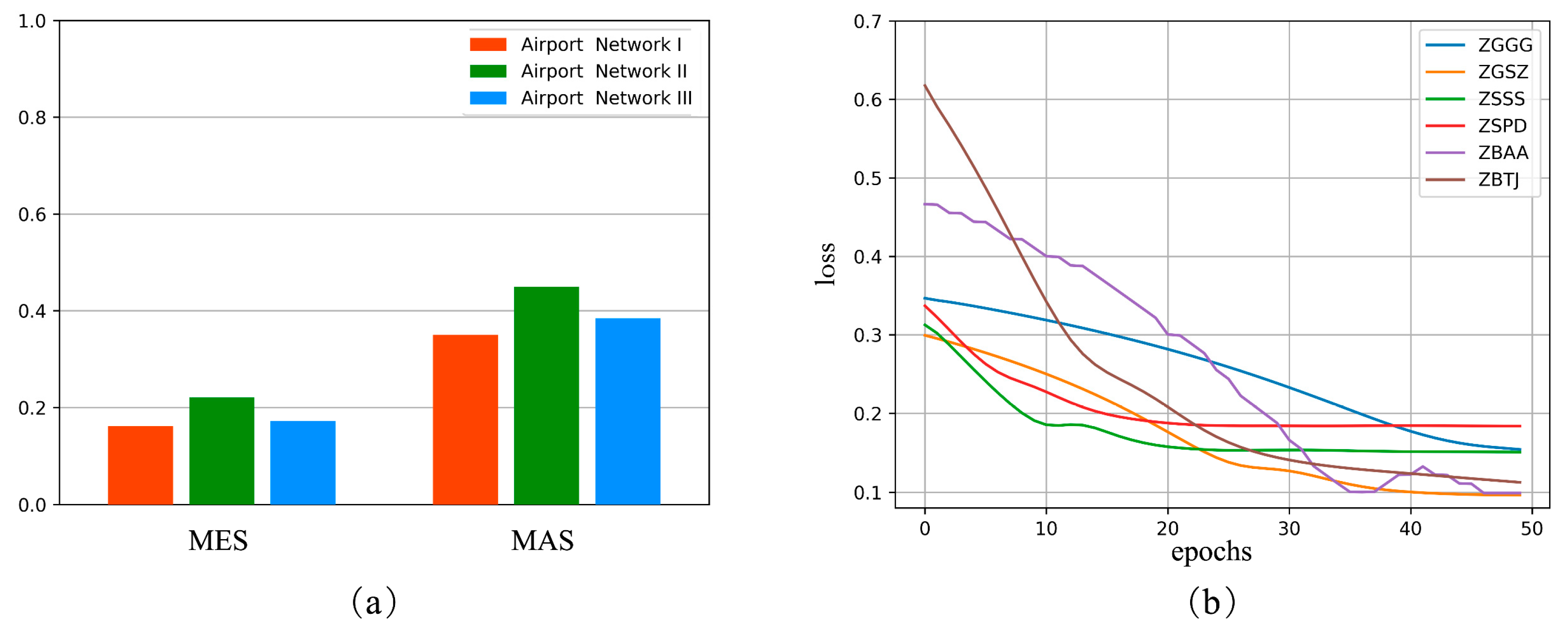
2.6. Objective Function
| Algorithm 1 ARGC training algorithm |
| Input: Airports number i∈V, Historical delay time of all airports in the network {xi}, i∈V, Time steps of input dataset Tstep, Time steps of output dataset Toutput_step, Delay time graph G = (V, E, A) Output: Delay time of airports, ARGC model with attention scores of the well-trained parameters // Prepare the training dataset Initialize a null set: Ɗ = Ø; for time interval t (1 ≤ t ≤ T) do Obtain the historical delay time of all airports at each previous Tstep: Xinput = {xijt-Tstep, …, xijt−1, xijt}, i∈V Obtain the historical delay time of all airports at each predicted time step: Xoutput = {xijt+1, xijt+2, …, xijt+Toutput_step}, i∈V Put the training sample into the dataset: (Xinput, Xoutput) → Ɗ; end for // Training ARGC model Initialize the hidden status, all weights and bias parameters; Concatenate the graphs at Tstep: [A1, A2, …, ATstep] → A; for n = 0 → number of epochs do Randomly select a batch of sample Ɗb from Ɗ as input, where b = 1, 2, …, B; Obtain the output through hidden GCN layers, followed by Equations (1)–(7); Obtain the attention score through Spatial Block, followed by Equations (8)–(10); Flatten the output into a latent vector; Obtain the output of LSTM by passing the flattened vector through Temporal Block, followed by Equations (11)–(15); Estimate the predicted delay time for each output time step: Yjt= σ (WFC • LSTM +bFC); Optimize W, b by minimizing the loss function defined in Equation (16); end for |
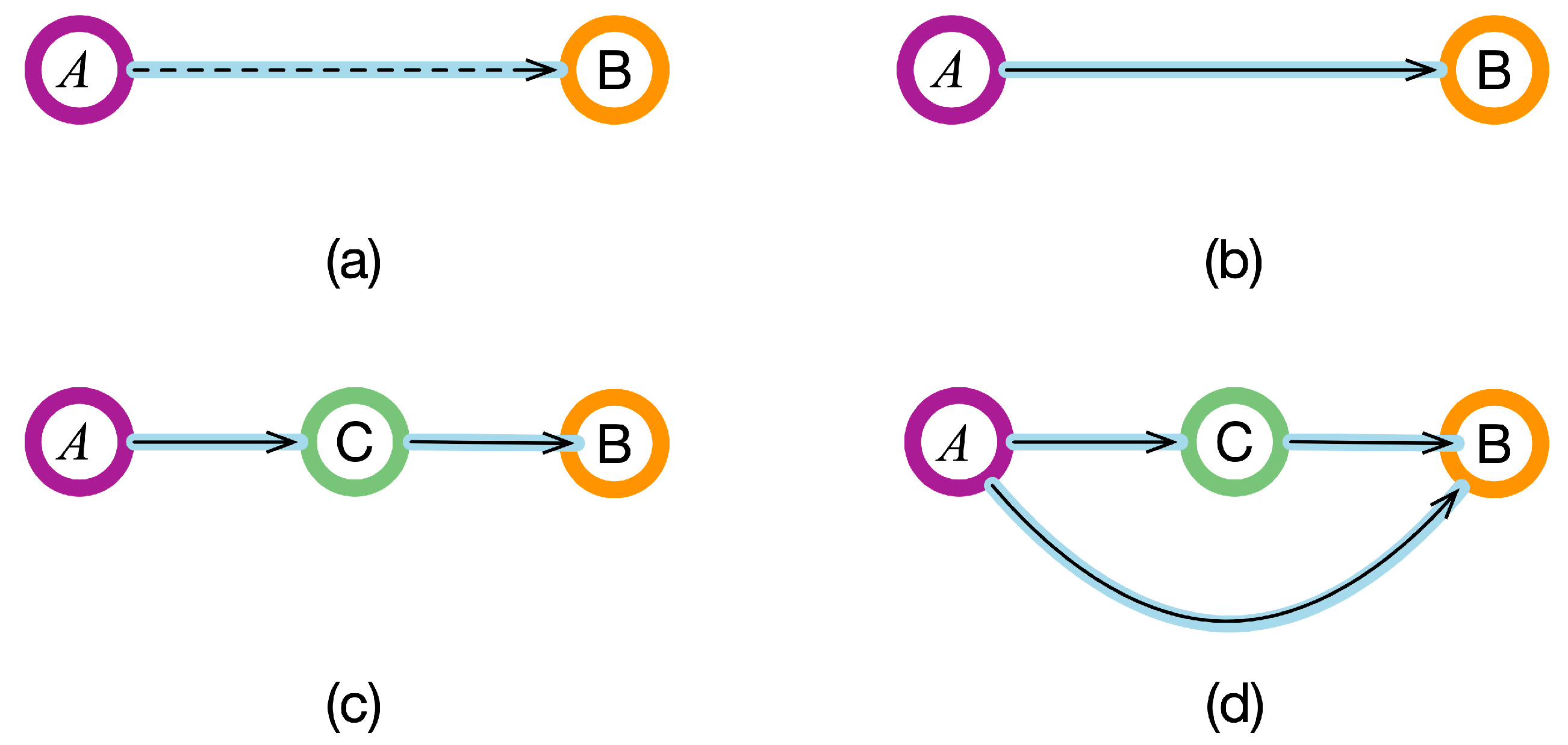
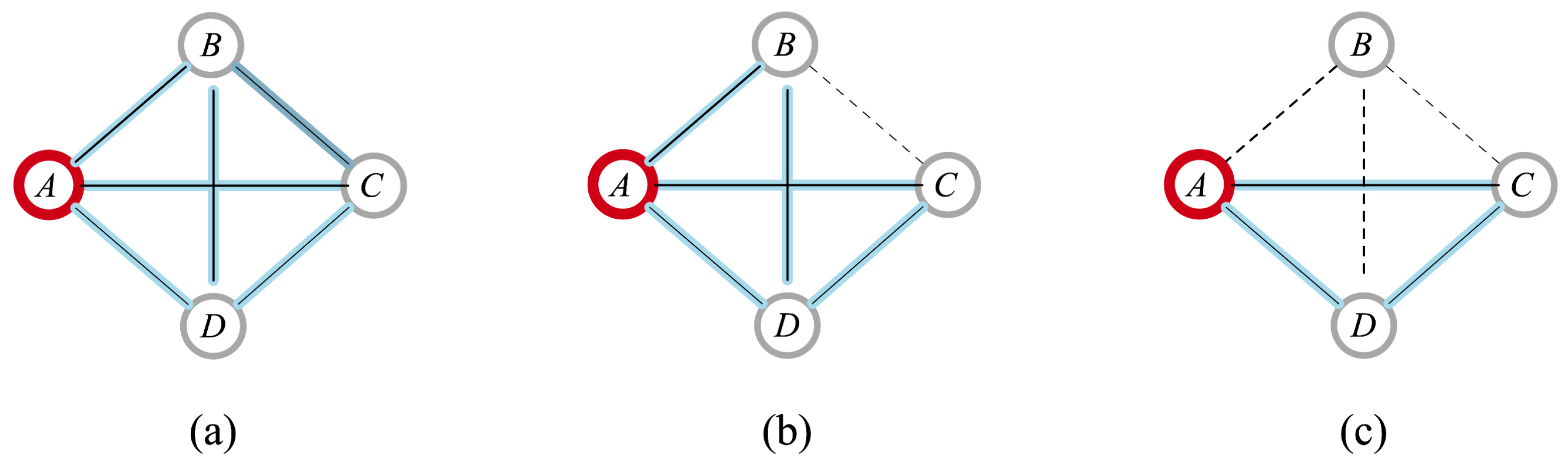
2.7. True Causality Relationship Test
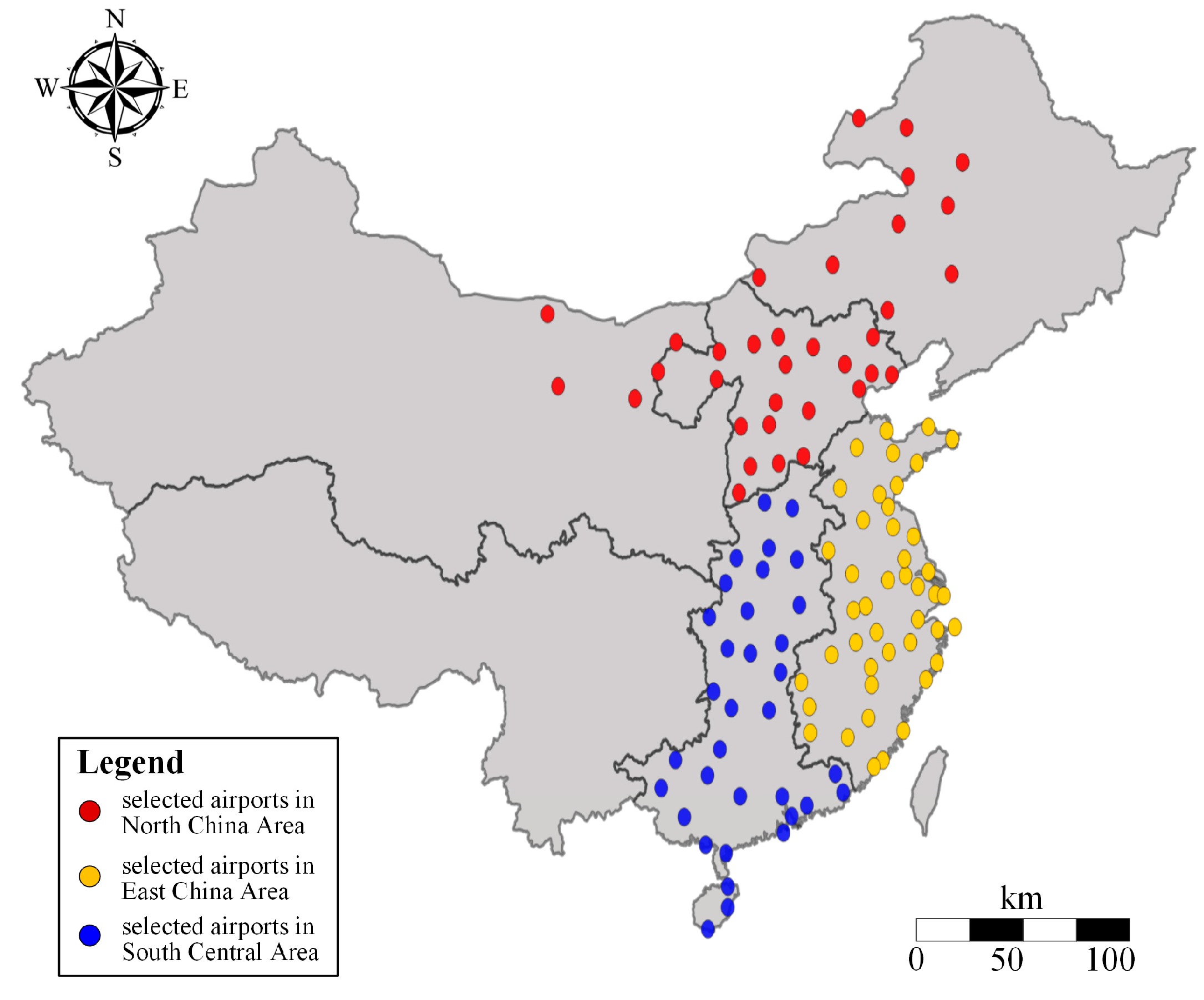
3. Data Source
4. Results of Data Analysis
4.1. Characteristics of Airport Network in Each Region
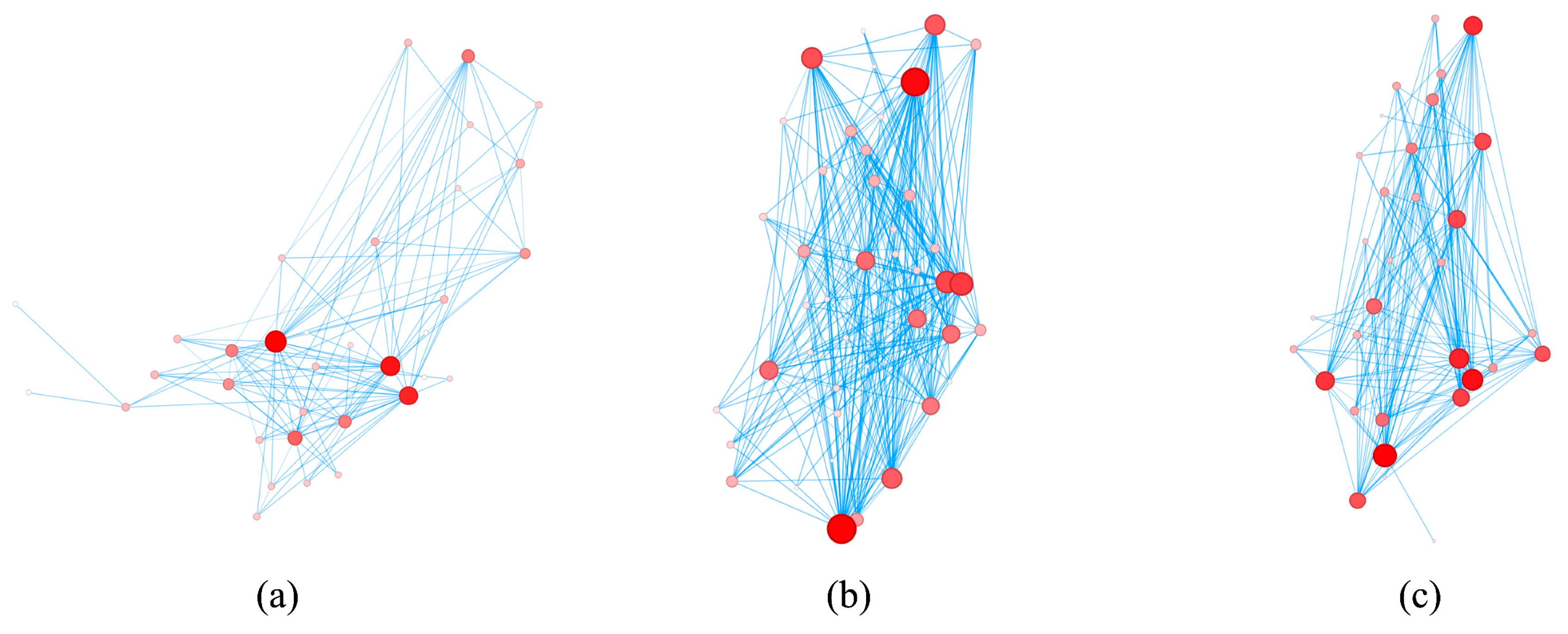
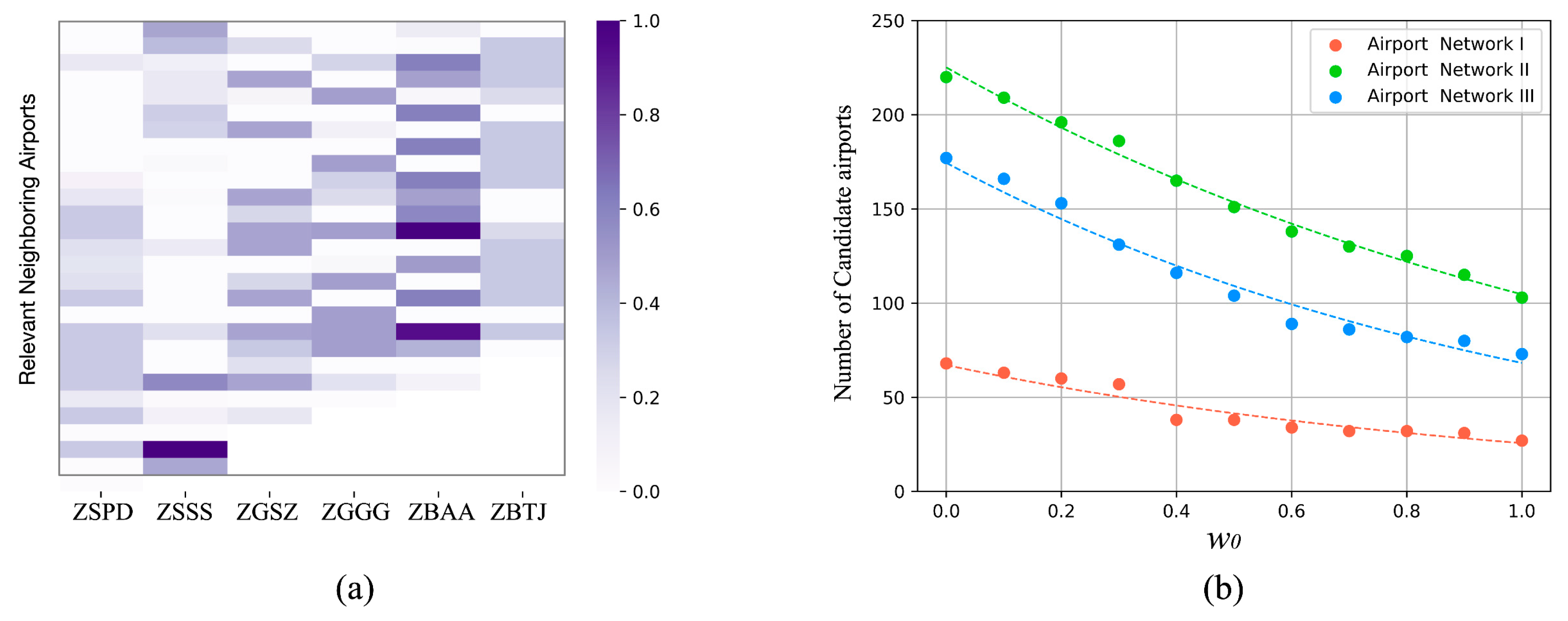
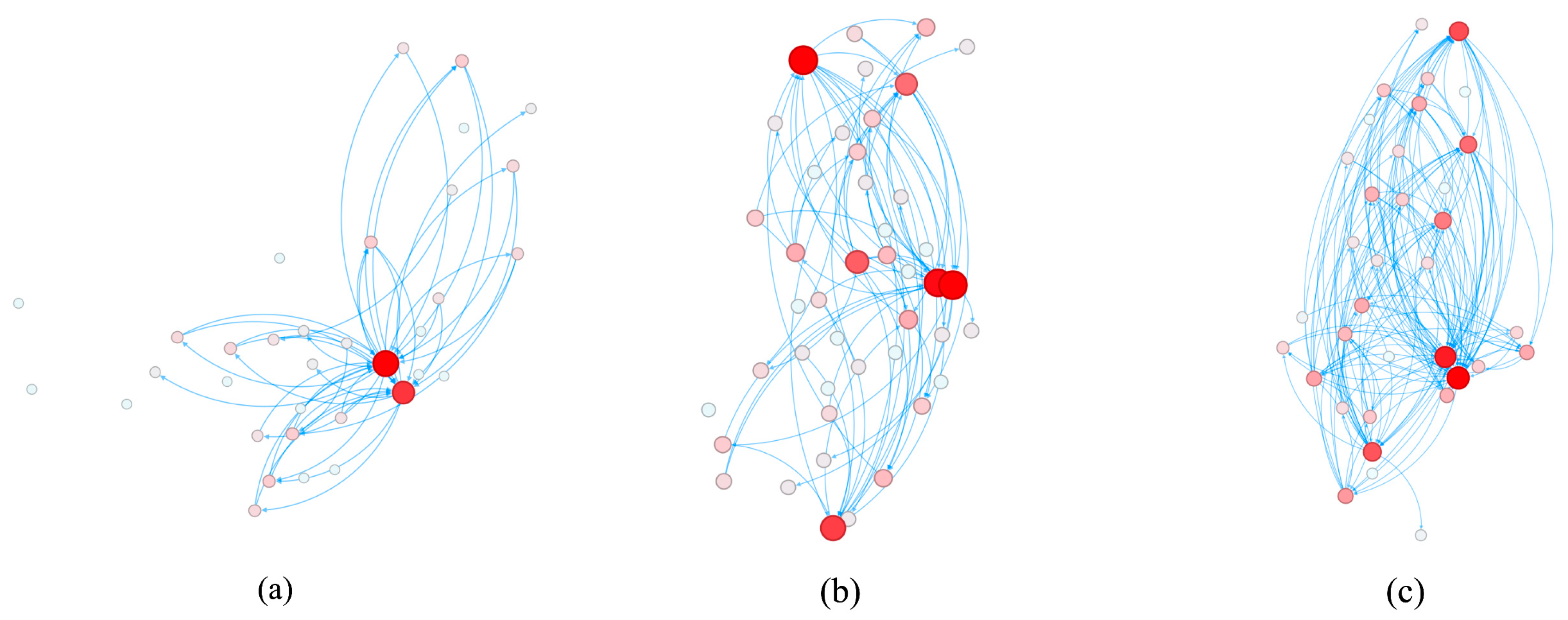
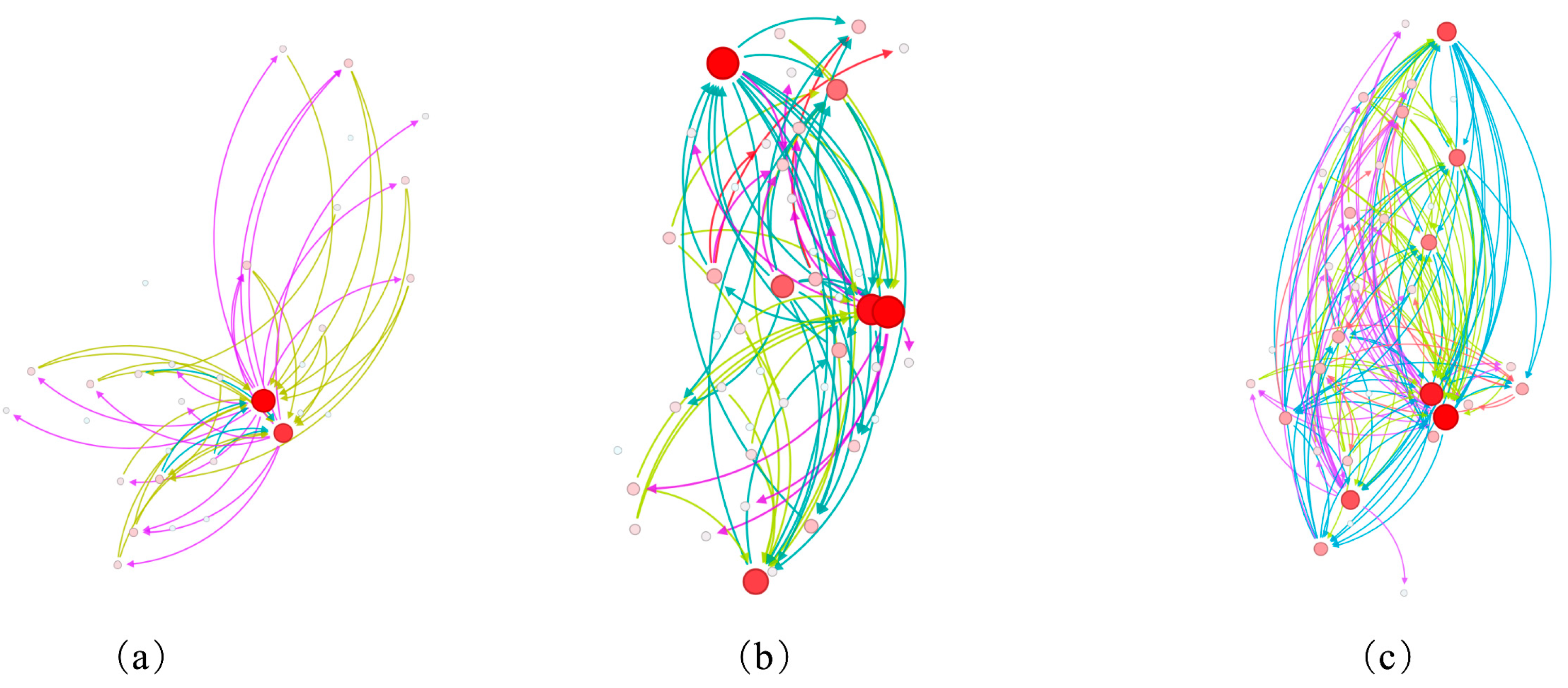
4.2. Causality Analysis Using the Proposed ARGC Model
4.3. Topological Analysis of the Delay Causality Network
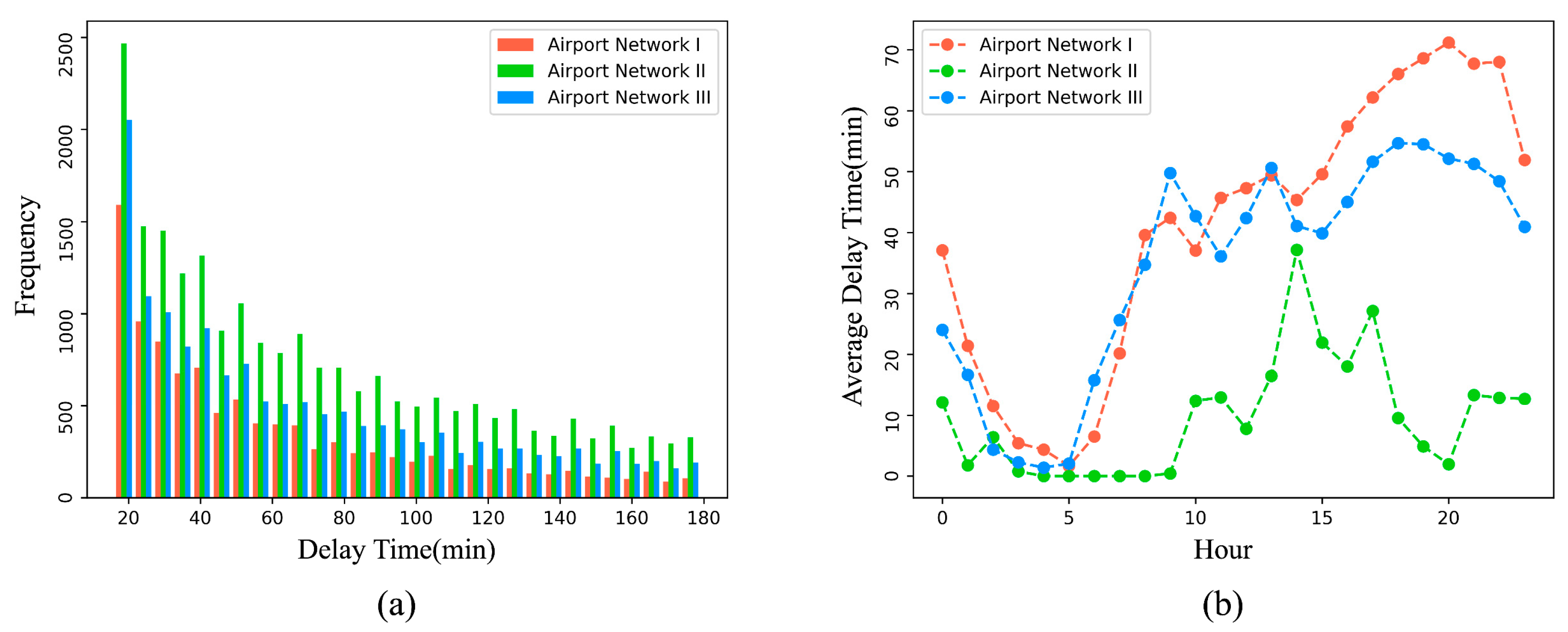
4.4. Delay State Transition Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vlachos, I.; Lin, Z. Drivers of airline loyalty: Evidence from the business travelers in China. Transp. Res. Part E Logis. Transp. Rev. 2014, 71, 1–17. [Google Scholar] [CrossRef]
- Total Delay Impact Study: A Comprehensive Assessment of the Costs and Impacts of Flight Delay in the United States. Available online: https://rosap.ntl.bts.gov/view/dot/6234 (accessed on 30 March 2023).
- Li, D.; Jiang, Y.; Kang, R.; Shlomo, H. Spatial correlation analysis of cascading failures: Congestions and blackouts. Sci. Rep. 2014, 4, 5381. [Google Scholar]
- Deshpande, V.; Arıkan, M. The impact of airline flight schedules on flight delays. Manuf. Serv. Oper. Manag. 2012, 14, 423–440. [Google Scholar] [CrossRef]
- Jetzki, M. The Propagation of Air Transport Delays in Europe. Master’s Thesis, RWTH Aachen University, Aachen, Germany, 2009. [Google Scholar]
- Kafle, N.; Zou, B. Modeling flight delay propagation: A new analytical-econometric approach. Transp. Res. Part B Methodol. 2016, 93, 520–542. [Google Scholar] [CrossRef]
- Malone, K.M. Dynamic Queueing Systems: Behavior and Approximations for Individual Queues and for Networks. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Pyrgiotis, N.; Malone, K.M.; Odoni, A. Modelling delay propagation within an airport network. Transp. Res. Part C Emerg. Technol. 2013, 27, 60–75. [Google Scholar] [CrossRef]
- Baspinar, B.; Koyuncu, E. A data-driven air transportation delay propagation model using epidemic process models. Int. J. Aerosp. Eng. 2016, 2016, 4836260. [Google Scholar] [CrossRef]
- Li, S.; Xie, D.; Zhang, X.; Zhang, Z.; Bai, W. Data-driven modeling of systemic air traffic delay propagation: An epidemic model approach. J. Adv. Transp. 2020, 2020, 8816615. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef]
- Zeng, L.; Wang, B.; Wang, T.; Wang, Z. Research on delay propagation mechanism of air traffic control system based on causal inference. Transp. Res. Part C Emerg. Technol. 2022, 138, 103622. [Google Scholar] [CrossRef]
- Runge, J.; Bathiany, S.; Bollt, E.; Camps-Valls, G.; Coumou, D.; Deyle, E.; Glymour, C.; Kretschmer, M.; Mahecha, M.D.; Muñoz-Marí, J.; et al. Inferring causation from time series in Earth system sciences. Nat. Commun. 2019, 10, 2553. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, X.; Zhang, Y.; Sun, L.; Dun, M.; Du, W. Propagation index on airport delays. Transp. Res. Rec. 2019, 2673, 536–543. [Google Scholar] [CrossRef]
- Tan, X.; Liu, Y.; Liu, D.; Zhu, D.; Zeng, W.; Wang, H. An Attention-Based Deep Convolution Network for Mining Airport Delay Propagation Causality. Appl. Sci. 2022, 12, 10433. [Google Scholar] [CrossRef]
- Lin, L.; He, Z.; Peeta, S. Predicting station-level hourly demand in a large-scale bike-sharing network: A graph convolutional neural network approach. Transp. Res. Part C Emerg. Technol. 2018, 97, 258–276. [Google Scholar] [CrossRef]
- Bao, J.; Liu, P.; Ukkusuri, S.V. A spatiotemporal deep learning approach for citywide short-term crash risk prediction with multi-source data. Accid. Anal. Prev. 2019, 122, 239–254. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.; Kang, J.; Yang, Z.; Chen, X. Forecasting network-wide multi-step metro ridership with an attention-weighted multi-view graph to sequence learning approach. Expert Syst. Appl. 2022, 210, 118475. [Google Scholar] [CrossRef]
- Zanin, M.; Belkoura, S.; Zhu, Y. Network analysis of Chinese air transport delay propagation. Chin. J. Aeronaut. 2017, 30, 491–499. [Google Scholar] [CrossRef]
- Du, W.; Zhang, M.; Zhang, Y.; Cao, X.; Zhang, J. Delay causality network in air transport systems. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 466–476. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- He, Y.; Li, L.; Zhu, X.; Tsui, K.L. Multi-Graph Convolutional-Recurrent Neural Network (MGC-RNN) for Short-Term Forecasting of Transit Passenger Flow. In Proceedings of the IEEE Transactions on Intelligent Transportation Systems, Blacksburg, VA, USA, 8–12 October 2022. [Google Scholar]
- Lee, K.; Rhee, W. DDP-GCN: Multi-graph convolutional network for spatiotemporal traffic forecasting. Transp. Res. Part C Emerg. Technol. 2022, 134, 103466. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Bao, J.; Yang, Z.; Zeng, W. Graph to sequence learning with attention mechanism for network-wide multi-step-ahead flight delay prediction. Transp. Res. Part C Emerg. Technol. 2021, 130, 103323. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Micheli, A. Neural network for graphs: A contextual constructive approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Boneau, C.A. The effects of violations of assumptions underlying the t test. Psychol. Bull. 1960, 57, 49. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Sarle, W.S. Stopped training and other remedies for overfitting. Comput. Sci. Stat. 1996, 352–360. [Google Scholar]
- Hu, J.; Qian, S.; Fang, Q.; Wang, Y.; Zhao, Q.; Zhang, H. Efficient graph deep learning in tensorflow with tf_geometric. In Proceedings of the 29th ACM International Conference on Multimedia, Ottawa, ON, Canada, 28 October–3 November 2021. [Google Scholar]
- Li, Q.; Jing, R. Characterization of delay propagation in the air traffic network. J. Air Transp. Manag. 2021, 94, 102075. [Google Scholar] [CrossRef]



| Indicators | Airport Network I | Airport Network II | Airport Network III | Mean | STD |
|---|---|---|---|---|---|
| Degree | 34 | 44 | 35 | 39 | 7.071 |
| Edge | 213 | 497 | 354 | 354.667 | 142.001 |
| Average Degree | 6.265 | 11.295 | 10.144 | 9.235 | 2.635 |
| Average Intensity | 18.277 | 29.006 | 31.463 | 26.249 | 7.012 |
| Density | 0.19 | 0.263 | 0.297 | 0.25 | 0.055 |
| Number of Communities | 3 | 4 | 5 | 4 | 1 |
| Modularity | 0.199 | 0.117 | 0.11 | 0.142 | 0.049 |
| Average Clustering Coefficient | 0.57 | 0.69 | 0.616 | 0.625 | 0.061 |
| Average Path Length | 2.059 | 1.807 | 1.759 | 1.875 | 0.161 |
| Eigenvector Centrality | 4.482 × 10−6 | 3.179 × 10−6 | 1.225 × 10−6 | 2.962 × 10−6 | 1.639 × 10−6 |
| Hyper-Parameter | Description | Hyper-Parameters in Airport Network I | Hyper-Parameters in Airport Network II | Hyper-Parameters in Airport Network III |
|---|---|---|---|---|
| Tstep | The time steps of input dataset | 5 | 4 | 4 |
| Toutput_step | The time steps of output dataset | 1 | 1 | 1 |
| HGCN | The number of hidden units in each GCN layer | 1 | 1 | 1 |
| activationGCN | The activation function of the GCN cell | Relu | Relu | Relu |
| HLSTM | The number of hidden units in each LSTM layer | 8 | 8 | 8 |
| activationLSTM | The activation function of the LSTM cell | Relu | Relu | Relu |
| HFC | The number of hidden units in each fully connected layer | 1 | 1 | 1 |
| ActivationFC | The activation function of the FC cell | Relu | Relu | Relu |
| Optimizer | Implemented optimizer during the training process | Adam | Adam | Adam |
| Learning rate | 0.005 | 0.01 | 0.01 | |
| B | Batch size | 16 | 16 | 16 |
| d | The dropout rate | 0.05 | 0.1 | 0.05 |
| Airport Network | Original Candidate Number | Candidate Number after Attention Score Selection | Candidate Number after t-test * Selection |
|---|---|---|---|
| Airport Network I | 221 | ||
| Airport Network II | 510 | ||
| Airport Network III | 362 |
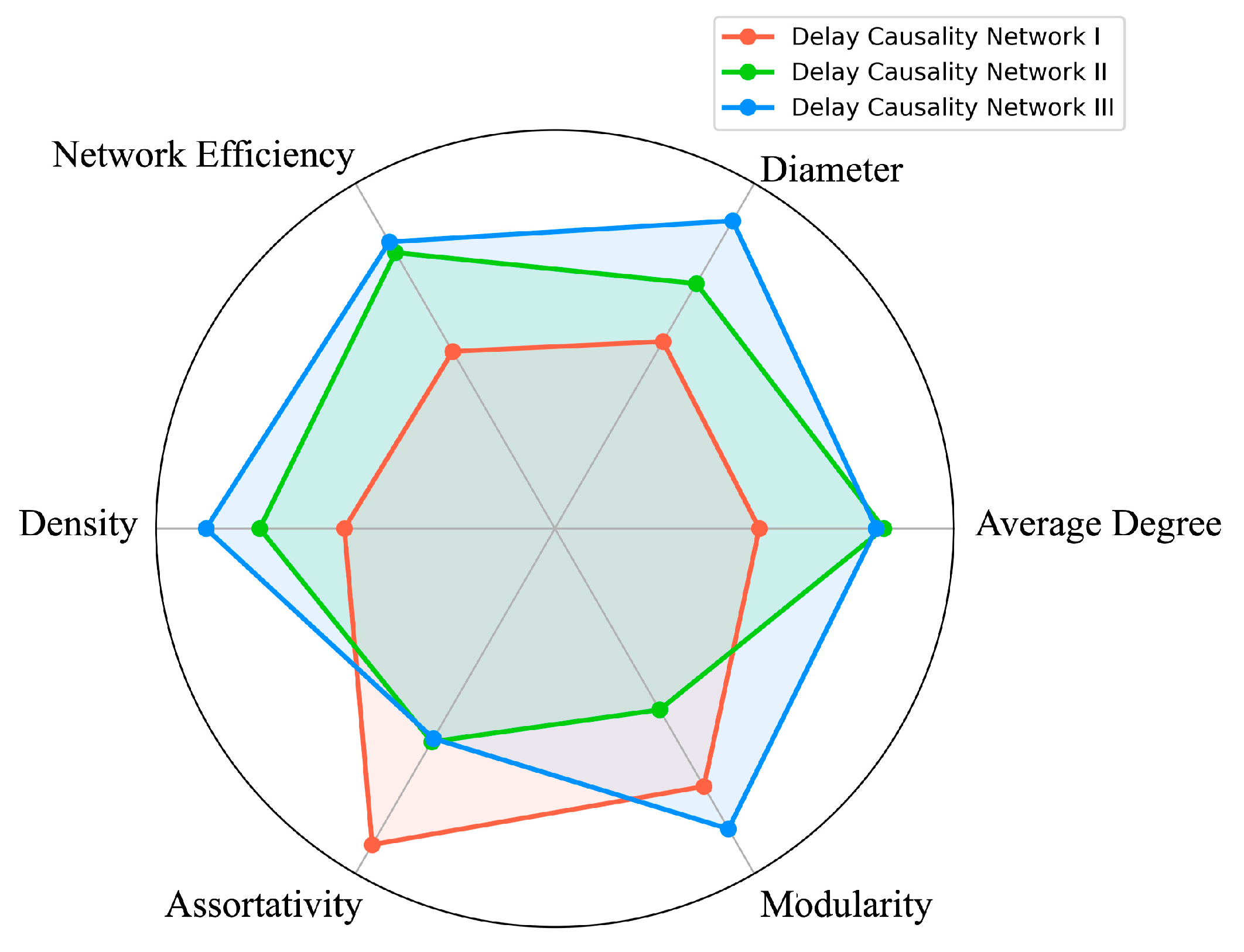
| Indicators | Delay Causality Network I | Delay Causality Network II | Delay Causality Network III | Mean | STD |
|---|---|---|---|---|---|
| Node | 34 | 44 | 33 | 37 | 4.966 |
| Edge | 53 | 88 | 65 | 68.667 | 14.522 |
| Average Degree | 1.853 | 4.681 | 4.515 | 3.683 | 1.295 |
| Diameter (KM) | 1137.51 | 1479.253 | 1849.669 | 1488.81 | 290.816 |
| Network Efficiency | 1.025 × 10−4 | 2.341 × 10−4 | 2.483 × 10−4 | 1.949 × 10−4 | 6.564 × 10−5 |
| Density | 0.056 | 0.108 | 0.141 | 0.101 | 0.034 |
| Assortativity | −0.065 | −0.033 | −0.032 | −0.043 | 0.015 |
| Modularity | 0.023 | 0.005 | 0.033 | 0.02 | 0.014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.; Yang, S.; Shan, X.; Bao, J.; Yang, Z. Exploring Delay Propagation Causality in Various Airport Networks with Attention-Weighted Recurrent Graph Convolution Method. Aerospace 2023, 10, 453. https://doi.org/10.3390/aerospace10050453
Kang J, Yang S, Shan X, Bao J, Yang Z. Exploring Delay Propagation Causality in Various Airport Networks with Attention-Weighted Recurrent Graph Convolution Method. Aerospace. 2023; 10(5):453. https://doi.org/10.3390/aerospace10050453
Chicago/Turabian StyleKang, Jiawei, Shangwen Yang, Xiaoxuan Shan, Jie Bao, and Zhao Yang. 2023. "Exploring Delay Propagation Causality in Various Airport Networks with Attention-Weighted Recurrent Graph Convolution Method" Aerospace 10, no. 5: 453. https://doi.org/10.3390/aerospace10050453
APA StyleKang, J., Yang, S., Shan, X., Bao, J., & Yang, Z. (2023). Exploring Delay Propagation Causality in Various Airport Networks with Attention-Weighted Recurrent Graph Convolution Method. Aerospace, 10(5), 453. https://doi.org/10.3390/aerospace10050453






