Small Space Target Detection Based on a Convolutional Neural Network and Guidance Information
Abstract
1. Introduction
- 1.
- Even though the intensities of the same target in different images or different targets in the same image change dramatically, they share high similarities with the distribution. However, it is difficult for traditional methods based on theoretical models to summarize a generalized distribution function of space targets that covers different situations.
- 2.
- In the stage of the final target confirmation, the thresholds are usually set based on the information from the global image. This can barely balance the detection of weak targets and a decrease in false alarms.
- 3.
- A star image contains a large number of targets that can be used to build a dataset, which provides a good foundation to build a deep convolutional neural network that can approximate the distribution function of different targets. Due to the diverse detectability of optical systems, even the images pointing to the same sky area contain different magnitudes and quantities of stars. Thus, although there are thousands of targets existing in an image, not all of them are certain, which results in a higher cost of annotation for a full image and lower validity of detection.
- 4.
- The common end-to-end detectors based on CNN [50] do not perform well for small target detection. Besides, most of the structures of existing networks are complex and bring high requirements for in-orbit hardware resources.
- 1.
- A method is presented to detect space targets by modeling the global detection of an image as local two-class recognition of several candidate regions so that manual labeling for a full image is not required.
- 2.
- We design a small architecture of the CNN to realize automatic feature extraction and target confirmation, which avoids the problem of threshold setting for the final target confirmation. Furthermore, the architecture can potentially be used in actual in-orbit services because it is easy to implement and requires only a low cost in terms of computing resources.
- 3.
- We added a module of information guidance to improve the detection ability. The former is applied to each candidate region to reduce the difference in intensity among targets, which confers a better generalization ability to the network. Furthermore, the latter is added to provide extra features. In this way, the interference caused by pixels in the non-central area is further reduced and the distribution characteristics of the target are enhanced. This method shows good performance in experiments.
2. Proposed Method
2.1. Problem Description
- 1.
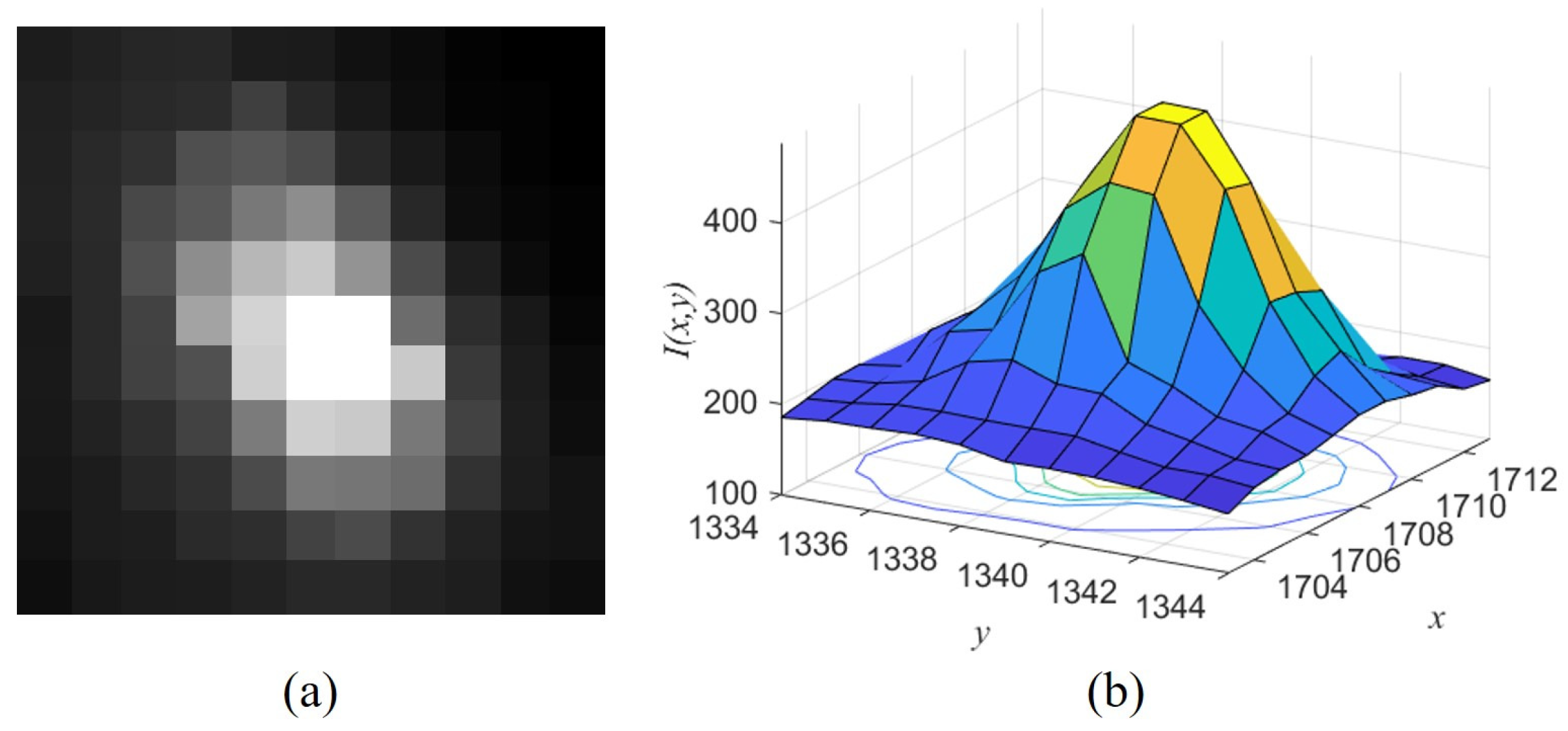
- The target center is the local maximum. Figure 1 shows the original images and corresponding intensity distribution of the same target with low SCR values in different frames, where the center of the target in each image is marked in red. The distribution of the target is easily influenced by the noise (Figure 1c) and the PSFs of close stars and other targets (Figure 1d). The intensity value of each pixel inside the target region is the superposition result of the target and other interference; thus, the target center still retains its saliency unless it is submerged.
- 2.
- When the target has no fast relative motion, its distribution approximates a Gaussian distribution. The difference is that the actual distribution extends in the direction of its motion because of motion blur if the exposure time is long or the target has a high speed, as shown in Figure 2.
2.2. Preprocessing Stage
2.3. Region Proposal Search
2.4. Target Detection with an SF-CNN
3. Implementation Details
3.1. Network Input
3.2. Network Structure
3.3. Guidance Information
3.4. Network Loss Calculation
4. Experimental Results
4.1. Experimental Settings
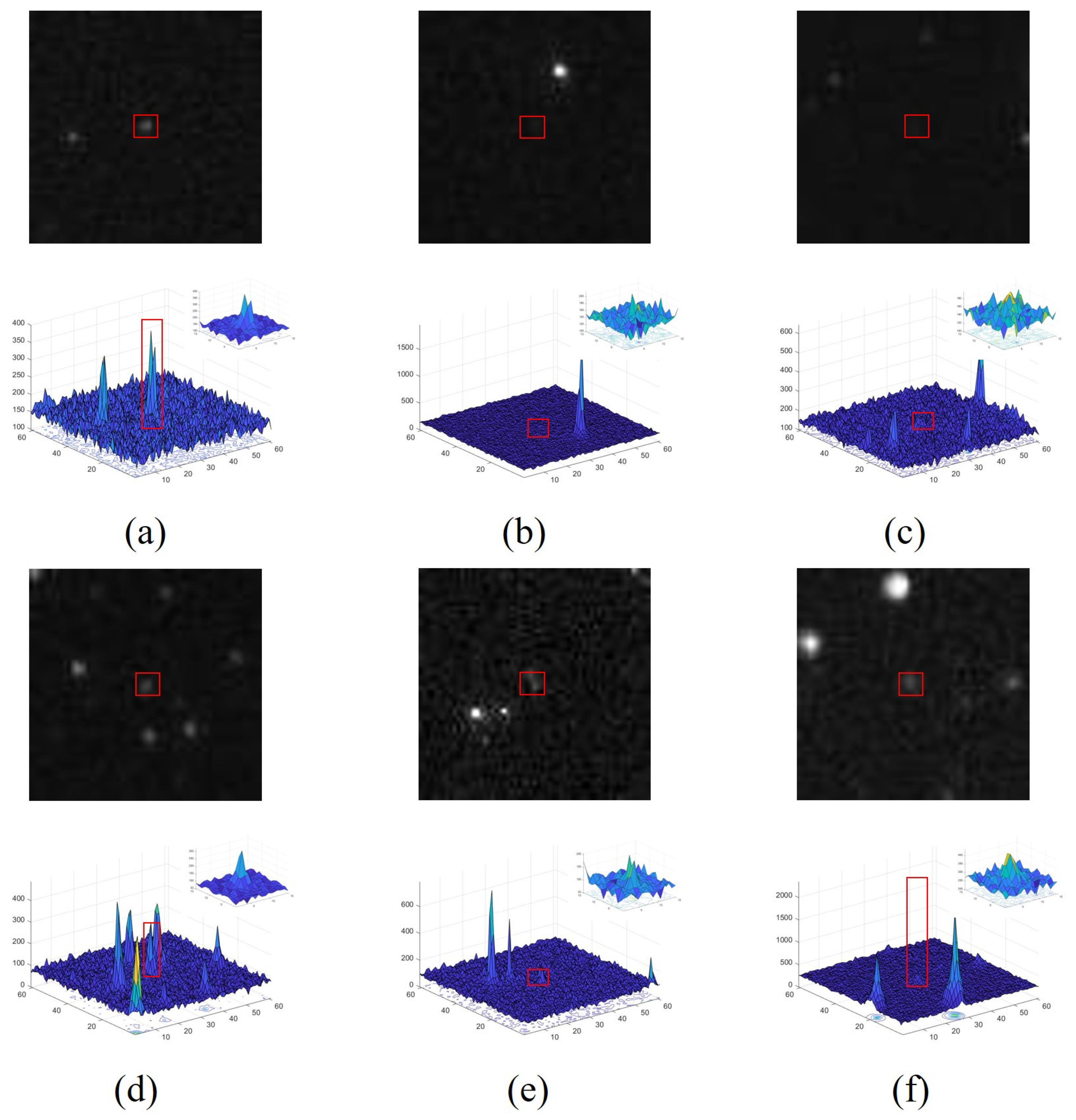
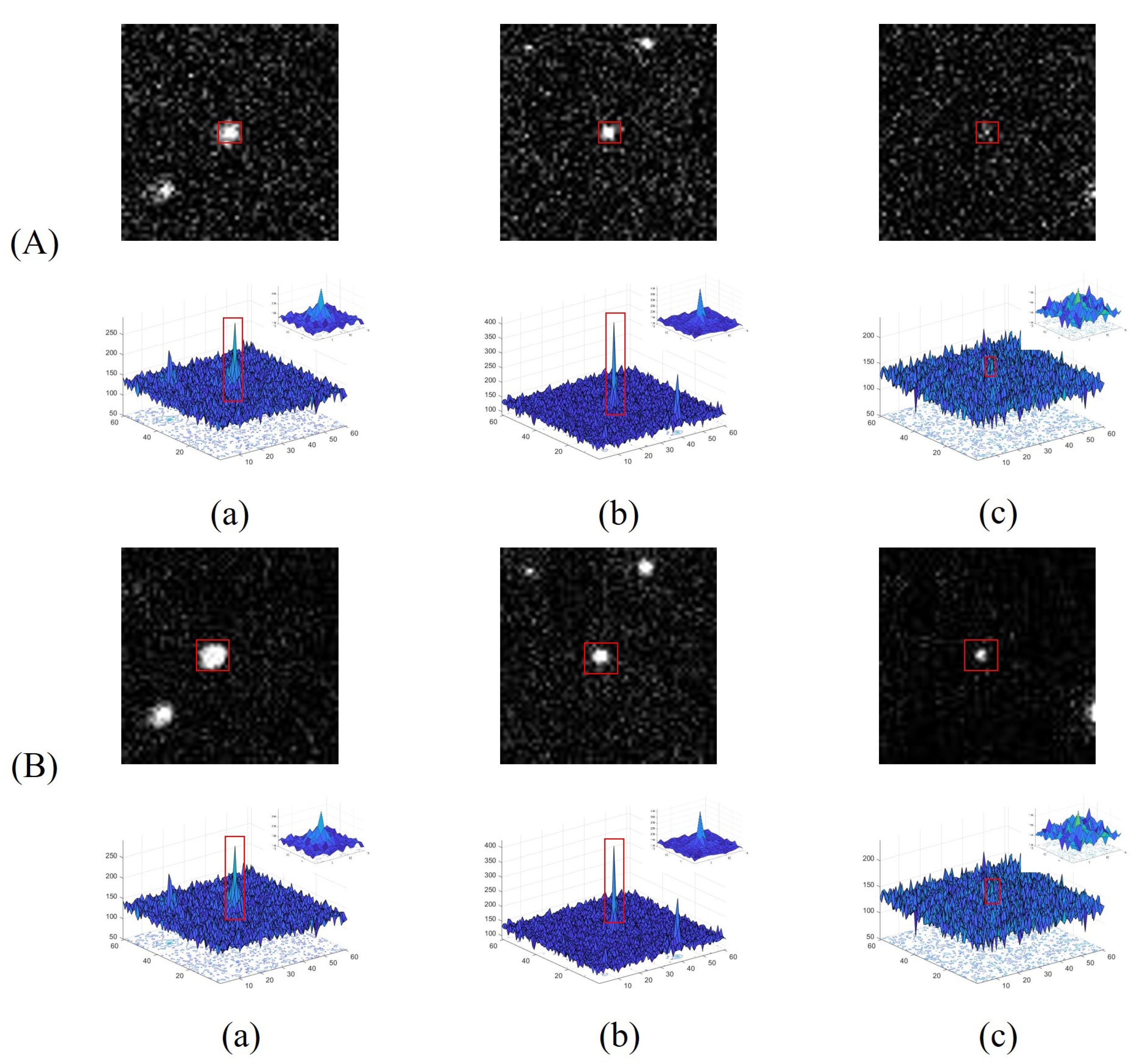
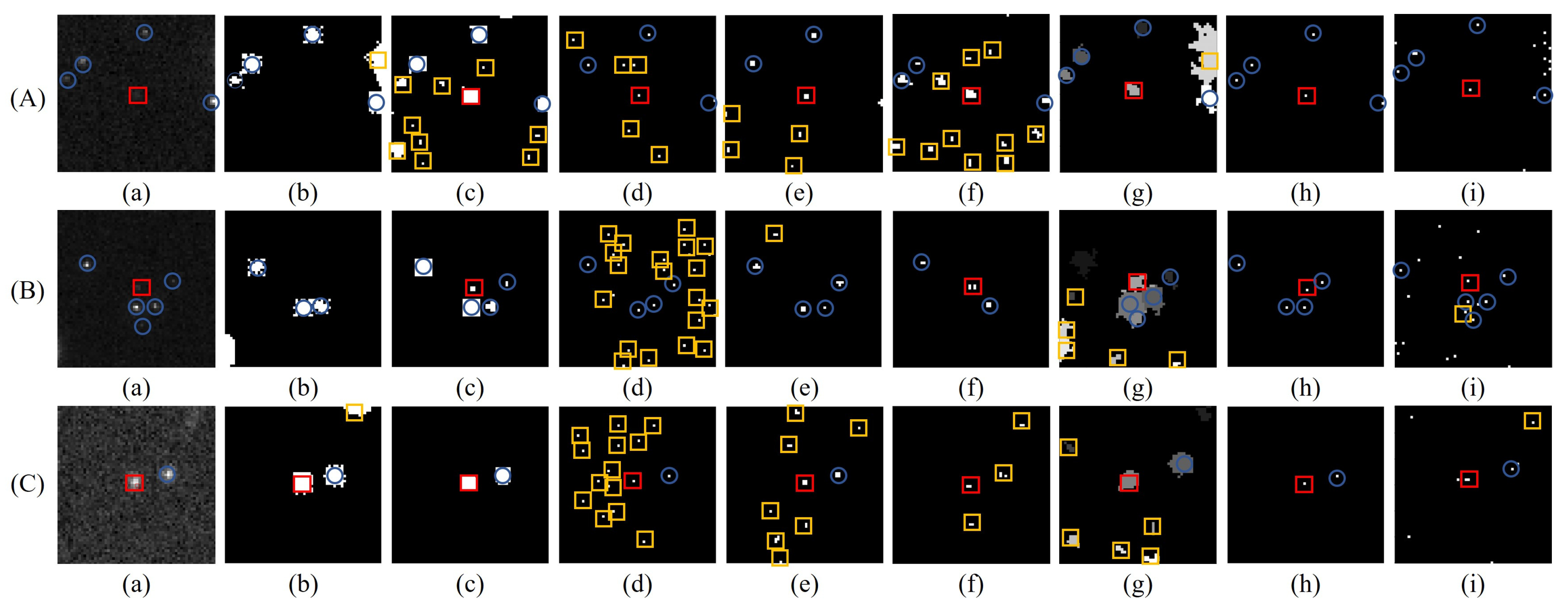
4.2. Comparative Analysis of the Processing Stage
4.3. Comparative Analysis of Ablation Experiments
4.4. Comparative Analysis of Experiments for Different Targets
4.5. Comparative Analysis of Experiments on the Same Targets with Different Saliency
5. Discussion
- 1.
- The global detection of a star image is converted to local two-class recognition of several candidate regions and certain targets are chosen as samples in order to solve the problems of uncertainty and a high cost of annotation.
- 2.
- The preprocessing can only filter the interference in a large area to reduce the false extraction of candidate points and improve algorithm efficiency. The distribution of a target and its surrounding region is almost unchanged so that the original image information is maintained, which guarantees similarity among samples.
- 3.
- Improvements in the network, including guidance information and bias loss, can contribute to a stronger detection ability.
- 4.
- There are many problems for common end-to-end detectors based on CNN, such as the construction of a dataset, small sizes of targets and so on, to be considered in this field. Thus, we did not choose deep-learning-based methods as baselines. The proposed method avoids the problem of threshold setting for the final target confirmation so that it has better performance than the baseline methods when targets deviate from the ideal distribution due to their movement or interference from the background.
- 5.
- With an increase in speed, a target may gradually change from point-like to streak-like, which will affect the detection ability of our method. In our future work, we will enhance the adaptability for targets of different shapes by the simulation of samples or improvements to the network.
- 6.
- In our future research, we will further improve the processing stage and the region proposal search to enhance the SCR of a target (while maintaining the distribution of the target) and reduce computations.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruprecht, J.D.; Stuart, J.S.; Woods, D.F.; Shah, R.Y. Detecting small asteroids with the Space Surveillance Telescope. Icarus 2014, 239, 253–259. [Google Scholar] [CrossRef]
- Stokes, G.; Vo, C.; Sridharan, R.; Sharma, J. The space-based visible program. Lincoln. Lab. J. 1998, 11, 205–238. [Google Scholar]
- Sharma, J. Space-based visible space surveillance performance. J. Guid. Control. Dyn. 2000, 23, 153–158. [Google Scholar] [CrossRef]
- Hu, Y.P.; Li, K.B.; Xu, W.; Chen, L.; Huang, J.Y. A novel space-based observation strategy for GEO objects based on daily pointing adjustment of multi-sensors. Adv. Space Res. 2016, 58, 505–513. [Google Scholar] [CrossRef]
- Porat, B.; Friedlander, B. A frequency domain algorithm for multiframe detection and estimation of dim targets. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 398–401. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Reed, I.S.; Gagliardi, R.M.; Stotts, L.B. Optical moving target detection with 3-D matched filtering. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 327–336. [Google Scholar] [CrossRef]
- Li, M.; Zhang, T.; Yang, W.; Sun, X. Moving weak point target detection and estimation with three-dimensional double directional filter in IR cluttered background. Opt. Eng. 2005, 44, 107007. [Google Scholar] [CrossRef]
- Liu, X.; Zuo, Z. A dim small infrared moving target detection algorithm based on improved three-dimensional directional filtering. In Chinese Conference on Image and Graphics Technologies; Springer: Berlin/Heidelberg, Germany, 2013; pp. 102–108. [Google Scholar]
- Wang, Z.; Tian, J.; Liu, J.; Zheng, S. Small infrared target fusion detection based on support vector machines in the wavelet domain. Opt. Eng. 2006, 45, 076401. [Google Scholar]
- Zhang, B.; Zhang, T.; Cao, Z.; Zhang, K. Fast new small-target detection algorithm based on a modified partial differential equation in infrared clutter. Opt. Eng. 2007, 46, 106401. [Google Scholar] [CrossRef]
- Stoveken, E.; Schildknecht, T. Algorithms for the optical detection of space debris objects. In Proceedings of the 4th European Conference on Space Debris, Darmstadt, Germany, 18–20 April 2005; pp. 18–20. [Google Scholar]
- Virani, S.; Murphy, T.; Holzinger, M.; Jones, B. Empirical Dynamic Data Driven Detection and Tracking Using Detectionless and Traditional FiSSt Methods. In Proceedings of the Advanced Maui Optical and Space Surveillance (AMOS) Technologies Conference, Maui, HI, USA, 19–22 September 2017; p. 41. [Google Scholar]
- Viggh, H.; Stokes, G.; Shelly, F.; Blythe, M.; Stuart, J. Applying electro-optical space surveillance technology to asteroid search and detection: The linear program results. In Proceedings of the 1998 Space Control Conference; American Society of Civil Engineers: HlAmerican Society of Civil Engineers: Reston, VA, USA, 1998; pp. 373–381. [Google Scholar]
- Zingarelli, J.C.; Pearce, E.; Lambour, R.; Blake, T.; Peterson, C.J.; Cain, S. Improving the space surveillance telescope’s performance using multi-hypothesis testing. Astron. J. 2014, 147, 111. [Google Scholar] [CrossRef]
- Hardy, T.; Cain, S.; Jeon, J.; Blake, T. Improving space domain awareness through unequal-cost multiple hypothesis testing in the space surveillance telescope. Appl. Opt. 2015, 54, 5481–5494. [Google Scholar] [CrossRef]
- Tompkins, J.; Cain, S.; Becker, D. Near earth space object detection using parallax as multi-hypothesis test criterion. Opt. Express 2019, 27, 5403–5419. [Google Scholar] [CrossRef] [PubMed]
- Bertin, E.; Arnouts, S. SExtractor: Software for source extraction. Astron. Astrophys. Suppl. Ser. 1996, 117, 393–404. [Google Scholar] [CrossRef]
- Bertin, E. Automated morphometry with SExtractor and PSFEx. In Astronomical Data Analysis Software and Systems XX; Astronomical Society of the Pacific: San Francisco, CA, USA, 2011; Volume 442, p. 435. [Google Scholar]
- Murphy, T.S.; Holzinger, M.J. Uncued Low SNR Detection with Likelihood from Image Multi Bernoulli Filter. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 20–23 September 2016; p. 30. [Google Scholar]
- Murphy, T.S.; Holzinger, M.J.; Flewelling, B. Space object detection in images using matched filter bank and bayesian update. J. Guid. Control. Dyn. 2017, 40, 497–509. [Google Scholar] [CrossRef]
- Lin, B.; Yang, X.; Wang, J.; Wang, Y.; Wang, K.; Zhang, X. A Robust Space Target Detection Algorithm Based on Target Characteristics. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Signal and Data Processing of Small Targets 1999; International Society for Optics and Photonics: Bellingham, DC, USA, 1999; Volume 3809, pp. 74–83. [Google Scholar]
- Bai, X.; Zhou, F.; Xue, B. Infrared dim small target enhancement using toggle contrast operator. Infrared Phys. Technol. 2012, 55, 177–182. [Google Scholar] [CrossRef]
- Hadhoud, M.M.; Thomas, D.W. The two-dimensional adaptive LMS (TDLMS) algorithm. IEEE Trans. Circuits Syst. 1988, 35, 485–494. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Han, J.; Ma, Y.; Zhou, B.; Fan, F.; Liang, K.; Fang, Y. A robust infrared small target detection algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2168–2172. [Google Scholar]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared small target detection utilizing the multiscale relative local contrast measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Lv, P.; Sun, S.; Lin, C.; Liu, G. A method for weak target detection based on human visual contrast mechanism. IEEE Geosci. Remote Sens. Lett. 2018, 16, 261–265. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared small target detection based on the weighted strengthened local contrast measure. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1670–1674. [Google Scholar] [CrossRef]
- Qin, Y.; Bruzzone, L.; Gao, C.; Li, B. Infrared small target detection based on facet kernel and random walker. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7104–7118. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Wei, L.; Dragomir, A.; Dumitru, E.; Christian, S.; Scott, R.; Cheng-Yang, F.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Jia, P.; Liu, Q.; Sun, Y. Detection and classification of astronomical targets with deep neural networks in wide-field small aperture telescopes. Astron. J. 2020, 159, 212. [Google Scholar] [CrossRef]
- Xi, J.; Xiang, Y.; Ersoy, O.K.; Cong, M.; Wei, X.; Gu, J. Space debris detection using feature learning of candidate regions in optical image sequences. IEEE Access 2020, 8, 150864–150877. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Yang, X.; Feng, P.; Liu, L.; Wu, N. Tbc-net: A real-time detector for infrared small target detection using semantic constraint. arXiv 2019, arXiv:2001.05852. [Google Scholar]
- Wang, H.; Zhou, L.; Wang, L. Miss detection vs. false alarm: Adversarial learning for small object segmentation in infrared images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8509–8518. [Google Scholar]
- Shi, M.; Wang, H. Infrared dim and small target detection based on denoising autoencoder network. Mob. Netw. Appl. 2020, 25, 1469–1483. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Fu, Q.; Han, Z. A novel pattern for infrared small target detection with generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4481–4492. [Google Scholar] [CrossRef]
- Du, J.; Lu, H.; Zhang, L.; Hu, M.; Chen, S.; Deng, Y.; Shen, X.; Zhang, Y. A Spatial-Temporal Feature-Based Detection Framework for Infrared Dim Small Target. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Hou, Q.; Wang, Z.; Tan, F.; Zhao, Y.; Zheng, H.; Zhang, W. RISTDnet: Robust infrared small target detection network. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Niu, Z.; Sun, Q.; Xiao, H.; Li, H. BSC-Net: Background Suppression Algorithm for Stray Lights in Star Images. Remote Sens. 2022, 14, 4852. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Abrahamyan, L.; Ziatchin, V.; Chen, Y.; Deligiannis, N. Bias Loss for Mobile Neural Networks. arXiv 2021, arXiv:2107.11170. [Google Scholar]









| Type | Filters | Size/Stride | Output |
|---|---|---|---|
| Convolution-1 | 6 | ||
| Maxpooling | - | ||
| Convolution-2 | 12 | ||
| Connected | - | 2 | - |
| Softmax | - | - | - |
| Parameter | Value |
|---|---|
| Focal length | 160 mm |
| Effective aperture | 150 mm |
| CCD pixel size | 9 m × 9 m |
| Total number of pixels | 4096 × 4096 |
| Center wavelength | 650 |
| Field angle | 13.1 |
| Shooting mode | Star mode |
| Gray level | 16 bit |
| Group | Target | Exposure Time | Information | ||||
|---|---|---|---|---|---|---|---|
| Number | Avg Intensity of Targets | Avg FWHM | Avg Intensity of Background | Avg SCR | |||
| 1 | 1 | 500 ms | 244 | 379.2 | 4.0 | 140.43 | 5.5 |
| 2 | 178 | 216.5 | 3.4 | 147.11 | 2.3 | ||
| 3 | 93 | 194.6 | 3.0 | 151.43 | 1.6 | ||
| 2 | 4 | 300 ms | 54 | 286.4 | 3.6 | 83.50 | 4.3 |
| 5 | 54 | 182.8 | 3.2 | 107.21 | 2.5 | ||
| 3 | 6 | 100 ms | 16 | 283.1 | 3.9 | 245.11 | 1.1 |
| 4 | 7 | 500 ms | 54 | 1142.5 | 5.11 | 457.95 | 5.3 |
| 100 ms | 54 | 266.7 | 3.12 | 131.30 | 4.5 | ||
| 8 | 500 ms | 54 | 738.4 | 3.46 | 448.96 | 6.3 | |
| 100 ms | 54 | 186.6 | 2.94 | 129.62 | 3.7 | ||
| 9 | 500 ms | 54 | 690.5 | 2.91 | 461.11 | 5.4 | |
| 100 ms | 54 | 173.5 | 2.74 | 131.61 | 3.4 | ||
| Condition | Number of Candidates | SCR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Star 1 | Star 2 | Star 3 | Star 4 | Star 5 | Star 6 | Star 7 | Star 8 | ||
| Before processing | 62,736 | 2.25 | 2.31 | 2.45 | 4.00 | 3.52 | 6.85 | 1.62 | 1.19 |
| After processing | 57,463 | 2.26 | 2.31 | 2.45 | 4.00 | 3.51 | 6.85 | 1.62 | 1.19 |
| Method | ||
|---|---|---|
| Training Dataset | Validation Dataset | |
| SFCNN + Cross entropy loss | 88.57% | 76.95% |
| SFCNN + Normalization + Cross entropy loss | 94.16% | 88.51% |
| SFCNN + Bias loss | 92.88% | 93.98% |
| SFCNN + Normalization + Guidance information + Cross entropy loss | 96.97% | 92.90% |
| SFCNN + Normalization + Guidance information + Bias loss | 98.05% | 97.85% |
| Target | Exposure Time | TD/TPR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Max-Mean | RLCM | NSM | WSLCM | FKRW | SExtractor | MLTC | SF-CNN | ||
| 1 | 500 ms | 238/97.54% | 241/98.77% | 232/95.08% | 234/95.90% | 207/84.84 | 243/99.59% | 241/98.77% | 244/100.00% |
| 2 | 54/30.33% | 154/86.52% | 75/42.13% | 151/84.83% | 125/70.22 | 167/93.82% | 170/95.51% | 178/100.00% % | |
| 3 | 55/59.13% | 80/86.02% | 21/22.58% | 81/87.10% | 143/80.34 | 87/93.54% | 88/94.62% | 90/96.77% | |
| 4 | 300 ms | 48/85.71% | 53/94.64% | 35/64.81% | 54/100.00% | 50/92.59 | 54/100.00% | 54/100.00% | 54/100.00% |
| 5 | 26/48.15% | 52/96.30% | 44/95.08% | 46/82.14% | 54/100.00% | 54/100.00% | 53/94.64% | 54/100.00% | |
| 6 | 100 ms | 9/56.25% | 16/100.00% | 13/81.25% | 14/87.50% | 16/100.00% | 16/100.00% | 16/100.00% | 16/100.00% |
| Method | Max-Mean | RLCM | NSM | WSLCM | FKRW | SExtractor | MLTC | SF-CNN |
|---|---|---|---|---|---|---|---|---|
| Time consumed (ms) | 141.28 | 538.37 | 1586.78 | 104.31 | 1140.12 | 15.55 | 12.89 | 53.85 |
| Method | Size of Input | MACs | Params |
|---|---|---|---|
| VGG13 | 9.02 G | 133.05 M | |
| AlexNet | 551.13 M | 61.1 M | |
| ResNet50 | 31.89 M 3.62 G | 25.56 M | |
| SF-CNN | 23.32 K 184.01 M | 1.14 k |
| Target | Exposure Time | TD/TPR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Max-Mean | RLCM | NSM | WSLCM | FKRW | SExtractor | MLTC | SF-CNN | ||
| 7 | 500 ms | 54/100.00% | 54/100.00% | 44/81.48% | 54/100.00% | 54/100.00% | 54/100.00% | 54/100.00% | 54/100.00% |
| 100 ms | 54/100.00% | 54/100.00% | 41/75.93% | 54/100.00% | 54/100.00% | 54/100.00% | 54/100.00% | 54/100.00% | |
| 8 | 500 ms | 50/92.59% | 54/100.00% | 30/55.56% | 54/100.00% | 54/100.00% | 54/100.00% | 53/98.15% | 54/100.00% |
| 100 ms | 48/88.89% | 54/100.00% | 25/46.30% | 54/100.00% | 43/79.63% | 49/90.74% | 48/88.89% | 54/100.00% | |
| 9 | 500 ms | 54/100.00% | 54/100.00% | 17/31.48% | 54/100.00% | 54/100.00% | 54/100.00% | 54/100.00% | 53/98.15% |
| 100 ms | 51/94.44% | 54/100.00% | 11/20.37% | 48/88.89% | 50/92.59% | 30/55.56% | 47/87.04% | 50/92.59% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, B.; Wang, J.; Wang, H.; Zhong, L.; Yang, X.; Zhang, X. Small Space Target Detection Based on a Convolutional Neural Network and Guidance Information. Aerospace 2023, 10, 426. https://doi.org/10.3390/aerospace10050426
Lin B, Wang J, Wang H, Zhong L, Yang X, Zhang X. Small Space Target Detection Based on a Convolutional Neural Network and Guidance Information. Aerospace. 2023; 10(5):426. https://doi.org/10.3390/aerospace10050426
Chicago/Turabian StyleLin, Bin, Jie Wang, Han Wang, Lijun Zhong, Xia Yang, and Xiaohu Zhang. 2023. "Small Space Target Detection Based on a Convolutional Neural Network and Guidance Information" Aerospace 10, no. 5: 426. https://doi.org/10.3390/aerospace10050426
APA StyleLin, B., Wang, J., Wang, H., Zhong, L., Yang, X., & Zhang, X. (2023). Small Space Target Detection Based on a Convolutional Neural Network and Guidance Information. Aerospace, 10(5), 426. https://doi.org/10.3390/aerospace10050426






