Abstract
During mission design, the concept of operations (ConOps) describes how the system operates during various life cycle phases to meet stakeholder expectations. ConOps is sometimes declined in a simple evaluation of the power consumption or data generation per mode. Different operational timelines are typically developed based on expert knowledge. This approach is robust when designing an automated system or a system with a low level of autonomy. However, when studying highly autonomous systems, designers may be interested in understanding how the system would react in an operational scenario when provided with knowledge about its actions and operational environment. These considerations can help verify and validate the proposed ConOps architecture, highlight shortcomings in both physical and functional design, and help better formulate detailed requirements. Hence, this study aims to provide a framework for the simulation and validation of operational scenarios for autonomous robotic space exploration systems during the preliminary design phases. This study extends current efforts in autonomy technology for planetary systems by focusing on testing their operability and assessing their performances in different scenarios early in the design process. The framework uses Model-Based Systems Engineering (MBSE) as the knowledge base for the studied system and its operations. It then leverages a Markov Decision Process (MDP) to simulate a set of system operations in a relevant scenario. It then outputs a feasible plan with the associated variation of a set of considered resources as step functions. This method was applied to simulate the operations of a small rover exploring an unknown environment to observe and sample a set of targets.
1. Introduction
From a system engineering view, the study of autonomous systems brings to the table different challenges, mainly:
- Formulation of effective and realistic requirements that do not constrain the future system operability [1,2].
- Interfaces’ design, check, and control between hardware, software, and the human operator [3].
- Verification of the requirements and validation of the architecture [4,5,6,7].
Autonomous systems have high interactions with their operative environment and must make decisions based on their resources and environment state. Those capabilities drive the overall system behaviour and operations and are hard to capture in conceptual and preliminary design in a set of well-formed requirements [1,2]. Moreover, autonomous systems combine highly integrated software with physical hardware while interacting with a human operator. This interaction may pose problems during the requirement formulation and the verification and validation processes [3]. In [8], the author highlights how important it is to establish correct interface requirements early in the design of autonomous systems. Autonomous systems operations involve concurrent activities to be processed and performed by tightly coupled subsystems [8].
Given the difficulty of realistically defining an autonomous robotic mission and related requirements, the problem this paper addresses can be formulated as: is it possible to provide an analysis or procedure to capture the interaction between an autonomous system, its environment, its mission goals and its resources during preliminary design phases? With preliminary design phases, the authors identify conceptual studies and concept and technology development studies, as defined by the NASA life cycle standard [9].
Heritage from previous missions can help guide the decisions during initial studies. There are a few examples of spacecraft guided predominately by AI-based processes, such as some successful missions that push toward almost complete autonomy, such as Deep Space 1 [10] or Earth Observing 1 [11]. In addition, different teams are studying AI-agents capabilities on analogue platforms on Earth such as the Field Integrated Design and Operations (FIDO) [12], or the Long Range Science Rover (Rocky) [13] or the Robotic Antarctic Meteorite Search [14]. Those missions look into planning and robotics-related theories during the later implementation phases and operations, not during the initial system design. The interest of this publication is to understand how an autonomous system may behave or plan its mission at a higher design level (namely conceptual and preliminary design). Different round tables and discussions with experts can provide mission system engineers with the knowledge to allocate autonomous functionalities well and define the possible bottlenecks or criticality of different autonomy architectures. On the other hand, providing system engineers with straightforward simulation tools to understand the impact of autonomy at a higher design level can be helpful, and it can speed up the design process.
This study proposes a framework to study and validate operational scenarios for autonomous robotic planetary exploration systems at early design stages. The objective is to understand how the system, provided with knowledge about its actions and their impact on different resources, plans its mission and interacts with the environment. The created plan can then be run easily on a robotic platform or a simulation as a further validation round of the computed architecture. Frameworks provide a general structure to be followed; however, they leave the designer room to implement different algorithms at any level. This framework would help the designer in both the mission definition and system sizing. As analysed in [15], if operational models can be executed, it is also possible to debug the described behaviour to match the expected performances or what the engineer meant to capture. They may test whether the designed system has enough resources for battery or data storage to complete the expected operational scenario(s). At the same time, it can help validate and verify the designed functional architecture. For example, if there is the need to consider additional operative modes or a function that was overlooked during the initial design phases. The simulation of the operational scenarios can help with stakeholder consultation. Presenting a straightforward simulation of resource variation associated with a given scenario can help better frame the mission and pinpoint discrepancies between what is expected from the stakeholders and what the designers are providing. This study innovates from the state of the art, as follows:
- It implements a simulation-backed analysis to study and validate the feasibility of operational scenarios;
- It stores all the mission instances in an MBSE model and provides traceability of changes;
- It defines the variables defining and MDP space starting from the resources defined in the MBSE model.
The knowledge base for the study is the MBSE model that encodes all the parameters and products of the study. The proposed framework provides a plan that can be easily interfaced with middleware, such as the Robot Operating System (ROS). Hence, it will be possible to simulate the studied operational scenario(s) directly on an analogue robotic platform or a physics-based simulator to cross-validate the identified operational capabilities. For instance, [16] proposed a virtual mission operation framework with a validation-in-the-loop of the design applied to the satellite and leveraging STK to simulate the autonomous manoeuvres’ sequences. However, nothing comparable has been found in the literature for planetary surface robotic systems.
As highlighted in Figure 1, the presented framework identifies the main mission driver for the definition of the mission scope. The focus then shifts toward defining the MBSE model in its functional and physical declinations. The MBSE model is then morphed into a Markov Decision Process (MDP) and applied to a reference scenario. A plan is computed, and if its output is satisfying, the designers may proceed with their study or test it on analogue platforms.
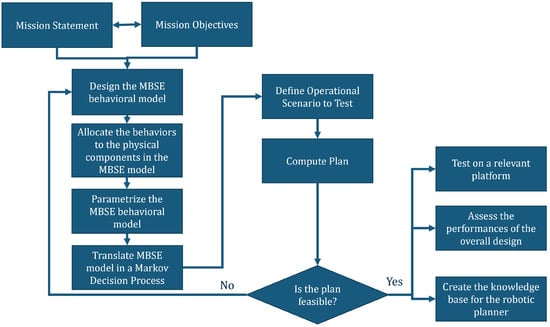
Figure 1.
MBSE to MDP theoretical workflow.
The study case is a small rover moving on the lunar surface. The designed system weighs around 30 kg, with 3.3 kg of payload and an expected power consumption around 100 W. It is assumed that the rover can freely recharge its batteries and relay its communications to Earth or another system on the surface. Therefore, no specific flight rules are imposed on when to communicate or recharge the batteries. The system should observe different waypoints and sample some of them based on their scientific reward. All the decisions can be left to the solving algorithm.
After this initial overview of the context and objective of this research, the remaining of the paper will be organized as follows: Section 2 provides a small overview of similar studies, Section 3 focuses on the background theories and definition guiding the proposed framework, Section 4 provides a set of sample results that can be obtained with the framework, Section 5 draws the main conclusions on this study and details its future development.
2. Related Work
Operational scenarios are usually studied as a part of the Concept of Operations (ConOps) analysis, as investigated in [17]. ConOps describe how the system will be operated during all various life cycle phases to meet stakeholder expectations [18]. They include evaluations of mission phases, operation timelines, operational scenarios, end-to-end communications strategy, command and data architecture, operational facilities, integrated logistic support and critical events [17]. In [17,19], ConOps are used to flow down requirements for complex aerospace products as habitable modules or transfer vehicles. Beyond the requirement definition, ConOps guarantees that the technical team thoroughly knows the stakeholders’ expectations and how the product may meet them [20]. If there are gaps or ambiguities in the requirement definition, the ConOps study should identify them and lead to additional refining rounds of the initial list of stakeholder objectives [20]. In addition, thinking through ConOps and use cases frequently reveals requirements and design features that would otherwise go unnoticed, as investigated in [20].
ConOps analysis is the design step when the systems engineers define the level of autonomy that will characterize the mission [21]. The operational timelines related to the space segments, the operational scenarios, and the command and data architecture are the ConOps’s evaluations mostly affected by autonomy. On the other hand:
- The mission phases depend only on the external operational environment;
- The end-to-end communications strategy depends on the overall mission architecture, existing relay satellites and celestial bodies’ positions;
- The operational facilities and the integrated logistic support depend on the mission context, stakeholders, and goals.
The study of operational scenarios would include elements of logistic support. The focus would be on how the operator interacts with the system when autonomous. This interaction can be viewed as sharing responsibilities, as detailed in [21]. ConOps have established themselves as the analysis to help design autonomous systems during conceptual design, as highlighted in [1,22,23]. For example, the authors of [1,22] employ operational analysis to pinpoint the requirements associated with different levels of autonomy and human-system interactions. Furthermore, different authors start looking for behavioural patterns and protocols to generalize the testing and early design definition of autonomous systems’ operations [24,25]. Moving toward a more model-based approach, ConOps’ operational scenarios can be captured in the MBSE functional architecture highlighting operational capabilities, activities, or actions the system can perform. Different studies on autonomous cars have started leveraging ontologies and MBSE to define testing scenarios for operational capabilities of the autonomous AI agent [23,26]. The objective is to avoid expensive re-design later in the system’s life cycle by introducing operational tests during conceptual design [23].
All of these studies, model-based or not, leave the verification and validation of the ConOps to a board of experts instead of a set of operations-related simulations. By leveraging MBSE, it should be possible to relay information to other tools to test the ConOps and better define requirements and mission architecture. Authors such as [15] emphasize how simulations effectively detect possible defects at an early design stage when changes are less expensive. In [15,27], executable MBSE models based on SysML are employed for requirement verification. The underlying idea of the executable systems’ engineering method (ESEM) is to create an MBSE model that ties together different subsystem models and the output of domain-specific practices such as CAD or CFD modelling. As stated by [15], with executable models, it is possible to debug a described behaviour checking whether it matches what the designer meant to capture. The simulation provides a benchmark to understand whether the system behaves as predicted. The level of MBSE maturity provided by frameworks similar to ESEM blurs the line between design and development. However, the ESEM methodology has been applied to automated systems, not autonomous ones.
The work presented in this paper extends the efforts of executable models, providing a simulation framework targeting operational scenarios. The defined simulation framework tests the operations of an autonomous system from its point of view, employing techniques of AI planning. The paper also proposes a new case study, autonomous systems, for applying executable MBSE models. AI planning is the branch of artificial intelligence that focuses on defining an action sequence for an agent to reach a specified goal. Space operations’ software uses planning and scheduling algorithms to achieve a high level of autonomy for both goal-oriented autonomy onboard a spacecraft and planning activities in the ground segment [28]. Most of the work employing AI planning focused on enabling long-term autonomous operations, such as in [7,28,29,30,31]. Some of those algorithms and frameworks were concretized in the Deep Space 1 mission [10,32] and in the Earth Observing 1 mission [33]. In these studies, automated planning techniques are used during the implementation and operation phases of the life cycle. The planners are developed following a series of requirements defined during the formulation phases. Hence, it can be helpful to leverage the ability of those algorithms to output a series of feasible plans (given a set of desired goals, knowledge of the environment, and the possible actions and resources available) to simulate an operational scenario defined in a ConOps at a conceptual design level. No prior studies have examined possible links or synergies between automated planning techniques and preliminary design for space systems, nor have they analysed the reuse of systems engineering models to define planning domains, as illustrated in Table 1.

Table 1.
Comparison between the literature employing MBSE or operations-based simulations and the study of this paper.
3. Methods and Materials
3.1. MBSE and the Parametric Functional Model
Model-based systems engineering is a discipline that emphasizes the use of models to design, develop, and test all parts of a system [35]. MBSE aims to shift the systems engineering paradigm from a document-centric approach to a coherent model from which the typical systems’ engineering documents are derived. The MBSE model includes a functional architecture (encompassing functions, use cases, activities, actions, and states of the system) and a physical one (including physical elements, resources, and variation law of those resources). In this study, the functional architecture includes the operational capabilities that the system can perform. Each of these capabilities is associated with a physical element that can perform them. The first step is the definition of the functional architecture. During the design formulation phases, it is possible to generalize a set of operational capabilities for a given system, as studied in [36]. The operational capabilities are high-level functions responding to a mission statement [36]. From a SysML point of view, they can be identified as primary use cases. Regardless of the mission architecture, the authors propose to generalize a set of common operational capabilities for rover-like planetary exploration systems:
- Payload related:
- –
- Observe target;
- –
- Collect target data;
- Platform related:
- –
- Communicate telemetry;
- –
- Receive command;
- –
- Recharge batteries;
- –
- Check resources;
- –
- Check goal;
- –
- Navigate to goal;
- –
- Wait instructions.
The technologies that guarantee those operational capabilities are met may differ based on the mission. For example, “navigate to goal” can be a shared operational capability for a rover or a drone, even if the mobility system is quite different. Even how those operational capabilities would be detailed or executed can vary. Different missions may require the system to check different types of resources or execute a different logic. For example, “collect target data” may encompass sampling activities, temperature or radiation recording activities, mapping activities or similar. Some of these operational capabilities are heavily linked to autonomous decision-making. For instance, a planetary rover can check the list of goals provided by the control centre and remove some or send a warning to the control centre if it detects that reaching them may endanger it. In comparison, other capabilities are shared between autonomous and automated platforms, as for “communicate telemetry”. Some of these listed operational capabilities may not be considered based on the mission’s objectives.
After identifying which high-level functions the system under study should perform, it is possible to focus on the physical architecture and identify the components. These components would impact resources such as power consumption, generated data or storage space. These parameters can derive from a database of components, previous studies, or a scale-up of existing systems. There is extensive literature on the rapid sizing of physical hardware for robotic space systems, as in [28,37,38]. This resource consumption can change or be refined during the different design phases. The MBSE model matures with the system development, encoding all the related information in a coherent model. The variation of resources due to the different components can be associated with the operational capabilities. Hence, it is possible to assimilate these variations in the related functions, creating a parametric functional model.
A parameterization of the functional architecture with time has already been studied in [15]. The idea of associating some parameters with functional entities is not unheard of in the system engineering domain. However, it appears to be less used. The branch of system research that focuses on developing data exchanges between MBSE and other engineering models (aerodynamic, propulsive, etc.) seems more open to adopting parametrization at the functional level and not only on the physical level. This study proposes to push beyond the time parametrization of [15], considering how other resources change during an operational scenario. A resource can be an available storage space for a sample, a battery capacity or the available memory to store some data. The steps to define a parametric functional model used in this paper are:
- 1.
- An initial functional model is defined;
- 2.
- The different functional instances can be associated with the physical element that can perform them;
- 3.
- The resource parameters associated with the component are back-traced to the functions;
- 4.
- A time parametrization is linked to the functions.
If different physical elements can answer one of the identified functionalities, a trade-off is conducted relying on the quality function deployment (QFD) tool, as in [39]. The different figures of merit are graded considering mission objectives and the stakeholder’s needs, as in the analysis of [39,40]. The design space is then narrowed down to a few solutions that can be quickly tested for feasibility with the proposed framework. This last analysis can provide new inputs for further refining trade-offs. From the definition of the parametric functional model, it is possible to identify the parameters that can define different states of the studied system during its mission. These states can then be formulated as an MDP state.
3.2. Markov Decision Process
Markov decision processes are a long-studied formalism for decision making [41]. In an MDP, the agent solves several decision problems in sequence, where each current decision influences the solution of the following problem [41,42]. This sequential nature of the decisions is typically found in probabilistic planning problems, which generalize shortest-path algorithms in a stochastic environment. The objective of solving an MDP is to find an optimal policy that associates an optimal action with any state [42]. Solving a Markov decision problem can be thought of as controlling the agent to behave optimally, maximizing an average accumulated income in the long run. The solutions are policies that specify the action to be taken in each possible state, assuming that the agent possesses a perfect knowledge of the process and its state at all times. MDP has been long used in robotics for:
- Task planning in a probabilistic environment, as analysed in [42].
- Allocating tasks between different robots, as investigated in [43].
- Managing failure scenarios with multiple robots. For example, in [44], failure reconfigurability comes with re-allocating tasks between robotic platforms. If a robot fails, another is ready to take on the task.
MDP follows the Markov property: all information relevant to the prediction of the future is contained in the present state. This property is referred to as memorylessness by experts: the action leading to the next state can be decided based on the system’s current state, as if the process’s complete history is known.
For the application of this paper, MDP is used instead of a partially observable Markov decision process (POMDP). The assumption is that during the initial design studies, complete knowledge is given to the agent about its state and environment. For the planetary rover, the environment is less dynamic and changing than autonomous systems on Earth. This assumption can stand during the initial conception phases. However, when more dynamic robotic systems, such as flying bots, are considered, looking toward POMDP can be a good solution. At the same time, failure models would benefit from a POMDP model as soon as sensors and monitoring equipment are defined. Most of the process in robotics falls into this category, like the work in [45]. An MDP problem can be easily solved if the state transition probabilities are known. The state transition functions depend only on the current state, not on how that state was reached. The solution of an MDP is to find an optimal policy. A policy is a mapping from states to actions. An optimal policy should ensure that, for a given state, no other action would provide a higher sum of discounted future rewards. Beyond classical MDP-solving techniques in planning, such as policy or value iteration, it is possible to define an optimal policy leveraging reinforcement learning. These techniques are used if the problem transition matrix is complex to compute. These strategies can be considered as planning with a simulator-type model. A simulator samples the following possible states starting from a current state and a reward function [46]. Those methods are called off-policy, as the values of the state transition probabilities are learnt with many trials and errors. Hence, the optimal policy can be learnt by the reinforcement learning algorithm. In [46], one of the identified drawbacks of this solving method is the significant degree of knowledge engineering spent in tweaking various parameters and somehow suggesting the solver of some optimal decision strategies.
In the application of this study, this drawback is tackled by defining the set of parameters that influence the functional architecture and the system operations from the MBSE model. The model can include flight rules to decrease the algorithm’s search space, such as communicating data only in specific time slots or when the memory is full of a defined amount. Suppose the application is a movable planetary system exploring a particular site of interest. In that case, routing problems can be used to suggest optimal movement strategies, as analysed in Section 3.3. Focusing back on the MDP-solving technique, the most used simulation-based optimization to find optimal policies of MDP with reinforcement learning is Q-learning [47]. However, this study suggests tree-based reinforcement learning algorithms such as the Monte Carlo tree search to solve operational problems similarly to [48].
A tree view is more adapted to represent the possible actions taken by an exploration system during its mission. Figure 2 shows a partial view of the decision tree, where an autonomous system should decide its following action. Each of the state-action pairs has an associated reward. Monte Carlo Tree Search is a policy-free reinforcement learning algorithm. The algorithm is often applied to find the winning strategies for board or video games, Figure 3. The algorithm learns from its trials, and when well-defined, it can provide a near-optimal or optimal operational plan respecting a series of constraints.
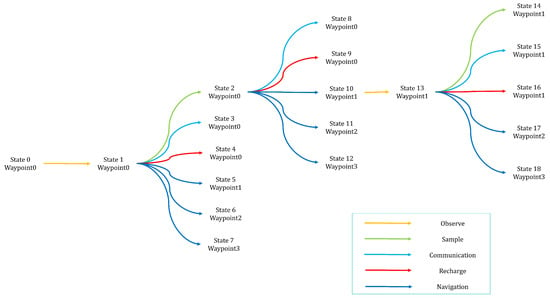
Figure 2.
Partial view of a decision tree for a rover exploring an unknown environment, touching different waypoints during its mission. The different actions bring to different states defined in terms of the rover energy, data, and sampling storage.
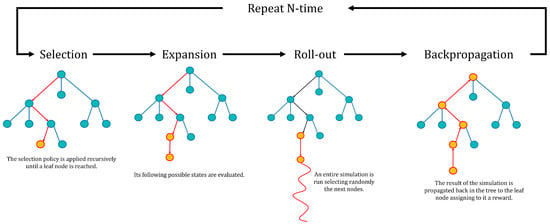
Figure 3.
Monte Carlo tree search algorithm (adapted from [49]).
In Monte Carlo Tree Search, a tree of states connected by the action is incrementally built, preserving data about the times the node was visited and the reward accumulated at the node. The root of this tree corresponds to the agent’s present position. The basic version of MCTS consists of four iterative phases:
- Selection: a root node is selected accordingly to a selection policy that can be random or guided by a heuristic.
- Expansion: the possible children of the selected node are identified.
- Roll-out: a complete simulation is played out starting from one of the added states. The moves can be again random or guided by a heuristic.
- Backpropagation: the simulated roll-out results are propagated back to the root node. The root node visit index and cumulative reward are updated.
An application of the Monte Carlo Tree Search and MDP for the scheduling of satellite operations is presented in [50,51]. On the other hand, in [46], a similar scheme is used to model a rover control problem. With respect to the work of this study, Ref. [46] lacks a knowledge base derived from the MBSE model to choose the most impactful state variables. Moreover, the study in [46] targeted implementation and operational phases. Its application pointed to the direct use of MDP onboard the robotic surface systems.
In Monte Carlo techniques, a complete simulation is run before associating a value to a specific state-action function. An exploration depth can be introduced if the possibility tree is remarkably ample. Instead of running the complete simulation, the algorithm simulates the next n-steps and then provides an indication of the goodness of that random path. The algorithm can take some exploration action to avoid local minima or follow the most promising path. The time the algorithm spends exploring or following the heuristic depends on an exploration weight that usually varies between 0.5 and 2 [52]. MCTS needs a good definition of the reward per each scenario. The simulations of this paper use a reward defined as a linear combination of: (i) the reward provided by exploring different sites , (ii) the reward provided by sampling the sites , (iii) the reward associated with an optimal path , as shown in Equation (1).
where:
- and are the ratios between the effective scenario reward and the maximum reward for observation and sampling for that scenario.
- is the reward linked to the distance.
- is the total number of communications sessions.
- is the total number of recharging sessions.
- is the total number of waypoints to be touched in the simulation.
The weights and sum up the unity. In the simulation results presented at the end of this section, the weights are: , . The algorithm works well when the reward is between 0 and 1. Therefore, the final value of is set to be at most equal to unity. For the simulations in this paper, the system had enough resources to communicate and recharge only two times over the ten touched waypoints. The is evaluated as in Equations (2) and (3), where:
- is a factor defining the equation’s sensitivity.
- is an optimal distance estimate to touch all the .
- is the travelled distance between the touched waypoints during the simulation.
Equation (2) tends toward one when the x evaluated in Equation (3) tends toward zero. The factor quantifies the boundaries from which there is a sensitive increment of the reward related to distance, as showed in Figure 4. For the simulations of this paper is assumed to be equal to 1000.
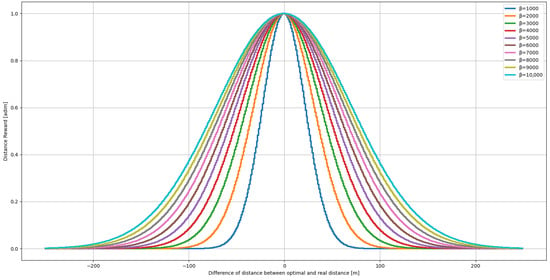
Figure 4.
Variation of the reward related to distance with the difference between the optimal and real distance travelled in the scenario with the variation of .
The optimal distance between a set of waypoints can be evaluated with routing algorithms. The results of the routing algorithms can be used in the MDP framework to provide a heuristic suggesting a preferential movement sequence. Different scenarios can have quite different reward formulations. Therefore, the algorithm requires a first tuning to define it.
3.3. Routing Problems
To lower the number of trials of the MCTS algorithm, the authors suggest using a routing problem to provide a heuristic guiding the path of the planetary exploration system. The formulation used to estimate an optimal path between the waypoints is the “open vehicle routing problem with reward with a distance constraint”. The formulation employed to define the problem is mixed-linear integer programming (MILP). There are formulations available for the “closed vehicle routing problems” [53], the “closed vehicle routing problems with reward” [54], and the “open vehicle routing problem” [55,56]. Indeed, the solving method used in this study circles back to the closed solution. The problem can be observed as a directional graph to which two phantom nodes are added if the initial point is not fixed:
- The distance from the first phantom node and all the other nodes is zero. However, the distance between the other nodes and the initial one is infinite (or set to a high value).
- The distance from all the nodes to the second phantom node is zero. However, the distance from the second phantom node is infinite for all but the first phantom node.
For example, if the problem has five nodes, the obtained distance matrix would look like the one in Equation (4), where are the distance between the waypoints and are the phantom nodes.
When the algorithm looks at the distance matrix, it can always evaluate a closed path using the two phantom nodes. The closed loop ensures an easy formulation. Let us assume that each vertex is connected by a branch identified as . If the routing problem is closed, then if that node is considered (), the sum of on the column and row associated with should equal one. This constraint is simple to enforce in a MILP formulation. If the initial position is fixed, the initial phantom node merges with the indicated initial position. Eventually, the MILP problem can be formulated as shown in Equations from (5) to (10): Maximize reward for every waypoint in V:
Subject to:
where:
- are the waypoints indexes. If a waypoint is not considered, then equals zero.
- is the scientific reward associated with those waypoints.
- is a weight defining the importance of the second optimization target. The suggested value used in this paper is 0.01.
- are the edges between the waypoints’ indexes.
- is the distance between the waypoint.
- is the maximum traversable distance under one battery discharge as evaluated from [57].
The scientific reward is evaluated as a specific waypoint’s scientific interest or priority. Equation (5) describes the objective function: maximizing the accumulated reward touching different waypoints while minimizing the distance to touch them. Equation (6) imposes a constraint on the maximum traversable distance. The aim is always to touch the more interesting waypoints with the highest reward, respecting energy constraints driven by the , while simultaneously lowering the overall travelled distance. If no energy constraints are needed, can be set to a high value. For example, in the code developed for the framework presented in this paper, when no distance constraint is imposed, is evaluated by solving a travelling salesman problem. If the robotic system can recharge when it reaches a waypoint, then the first constraints’ (Equation (6)) can be dropped. A reachability analysis is used when defining the distance matrix. If the distance between two waypoints is more than the , then the related is set to be infinitely distant. Equations (7) and (8) impose that if a node is selected, then there must be one incoming and one outcoming edge. The index i represent the rows, while index j represents the columns. Equation (9) is imposed to avoid subtours. It avoids that the number of selected arcs within S (a subset of V) to be equal to or larger than the number of nodes in S [58]. Equation (10) defines the allowed values for and .
The distance between the waypoints can be evaluated as a simple Euclidean distance or using more refined path planning algorithms such as A*. If the environment the system explores is not particularly texturized, the Euclidean distance may provide a good enough estimate of the travelled distance. A simple example of a routing plan considering the Euclidean distance and the “open vehicle routing problem with reward with a distance constraint” is shown in Figure 5. Figure 6 shows the same simulation considering an A* algorithm to assess the path between the different waypoints. The green areas in Figure 6 represent clusters of obstacles the system should avoid. The distance evaluated with the A* algorithm and the one estimated as Euclidean distance differ by about 10%.
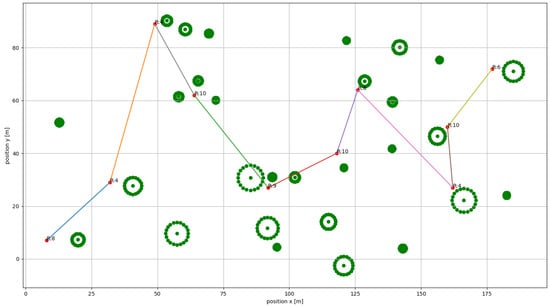
Figure 5.
Example of path evaluated with the “open vehicle routing problem with reward with a distance constraint”. The numbers at each waypoint indicate the associated scientific reward. The minimum covered distance is evaluated as Euclidean distance, and it is equal to 327 m.
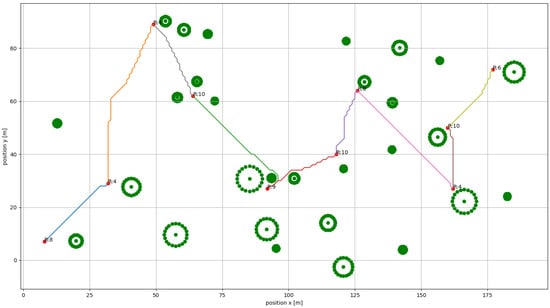
Figure 6.
Example of path evaluated with the “open vehicle routing problem with reward with a distance constraint” routing problem. The numbers at each waypoint indicate the associated scientific reward. The distance between waypoints is evaluated with an A* algorithm, and it is equal to 360 m.
4. Results and Discussion
As highlighted in the previous section, the first step is to study and analyse the functional architecture related to the studied system. The tool used for the modelling is Papyrus, an open-source MBSE tool based on the system modelling language (SysML). In the study case, the rover should touch different waypoints, each with a scientific rating related to observing or sampling the site. The objective of the simulation is:
- To verify whether the identified operational capabilities cover all the functions that the system should perform for a successful mission;
- To check whether the rover has enough resources to complete its mission;
- To understand how the rover will plan its mission to touch the different waypoints if given the freedom to decide its own plan.
The operational capabilities identified in Section 3.1 are the starting point for the functional architecture. Their relationships with physical elements can be visualized in a use case diagram, such as the one in Figure 7. At the same time, their interactions can be investigated, leveraging an activity diagram, as in Figure 8.
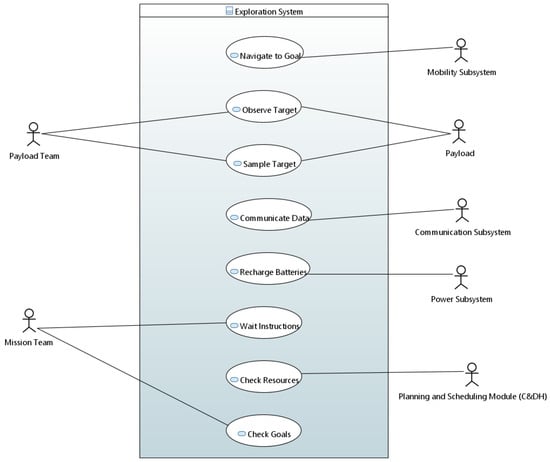
Figure 7.
Set of operational capabilities typical of exploration system.
The payload team provides a set of mission goals associated with observing or sampling a site of interest on the map. The mission team may provide the system with further directions, or they can initiate communication with the system. The system and its software or hardware components should take care of most of the operational capabilities, making the system highly autonomous. The subsystems are modelled as secondary actors. The primary actors invoke the use case, while the secondary actors participate in the use case by performing actions, as analysed in [59].
After the initial modelling of the functional architecture and identification of the main elements of the physical architecture, it is possible to parametrize the functional model. In this simple example, the different operational capabilities are directly linked to the different hardware that can perform them. The parametrization can be manual, or the XMI file in the backend of Papyrus can be extracted and converted into a tabulated and human-readable file with:
- The list of functions performed by the system.
- The physical components’ parameters associated with the functions.
- A time specification for the function.
The time for the operational capability “navigate to goal” depends on the distance to be covered and the exploration system velocity (a parameter of the mobility system set to 0.1 m/s for the presented simulations). Similarly, the amount of data to communicate or time to recharge the battery drives the time allocated to these operational capabilities. The time specifications for the “observe target” and “sample target” are set to be around 10 min. While the “check resources” is an almost instantaneous loop evaluating whether the system has enough resources to perform a specific operation. This check also lowers the number of possible outcomes in the MCTS algorithm.
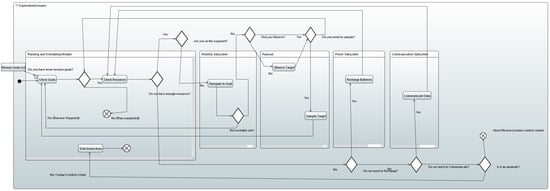
Figure 8.
Activity diagram view of a generic exploration mission with a high degree of autonomy.
Table 2 and Table 3 show the results of the analysis on the parametrization with respect to the power consumption and data generation. The operational capabilities’ names in the tables are shortened to just the verb, instead of the conventional verb plus noun that is typical of systems engineering. The values in the tables have been identified through an analogue system tested on Earth during the IGLUNA analogue mission. The details of the IGLUNA testing are provided in [60]. They can be used as reference values for a small rover (up to 30 kg), and they agree with the available literature on small planetary robotic platforms, as in [37,38,61].

Table 2.
Power consumption per operational capability per component in [W] (Comm is the abbreviation for Communicate).

Table 3.
Data Generation per operational capability per component in [kbytes/s] (Comm is the abbreviation for Communicate).
The IGLUNA rover has two batteries, one dedicated to the mobility system and one for the payload. The rover base is a commercial platform called Leo Rover [62]. It has its own battery dedicated to navigation capabilities. The base is then enriched with a set of sensors (the payload), the robotic arm, a new onboard computer (connected to the bottom one) and a dedicated battery for the payload.
After defining the MBSE model, the designer can define the variables that identify the system’s state. The state should provide the system with all the needed information to decide on the best next step. For a planetary exploration system, this state has been defined as described in Table 4:

Table 4.
Set of variables that define a state of the rover.
- Waypoint to visit indicates which waypoints have been visited and which have not during the given simulated episode.
- The last action performed poses a limit to which actions can be chosen at a lower level of the tree based on the provided flight rules.
- The current waypoint is an indication of where the system is at a given moment. It is most useful during debugging.
- The battery capacity, storage capacity and data volume capacity are linked to the constraints the system should not overshoot.
- The number of recharges, number of communication, idle time, and mission time are metrics used to evaluate the performances of the given scenario: does the system have enough capacity to store the data, or does it need an almost continuous communication?
All this information is written as a tuple that defines a specific scenario. At the end of the simulation, a reward characterizes each scenario. The reward defines how appropriate or suitable this scenario is with respect to others, helping the algorithm prune some branches of the tree. During the preliminary design phases, the objective is to study the feasibility of the proposed architecture and operational scenario. During the analysis, the systems’ engineers may point toward a near-optimal or optimal solution. In this second case, some time should be allocated to defining the exploration parameter of the MCTS algorithm and the number of samples before deciding on the following best path. However, to test the feasibility of the design, a near-optimal solution can be satisfying. In the results presented in this paper, the authors focus on near-optimal solutions, setting the MCTS exploration parameter to 1.5 and the number of samples before the decision to 100. To lower the number of samples, it is possible to impose flight rules suggesting preferential algorithm-solving strategies. For the example in this study, the engineers may suggest the algorithm preferential bounds on when to recharge or communicate. After testing the feasibility of the scenario and obtaining a suboptimal solution without any alteration, the engineers can tweak some boundaries so that the MCTS follows a preferential branch. This interaction may provide further insights and test cases on the performances of the system in its operative environment. In the results of this paper, the system is biased toward communicating data when the storage of its flash memory is equal to or above 60% of its maximum. The system is also biased toward recharging when one of its batteries is below 20% of its charging state. These values were set after two algorithm runs, to help optimise the results without sacrificing a quick run time. The overall run time is relatively low, taking only a handful of minutes to assess the feasibility of a scenario.
At the end of the simulation, the designers will be able to visualize a plan and the variation of the system resources during the simulated scenario. An example of the results that this analysis can provide is shown from Figure 9, Figure 10, Figure 11 and Figure 12. The visualization of the plan in Figure 9 is heavily inspired by the tools routinely used in mission control centres. It is an intuitive view, defined as a function of mission time. This view can provide an initial operational timeline to be discussed in round tables with the stakeholders or refined during the different design phases. It is interesting to pinpoint that this operational timeline is directly generated from the identified set of system functionalities. Hence, timelines with different granularity can be generated while detailing the functional architecture. Figure 10 shows the two batteries’ (lower and upper) consumptions clearly. The performances agree with what was recorded from IGLUNA and the specification of the Leo rover [62]. The battery connected to mobility has a capacity of around five hours. In comparison, the upper battery has more capacity but a higher power consumption. For example, during IGLUNA the upper battery was the one depleting the fastest due to the high power requirements of navigation equipment such as LiDAR and the cameras. Figure 11 shows the data generated. The system needs to relay data multiple times not to surpass the provided limit of 2 Gbytes. The rover has a sampling storage set at 1 g, while a sample weighs around 0.2 g. The system can only sample some of the waypoints, trying to maximize its sampling-related reward set as . The optimal path evaluated with the routing algorithm provides a reference for the optimal navigation actions. These optimal actions are suggested to the algorithm. Figure 12 shows the path followed by the simulated system. The green points delimit areas with rugged terrain or obstacles not-traversable for the rover. The path planning algorithm used during the simulation is an A*. The battery does not limit the distance, as the rover can recharge multiple times during its traverse.
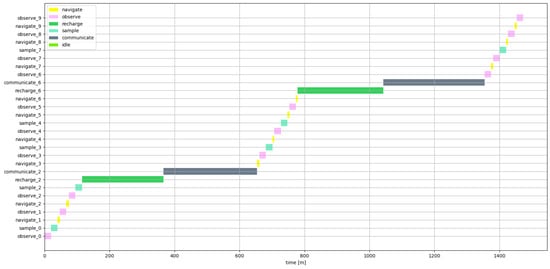
Figure 9.
Output plan for the simulated scenario.
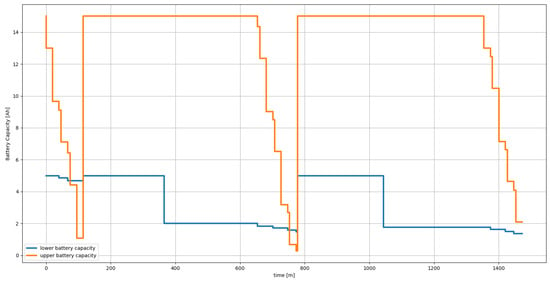
Figure 10.
Battery consumption and recharge cycles throughout the simulated scenario.
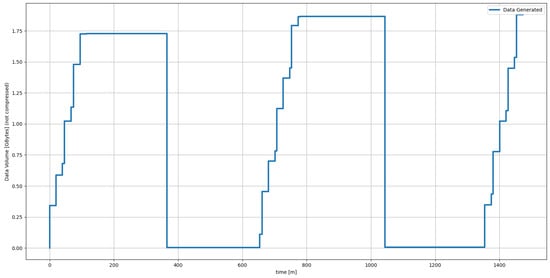
Figure 11.
Data generation and dumping throughout the simulated scenario.
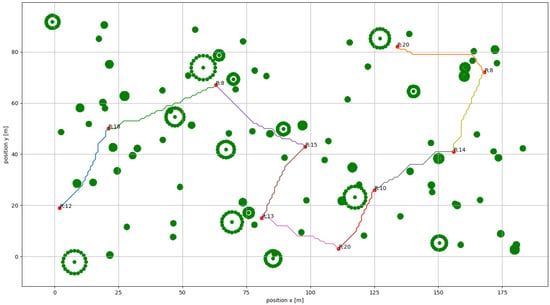
Figure 12.
Path of the rover between the different waypoints. The green dots identify areas that the system cannot traverse. The path is evaluated with an A* algorithm. The displayed reward is the sum of the observation and sampling rewards associated with that specific waypoint.
The results, from Figure 9, Figure 10, Figure 11 and Figure 12, show how the presented framework can provide an indication on:
- The plan that an autonomous system, knowing its resources and action, can lay down for an identified operational scenario;
- The variation of the main rover resources during a typical mission;
- An operational timeline as a product of the MBSE model simulated as an MDP.
These outcomes show that the system has enough resources to complete the particular considered mission, touching all waypoints. All of these results are products of the MBSE model and may be traced back to it, creating one knowledge base for the overall design.
The plan can be directly interfaced in a simulated or analogue platform as soon as it is generated. The authors used the Robot Operating System (ROS) to interface a similar plan with the IGLUNA rover in [60], testing the overall feasibility of this approach.
5. Conclusions and Future Work
This paper presents a framework to simulate operational scenarios for autonomous robotic systems during the initial design phases. During the design of a mission, an MBSE model is created. The MBSE models group both a functional architecture and a physical one. From those inputs, a simulation of the studied system in a relevant scenario is laid out, relying on MDP and MCTS. The simulation is developed from the system point of view, in which knowing its resources and mission goals provides the user with a feasible plan to maximize the scientific return. The framework introduces the concept of a parametric functional model. The functional architecture inherits the parameters of the physical architecture linked to that specific function. Moreover, the functions are enriched with a definition of time to perform them. These parameters are then used in the MDP to advance the plan based on the mission goals and a set of resources.
This study highlights how MBSE is a versatile concept that adapts well to different applications. The designers can easily capture their operations’ definition in the MBSE model and validate it in this framework. As a result, they can understand the performance of a system under constrained resources. They can assess the feasibility of a relevant scenario from both a functional point of view, with the operational capabilities, and a physical one, looking at the system resources and the mission time. It is possible to use this framework also to size variables in the system. For example, instead of imposing a data limit, the user can set a flight rule that enforces communicating only in certain circumstances or temporal windows. These flight rules can be easily added to the model through some heuristics or an if-then condition in the MDP model. The framework can also be used to understand the impact of different faults or failures on the mission. If, for example, a fault in the mobility system makes it consume more than the nominal value, the system may need to reconfigure its mission accordingly, as it is trying to maximize its scientific reward under these new power constraints.
The framework allows a modular approach to design. At the same time, it eases reusability between similar projects. For example, the generalized set of operational capabilities for a planetary exploration system identified in Section 3.1 can be re-employed as a starting functional analysis (focusing on operations) across different projects. This preferential behavioural model can be used on different simulated platforms, helping assess their likely-to-be performances on a particular mission of different solutions. The change in the physical model will define a different resource consumption or generation associated with an operational capability.
The work presented in this paper will be extended toward applying multiple collaborating systems. The framework should suggest to the designers a promising subdivision of tasks between different systems, starting from their system modelling. On the other hand, part of the future work related to this study will focus on exploring a different simulation-based optimization to find the MDP policy. The solution explored in this paper provides a near-optimal solution with around 100 samples. However, around 500 samples are needed to find the optimal policy for the paper’s case study (without suggesting some winning solution to the algorithm). The authors are exploring other algorithms and implementations of MCTS with neural networks to reach the optimal solution faster. The framework may be useful to outline the first feasible operational timeline for control centres. It can be included in a mixed-initiative tool where the AI and operator can interact and optimize the operations of an analysed system together. MDP and MCTS can help the mission architect explore the design space. The MCTS algorithm can be coupled with deep neural networks to explore the design space quickly and more efficiently. In this case, the MDP state would be defined in terms of the cost, maturity, and development time of a specific physical element, not only in terms of the power consumed and data generated. The trade-space exploration will rely on a precompiled database of technologies and related functionality, as developed in [36].
Author Contributions
Conceptualization, J.R.; methodology, J.R.; software, J.R.; validation, N.V. and S.L.-D.; formal analysis, J.R.; investigation, J.R.; writing—original draft preparation, J.R.; writing—review and editing, N.V. and S.L.-D.; supervision, N.V. and S.L.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
A simplified version of the MBSE model implemented in Papyrus used in this study can be found at https://github.com/JasmineRimani/PapyrusModelsRepository (accessed on 23 February 2023). The version includes all the links in the functional model, the links between the functional and the physical architecture, and an example of the links between the physical architecture and the mathematical formulations that can be traced back to the functional architecture.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CAD | Computer-Aided Design |
| CFD | Computational Fluid Dynamics |
| ConOps | Concept of Operations |
| ESEM | Executable Systems Engineering Method |
| HDDL | Hierarchical Domain Definition Language |
| MBSE | Model-Based System Engineering |
| MILP | Mixed-Integer Linear Programming |
| MDP | Markov Decision Process |
| MCTS | Monte Carlo Tree Search |
| OR | Operational Research |
| QFD | Quality Function Deployment |
References
- Vassev, E.; Hinchey, M. Autonomy requirements engineering. In Autonomy Requirements Engineering for Space Missions; Springer: Cham, Switzerland, 2014; pp. 105–172. [Google Scholar]
- Pinto, A. Requirement Specification, Analysis and Verification for Autonomous Systems. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1315–1318. [Google Scholar]
- Luckcuck, M. Using formal methods for autonomous systems: Five recipes for formal verification. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2021, 237. [Google Scholar] [CrossRef]
- Bensalem, S.; Havelund, K.; Orlandini, A. Verification and validation meet planning and scheduling. Int. J. Softw. Tools Technol. Transf. 2014, 16, 1–2. [Google Scholar] [CrossRef]
- Koopman, P.; Wagner, M. Challenges in autonomous vehicle testing and validation. SAE Int. J. Transp. Saf. 2016, 4, 15–24. [Google Scholar] [CrossRef]
- Cardoso, R.C.; Kourtis, G.; Dennis, L.A.; Dixon, C.; Farrell, M.; Fisher, M.; Webster, M. A Review of Verification and Validation for Space Autonomous Systems. Curr. Robot. Rep. 2021, 2, 273–283. [Google Scholar] [CrossRef]
- Truszkowski, W.; Hallock, H.; Rouff, C.; Karlin, J.; Rash, J.; Hinchey, M.; Sterritt, R. Autonomous and Autonomic Systems: With Applications to NASA Intelligent Spacecraft Operations and Exploration Systems; Springer Science & Business Media: London, UK, 2009. [Google Scholar]
- Frost, C.; Butt, A.; Silva, D. Challenges and opportunities for autonomous systems in space. In Proceedings of the Frontiers of Engineering: Reports on Leading-Edge Engineering from the 2010 Symposium, Armonk, NY, USA, 23–25 September 2010. [Google Scholar]
- Shishko, R.; Aster, R. NASA Systems Engineering Handbook; NASA: Washington, DC, USA, 1995; Volume 6105. [Google Scholar]
- Muscettola, N.; Fry, C.; Rajan, K.; Smith, B.; Chien, S.; Rabideau, G.; Yan, D. On-board planning for new millennium deep space one autonomy. In Proceedings of the 1997 IEEE Aerospace Conference, Snowmass, CO, USA, 13 February 1997; IEEE: Piscataway, NJ, USA, 1997; Volume 1, pp. 303–318. [Google Scholar]
- Rabideau, G.; Tran, D.; Chien, S.; Cichy, B.; Sherwood, R.; Mandl, D.; Frye, S.; Shulman, S.; Szwaczkowski, J.; Boyer, D.; et al. Mission operations of earth observing-1 with onboard autonomy. In Proceedings of the 2nd IEEE International Conference on Space Mission Challenges for Information Technology (SMC-IT’06), Pasadena, CA, USA, 17–20 July 2006; IEEE: Piscataway, NJ, USA, 2006; p. 7. [Google Scholar]
- Schenker, P.; Baumgartner, E.; Backes, P.; Aghazarian, H.; Dorsky, L.; Norris, J.; Huntsberger, T.; Cheng, Y.; Trebi-Ollennu, A.; Garrett, M. FIDO: A Field Integrated Design & Operation rover for Mars surface exploration. Proceeding of the 6th International Symposium on Artificial Intelligence and Robotics & Automation in Space, i-SAIRAS 2001, Montreal, QC, Canada, 18–22 June 2001. [Google Scholar]
- Hayati, S.; Arvidson, R. Long Range Science Rover (Rocky7) Mojave Desert Field Tests. Proc. i-SAIRAS’97 1997, 3, 361–367. [Google Scholar]
- Apostolopoulos, D.; Wagner, M.; Whittaker, W. Technology and Field Demonstration Results in the Robotic Search for Antarctic Meteorites. 2000. Available online: https://kilthub.cmu.edu/articles/journal_contribution/Technology_and_Field_Demonstration_Results_in_the_Robotic_Search_for_Antarctic_Meteorites/6561158 (accessed on 22 February 2023).
- Karban, R.; Dekens, F.G.; Herzig, S.; Elaasar, M.; Jankevičius, N. Creating system engineering products with executable models in a model-based engineering environment. In Proceedings of the Modeling, Systems Engineering, and Project Management for Astronomy VII, Edinburgh, UK, 26 June–1 July 2016; Volume 9911, pp. 96–111. [Google Scholar]
- Lee, M.; Weidner, R.J. Virtual mission operation framework. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No. 04TH8720), Big Sky, MT, USA, 6–13 March 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 6, pp. 4015–4025. [Google Scholar]
- Viscio, M.A.; Viola, N.; Fusaro, R.; Basso, V. Methodology for requirements definition of complex space missions and systems. Acta Astronaut. 2015, 114, 79–92. [Google Scholar] [CrossRef]
- Viola, N.; Corpino, S.; Fioriti, M.; Stesina, F. Functional analysis in systems engineering: Methodology and applications. In Systems Engineering-Practice and Theory; IntechOpen: London, UK, 2012. [Google Scholar]
- Li, R.; Verhagen, W.J.; Curran, R. Toward a methodology of requirements definition for prognostics and health management system to support aircraft predictive maintenance. Aerosp. Sci. Technol. 2020, 102, 105877. [Google Scholar] [CrossRef]
- Shea, G. NASA Systems Engineering Handbook Revision 2; National Aeronautics and Space Administration: Washington, DC, USA, 2017. [Google Scholar]
- Tessier, C. Robots autonomy: Some technical issues. In Autonomy and Artificial Intelligence: A Threat or Savior? Springer: Cham, Switzerland, 2017; pp. 179–194. [Google Scholar]
- Schuchardt, B.I.; Becker, D.; Becker, R.G.; End, A.; Gerz, T.; Meller, F.; Metz, I.C.; Niklaß, M.; Pak, H.; Schier-Morgenthal, S.; et al. Urban Air Mobility Research at the DLR German Aerospace Center—Getting the HorizonUAM Project Started. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021; p. 3197. [Google Scholar]
- Damak, Y.; Leroy, Y.; Trehard, G.; Jankovic, M. Operational Context-Based Design Method of Autonomous Vehicles Logical Architectures. In Proceedings of the 2020 IEEE 15th International Conference of System of Systems Engineering (SoSE), Budapest, Hungary, 2–4 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 439–444. [Google Scholar]
- Sifakis, J. System Design in the Era of IOT—Meeting the Autonomy Challenge. arXiv 2018, arXiv:1806.09846. [Google Scholar] [CrossRef]
- Väätänen, A.; Laarni, J.; Höyhtyä, M. Development of a concept of operations for autonomous systems. In Proceedings of the International Conference on Applied Human Factors and Ergonomics, Washington, DC, USA, 24–28 July 2019; Springer: Cham, Switzerland, 2019; pp. 208–216. [Google Scholar]
- Bagschik, G.; Menzel, T.; Maurer, M. Ontology based scene creation for the development of automated vehicles. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1813–1820. [Google Scholar]
- Karban, R. Using Executable SysML Models to Generate System Engineering Products. 2016. Available online: https://ntrs.nasa.gov/citations/20190033608 (accessed on 22 February 2023).
- Gao, Y.; Burroughes, G.; Ocón, J.; Fratini, S.; Policella, N.; Donati, A. Mission Operations and Autonomy; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Volpe, R.; Nesnas, I.; Estlin, T.; Mutz, D.; Petras, R.; Das, H. The CLARAty architecture for robotic autonomy. In Proceedings of the 2001 IEEE Aerospace Conference Proceedings (Cat. No. 01TH8542), Big Sky, MT, USA, 10–17 March 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 1, pp. 1–121. [Google Scholar]
- Fong, T. NASA Autonomous Systems & Robotics: Roadmap and Investments. In Proceedings of the Lunar Surface Innovation Consortium Fall 2021 Meeting, Bowie, MD, USA, 3–4 November 2021; 2021. [Google Scholar]
- Watson, D.P.; Scheidt, D.H. Autonomous systems. Johns Hopkins APL Tech. Dig. 2005, 26, 368–376. [Google Scholar]
- Rayman, M.D.; Varghese, P.; Lehman, D.H.; Livesay, L.L. Results from the Deep Space 1 technology validation mission. Acta Astronaut. 2000, 47, 475–487. [Google Scholar] [CrossRef]
- Tran, D.; Chien, S.; Rabideau, G.; Cichy, B. Flight Software Issues in Onboard Automated Planning: Lessons Learned on EO-1. 2004. Available online: https://dataverse.jpl.nasa.gov/dataset.xhtml?persistentId=hdl:2014/37970 (accessed on 22 February 2023).
- Vassev, E.; Hinchey, M. On the autonomy requirements for space missions. In Proceedings of the 16th IEEE International Symposium on Object/Component/Service-Oriented Real-Time Distributed Computing (ISORC 2013), Paderborn, Germany, 19–21 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–10. [Google Scholar]
- Kolcio, K.; Fesq, L. Model-based off-nominal state isolation and detection system for autonomous fault management. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–13. [Google Scholar]
- Viola, N.; Fusaro, R.; Vercella, V. Technology roadmapping methodology for future hypersonic transportation systems. Acta Astronaut. 2022, 195, 430–444. [Google Scholar] [CrossRef]
- Lamamy, J.A.; Miller, D.W. Designing the Next Generation of Rovers through a Mid-rover Analysis. ASTRA 2006, 2006, 28–30. [Google Scholar]
- De Paor, C.; Roque, A.; Rimani, J.; Lizy-Destrez, S. An Integrated Design Platform to Analyse and Size Planetary Exploration Systems Applied to Lunar Lava Tube Exploration. In Proceedings of the 73rd International Astronautical Congress (IAC 2022), Paris, France, 18–22 September 2022. [Google Scholar]
- Fusaro, R.; Viola, N.; Fenoglio, F.; Santoro, F. Conceptual design of a crewed reusable space transportation system aimed at parabolic flights: Stakeholder analysis, mission concept selection, and spacecraft architecture definition. Ceas Space J. 2017, 9, 5–34. [Google Scholar] [CrossRef]
- Governale, G.; Rimani, J.; Viola, N.; Villace, V.F. A trade-off methodology for micro-launchers. Aerosp. Syst. 2021, 4, 209–226. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Chanel, C.C.; Teichteil-Königsbuch, F.; Lesire, C. Multi-target detection and recognition by uavs using online pomdps. In Proceedings of the AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013; Volume 27, pp. 1381–1387. [Google Scholar]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Decision making in multiagent systems: A survey. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 514–529. [Google Scholar] [CrossRef]
- Asikin, D.; Dolan, J.M. Reliability impact on planetary robotic missions. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 4095–4100. [Google Scholar]
- Chanel, C.P.C.; Lesire, C.; Teichteil-Königsbuch, F. A robotic execution framework for online probabilistic (re)planning. In Proceedings of the Twenty-Fourth International Conference on Automated Planning and Scheduling, Portsmouth, NH, USA, 21–26 June 2014. [Google Scholar]
- Bernstein, D.; Zilberstein, S.; Washington, R.; Bresina, J. Planetary rover control as a markov decision process. In Proceedings of the Sixth International Symposium on Artificial Intelligence, Robotics, and Automation in Space, Montreal, QC, Canada, 21–26 October 2001. [Google Scholar]
- Gosavi, A. Solving Markov decision processes via simulation. In Handbook of Simulation Optimization; Springer: New York, NY, USA, 2015; pp. 341–379. [Google Scholar]
- Fu, M.C. AlphaGo and Monte Carlo tree search: The simulation optimization perspective. In Proceedings of the 2016 Winter Simulation Conference (WSC), Washington, DC, USA, 11–14 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 659–670. [Google Scholar]
- Pepels, T.; Winands, M.H.; Lanctot, M. Real-time monte carlo tree search in ms pac-man. IEEE Trans. Comput. Intell. AI Games 2014, 6, 245–257. [Google Scholar] [CrossRef]
- Eddy, D.; Kochenderfer, M. Markov decision processes for multi-objective satellite task planning. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–12. [Google Scholar]
- Herrmann, A.; Schaub, H. Autonomous spacecraft tasking using monte carlo tree search methods. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Charlotte, NC, USA, 1–4 January 2021. [Google Scholar]
- Lapan, M. Deep Reinforcement Learning Hands-On: Apply Modern RL Methods, with Deep Q-Networks, Value Iteration, Policy Gradients, TRPO, AlphaGo Zero and More; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. Ann. Oper. Res. 2022, 314, 255–275. [Google Scholar] [CrossRef]
- Ralphs, T.K.; Kopman, L.; Pulleyblank, W.R.; Trotter, L.E. On the capacitated vehicle routing problem. Math. Program. 2003, 94, 343–359. [Google Scholar] [CrossRef]
- Sariklis, D.; Powell, S. A heuristic method for the open vehicle routing problem. J. Oper. Res. Soc. 2000, 51, 564–573. [Google Scholar] [CrossRef]
- Li, F.; Golden, B.; Wasil, E. The open vehicle routing problem: Algorithms, large-scale test problems, and computational results. Comput. Oper. Res. 2007, 34, 2918–2930. [Google Scholar] [CrossRef]
- Xiao, X.; Whittaker, W.L. Energy Utilization and Energetic Estimation of Achievable Range for Wheeled Mobile Robots Operating on a Single Battery Discharge; Robotics Institute: Pittsburgh, PA, USA, 2014. [Google Scholar]
- De Giovanni, L.; Marco, D.S. Lecture notes in Methods and Model for Combinatorial Optimization. Available online: https://www.math.unipd.it/~luigi/courses/metmodoc1718/m08.01.TSPexact.en.pdf (accessed on 20 April 2023).
- Delligatti, L. SysML Distilled: A Brief Guide to the Systems Modeling Language; Addison-Wesley: Boston, MA, USA, 2013. [Google Scholar]
- Rimani, J.; Viola, N.; Lizy-Destrez, S. Application of a hierarchical task planner to a lunar lava tube analogue robotic mission. In Proceedings of the International Astronautical Congress, Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Della Torre, A.; Finzi, A.E.; Genta, G.; Curti, F.; Schirone, L.; Capuano, G.; Sacchetti, A.; Vukman, I.; Mailland, F.; Monchieri, E.; et al. AMALIA Mission Lunar Rover—The conceptual design of the Team ITALIA Rover, candidate for the Google Lunar X Prize Challenge. Acta Astronaut. 2010, 67, 961–978. [Google Scholar] [CrossRef]
- Leo Rover. Available online: https://www.leorover.tech/ (accessed on 22 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).