A New Adaptive Control Algorithm of IGC System for Targets with Several Maneuvering Modes Based on GTSMC-DNN
Abstract
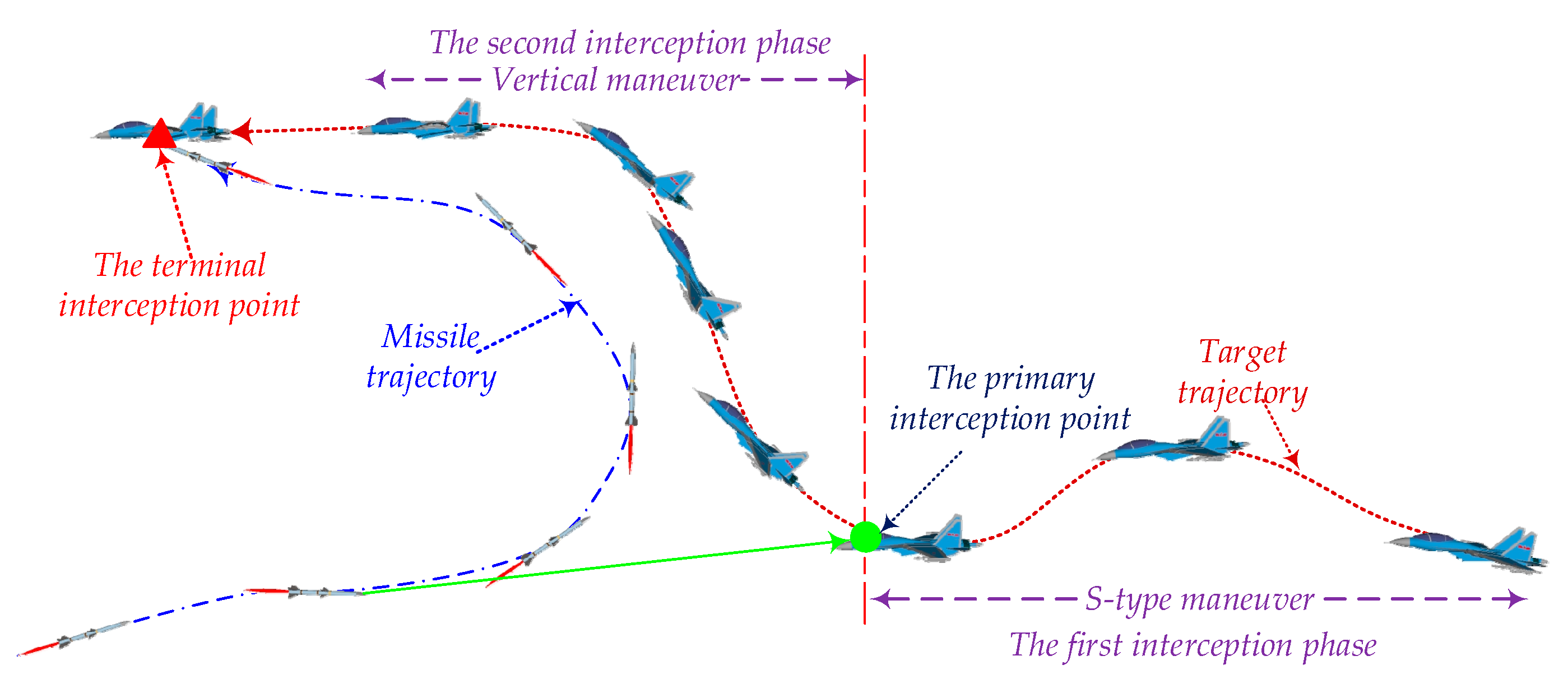
1. Introduction
- 1.
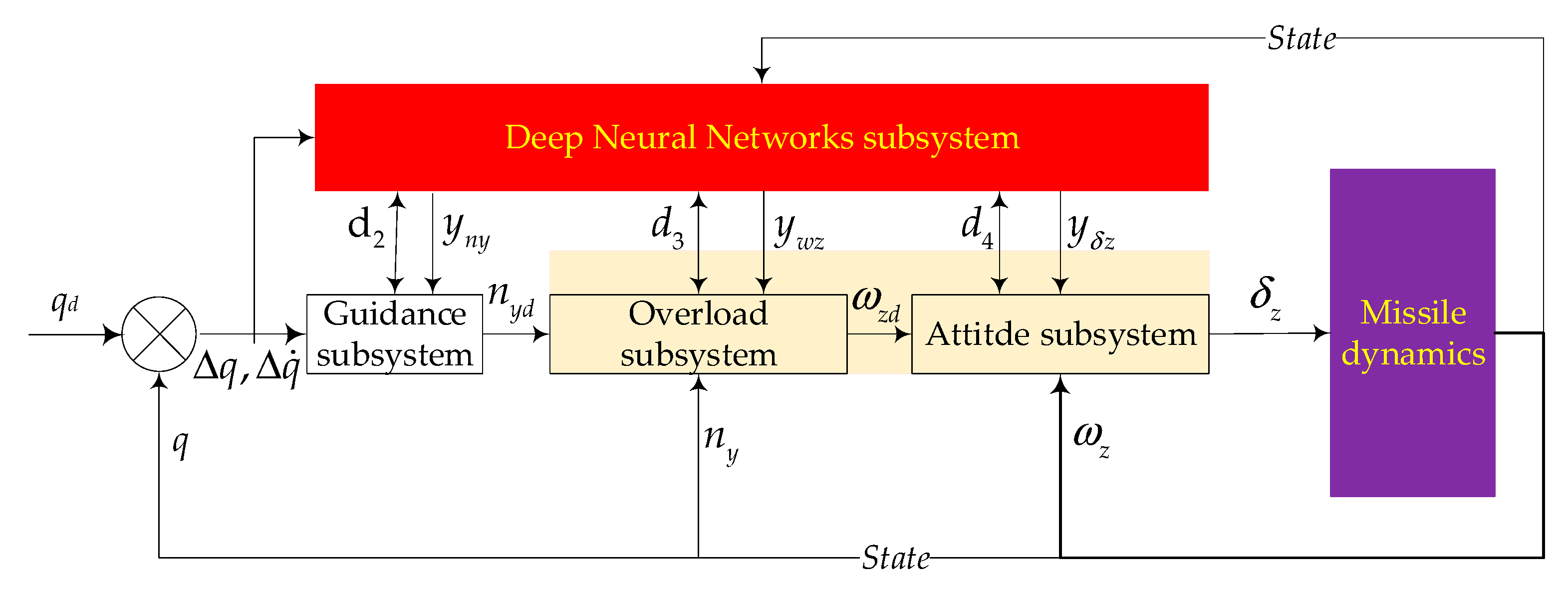
- In order to improve the adaptive interception capability of the missile, a new adaptive IGC nonlinear mathematic dynamic model with deep neural network is established. In this model, the IGC system is divided into four subsystems including guidance subsystem, overload subsystem, attitude subsystem and the deep neural subsystem.
- 2.
- Aiming to transform the control signal between each subsystem and avoid the “differential explosion”, the paper defines a new SOF (Second Order Filter). Additionally, to formulate the uncertain items, the paper defines the corresponding equation.
- 3.
- Combined with GTSMC, SOF and DNN, the paper designs a new IGC adaptive controller to intercept the maneuvering target, which has different maneuvering modes and changes the maneuvering mode suddenly during the interception process.
- 4.
- Using Lyapunov’s theory, the closed-loop system was proved to be stable. Finally, several simulation results demonstrated the superiority of the method proposed in this paper, compared with the previous approaches.
2. Problem Formulation
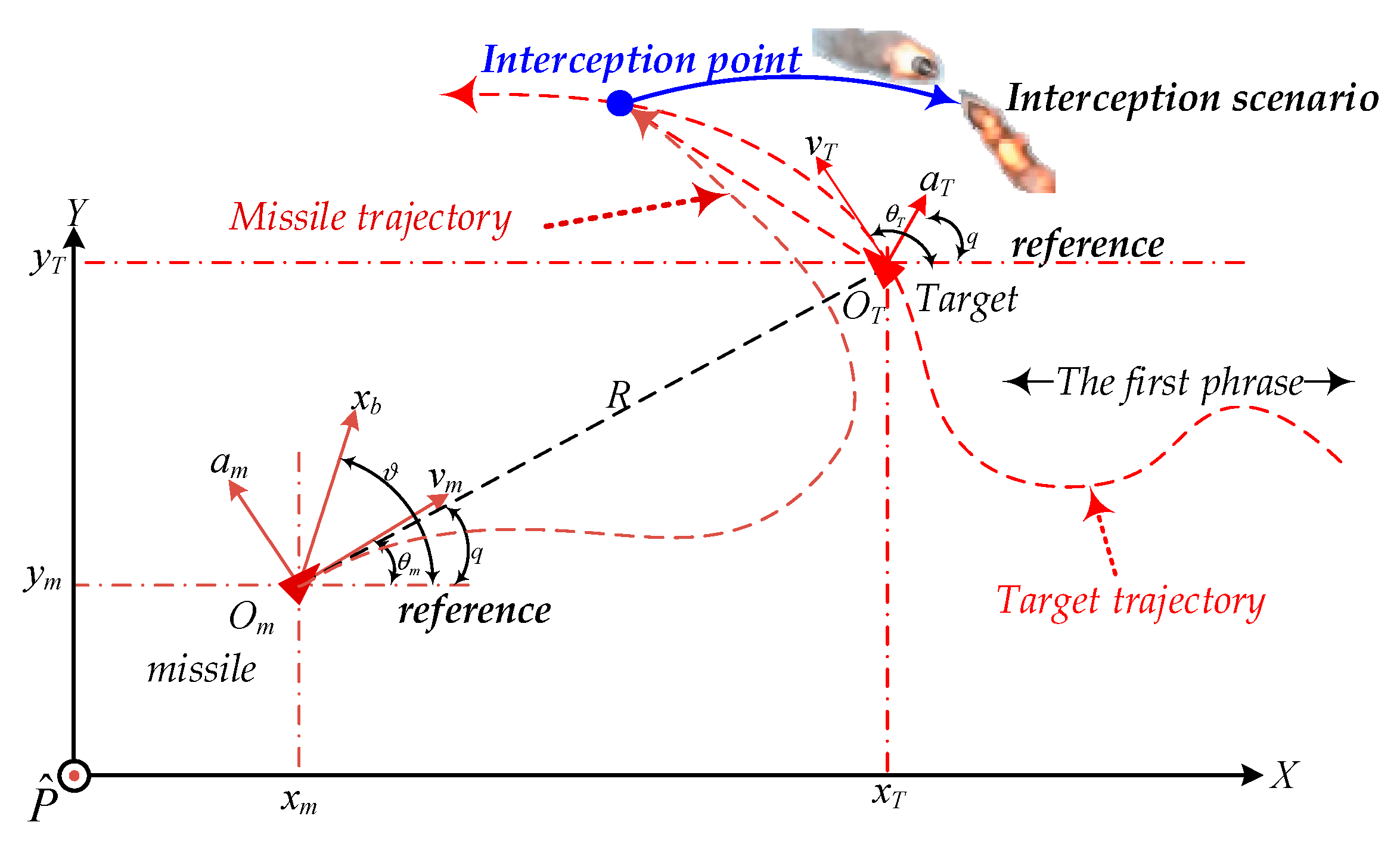
2.1. Engagement Kinematics
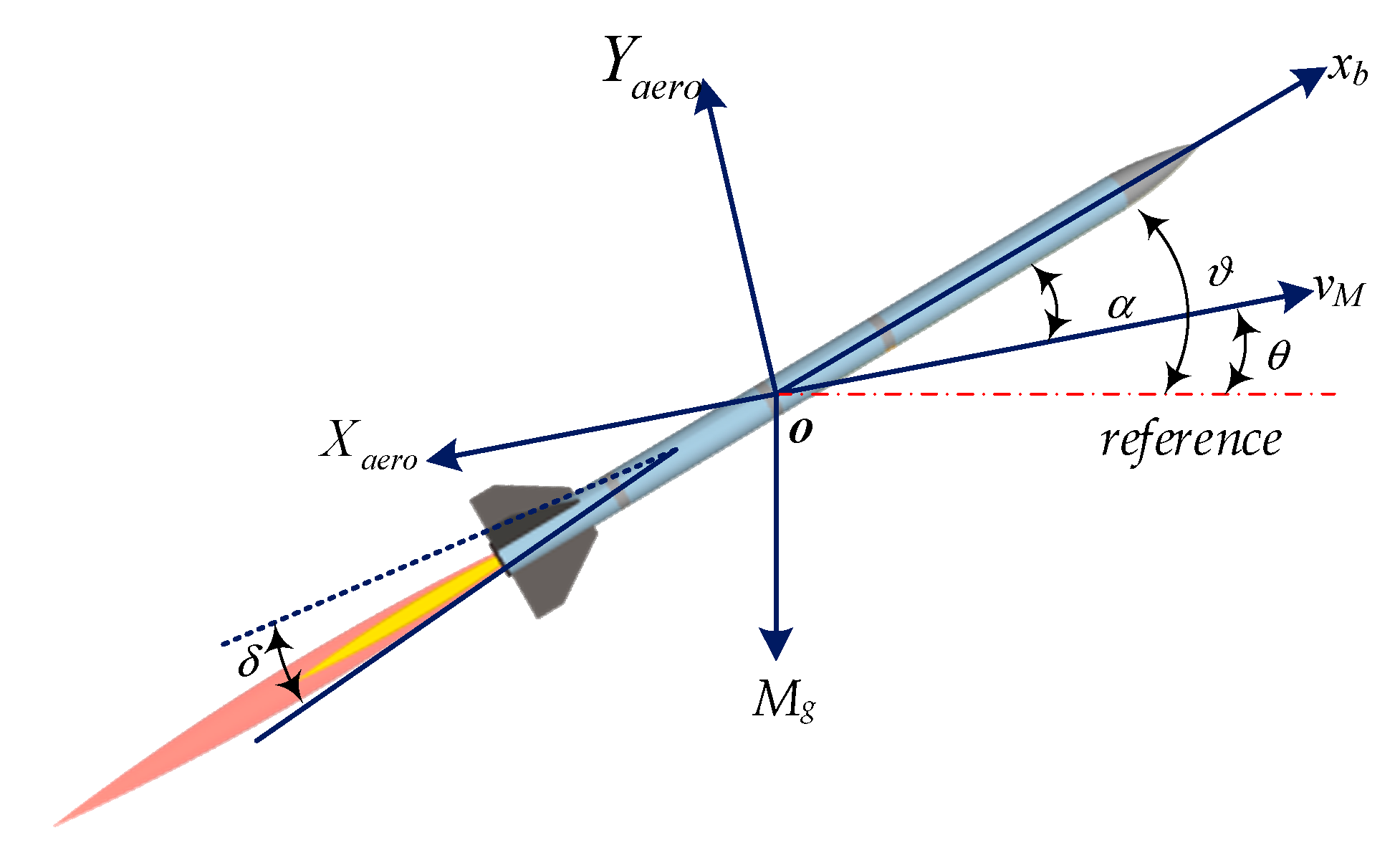
2.2. The Missile Dynamics with Uncertain Items
2.3. Fourth-Order IGC Model in State Space
3. Adaptive Controller Design with Deep Neural Network
3.1. Design Objectives
- (1)
- The LOS angle can be soon converged to the desire angle ;
- (2)
- The controller has a strong adaptability against maneuvering targets with different maneuver modes;
- (3)
- When considering the relationship between each control loop, a small miss distance can be achieved;
- (4)
- The stability of the closed-loop system of the system states should be ensured.
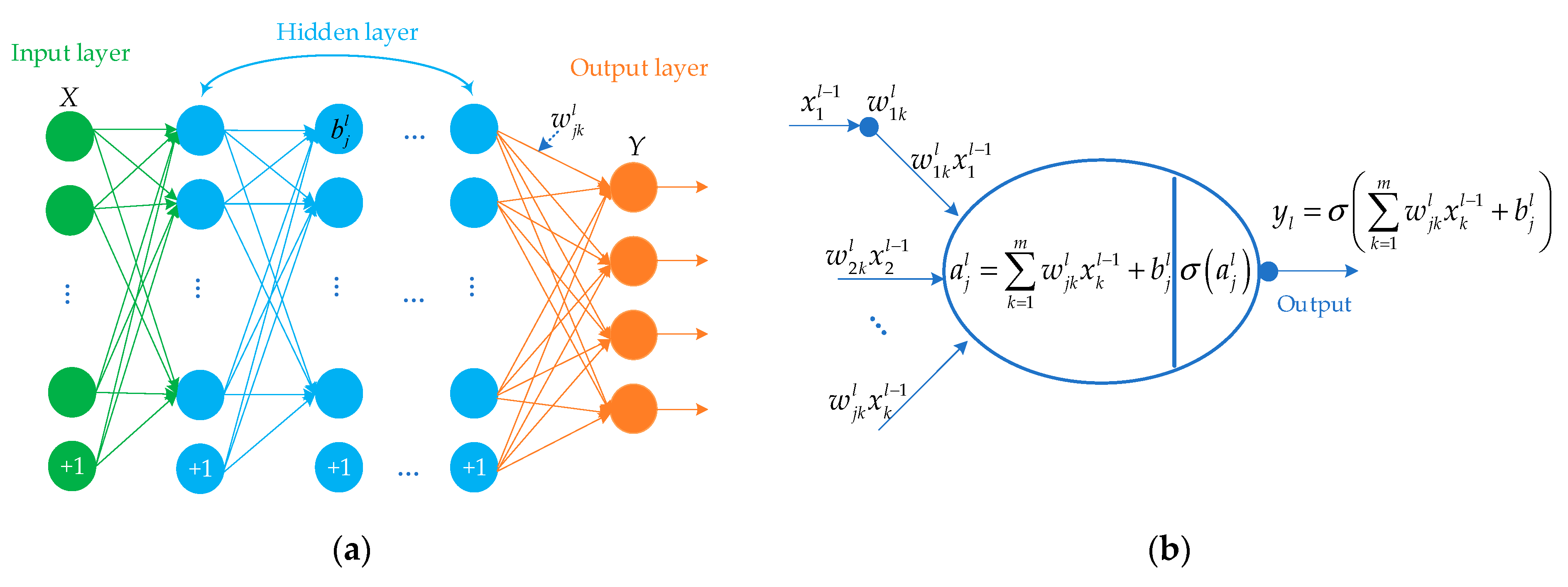
3.2. Deep Neural Network
3.3. Second Order Filter Definition
3.4. Adaptive Control Law Design Based on GTSMC-DNN
- Step 1: guidance subsystem with DNN
- Step 2: overload subsystem with DNN
- Step 3: attitude subsystem with DNN
4. Stability Analysis
5. Simulation Cases and Analysis
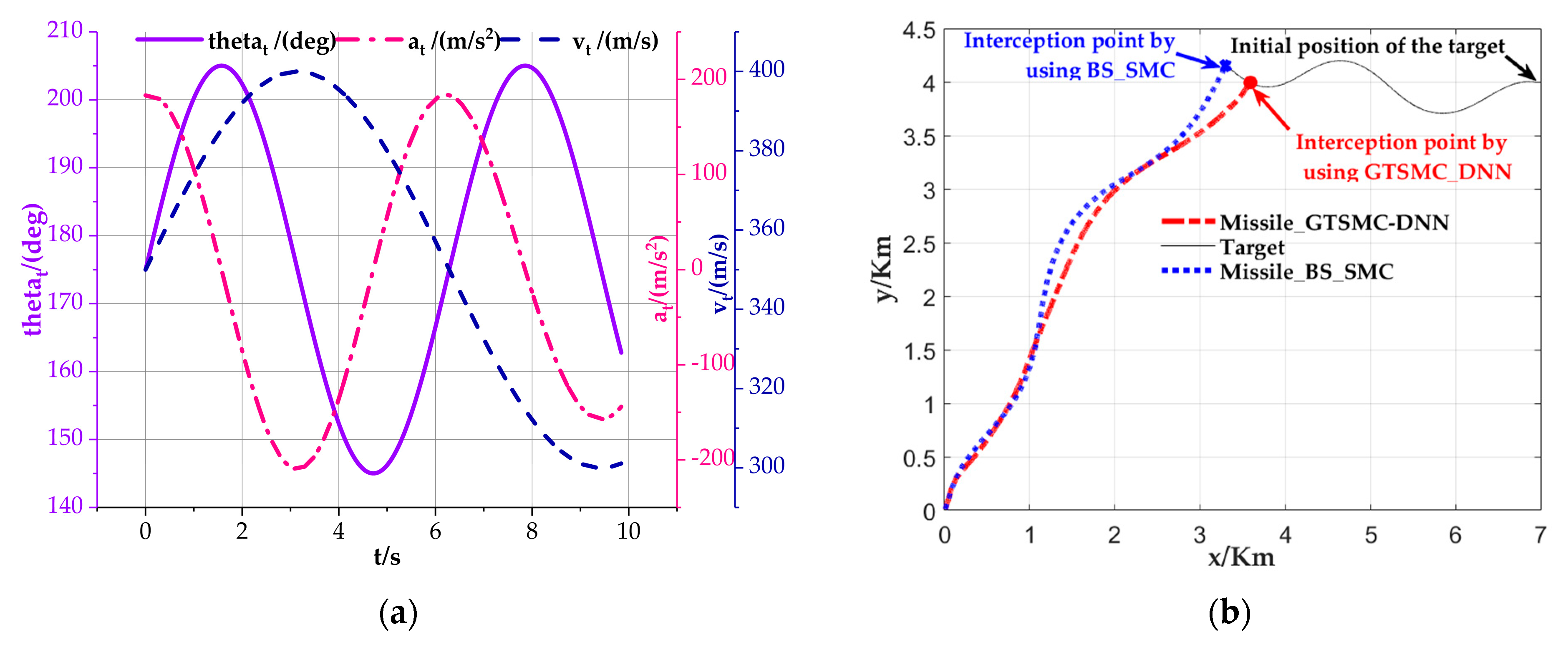
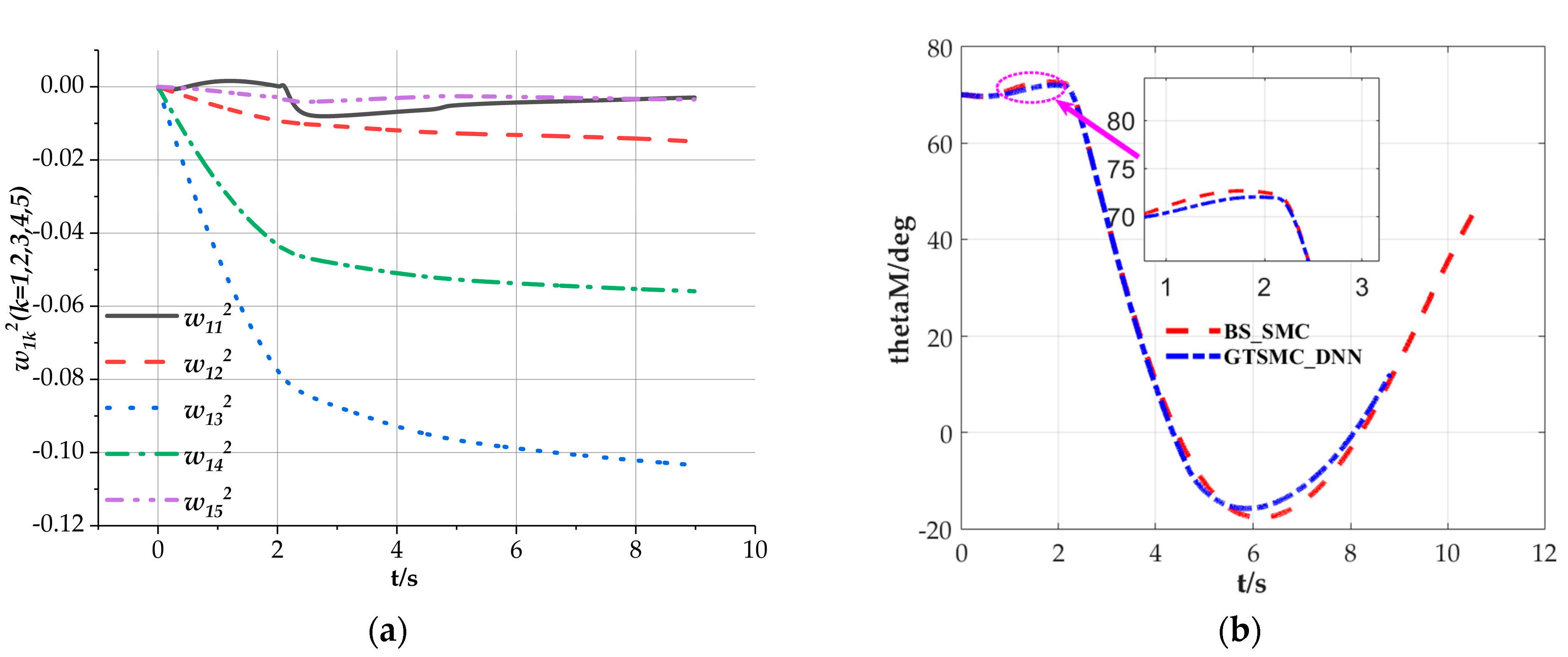
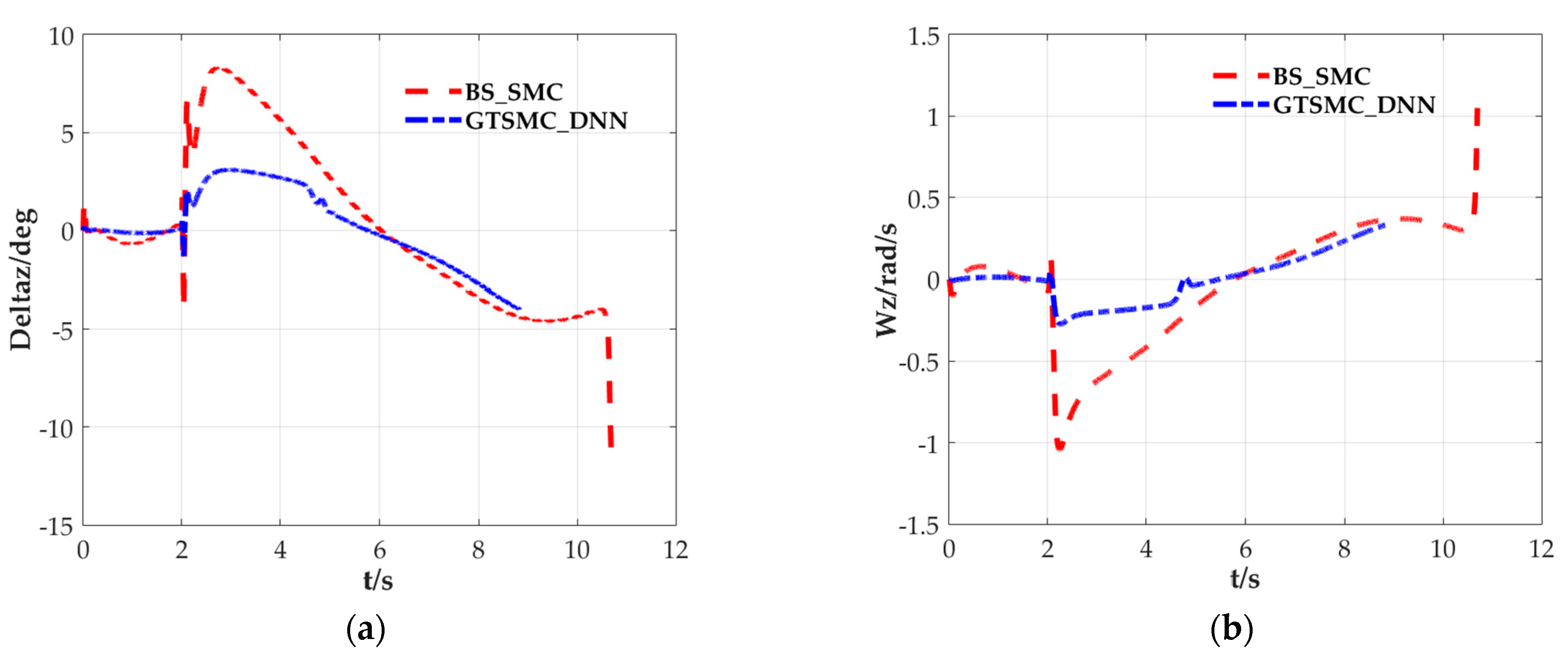
5.1. Case I
5.2. Case II
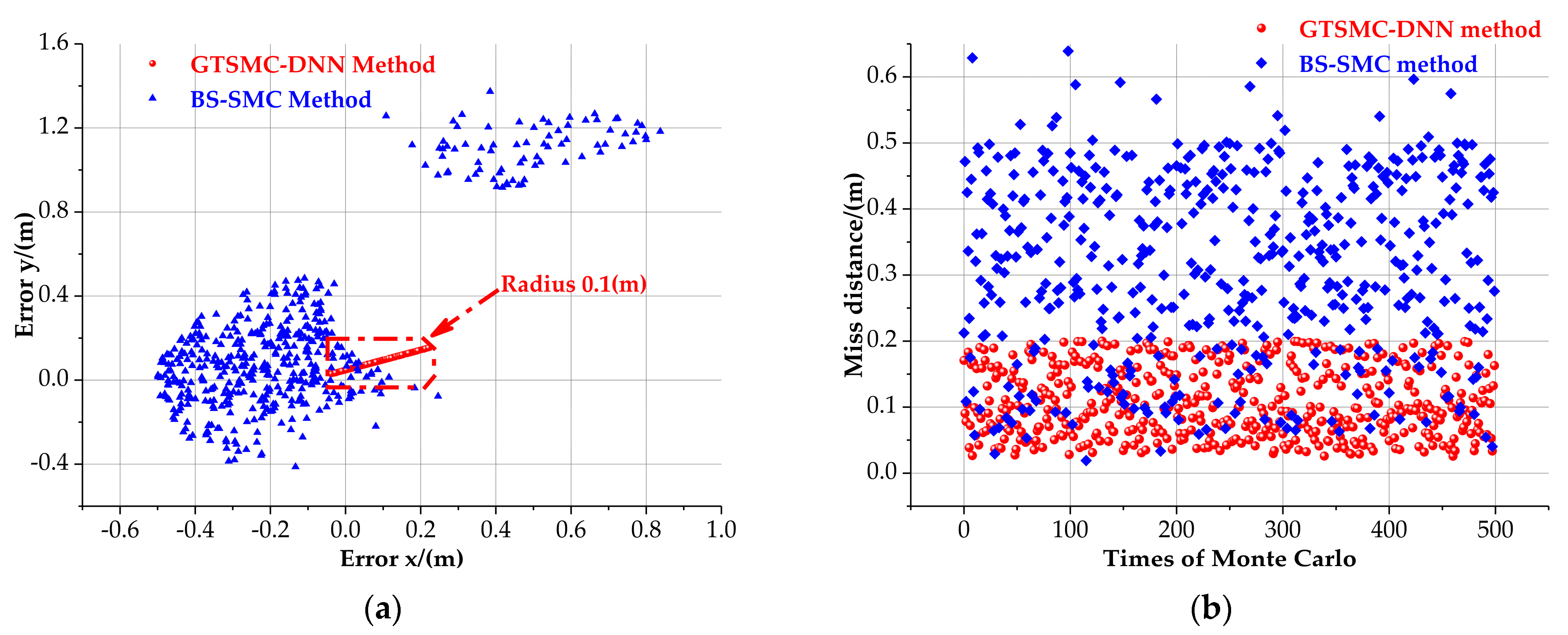
5.3. Case III (Monte Carlo Simulations)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niu, K.; Chen, X.; Yang, D.; Li, J.; Yu, J. A New Sliding Mode Control Algorithm of IGC System for Intercepting Great Maneuvering Target Based on EDO. Sensors 2022, 22, 7618. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.W.; Wang, W.; Fan, J.F.; Ji, Y. Impact angle constraint guidance law using fully-actuated system approach. Aerosp. Sci. Technol. 2023, 136, 108220. [Google Scholar] [CrossRef]
- Guo, J.G.; Xiong, Y.; Zhou, J. A new sliding mode control design for integrated missile guidance and control system. Aerosp. Sci. Technol. 2018, 78, 54–61. [Google Scholar] [CrossRef]
- Santoso, F.; Garratt, M.A.; Anavatti, S.G. State-of-the-art integrated guidance and control systems in unmanned vehicles: A Review. IEEE Syst. J. 2021, 15, 3312–3323. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Lin, D.; Wang, W. Nonlinear Guidance Laws for Maneuvering Target Interception With Virtual Look Angle Constraint. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2807–2822. [Google Scholar] [CrossRef]
- Dong, M.; Xu, X.; Xie, F. Constrained Integrated Guidance and Control Scheme for Strap-Down Hypersonic Flight Vehicles with Partial Measurement and Unmatched Uncertainties. Aerospace 2022, 9, 840. [Google Scholar] [CrossRef]
- Tian, Y.T.; Jing, W.X.; Gao, C.S.; An, R. Adaptive improved super-twisting integral sliding mode guidance law against maneuvering target with terminal angle constraint. Aerosp. Sci. Technol. 2022, 129, 107820. [Google Scholar]
- Garone, E.; Di Cairano, S.; Kolmanovsky, I. Reference and command governors for systems with constraints: A survey on theory and applications. Automatica 2017, 75, 306–328. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Chen, Z.; Wang, T.; Shi, H. Fixed-Time Circular Impact-Time Guidance with Look Angle Constraint. Aerospace 2022, 9, 356. [Google Scholar] [CrossRef]
- Ming, C.; Wang, X.; Sun, R. A novel non-singular terminal sliding mode control-based integrated missile guidance and control with impact angle constraint. Aerosp. Sci. Technol. 2019, 94, 105368. [Google Scholar] [CrossRef]
- Liu, W.; Wei, Y.; Duan, G. Barrier Lyapunov function-based integrated guidance and control with input saturation and state constraints. Aerosp. Sci. Technol. 2018, 84, 845–855. [Google Scholar] [CrossRef]
- Li, K.B.; Liao, X.P.; Liang, Y.G.; Li, C.Y.; Chen, L. Guidance strategy with impact angle constraint based on pure proportional navigation. Acta Aeronaut. Astronaut. Sin. 2020, 41, 79–88. [Google Scholar]
- Wang, C.; Dong, W.; Wang, J.; Shan, J. Nonlinear suboptimal guidance law with impact angle constraint: An SDRE-based approach. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4831–4840. [Google Scholar] [CrossRef]
- Han, T.; Xi, Y.; Chen, G.; Hu, Q. Three-Dimensional Impact Time and Angle Guidance via Controlling Line-of-Sight Dynamics. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 2850–2855. [Google Scholar]
- Chen, Y.; Shan, J.; Liu, J.; Wang, J.; Xin, M. Impact time and angle constrained guidance via range-based line-of-sight shaping. Int. J. Robust Nonlinear Control 2022, 32, 3606–3624. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, W.; Li, J.; Yu, W. Guidance algorithm for impact time, angle, and acceleration control under varying velocity condition. Aerosp. Sci. Technol. 2022, 123, 107462. [Google Scholar] [CrossRef]
- Hu, Q.; Han, T.; Xin, M. Sliding-Mode Impact Time Guidance Law Design for Various Target Motions. J. Guid. Control Dyn. 2019, 42, 136–148. [Google Scholar] [CrossRef]
- Hou, Z.; Yang, Y.; Liu, L.; Wang, Y. Terminal sliding mode control based impact time and angle constrained guidance. Aerosp. Sci. Technol. 2019, 93, 105142. [Google Scholar] [CrossRef]
- Ma, S.; Wang, X.; Wang, Z. Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control. Aerospace 2021, 8, 251. [Google Scholar] [CrossRef]
- Zhou, X.H.; Wang, W.H.; Liu, Z.H. Fixed-time cooperative guidance for multiple missiles with impact angle constraint. J. Aerosp. Eng. 2021, 236, 1984–1998. [Google Scholar] [CrossRef]
- Zhang, W.G.; Yi, W.J.; Guan, J.; Qu, Y. Three-dimensional impact angle guidance law based on robust repetitive control. SN Appl. Sci. 2019, 1, 1–7. [Google Scholar] [CrossRef]
- Kang, S.; Tekin, R.; Holzapfel, F. Generalized impact time and angle control via look-angle shaping. J. Guid. Control Dyn. 2019, 42, 695–702. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S.; Holzapfel, F. Impact Time Control with Generalized-Polynomial Range Formulation. J. Guid. Control Dyn. 2018, 41, 1190–1195. [Google Scholar] [CrossRef]
- Cao, L.F.; Cao, H.S.; Liu, P.F.; Liu, H.; Xiao, Y. Parameter optimization of proportional navigation guidance for 2D trajectory correction projectile with fixed canard. Acta Aeronaut. Astronaut. Sin. 2021, 42, 604–614. [Google Scholar]
- Wang, C.; Yu, H.; Dong, W.; Wang, J. Three-dimensional impact angle and time control guidance law based on two-stage strategy. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5361–5372. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; He, S.; Lee, C.-H. Nonlinear optimal 3-d impact-angle-control guidance against maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2467–2481. [Google Scholar] [CrossRef]
- Lin, L.-G.; Xin, M. Missile guidance law based on new analysis and design of sdre scheme. J. Guid. Control Dyn. 2019, 42, 853–868. [Google Scholar] [CrossRef]
- Kumar, S.R.; Maity, A. Finite-horizon robust suboptimal control-based impact angle guidance. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1955–1965. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R.; Linares, R. Reinforcement learning for angle-only intercept guidance of maneuvering targets. Aerosp. Sci. Technol. 2020, 99, 105746. [Google Scholar] [CrossRef]
- Gong, X.; Chen, W.; Chen, Z. All-aspect attack guidance law for agile missiles based on deep reinforcement learning. Aerosp. Sci. Technol. 2022, 127, 107677. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Wang, X.; Zhang, D.; Jia, J.; Li, Q. Time and FOV constraint guidance applicable to maneuvering target via sliding mode control. Aerosp. Sci. Technol. 2023, 133, 108104. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Wang, X.L. Impact time and angle control optimal guidance with field-of-view constraint. J. Guid. Control Dyn. 2022, 45, 2369–2378. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, F.; Zhang, P. A new three-dimensional fixed time sliding mode guidance with terminal angle constraints. Aerosp. Sci. Technol. 2022, 121, 107370. [Google Scholar] [CrossRef]
- Yang, B.; Jing, W.X.; Gao, C.S. Three-dimensional cooperative guidance law for multiple missiles with impact angle constraint. J. Syst. Eng. Electron. 2020, 31, 1286–1296. [Google Scholar]
- Guo, J.; Li, Y.; Zhou, J. A new continuous adaptive finite time guidance law against highly maneuvering targets. Aerosp. Sci. Technol. 2018, 85, 40–47. [Google Scholar] [CrossRef]
- Lee, S.; Cho, N.; Kim, Y. Impact-time-control guidance strategy with a composite structure considering the seeker’s field-of-view constraint. J. Guid. Control Dyn. 2020, 43, 1566–1574. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Zhou, J. Qualitative indicator-based guidance scheme for bank-to-turn missiles against couplings and maneuvering targets. Aerosp. Sci. Technol. 2020, 106, 106196. [Google Scholar] [CrossRef]
- Wang, X.; Lu, H.; Huang, X.; Yang, Y.; Zuo, Z. Three-dimensional time-varying sliding mode guidance law against maneuvering targets with terminal angle constraint. Chin. J. Aeronaut. 2021, 35, 303–319. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.; Wang, J.; Xin, M. Three-dimensional nonsingular cooperative guidance law with different field-of-view constraints. J. Guid. Control Dyn. 2021, 44, 2001–2015. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y. Capturability of impact-angle control composite guidance law considering field-of-view limit. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1077–1093. [Google Scholar] [CrossRef]
- Hu, Q.; Cao, R.; Han, T.; Xin, M. Field-of-view limited guidance with impact angle constraint and feasibility analysis. Aerosp. Sci. Technol. 2021, 114, 106753. [Google Scholar] [CrossRef]
- Duvvuru, R.; Maity, A.; Umakant, J. Three-dimensional field of view and im-pact angle constrained guidance with terminal speed maximization. Aerosp. Sci. Technol. 2022, 126, 107552. [Google Scholar] [CrossRef]


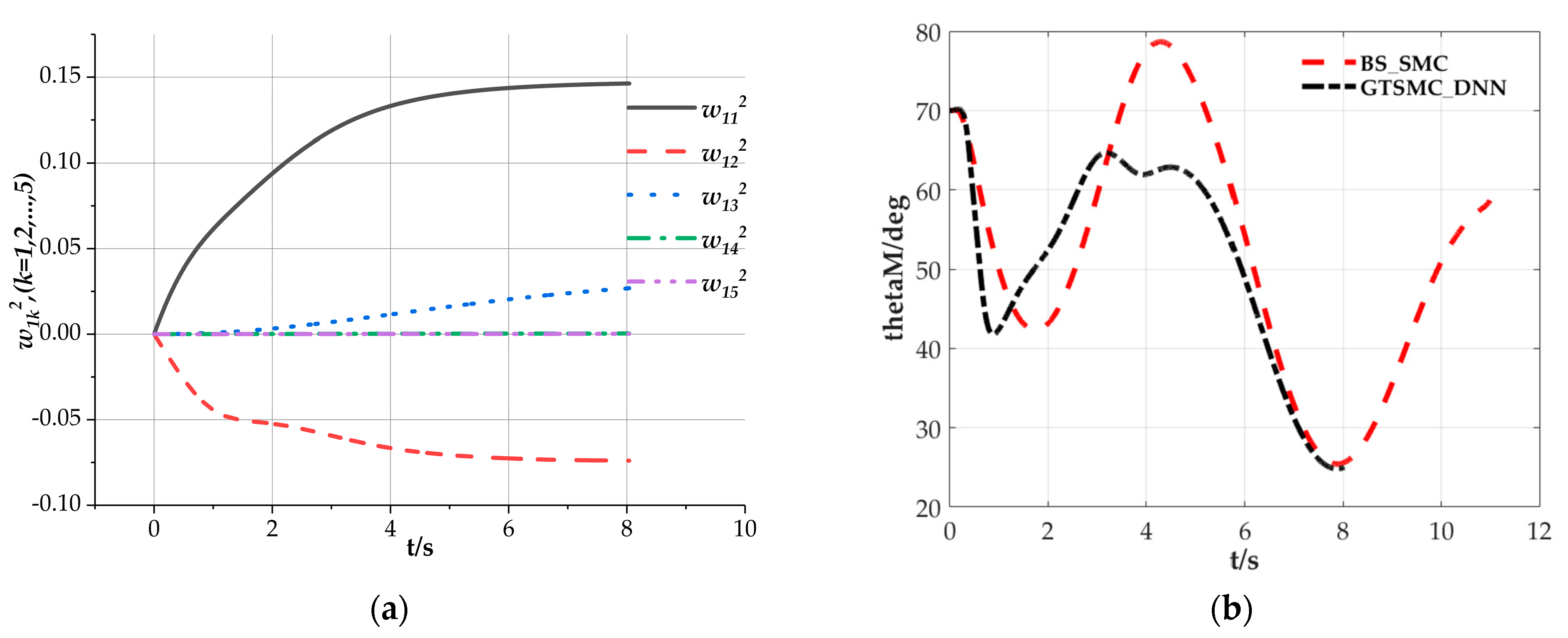
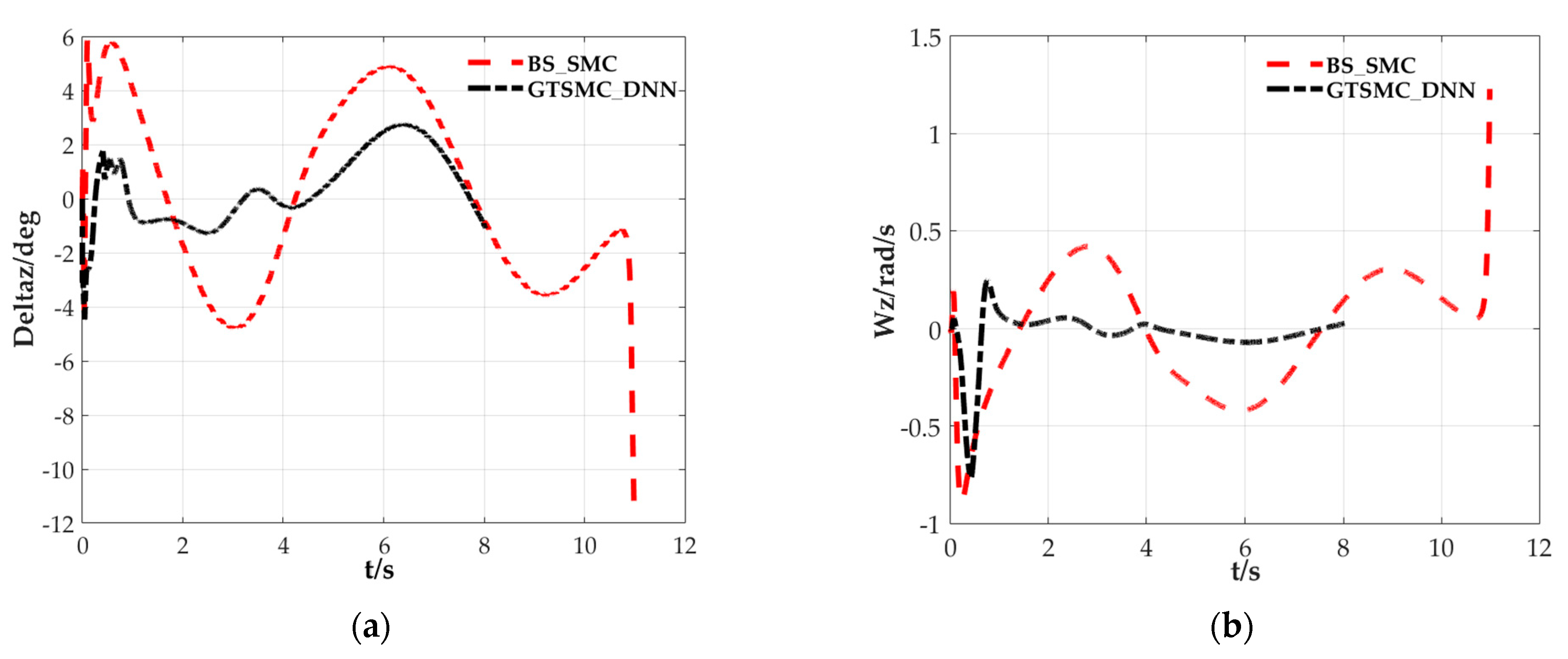
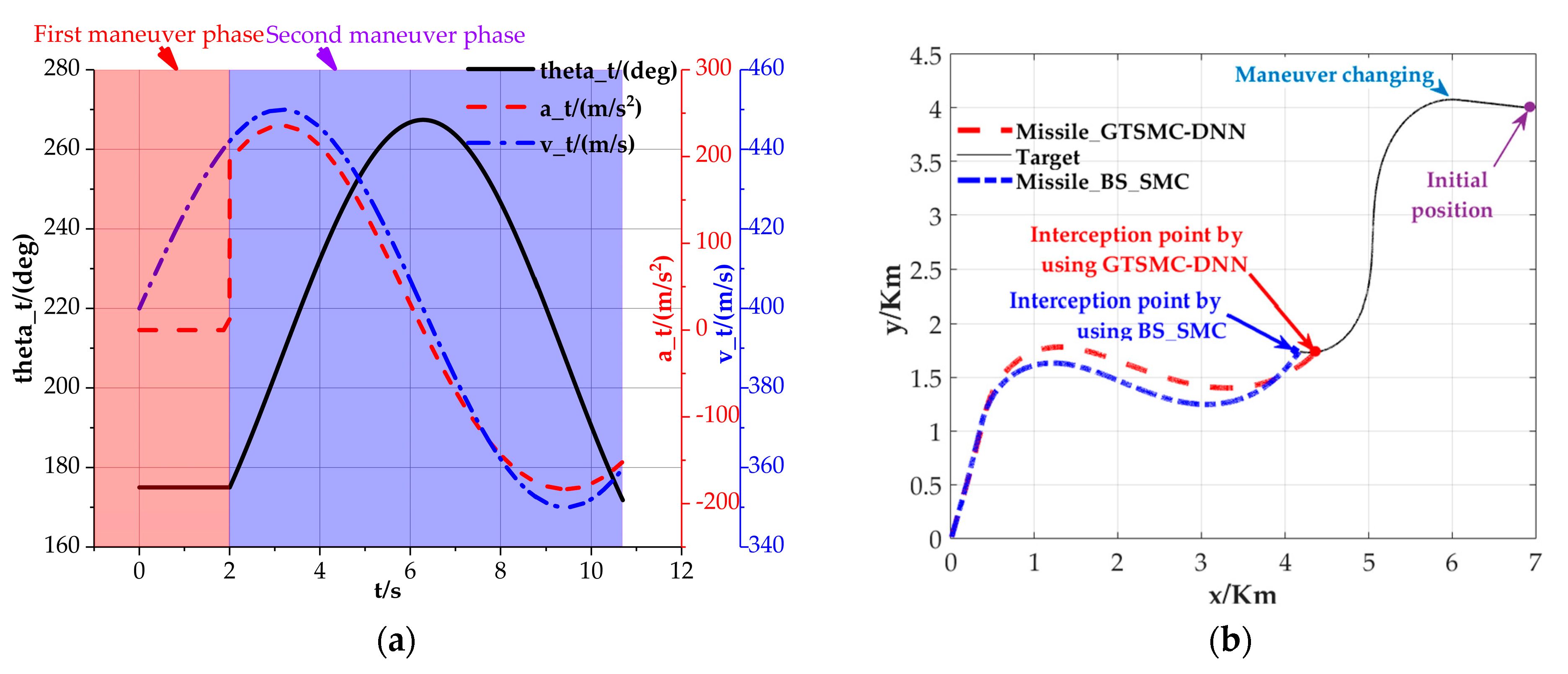
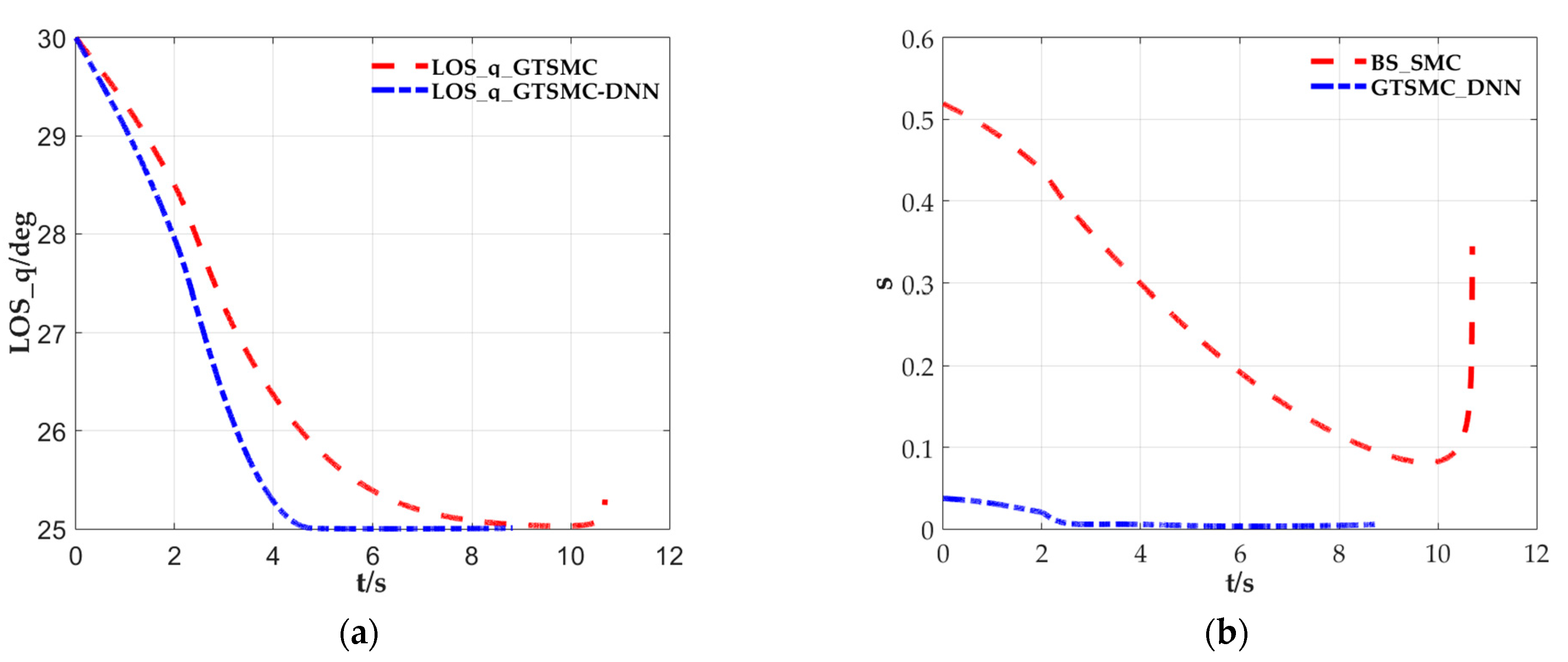
| kl | C3 | C2 |
|---|---|---|
| Item | Initial Value | Unit |
|---|---|---|
| m | ||
| m | ||
| deg | ||
| deg | ||
| m/s | ||
| m/s | ||
| deg | ||
| deg |
| Item | GTSMC-DNN | BS-SMC | Unit |
|---|---|---|---|
| Miss distance of M-T | 0.257 | 2.207 | m |
| Terminal LOS | 25.126 | 25.754 | deg |
| Symbol | Quantity | Values |
|---|---|---|
| flight path angle of missile | ||
| LOS | ||
| velocity of the missile | ||
| the rate of pitch angle | ||
| Initial position in x | ||
| Initial position in y | ||
| pitch angle | ||
| Initial position in x | ||
| Initial position in y | ||
| velocity of the T | ||
| flight path angle of T | ||
| acceleration of T | ||
| rudder deflection |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, K.; Bai, X.; Chen, X.; Yang, D.; Li, J.; Yu, J. A New Adaptive Control Algorithm of IGC System for Targets with Several Maneuvering Modes Based on GTSMC-DNN. Aerospace 2023, 10, 380. https://doi.org/10.3390/aerospace10040380
Niu K, Bai X, Chen X, Yang D, Li J, Yu J. A New Adaptive Control Algorithm of IGC System for Targets with Several Maneuvering Modes Based on GTSMC-DNN. Aerospace. 2023; 10(4):380. https://doi.org/10.3390/aerospace10040380
Chicago/Turabian StyleNiu, Kang, Xu Bai, Xi Chen, Di Yang, Jiaxun Li, and Jianqiao Yu. 2023. "A New Adaptive Control Algorithm of IGC System for Targets with Several Maneuvering Modes Based on GTSMC-DNN" Aerospace 10, no. 4: 380. https://doi.org/10.3390/aerospace10040380
APA StyleNiu, K., Bai, X., Chen, X., Yang, D., Li, J., & Yu, J. (2023). A New Adaptive Control Algorithm of IGC System for Targets with Several Maneuvering Modes Based on GTSMC-DNN. Aerospace, 10(4), 380. https://doi.org/10.3390/aerospace10040380






