Abstract
Morphing wings are a typical application of shape-adaptive structures in aviation, which play an important role in improving the comprehensive performance of an aircraft. However, traditional morphing wings based on purely mechanical, rigid-flexible coupling, or purely flexible structures usually cannot achieve a distributed morphing ability and have limitations in weight, intelligence level, and reliability. In this paper, a distributed morphing lattice structure based on variable geometry digital metamaterials is proposed. The innovative structural concept consists of three types of fundamental cells featuring remarkably different mechanical properties and three other types of derived cells. One type of the derived cells embedded with micro-actuators, named an active cell, can autonomously extend or contract. All these cells can be reversibly assembled in a random sequence to form an active distributed morphing lattice structure with the ability to realize different target aerodynamic contours. In addition, taking a simplified variable thickness wing as a designing case, this paper develops a cell combination optimization methodology on the basis of a heuristic algorithm to determine the optimal combination sequence of the six types of basic cells and the actuator inputs of active cells collaboratively. Final results show that the optimized lattice structure can morph its outer surface into a predefined aerodynamic contour with a maximum deviation of 3 mm.
1. Introduction
Shape-adaptive structures can improve the performance of both macroscale and microscale structures because they can alter their structural shape actively according to its working environment [1,2], especially in the fields of aviation [3,4,5,6], aerospace [7], and micromachines [8]. Among them, morphing wings are a typical application of shape-adaptive structures in the aviation field, which can effectively reduce aerodynamic drag and noise and improve the maneuvering performance of an aircraft.
The biggest challenge of morphing wing design is to develop an actively deformable structure which can meet the demands of large deformability and high load-bearing capacity. To solve these issues, a large number of structure concepts and design methods have been proposed, and some positive progress has been achieved, as illustrated in the literature reviews [9,10,11,12,13]. In general, these proposed concepts can be summarized into three categories: purely mechanical type, rigid-flexible coupling type, and purely flexible type. The purely mechanical morphing wings are mainly realized merely through the relative rotation or sliding of its rigid mechanical parts [14,15,16]. The rigid-flexible morphing wings always passively deform a one-piece compliant skin through an internal rigid mechanism to coordinate the high load-bearing ability and the large deformability [4,17,18,19,20,21,22,23]. The purely flexible morphing wings otherwise morph by a pure elastic deformation of a one-piece compliant structure under an internal centralized actuator [14,24,25,26,27,28]. However, these three types generally cannot achieve a revolutionary change in weight and sometimes even offset the aerodynamic advantages due to their excessive weight [3,29,30]. Most important of all, most of these existing concepts possess only a single deformable degree of freedom, which means they can only transform from a certain aerodynamic state to another rather than realize multiple accurately distributed morphed shapes [3].
With the maturity of lattice structures and additive manufacturing technologies, a morphing wing based on ultra-light lattice is expected to solve these issues [31,32,33]. For instance, Alsaidi et al. [34] developed an active twist wing with lattice structures, which greatly improved the aerodynamic and maneuvering performance of a UAV. However, as a one-piece lattice structured is adopted, the concept is limited by the additive manufacturing equipment size and is difficult to be extensively applied for large-scale aircraft. However, digital metamaterials are extremely suitable for the manufacturing and assembling of a large-scale structure due to their building-block feature [35]. Cheung et al. [3] firstly proposed the concept of digital morphing wings based on a digital metamaterial consisting of uniform octahedral voxels and realized an actively torsional morphing through a single torsion carbon tube. On this basis, Zhang et al. [36] proposed a digital morphing wing with the same octahedral cells but varied its cell density; they also used a torsion tube as its actuator. These research works shows that morphing wings based on digital metamaterials can better meet the demands of lightweight, active deformability and scalability, and has great application potential in engineering. However, within all these concepts, uniform cells and one single actuating degree of freedom are used. This will limit its performance to a great extent, although it can reduce its manufacturing complexity in some extent. On one hand, there are a wide range of flight conditions within the overall envelop of an aircraft, and different conditions correspond to distinctly different aerodynamical shapes, which requires a morphing wing to have multiple actuating degrees of freedom distributed in the whole structure; on the other hand, in actual engineering, one specific morphed shape needs to be identical to the optimal one at every single point on the overall aerodynamic surface, especially for a laminar flow wing [37], which means the deformability should be executed in a distributed way and the stiffness distribution should be optimized subtly. These two requirements imply that the design degrees of freedom of a digital morphing wing should be as many as possible. However, if a uniform cell is used, as shown in the existing literature, the deformability would be limited severely and the advantages of the digital metamaterial cannot be fully exploited [35]. Conversely, if a digital metamaterial with varied cell geometries is utilized and intelligent cells are embedded in a morphing wing, the design degrees of freedom will be significantly expanded, and an arbitrary aerodynamic shape is expected to be achieved.
Therefore, this paper proposes a morphing wing concept based on distributed active lattice structures with varied cell geometries in Section 2. Additionally, the building-block concept, fundamental cells and derived cells, and a reversibly assembled method of the active morphing lattice structure are presented in detail. Next, considering a variable thickness wing as a design case, a collaborative optimization method based on a heuristic algorithm is illustrated in Section 3 to validate the reasonability of the proposed concept. Finally, some conclusions are presented, and the advantages and disadvantages of the innovative concept are discussed in Section 4.
2. Reversibly Assembled Active Morphing Lattice Structures
2.1. Building-Block Concept
As aforementioned, an ideal morphing structure should be able to accurately realize multiple aerodynamic shapes or even an arbitrary one. This feature can be further interpreted as distributed deformability and accurate deformability. Distributed deformability means that a structure can be deformed into a target contour in a wide surface area, which requires a customized design of its structural stiffness distribution. Accurate deformability means that the structure can be deformed into a target contour exactly at every single point on the surface, which requires as many active degrees of freedom as possible.
Therefore, a building-block concept is utilized to develop the active morphing lattice structure. As shown in Figure 1, the design workflow based on the building-block concept is firstly to extract the design area and then configure and assemble the basic cells through a reversible assembly manner. In this paper, the building-block structure consists of five types of passive cells and one type of active cell. Among the passive cells, three types are fundamental cells. The other two types together with the active cell constitute the derived cells. With different combination sequences, the building-block structure can possess different mechanical property distributions. Actuated by the embedded active cells, passive cells can be driven and obtain a target outer surface shape predefined by aerodynamic calculations.
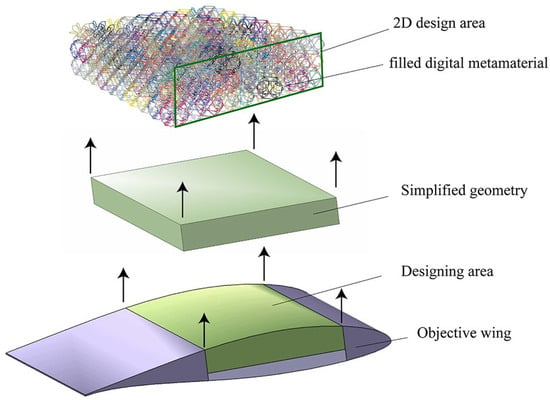
Figure 1.
Schematic diagram of variable thickness wing based on digital metamaterial with varied cell geometries.
To validate the rationality of this concept, a variable thickness wing design will be taken as an example, as shown in Figure 1. Without affecting the generality of the design method, the variable thickness area of the wing will be simplified into a cuboid structure filled with digital metamaterials. Ignoring the influence of the wingtip-to-root ratio of the three-dimensional wing, the structural design problem can be further simplified into a two-dimensional problem, as shown in Figure 2, where the red curve is the target aerodynamic profile and the blue one is the initial aerodynamic profile. The design objective is to determine the optimal cell configuration so that the upper surface of the digital metamaterial can be actively morphed into the red target one under a specific actuator signal. In the initial phase, considering the minimal size limitation of the micro-motor in the active cell, 11 cells along the horizontal axis and 3 cells along the vertical axis are arranged, with a cell size of 75 mm. The detail of the active cell is presented in Section 2.3.
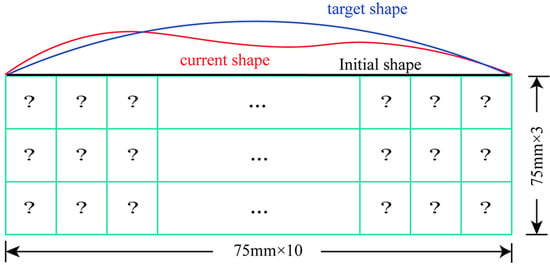
Figure 2.
Two-dimensional schematic diagram of the design of the distributed variable thickness structure based on digital metamaterials.
2.2. Fundamental Cells
To extend the design degrees of freedom, the combination of elementary cells should produce mechanical property distributions as diverse as possible. However, to reduce processing complexity, the number of basic cell types should be kept as small as possible. Therefore, three types of fundamental cells with distinctly different mechanical properties are constructed, as shown in Figure 3: rigid cell, compliant cell, and auxetic cell. The larger the difference in the mechanical properties of the fundamental cells, the richer the distribution of mechanical properties that can be produced through altering their combination sequence in space. Relevant studies have shown [36] that the rigid cell, as shown in Figure 3, is subjected mainly to a tensile and compressive deformation of the beams during a deformation process, and it has a high elastic modulus and positive Poisson’s ratio, while the compliant cell transmits load mainly through the elastic deformation of the plane-bending beams, and the Poisson’s ratio is close to 0. However, the auxetic cell transfers its load through the bending deformation of its curved beams, which features a negative Poisson’s ratio. Therefore, from the perspective of the stiffness and Poisson’s ratio, it can be qualitatively considered that the mechanical properties of these three cells are quite different.
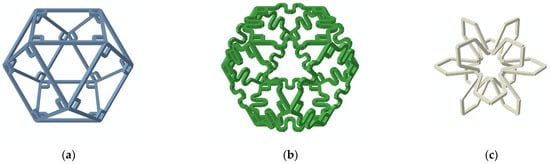
Figure 3.
Three types of fundamental cells: (a) Rigid cell; (b) Compliant cell; and (c) Auxetic cell.
To quantitatively understand its deforming mechanism and verify the aforementioned conclusions, the stiffness and Poisson’s ratio of the three types of fundamental cells are analyzed through a parametric finite element analysis. The analysis result can further provide some guidance for the selection of the specific geometric parameters of each type of cell. In engineering, the Euler–Bernoulli beam theory is relatively commonly utilized [36] and is quite suitable for the compliant and auxetic cells featured with bending deformation. In the lattice structure, the cell edges connected between vertexes are simplified as a range of beam elements, and each beam element has 12 degrees of freedom. As shown in Equation (1), by superposing each sub-stiffness matrix together, the overall stiffness matrix of the structure can be generated. After displacement and force boundary conditions are applied, a nonsingular numerical model of the structural analysis problem can be obtained by eliminating the matrix rows and columns corresponding to the fixed boundary conditions. It is worth noting that the compliant and auxetic cells have a large bending deformation. Thus, the geometric nonlinear effect must be considered in the analysis, which can be solved by an iterative method, although this will increase its computational complexity.
where is the nonlinear stiffness matrix related to displacement; is a node displacement vector; is the corresponding sub-stiffness matrix of non-free nodes; is the corresponding sub-stiffness matrix of the free nodes; is the crossing stiffness submatrix; is the displacement of non-free nodes; is the displacement of free nodes; and is the nonlinear force vector related to the displacement vector.
In fact, to obtain the macro scale material property of a lattice structure, periodic boundary conditions are generally utilized to simply its analysis model, for instance, as shown in Z. WANG’s work [38]. However, as presented in Section 2.1, the possible final lattice of a variable thickness wing would likely not be combined by homogeneous unit cells, which means it would not be an isotropic lattice. For a certain type of unit cell, it may or may not be separated by the other types, and the number of the consecutive identical cells are different. Therefore, except for the macro property, it is also necessary to examine the relationship between the macro property of the lattice and its unit cell number. Therefore, this paper does not utilize periodic boundary conditions to analysis the lattice. Furthermore, as found by Z. WANG et al. [38], an anisotropic transition may occur if large displacement exists in a lattice. However, in the morphing wing concept proposed here, the number and driving displacement of the active unit cells can be adjusted or constrained to avoid too large local displacement. Therefore, in this paper the anisotropic transition problem is neglected, and it will also not influence the subsequent optimization design. Figure 4 presents the final analysis models of the macro mechanical properties of the three types of fundamental cells. In all these models, a fixed boundary condition is applied on their bottom surfaces and a compressed load on their upper surfaces. To simplify the load condition, as shown in Figure 4, the points of action are coupled with all their nodes on the upper surfaces. Convergence analysis of the mesh size shows that the mechanical properties of one single cell no longer change when the mesh size is less than 3.7 mm. Therefore, the mesh size of the three types of cells is set to 3.7 mm. Regarding its manufacturing process, a type of durable resin material developed by FormLabs® is selected here. This material can be additively manufactured through a stereo-lithography process, which has a good fatigue property and a high machining accuracy. Considering the curing process, its specific mechanical properties are shown in Table 1.
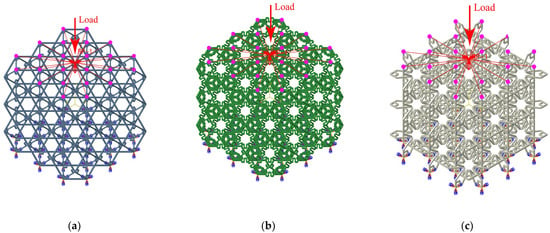
Figure 4.
The finite element models of the three types of fundamental cells for macro-mechanical performance analysis, for instance, with 3 × 3 × 3 unit cells: (a) Rigid lattice; (b) Compliant lattice; and (c) Auxetic lattice.

Table 1.
Mechanical property parameters of the material.
2.2.1. Rigid Cell
The deformation mechanism diagram and its geometric parameter are shown in Figure 5. As its cell size is predefined as 70 mm, there remains only one variable geometric parameter, namely the thickness of the cross section of its square beams. From the diagram it can be seen that the straight beams can withstand an external force effectively through tensile-dominated deformation, which causes the rigid cell to have a positive Poisson’s ratio. Figure 6a presents the relationship between the elastic modulus and the number of rigid cells (n × n × n) with different beam section sizes (t = 0.5 mm, 1.5 mm, 2.5 mm, 3.5 mm, and 4.5 mm), and it shows that the elastic modulus depends heavily on the beam section size and increases with the increase of it. When the number of the cells is 5 × 5 × 5 and the beam size 4.5, the elastic modulus can reach 9.34 Mpa, equivalent to some engineering continuous polymers. However, Figure 6b shows that its Poisson’s ratio is almost unaffected by the beam section size and is stable at approximately positive 0.4. These results verify the aforementioned conclusion about the high stiffness and positive Poisson’s ratio of the rigid cell. Therefore, the rigid cells can be distributed at some locations where small deformation is permitted and high stiffness material is needed.
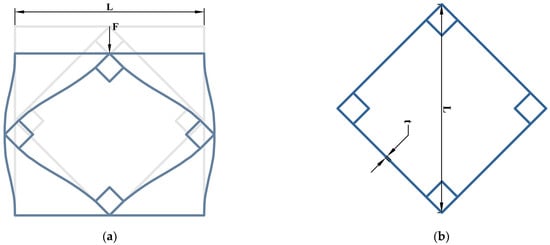
Figure 5.
The deformation mechanism diagram and geometric parameter of the rigid unit cell: (a) Deformation mechanism of the rigid cell under an external load; (b) The beam section size of the rigid cell (L = 70 mm).
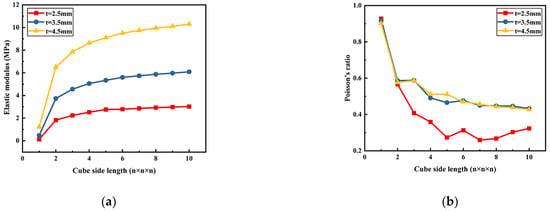
Figure 6.
Mechanical properties of the rigid lattice. (a) The relationship between the elastic modulus and the cube side length of the rigid lattice (t = 2.5–4.5 mm); (b) The relationship between the Poisson’s ratio the cube side length of the rigid lattice (t = 2.5–4.5 mm).
2.2.2. Compliant Cell
As shown in Figure 3b, the compliant cell consists of six quadrilateral face elements, each consisting of four S-shaped beams. Figure 7a illustrates the deformation mechanism of the complaint unit cell. It also shows that the S-shaped beams suffer plane-bending deformation under an external load and feature a nearly zero Poisson’s ratio. If the cell size is constrained, the remaining geometric parameters of the compliant cell include the width of the S-shaped bulge, the height of the S-shaped bulge, and the beam section size.
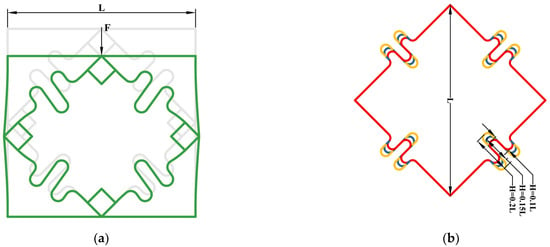
Figure 7.
The deformation mechanism diagram and one of the geometric parameters of the compliant unit cell: (a) Deformation mechanism of the compliant cell under an external load; (b) Different S-shaped bulge heights of the compliant cell (L = 70 mm).
As shown in Figure 7b, we first investigate the relationship between the mechanical properties and the height of the S-shaped bulge. The height varied from H = 0.1 L to H = 0.2 L, and the beam section size and the width of the S-shaped bulge is constrained as 2.5 mm × 2.5 mm and 0.05 L, respectively. Figure 8 presents the influence of the height on the elastic modulus and Poisson’s ratio of the macro-lattice. It can be seen that as the height of the S-shaped bulge increases, the elastic modulus value decreases reversely. This indicates that increasing the height is beneficial to improving the deformation ability of the compliant cell. Meanwhile, the elastic modulus value barely changes with the increase of the cell numbers (n × n × n). This phenomenon can be attributed to the spring-like behavior of the curve beams, for both the effective area and the parallel spring number of the whole lattice are proportional to the square of the side length (n × n × n). By comparing the rigid and compliant results, we can see that the elastic modulus of the compliant cell is one order of magnitude smaller than that of the rigid one, which also verifies the above conclusion that the deformation ability of compliant cells is relatively large. Figure 8b presents the change of Poisson’s ratio under different heights of the S-shaped bulge. It can be seen that with the increase in the height of the S-shaped bulge, the Poisson’s ratio decreases close to zero.
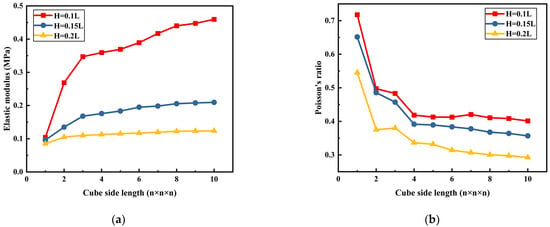
Figure 8.
Mechanical properties of the compliant lattice with different S-shaped heights: (a) The relationship between the elastic modulus and the cube side length (with H = 0.1–0.2 L); (b) The relationship between the Poisson’s ratio and the cube side length (with H = 0.1–0.2 L).
Furthermore, the influence of different widths of the S-shaped bulge and beam section sizes on its mechanical properties is also analyzed parametrically here. Figure 9 illustrates the schematic diagram of different widths of the S-shaped bulge and beam section size of the compliant cell. Figure 10a,b present the elastic modulus curve and the Poisson’s ratio curve of the compliant lattice as the S-shaped beam widths changes from W = 0.05 L to W = 0.09 L, with a beam section size of 2.5 mm × 2.5 mm and a height of the S-shaped bulge of 0.2 L. Figure 10c,d show the influence of different beam sizes (t = 0.5 mm, 1.5 mm, 2.5 mm, 3.5 mm, and 4.5 mm) on its elastic modulus and Poisson’s ratio with a S-shaped width of 0.07 L. It can be seen that the elastic modulus of the lattice is greatly affected by the width of the S-shape bulge and the beam section size. Increasing the width of the S-shape bulge and decreasing the beam size will lead to a decrease in the elastic modulus, which can improve the deformation ability of the whole lattice. This is mainly because as the width of the S-shape increase and the beam size decrease, the bending deformation of the curved beam dominates more than the stretching one. The results also show that the Poisson’s ratio of compliant cells has little relationship with the width of S-shaped bulge width and the beam section size, and the Poisson’s ratio value is close to zero as the cell number of the lattice continues to increase.
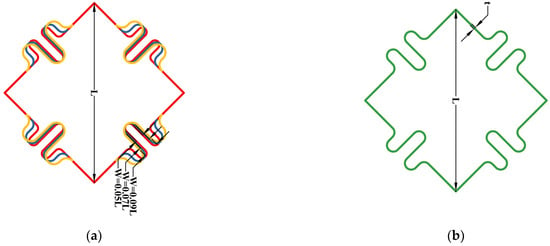
Figure 9.
Schematic diagram of different geometric parameters of the S-shaped bulge of the facet element of the compliant cell: (a) different widths of the S-shaped bulge; (b) schematic of the beam section size of the compliant cell.
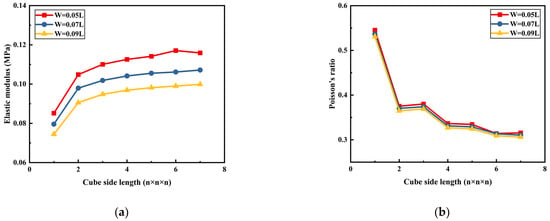
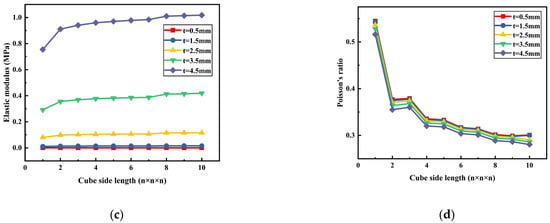
Figure 10.
Mechanical properties of compliant lattice with different S-shaped bulge widths and beam section sizes: (a) The relationship between the elastic modulus and the cube side length (W = 0.05–0.09 L); (b) The relationship between the Poisson’s ratio and the cube side length (W = 0.05–0.09 L); (c) The relationship between the elastic modulus and the cube side length (t = 0.5–4.5 mm); and (d) The relationship between the Poisson’s ratio and the cube side length (t = 0.5–4.5 mm).
2.2.3. Auxetic Cell
Figure 11 illustrates the deformation mechanism diagram and different geometric parameters of the auxetic unit cell. It can be seen that the auxetic cell withstands its external load through out-of-plane bending of its curve beams, which causes the auxetic cell to feature a negative Poisson’s ratio. Regarding its specific geometry, if the cell length is constrained as 70 mm, there remain two geometric parameters, which are beam section size and concave depth, as shown in Figure 11b,c. Figure 12a,b show the influence of different concave depths (d = 0.1 L, 0.2 L, 0.3 L, and 0.4 L) on the elastic modulus and Poisson’s ratio of the auxetic cells with a fixed beam section size of 2.5 mm × 2.5 mm. It shows that the elastic modulus and Poisson’s ratio of the lattice decreases rapidly with the increase of the concave depth. Figure 12c,d present the influence of different beam section sizes (t = 0.5 mm, 1.5 mm, 2.5 mm, 3.5 mm, and 4.5 mm) on the elastic modulus and Poisson’s ratio of the auxetic cell with a fixed concave depth of 0.4 L. The results show that with the increase in beam section size, the elastic modulus becomes higher. However, its Poisson’s ratio changes with an opposite trend. In addition, it can be seen that Poisson’s ratio of auxetic cells is negative overall. This means that the feature of a negative Poisson’s ratio becomes increasingly more obvious.
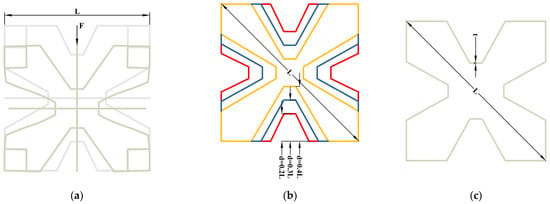
Figure 11.
The deformation mechanism diagram and different geometric parameters of the auxetic unit cell: (a) Deformation mechanism of the auxetic cell under an external load; (b) Different concave depths of the auxetic cell (L = 70 mm); (c) Shematic diagram of the beam section size of the auxetic cell.
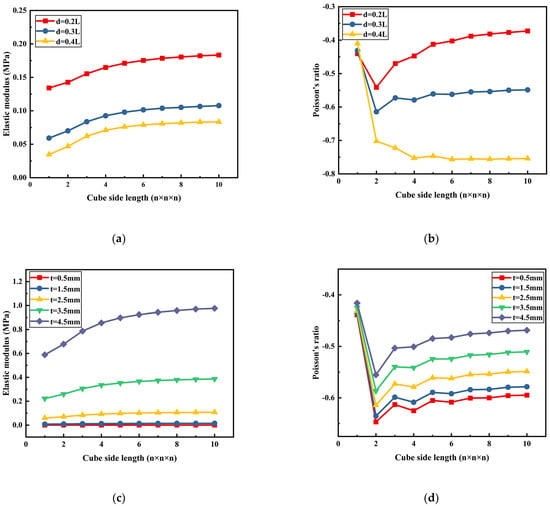
Figure 12.
Mechanical properties of the auxetic lattice: (a) The relationship between the elastic modulus and the cube side length (d = 0.2 L~0.4 L); (b) The relationship between the Poisson’s ratio and the cube side length (d = 0.2L~0.4 L); (c) The relationship between the elastic modulus and the cube side length (t = 0.5 mm~4.5 mm); and (d) The relationship between the Poisson’s ratio and the cube side length (t = 0.5 mm~4.5 mm).
In summary, several conclusions can be drawn. (1) The rigid cell has the highest elastic modulus among the three types and, overall, features a positive Poisson’s ratio. (2) The elastic modulus of the compliant cell is related to several geometric parameters, but it is generally one order of magnitude lower than that of the rigid cell, and Poisson’s ratio of the compliant cell is generally close to zero. (3) The elastic modulus of the auxetic cell is in the same order of magnitude as that of the compliant cell, but the Poisson’s ratio is negative. (4) The Poisson’s ratio of compliant cells decreases with the increase of the height of the S-shaped bulge, but it is not affected by the width of the S-shaped bulge and beam section size. (5) The elastic modulus of the rigid cell is heavily dependent on the beam section size, and it also shows an increasing trend with the increase of cell size.
The above conclusions confirm the previous claim that rigid, compliant, and auxetic cells have quite different mechanical properties, which means that different combinations of these three types of cells may produce various mechanical property distributions. Moreover, it proves the rationality of utilizing these three types of cells as fundamental cells.
2.3. Derived Cells
To further expand the design degrees of freedom and develop an active lattice structure, three other types of derived cells are constructed creatively in this paper. Generally, some local positions of the shape-adaptive structure (such as the surface) usually need to achieve an elongation deformation in only one direction, while it is not expected in the other. In this case, we need a single-direction tensile cell to make the structure more efficient. However, in the other case, some local area of the shape adaptive structure basically has no tensile deformation, and only a bending ability is needed. Therefore, it is also necessary to construct a pure bending cell.
By examining the geometries and deformation features of the rigid cell and compliant cell, it can be found that combining the elements of the rigid cell and compliant cell can just achieve the tensile cell and the bending cell, as shown in Figure 13. As the S-shaped beams are arranged along the vertical direction, the tensile cell possesses high tensile ability along the vertical direction but low ability along the horizontal direction. However, regarding the bending cell, all facet elements along the vertical direction are constituted by straight beams, which cause the cell to have a bending deformation feature.
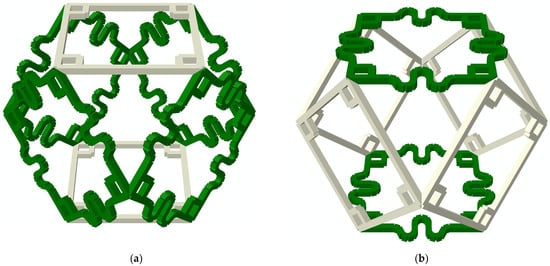
Figure 13.
Two types of derived passive cells: (a) Tensile cell; (b) Bending cell.
As for the active cell, it must have the ability to produce a large deformation during a driving process, and it needs to have a uniform assembly interface with other cells to ensure modularity. The above analysis shows that the compliant cell has large deformation ability and can meet the requirements well. Therefore, on the basis of the compliant cell, an active cell embedded with smart actuators can be developed. As a preliminary demo, the driving displacement of the active cell is produced by a micro-electric motor in this paper. The micro-actuator is developed by Shaoteng company, Changzhou, China (12V, LA-T8-12-15). With the maturity of smart materials and 4D printing technology, we will integrate smart materials (such as shape memory alloys, shape memory polymers, piezoelectric materials with displacement amplification, etc.) into the active cells in the future to truly realize an intelligent digital metamaterial.
Specifically, Figure 14 shows the assembly process of an active cell. In the active cell, a driving motor and a chip circuit are integrated and connected by two solid pads at both ends. Similar to a compliant cell, the active cell has zero Poisson’s ratio in the direction perpendicular to the driving displacement, which helps to achieve a pure extending driving in a single direction. Figure 15 shows the schematic diagram of the active cell before and after deformation.
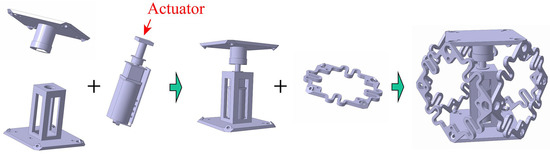
Figure 14.
Assembly process of an active cell embedded with a micro-actuator.
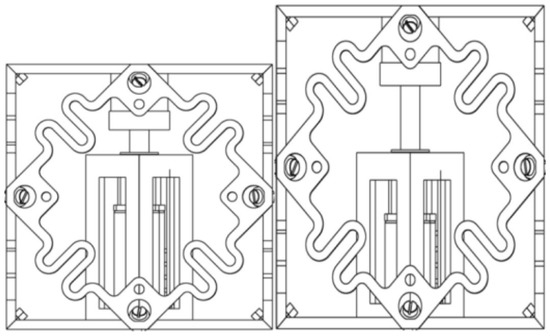
Figure 15.
Schematic diagram of the active cell with different excitement signal.
To simulate the active cell in the subsequent optimization process, an axial connector element, as shown in Figure 16, is adopted in this paper. A relative translation along the axis direction can occur between Reference Point 1 and Reference Point 2, and the driving displacement is the value of the relative displacement. The two reference points are connected further with four corner nodes through four coupling connector elements.
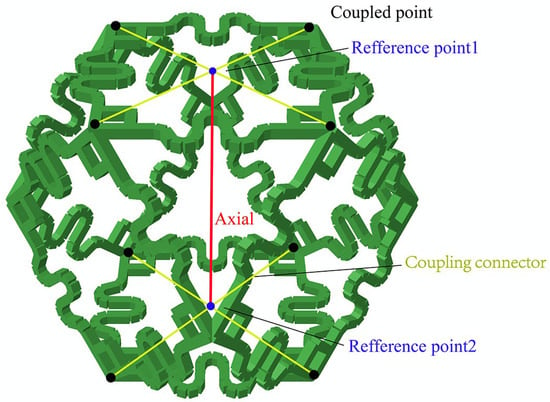
Figure 16.
Schematic diagram of the active drive cell and axial unit.
2.4. Reversible Assembly Manner
A basic principle to qualify a lattice structure as a digital metamaterial is based on whether the lattice is reversibly assembled. This characteristic ensures the structure to be replaceable in the event of local failure. Therefore, how to define a reversible assembly manner is very important. Similar to the method in the literature [35], this paper adopts a screw connection method for the reversible assembly within and between different cells. By examining the internal structure of the three basic cells, it can be found that every unit cell can be further divided into six identical facet elements. Therefore, these facet elements can be used as the most basic parts and fabricated by additive manufacturing. The specific geometries of the three types of facet elements are shown in Figure 17. The connection area at the corner of each facet element consists of two connection holes, one for the connection within a cell and the other for between the cells.
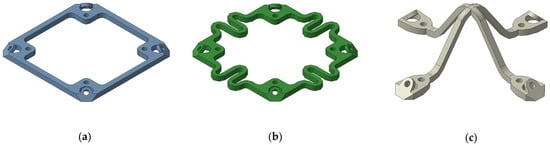
Figure 17.
Component-level facet elements: (a) Facet element of the rigid cell; (b) Facet element of the compliant cell; (c) Facet element of the auxetic cell.
Considering a rigid cell as an example, Figure 18 introduces the connection process of the facet element. It can be seen that the rigid cell is connected by six facet elements through screws at the midpoints of the 12 edges of the cube. It is recommended that these screw connections should be smeared with glue to ensure that the screw will not come loose in a long-term use.
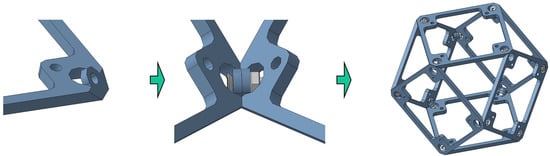
Figure 18.
Schematic diagram of a screw connection within a single cell.
Figure 19 shows the connection methodology for the case of multiple cells. It is worth noting that the positions and radii of the holes reserved on all facet elements are consistent, so a series of cells with different functions and mechanical properties can be arbitrarily assembled according to a specific functional need. Finally, a complex structural system can be constructed.
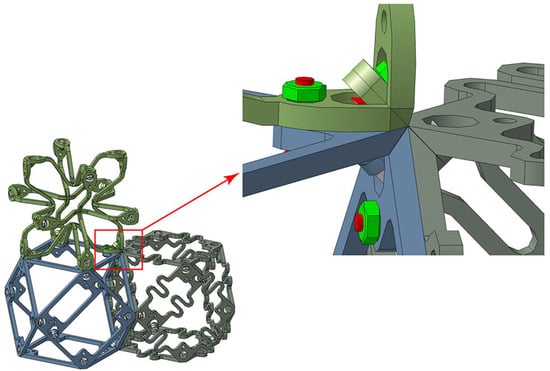
Figure 19.
Schematic diagram the screw connection between several cells.
The reversible assembly way enables the structural components to be disassembled and replaced in time when some failure occurs. In the process of replacement, it can even be printed on demand through on-site additive manufacturing, avoiding structural storage problems. The component-level additive manufacturing method can effectively make up for the shortcomings of traditional additive manufacturing method, such as scalability, and greatly reduce the processing and manufacturing costs [3]. The modularized structure is also conducive to standardized and mass-processing operations. These features make parallel and automated assembly possible. In fact, this has been realized through some micro-assembly robots [39]. Therefore, the reversible assembly will greatly improve the efficiency of manufacturing in the future.
Moreover, the reversible cell assembly method proposed in this paper can be extended and applied to heterogeneous cells. It has been shown that heterogeneous cells can exponentially improve the combination possibilities of mechanical metamaterials, and even arbitrary elasticity tensors can be obtained. Therefore, if the assembly method is combined with heterogeneous cells, the design space of a structure will be expanded further. This makes it possible for the discrete cell structure to achieve arbitrarily complex stiffness distribution.
However, the detachable screw connection method is prone to loosening in practical application, which is detrimental to the reliability of aircraft structures. This problem is expected to be solved through a connection method innovation. In addition, the connection way requires very high assembly accuracy; otherwise, the assembled structure is predisposed to initial assembly stress, which is also disadvantageous for practical applications. As shown in the literature [39], the automatic assembly method of reversible lattice structures based on micro-robots can be accurate enough for the assembly of lattice structures. In the future, it is expected that micro-robots will be used to improve assembly accuracy, reduce assembly stress, and enhance assembly efficiency.
3. Optimization Methodology
As mentioned in Section 2, the design of a variable thickness structure can be simplified as a two-dimensional combinational optimization problem. In this optimization problem, there are six alternative types of basic cells, namely the rigid cell, compliant cell, auxetic cell, tensile cell, bending cell, and active cell. To mathematize the design variables, these cell categories can be represented by 1, 2, 3, 4, 5, and 6, respectively. Figure 20 is a schematic diagram of a lattice structure corresponding to a specific cell combinational sequence. To generate a predefined target aerodynamic profile as shown in Figure 2, some active cells should be embedded into the lattice, and the driving displacement of each active cell also needs to be determined. Therefore, the combination optimization problem of the distributed variable thickness lattice structure is a multi-class-variable optimization problem because the combination sequence of lattice cells is a discrete variable, while the driving displacements of active cells are continuous variables. Compared with gradient-based algorithms, genetic algorithms perform better in discrete variable optimization problems, so they are more suitable for solving the problem.
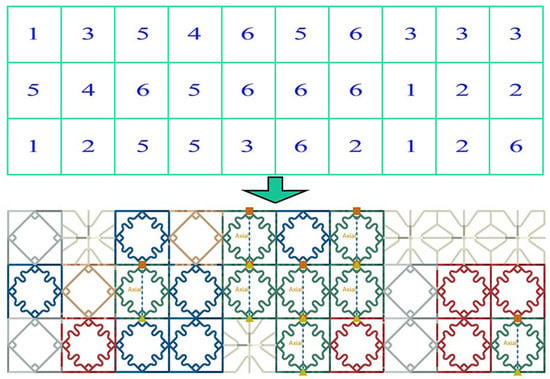
Figure 20.
Diagram of the corresponding relationship between a specific sequence and its cell combination configuration.
A genetic algorithm is a population-based optimization method, which consists of a certain number of individuals encoded by genes. Each individual carries different chromosomes. As the main carriers of genetic material, chromosomes represent a certain combination of genes, which determines the external performance of individual traits (or fitness function). Therefore, after the generation of the primitive population, the appropriate individuals are selected according to a fitness rule of the individuals, and the genetic operators of natural genetics are used to crossover and mutate. Finally, new individuals are generated. By replacing the worst individuals in the offspring, the overall fitness of the offspring will be improved. In this way, a better progeny is produced repeatedly, and the optimal population of the problem is finally obtained.
The establishment of optimization mathematical models based on genetic algorithms requires solving the issues of coding/decoding, selection, crossover, and mutation. In addition, for this problem, the number of driving displacement variables of active cells directly depends on the number of active cells, which is, however, unknown during the optimization process. Therefore, it is necessary to solve the problem that the number of design variables is always changing. All these issues will be elaborated on in the following.
3.1. Encoding and Decoding
Each gene in a chromosome corresponds to a cell type, which is a discrete variable. When the discrete variable is mixed with the continuous one of the driving displacement, it is difficult to carry out the optimization process. Therefore, this paper proposes a method to transform the discrete variables into continuous ones. The range of each variable can be defined as (0 + , 1 + ), where represents the coding difference of the allowable cell type. For this problem, the variable can be 1, 2, 3, 4, 5, or 6, which means . The relationship between the value of the gene and the value of the actual cell type is:
where the symbol represents a round-down operator, which returns a maximum integer no greater than the number in the parentheses.
3.2. Selection
The selection operator in the algorithm is a tournament selection or competitive selection. The selection operator has both random and deterministic characteristics. This method randomly selects several individuals and selects the best one. The number of the selected individuals is called the tournament size. In this paper, the size is set as 2, which is also the most common setting [40]. This situation is called a binary tournament. For a structural design, the implementation of the binary tournament is as follows. Firstly, two individuals are randomly selected from the group for comparison. When both individuals meet the constraints, the one with the smaller fitness is considered the outstanding individual; when one individual satisfies the constraint and the other does not, the one that satisfies the constraint is the excellent individual. If both of them do not meet the constraint, the one with a small degree of constraint violation is the outstanding individual, and the outstanding individual will be selected to enter into the next generation. The tournament selection is characterized by individuals with good fitness having a greater chance of survival. At the same time, it uses only the relative value of fitness as the selection criterion, which is not proportional to the value of fitness, to avoid the influence of super individuals but also to allow the new individuals with lower fitness the chance to be selected into the next generation, which reduces the loss of population diversity to avoid premature convergence and the stagnation phenomenon.
3.3. Crossover
Since the design variables are uniformly transformed into continuous variables, a simulated binary crossover (SBX) operator is used to transfer the excellent genes from the two parental chromosomes to the next generation. SBX is a type of arithmetic crossover operator, which adds arithmetic operation between gene pairs on the basis of a gene exchange. Therefore, SBX can generate not only new individuals but also new genes. Assuming that the two parent individuals involved in the crossover are x(1) and x(2), and the two offspring individuals after the crossover are y(1) and y(2), the crossover process can be illustrated with the following equations:
where is a random number and satisfies ; is the lower limit and the upper limit of the i-th variable, respectively; and is the cross-distribution index, which represents the balance between global search and local search. When it is large, the local search is more important.; when it is small, it focuses on global search. In this paper, we take .
3.4. Mutation
In this paper, a polynomial mutation operator is applied to two parental chromosomes. Assuming that the new offspring y is generated after the mutation of the parent x, the individual mutation process is as follows:
where is a random number and satisfies and is variation distribution coefficient; is taken in this paper.
3.5. Changing Number of Design Variables
The variables to be determined in this problem include the combination sequence of different types of cells, the driving displacements of the active cells, and the position of the active cells. Compared with normal combinatorial optimization problems, the problem in this paper has a special feature: the number of design variables changes with the variation of the combination sequences. This is because when the number of active cells changes, the number of driving displacement variables also changes, and then the total number of design variables changes. However, in regard to a practical algorithm, the individual chromosome length must be a constant number, otherwise, the number of the genetic operator cannot be executed. To solve the problem, this paper proposes an innovative coding strategy based on dummy variables. This means whether a cell is active or passive, a dummy displacement variable is assigned to it. In the decoding process, only when the cell is active, its drive displacement is decoded and is equal to its dummy variable. Although this method will increase the number of design variables and reduce the solution speed, it can effectively solve the problem that the number of design variables changes.
3.6. Optimization Model and Results
After considering the dummy variables, the design variables include 30 serial numbers of the cell types and 30 dummy drive displacements for the two-dimensional variable thickness wing shown in Figure 2. To achieve an accurate shape control, more active cells are more beneficial. However, more active cells will lead to a more complicated control system. Therefore, the problem is actually a multi-objective optimization problem, which means that the deformation error and the number of drivers need to be considered collaboratively. The deformation error is generally described by the least square error (LSE), which is defined as the coordinates error between the actual contour and the target contour [30,41,42]. To transform the multi-objective problem into a single-objective problem, as has been done in the literature [40,43], an equivalent objective function is adopted, which is presented as follows:
where and are chosen to be 0.01 and 10, respectively; the MaxActuatorNum is 5, that is, it is expected that the number of drives is less than or equal to 5.
Since the driving displacement range of the micro linear motor selected in this paper is 0~15 mm, the dummy variable of each active cell is less than 15 mm. The final mathematical optimization model is expressed as follows:
As mentioned before, the lattice structure constructed in this paper has large bending and rotational displacement for its beam elements in a morphing process. Therefore, the problem is a geometrically nonlinear problem, and the Newton–Raphson iterative method [44] is used to solve the equilibrium equation. For an ideal simulation, the global and local buckling behaviors of the beams of the lattice need to be considered [45]. However, one of the original intentions of the usage of the distributed active lattice structure is to decrease the maximum structural strain, which means that the whole strain energy will be distributed in as many unit cells as possible. In fact, this can be controlled through constraining the maximum driving displacement of the active unit cells. Furthermore, the buckling behavior can be avoided. Therefore, the global and local buckling behaviors are not considered in the finite element model.
After 94 iterations, the error of the fitness or objective function LSE converged to 3.4 mm. The iterative process of the objective function of the optimization problem is shown in Figure 21. This means that after the optimization, the average deformation error of the distributed lattice structure is 3.4 mm between the target shape and the final realized shape.
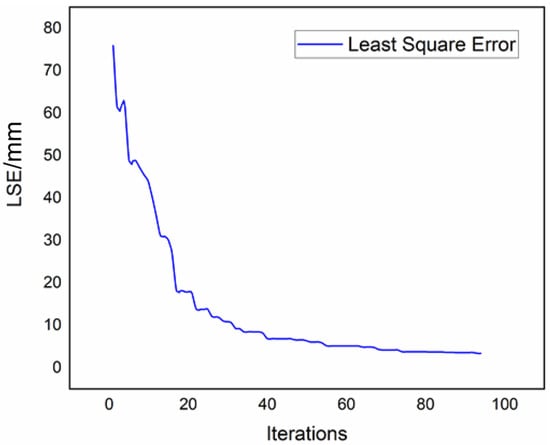
Figure 21.
The iterative process of the objective function of the optimization problem.
Figure 22 presents the diagram of the optimized lattice combination after convergence. It can be seen that to achieve the optimal target shape defined in Figure 2, five active drive cells are required, but they are all distributed in the top layer of the lattice structure as green cells shown in Figure 22. The reason for the phenomenon is that the maximum displacement of the target profile from its initial profile is approximately 13 mm, while the displacement range of the actuator is 15 mm. Therefore, the target profile can be achieved immediately by executing only the specified drive displacement of the uppermost layer. However, in practice, in addition to the deformation accuracy, the total driving energy and the maximum strain of the structure also need to be considered. Therefore, other constraints need to be further added in the future to avoid the problem of excessive local strain caused by all the actuators appearing on the top layer.
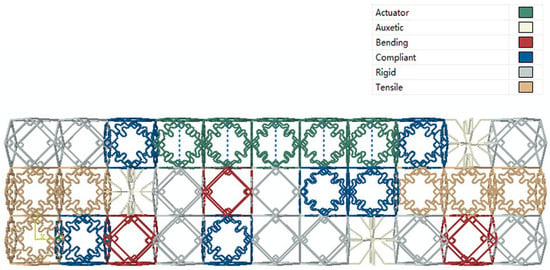
Figure 22.
The optimal cell arrangement after convergence.
Figure 23 is its final displacement contour correspondingly, and it is compared with the target contour, as shown in Figure 24. It can be seen that they are quite close to each other in general. The maximum deviation between the final achieved curve and the target curve is approximately 3 mm, occurring around the left of the midpoint. If a large number of active cells are permitted, the final achieved curve will agree better with the target curve.
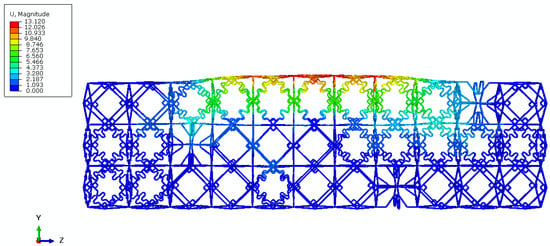
Figure 23.
The finite element analysis result of the optimal cell arrangement.
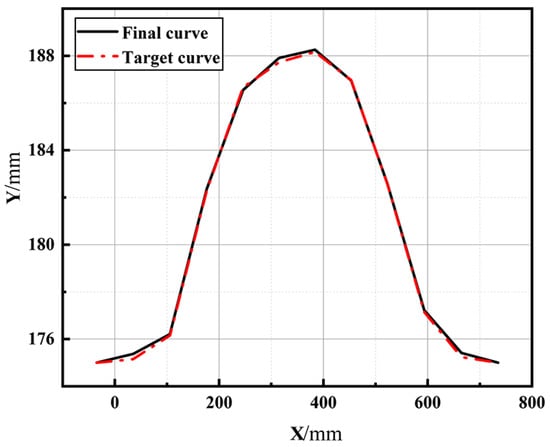
Figure 24.
The comparison between the target curve and the final curve of the optimal cell arrangement.
As for the weight of the optimized lattice, we can examine its density to analysis whether it has a weight advantage compared with tradition structures. In the obtained lattice, the numbers of six types of fundamental unit cells are presented in Table 2. As the density of the used material is 1.005 × 103 kg/m3 and the weight of a micro-actuator is approximately 0.03 kg, the final overall weight is 0.5602 kg; as the overall space volume is 0.0139 m3, the final macro density is calculated as 40.4964 kg/m3, which is very close the critical value of the ultralight materials (below 10 kg/m3) [46]. Therefore, it can be said that the concept has an obvious weight advantage compared with other traditional metal materials (or non-ultralight structures).

Table 2.
Number and weight of six kinds of fundamental unit cells.
As an initial phase of the exploration of the morphing wing concept, this paper realized only one target aerodynamic shape for a single target working condition. However, as several active actuators are utilized here, the lattice morphing wing features a distributive morphing ability and has the potential to realize multiple target aerodynamic shapes. This can be further completed with some muti-objective optimization methods.
4. Conclusions
In this paper, we propose a modular distributed variable thickness structure based on a reversible assembly digital metamaterial. In the concept, three types of fundamental cells and three types of derived cells have been constructed innovatively. A quantitative analysis of the mechanical properties of the fundamental cells has shown that the three types of fundamental cells have distinct differences in mechanical properties, which can expand the design space of the lattice morphing structure through changing their combination sequence. Specifically, the rigid cell has the highest elastic modulus among the three fundamental cell types and features a positive Poisson’s ratio overall. However, the elastic modulus of compliant cells is generally one order of magnitude lower than that of rigid cells, and the Poisson’s ratio of the compliant cell is generally close to zero. In addition, the elastic modulus of auxetic cells is in the same order of the magnitude as that of compliant cells, but the Poisson’s ratio is negative. On the basis of the complaint cell, an active cell with an embedded micro-motor is further developed, which can be reversibly assembled and connected with other passive cells and enable the whole lattice cell structure to have an active distributed morphing ability.
To ensure high active deformation accuracy, a collaborative optimization method based on a heuristic optimization algorithm for the design of the lattice combination sequence is proposed. This optimization method adopts a continuous encoding method to solve the issue of multi-class variable optimization, and an objective function considering the actuator number in the optimization process is used to simplify the actuator system. The final optimization results show that the optimal cell combination can accurately achieve a distributed target contour with a maximum deformation error of approximately 3 mm.
Therefore, the morphing lattice structure with reversible assembly has a number of advantages, such as being lightweight and replaceable, having distributed morphing ability and functional integration, and being better able to coordinate the contradiction between size and accuracy existing in traditional additive manufacturing. However, in a practical application, the connection problem of high reliability and the assembly stress problem still need to be further investigated. This work will be studied in the future.
Author Contributions
Conceptualization, Z.W. and Y.Y.; methodology, Z.W. and Q.W.; software, Z.W. and Y.L.; validation, Z.W. and P.B.; formal analysis, Z.W. and Q.W.; investigation, Z.W. and Q.W.; resources, Y.Y. and D.L.; data curation, Q.W.; writing—original draft preparation, Z.W., Q.W. and P.B.; writing—review and editing, Y.Y., X.S. and J.X.; visualization, Z.W.; supervision, D.L., J.X., and X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A Review of Modelling and Analysis of Morphing Wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Cramer, N.B.; Cellucci, D.W.; Formoso, O.B.; Gregg, C.E.; Jenett, B.E.; Kim, J.H.; Lendraitis, M.; Swei, S.S.; Trinh, G.T.; Trinh, K.V.; et al. Elastic Shape Morphing of Ultralight Structures by Programmable Assembly. Smart Mater. Struct. 2019, 28, 055006. [Google Scholar] [CrossRef] [PubMed]
- De Gaspari, A.; Ricci, S. A Two-Level Approach for the Optimal Design of Morphing Wings Based on Compliant Structures. J. Intell. Mater. Syst. Struct. 2011, 22, 1091–1111. [Google Scholar] [CrossRef]
- Chen, Y.; Yin, W.; Liu, Y.; Leng, J. Structural Design and Analysis of Morphing Skin Embedded with Pneumatic Muscle Fibers. Smart Mater. Struct. 2011, 20, 085033. [Google Scholar] [CrossRef]
- Cramer, N.B.; Cheung, K.; Swei, S.S.-M. Design and Testing of a Lattice-Based Cellular Component Active Twist Wing. In Proceedings of the American Institute of Aeronautics and Astronautics (AIAA), San Diego, CA, USA, 4 January 2016. [Google Scholar]
- McHale, C.; Telford, R.; Weaver, P.M. Morphing Lattice Boom for Space Applications. Compos. Part B Eng. 2020, 202, 108441. [Google Scholar] [CrossRef]
- Chen, Q.; Lv, P.; Huang, J.; Huang, T.-Y.; Duan, H. Intelligent Shape-Morphing Micromachines. Research 2021, 2021, 9806463. [Google Scholar] [CrossRef]
- Özgen, S.; Yaman, Y.; Insuyu, T.; Yilmaz, A.; Şahin, M.; Seber, G.; Ünlüsoy, L.; Sakarya, E.; İnsuyu, T.; Bulvarı, İ.; et al. Morphing Air Vehicle Concepts. In Proceedings of the International Workshop on Unmanned Vehicles-UVW, Istanbul, Turkiye, 10–12 June 2010. [Google Scholar]
- Sun, J.; Guan, Q.; Liu, Y.; Leng, J. Morphing Aircraft Based on Smart Materials and Structures: A State-of-the-Art Review. J. Intell. Mater. Syst. Struct. 2016, 27, 2289–2312. [Google Scholar] [CrossRef]
- Vasista, S.; Tong, L.; Wong, K.C. Realization of Morphing Wings: A Multidisciplinary Challenge. J. Aircr. 2012, 49, 11–28. [Google Scholar] [CrossRef]
- Sofla, A.Y.N.; Meguid, S.A.; Tan, K.T.; Yeo, W.K. Shape Morphing of Aircraft Wing: Status and Challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, G.; Li, H.; Dong, M. Intelligent and Flexible Morphing Wing Technology: A Review. Jixie Gongcheng Xuebao/J. Mech. Eng. 2018, 54, 28–42. [Google Scholar] [CrossRef]
- Joo, J.J.; Marks, C.R.; Zientarski, L.; Culler, A. Variable Camber Compliant Wing-Design. In Proceedings of the 23rd AIAA/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA. [Google Scholar]
- Gilbert, W.W. Mission Adaptive Wing System for Tactical Aircraft. J. Aircr. 1981, 18, 597–602. [Google Scholar] [CrossRef]
- Popov, A.V.; Grigorie, L.T.; Botez, R.; Mamou, M.; Mébarki, Y. Closed-Loop Control Validation of a Morphing Wing Using Wind Tunnel Tests. J. Aircr. 2010, 47, 1309–1317. [Google Scholar] [CrossRef]
- Schmitz, A.; Horst, P. A Finite Element Unit-Cell Method for Homogenised Mechanical Properties of Heterogeneous Plates. Compos. Part A Appl. Sci. Manuf. 2014, 61, 23–32. [Google Scholar] [CrossRef]
- Bishay, P.L.; Finden, R.; Recinos, S.; Alas, C.; Lopez, E.; Aslanpour, D.; Flores, D.; Gonzalez, E. Development of an SMA-Based Camber Morphing UAV Tail Core Design. Smart Mater. Struct. 2019, 28, 075024. [Google Scholar] [CrossRef]
- Rudenko, A.; Hannig, A.; Monner, H.P.; Horst, P. Extremely Deformable Morphing Leading Edge: Optimization, Design and Structural Testing. J. Intell. Mater. Syst. Struct. 2018, 29, 764–773. [Google Scholar] [CrossRef]
- Vasista, S.; Nolte, F.; Monner, H.P.; Horst, P.; Burnazzi, M. Three-Dimensional Design of a Large-Displacement Morphing Wing Droop Nose Device. J. Intell. Mater. Syst. Struct. 2018, 29, 3222–3241. [Google Scholar] [CrossRef]
- Wang, C.; Haddad Khodaparast, H.; Friswell, M.I.; Magrini, A.; Ponza, R.; Benini, E.; Landersheim, V.; Laveuve, D.; Contell Asins, C. Conceptual-Level Evaluation of a Variable Stiffness Skin for a Morphing Wing Leading Edge. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5703–5716. [Google Scholar] [CrossRef]
- Sodja, J.; Martinez, M.J.; Simpson, J.C.; De Breuker, R. Experimental Evaluation of the Morphing Leading Edge Concept. In Proceedings of the 23rd AIAA/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA. [Google Scholar]
- Asins, C.C.; Landersheim, V.; Laveuve, D.; Adachi, S.; May, M.; Wacker, J.D.; Decker, J. Analysis and Design of a Leading Edge with Morphing Capabilities for the Wing of a Regional Aircraft—Gapless Chord-and Camber-Increase for High-Lift Performance. Appl. Sci. 2021, 11, 2752. [Google Scholar] [CrossRef]
- Baker, D.; Friswell, M.I. Determinate Structures for Wing Camber Control. Smart Mater. Struct. 2009, 18, 035014. [Google Scholar] [CrossRef]
- Cavalieri, V.; de Gaspari, A.; Ricci, S. Optimization of Compliant Adaptive Structures in the Design of a Morphing Droop Nose. Smart Mater. Struct. 2020, 29, 075020. [Google Scholar] [CrossRef]
- Trease, B.; Kota, S. Design of Adaptive and Controllable Compliant Systems with Embedded Actuators and Sensors. J. Mech. Des. Trans. ASME 2009, 131, 1110011–11100112. [Google Scholar] [CrossRef]
- Milojević, A.P.; Pavlović, N.D. Development of a New Adaptive Shape Morphing Compliant Structure with Embedded Actuators. J. Intell. Mater. Syst. Struct. 2016, 27, 1306–1328. [Google Scholar] [CrossRef]
- Geier, S.; Kintscher, M.; Mahrholz, T.; Wierach, P.; Monner, H.-P.; Wiedemann, M. Experimental and Finite Element Analyses of Multifunctional Skins for Morphing Wing Applications. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2016, Las Vegas, NV, USA, 20 April 2016; SPIE: Washington, DC, USA; Volume 9803, p. 980328. [Google Scholar]
- Kintscher, M.; Wiedemann, M.; Monner, H.P.; Heintze, O.; Kühn, T. Design of a Smart Leading Edge Device for Low Speed Wind Tunnel Tests in the European Project SADE. Int. J. Struct. Integr. 2011, 2, 383–405. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Wang, B.; Lyu, S. Optimization, Design and Testing for Morphing Leading Edge. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 095440622094188. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Computational Analysis of 3D Lattice Structures for Skin in Real-Scale Camber Morphing Aircraft. Aerospace 2019, 6, 79. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M. Static Aeroelastic Response of Chiral-Core Airfoils. J. Intell. Mater. Syst. Struct. 2007, 18, 1067–1075. [Google Scholar] [CrossRef]
- Fasel, U.; Keidel, D.; Baumann, L.; Cavolina, G.; Eichenhofer, M.; Ermanni, P. Composite Additive Manufacturing of Morphing Aerospace Structures. Manuf. Lett. 2020, 23, 85–88. [Google Scholar] [CrossRef]
- Keidel, D.; Lienhard, M.; Fasel, U.; Ermanni, P. Design and Testing of a Lattice Morphing Wing. In Proceedings of the ASME 2020 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Virtual, Online, 15 September 2020; American Society of Mechanical Engineers: New York, NY, USA; p. V001T04A011. [Google Scholar]
- Jenett, B.; Cameron, C.; Tourlomousis, F.; Rubio, A.P.; Ochalek, M.; Gershenfeld, N. Discretely Assembled Mechanical Metamaterials. Sci. Adv. 2020, 6, eabc9943. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Song, C.; Yang, C. A Morphing Wing with Cellular Structure of Non-Uniform Density. Smart Mater. Struct. 2021, 30, 105005. [Google Scholar] [CrossRef]
- Youngren, H. Multi-Point Design and Optimization of a Natural Laminar Flow Airfoil for a Mission Adaptive Compliant Wing. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Wang, Z.-P.; Poh, L.H. Optimal Form and Size Characterization of Planar Isotropic Petal-Shaped Auxetics with Tunable Effective Properties Using IGA. Compos. Struct. 2018, 201, 486–502. [Google Scholar] [CrossRef]
- Jenett, B.; Cellucci, D. A Mobile Robot for Locomotion through a 3D Periodic Lattice Environment. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May 2017–3 June 2017; IEEE: Singapore; pp. 5474–5479. [Google Scholar]
- Yang, J.; Song, B.; Zhong, X.; Jin, P. Optimal Design of Blended Composite Laminate Structures Using Ply Drop Sequence. Compos. Struct. 2016, 135, 30–37. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Lyu, S. Comparative Study of Two Lay-up Sequence Dispositions for Flexible Skin Design of Morphing Leading Edge. Chin. J. Aeronaut. 2021, 34, 271–278. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y. Design of a Variable-Stiffness Compliant Skin for a Morphing Leading Edge. Appl. Sci. 2021, 11, 3165. [Google Scholar] [CrossRef]
- Soremekun, G.; Gürdal, Z.; Kassapoglou, C.; Toni, D. Stacking Sequence Blending of Multiple Composite Laminates Using Genetic Algorithms. Compos. Struct. 2002, 56, 53–62. [Google Scholar] [CrossRef]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003; ISBN 978-0-521-00794-8. [Google Scholar]
- Wang, D.; Abdalla, M.M. Global and Local Buckling Analysis of Grid-Stiffened Composite Panels. Compos. Struct. 2015, 119, 767–776. [Google Scholar] [CrossRef]
- Jenett, B.; Calisch, S.; Cellucci, D.; Cramer, N.; Gershenfeld, N.; Swei, S.; Cheung, K.C. Digital Morphing Wing: Active Wing Shaping Concept Using Composite Lattice-Based Cellular Structures. Soft Robot. 2017, 4, 33–48. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).