Fault-Tolerant Attitude Control Incorporating Reconfiguration Control Allocation for Supersonic Tailless Aircraft
Abstract
1. Introduction
2. Fault-Tolerant Attitude Control Incorporating Control Allocation Problem Statement
2.1. Backstepping Attitude Controller Design
2.2. Fault-Tolerant Control Allocation Problem
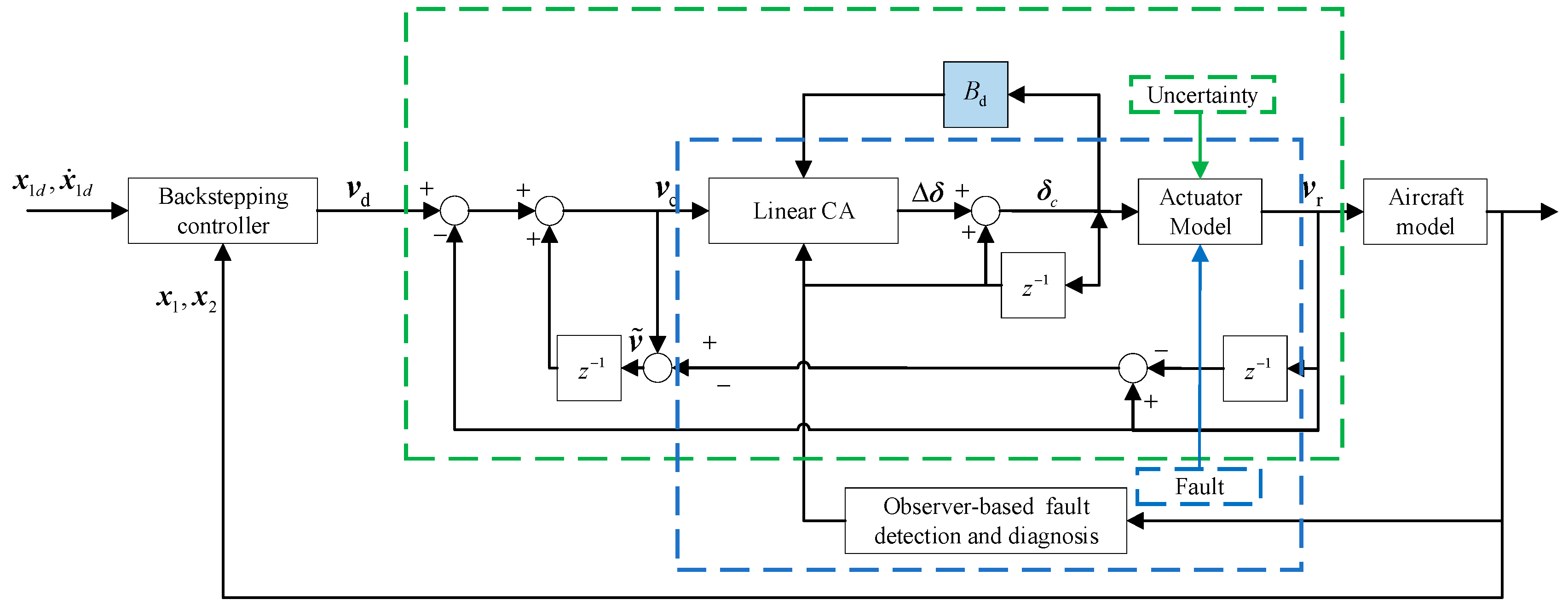
3. Incremental Reconfiguration Closed-Loop Control Allocation Scheme Design
- (1)
- th actuator with lock-in-place faultReferring to Equation (15), under the lock-in-place fault, the control effectiveness matrix is reconfigured to be , where contains the lock-in-place fault information. The actual output of IRCCA is derived as Equation (22). The additional moment generated by the fault actuator due to the lock-in-place fault reduces the accuracy of control allocation. Therefore, the virtual input is demanded to subtract the additional part. Referring to Equation (15), the additional part is derived as . However, cannot be gained in the actual situation due to being unknown. We replace by , and can be gained by . Then the and are rewritten in Equations (23) and (24).
- (2)
- th actuator with loose faultReferring to Equation (15), under the loose fault, the control effectiveness matrix is reconfigured to be , where contains the loose fault information. Additionally, with the loose fault, the fault actuator deflection is 0 deg. The control input is transformed into . The actual output of IRCCA is derived as Equation (25). The actuator with a loose fault cannot generate additional moments. Therefore, the and retain the form of Equations (20) and (21).
- (3)
- th actuator with a loss of effectiveness faultReferring to Equation (15), under the loss of effectiveness fault, the control effectiveness matrix is reconfigured to be , where contains the loss of effectiveness fault information. The actual output of IRCCA is derived as Equation (26). The actuator with the loss of effectiveness fault cannot generate additional moments. Therefore, the and retain the form of Equations (20) and (21).
- (4)
- multiple fault scenariosConsidering the multiple fault scenarios, the control effectiveness matrix is reconfigured to be . Additionally, with the loose fault, the fault actuator deflection is 0 deg. The control input is transformed into . The actual output of IRCCA is derived as Equation (27). The actuator with the loss of effectiveness fault and loose fault cannot generate additional moments. Therefore, the and retain the form of Equations (23) and (24).the whole fault-tolerant attitude control incorporating reconfiguration control allocation scheme is shown in Figure 1.
4. Stability Analysis
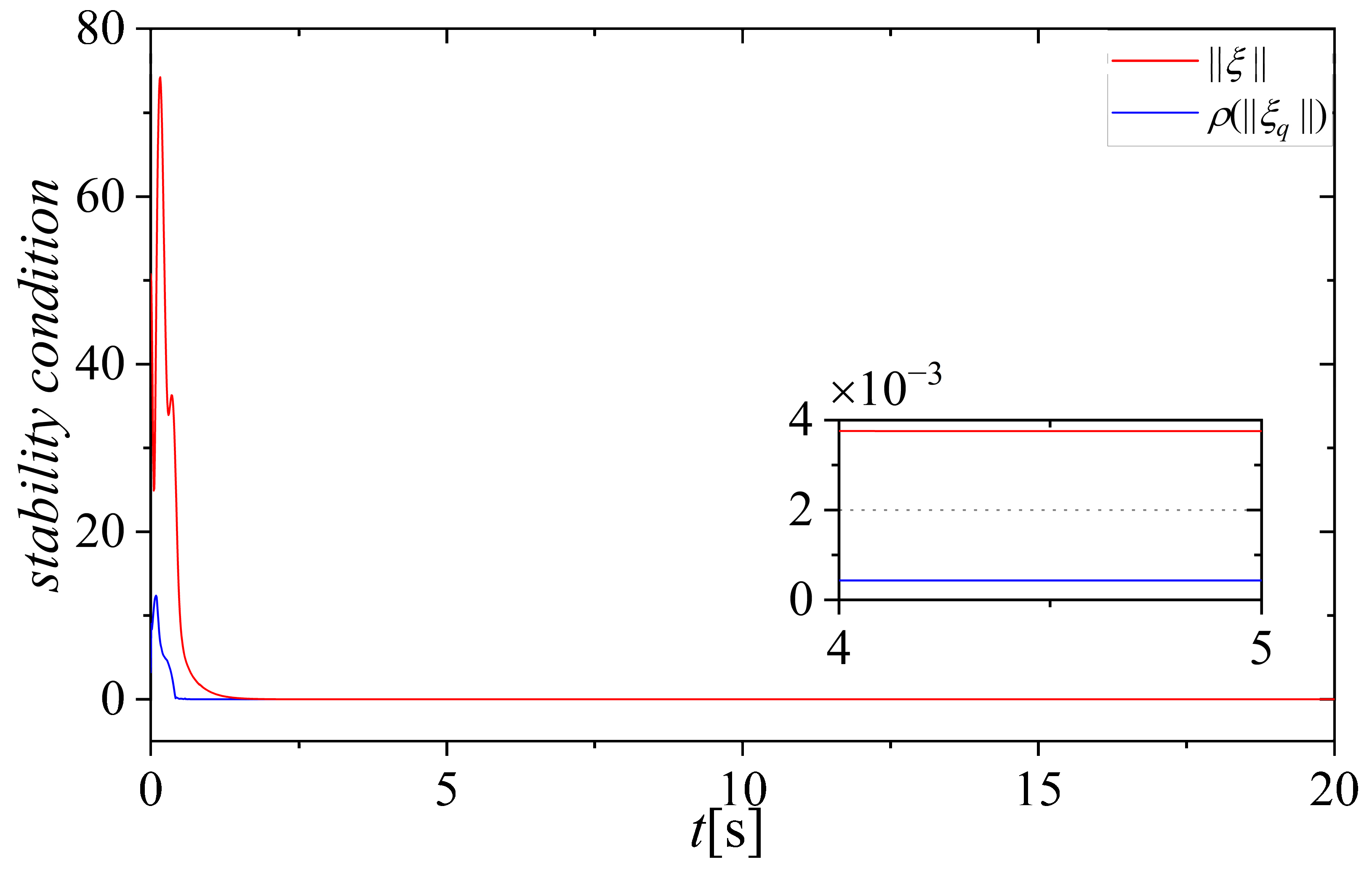
4.1. Stability Analysis for Incremental Reconfiguration Closed-Loop Control Allocation
4.1.1. Stability in the Absence of Actuator Faults
4.1.2. Stability in the Presence of Control Effectiveness Matrix Uncertainty
4.1.3. Stability in the Presence of Actuator Fault
4.2. Stability Analysis for Fault-Tolerant Attitude Control System
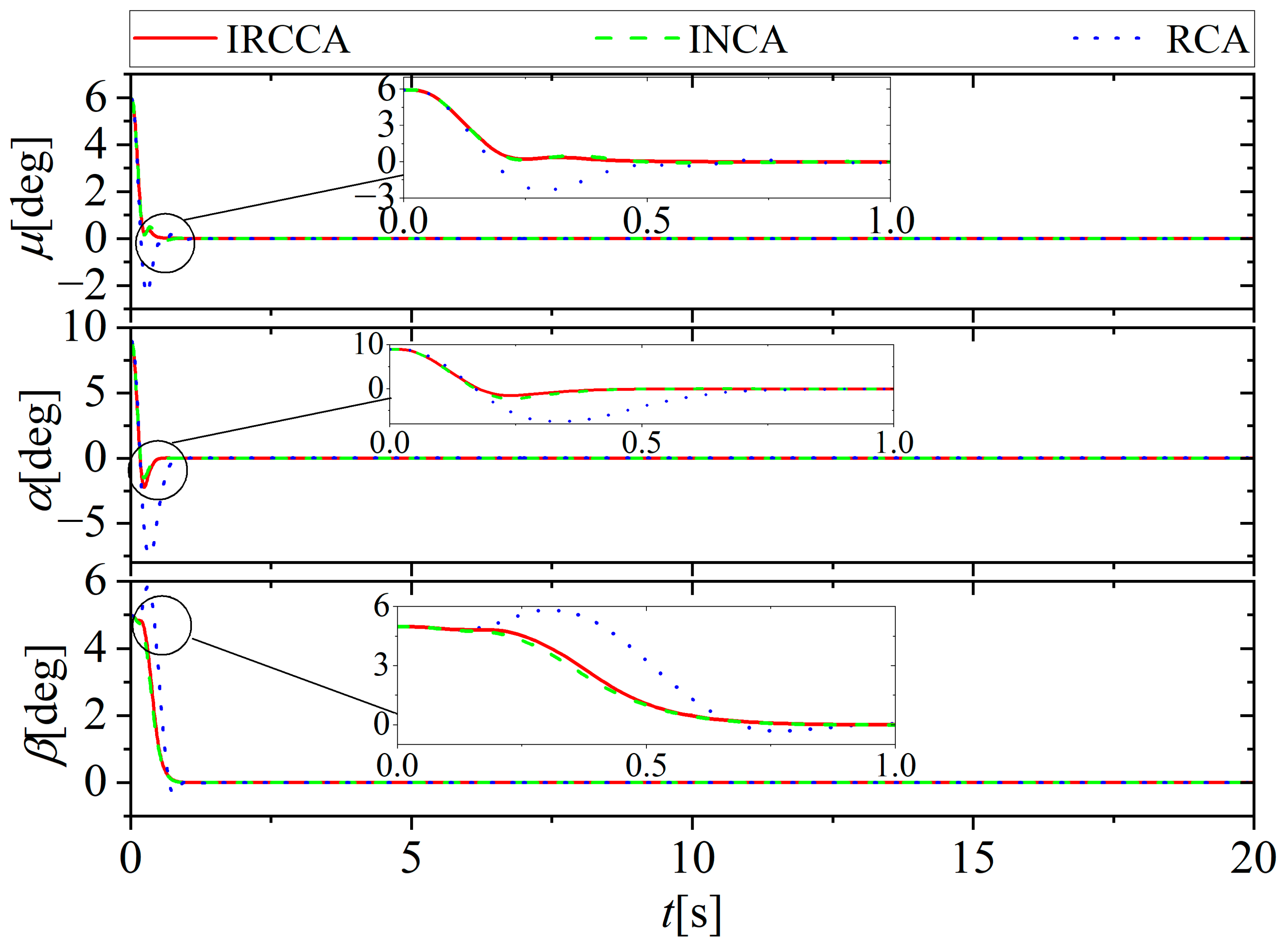
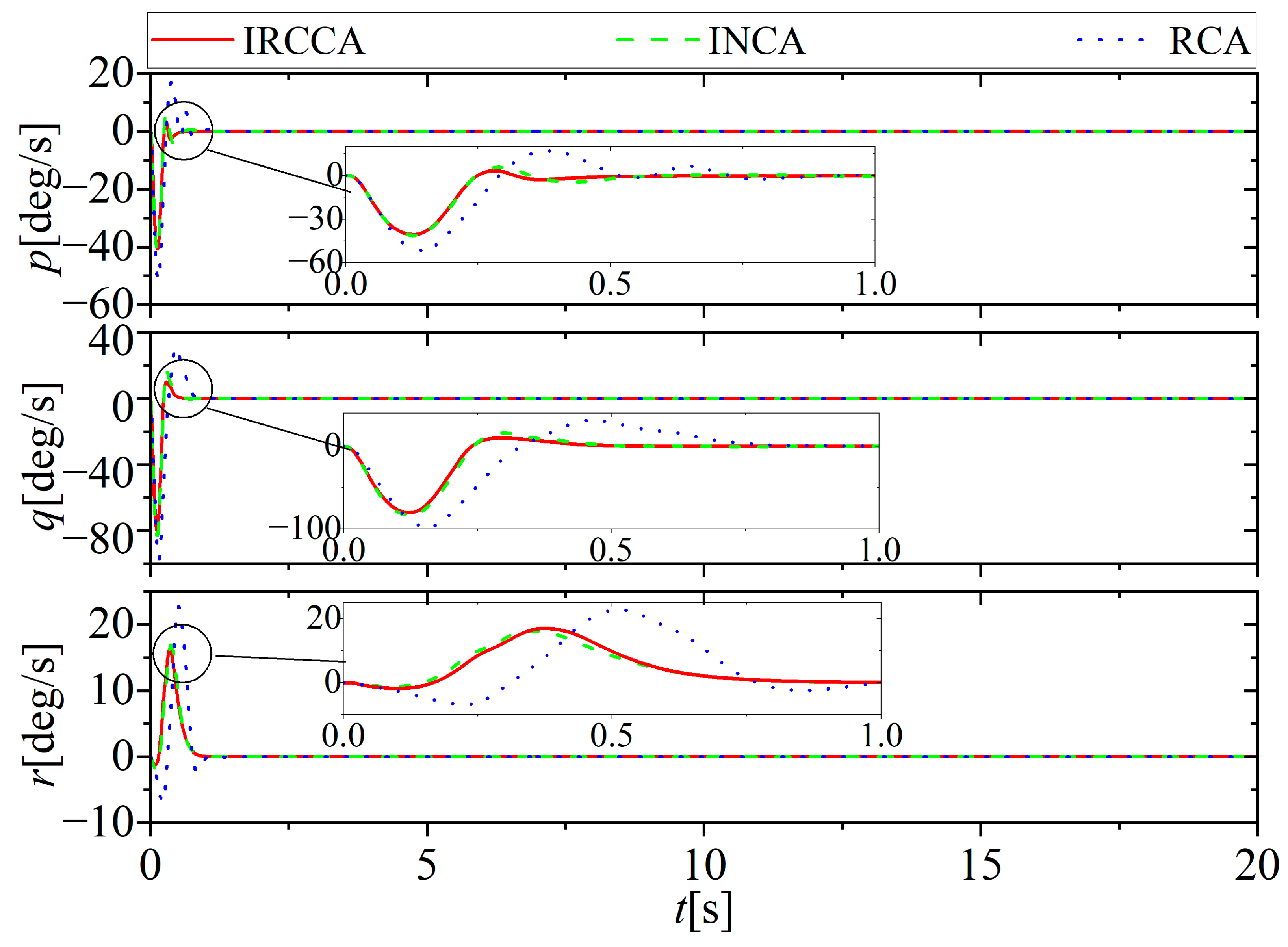
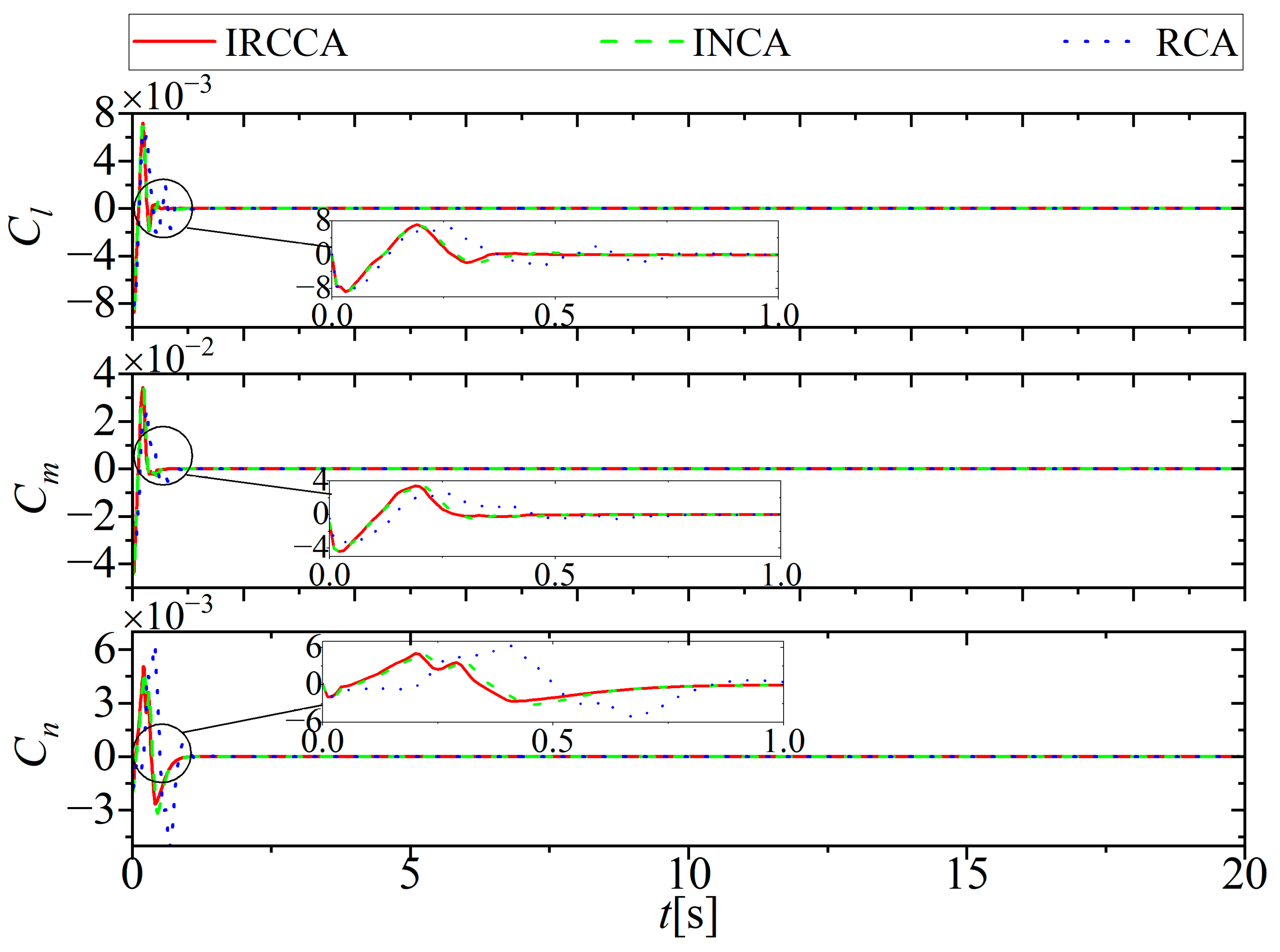
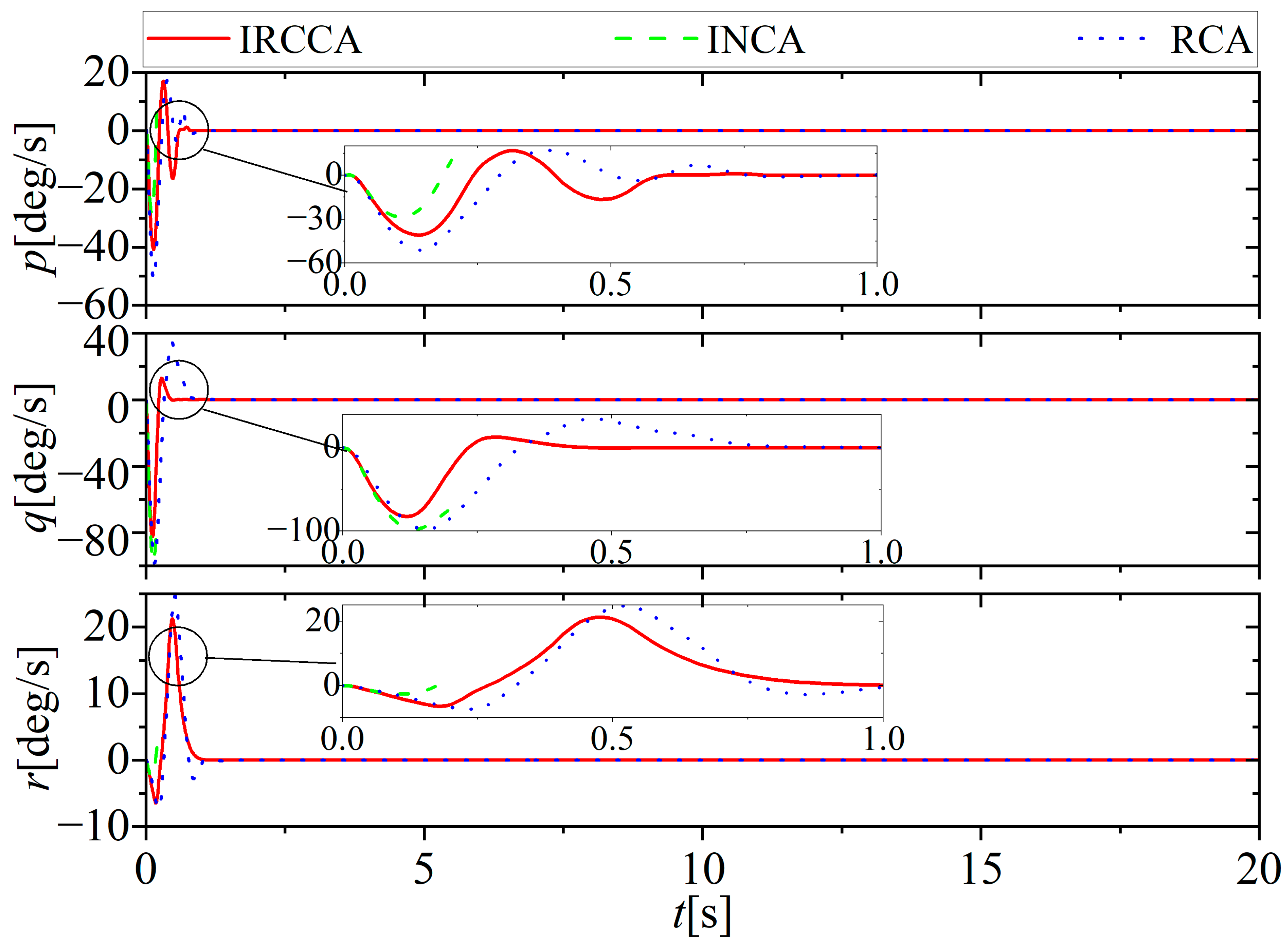
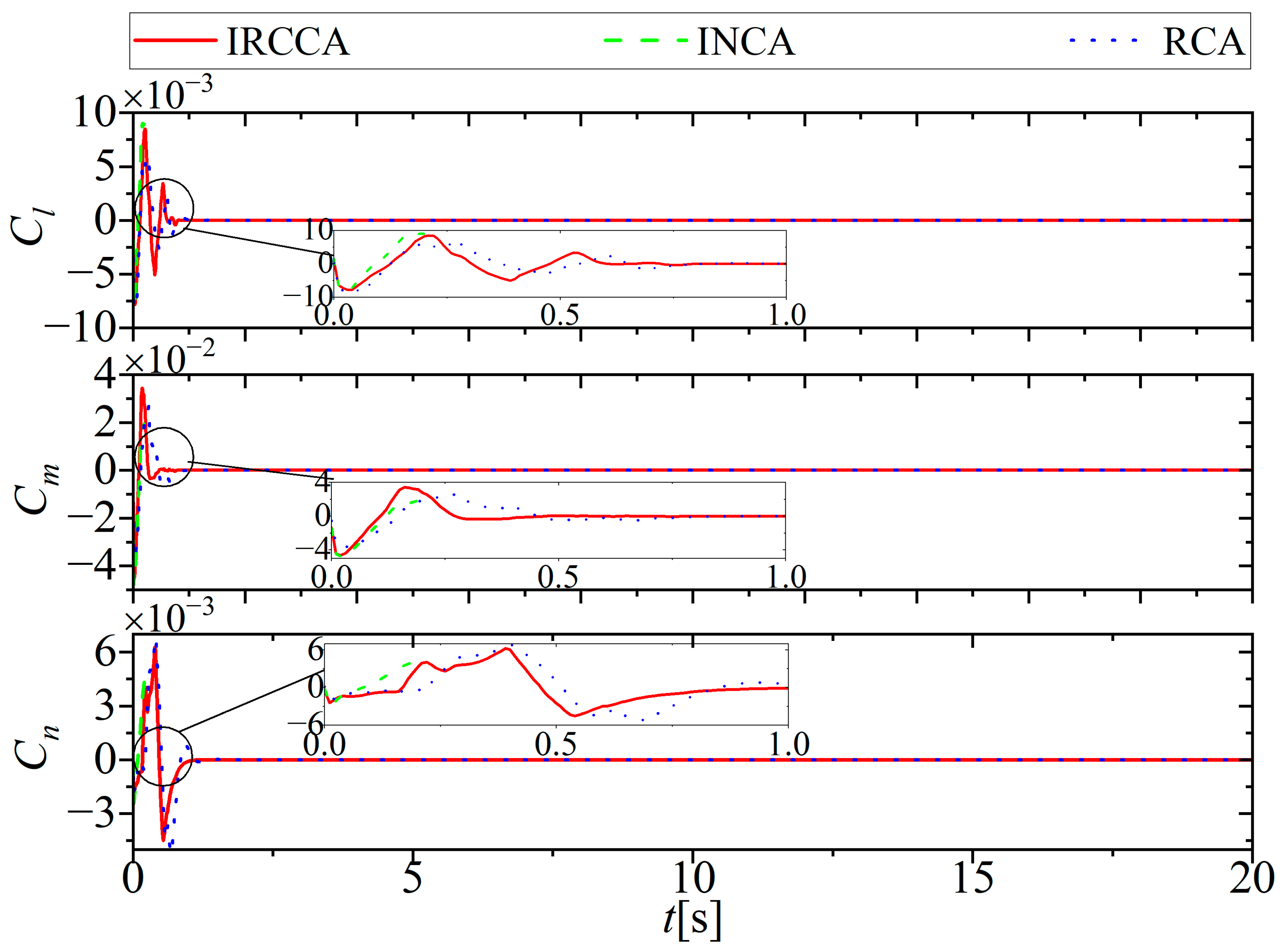
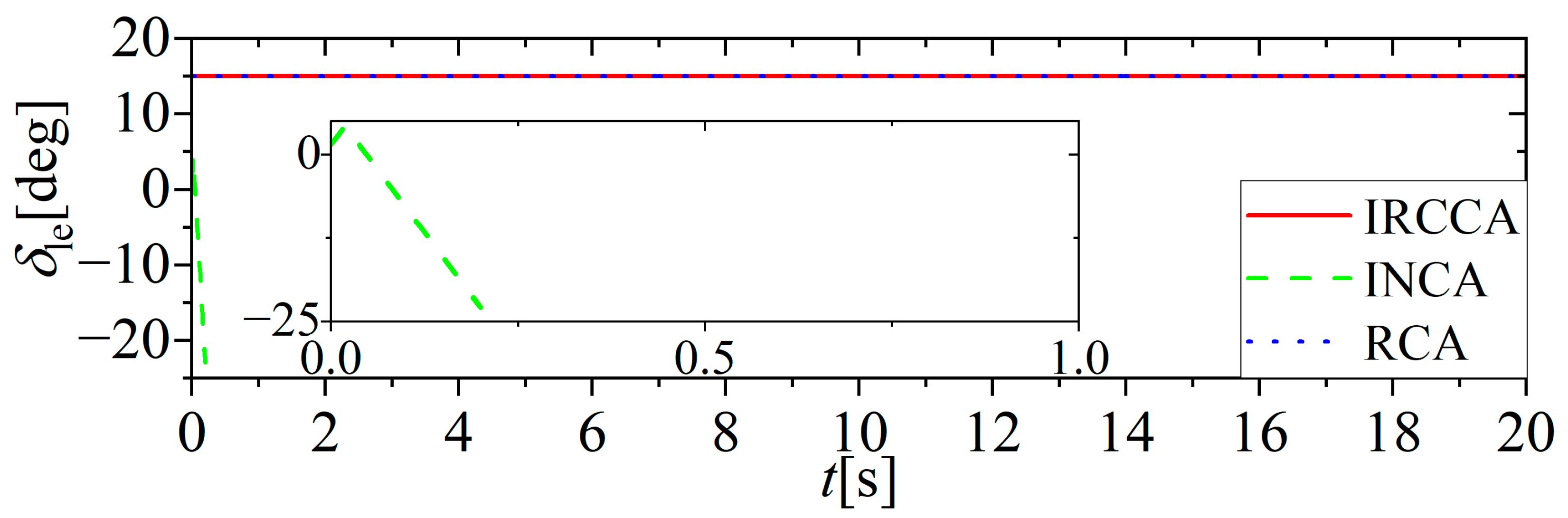
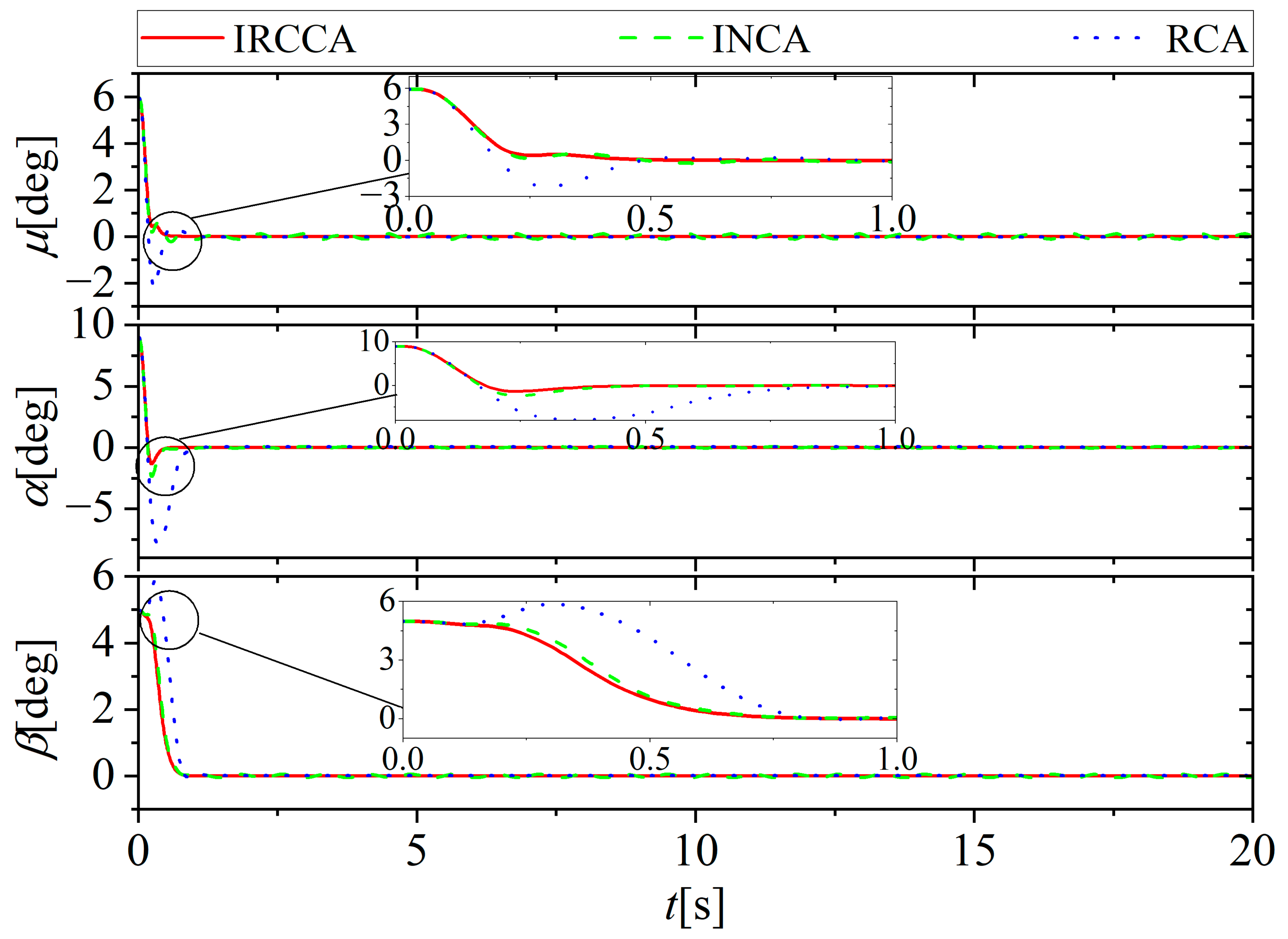
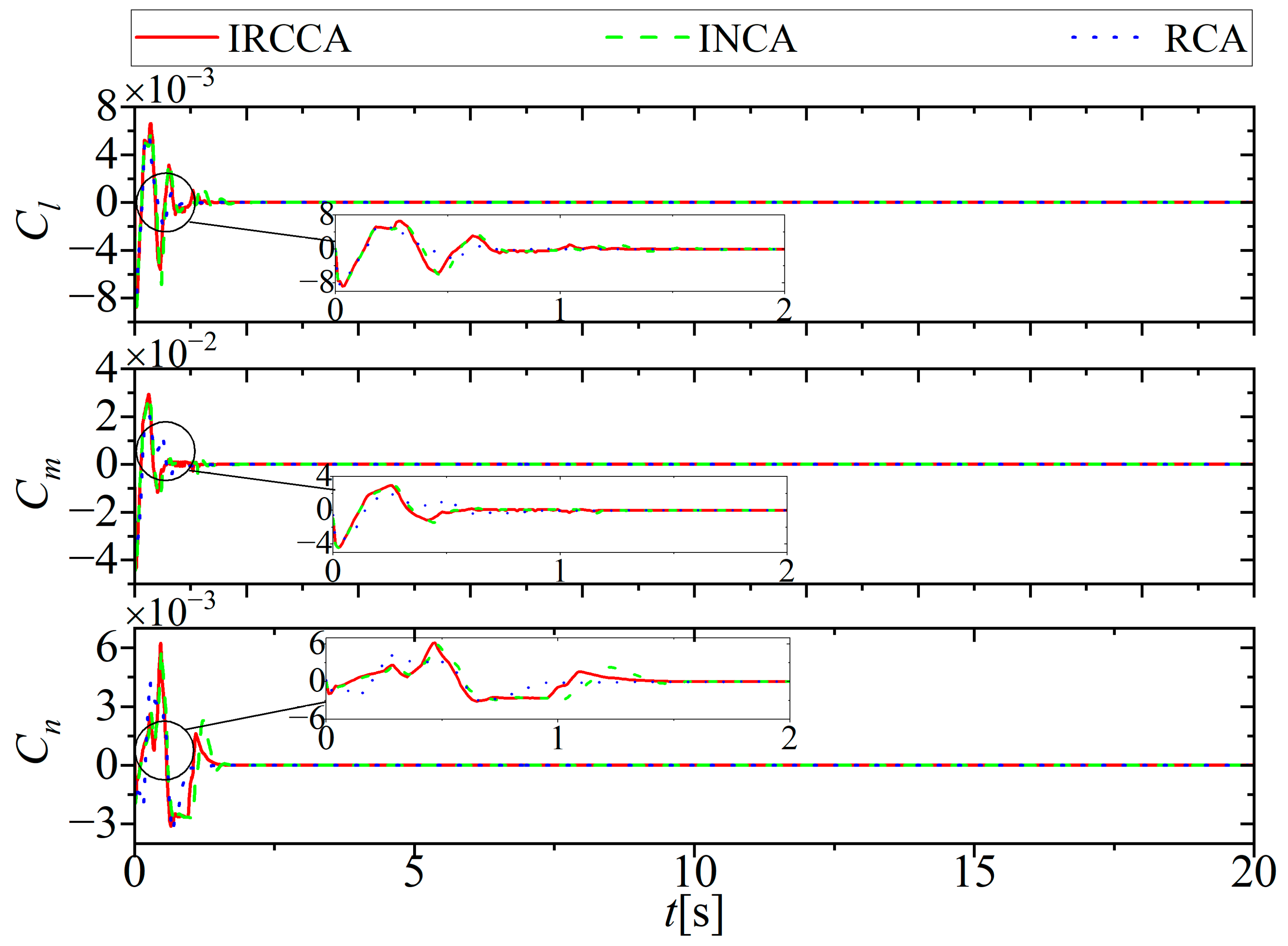
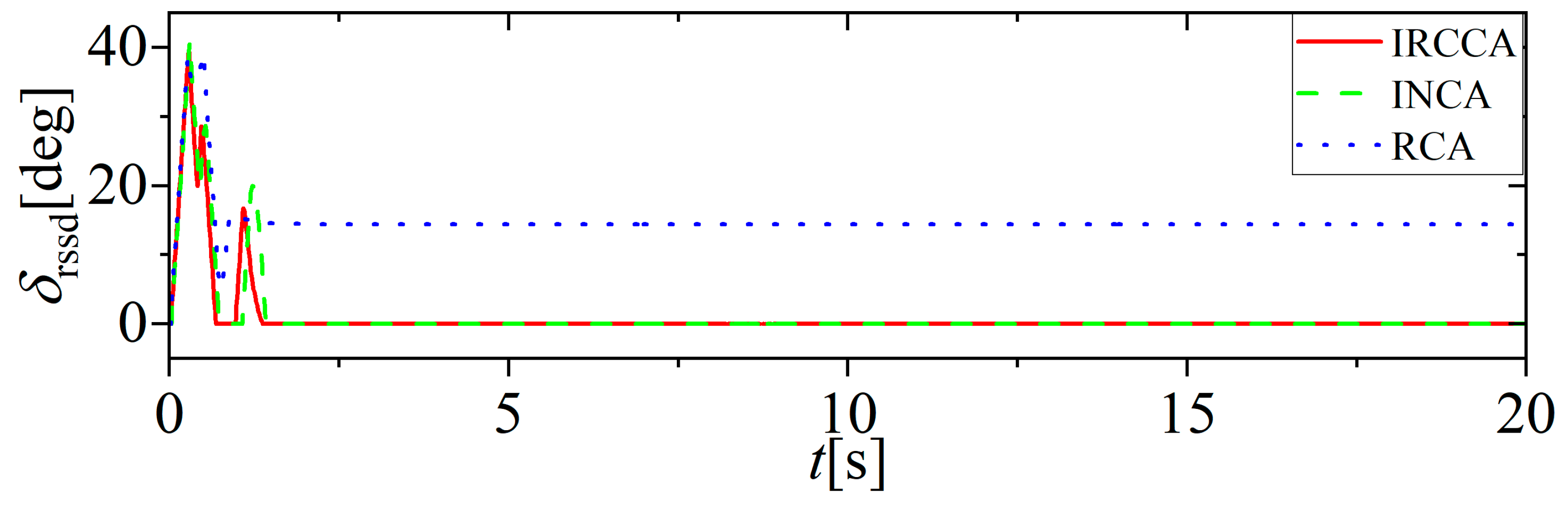
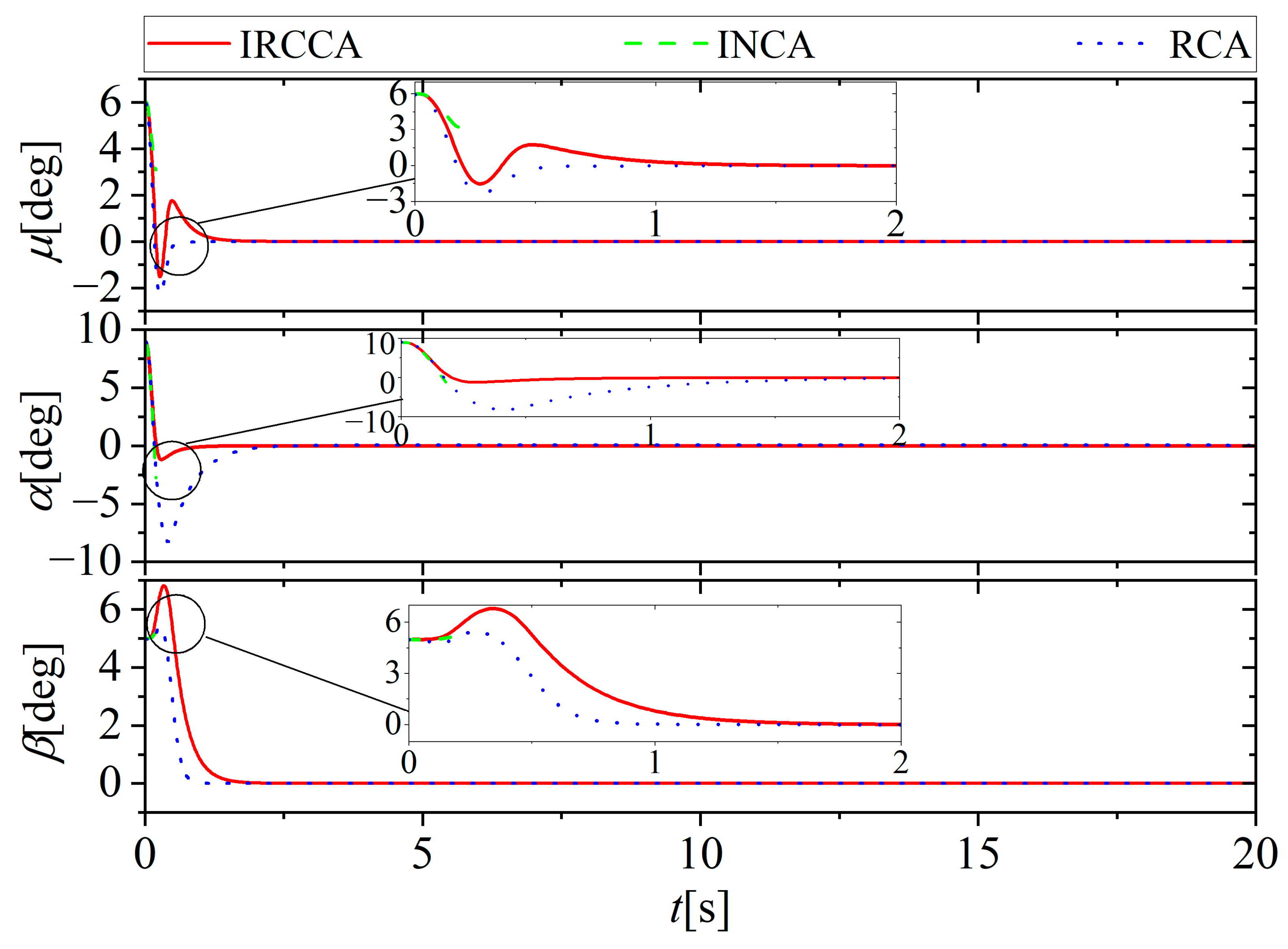
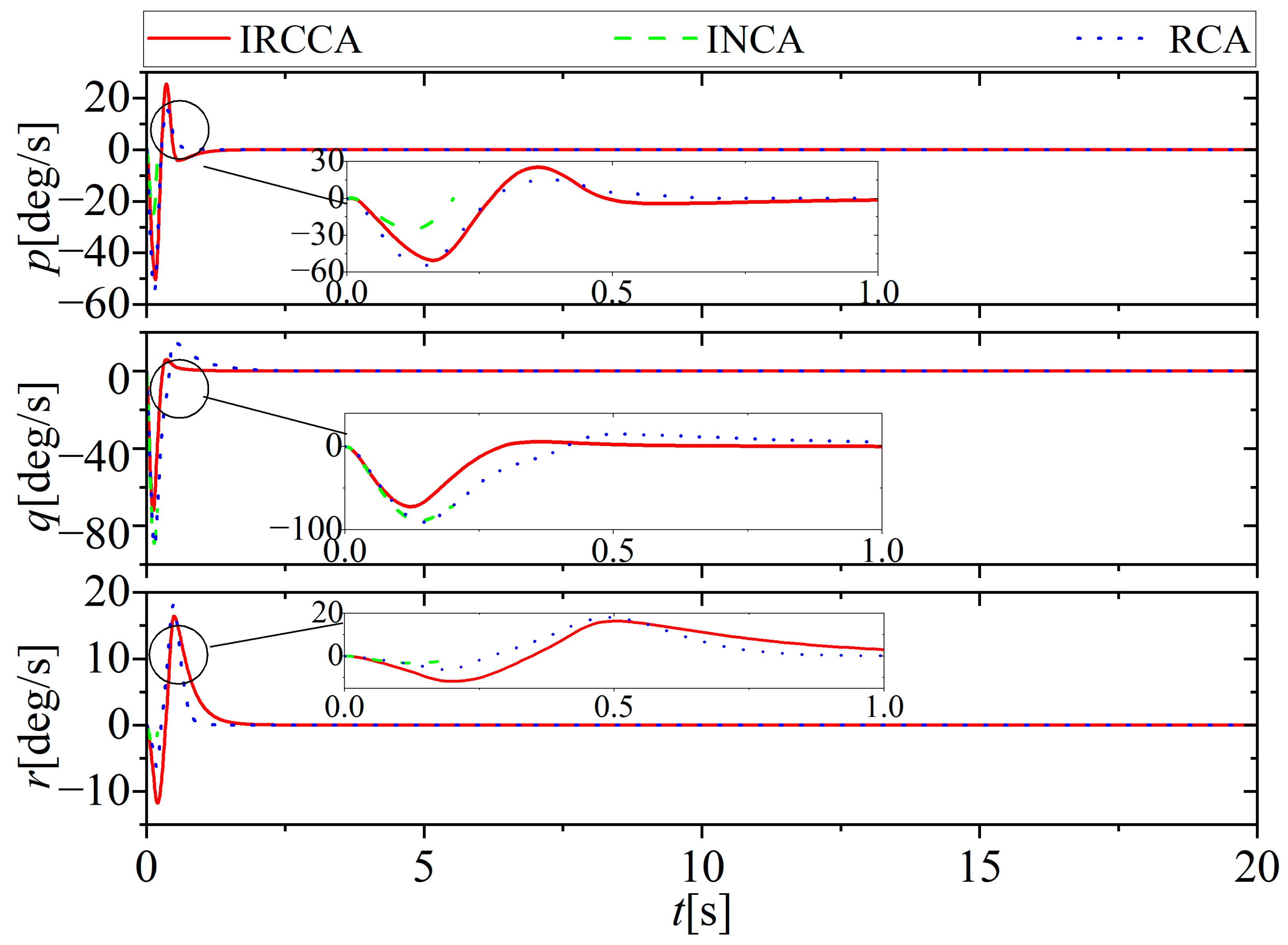
5. Simulation Results and Discussion
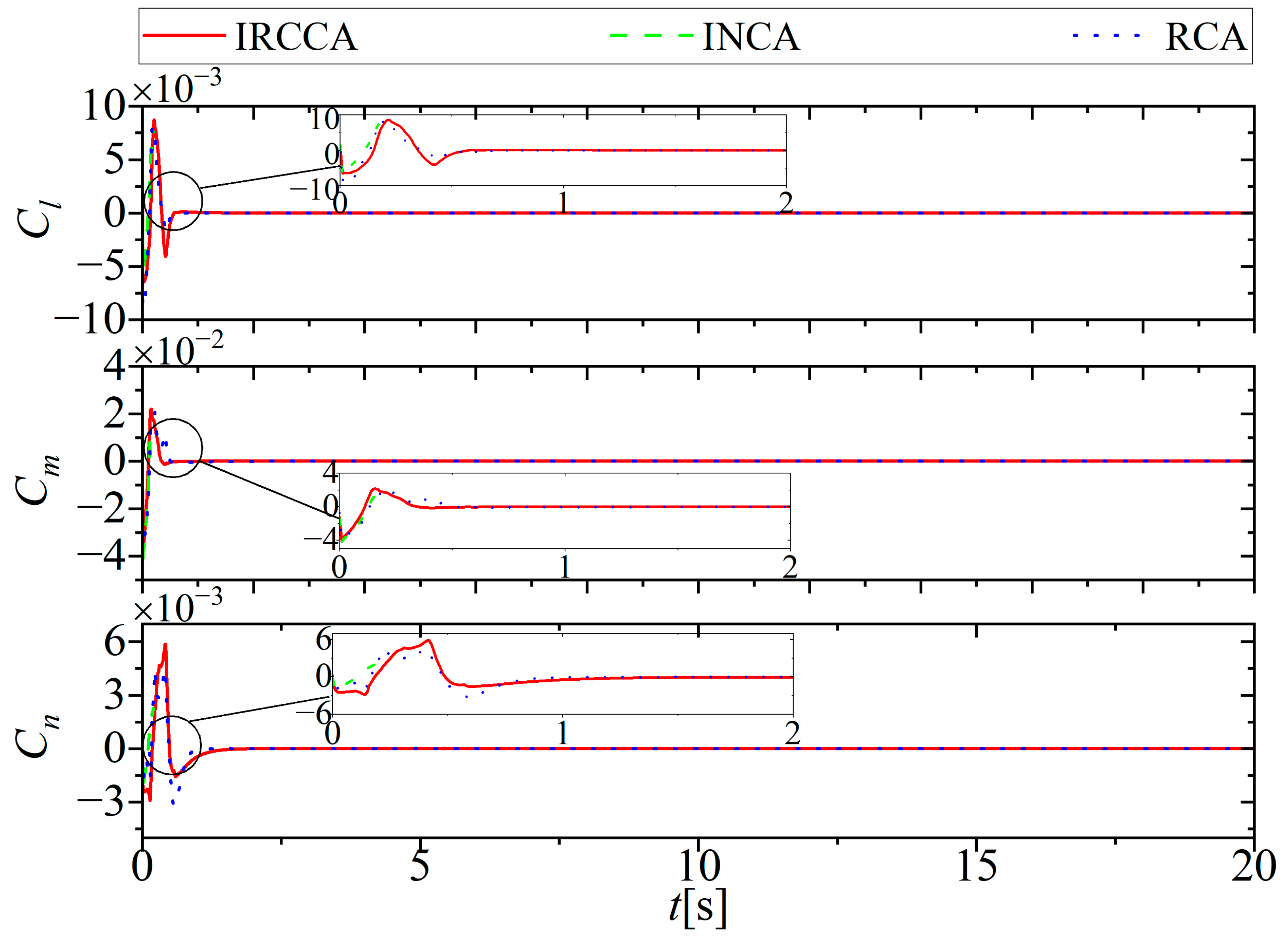
5.1. No Actuator Fault
5.2. Lock-in-Place Fault
5.3. Loose Fault
5.4. Loss of Effectiveness Fault
5.5. Multiple Faults
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niestroy, M.A.; Dorsett, K.M.; Markstein, K. A tailless fighter aircraft model for control-related research and development. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Hou, Y.; Lv, M.; Liang, X.; Yang, A. Fuzzy adaptive fixed-time fault-tolerant attitude tracking control for tailless flying wing aircrafts. Aerosp. Sci. Technol. 2022, 130, 107950. [Google Scholar] [CrossRef]
- Li, H.; Sun, L.; Tan, W.; Liu, X.; Dang, W. Incremental dual heuristic dynamic programming based hybrid approach for multi-channel control of unstable tailless aircraft. IEEE Access 2022, 10, 31677–31691. [Google Scholar] [CrossRef]
- He, Z.; Hu, J.; Wang, Y.; Cong, J.; Han, L.; Su, M. Sample entropy based prescribed performance control for tailless aircraft. ISA Trans. 2022, 131, 349–366. [Google Scholar] [CrossRef]
- He, Z.; Hu, J.; Wang, Y.; Cong, J.; Han, L.; Su, M. Incremental Backstepping Sliding-Mode Trajectory Control for Tailless Aircraft with Stability Enhancer. Aerospace 2022, 9, 352. [Google Scholar] [CrossRef]
- Shayan, K.; Van Kampen, E.-J. Online Actor-Critic-Based Adaptive Control for a Tailless Aircraft with Innovative Control Effectors. In Proceedings of the AIAA Scitech 2021 Forum, Online, 11–15 and 19–21 January 2021. [Google Scholar] [CrossRef]
- Harris, J.; Elliott, C.M.; Tallant, G.S. L1 Adaptive Nonlinear Dynamic Inversion Control for the Innovative Control Effectors Aircraft. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Cai, W.; Liao, X.H.; Song, Y.D. Indirect Robust Adaptive Fault-Tolerant Control for Attitude Tracking of Spacecraft. J. Guid. Control Dyn. 2008, 31, 1456–1463. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Jiang, H.; Sun, X. Passive fault-tolerant path following control of autonomous distributed drive electric vehicle considering steering system fault. Mech. Syst. Signal Process. 2019, 123, 298–315. [Google Scholar] [CrossRef]
- Zhu, G.; Du, J.; Li, J.; Kao, Y. Robust adaptive NN tracking control for MIMO uncertain nonlinear systems with completely unknown control gains under input saturations. Neurocomputing 2019, 365, 125–136. [Google Scholar] [CrossRef]
- Yazar, I.; Caliskan, F.; Kiyak, E. Multiple fault-based FDI and reconfiguration for aircraft engine sensors. Aircr. Eng. Aerosp. Technol. 2017, 89, 397–405. [Google Scholar] [CrossRef]
- Kilic, U.; Unal, G. Sensor fault detection and reconstruction system for commercial aircrafts. Aeronaut. J. 2022, 126, 889–905. [Google Scholar] [CrossRef]
- Unal, G. Fuzzy robust fault estimation scheme for fault tolerant flight control systems based on unknown input observer. Aircr. Eng. Aerosp. Technol. 2021, 93, 1624–1631. [Google Scholar] [CrossRef]
- Kilic, U.; Unal, G. Aircraft air data system fault detection and reconstruction scheme design. Aircr. Eng. Aerosp. Technol. 2021, 93, 1104–1114. [Google Scholar] [CrossRef]
- Li, B.; Hu, Q.; Ma, G.; Yang, Y. Fault-Tolerant Attitude Stabilization Incorporating Closed-Loop Control Allocation Under Actuator Failure. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1989–2000. [Google Scholar] [CrossRef]
- Li, Y.; Hou, M.; Liang, S.; Jiao, G. Predefined-time adaptive fault-tolerant control of hypersonic flight vehicles without overparameterization. Aerosp. Sci. Technol. 2020, 104, 105987. [Google Scholar] [CrossRef]
- Unal, G. Integrated design of fault-tolerant control for flight control systems using observer and fuzzy logic. Aircr. Eng. Aerosp. Technol. 2021, 93, 723–732. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, C.; Ji, K.; Zhang, H. Prescribed performance incremental adaptive optimal fault-tolerant control for nonlinear systems with actuator faults. ISA Trans. 2022, 120, 99–109. [Google Scholar] [CrossRef]
- Cui, L.; Zuo, Z.; Yang, Y. A Control-Theoretic Study on Iterative Solution to Control Allocation for Over-Actuated Aircraft. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3429–3439. [Google Scholar] [CrossRef]
- Su, Y.; Yu, P.; Gerber, M.J.; Ruan, L.; Tsao, T.-C. Nullspace-Based Control Allocation of Overactuated UAV Platforms. IEEE Robot. Autom. Lett. 2021, 6, 8094–8101. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, Z. A New Method for Control Allocation of Aircraft Flight Control System. IEEE Trans. Autom. Control 2020, 65, 1413–1428. [Google Scholar] [CrossRef]
- Tohidi, S.S.; Yildiz, Y.; Kolmanovsky, I. Adaptive control allocation for constrained systems. Automatica 2020, 121, 109161. [Google Scholar] [CrossRef]
- de Almeida, F.A. Robust off-line control allocation. Aerosp. Sci. Technol. 2016, 52, 1–9. [Google Scholar] [CrossRef]
- Servidia, P.; Pena, R. Spacecraft thruster control allocation problems. IEEE Trans. Autom. Control 2005, 50, 245–249. [Google Scholar] [CrossRef]
- Oppenheimer, M.W.; Doman, D.B.; Bolender, M.A. Control Allocation for Over-actuated Systems. In Proceedings of the 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006; pp. 1–6. [Google Scholar]
- Harkegard, O. Efficient active set algorithms for solving constrained least squares problems in aircraft control allocation. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 2, pp. 1295–1300. [Google Scholar]
- Luo, Y.; Serrani, A.; Yurkovich, S.; Doman, D.; Oppenheimer, M.W. Model predictive dynamic control allocation with actuator dynamics. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 2, pp. 1695–1700. [Google Scholar] [CrossRef]
- Galeani, S.; Sassano, M. Data-driven dynamic control allocation for uncertain redundant plants. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 5494–5499. [Google Scholar]
- Naderi, M.; Sedigh, A.K.; Johansen, T.A. Guaranteed feasible control allocation using model predictive control. Control Theory Technol. 2019, 17, 252–264. [Google Scholar] [CrossRef]
- Elsisi, M.; Zaini, H.G.; Mahmoud, K.; Bergies, S.; Ghoneim, S.S. Improvement of Trajectory Tracking by Robot Manipulator Based on a New Co-Operative Optimization Algorithm. Mathematics 2021, 9, 3231. [Google Scholar] [CrossRef]
- Elsisi, M.; Tran, M.Q. Development of an IoT Architecture Based on a Deep Neural Network against Cyber Attacks for Automated Guided Vehicles. Sensors 2021, 21, 8467. [Google Scholar] [CrossRef]
- Gai, W.; Wang, H. Closed-loop dynamic control allocation for aircraft with multiple actuators. Chin. J. Aeronaut. 2013, 26, 676–686. [Google Scholar] [CrossRef]
- Hu, Q.; Li, B.; Zhang, Y. Nonlinear proportional derivative control incorporating closed-loop control allocation for spacecraft. J. Guid. Control Dyn. 2014, 37, 799–812. [Google Scholar] [CrossRef]
- Chen, L.; Duan, D.; Sun, D. Design of a multi-vectored thrust aerostat with a reconfigurable control system. Aerosp. Sci. Technol. 2016, 53, 95–102. [Google Scholar] [CrossRef]
- Almutairi, S.H.; Aouf, N. Reconfigurable dynamic control allocation for aircraft with actuator failures. Aeronaut. J. 2017, 121, 341–371. [Google Scholar] [CrossRef]
- Ergocmen, B. Reconfigurable Dynamic Control Allocation with SDRE As a FTFC for NASA GTM Design. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021. [Google Scholar]
- Doman, D.; Sparks, A. Concepts for constrained control allocation of mixed quadratic and linear effectors. In Proceedings of the 2002 American control conference, Anchorage, AK, USA, 8–10 May 2002; Volume 5, pp. 3729–3734. [Google Scholar]
- Poonamallee, V.; Yurkovich, S.; Serrani, A.; Doman, D.; Oppenheimer, M.W. A nonlinear programming approach for control allocation. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 1689–1694. [Google Scholar] [CrossRef]
- Bolender, M.A.; Doman, D.B. Nonlinear Control Allocation Using Piecewise Linear Functions. J. Guid. Control Dyn. 2004, 27, 1017–1027. [Google Scholar] [CrossRef]
- Tol, H.J.; De Visser, C.C.; Van Kampen, E.; Chu, Q.P. Nonlinear Multiariate spline-based control allocation for high-performance aircraft. J. Guid. Control Dyn. 2014, 37, 1840–1862. [Google Scholar] [CrossRef]
- Matamoros, I. Incremental Nonlinear Control Allocation for a Tailless Aircraft with Innovative Control Effectors. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Tang, X.; Zhai, D.; Li, X. Adaptive fault-tolerance control based finite-time backstepping for hypersonic flight vehicle with full state constrains. Inf. Sci. 2019, 507, 53–66. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Y.; Lv, M.; Chang, J.; Pei, B. Predefined-time anti-saturation fault-tolerant attitude control for tailless aircraft with guaranteed output constraints. Nonlinear Dyn. 2022, 111, 1399–1416. [Google Scholar] [CrossRef]
- Cui, Y.; Li, A.; Duan, B.; Wasif, S. Reconfiguration Control Design of UAV against Actuator Faults Based on Control Allocation Method. Int. J. Aerosp. Eng. 2022, 2022, 4481553. [Google Scholar] [CrossRef]
- Johann, K. Advanced Flight Control Design And evaluation: An Application of Time Delayed Incremental Backstepping. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Smeur, E.J.; Chu, Q.P.; de Croon, G.C. Adaptive Incremental Nonlinear Dynamic Inversion for Attitude Control of Micro Aerial Vehicles. J. Guid. Control Dyn. 2016, 39, 450–461. [Google Scholar] [CrossRef]
- Jury, E.I. A Simplified Stability Criterion for Linear Discrete Systems. Proc. IRE 1962, 50, 1493–1500. [Google Scholar] [CrossRef]
- Liberzon, D. Hybrid feedback stabilization of systems with quantized signals. Automatica 2003, 39, 1543–1554. [Google Scholar] [CrossRef]
- Stolk, A.J. Minimum Drag Control Allocation for the Innovative Control Effector Aircraft. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]

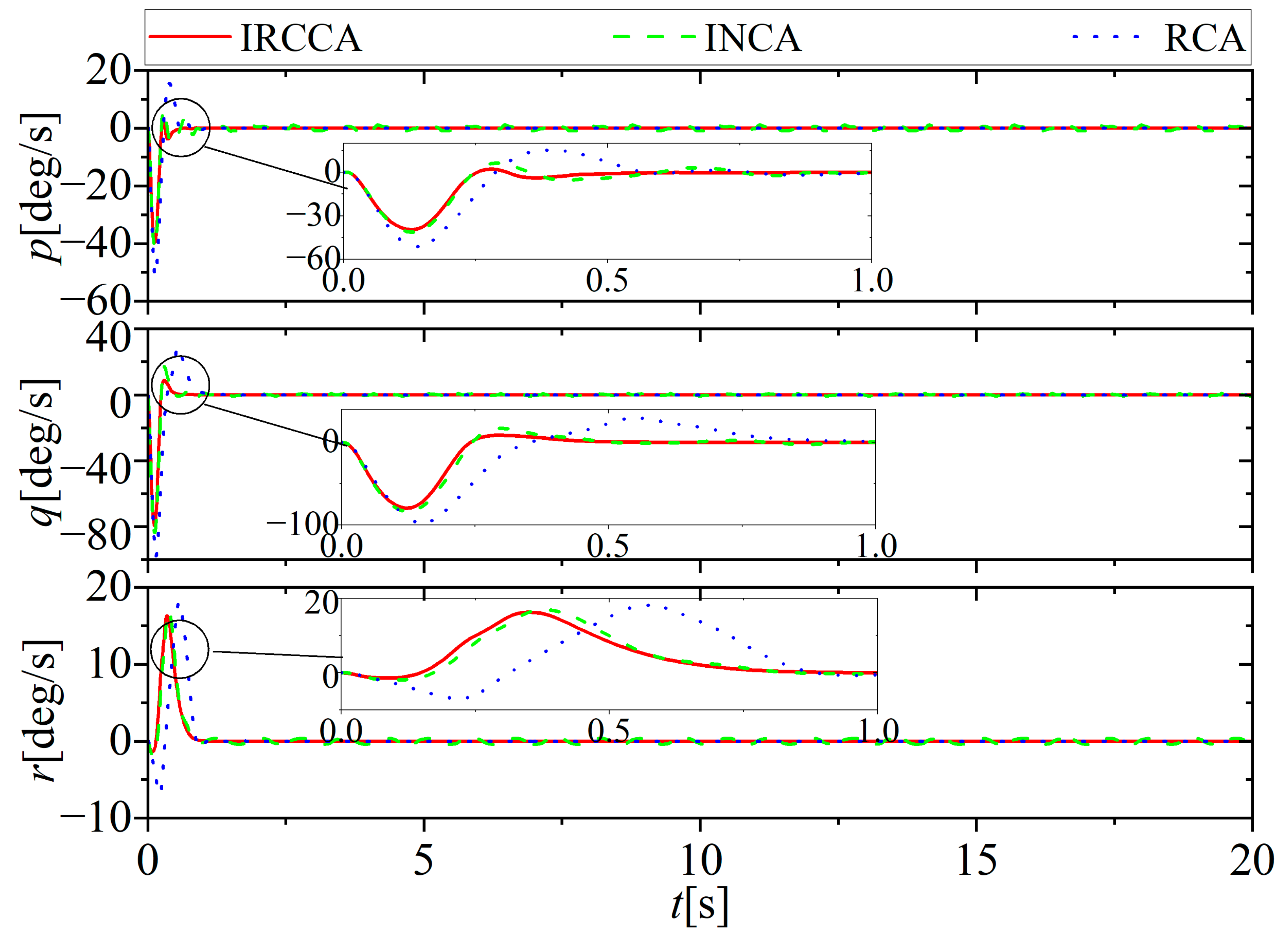
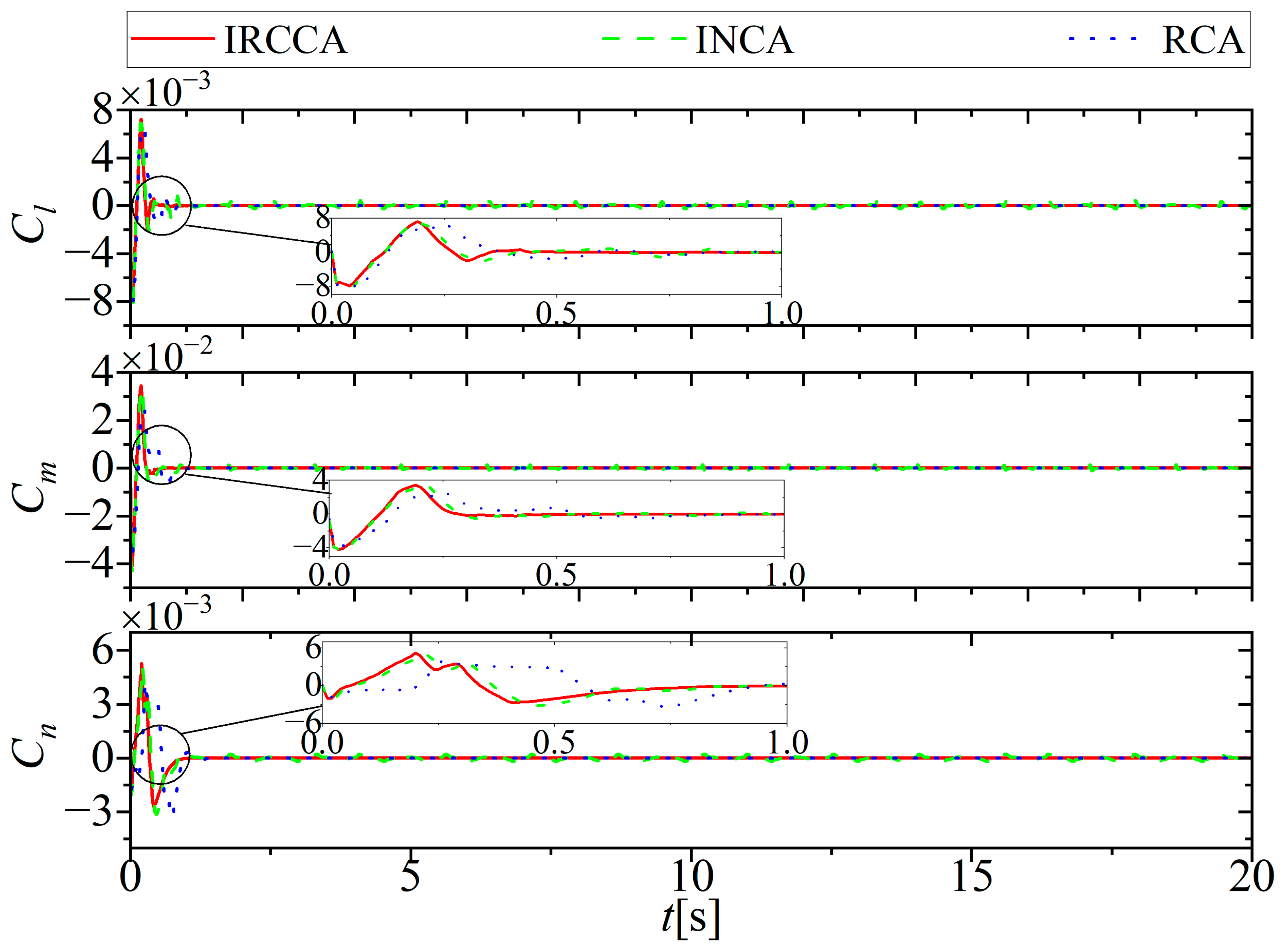
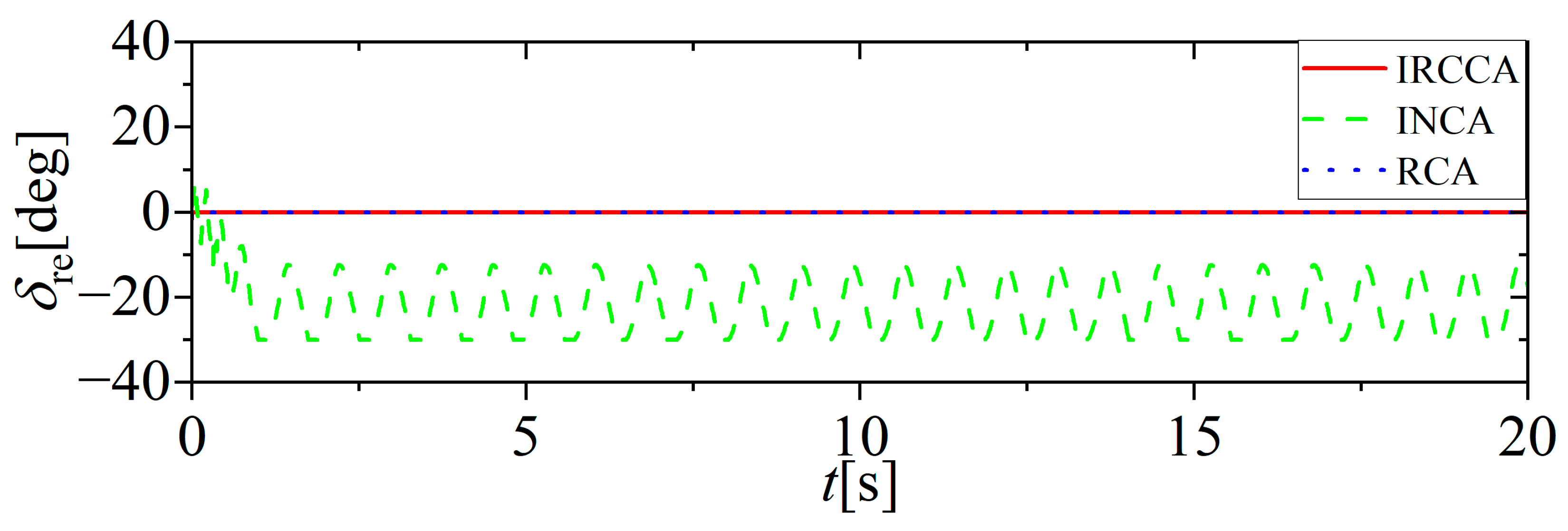
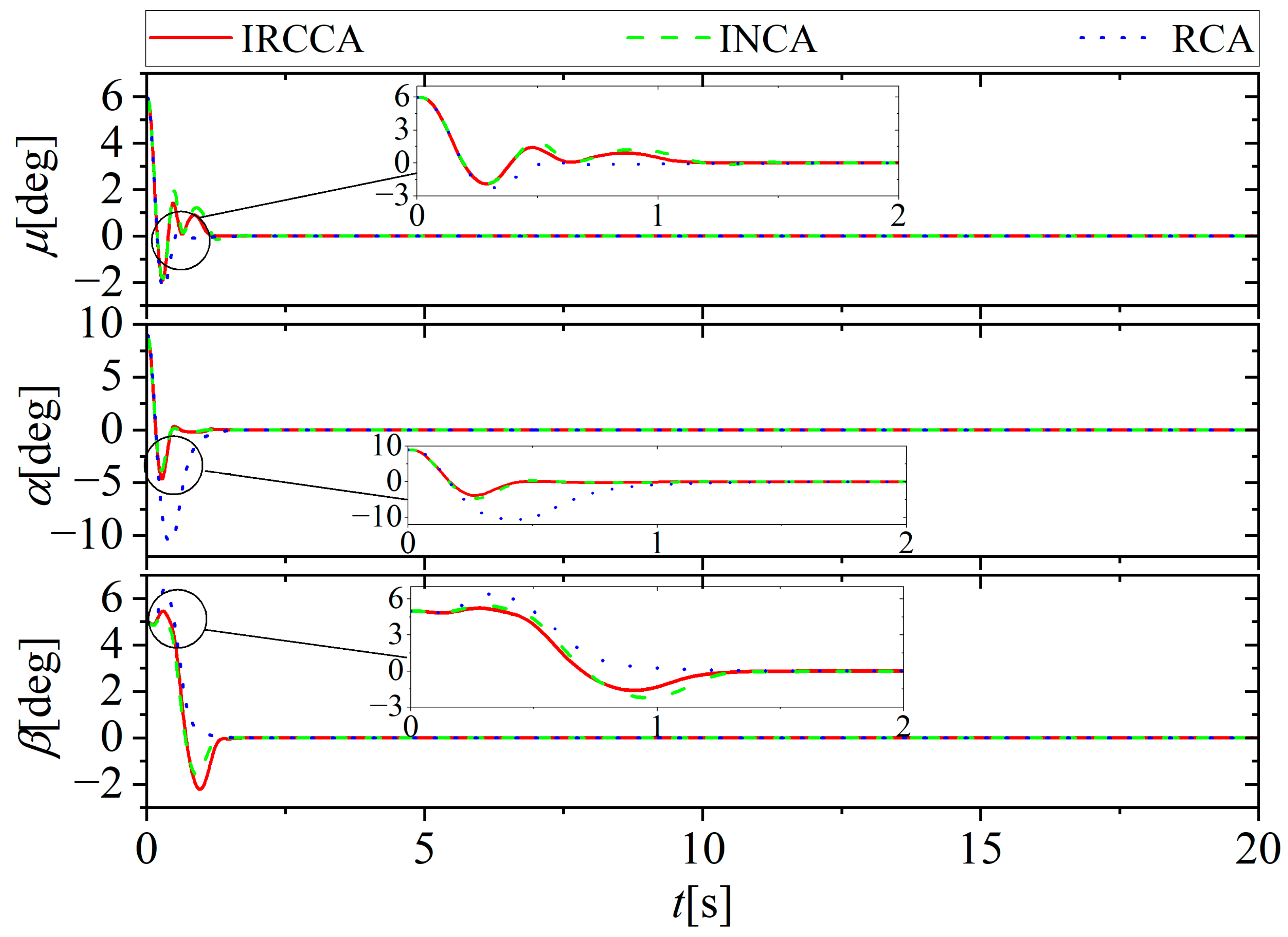

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 37.5 [ft] | 81,903 [slug-ft2] | ||
| 28.75 [ft] | 118,379 [slug-ft2] | ||
| 808.6 [ft2] | −525 [slug-ft2] | ||
| 42,576 [slug-ft2] | −525 [slug-ft2] |
| Parameter | The Operation Range [deg] | Parameter | The Operation Range [deg/s] |
|---|---|---|---|
| [−5,30] | [−100,100] | ||
| [−20,20] | [−100,100] | ||
| [−90,90] | [−100,100] |
| Control Actuator | Notation | Position Limit [deg] | Rate Limit [deg/s] |
|---|---|---|---|
| Inboard leading-edge flap (ILEF) | [0,40] | 40 | |
| Outboard leading-edge flap (OLEF) | [−40,40] | 40 | |
| All moving wing tips (AMT) | [0,60] | 150 | |
| Elevons | [−30,30] | 150 | |
| Spoiler-slot deflectors (SSD) | [0,60] | 150 | |
| Pitch flaps (PF) | [−30,30] | 150 |
| Fault Matrix | Parameters of Actuator Faults |
|---|---|
| Method | RCA | INCA | IRCCA |
|---|---|---|---|
| Simulation time | 8.796 s | 16.051 s | 16.771 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, J.; Hu, J.; Wang, Y.; He, Z.; Han, L.; Su, M. Fault-Tolerant Attitude Control Incorporating Reconfiguration Control Allocation for Supersonic Tailless Aircraft. Aerospace 2023, 10, 241. https://doi.org/10.3390/aerospace10030241
Cong J, Hu J, Wang Y, He Z, Han L, Su M. Fault-Tolerant Attitude Control Incorporating Reconfiguration Control Allocation for Supersonic Tailless Aircraft. Aerospace. 2023; 10(3):241. https://doi.org/10.3390/aerospace10030241
Chicago/Turabian StyleCong, Jiping, Jianbo Hu, Yingyang Wang, Zihou He, Linxiao Han, and Maoyu Su. 2023. "Fault-Tolerant Attitude Control Incorporating Reconfiguration Control Allocation for Supersonic Tailless Aircraft" Aerospace 10, no. 3: 241. https://doi.org/10.3390/aerospace10030241
APA StyleCong, J., Hu, J., Wang, Y., He, Z., Han, L., & Su, M. (2023). Fault-Tolerant Attitude Control Incorporating Reconfiguration Control Allocation for Supersonic Tailless Aircraft. Aerospace, 10(3), 241. https://doi.org/10.3390/aerospace10030241






