Abstract
The aim of this study is to analyze lunar trajectories with the optimal junction point of geocentric and selenocentric segments. The major motivation of this research is to answer two questions: (1) how much of the junction of the trajectory segments at the libration point between the Earth and the Moon is non-optimal? and (2) how much can the trajectory be improved by optimizing the junction point of the two segments? The formulation of the end-to-end optimization problem of power-limited trajectories to the Moon and a description of the method of its solution are given. The proposed method is based on the application of the maximum principle and continuation method. Canonical transformation is used to transform the costate variables between geocentric and selenocentric coordinate systems. For the initial guess, a collinear libration point between the Earth and the Moon is used as a junction point, and the transformation to the optimal junction of these segments is carried out using the continuation method. The developed approach does not require any user-supplied initial guesses. It provides the computation of the optimal transfer duration for trajectories with a given angular distance and facilitates the incorporation of the perturbing accelerations in the mathematical model. Numerical examples of low-thrust trajectories from an elliptical Earth orbit to a circular lunar orbit considering a four-body ephemeris model are given, and a comparison is made between the trajectories with an optimal junction point and the trajectories with a junction of geocentric and selenocentric segments at the libration point.
1. Introduction
The use of electric propulsion systems (EPS) for space transportation between an Earth orbit and a lunar orbit is an urgent issue for advanced lunar missions, including the problems of cargo support for lunar manned programs and the transportation of robotic spacecrafts, which are launched into Earth orbits as a piggyback payload, to the Moon. To successfully implement these missions, it is necessary to develop new methods and improve existing methods to calculate and optimize low-thrust Earth–Moon trajectories. An efficient, fast, and stable method to solve the problem of the end-to-end optimization of low-thrust trajectories, which takes into account the gravity of the Earth, the Moon, and the Sun in all segments of trajectory between an Earth orbit and a lunar orbit, is critically important for space mission analysis and design.
In [1], the problem of the end-to-end optimization of low-thrust trajectories from the geosynchronous orbit to the final lunar orbit using nonlinear programming (NLP) was considered, along with all the advantages and disadvantages of this approach. One of the disadvantages of this method is the need to solve a high-dimensional problem of NLP. Therefore, due to the problems with convergence, in [1], solutions to the minimum-time problem are shown only with relatively large values of the thrust acceleration of EPS (about 10−3 m/s).
A solution to the minimum-fuel problem was presented in [2], based on the maximum principle and the continuation method. In this article, low-energy low-thrust lunar trajectories were considered in the framework of the bicircular four-body problem (BR4BP) model. In the considered scheme of transfer in this article, there was no multi-revolution geocentric segment for escape from the initial Earth orbit. The similarity between the optimal geocentric trajectories considered in [2] and impulsive WSB trajectories was noted by the author of this article.
The author of [3] considered a method of designing lunar captures for spacecrafts, starting from a high-energy trajectory around the Earth to a lunar orbit, i.e., the considered scheme of transfer was close to the one that was considered in [2] but with a higher level of thrust acceleration.
In many studies, the approach of dividing trajectory into several segments has been considered to solve the optimization problem of low-thrust trajectories to the Moon. For example, in [4,5,6,7], trajectory with three segments (1) a geocentric segment with an operating EPS; (2) an intermediate segment with a non-operating EPS; and (3) a selenocentric segment with an operating EPS was considered. Sometimes, the number of segments of trajectory was increased to five, with the addition of an initial segment of transfer between low and high orbits around the Earth and a final segment of transfer between high and low orbits around the Moon. The necessity of dividing trajectory into segments is associated, first of all, with the difficulty of ensuring the computational stability of methods to solve the optimization problems of multi-revolution trajectories with a change in the central celestial body using the numerical integration of differential equations of motion written in any fixed (geocentric, selenocentric, or barycentric) coordinate system.
If a trajectory is divided into several segments with the connecting conditions of segments specified in the state space, and the separate trajectory optimization problem is solved on each segment, then the necessary optimality conditions are usually not satisfied at the junction points of these segments; in particular, the discontinuities appear in the optimal control. A violation of the necessary optimality conditions at the junction points of segments of trajectory leads to the deviation of the obtained “patched” trajectories from the optimal ones. To calculate an optimal trajectory, it is necessary to solve the end-to-end optimization problem, which includes the optimization of junction points for each segment of trajectory.
To reduce the number of divisions of trajectory and obtain trajectories sufficiently close to optimal ones with insignificant losses in the cost function (transfer duration or fuel consumption), as an initial guess, some have recommended considering trajectories consisting of one geocentric segment and one selenocentric segment, with the junction of these segments at the libration point EML1 of the Earth–Moon system (intermediate EML1 rendezvous) [8]. The need to pass through the vicinity of the libration point EML1 is a well-known property of low-thrust transfer between an Earth orbit and a lunar orbit. However, the degree of non-optimality of the solution using EML1 as the junction point of geocentric and selenocentric segments of trajectory has not been sufficiently studied so far.
In this article, we consider an approach to optimize trajectories based on the application of the maximum principle for the reduction of the optimal control problem to a boundary value problem and a continuation method to solve this boundary value problem.
We use a system of differential equations of the geocentric and selenocentric motions of spacecrafts in modified equinoctial elements (MEE) [9] and an auxiliary longitude as an independent variable [10,11], which ensures the high computational stability of the solution to the problem of optimizing multi-revolution trajectories. The transformation from the geocentric coordinate system to the selenocentric one (or vice versa) is conveniently performed in the Cartesian coordinate system. In this case, the transformation is reduced to a simple translation of the origin of the coordinate system. The proposed scheme for the transformation from the geocentric coordinate system to the selenocentric coordinate system is as follows: (1) transformation from the geocentric MEE to the geocentric Cartesian coordinate system; (2) transformation from the geocentric Cartesian coordinate system to the selenocentric Cartesian coordinate system; (3) transformation from the selenocentric Cartesian coordinate system to the selenocentric MEE. For each of these coordinate transformations, a canonical transformation of costate variables is derived.
The canonical transformations, which are necessary to preserve the Hamiltonian structure of the equations of optimal motion when replacing the state variables, are often used in optimal control problems. For example, in [12], canonical transformations were used to ensure the continuity of costate variables at the junction point of trajectory segments. Canonical transformations between the spherical coordinates, the Cartesian coordinates (CC), the Keplerian, and the equinoctial elements were presented in [13]. In [14], to solve the problem of optimizing multi-revolution interplanetary transfers using CC, the authors proposed using costate values from modified equinoctial elements as an initial guess. To implement this proposal, a canonical transformation of costate variables from the modified equinoctial elements into a Cartesian coordinate system was used.
In [15], the authors performed a numerical experiment to compare the computational productivity of solving the optimization problem for low-thrust multi-revolution trajectories using different state variables. The results of testing with various types of “solvers” showed that the time needed to solve the problem using MEE was 10 to 35 times lower than the time needed when using Cartesian or spherical coordinates.
Therefore, to calculate trajectories, including segments of multi-revolution escape around the Earth and capture around the Moon, it is advisable to use MEE. In this case, however, the form of the canonical transformation of costate variables at the junction point of the geo- and selenocentric segments of trajectory, which is necessary for end-to-end trajectory optimization, becomes more complicated. To implement this, the authors of this article had to develop a special procedure to calculate it.
The main advantages of the presented method of end-to-end optimization of trajectories to the Moon in this study are the absence of the need to use any initial guess to calculate an optimal trajectory, the automatic calculation of the optimal transfer duration for a given angular distance of its segments, and the simplicity of including arbitrary perturbing accelerations in the mathematical model of motion due to the high-precision calculation of derivatives using complex dual number automatic differentiation (CDNAD).
It should be noted that in the studies known to us, we could not find the derivation of the necessary optimality conditions at the junction point of the segments of trajectory with different gravity centers in the problem statement we are considering. Meanwhile, the analysis of these conditions leads to the conclusion that the assumption of the continuity of all costate variables at the junction point is unfounded. This article shows that there is a discontinuity in some costate variables at the junction point while maintaining the continuity of the optimal control. In the case of the method using zero sphere of influence, the existence of such a discontinuity caused by a discontinuity in acceleration on the sphere of influence was shown in [16]. We show that a discontinuity in terms of costate variables also exists for the identical mathematical models of acceleration in different segments. This discontinuity is associated with a translation of the origin of a coordinate system in the calculation of connected segments of the trajectory.
To date, there are many different problem statements that consider low-thrust transfers and methods for their solution [17]. In this article, we consider the problem of optimizing power-limited trajectories to the Moon. The problem in this formulation has already been considered in a number of studies, for example [18,19]. A solution to the power-limited trajectory optimization problem makes it possible to obtain the estimates of fuel consumption for the transfer of spacecrafts with constant exhaust velocity and limited thrust [10]. The practical significance of the problem of optimizing power-limited trajectories is associated with the possibility of using the solution of this problem as an initial guess to optimize the trajectories with constant exhaust velocity and limited thrust (CEV-problem) [11,20].
The article has the following structure. Section 2 formulates the end-to-end optimization problem of power-limited trajectories to the Moon, including the derivation of the necessary optimality conditions at the junction point of the geocentric and selenocentric segments of trajectory. Section 3 presents the canonical transformations of costate variables, which are necessary to solve the problem of the end-to-end optimization of trajectories. Section 4 describes a method for solving the boundary value problem, to which the trajectory optimization problem is reduced after applying the maximum principle. Section 5 presents numerical examples of optimal low-thrust trajectories to the Moon with optimal junction points of the geocentric and selenocentric segments and their comparison with the optimal trajectories with intermediate EML1 rendezvous. Concluding remarks are presented in Section 6.
2. End-to-End Optimization of the Perturbed Power-Limited Trajectories
Let us consider the problem of optimizing the trajectories of spacecrafts with limited power to the Moon, which is called the LP-problem. We take into account the gravity of the Earth, the Moon, and the Sun on all segments of trajectory, and the position and velocity vectors of the primaries are calculated using JPL ephemeris software [21].
We use the approach given in [10,11] to solve the problem of optimizing the multi-revolution power-limited orbital transfer with a fixed angular distance and free transfer duration. In [10,11], the optimization problems of unperturbed power-limited orbital transfer were considered. In this article, we consider the problem of optimizing perturbed LP-trajectories to the Moon. The dynamic equations of the perturbed motion of spacecrafts with limited power have the following form:
where p is the semi-latus rectum, , are the components of eccentricity vector, , are the components of inclination vector, LK = L − K is the deviation of true longitude from auxiliary longitude K, e is the eccentricity, ω is the argument of perigee, Ω is the right ascension of ascending node, i is the inclination, ν is the true anomaly, , , , μ is the gravitational parameter of the central celestial body, aLPr, aLPt, aLPn are the circumferential, radial, and binormal components of the thrust acceleration, respectively, and apt, apr, and apn are the components of the perturbing acceleration.
It was shown in [10] that for transfers in the central Newtonian gravitational field and in the case when the perturbing accelerations do not explicitly depend on time, the differential equation for time can be excluded from the system of differential equations of motion, and the time costate variable has the form dpt/dK ≡ 0. However, during the process of designing multi-revolution trajectories to the Moon, it is necessary to take into account perturbing accelerations from the gravity of other celestial bodies, which explicitly depend on time. Therefore, the differential equation for t must be included in system (1).
In many studies [8,10,11,22] that used the auxiliary longitude K as an independent variable, the problems of a transfer with a fixed angular distance ΔL and a free transfer duration were considered. These studies showed that the value of LK varies very little in typical multi-revolution optimal trajectories. For example, in the 500-revolution optimal perturbed orbit transfer presented in [23], the value of LK varies from 0 to −0.092 degrees. Therefore, in this article, we will limit ourselves to considering the problems of transfer with a fixed angular distance along the auxiliary longitude ΔK instead of ΔL, and we will optimize the values of LK at the left or right ends of the trajectory. In this case, the final value of the auxiliary longitude will be fixed: Kf = K0 + ΔK.
To calculate the trajectory, we will separately compute the geocentric and selenocentric segments, integrate the system of differential Equation (1), and connect them at the junction point that satisfies the necessary optimality conditions. On the geocentric segment of trajectory, the central celestial body is the Earth, and on the selenocentric segment, it is the Moon. Therefore, on the right-hand side of differential Equation (1), the gravitational parameter μ is determined by the segment of trajectory. Further, the parameters associated with the geocentric segment of trajectory will be denoted by the subscript “gc”, and those associated with the selenocentric segment of trajectory by the subscript “sc”.
The mathematical model of the perturbing acceleration vector on the geocentric apgc and selenocentric apsc segments has the form:
respectively, where r is the vector of the spacecraft’s position with respect to the central celestial body, rM is the vector of the geocentric position of the Moon, rE is the vector of the selenocentric position of the Earth, rS is the vector of the geocentric or the selenocentric position of the Sun, and μE, μM, and μS are the gravitational parameters of the Earth, the Moon, and the Sun.
The power-limited trajectory optimization problem is considered. It is assumed that the power of the EPS Pb = Tc/2 is given, but within this limitation, the thrust magnitude T and the exhaust velocity magnitude c can be varied arbitrarily. It is known that the differential equations of the optimal motion of a spacecraft for the LP-problem are divided into dynamic and parametric parts [24]. The dynamic part (1) does not depend on the spacecraft mass m. The dependence of the spacecraft mass on time t is calculated by the relation , where and . Therefore, in the case under consideration, the problem of minimizing fuel consumption mp = m0 − mf is equivalent to the problem of minimizing the cost function JLP [10]. The cost function of the form JLP is often called the “energy” criteria. The choice of this cost function facilitates the numerical solution of the problem. However, the main reason for choosing such a criterion is the possibility of the continuation of the obtained solutions to optimal trajectories with a constant exhaust velocity and finite thrust [11,20,22].
After replacing the independent variable t by K, taking into account the last equation in (1), the expressions for the considered cost function on the geocentric and selenocentric segments of trajectory will take the form [10,11]:
where t1 is the time of passing the junction point of the geocentric and selenocentric segments, and K1 is the intermediate value of the auxiliary longitude value K0 < K1 < Kf. The value of is calculated by the relation of , and the final auxiliary longitude is . As was shown in [10,11], the zero value of K0 and can be used without a loss of generality.
The Pontryagin function of the optimal control problem (1), (2) has the form:
where , , and are the parts of the Pontryagin function depending, respectively, on the thrust acceleration aLP, the perturbing accelerations, and the time costate variable, aLP = [aLPt, aLPr, aLPn]T, aLP = |aLP|, AT = (At, Ar, An),
and pp, pex, pey, pix, piy, pLK, pm, and pt are the costate variables to the corresponding state variables of the system p, ex, ey, ix, iy, LK, m, t, , . From the maximum condition for the Pontryagin function (3) with respect to the control aLP, it is easy to obtain an expression for the optimal control:
substituting an expression for the Hamiltonian of the optimal control problem under consideration, which we obtain in (3):
where . In contrast to the unperturbed problem, the Hamiltonian explicitly depends on time; therefore, dpt/dK ≠ 0 and pt(K) ≠ 0. The equations of optimal motion have the form:
where xT = (p, ex, ey, ix, iy), pxT = (pp, pex, pey, pix, piy).
When calculating trajectories to the Moon, the time t1 of passing the junction point (optimal junction point or libration point EML1), is fixed and the time of departure from the initial Earth orbit and the time of insertion into the final lunar orbit must satisfy the necessary optimality conditions.
The initial conditions of the geocentric segment of trajectory, considering the possibility to set K0 = 0 without loss of generality [10], can be written as:
The final conditions of the selenocentric segment of trajectory can be written as:
To ensure the continuity of the state vector, the conditions for connecting the geocentric and selenocentric segments of trajectory at the given time t1 have the following form:
where the orbital elements at the end of the geocentric and at the beginning of the selenocentric segments of trajectory are calculated in the geocentric coordinate system, .
To solve the boundary value problem (7)–(10), it is necessary to calculate five components of the vector px(0), initial values of LK and t for the geocentric segment, as well as five components of the vector px(K1+), the initial value of pt, and the final value of LK for the selenocentric segment (a total of 14 decision variables). In addition, the six elements of the geocentric orbit x(K1+) and LK(K1+) at the junction point at the beginning of the selenocentric segment are unknown. Thus, the problem under consideration contains 14 + 6 = 20 decision variables.
Boundary conditions (8), (9), and (10) determine only seven equations for the geocentric segment and seven equations for the selenocentric segment, which, in total, is 7 + 7 = 14 equations to calculate these 20 decision variables. These 14 equations must be supplemented with 6 additional necessary optimality conditions for the junction point.
The choice of the condition type, under which the transformation from the geocentric motion to the selenocentric motion occurs, is rather arbitrary. From our point of view, it is convenient to locate the junction point of the geocentric and the selenocentric segments of trajectory on the instantaneous Hill sphere of the Moon, i.e., on the sphere with the center at the Moon’s center and with the radius r1*, which is equal to the selenocentric distance of the EML1 point at the junction moment t1. This choice allows us to use a smooth continuation from the trajectory with intermediate EML1 rendezvous to the trajectory with an optimal junction point.
The conditions for continuity of the trajectory at the junction point of geocentric and selenocentric segments (10) at a given time t1 can be rewritten using variables in Cartesian coordinates:
where r− and v− are the position and velocity vectors of the spacecraft in the geocentric coordinate system at the final moment t− of the geocentric segment, r+ and v+ are the position and velocity vectors of the spacecraft in the selenocentric coordinate system at the initial moment t+ of the selenocentric segment, and rM and vM are the position and velocity vectors of the Moon in the geocentric coordinate system at a fixed moment of junction t1, and .
The selected junction condition on the Hill sphere of the Moon has the form:
where r+ = |r+|.
To derive the necessary optimality conditions at the junction point, we write the Lagrange endpoint function in the form:
where are the Lagrange multipliers. For such a Lagrange endpoint function, the transversality conditions take the following form:
From these conditions follow the relations and
To calculate the boundary conditions (11) and (12), the transformation from the system of modified equinoctial elements into a Cartesian state vector is required, and to calculate the necessary optimality conditions (15), the corresponding canonical transformation of the costate vector is required. The required transformation functions to calculate (11), (12), and (15) are given in the next section and in the Appendix A of the article. It follows from the Equation (15) that the vector pv is continuous at the junction point, the vector pr undergoes a discontinuity along the selenocentric radius of the junction point, and the time costate variable pt also undergoes a discontinuity due to the fixed value of t1.
The conditions (12) and (15) close the system of boundary conditions for the considered boundary value problem of the maximum principle. The decision vector of the boundary value problem (7)–(10), (12), (15) consists of the following decision variables:
- the values of five components of the vector px(0);
- the initial values of LK and t for the geocentric segment;
- the values of five components of the vector px(K1+);
- the initial value of pt(K1+) and the final value of LK(Kf) for the selenocentric segment;
- the values of six osculating elements of the orbit (x(K1), LK(K1)) at the junction point;
- the value of Lagrange multiplier λ1.
The values of these 21 decision variables must be chosen to satisfy 7 equations in (9), 7 equations in (10), 1 equation in (12), and 6 equations in (15) (21 equations in total).
3. Canonical Transformation of Costate Variables
The division of the entire trajectory into geocentric and selenocentric segments requires the transformation of state and costate variables. To transform state variables between non-rotating Cartesian geoequatorial geocentric and selenocentric coordinate systems, only the translation of the origin of the coordinate system between the centers of the Earth and the Moon is necessary. If the MEEs are used as state variables, then it is additionally required to calculate the geocentric vectors of the position and velocity of spacecraft from the known values of the geocentric orbital elements at the junction point. Additionally, during the calculation of the selenocentric vectors of the position and velocity of spacecraft at the junction point, it is necessary to calculate the selenocentric orbital elements.
To transform costate variables from the geocentric coordinate system to the selenocentric one (or vice versa), a canonical transformation [25] that preserves the Hamiltonian form of Equation (7) must be used. Canonical transformations are often used in optimal control problems for the transformation of the costate variables between different coordinate systems and/or orbital elements [13,14].
Let x = (x1, x2, …, xn)T, p = (p1, p2, …, pn)T represent the (old) system of state and costate variables and x* = (x*1, x*2, …, x*n)T, p* = (p*1, p*2, …, p*n)T represent another (new) system. The transformation between the coordinates x and x* can be expressed in terms of the transformation function of the state variable F:
If the transformation of state variables (16) is used, then the old and new costate variables of the Hamiltonian system are obeyed to the following canonical transformation:
A transformation of costate variables in the opposite direction, i.e., from the old system to the new one can be represented as:
where S is the transformation function of the state variables from x* to x.
Thus, to calculate new costate variables p*, it is necessary to calculate the Jacobian matrix ∂S(x*)/∂x*. If the vector function S has a complex analytical representation that makes it difficult to calculate its Jacobian, and the vector function of the direct transformation of state variables F is simpler, then the second part of the Equation (18) can be used, for which the matrix ∂F(x)/∂x must be calculated. The high-precision calculation of the matrices ∂S(x*)/∂x* and ∂F(x)/∂x is possible via the complex step differentiation [26] or via automatic differentiation using the algebra of dual numbers [27] if necessary.
In this study, the modified equinoctial orbital elements are used as state variables, and the necessary optimality conditions of the junction point are most conveniently represented in the Cartesian coordinate system using state variables . In this regard, canonical transformations are needed from the system of modified equinoctial elements to the Cartesian coordinate system at the end of the geocentric segment, between the geocentric and selenocentric Cartesian coordinate systems considering the necessary optimality conditions at the junction point, and from the Cartesian coordinate system to the system of modified equinoctial elements at the beginning of the selenocentric segment of trajectory.
To transform between the Cartesian coordinates and the modified equinoctial elements at the known value of the auxiliary longitude K, the transformation functions Q and G are used:
Expressions for these transformation functions are given in the Appendix A.
For the canonical transformation from a system of modified equinoctial elements to a non-rotating Cartesian coordinate system, the first equation in (19) must be supplemented with one of the following equations:
where , . It is obvious that the analytic representation of the transformation Q is much simpler than that of G, so it is reasonable to use the second equation in (20) for the canonical transformation.
To implement the inverse canonical transformation (from a non-rotating Cartesian coordinate system to a system of modified equinoctial elements), it is necessary to supplement the second equation in (19) with the equation:
The accuracy of canonical transformations was verified via comparison with the results presented in [14]. The values of costate variables after canonical transformations (20) and (21) coincided with the corresponding values from [14] up to 12 decimal places.
4. General Scheme for The Solution of End-to-End Trajectory Optimization
The boundary value problem (7), (8), (9), (10), (12), and (15) of the maximum principle can be formally represented as the system of nonlinear equations for residuals on the geocentric segment of trajectory fgc, at the junction point fjunc, and on the selenocentric segment of trajectory fsc: f = [fgcT, fjuncT, fscT]:
where Ggc is the transformation function from xcc to xmee in geocentric motion (using the gravitational parameter of the Earth), Qsc is the transformation function from xmee to xcc in selenocentric motion (using the gravitational parameter of the Moon), and is the vector of geocentric position and the velocity of the Moon. To solve systems (22), (23), and (24), it is necessary to calculate the decision vector z = [zgcT, zjuncT, zscT], which includes eight decision variables of the geocentric segment zgc = [pxT (0), LK (0), t (0), λ1]T, six decision variables of the junction zone , and seven decision variables of the selenocentric segment zsc = [pr+T, pv+T, pt+]T. A canonical transformation, based on function Q, is used to calculate the Cartesian coordinates, the components of velocity, and their costate variables at the junction point.
It should be noted that Equation (23) is introduced into the vector of residuals to improve the convergence and stability of the numerical method in the same way as using the intermediate nodes in the multiple shooting method. This approach makes it possible to reduce the sensitivity of the vector of residuals f to variations of the decision vector z in the process of solving the boundary value problem.
An effective method of solving the considered class of boundary value problems is the continuation method [10,11,20,22]. To calculate the right-hand sides of differential equations of the continuation method, it is required to calculate the partial derivatives of the residual vector with respect to decision vector of the boundary value problem:
When calculating the trajectory, we will separately compute the geocentric and selenocentric segments so that the decision variables of the selenocentric segment do not affect to the residual vector of the geocentric segment: ∂fgc/∂zsc = 0.
The following scheme for solving the end-to-end optimization problem of trajectories to the Moon is used:
- The input data are set: the time t1 of passing the junction point (in the case of solving the optimization problem of trajectories with intermediate EML1 rendezvous, t1 is equal to the time tEML1 of passing the libration point), the elements of the initial Earth orbit x0gc = (p0gc, ex0gc, ey0gc, ix0gc, iy0gc)T, the elements of the final lunar orbit xfsc = (pfsc, exfsc, eyfsc, ixfsc, iyfsc)T, the angular distance of geocentric segment of trajectory ΔKgc, and the angular distance of selenocentric segment of trajectory ΔKsc;
- The continuation method is used to solve a boundary value problem for calculating the optimal perturbed LP-trajectory with a junction of the geocentric and selenocentric segments at the EML1 point. The continuation parameter τ is introduced into the right-hand sides of the differential equations for the state and costate variables in such a way that for τ = 0, the differential equations coincide with the equations of the unperturbed LP-problem, and for τ = 1, they coincide with the equations of the perturbed LP-problem, including the perturbed part of the Hamiltonian Hp and the pt-dependent part of Hamiltonian Ht (with additional equations for the time variable and its costate variable). To use the Hamiltonian form of writing these equations, the Hamiltonian must have the form HLP + τ∙(Hp + Ht). As an initial guess for the decision vector, the zero values of costate variables are used in both segments of the trajectory: pp(0) = pex(0) = pey(0) = pix(0) = piy(0) = pLK(0) = 0 (which corresponds to the coasting motion of the spacecraft along the initial orbit of each segment of trajectory). At first, the geocentric segment of the LP-trajectory is calculated, and then, the selenocentric segment of the LP-trajectory is sequentially calculated;
- The continuation method is used to solve a boundary value problem for calculating the optimal perturbed LP-trajectory with an optimal junction point. The values obtained for the perturbed LP-trajectory with intermediate EML1 rendezvous are used as an initial guess for the decision vector of the end-to-end optimization problem. After setting the initial conditions, the system of differential equations of geocentric motion is numerically integrated from K0 to . The residual vector of the boundary value problem of geocentric segment fgc is calculated after integrating the differential equations of the geocentric motion using the technique specified in Section 3. The vector of residuals fjunc is calculated using (23). The initial conditions of the selenocentric segment are set at , and the numerical integration of the system of differential equations of selenocentric motion from to Kf is carried out. The vector of residuals of the boundary value problem of selenocentric segment fsc is calculated. The matrix ∂f/∂z, which is required to calculate the right-hand sides of the differential equations of the continuation method, is calculated based on the use of automatic differentiation using CDNAD [22].
One of the ways to estimate the degree of difference between the trajectory with an optimal junction point and with a junction at the EML1 point is the magnitude of the velocity when passing through the junction point of two segments. To calculate the velocity of a spacecraft in a rotating coordinate system at the time of passing the optimal junction point in the framework of the perturbed ephemeris model, it is necessary to transform from the inertial coordinate system J2000 to the rotating coordinate system.
Let us introduce a rotating coordinate system related to the current position and velocity of the Moon in the geocentric coordinate system J2000 as follows. The unit vectors along the coordinate axes of this system in the J2000 system are calculated via the following expressions:
and the instantaneous angular velocity of the Moon’s rotation is calculated by the expression:
The position and velocity vectors of the spacecraft relative to the Earth in the inertial coordinate system can be expressed using the coordinates and the components of velocity of the spacecraft in the rotating system relative to the Earth in the following form:
where are the position vector and velocity vector of the spacecraft in the rotating system. Further, the adimensional position vector of the spacecraft in the rotating coordinate system will be used to present the numerical results.
5. Numerical Examples
We consider the results of calculating the trajectories with an optimal junction point from the initial highly elliptical Earth orbit having the perigee altitude of 4500 km, the apogee altitude of 50,000 km, the inclination of 25°, the argument of perigee of 248°, and the right ascension of the ascending node (RAAN) of 4° to the circular orbit around the Moon having the altitude of 5000 km, the inclination of 30°, and the RAAN of 4°. The size, shape, and inclination of the selected departure orbit in the considered numerical example are close to typical super geostationary transfer orbit (GTO) when launching via the “Proton-M” launch vehicle. The values of the argument of perigee and the RAAN are chosen close to the values of the corresponding osculating orbital elements of EML1 for a given date of passing the junction point. The problem of optimizing the argument of perigee and the RAAN of the initial orbit was not considered in this study.
For the geocentric segment of trajectory, all altitudes are given relative to the mean radius of the Earth, 6371 km, and the gravitational parameter of the Earth is taken equal to 398,600.436 km3/s2. For the selenocentric segment of trajectory, all altitudes are given relative to the mean radius of the Moon, 1738 km, and the gravitational parameter of the Moon is taken equal to 4902.799 km3/s2. The gravitational parameter of the Sun is taken equal to 132,712,440,018 km3/s2. The date of passing the junction point is 25 December 2023, 00:00:00 UTC. On the corresponding fixed date of the passage of the junction point, the radius of the Hill sphere of the Moon in the selenocentric inertial coordinate system is 58,082.52 km.
The trajectories with an optimal junction point are compared with the trajectories with a junction of the geocentric and selenocentric segments at the EML1 point for the identically given orbital elements of the boundary orbits and time of passing the optimal junction point and the libration point EML1. The angular distances of the transfer are fixed from 4 to 28 revolutions for the geocentric segment and from 1 to 7 revolutions for the selenocentric segment. The total value of the angular distances for transfer to the Moon is calculated as the sum of these values in the geocentric and selenocentric segments: ΔKΣ = ΔKgc + ΔKsc. In this study, trajectories with a ratio of the number of revolutions in the geocentric and selenocentric segments of 4:1 are considered, and the total number of revolutions will be varied in the range of 5 to 35 revolutions. The main criterion to choose the angular distance of trajectory segments is the level of thrust acceleration of EPS. The ratio of the number of revolutions in the geo- and selenocentric segments was selected from the approximate equality condition of the average values of thrust acceleration in these segments.
Table 1 and Table 2 present the main parameters of the optimal trajectories with an optimal junction point and with an intermediate EML1 rendezvous for the different angular distances of transfer.

Table 1.
The main parameters of the optimal trajectories with an optimal junction point.

Table 2.
The main parameters of the optimal trajectories with an intermediate EML1 rendezvous.
In Table 1 and Table 2, we use the following symbols: Δt is the total time of transfer to the Moon, Δvch is the characteristic velocity, JLP is the cost function of the considered problem, and are the mean values of the thrust acceleration for the geocentric and selenocentric segments of the LP-trajectory, and ΔLgc and ΔLsc are the increments of the true longitudes on the geocentric and selenocentric segments of trajectory.
As can be seen from Table 1 and Table 2, the optimization of the junction point leads not only to a decrease in the value of cost function but also to a decrease in the required characteristic velocity value. The cost function of the problem under consideration decreases by a minimum of 7.661% (on the 5-revolution trajectory) and a maximum of 9.842% (on the 30-revolution trajectory), while the characteristic velocity value decreases by a minimum of 8.600% (on the 35-revolution trajectory) and a maximum of 9.685% (on the 15-revolution trajectory).
In the considered cases, the optimization of the junction point made it possible to reduce the total transfer duration along the LP-trajectory to the Moon by at least 10.967% (on the 30-revolution trajectory) and by a maximum of 23.582% (on the 5-revolution trajectory).
Figure 1 shows the projections of the optimal trajectories, which have the angular distance of 5, 20, and 35 revolutions, with an optimal junction point and with a junction of the geocentric and selenocentric segments at the EML1 point in the inertial coordinate system J2000. In Figure 1 and everywhere else in this article, the position of the EML1 libration point is indicated by the red marker “×”, and the position of the optimal junction point is indicated by the red circle. The motion of the Moon is indicated by the dashed gray line. Everywhere else in this article, the solution associated with the trajectory with an optimal junction point is indicated by a blue line, and the trajectory with an intermediate EML1 rendezvous by an orange line.
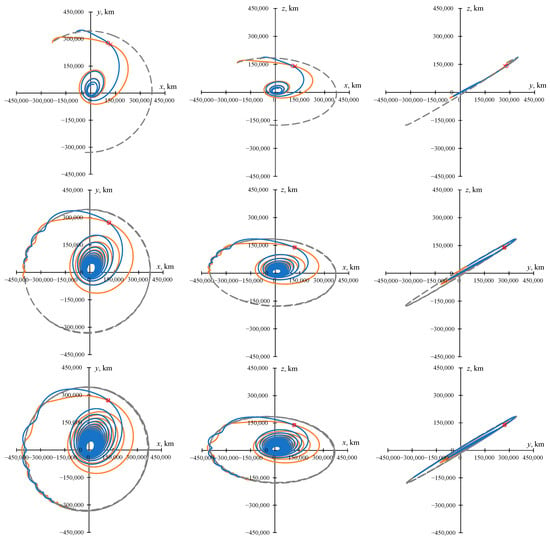
Figure 1.
The projection of the optimal 5-(upper row), 20-(middle row), and 35-(lower row) revolution trajectories with an optimal junction point and with an intermediate EML1 rendezvous in the inertial coordinate system J2000.
On the last revolution of the optimal trajectories with a junction at the EML1 point, the radius of perigee increases compared to trajectories with an optimal junction point, and this is necessary to ensure the approach to the libration point with zero relative velocity. Figure 2 shows the projections of the same optimal trajectories as in Figure 1 onto the XY plane of the rotating coordinate system.
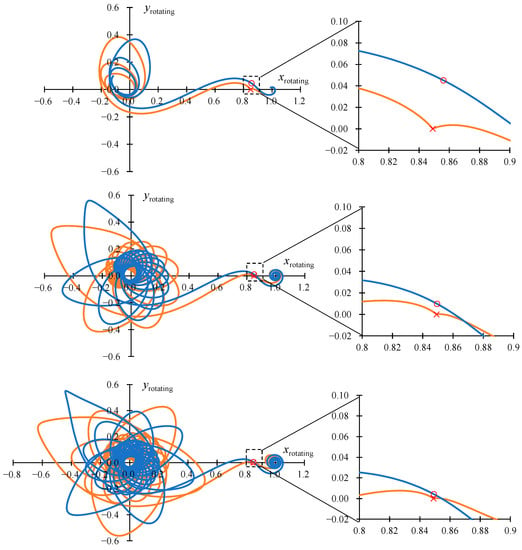
Figure 2.
The projection of optimal 5-(upper row), 20-(middle row), and 35-(lower row) revolution trajectories with an optimal junction point and with an intermediate EML1 rendezvous onto the XY plane in the rotating coordinate system.
This figure shows a significant difference between the optimal LP-trajectories with an optimal junction point and with a junction at the EML1 point in the rotating coordinate system. On the right side of Figure 2, a part of the trajectories near the junction point are shown on an enlarged scale.
According to the results of calculation, as expected, an increase in the number of revolutions leads to a decrease in thrust acceleration (see Table 1) and to a decrease in the distance from the optimal junction point to EML1 point. This is due to the fact that the smaller the thrust acceleration magnitude, the narrower the allowable size of the opening in the vicinity of the libration point EML1 when spacecraft enters into the Hill sphere of the Moon and passes through the opening in such a way that it makes it possible to capture spacecrafts in the orbit around the Moon.
Figure 3 presents the dependences of the optimal thrust acceleration magnitudes on time for the trajectories with an angular distance of 5 (on the left), 20 (on the middle), and 35 (on the right) revolutions. The solution with an optimal junction of two segments makes it possible to ensure the continuity of the optimal control program (thrust acceleration vector) at the junction point and the smooth connection between the geocentric and selenocentric segments of the trajectory. The trajectories with an intermediate EML1 rendezvous, on the contrary, have fractures and discontinuities in the control program at the EML1 point (Figure 2 and Figure 3).
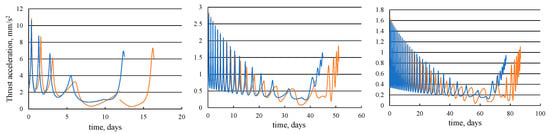
Figure 3.
The time dependence of thrust acceleration for the transfer to the Moon.
Figure 4 presents the time dependences of the adimensional values of costate variables to the vectors r and v on the 4-revolution LP-trajectory to the Moon. For the trajectory with an intermediate EML1 rendezvous (orange line), there is a discontinuity in all six costate variables, since two separate optimization problems for the geocentric and selenocentric segments of trajectory are being solved. In the case of the trajectory with an optimal junction of two segments (blue line), the dependences of the costate variables to the components of the velocity vector pv are continuous, but the costate variables to the components of the position vector pr have a discontinuity λ1·r+/r+ at the junction point.
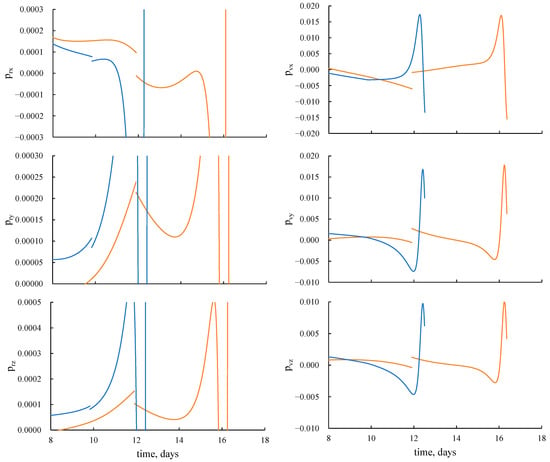
Figure 4.
Variation of the adimensional values of costate variables on the 4-revolution LP-trajectory to the Moon.
The magnitudes of discontinuity of the costate variables to the vector r at the junction moment are = −2.0424·10−5, = −2.18182·10−5, = −1.25671·10−5 for the 4-revolution trajectory, = 1.18001·10−6, = 2.16396·10−6, = 1.22789·10−6 for the 20-revolution trajectory, and = 6.48896·10−7, = 1.31404·10−6, = 7.40291·10−7 for the 35-revolution trajectory. Therefore, the magnitude of the discontinuity in pr decreases as the number of revolutions increases.
Table 3 presents the magnitudes of position and velocity vectors of the optimal junction point in the geocentric rotating coordinate system for transfer with a different number of revolutions.

Table 3.
The magnitudes of adimensional position and dimensional velocity vectors of the optimal junction point in the rotating coordinate system.
In the geocentric rotating coordinate system, the adimensional position vector of the libration point EML1 is equal to (0.849073, 0, 0), and the velocity vector of the EML1 point is equal to (32.18877, 0, 0) m/s. The nonzero value of the first component of the velocity vector of the libration point is due to the use of the ephemeris model of motion, in which the radial velocity of the Moon is not equal to zero. Table 3 shows that the trajectory with the optimal junction point has large values of the velocity components in the rotating coordinate system when passing through the junction point of two segments compared to the trajectories with an intermediate EML1 rendezvous.
The time dependences of velocity in the rotating coordinate system on the 5-, 20-, and 30-revolution trajectories with an optimal junction point and with the intermediate EML1 rendezvous are presented in Figure 5. The deviations of the velocity magnitude Δvrotating in the rotating coordinate system from the velocity magnitude of the libration point EML1 at the junction point of two segments of trajectory are 266.7827 m/s for a 5-revolution trajectory, 224.6906 m/s for a 20- revolution trajectory, and 218.0903 m/s for a 35-revolution trajectory
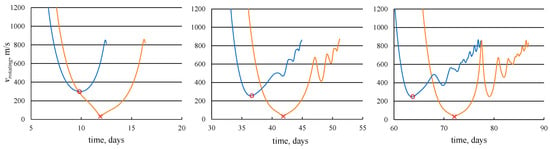
Figure 5.
The time dependences of the velocity in the rotating coordinate system on the 5-(on the left), 20-(in the middle), and 35-revolution (on the right) trajectories with an optimal junction point and with an intermediate EML1 rendezvous.
Figure 6 presents the positions of the optimal junction points of the geocentric and selenocentric segments onto the XY and XZ planes in the rotating coordinate system for the considered trajectories with an angular distance of 5 to 35 revolutions. On the graphs, the libration point is indicated by the red dot, and the optimal junction points of the two segments are indicated by the blue squares. The optimal junction point approaches the libration point EML1 as the total number of revolutions increases (dashed trend lines in Figure 6).
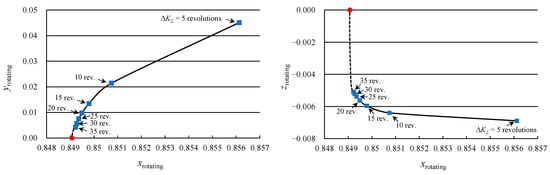
Figure 6.
The positions of the optimal junction points in the rotating coordinate system onto the XY (on the left) and XZ (on the right) planes.
Figure 7 presents the dependencies of the distance djunction point between the optimal junction point and the libration point EML1 on the total number of revolutions of trajectories in the inertial coordinate system. In this Figure, the obtained values of distance between two points are indicated by the black squares. The graph shows the dependence of djunction point on the total increment value of the angular variable K with extrapolation to the region of large values of the angular distance (dashed line).
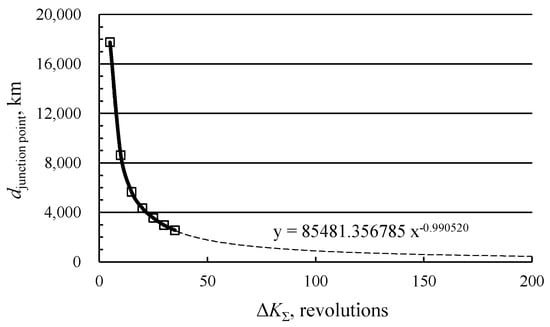
Figure 7.
The dependence of distance between the optimal junction point and the libration point EML1 on the total value of angular variable K in the inertial coordinate system.
With an increase in the total number of revolutions of the trajectories to the Moon in the considered range of 5 to 35 revolutions, the distance between the optimal junction point and the libration point rapidly decreases from 17,760.037 km to 2560.7455 km (thin solid line) and then asymptotically approaches the zero value, i.e., the EML1 point. According to the prediction of our study, this distance will decrease to 893 km on a 100-revolution trajectory and to 449 km on a 200-revolution trajectory.
To demonstrate the capabilities of the developed method, as an additional example, we present the trajectory from a GTO having the perigee altitude hp of 300 km and the apogee altitude ha of 35,793 km to an elliptical lunar orbit having the perilune altitude hp of 1000 km and an apolune altitude ha of 10,000 km. The full set of elements of the initial and final orbits used in this example is presented in Table 4.

Table 4.
Parameters of the initial GTO and final elliptical lunar orbit.
To ensure the close level of thrust acceleration of EPS in the geo- and selenocentric segments, the ratio of the number of revolutions in two segments of the trajectory is set to 8:1 in this example. Figure 8 shows the optimal trajectories with 16 revolutions in the geocentric segment and 2 revolutions in the selenocentric segment. As before, the orange line corresponds to the trajectory with an intermediate EML1 rendezvous, and the blue line corresponds to the trajectory with an optimal junction point. The main parameters of these trajectories are presented in Table 5.
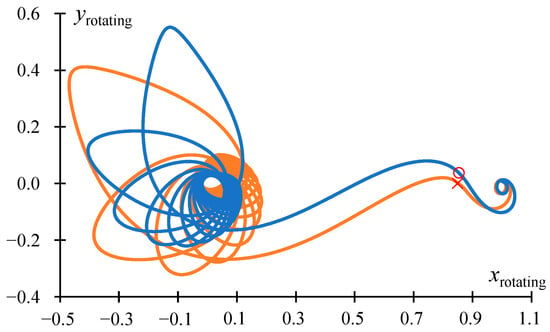
Figure 8.
The projection of optimal 18-revolution trajectories from GTO with low perigee altitude of 300 km to elliptical lunar orbit onto the XY plane in the rotating coordinate system.

Table 5.
The results of the optimal 18-revolution trajectories from GTO with perigee altitude of 300 km to elliptical lunar orbit.
6. Conclusions
The article proposed an approach to solve the problem of the end-to-end optimization of power-limited trajectories to the Moon, based on the use of the maximum principle, the continuation method, and the canonical transformation at the junction point of the geocentric and selenocentric segments of trajectory.
The problem of optimizing trajectories to the Moon with a fixed angular distance and free time of fight was considered. An ephemeris model of the motion of celestial bodies was used to calculate the perturbing accelerations, and the equations of motion of the spacecraft were presented in modified equinoctial orbital elements with the angular independent variable (auxiliary longitude) as the independent variable. The necessary optimality conditions for the junction point of the geocentric and selenocentric segments of trajectory were obtained, and a boundary value problem, which follows from the application of the maximum principle to the considered problem of the end-to-end optimization of the transfer between the orbits around the Moon and around the Earth, was formulated.
As an initial guess for the trajectory with the optimal junction point of the geocentric and selenocentric segments, the optimal trajectory with the junction of these segments at the libration point EML1 of the Earth–Moon system was used. The numerical results of the end-to-end optimization of power-limited trajectories to the Moon were presented. The comparison was made between the obtained trajectories with the optimal junction point and with the intermediate EML1 rendezvous.
As a result of the calculations, it was shown that optimization of a junction point of the geocentric and selenocentric segments of trajectory leads not only to a decrease in the cost function (in the considered example, by 7.7–9.8% with a total angular distance of 5–35 revolutions) but also to a decrease in the characteristic velocity of transfer (by 8.6–9.7%) and the optimal transfer duration (by 11.0–23.6%). So, we consider that optimal junction will be important for future space missions.
A significant difference between the shapes of the trajectories with an optimal junction point and with a junction at the libration point EML1 was shown. The optimal junction point can be quite far from the libration point EML1 (by 2560–17,760 km in the considered numerical examples) and the velocity of the spacecraft at this point can differ significantly from the velocity of the libration point (by 218–267 m/s). It was shown that with an increase in the total number of revolutions, the optimal junction point approaches EML1, and the velocity of the spacecraft at the optimal junction point relative to the velocity of EML1 asymptotically tends to zero with increasing angular distance of transfer.
The stability of the solution of end-to-end optimization problem has been demonstrated by varying the number of revolutions in the range of 5–35 revolutions. The dependence between the stability of the capture orbit and the total number of revolutions has not been specifically studied. As the total number of revolutions increases, the convergence and numerical stability of the proposed method deteriorate. This can be explained by the following reasons: (1) in the process of optimization, a change in the initial values of costate variables in the geocentric segment strongly affects not only the intermediate boundary conditions in the junction zone but also the parameters of the final lunar orbit. These effects increase as the number of revolutions increases; (2) as the number of revolutions increases, the difference between the perturbed trajectory and the trajectory of the initial guess that does not consider the perturbating acceleration during calculation increases. Because the transfer duration increases as the number of revolutions increases, this increases the integral influence of the perturbating acceleration. In the future, we plan to incorporate the multiple shooting method into our approach to improve convergence with a large number of revolutions.
The developed approach to solve the problem of the end-to-end optimization of a transfer between a given Earth orbit and a lunar orbit can be used to solve more complex and realistic problems, for example, the problem of minimizing thrust or minimizing fuel consumption using the engine model with a limited thrust and a constant specific impulse.
Author Contributions
Authors contributed equally to this work. Conceptualization, V.P.; methodology, V.P. and S.W.Y.; software, V.P. and S.W.Y.; validation, S.W.Y.; formal analysis, V.P. and S.W.Y.; investigation, V.P. and S.W.Y.; resources, V.P. and S.W.Y.; data curation, V.P. and S.W.Y.; writing—original draft preparation, V.P. and S.W.Y.; writing—review and editing, V.P. and S.W.Y.; visualization, S.W.Y.; supervision, V.P.; project administration, V.P. and S.W.Y.; funding acquisition, V.P. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the Russian Science Foundation grant no. 22-19-00329, https://rscf.ru/project/22-19-00329/.
Data Availability Statement
Data is unavailable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The Cartesian coordinates xcc can be expressed in terms of the modified equinoctial elements xmee with the following expressions (here, true longitude can be represented as L = LK + K):
where r = p/(1 + excosL + eysinL), α2 = ix2 − iy2.
The modified equinoctial elements xmee can be expressed in terms of the Cartesian coordinates xcc with the following expressions:
where
References
- Herman, A.L.; Conway, B.A. Optimal, Low-Thrust, Earth–Moon Orbit Transfer. J. Guid. Control. Dyn. 1998, 21, 141–147. [Google Scholar] [CrossRef]
- Pérez-Palau, D.; Epenoy, R. Fuel optimization for low-thrust Earth–Moon transfer via indirect optimal control. Celest. Mech. Dyn. Astr. 2018, 130, 21. [Google Scholar] [CrossRef]
- Carletta, S. Design of fuel-saving lunar captures using finite thrust and gravity-braking. Acta Astronaut. 2021, 181, 190–200. [Google Scholar] [CrossRef]
- Taheri, E.; Abdelkhalik, O. Fast initial trajectory design for low-thrust Restricted Three-Body Problems. J. Guid. Control. Dyn. 2015, 38, 2146–2160. [Google Scholar] [CrossRef]
- Yang, G. Earth-moon Trajectory Optimization Using Solar Electric Propulsion. Chin. J. Aeronaut. 2007, 20, 452–463. [Google Scholar] [CrossRef][Green Version]
- Kluever, C.A.; Pierson, B.L. Optimal earth-moon trajectories using nuclear electric propulsion. J. Guid. Control. Dyn. 1997, 20, 239–245. [Google Scholar] [CrossRef][Green Version]
- Gao, Y.; Wang, Z.; Zhang, Y. Low thrust Earth–Moon transfer trajectories via lunar capture set. Astrophys. Space Sci. 2019, 364, 219. [Google Scholar] [CrossRef]
- Yoon, S.W.; Petukhov, V.G.; Ivanyukhin, A.V. Minimum-Thrust Lunar Trajectories. In Proceedings of the 72nd International Astronautical Congress (IAC), Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Walker, M.; Ireland, B.; Owens, J. A set of modified equinoctial elements. Celest. Mech. 1985, 36, 409–419, Erratum in 1986, 38, 391–392. [Google Scholar] [CrossRef]
- Ivanyukhin, A.V.; Petukhov, V.G. Optimization of Multi-revolution Limited Power Trajectories Using Angular Independent Variable. J. Optim. Theory Appl. 2021, 191, 575–599. [Google Scholar] [CrossRef]
- Petukhov, V.; Ivanyukhin, A.; Popov, G.; Testoyedov, N.; Yoon, S.W. Optimization of finite-thrust trajectories with fixed angular distance. Acta Astronaut. 2022, 197, 354–367. [Google Scholar] [CrossRef]
- Ranieri, C.L.; Ocampo, C.A. Indirect optimization of low Earth orbit to low lunar orbit transfers. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, American Institute of Aeronautics and Astronautics, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Haissig, C.M.; Mease, K.D.; Vinh, N.X. Canonical transformations for space trajectory optimization. In Proceedings of the AIAA/AAS Astrodynamics Conference, Hilton Head, SC, USA, 10–12 August 1992. [Google Scholar]
- Taheri, E.; Arya, V.; Junkins, J.L. Costate mapping for indirect trajectory optimization. Astrodynamics 2021, 5, 359–371. [Google Scholar] [CrossRef]
- Junkins, J.L.; Taheri, E. State vector representations for low-thrust trajectory optimization. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Snowbird, UT, USA, 19–23 August 2018. [Google Scholar]
- Ivashkin, V.V. Optimization of Space Maneuvers at Limited Distances from the Planets; Nauka Press: Moscow, Russia, 1975; p. 392. (In Russian) [Google Scholar]
- Morante, D.; Rivo, M.S.; Soler, M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]
- Golan, O.M.; Breakwell, J.V. Minimum fuel lunar trajectories for a low-thrust power-limited spacecraft. Dyn. Control. 1994, 4, 383–394. [Google Scholar] [CrossRef]
- Ozimek, M.T.; Howell, K.C. Low-thrust transfers in the Earth-Moon system, including applications to libration point orbits. J. Guid. Control Dyn. 2010, 33, 533–549. [Google Scholar] [CrossRef]
- Petukhov, V.G. Method of continuation for optimization of interplanetary low-thrust trajectories. Cosm. Res. 2012, 50, 249–261. [Google Scholar] [CrossRef]
- Standish, E.M.; Newhall, X.X.; Williams, J.G.; Folkner, W.M. JPL Planetary and Lunar Ephemerides, DE403/LE403. Interoff. Memo. 1995, 314.10-127. [Google Scholar]
- Petukhov, V.G.; Yoon, S.W. Optimization of perturbed spacecraft trajectories using complex dual numbers. Part 1: Theory and method. Cosmic Res. 2021, 59, 401–413. [Google Scholar] [CrossRef]
- Petukhov, V.G.; Yoon, S.W. Optimization of perturbed spacecraft trajectories using complex dual numbers. Part 2: Numerical Results. Cosmic Res. 2021, 59, 517–528. [Google Scholar] [CrossRef]
- Irving, J.H. Low Thrust Flight: Variable Exhaust Velocity in Gravitational Fields. In Space Technology; Seifert, H.S., Ed.; Wiley and Sons Inc.: New York, NY, USA, 1959. [Google Scholar]
- Szebehely, V. Theory of Orbits: The Restricted Problem of Three Bodies; Academic Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Martins, J.R.R.A.; Sturdza, P.; Alonso, J.J. The Connection Between the Complex-Step Derivative Approximation and Algorithmic Differentiation. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Yu, W.; Blair, M. DNAD, a Simple Tool for Automatic Differentiation of Fortran Codes Using Dual Numbers. Computer Physics Communications 2013, 184, 1446–1452. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).