A Review of Solution Stabilization Techniques for RANS CFD Solvers
Abstract
1. Introduction
2. Theoretical Background
2.1. Time-Marching Nonlinear RANS Equation Systems
2.2. Time-Marching Linearized RANS Equation Systems
3. Stabilization Techniques
3.1. Recursive Projection Method (RPM)
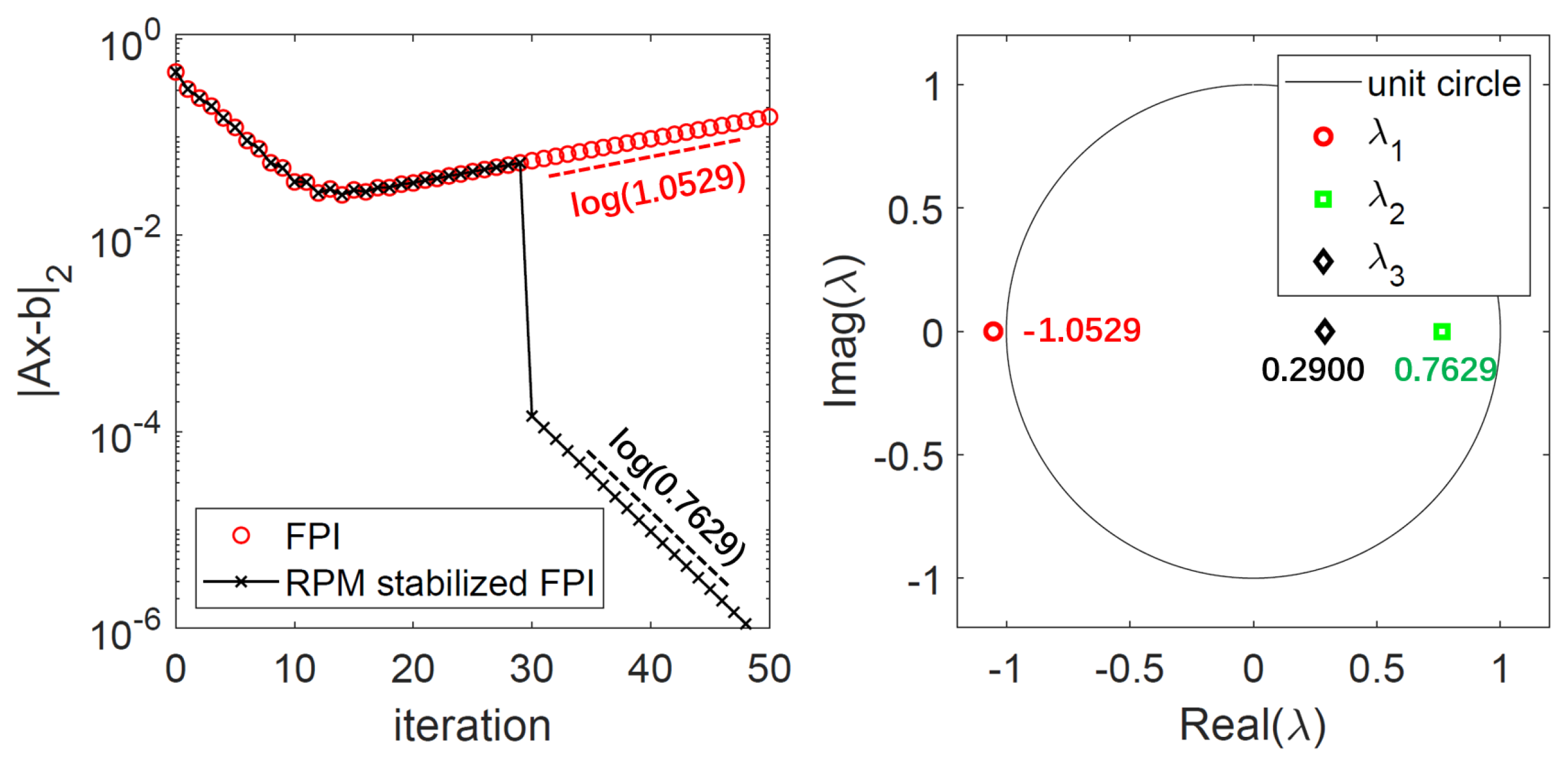
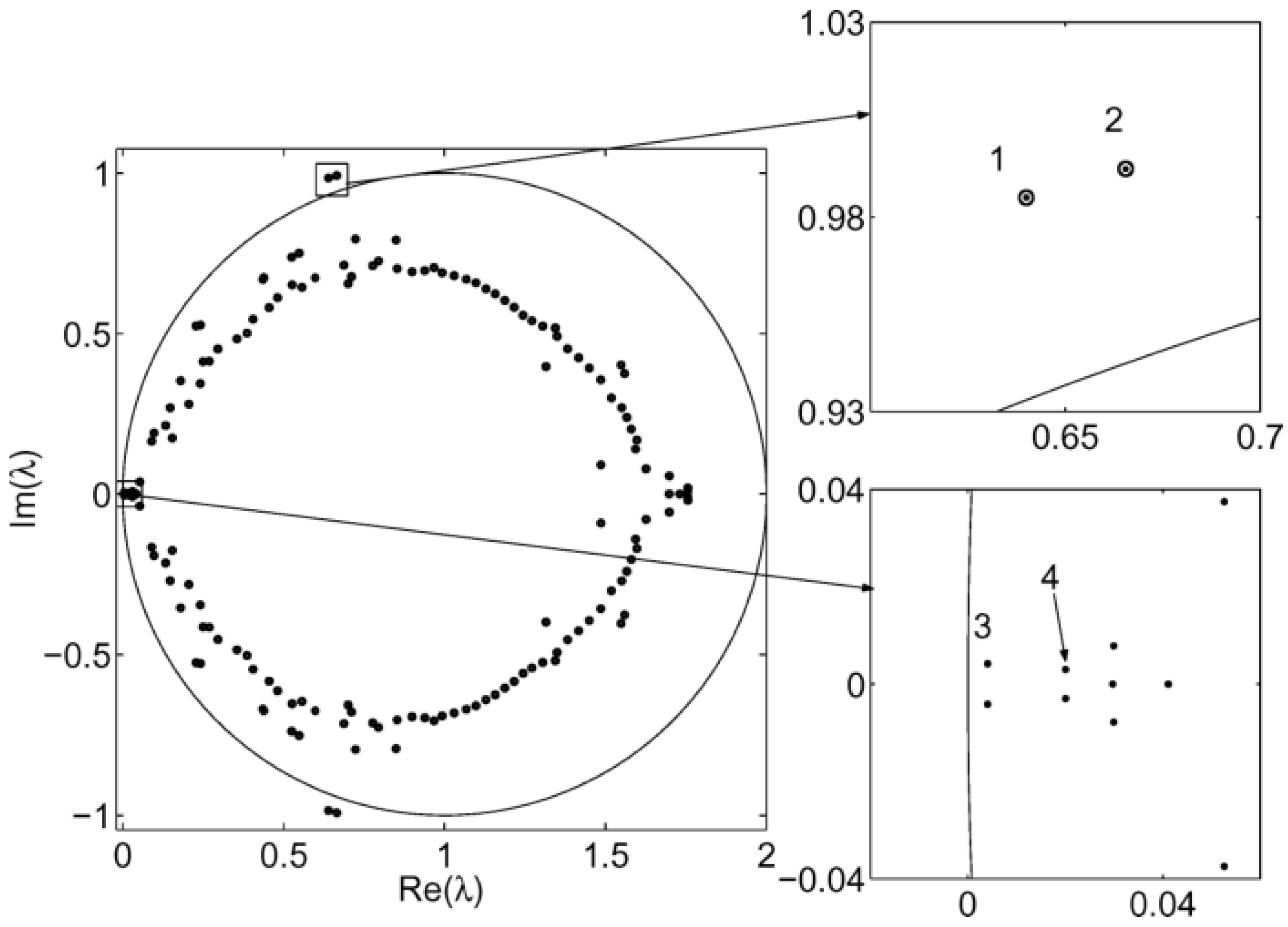
3.1.1. Theory and Examples
3.1.2. Rpm Stabilized Time-Linearized Analysis
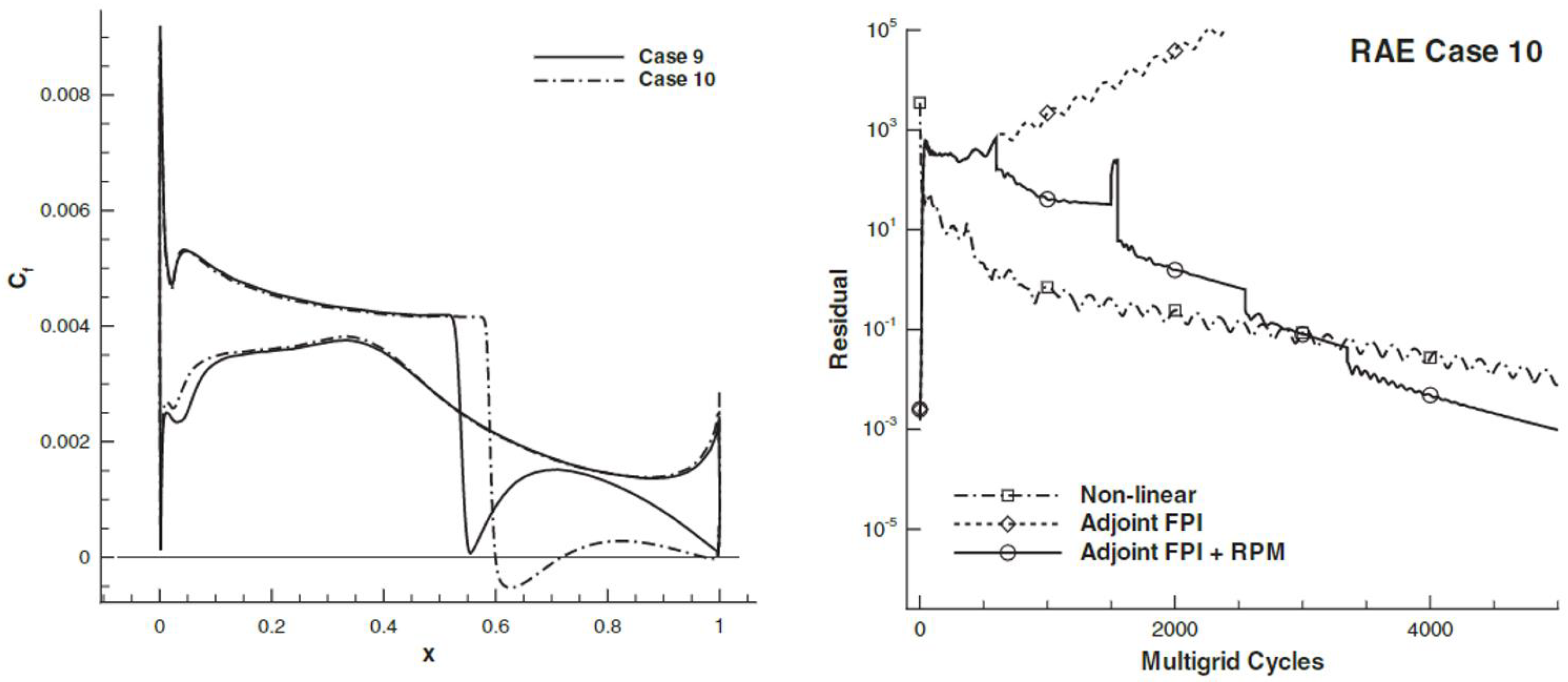
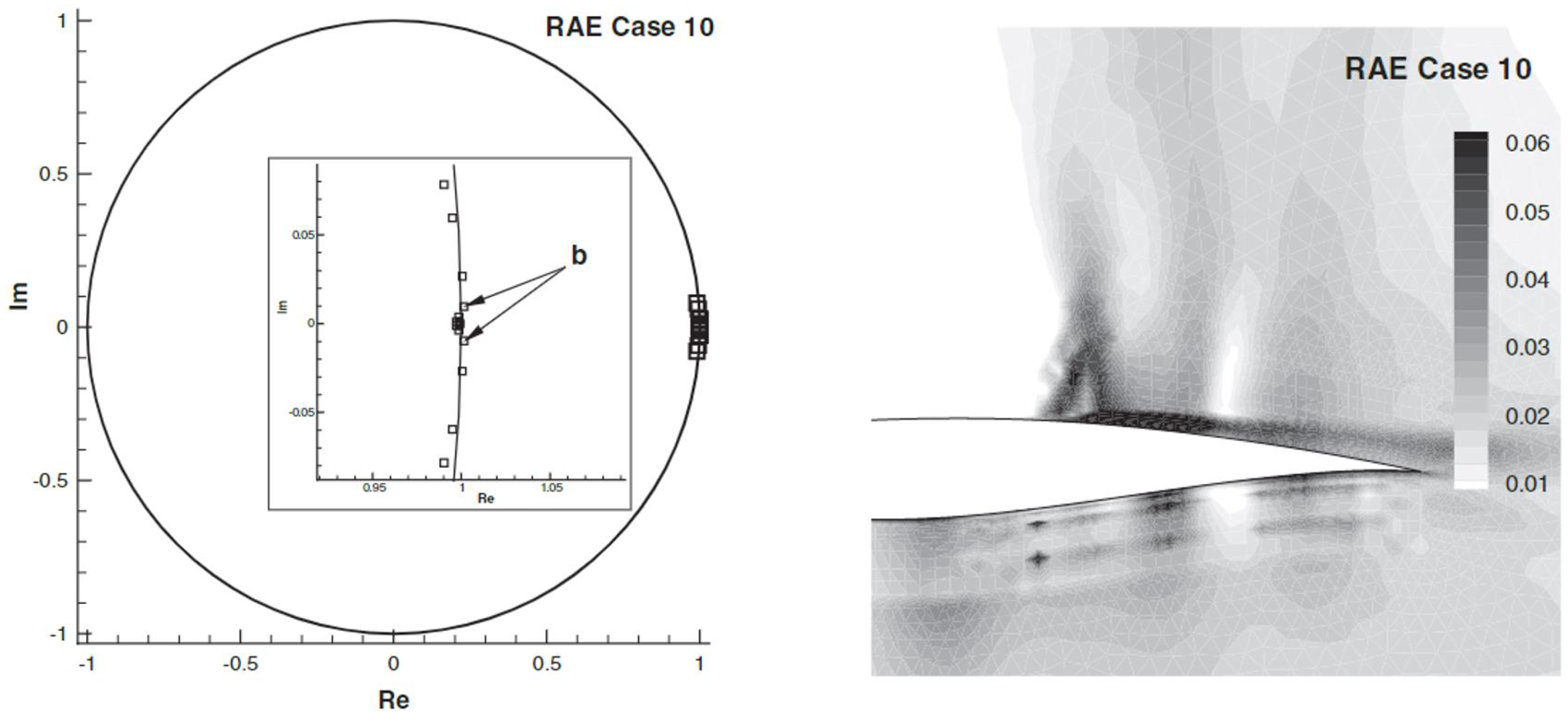
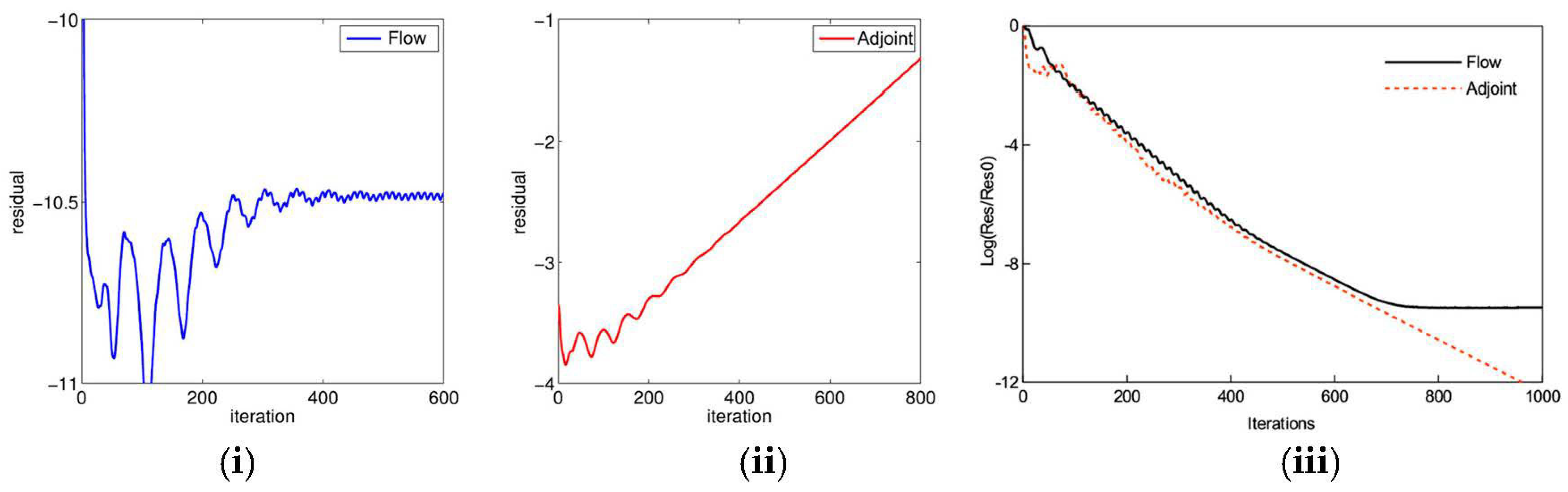
3.1.3. Rpm Stabilized Adjoint Analysis
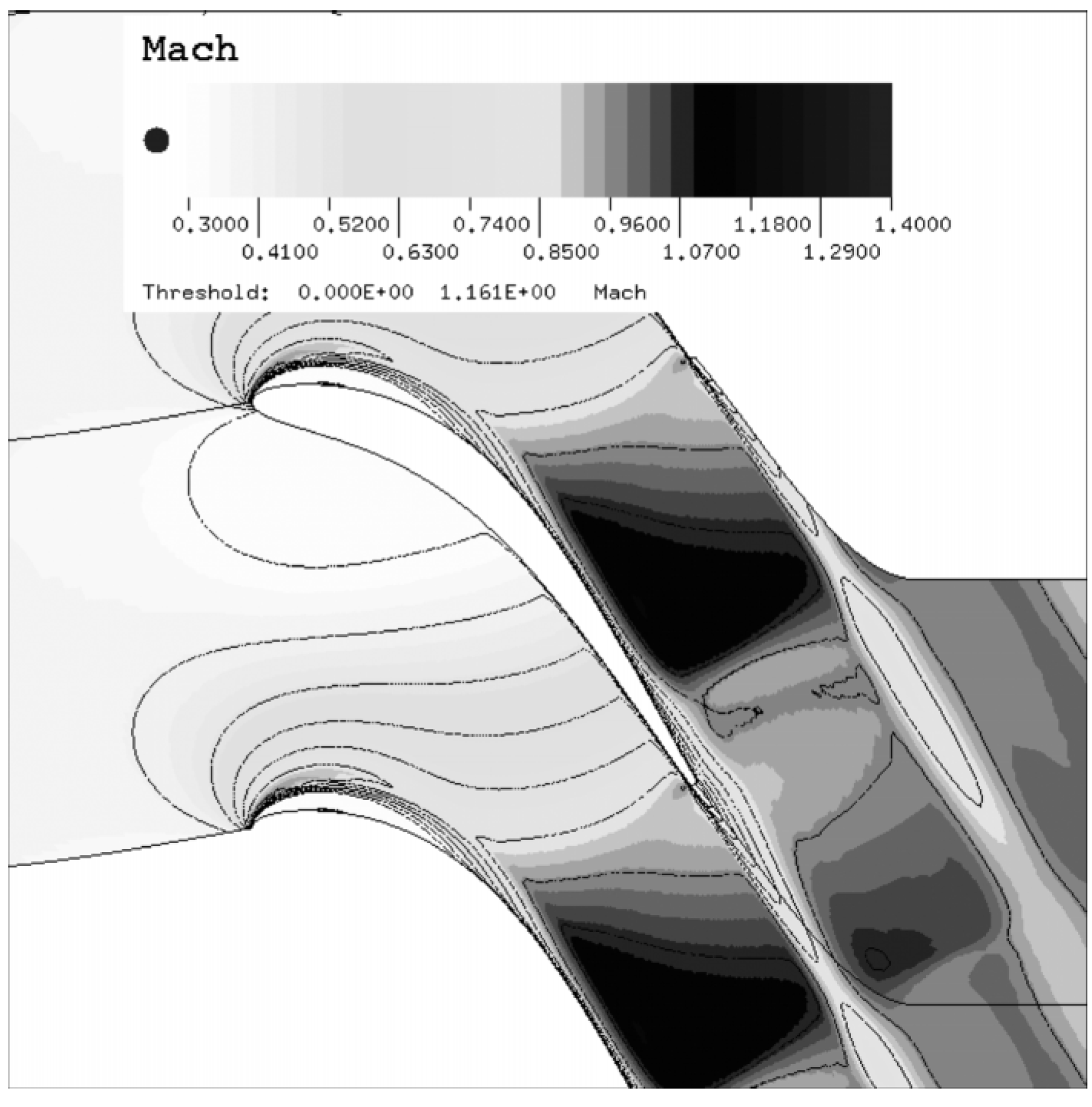
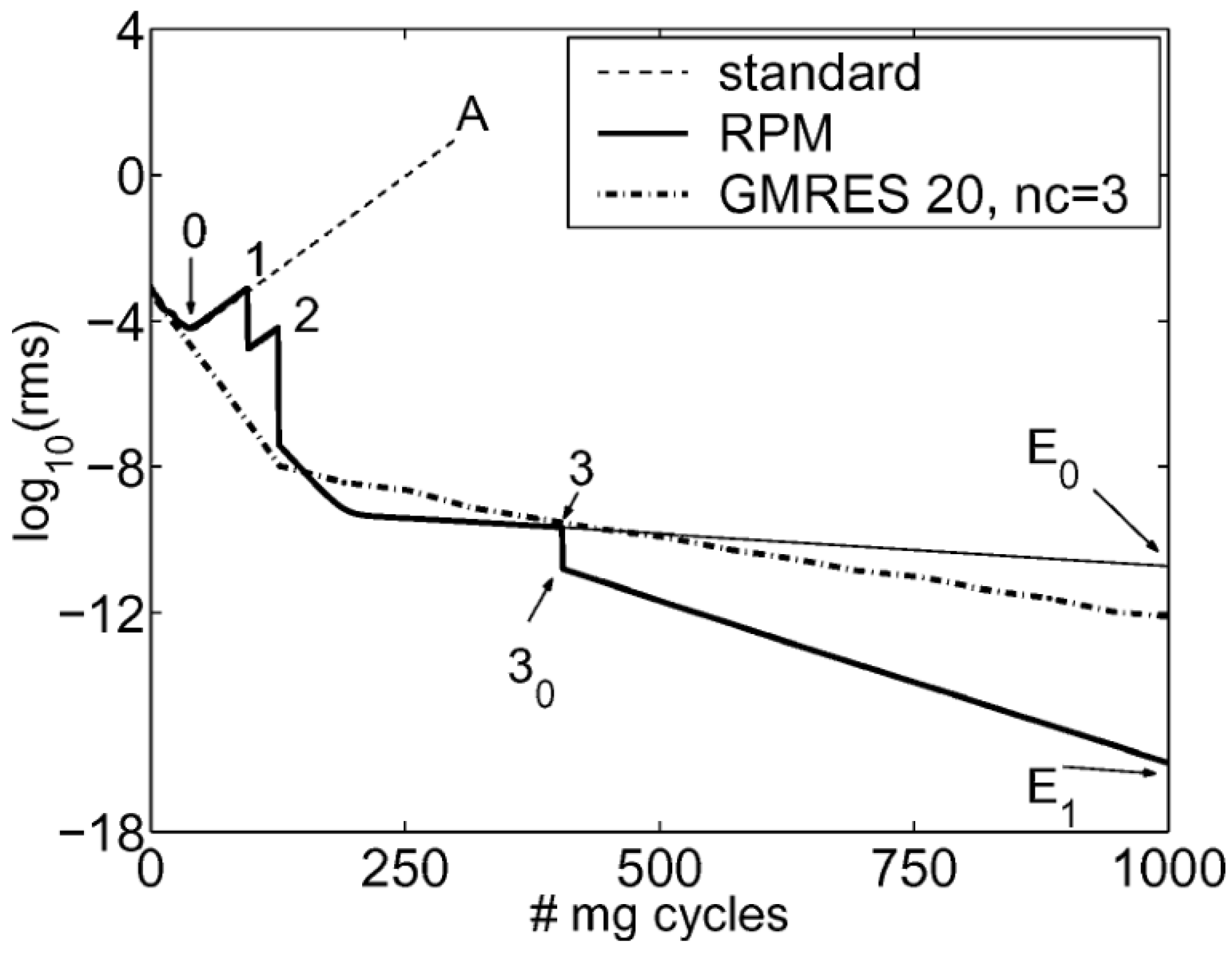
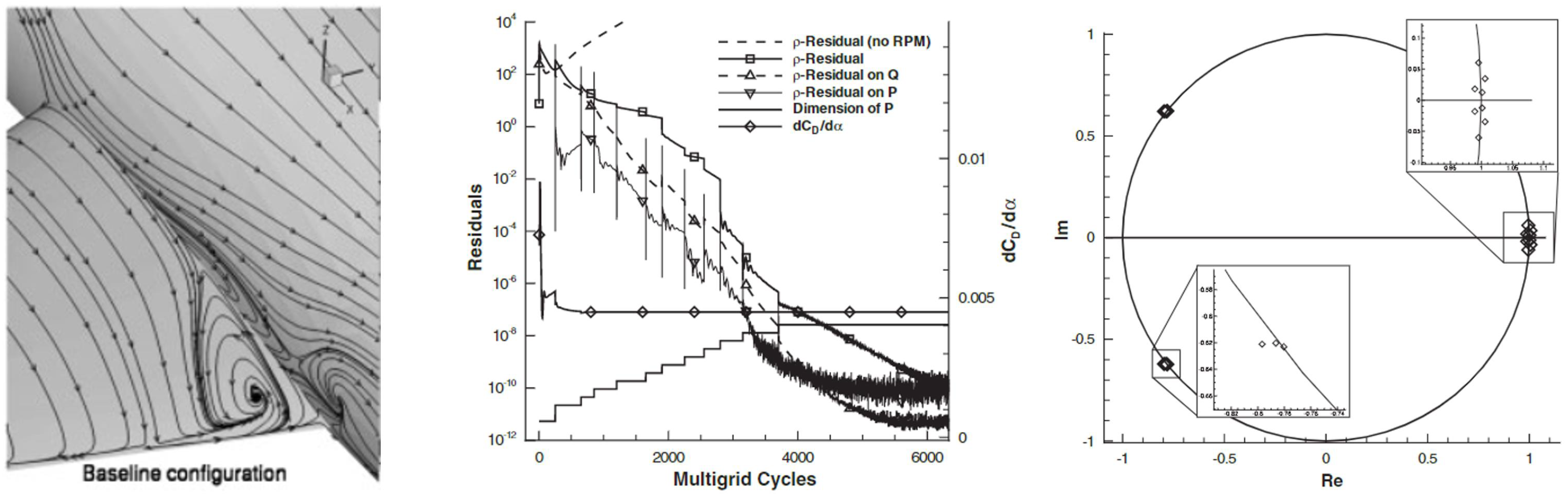
3.1.4. Rpm Accelerated RANS Nonlinear and Linear Calculations
3.1.5. Summary of Current Status and Direction for Further Development
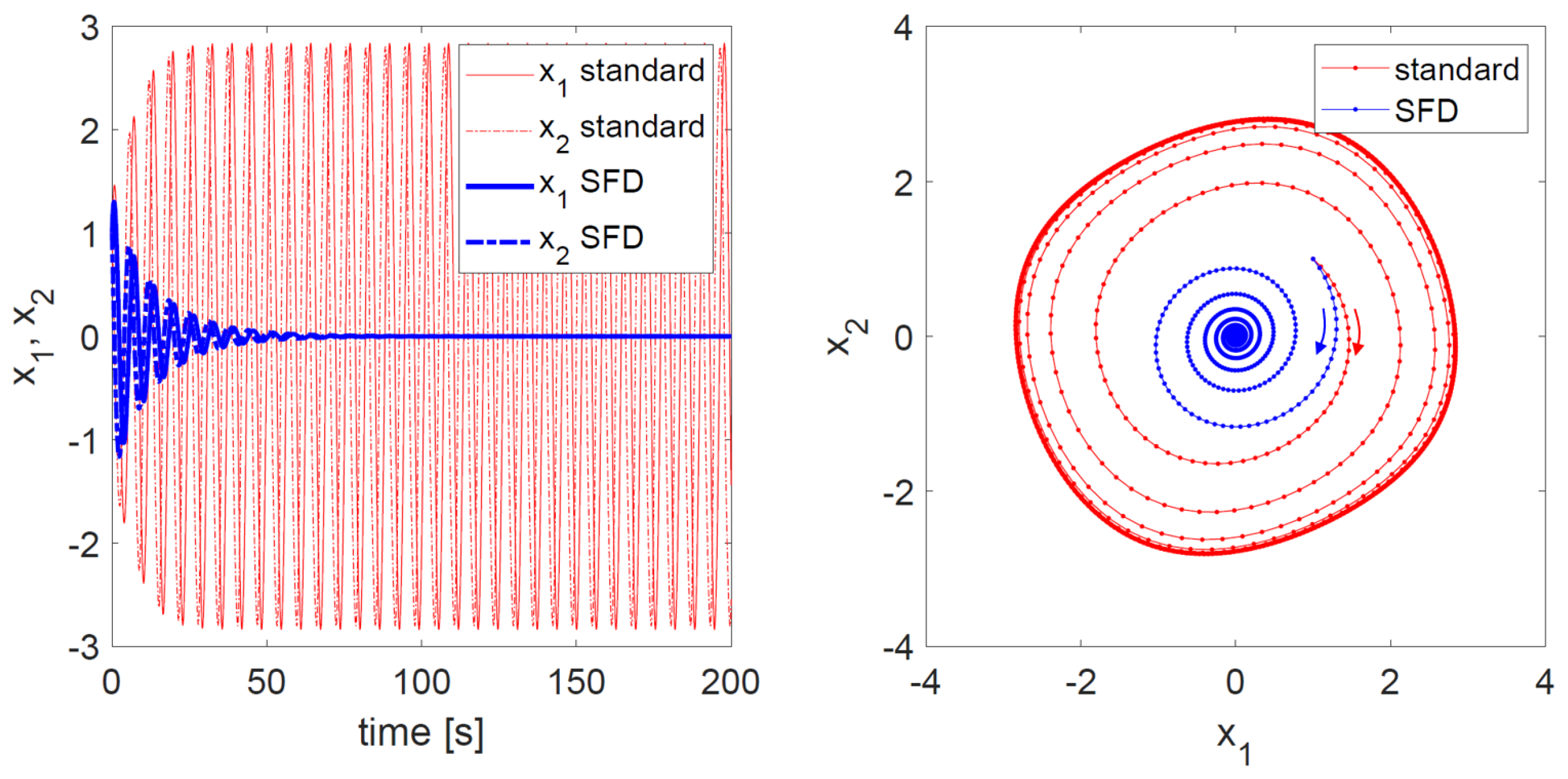
3.2. Selective Frequency Damping (SFD) Method
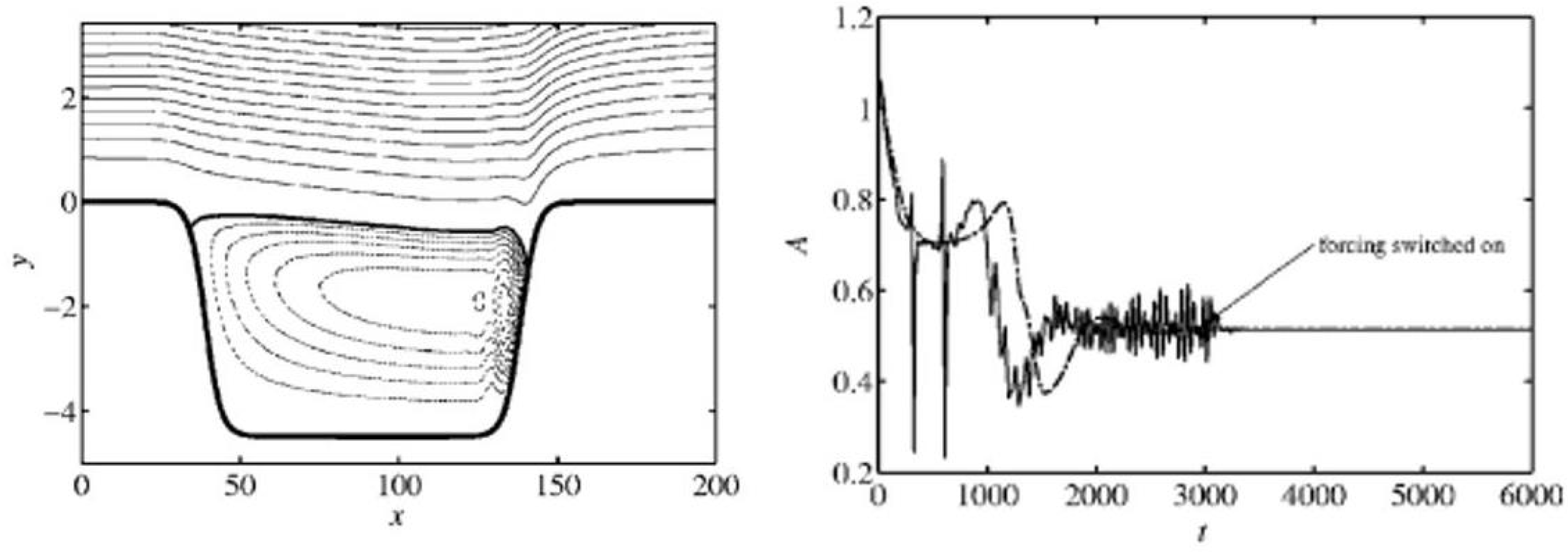
3.2.1. Theory and Examples
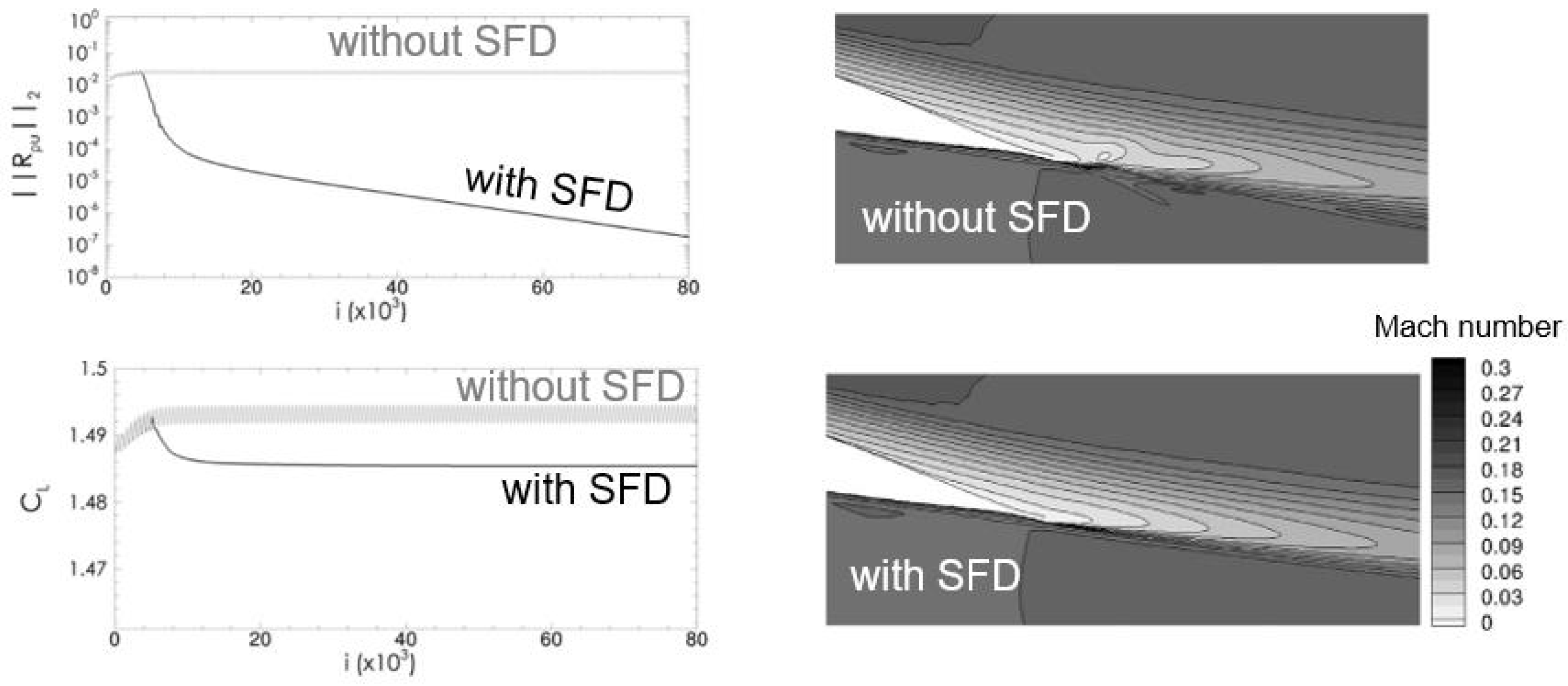
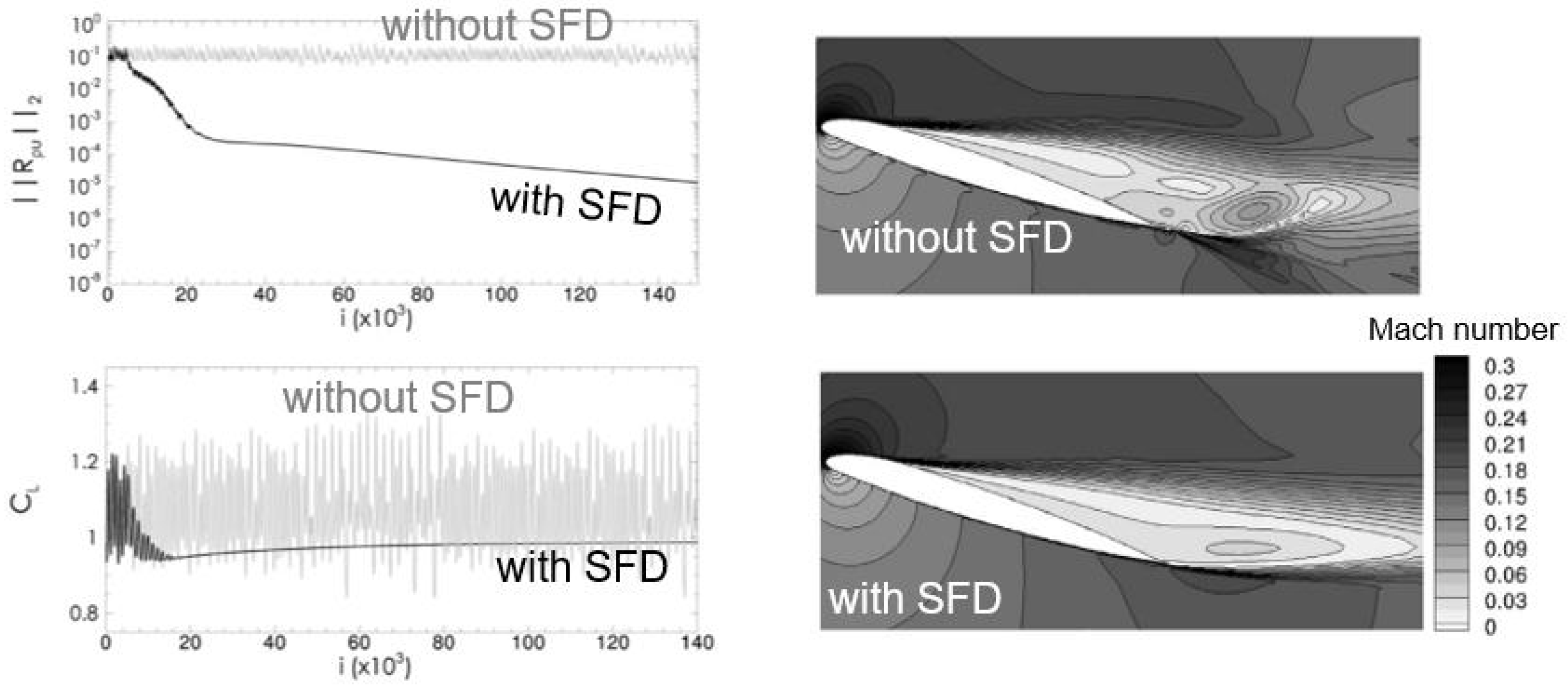
3.2.2. Sfd Stabilized Nonlinear Steady Flow Calculations
3.2.3. Sfd Accelerated Nonlinear Flow Solvers
3.2.4. Summary of Current Status and Suggestions for Further Development
3.3. Boostconv Method
3.3.1. Theory
3.3.2. Summary of Current Status and Suggestions for Further Development
3.4. Newton’S Method
3.4.1. Theory and Mathematical Formulation
| Algorithm 1: Arnoldi process |
|
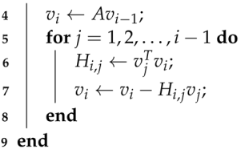 |
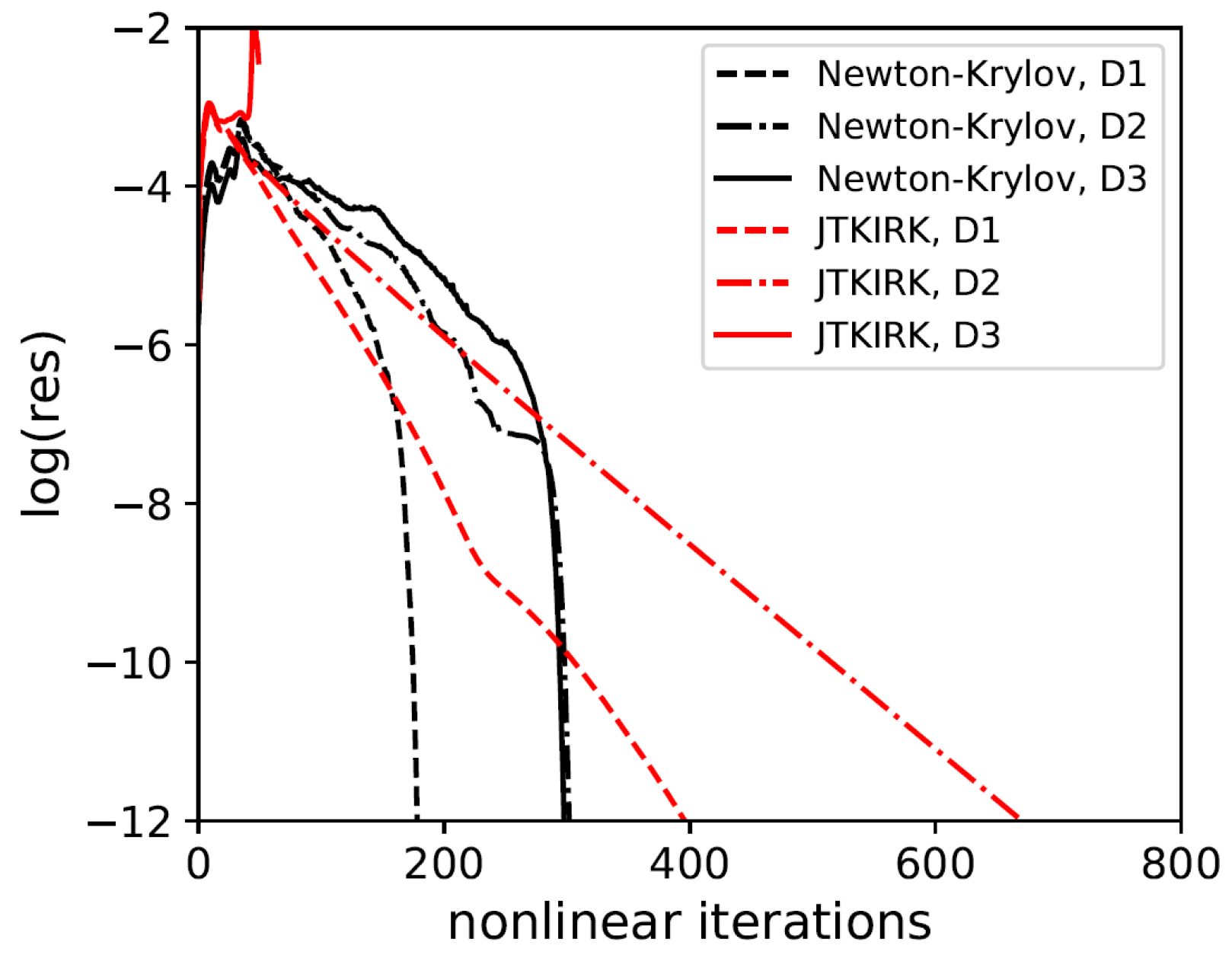
3.4.2. Stabilization and Acceleration of Nonlinear and Linear Solutions
3.4.3. Summary of Current Status and Suggestions for Future Development
3.5. Implicit Methods
3.5.1. Stabilization of Nonlinear Steady and Adjoint Solvers
3.5.2. Stabilization and Acceleration of Frequency Domain Solvers
4. Conclusions
- RPM: methods for efficiently resolving the unstable modes are worthy of further investigations and more comprehensive evaluations of the method for large scale cases with challenging flows on complex geometries are needed;
- SFD: methods for adaptively setting the optimal values of and are worthy of further development, as some reported overwhelming slow convergence when SFD is switched on;
- BoostConv: more applications of the method on realistic three-dimensional cases are desired in order to better evaluate the performance of this method, as it is relatively new compared with all other methods, and application examples are limited;
- Newton’s method
- -
- more work on startup strategy is needed. The work in [70] probably is the only algorithm that achieves a completely parameter-free smooth transition between weak implicit and NK algorithms, while the work in [71] is also quite elegant but a hardwired threshold of the residual level below which NK is activated needs to be manually specified. The logic behind both approaches is to smoothly blend a robust implicit algorithm with a moderate Courant number and a fully implicit NK algorithm towards the end;
- -
- recent progress made in scalable and efficient Krylov subspace solvers and preconditioning techniques need to be consolidated into the CFD community, and there currently seems to be a gap in the knowledge between the mathematical and engineering research communities.
- implicit methods: unlike NK, which can strictly follow a set of development guidelines backed up by rigorous theories, implicit methods instead require more tricks and experiences to fine tune the algorithm, especially regarding how the Jacobian matrix is approximated. An approximation too crude leads to either non-convergence or a diminishing Courant number (thus slow or stalled convergence), while an approximate too accurate leads to a drastically increased memory overhead and development difficulty. From this perspective, the exact Jacobian can be used as a reference to guide the fine tuning of the approximate Jacobian and increase the robustness of implicit methods, either with LU-SGS or ANK.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jameson, A. Aerodynamic Design via Control Theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Pinto, R.; Afzal, A.; D’Souza, L.; Ansari, Z.; Samee, M. Computational fluid dynamics in turbomachinery: A review of state of the art. Arch. Comput. Methods Eng. 2017, 24, 467–479. [Google Scholar] [CrossRef]
- Johnson, F.T.; Kamenetskiy, D.S.; Melvin, R.G.; Venkatakrishnan, V.; Wigton, L.B.; Young, D.P.; Allmaras, S.R.; Bussoletti, J.E.; Hilmes, C.L. Observations Regarding Algorithms Required for Robust CFD Codes. Math. Model Nat. Phenom. 2011, 6, 2–27. [Google Scholar] [CrossRef]
- Xu, S.; Timme, S.; Badcock, K.J. Enabling off-design linearised aerodynamics analysis using Krylov subspace recycling technique. Comput. Fluids 2016, 140, 385–396. [Google Scholar] [CrossRef]
- Campobasso, S.; Giles, M. Stabilization of Linear Flow Solver for Turbomachinery Aeroelasticity Using Recursive Projection Method. AIAA J. 2004, 42, 1765–1774. [Google Scholar] [CrossRef]
- Sartor, F.; Mettot, C.; Sipp, D. Stability, Receptivity, and Sensitivity Analyses of Buffeting Transonic Flow over a Profile. AIAA J. 2015, 53, 1980–1993. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Strelets, M. Global instability in the onset of transonic-wing buffet. J. Fluid Mech. 2019, 881, 3–22. [Google Scholar] [CrossRef]
- Timme, S. Global instability of wing shock-buffet onset. J. Fluid Mech. 2020, 885, A37. [Google Scholar] [CrossRef]
- Giles, M.; Duta, M.; Müller, J.D.; Pierce, N. Algorithm developments for discrete adjoint methods. AIAA J. 2003, 41, 198–205. [Google Scholar] [CrossRef]
- Dwight, R.; Brezillon, J. Efficient and Robust Algorithms for Solution of the Adjoint Compressible Navier–Stokes Equations with Applications. Int. J. Numer. Methods Fluids 2009, 60, 365–389. [Google Scholar] [CrossRef]
- Xu, S.; Radford, D.; Meyer, M.; Mueller, J.D. Stabilisation of discrete steady adjoint solvers. J. Comput. Phys. 2015, 299, 175–195. [Google Scholar] [CrossRef]
- Shroff, G.M.; Keller, H. Stabilization of unstable procedures: The recursive projection method. SIAM J. Math. Anal. 1993, 30, 1099–1120. [Google Scholar] [CrossRef]
- Åkervik, E.; Brandt, L.; Henningson, D.; Hoepffner, J.; Marxen, O.; Schlatter, P. Steady solutions of the Navier-Stokes equations by selective frequency damping. Phys. Fluids 2006, 18, 068102. [Google Scholar] [CrossRef]
- Citro, V.; Luchini, P.; Giannetti, F.; Auteri, F. Efficient stabilization and acceleration of numerical simulation of fluid flows by residual recombination. J. Comput. Phys. 2017, 344, 234–246. [Google Scholar] [CrossRef]
- Venkatakrishnan, V.; Mavriplis, D.J. Implicit solvers for unstructured meshes. J. Comput. Phys. 1993, 105, 83–91. [Google Scholar] [CrossRef]
- Knoll, D.A.; Keyes, D.E. Jacobian-free Newton–Krylov methods: A survey of approaches and applications. J. Comput. Phys. 2004, 193, 357–397. [Google Scholar] [CrossRef]
- Chisholm, T.T.; Zingg, D.W. A Jacobian-free Newton–Krylov algorithm for compressible turbulent fluid flows. J. Comput. Phys. 2009, 228, 3490–3507. [Google Scholar] [CrossRef]
- Nadarajah, S.; Jameson, A. Studies of the continuous and discrete adjoint approaches to viscous automatic aerodynamic shape optimization. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 2530. [Google Scholar] [CrossRef]
- Anderson, W.K.; Venkatakrishnan, V. Aerodynamic design optimization on unstructured grids with a continuous adjoint formulation. Comput. Fluids 1997, 28, 443–480. [Google Scholar] [CrossRef]
- Möller, J. Aspects of The Recursive Projection Method Applied to Flow Calculations. Ph.D. Thesis, KTH Royal Institute of Technology in Stockholm, Stockholm, Sweden, 2005. [Google Scholar]
- Görtz, S.; Möller, J. Evaluation of the recursive projection method for efficient unsteady turbulent CFD simulation. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004; pp. 1–13. [Google Scholar]
- Sergio Campobasso, M.; Giles, M.B. Stabilization of a linearized Navier-Stokes solver for turbomachinery aeroelasticity. In Computational Fluid Dynamics 2002; Springer: Berlin/Heidelberg, Germany, 2003; pp. 343–348. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar] [CrossRef]
- Langer, S. Agglomeration multigrid methods with implicit Runge–Kutta smoothers applied to aerodynamic simulations on unstructured grids. J. Comput. Phys. 2014, 277, 72–100. [Google Scholar] [CrossRef]
- Renac, F. Improvement of the recursive projection method for linear iterative scheme stabilization based on an approximate eigenvalue problem. J. Comput. Phys. 2011, 230, 5739–5752. [Google Scholar] [CrossRef]
- Ekici, K.; Hall, K.C.; Huang, H.; Thomas, J.P. Stabilization of Explicit Flow Solvers Using a Proper-Orthogonal-Decomposition Technique. AIAA J. 2013, 51, 1095–1104. [Google Scholar] [CrossRef]
- Richez, F.; Leguille, M.; Marquet, O. Selective frequency damping method for steady RANS solutions of turbulent separated flows around an airfoil at stall. Comput. Fluids 2016, 132, 51–61. [Google Scholar] [CrossRef]
- Cambier, L.; Heib, S.; Plot, S. The Onera elsA CFD software: Input from research and feedback from industry. Mech. Ind. 2013, 14, 159–174. [Google Scholar] [CrossRef]
- Cantwell, C.D.; Moxey, D.; Comerford, A.; Bolis, A.; Rocco, G.; Mengaldo, G.; De Grazia, D.; Yakovlev, S.; Lombard, J.E.; Ekelschot, D.; et al. Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 2015, 192, 205–219. [Google Scholar] [CrossRef]
- Proskurin, A.V. Mathematical modelling of unstable bent flow using the selective frequency damping method. J. Phys. Conf. Ser. 2021, 1809, 012012. [Google Scholar] [CrossRef]
- Bagheri, S.; Schlatter, P.; Schmid, P.J.; Henningson, D.S. Global stability of a jet in crossflow. J. Fluid Mech. 2009, 624, 33–44. [Google Scholar] [CrossRef]
- Plante, F.; Laurendeau, É. Acceleration of Euler and RANS solvers via Selective Frequency Damping. Comput. Fluids 2018, 166, 46–56. [Google Scholar] [CrossRef]
- Li, F.; Ji, C.; Xu, D. A novel optimization algorithm for the selective frequency damping parameters. Phys. Fluids 2022, 34, 124112. [Google Scholar] [CrossRef]
- Liguori, V.; Plante, F.; Laurendeau, E. Implementation of an efficient Selective Frequency Damping method in a RANS solver. AIAA Scitech 2021, 2021, 0359. [Google Scholar] [CrossRef]
- Cunha, G.; Passaggia, P.Y.; Lazareff, M. Optimization of the selective frequency damping parameters using model reduction. Phys. Fluids 2015, 27, 094103. [Google Scholar] [CrossRef]
- Jordi, B.E.; Cotter, C.J.; Sherwin, S.J. Encapsulated formulation of the Selective Frequency Damping method. Phys. Fluids 2014, 26, 034101. [Google Scholar] [CrossRef]
- Citro, V.; Giannetti, F.; Luchini, P.; Auteri, F. Global stability and sensitivity analysis of boundary-layer flows past a hemispherical roughness element. Phys. Fluids 2015, 27, 084110. [Google Scholar] [CrossRef]
- Citro, V. Simple and efficient acceleration of existing multigrid algorithms. AIAA J. 2019, 57, 2244–2247. [Google Scholar] [CrossRef]
- Dicholkar, A.; Zahle, F.; Sørensen, N.N. Convergence enhancement of SIMPLE-like steady-state RANS solvers applied to airfoil and cylinder flows. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104863. [Google Scholar] [CrossRef]
- Xu, S.; Mohanamuraly, P.; Wang, D.; Müller, J.D. Newton–Krylov Solver for Robust Turbomachinery Aerodynamic Analysis. AIAA J. 2020, 58, 1320–1336. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.; Maki, K.J. DAFOAM: An open-source adjoint framework for multidisciplinary design optimization with openfoam. AIAA J. 2020, 58, 1304–1319. [Google Scholar] [CrossRef]
- Gebremedhin, A.H.; Manne, F.; Pothen, A. What color is your Jacobian? Graph coloring for computing derivatives. SIAM Rev. 2005, 47, 629–705. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Huang, X.; Wang, D. Robust Newton–Krylov Adjoint Solver for the Sensitivity Analysis of Turbomachinery Aerodynamics. AIAA J. 2021, 59, 4014–4030. [Google Scholar] [CrossRef]
- Mader, C.A.; Martins, J.R.; Alonso, J.J.; Van Der Weide, E. ADjoint: An approach for the rapid development of discrete adjoint solvers. AIAA J. 2008, 46, 863–873. [Google Scholar] [CrossRef]
- Dwight, R.P.; Brezillon, J. Effect of approximations of the discrete adjoint on gradient-based optimization. AIAA J. 2006, 44, 3022–3031. [Google Scholar] [CrossRef]
- Nemec, M.; Zingg, D.W. Newton-Krylov Algorithm for Aerodynamic Design Using the Navier-Stokes Equations. AIAA J. 2002, 40, 1146–1154. [Google Scholar] [CrossRef]
- Morgan, R.B. GMRES with deflated restarting. SIAM J. Sci. Comput. 2002, 24, 20–37. [Google Scholar] [CrossRef]
- Parks, M.L.; De Sturler, E.; Mackey, G.; Johnson, D.D.; Maiti, S. Recycling Krylov subspaces for sequences of linear systems. SIAM J. Sci. Comput. 2006, 28, 1651–1674. [Google Scholar] [CrossRef]
- Mohamed, K.; Nadarajah, S.; Paraschivoiu, M. Krylov recycling techniques for unsteady simulation of turbulent aerodynamic flows. In Proceedings of the 26th International Congress of the Aeronautical Sciences, Anchorage, Alaska, 14–19 September 2008; International Council of The Aeronautical Sciences: Stockholm, Sweden, 2008; Volume 2, pp. 3338–3348. [Google Scholar]
- Xu, S.; Timme, S. Robust and efficient adjoint solver for complex flow conditions. Comput. Fluids 2017, 148, 26–38. [Google Scholar] [CrossRef]
- Gomes, P.; Palacios, R. Pitfalls of discrete adjoint fixed-points based on algorithmic differentiation. AIAA J. 2022, 60, 1251–1256. [Google Scholar] [CrossRef]
- Pueyo, A.; Zingg, D.W. Efficient Newton-Krylov solver for aerodynamic computations. AIAA J. 1998, 36, 1991–1997. [Google Scholar] [CrossRef]
- Liu, W.H.; Sherman, A.H. Comparative analysis of the Cuthill–McKee and the reverse Cuthill–McKee ordering algorithms for sparse matrices. SIAM J. Math. Anal. 1976, 13, 198–213. [Google Scholar] [CrossRef]
- Dwight, R.P. Efficiency Improvements of RANS-Based Analysis and Optimization Using Implicit and Adjoint Methods on Unstructured Grids; The University of Manchester: Manchester, UK, 2006. [Google Scholar]
- Nejat, A.; Ollivier-Gooch, C. Effect of discretization order on preconditioning and convergence of a high-order unstructured Newton-GMRES solver for the Euler equations. J. Comput. Phys. 2008, 227, 2366–2386. [Google Scholar] [CrossRef]
- Trottenberg, U.; Oosterlee, C.W.; Schuller, A. Multigrid; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Moinier, P.; Muller, J.D.; Giles, M.B. Edge-based multigrid and preconditioning for hybrid grids. AIAA J. 2002, 40, 1954–1960. [Google Scholar] [CrossRef]
- Müller, J.D. Anisotropic adaptation and multigrid for hybrid grids. Int. J. Numer. Methods Fluids 2002, 40, 445–455. [Google Scholar] [CrossRef]
- Ruge, J.W.; Stüben, K. Algebraic multigrid. In Multigrid Methods; SIAM: Philadelphia, PA, USA, 1987; pp. 73–130. [Google Scholar]
- Stüben, K. A review of algebraic multigrid. In Numerical Analysis: Historical Developments in the 20th Century; Elsevier: Amsterdam, The Netherlands, 2001; pp. 331–359. [Google Scholar]
- Naumovich, A.; Förster, M.; Dwight, R. Algebraic multigrid within defect correction for the linearized Euler equations. Numer. Linear Algebra Appl. 2010, 17, 307–324. [Google Scholar] [CrossRef]
- Förster, M.; Pal, A. A linear solver based on algebraic multigrid and defect correction for the solution of adjoint RANS equations. Int. J. Numer. Methods Fluids 2014, 74, 846–855. [Google Scholar] [CrossRef]
- Walker, H.F. A GMRES-backtracking Newton iterative method. In Proceedings of the Copper Mountain Conference on Iterative Methods, Copper Mountain, CO, USA, 9–14 April 1992. [Google Scholar]
- Eisenstat, S.C.; Walker, H.F. Choosing the forcing terms in an inexact Newton method. SIAM J. Sci. Comput. 1996, 17, 16–32. [Google Scholar] [CrossRef]
- Shadid, J.N.; Tuminaro, R.S.; Walker, H.F. An inexact Newton method for fully coupled solution of the Navier–Stokes equations with heat and mass transport. J. Comput. Phys. 1997, 137, 155–185. [Google Scholar] [CrossRef]
- Tuminaro, R.S.; Walker, H.F.; Shadid, J.N. On backtracking failure in Newton–GMRES methods with a demonstration for the Navier–Stokes equations. J. Comput. Phys. 2002, 180, 549–558. [Google Scholar] [CrossRef]
- Kelley, C.T.; Keyes, D.E. Convergence analysis of pseudo-transient continuation. SIAM J. Math. Anal. 1998, 35, 508–523. [Google Scholar] [CrossRef]
- Mulder, W.A.; Van Leer, B. Experiments with implicit upwind methods for the Euler equations. J. Comput. Phys. 1985, 59, 232–246. [Google Scholar] [CrossRef]
- Kamenetskiy, D.S.; Bussoletti, J.E.; Hilmes, C.L.; Venkatakrishnan, V.; Wigton, L.B.; Johnson, F.T. Numerical evidence of multiple solutions for the Reynolds-averaged Navier–Stokes equations. AIAA J. 2014, 52, 1686–1698. [Google Scholar] [CrossRef]
- Mavriplis, D.J. A residual smoothing strategy for accelerating Newton method continuation. Comput. Fluids 2021, 220, 104859. [Google Scholar] [CrossRef]
- Yildirim, A.; Kenway, G.K.; Mader, C.A.; Martins, J.R. A Jacobian-free approximate Newton–Krylov startup strategy for RANS simulations. J. Comput. Phys. 2019, 397, 108741. [Google Scholar] [CrossRef]
- Langer, S. Preconditioned Newton Methods to Approximate Solutions of the Reynolds- Averaged Navier–Stokes Equations. Ph.D. Thesis, Deutschen Zentrum für Luft-und Raumfahrt, Köln, Germany, 2018. [Google Scholar]
- Kenway, G.; Martins, J. Buffet-Onset Constraint Formulation for Aerodynamic Shape Optimization. AIAA J. 2017, 55, 1–18. [Google Scholar] [CrossRef]
- Campobasso, M.S.; Giles, M.B. Effects of Flow Instabilities on the Linear Analysis of Turbomachinery Aeroelasticity. J. Propuls. Power 2003, 19, 250–259. [Google Scholar] [CrossRef]
- Krakos, J.A.; Darmofal, D.L. Effect of Small-Scale Output Unsteadiness on Adjoint-Based Sensitivity. AIAA J. 2015, 48, 2611–2623. [Google Scholar] [CrossRef]
- Gaul, A.; Gutknecht, M.H.; Liesen, J.; Nabben, R. A framework for deflated and augmented Krylov subspace methods. SIAM J. Matrix Anal. Appl. 2012, 34, 495–518. [Google Scholar] [CrossRef]
- Ghysels, P.; Ashby, T.J.; Meerbergen, K.; Vanroose, W. Hiding Global Communication Latency in the GMRES Algorithm on Massively Parallel Machines. SIAM J. Sci. Comput. 2013, 35, C48–C71. [Google Scholar] [CrossRef]
- Grigori, L.; Moufawad, S. Communication Avoiding ILU0 Preconditioner. SIAM J. Sci. Comput. 2015. [Google Scholar] [CrossRef]
- Yoon, S.; Jameson, A. Lower-upper Symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations. AIAA J. 1988, 26, 1025. [Google Scholar] [CrossRef]
- Pierce, N.A.; Giles, M.B. Preconditioned multigrid methods for compressible flow calculations on stretched meshes. J. Comput. Phys. 1997, 136, 425–445. [Google Scholar] [CrossRef]
- Swanson, R.C.; Turkel, E.; Rossow, C.C. Convergence acceleration of Runge–Kutta schemes for solving the Navier–Stokes equations. J. Comput. Phys. 2007, 224, 365–388. [Google Scholar] [CrossRef]
- Rossow, C.C. Efficient computation of compressible and incompressible flows. J. Comput. Phys. 2007, 220, 879–899. [Google Scholar] [CrossRef]
- Swanson, R.C.; Rossow, C.C. An efficient solver for the RANS equations and a one-equation turbulence model. Comput. Fluids 2011, 42, 13–25. [Google Scholar] [CrossRef]
- Wang, D.; Huang, X. Solution Stabilization and Convergence Acceleration for the Harmonic Balance Equation System. J. Eng. Gas Turbine Power 2017, 139, 092503. [Google Scholar] [CrossRef]
- Huang, X.; Wu, H.; Wang, D. Implicit solution of harmonic balance equation system using the LU-SGS method and one-step Jacobi/Gauss-Seidel iteration. Int. J. Comput. Fluid D. 2018, 32, 218–232. [Google Scholar] [CrossRef]
- Sicot, F.; Puigt, G.; Montagnac, M. Block-Jacobi implicit algorithms for the time spectral method. AIAA J. 2008, 46, 3080–3089. [Google Scholar] [CrossRef]
- Mundis, N.; Mavriplis, D. Toward an optimal solver for time-spectral fluid-dynamic and aeroelastic solutions on unstructured meshes. J. Comput. Phys. 2017, 345, 132–161. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Zhao, J.; Wu, H.; Zhang, S.; Müller, J.-D.; Huang, H.; Rahmati, M.; Wang, D. A Review of Solution Stabilization Techniques for RANS CFD Solvers. Aerospace 2023, 10, 230. https://doi.org/10.3390/aerospace10030230
Xu S, Zhao J, Wu H, Zhang S, Müller J-D, Huang H, Rahmati M, Wang D. A Review of Solution Stabilization Techniques for RANS CFD Solvers. Aerospace. 2023; 10(3):230. https://doi.org/10.3390/aerospace10030230
Chicago/Turabian StyleXu, Shenren, Jiazi Zhao, Hangkong Wu, Sen Zhang, Jens-Dominik Müller, Huang Huang, Mohammad Rahmati, and Dingxi Wang. 2023. "A Review of Solution Stabilization Techniques for RANS CFD Solvers" Aerospace 10, no. 3: 230. https://doi.org/10.3390/aerospace10030230
APA StyleXu, S., Zhao, J., Wu, H., Zhang, S., Müller, J.-D., Huang, H., Rahmati, M., & Wang, D. (2023). A Review of Solution Stabilization Techniques for RANS CFD Solvers. Aerospace, 10(3), 230. https://doi.org/10.3390/aerospace10030230








