Influence of Ablation Deformation on Aero-Optical Effects in Hypersonic Vehicles
Abstract
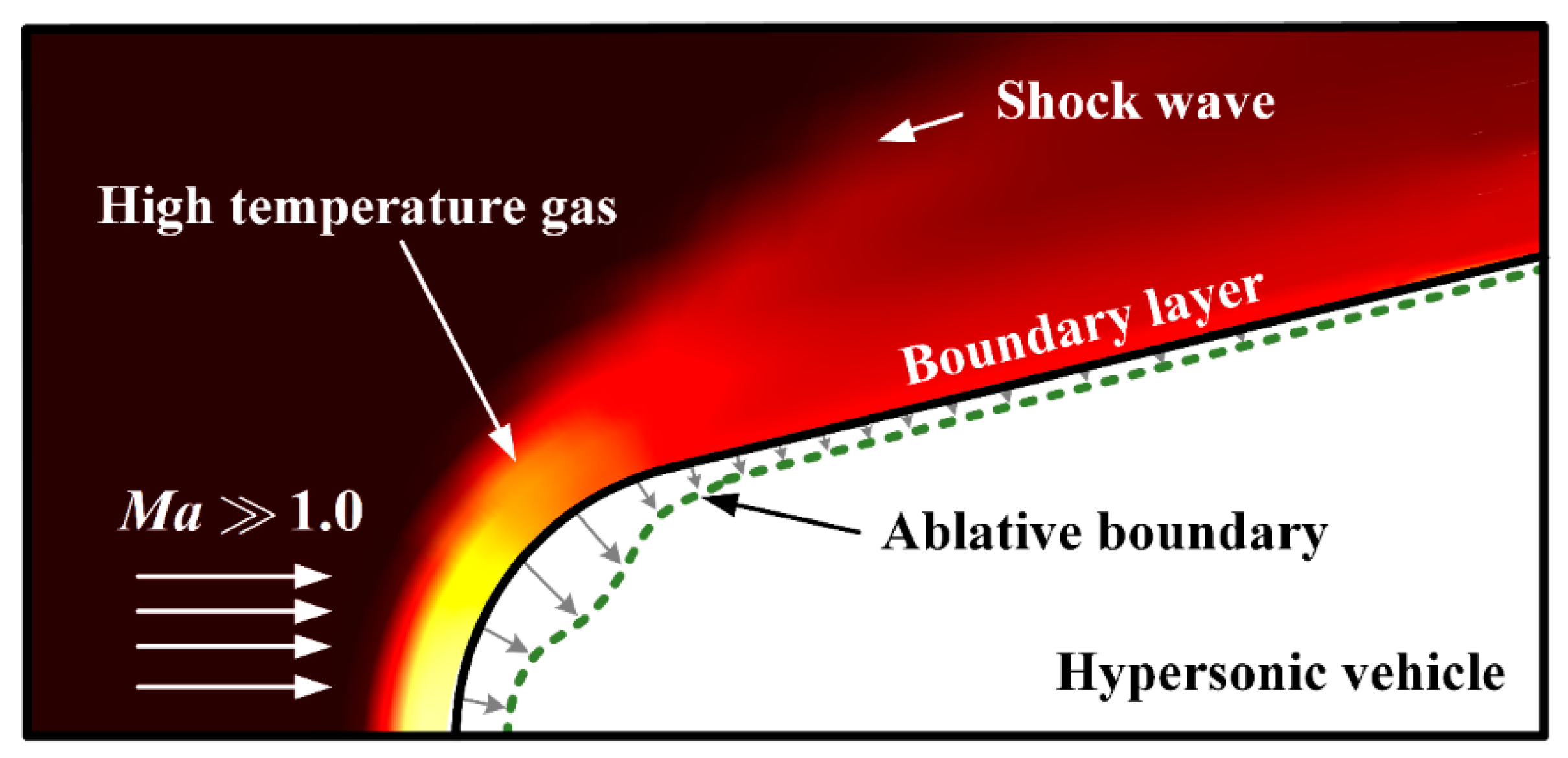
1. Introduction
2. Simulation of Head Ablation and Optical Window Thermal Deformation
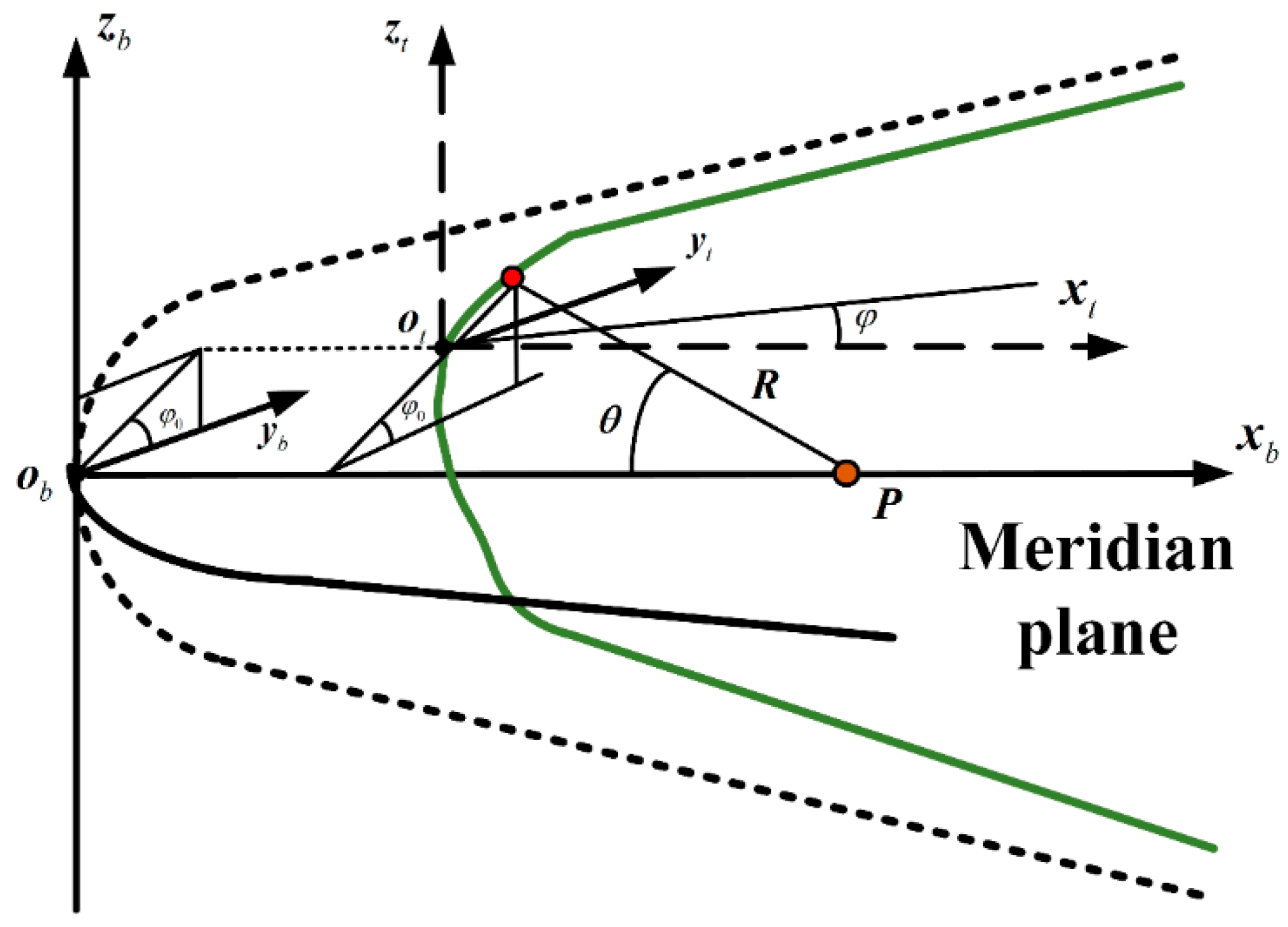
2.1. Head Ablation Profile of Hypersonic Vehicles
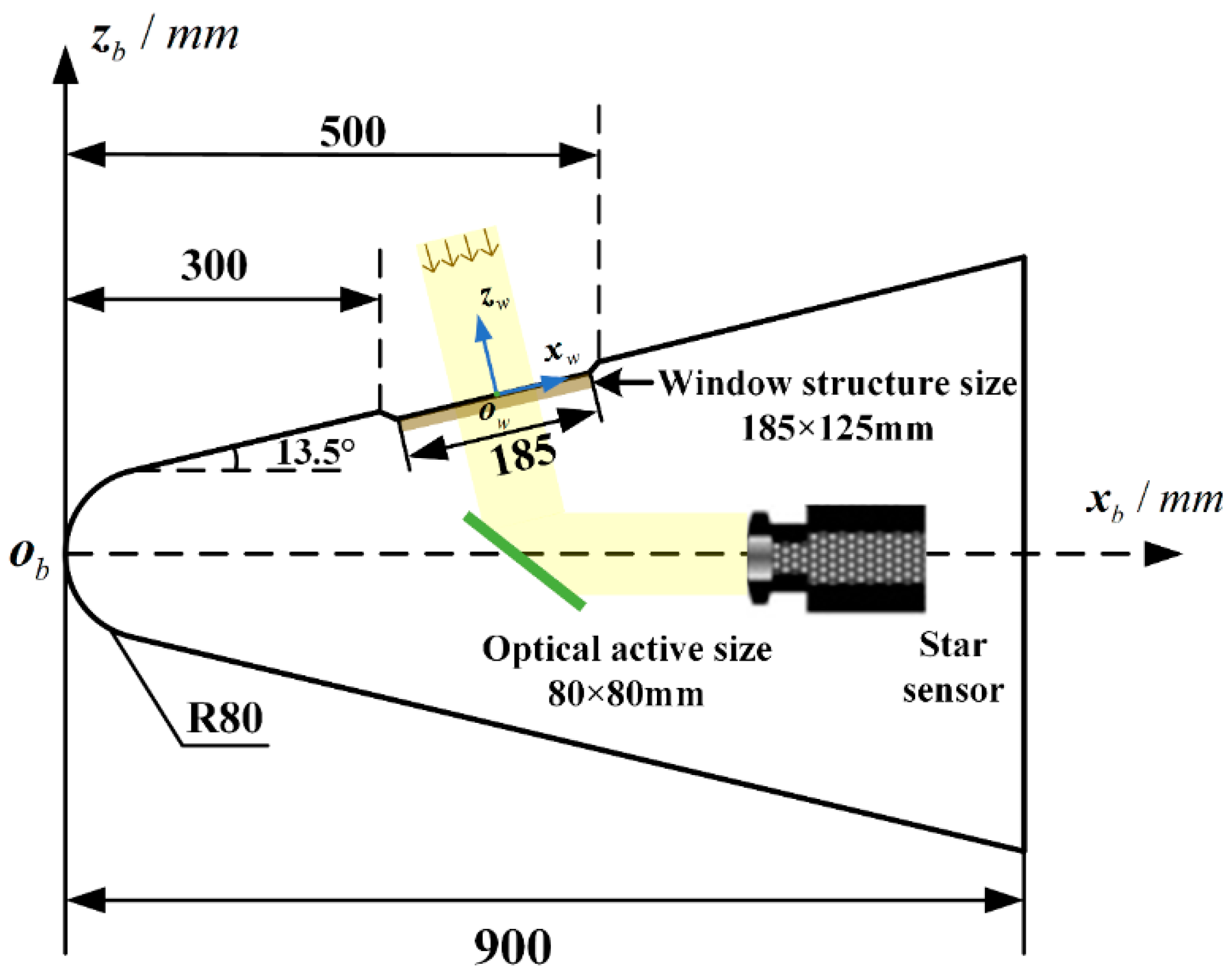
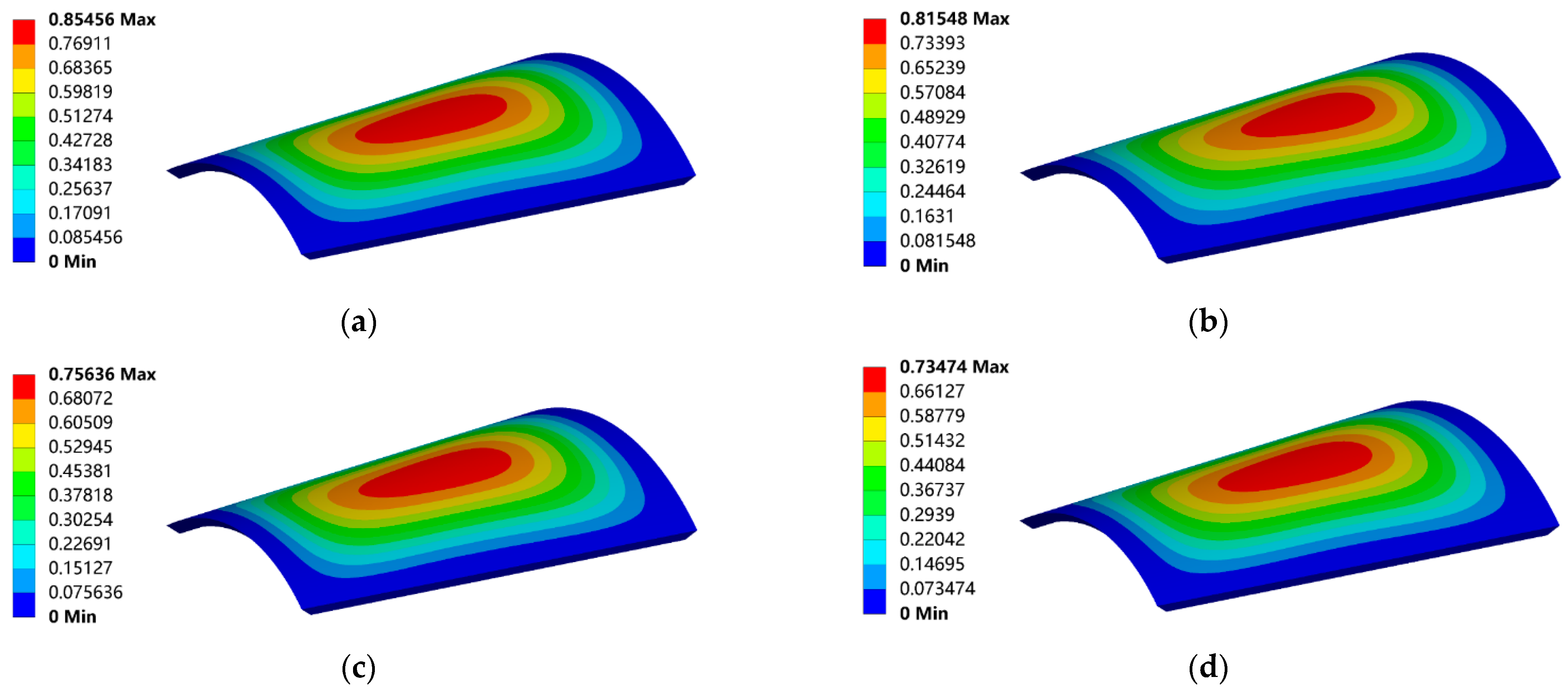
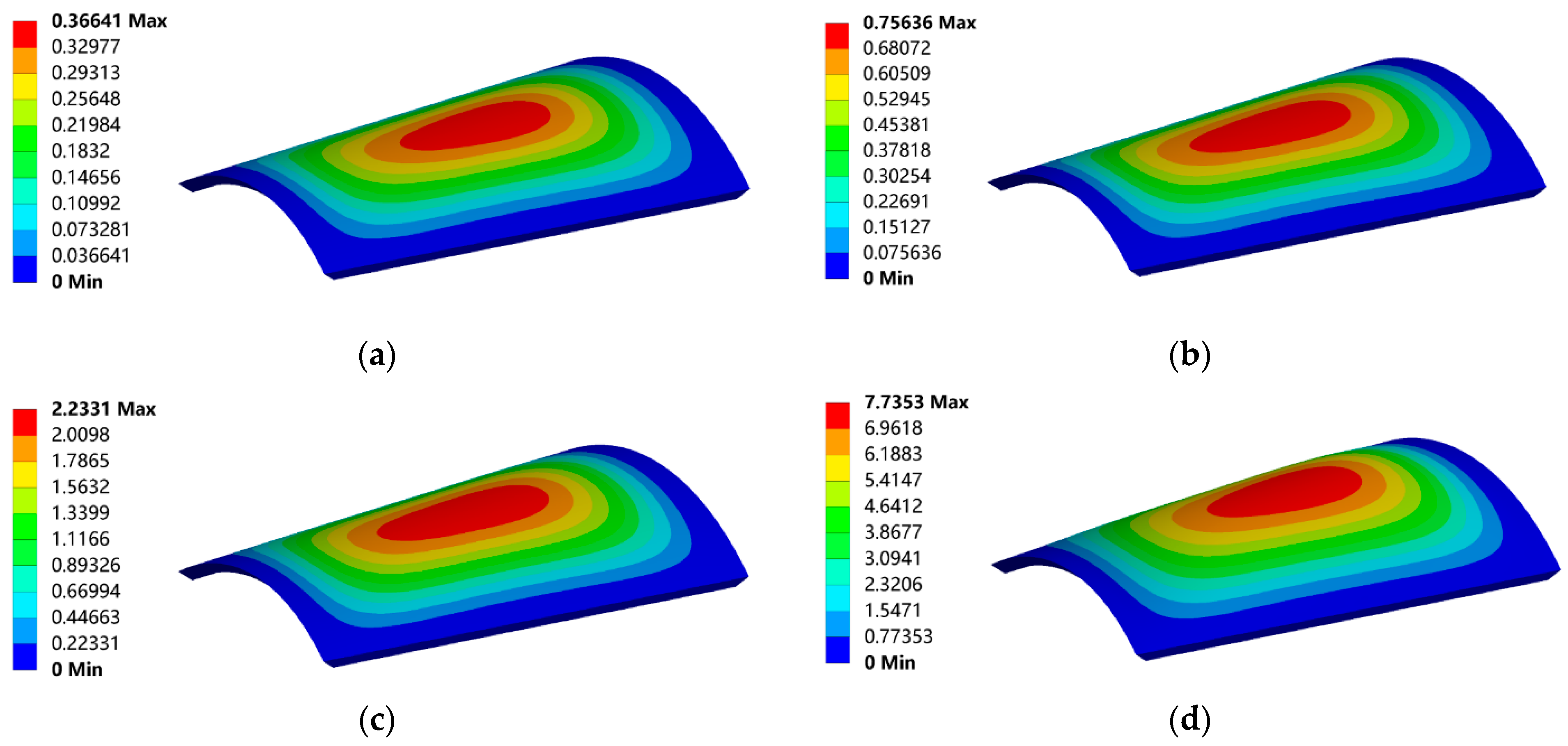
2.2. Thermal Deformation of Optical Window
3. Design of Aero-Optical Effects under Aerodynamic Heating Environment
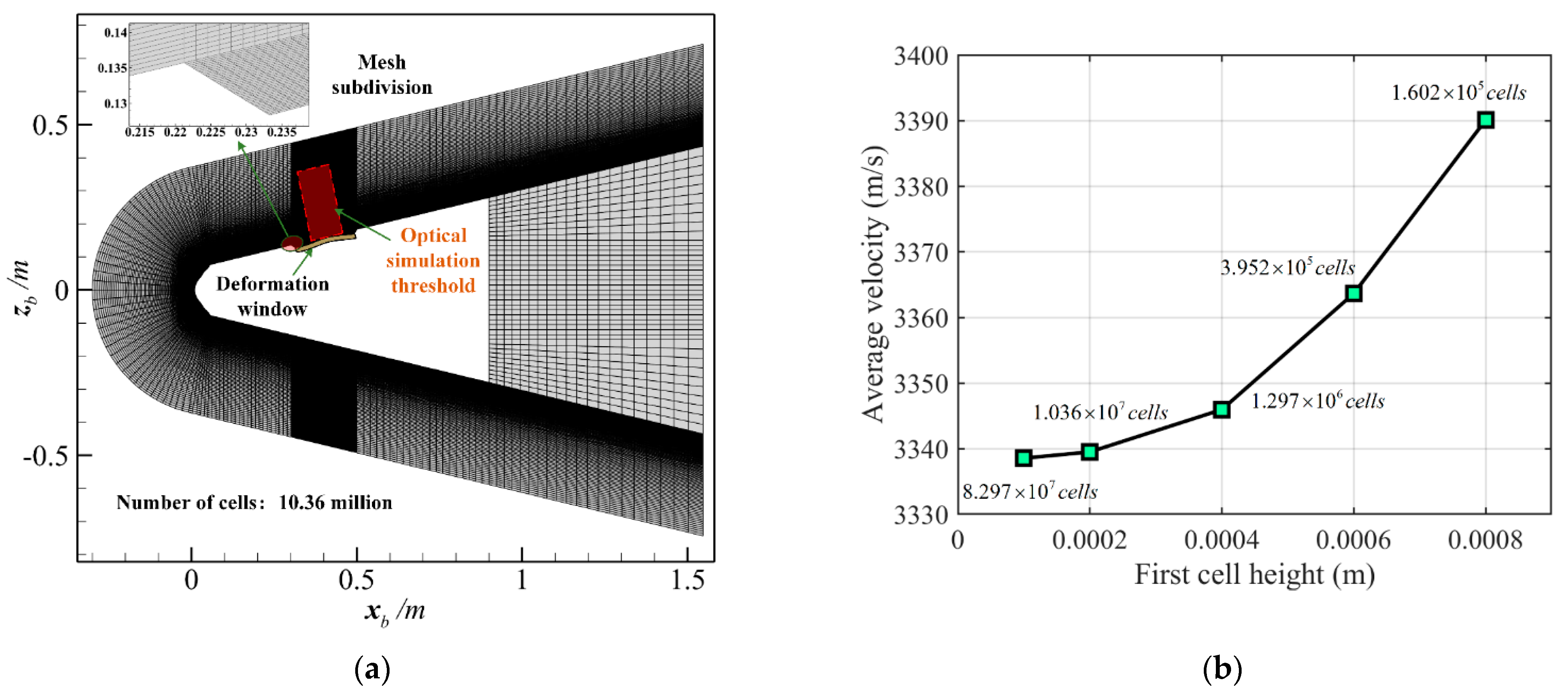
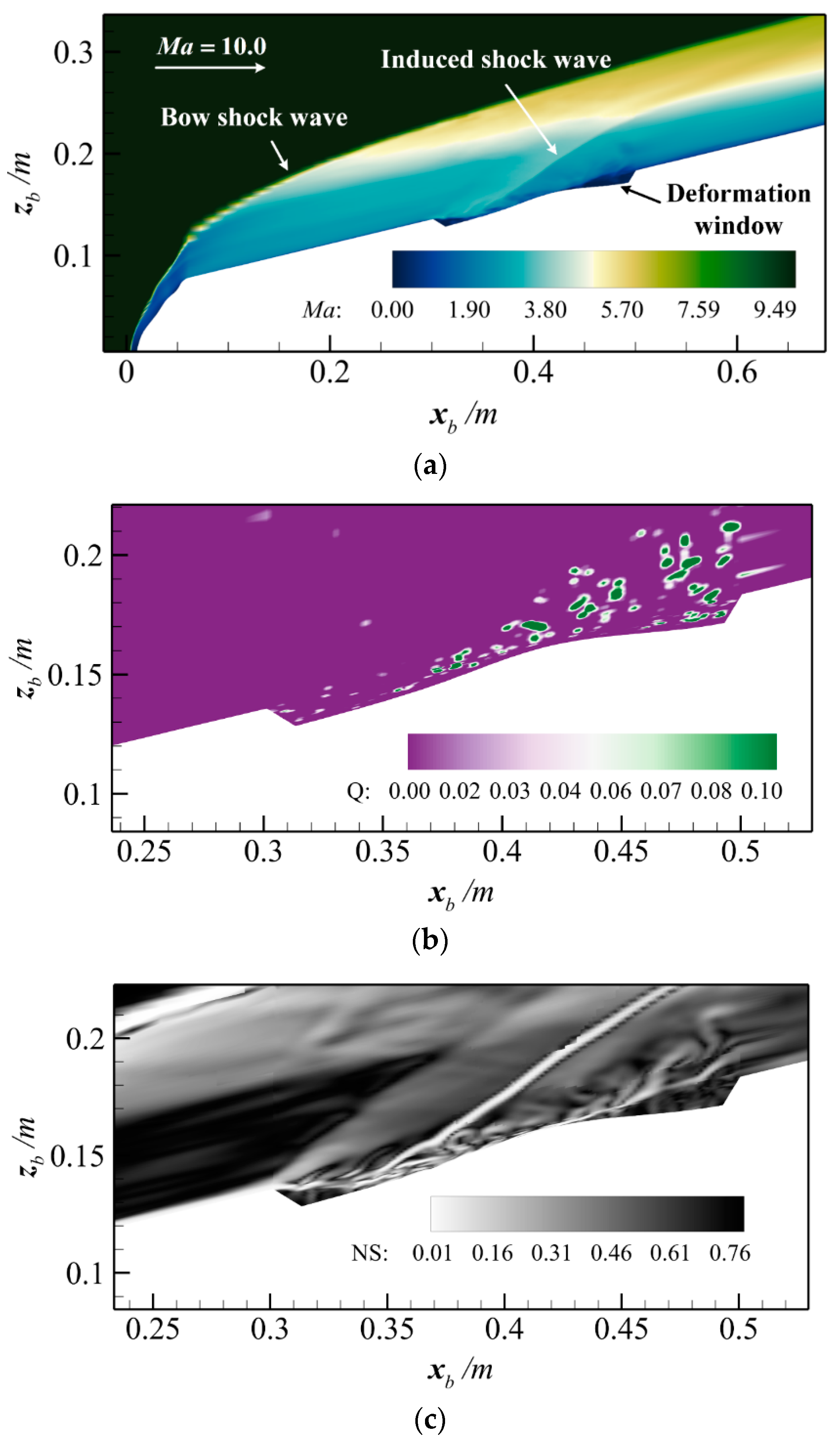
3.1. High-Speed Turbulence of Structures with Thermal Deformation
3.2. Description of Aero-Optical Effects Based on Photon Transmission Theory
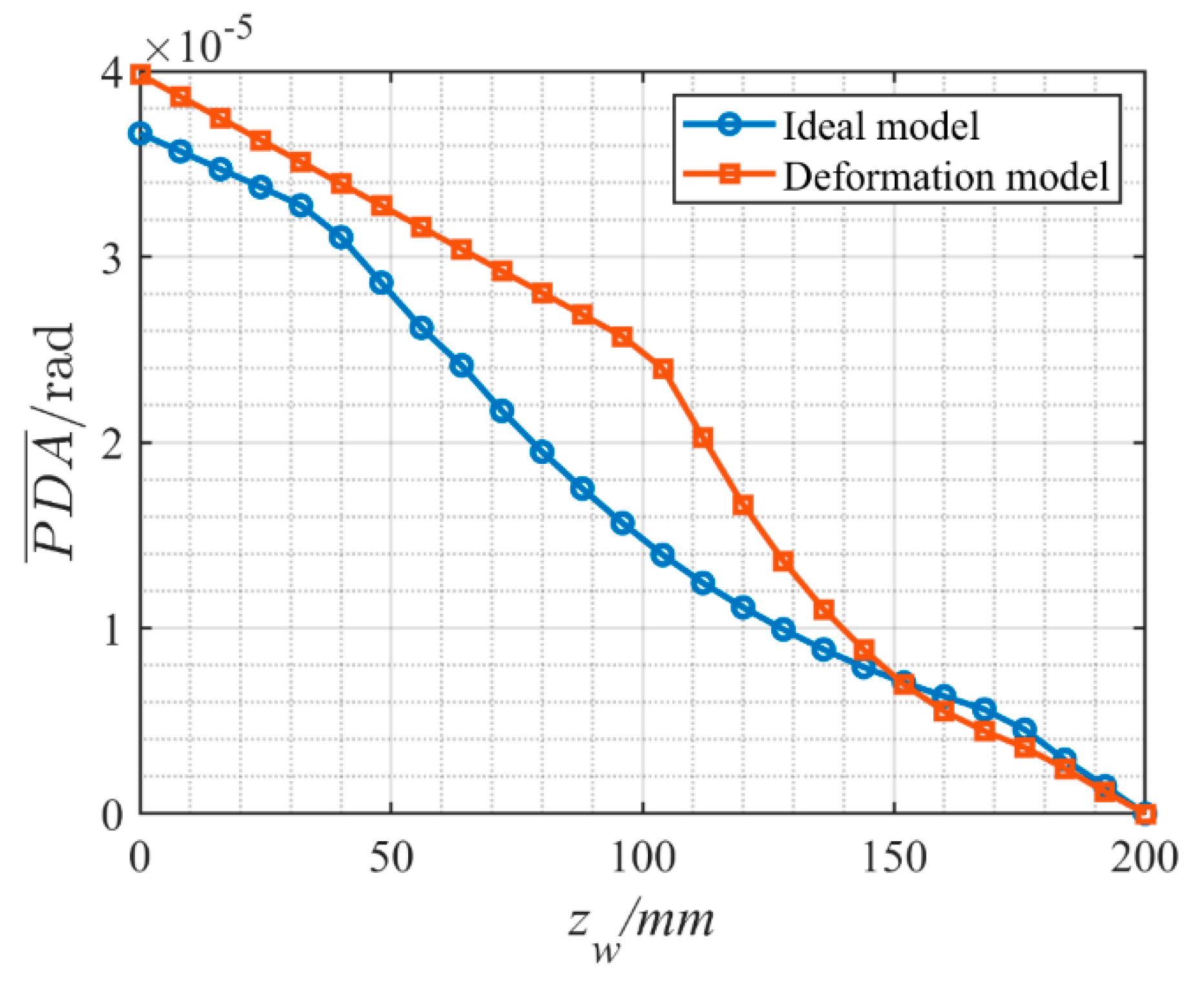
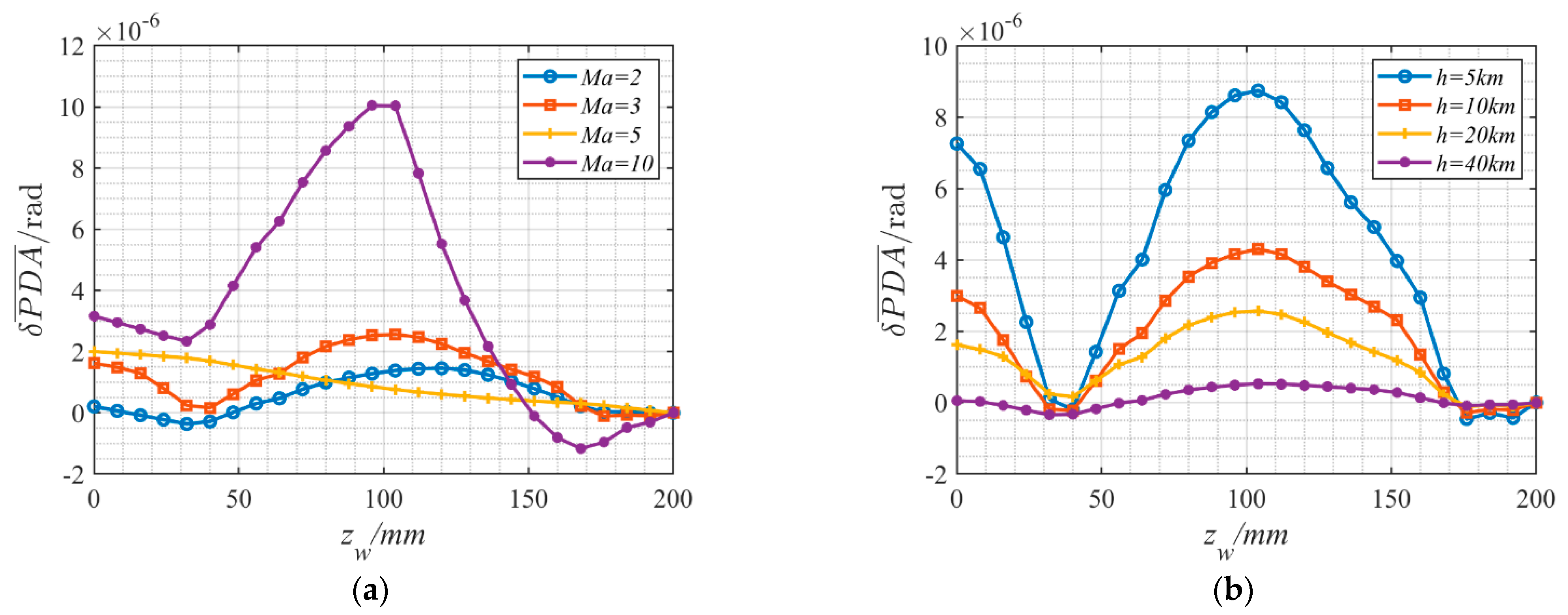
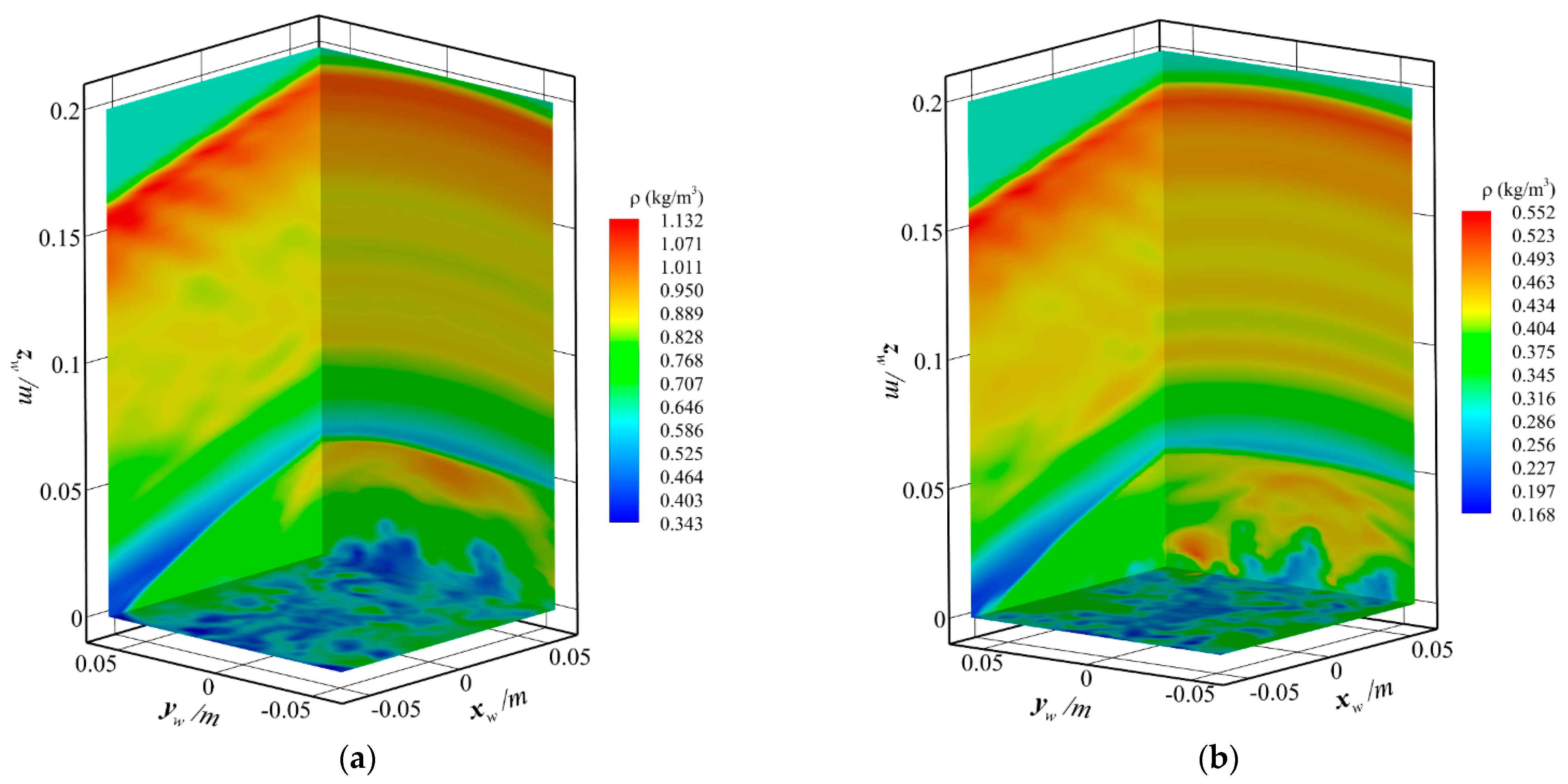
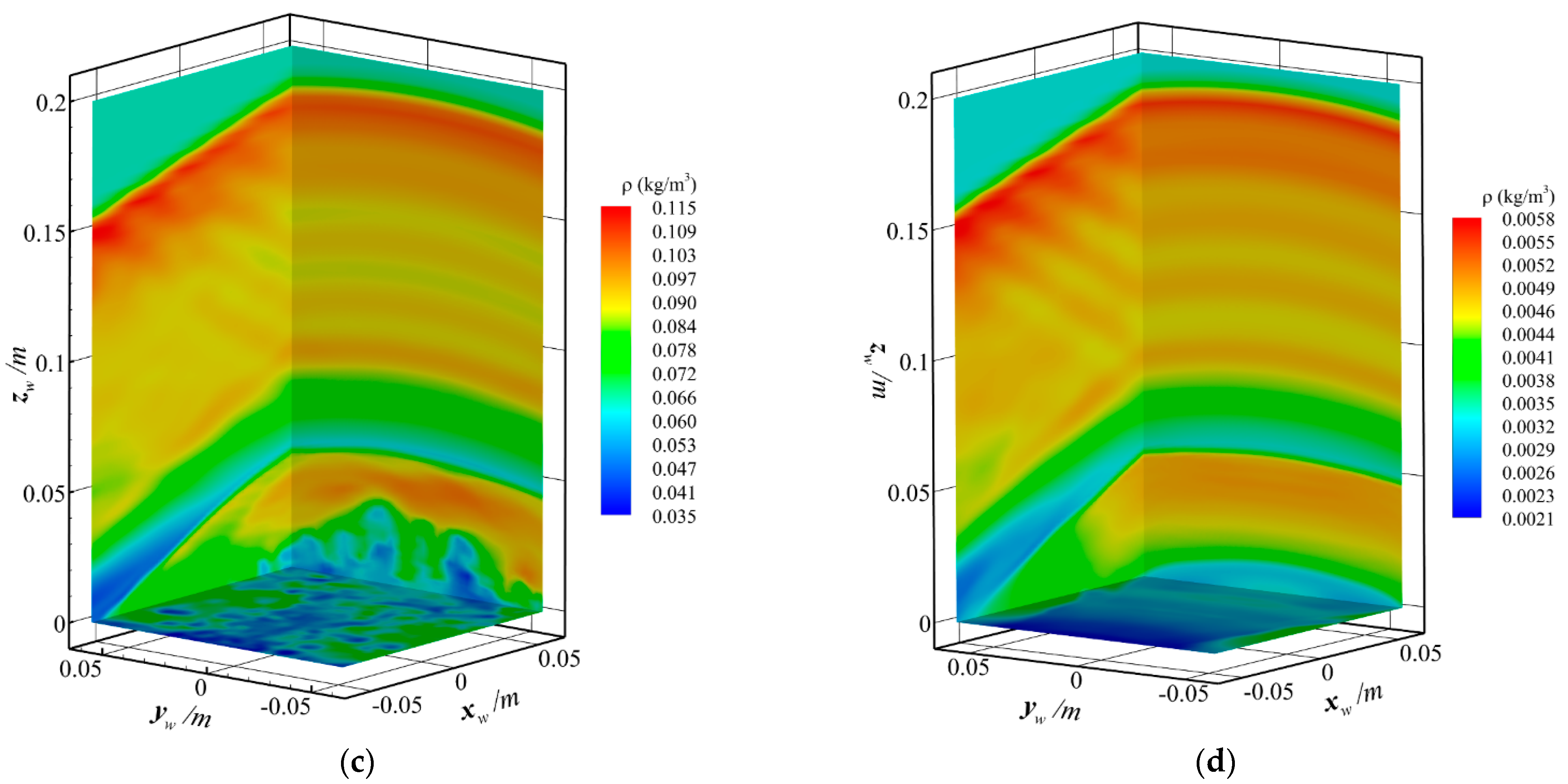
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| : | Ablation rate of vehicle surface. |
| : | Moving speed of the coordinate origin. |
| : | Stagnation point. |
| : | Polar diameter from the origin to the ablation surface. |
| : | Spherical center angle. |
| : | Meridian angle. |
| : | Heat flow of the stagnation point. |
| : | Prandtl number. |
| : | Wall density. |
| : | Density of the stationary point. |
| : | Viscosity coefficient of the stationary point. |
| : | Wall viscosity coefficient. |
| : | Velocity immediately outside the boundary layer. |
| : | Dissociation enthalpy of air. |
| : | Wall enthalpy. |
| : | Lewis number. |
| : | Laminar state. |
| : | Turbulent state. |
| : | Intermittence factor. |
| : | Reynolds number at the beginning of transition. |
| : | Average Reynolds number. |
| : | Reynolds number at the end of transition. |
| : | Current Reynolds number. |
| : | Convection heat transfer coefficient. |
| : | Sum of convective heating and recombined heating. |
| : | Emissivity. |
| : | Stefan–Boltzmann constant |
| : | Thermal blocking factor. |
| : | Mechanical denudation factor. |
| : | Wall temperature. |
| : | Enthalpy of the cold wall. |
| : | Mass loss rate per unit area of the material. |
| : | Density of the material. |
| : | Thermal conductivity values in the of the optical window. |
| : | Temperature distribution in the optical window. |
| : | Temperature distribution of boundary . |
| : | Direction cosine of the coordinate axis pointing to the outside normal. |
| : | Heat flux of boundary . |
| : | Convection heat transfer coefficient. |
| : | External ambient temperature of boundary . |
References
- Di Giorgio, S.; Quagliarella, D.; Pezzella, G.; Pirozzoli, S. An aerothermodynamic design optimization framework for hypersonic vehicles. Aerosp. Sci. Technol. 2019, 84, 339–347. [Google Scholar] [CrossRef]
- Eyi, S.; Hanquist, K.; Boyd, I. Aerothermodynamic design optimization of hypersonic vehicles. J. Thermophys. Heat Transf. 2019, 33, 392–406. [Google Scholar] [CrossRef]
- Guo, G.; Liu, H.; Zhang, B. Aero-optical effects of an optical seeker with a supersonic jet for hypersonic vehicles in near space. Appl. Opt. 2016, 55, 4741–4751. [Google Scholar] [CrossRef] [PubMed]
- Jumper, E.; Gordeyev, S. Physics and measurement of aero-optical effects: Past and present. Annu. Rev. Fluid Mech. 2017, 49, 419–441. [Google Scholar] [CrossRef]
- Gordeyev, S.; Smith, A.; Cress, J.; Jumper, E. Experimental studies of aero-optical properties of subsonic turbulent boundary layers. J. Fluid Mech. 2014, 740, 214–253. [Google Scholar] [CrossRef]
- Hopkins, K.; Porat, H.; McIntyre, T.; Wheatley, V.; Veeraragavan, A. Measurements and analysis of hypersonic tripped boundary layer turbulence. Exp. Fluids 2021, 62, 1–12. [Google Scholar] [CrossRef]
- Knutson, A.; Thome, J.; Candler, G. Numerical simulation of instabilities in the boundary-layer transition experiment flow field. J. Spacecr. Rocket. 2021, 58, 90–99. [Google Scholar] [CrossRef]
- Bo, Y.; Zichen, F.; He, Y. Aero-optical effects simulation technique for starlight transmission in boundary layer under high-speed conditions. Chin. J. Aeronaut. 2020, 33, 1929–1941. [Google Scholar]
- Yang, B.; Yu, H.; Liu, C.; Wei, X.; Fan, Z.; Miao, J. A New Method for Analyzing the Aero-Optical Effects of Hypersonic Vehicles Based on a Microscopic Mechanism. Aerospace 2022, 9, 618. [Google Scholar] [CrossRef]
- Gordeyev, S.; Jumper, E.; Hayden, T. Aero-optical effects of supersonic boundary layers. AIAA J. 2012, 50, 682–690. [Google Scholar] [CrossRef]
- Saxton-Fox, T.; McKeon, B.J.; Gordeyev, S. Effect of coherent structures on aero-optic distortion in a turbulent boundary layer. AIAA J. 2019, 57, 2828–2839. [Google Scholar] [CrossRef]
- Mathews, E.; Wang, K.; Wang, M.; Jumper, E.J. Turbulence scale effects and resolution requirements in aero-optics. Appl. Opt. 2021, 60, 4426–4433. [Google Scholar] [CrossRef] [PubMed]
- Emelyanov, V.; Karpenko, A.; Volkov, K. Simulation of hypersonic flows with equilibrium chemical reactions on graphics processor units. Acta Astronaut. 2019, 163, 259–271. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research progress on active thermal protection for hypersonic vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Canning, T.; Tauber, M.; Wilkins, M. Influence of turbulence structure with different scale on aero-optics induced by supersonic turbulent boundary layer. AIAA J. 1968, 6, 174–175. [Google Scholar] [CrossRef]
- Kuntz, D.; Hassan, B.; Potter, D. Predictions of ablating hypersonic vehicles using an iterative coupled fluid/thermal approach. J. Thermophys. Heat Transf. 2001, 15, 129–139. [Google Scholar] [CrossRef]
- Hall, D.; Nowlan, D. Aerodynamics of ballistic re-entry vehicles with asymmetric nosetips. J. Spacecr. Rocket. 1978, 15, 55–61. [Google Scholar] [CrossRef]
- Katte, S.; Das, S.; Venkateshan, S. Two-dimensional ablation in cylindrical geometry. J. Thermophys. Heat Transf. 2000, 14, 548–556. [Google Scholar] [CrossRef]
- Raimondo, F.; Sellitto, A.; Carandente, V.; Scigliano, R.; Tescione, D. Optimum design of ablative thermal protection systems for atmospheric entry vehicles. Appl. Therm. Eng. 2017, 119, 541–552. [Google Scholar]
- Martin, A.; Boyd, I. Strongly coupled computation of material response and nonequilibrium flow for hypersonic ablation. J. Spacecr. Rocket. 2015, 52, 89–104. [Google Scholar] [CrossRef]
- Alba, C.; Greendyke, R.; Lewis, S.; Morgan, R.; McIntyre, T. Numerical modeling of earth reentry flow with surface ablation. J. Spacecr. Rocket. 2016, 53, 84–97. [Google Scholar] [CrossRef]
- Paglia, L.; Tirillò, J.; Marra, F.; Bartuli, C.; Simone, A.; Valente, T.; Pulci, G. Carbon-phenolic ablative materials for re-entry space vehicles: Plasma wind tunnel test and finite element modeling. Mater. Des. 2016, 90, 1170–1180. [Google Scholar] [CrossRef]
- Bianchi, D.; Nasuti, F.; Martelli, E. Navier-Stokes simulations of hypersonic flows with coupled graphite ablation. J. Spacecr. Rocket. 2010, 47, 554–562. [Google Scholar] [CrossRef]
- Lee, S.; Park, G.; Kim, J.; Paik, J. Evaluation system for ablative material in a high-temperature torch. Int. J. Aeronaut. Space Sci. 2019, 20, 620–635. [Google Scholar] [CrossRef]
- Yu, L.; Pan, B. Overview of high-temperature deformation measurement using digital image correlation. Exp. Mech. 2021, 61, 1121–1142. [Google Scholar] [CrossRef]
- Wu, D.; Lin, L.; Ren, H.; Zhu, F.; Wang, H. High-temperature deformation measurement of the heated front surface of hypersonic aircraft component at 1200 °C using digital image correlation. Opt. Lasers Eng. 2019, 122, 184–194. [Google Scholar] [CrossRef]
- Chakradhar, K.; Pal, M. Design and analysis of constant volume optical chamber for spray and combustion characterization. Mater. Today 2022, 56, 1418–1423. [Google Scholar] [CrossRef]
- Hossen, M.; MulayathVariyath, A.; Alam, J. Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace 2021, 8, 375. [Google Scholar] [CrossRef]
- Crowell, P.G. Finite Difference Schemes for the Solution of the Nosetip Shape Change Equations; Aerospace Corporation, Vehicle Engineering Division: El Segundo, CA, USA, 2017. [Google Scholar]
- Zhang, Z.; Zhang, X. Aerothermal Heating and Thermal Protection of Spacecraft at Hypersonic Conditions; National Defend Industry Press: Beijing, China, 2003. [Google Scholar]
- Zhou, S.; Guo, Y.; He, L.; Liu, X. Simulation of 3D asymmetric ablation shape of reentry missile. Acta Aeronaut. Astronaut. Sin. 2017, 38, 121397. [Google Scholar]
- Chen, Z.; Zhang, X.; Wang, Z.; Xu, Y.; Xu, X. Hypersonic aircraft’s carbon-based nose ablation shape calculation. Acta Aeronaut. Astronaut. Sin. 2016, 37, S38–S45. [Google Scholar]
- Wakaki, M.; Shibuya, T.; Kudo, K. Physical Properties and Data of Optical Materials; CRC Press: Boca Raton, FL, USA, 2018; pp. 383–585. [Google Scholar]
- Li, T.; Sun, H.; Yang, M.; Zhang, C.; Lv, S.; Li, B.; Sun, D. All-Ceramic, compressible and scalable nanofibrous aerogels for subambient daytime radiative cooling. Chem. Eng. 2023, 452, 139518. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, W.; Yang, Y.; Han, Z.; Bao, Y. Finite element analysis of heat transfer performance of vacuum glazing with low-emittance coatings by using ANSYS. Energy Build. 2020, 206, 109584. [Google Scholar] [CrossRef]
- Memon, S. Experimental measurement of hermetic edge seal’s thermal conductivity for the thermal transmittance prediction of triple vacuum glazing. Case Stud. Therm. Eng. 2017, 10, 169–178. [Google Scholar] [CrossRef]
- Wu, M.; Martin, M. Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp. AIAA J. 2007, 45, 879–889. [Google Scholar] [CrossRef]
- Oughstun, K.; Cartwright, N. On the Lorentz-Lorenz formula and the Lorentz model of dielectric dispersion. Opt. Express 2003, 11, 1541–1546. [Google Scholar] [CrossRef] [PubMed]
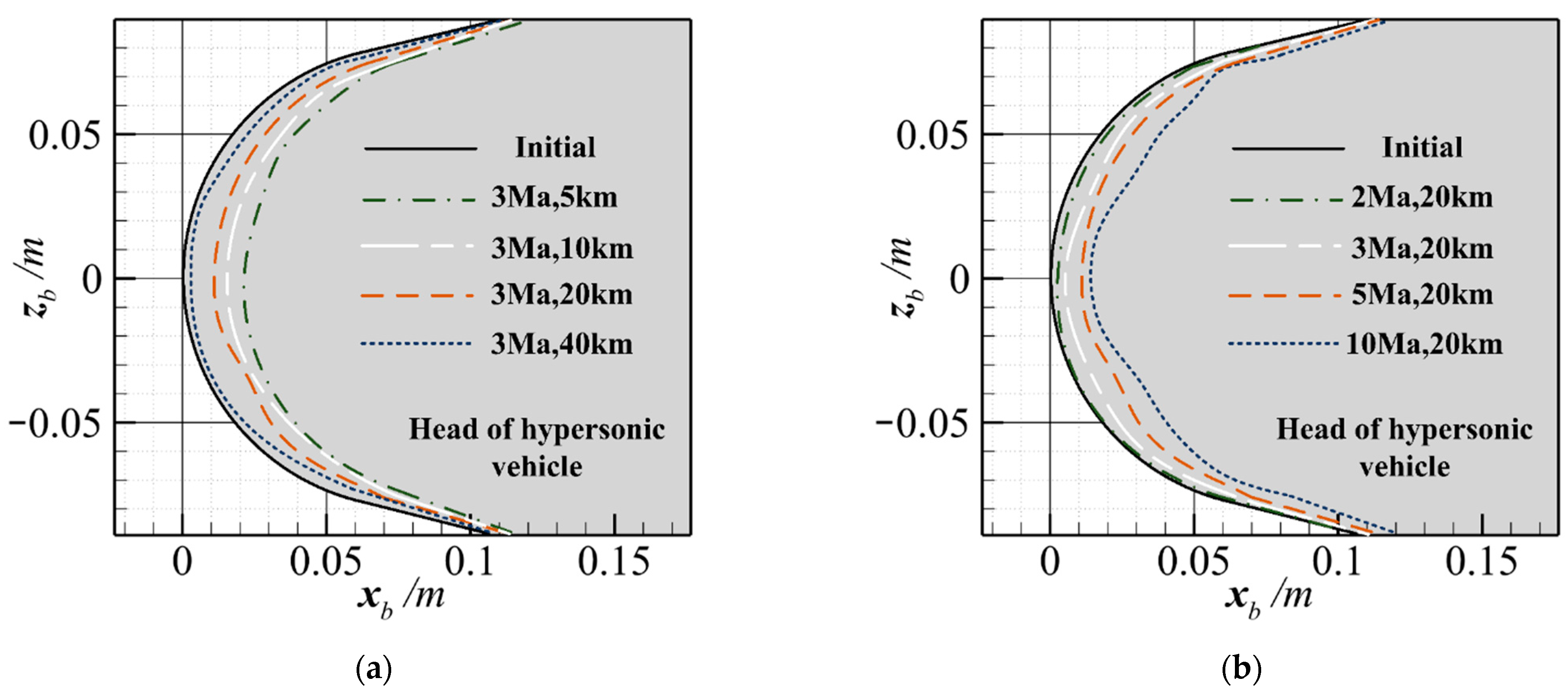


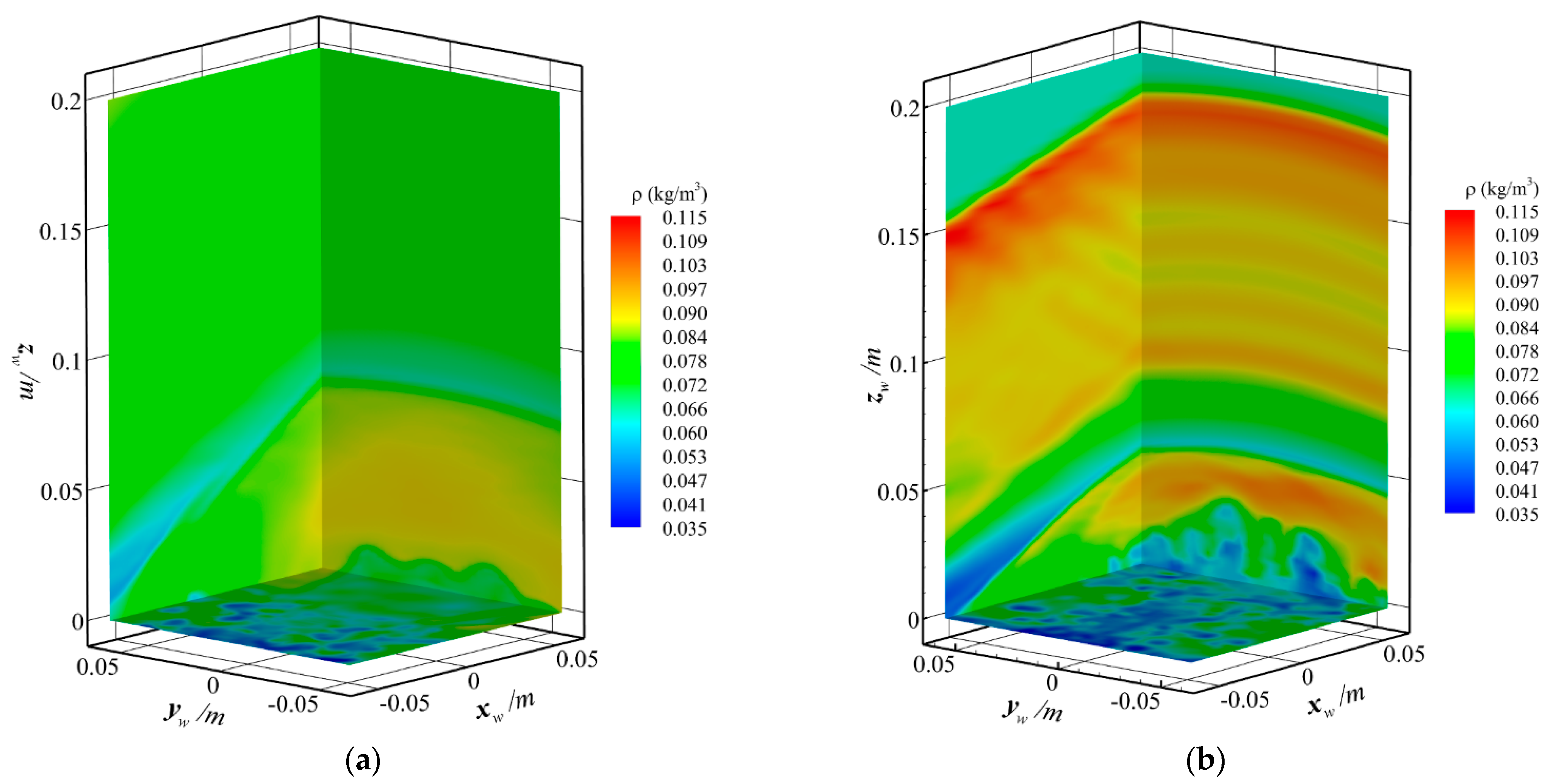
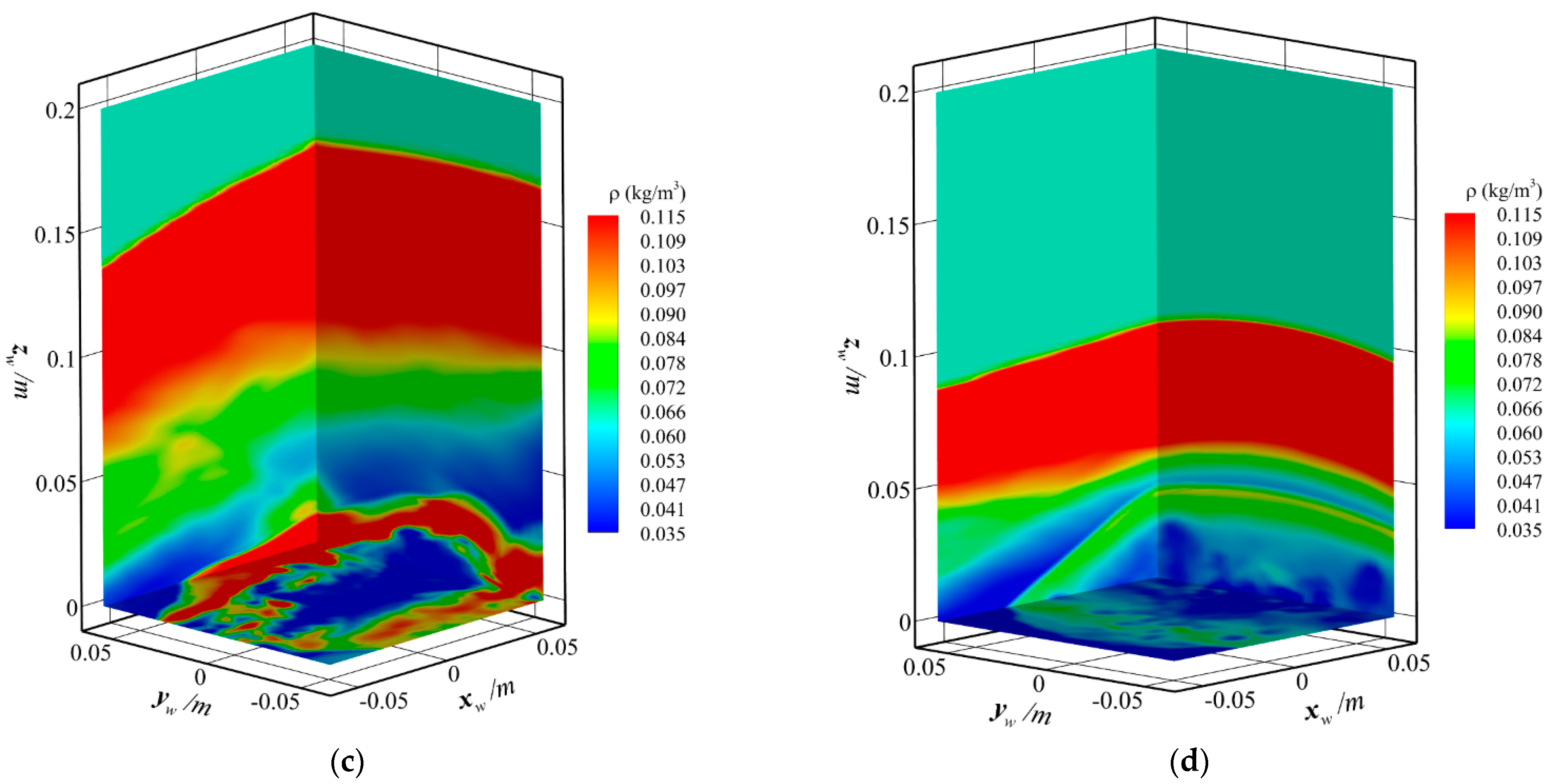
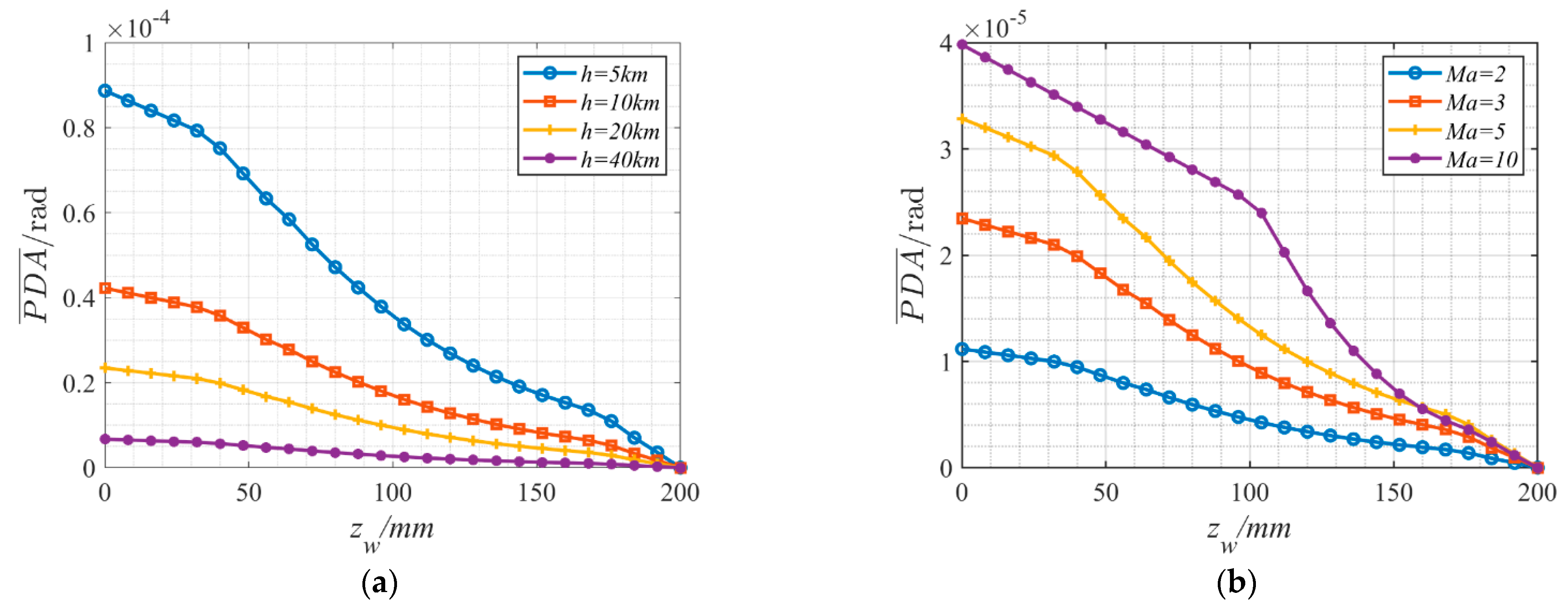
| Number | Altitude | Velocity |
|---|---|---|
| 1 | 5 km | 3 Ma |
| 2 | 10 km | 3 Ma |
| 3 | 20 km | 3 Ma |
| 4 | 40 km | 3 Ma |
| 5 | 20 km | 2 Ma |
| 6 | 20 km | 5 Ma |
| 7 | 20 km | 10 Ma |
| Physical Quantity | Value |
|---|---|
| Elastic modulus | 344 GPa |
| Poisson’s ratio | 0.27 |
| Density | 3980 kg·m−3 |
| Thermal conductivity | 36 W·m−1·K−1 |
| Constant pressure heat capacity | 750 J·kg−1·K−1 |
| Coefficient of thermal expansion | 5.3 × 10−6 K−1 |
| Boundary | Thermal Boundary | Solid Mechanical Boundary |
|---|---|---|
| Outer surface | The first kind of boundary (temperature distribution from external flow field) | Applied load (the pressure distribution from external flow field) |
| Inner surface | The third kind of boundary (T = 300 K, h = 10 W·m−2·K−1) | Applied load (P = 101,325 Pa) |
| Window edge | The second kind of boundary (q = 0) | Fixed constraint |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Yu, H.; Liu, C.; Wei, X.; Fan, Z.; Miao, J. Influence of Ablation Deformation on Aero-Optical Effects in Hypersonic Vehicles. Aerospace 2023, 10, 232. https://doi.org/10.3390/aerospace10030232
Yang B, Yu H, Liu C, Wei X, Fan Z, Miao J. Influence of Ablation Deformation on Aero-Optical Effects in Hypersonic Vehicles. Aerospace. 2023; 10(3):232. https://doi.org/10.3390/aerospace10030232
Chicago/Turabian StyleYang, Bo, He Yu, Chaofan Liu, Xiang Wei, Zichen Fan, and Jun Miao. 2023. "Influence of Ablation Deformation on Aero-Optical Effects in Hypersonic Vehicles" Aerospace 10, no. 3: 232. https://doi.org/10.3390/aerospace10030232
APA StyleYang, B., Yu, H., Liu, C., Wei, X., Fan, Z., & Miao, J. (2023). Influence of Ablation Deformation on Aero-Optical Effects in Hypersonic Vehicles. Aerospace, 10(3), 232. https://doi.org/10.3390/aerospace10030232






