Theoretical Research on Magnetic Confinement Mechanism of Applied-Field Magnetoplasmadynamic Thruster

Abstract

Since the invention of rockets, mankind has been constantly trying to explore the universe. It was not until the beginning of the last century that electric propulsion technology was introduced. With the same weight of fuel consumed as chemical propulsion, electric propulsion technology can transport a spacecraft to a more distant universe. With its excellent performance in terms of specific impulse and thrust, the MPDT (MagnetoPlasmaDynamic Thruster) is garnering significant attention in the field of electric propulsion. Recent research has focused on improving its propulsion performance and service life. Due to the complexity of its working mechanism, there is no perfect explanation for it. Further analysis of its working mechanism may lead to a solution to the improvement of certain significant performance aspects such as thrust. An ideal magnetic fluid model of the MPDT is established based on the MHD method, and the working mechanism is analyzed and summarized according to simulations and experiments. The results of the analysis indicate that reducing the size of the cathode could significantly improve the thruster’s performance.

1. Introduction

The theory of electric propulsion started in the early 20th century. At that time, the low specific impulse of chemical propulsion made it difficult for the spacecraft to travel beyond our solar system. The invention of electric propulsion technology can be said to be an important milestone in the history of aerospace. The extremely high specific impulse of electric propulsion technology greatly reduces the fuel required for aircraft acceleration. Currently, electric propulsion technology has been applied to all kinds of spacecraft.

The MPDT (MagnetoPlasmaDynamic Thruster) is the most powerful electric propulsion technology [1] that can produce extremely high thrust and a specific impulse, making it one of the most desirable candidates for deep-space-exploration missions [2,3,4]. There are two types of thrusters: The Self-field MPDT (SF-MPDT) and the Applied-field MPDT (AF-MPDT). The AF-MPDT has lower power requirements compared with the SF-MPDT (10 kW vs. 100 kW) [5], and the main subject of this article is the AF-MPDT. As shown in Figure 1, it consists of a ring anode and a hollow cathode. When the propellant (argon gas) is injected through the cathode, it is ionized by a discharge arc between the cathode and anode to form a high-temperature plasma, which creates a high current between the cathode and anode. The interaction between the applied magnetic field and the plasma current generates the Lorentz force to accelerate the propellant, which, in turn, produces thrust.

The magnetic field formed by the high-speed flowing plasma will interact with the existing electric and magnetic fields, affecting the flow properties of the plasma inversely. Therefore, the working process is extremely complex, and the current theoretical findings are not yet sufficient for large-scale applications [6].

Since the MPDT was proposed, scientists in various countries have been continuously working on its theoretical analysis and simulation. Early simulations were mostly based on fluid models, such as that of Brushlinskii and Morozov [7,8], who first carried out numerical simulations of a high-power MPDT using fluid models in the 1960s and obtained the relationship between the MPDT current and the plasma axial density.

There is still a great deal of uncertainty regarding the thrust theory and mechanism of MPD thrusters. Dr. Mikellides [9,10] of Ohio State University developed an MHD model for the SF-MPDT made by Princeton University and a steady-state AF-MPDT at NASA Lewis Research Center using the time-dependent two-dimensional axisymmetric MHD code MACH2, and the results were in good agreement with the experimental results.

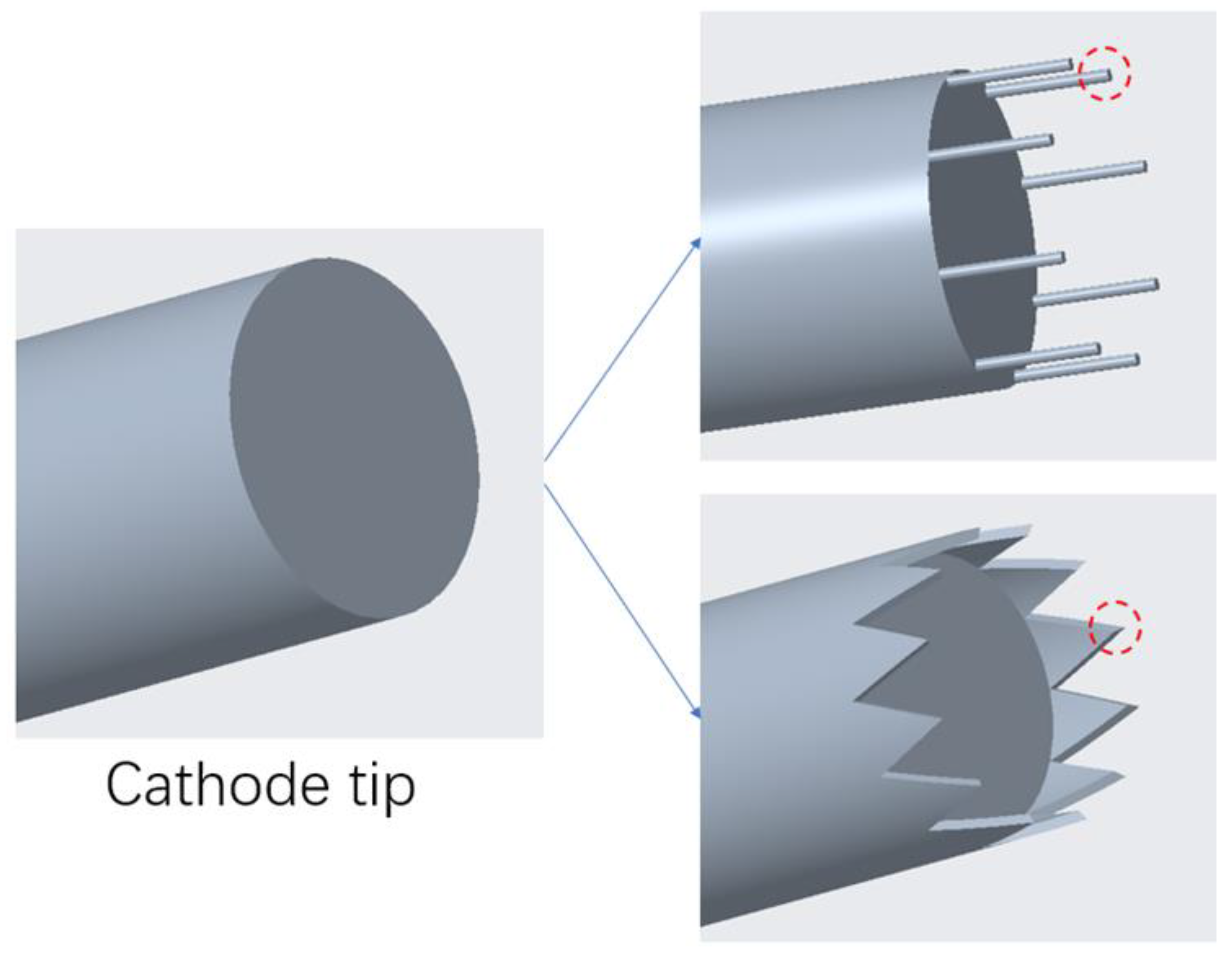
MPDT R&D is currently facing two main challenges: The short service life and the incomplete working mechanism. According to the plasma generation principle of MPDT, the cathode tip will be severely corroded by a large number of high-energy particles during the operation of the thruster, including the moment of ignition, thereby severely reducing its lifespan. Moreover, some high-energy particles are impacting the thruster along the magnetic line in the opposite direction, resulting in a reduction in its propulsion efficiency and corrosion of the thruster walls.

This article indicates that several factors will influence thruster life and propulsion efficiency, including the size of the cathode and anode, the additional magnetic field strength, and other operating conditions. In order to maximize thruster performance, each operating condition must be considered when evaluating the thruster performance improvement method. The paper presents a two-dimensional axisymmetric ideal magneto-fluid model of the MPDT using the MHD method, and simulation results and experimental images were observed under various working conditions. To analyze its working mechanism, we also developed a three-dimensional electromagnetic field model and predicted the most effective method for improving propulsion performance.

2. Model Description

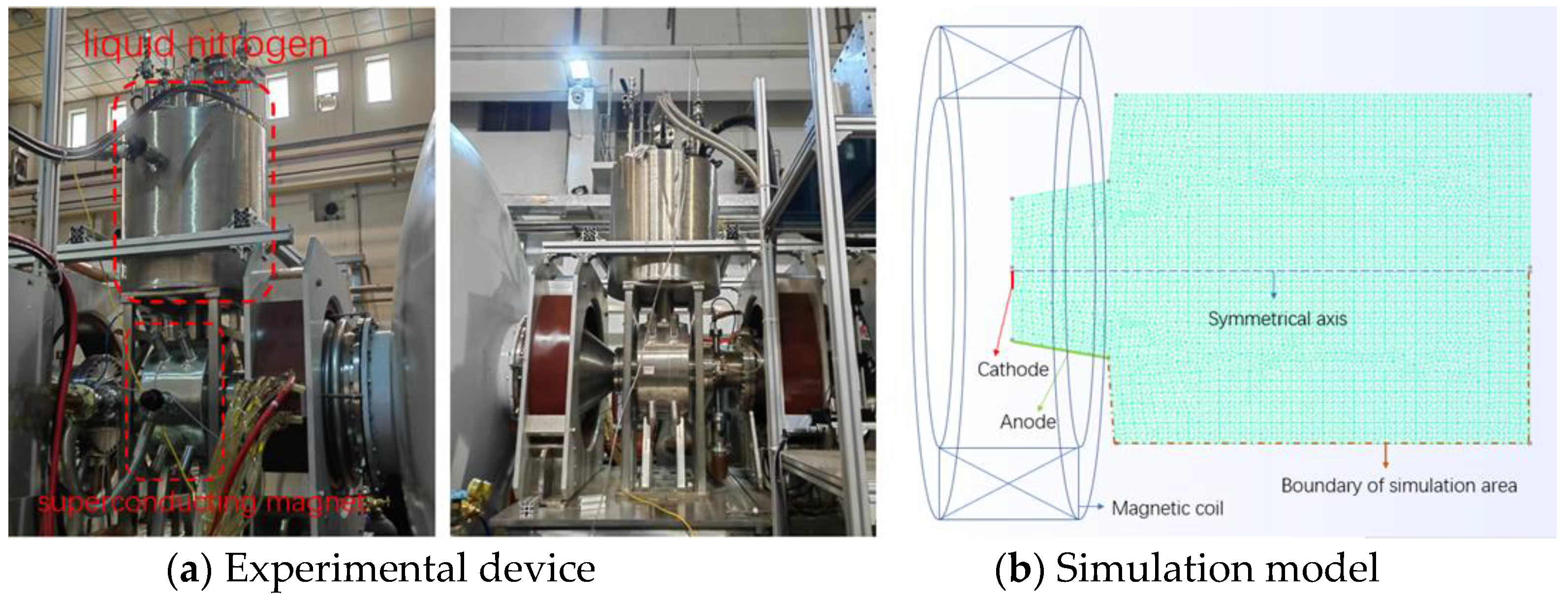
The article takes the AF-MPDT as the research object with a plasma magnetic confinement device (Figure 2a) as the experimental space. The propulsion model is shown in Figure 2b. An electric field is generated between the cathode and anode, and a magnetic field is generated by the magnetic coil. The propellant is sent into the simulation space from the cathode, and we only analyze the space within the boundaries of the simulation area.

The basic composition of the thruster includes a hollow cathode and a toroidal anode. Due to the large number of simulation comparison results needed, a two-dimensional axisymmetric model is used, and several models are designed for various operating conditions. Models differ primarily in terms of cathode and anode sizes and the simulated area. To simplify the calculation process, the ionization process is omitted. Instead, the plasma is injected directly from the cathode, simulating its behavior under the action of a magnetic field.

In order to study the mechanism of plasma motion in the ionization cavity, a complex system of coupled equations was used. It consists of continuity equations, momentum equations, energy equations, Maxwell’s set of equations, and Ohm’s law [11].

The form of the mass equation is as follows:

$$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho V\right)=0$$

(1)

where $\rho$ is the plasma density and $V$ the plasma velocity vector.

The form of the momentum equation can be expressed as:

$$\frac{\partial \left(\rho V\right)}{\partial t}+\nabla \cdot \left(\rho VV\right)=\nabla \cdot \overline{\overline{\sigma }}+\rho f$$

(2)

where $f$ denotes the volume force and $\overline{\overline{\sigma }}$ denotes the stress tensor.

The energy equation has the following form:

$$\frac{\partial }{\partial t}\left(\rho e_t\right)+\nabla \cdot \left(\rho e_{t}U\right)=\nabla \cdot \left(\overline{\overline{\sigma }}\cdot U\right)+\rho f\cdot V+\nabla \cdot q+\dot{q}$$

(3)

where $\rho e_t=\rho e+\rho \frac{V^2}{2}$ is the total energy, $q$ is the surface heat flow vector (heat transfer), and $\dot{q}$ includes the arbitrary heat addition (e.g., heat source, radiation, etc.) other than viscous dissipation.

The above equation is for the hydrodynamic part, and due to the presence of the magnetic field inside the plasma, it is necessary to further introduce Maxwell’s set of equations:

$$\begin{gathered} \nabla \cdot E=\frac{{\rho }_q}{{\epsilon }_0} \\ \nabla \times E=-\frac{\partial B}{\partial t} \\ \nabla \cdot B=0 \\ \nabla \times B={\epsilon }_0{\mu }_0\frac{\partial E}{\partial t}+{\mu }_{0}J \end{gathered}$$

(4)

where $\rho$ is the charge density and $J$ is the current density vector.

Based on Ohm’s law, we can conclude that:

$$J=\sigma \left(E+u\times B\right)+{\rho }_{q}u$$

(5)

where ${\rho }_q$ is given by the first of Maxwell’s Equations. We assume that the plasma is approximately in local thermal equilibrium (LTE).

We consider a functional equation in the convective form:

$$R\left(Q\right)={\partial }_{t}Q+\nabla \cdot F\left(Q\right)=0$$

(6)

bringing the set of ideal magnetic fluid equations into it:

$$Q=\left[\begin{array}{c}\rho \\ \rho {\nu }_x\\ \rho {\nu }_y\\ \rho {\nu }_z\\ E\\ b_x\\ b_y\\ b_z\end{array}\right]; F_x\left(Q\right)=\left[\begin{array}{c}\rho {\nu }_x\\ \rho {\nu }_x{\nu }_x+P_t-b{x}^2\\ \rho {\nu }_x{\nu }_y-b_x{b}_y\\ \rho {\nu }_x{\nu }_z-b_x{b}_z\\ \left(E+P_t\right)v_x-\left(b\cdot v\right)b_x\\ 0\\ b_y{\nu }_x-b_x{b}_y\\ b_z{b}_x-b_x{v}_z\end{array}\right]$$

(7)

where $\rho$ is the plasma density, v is the fluid velocity, b is the magnetic field, and $P_t$ is the total pressure. The electric field E is composed of dynamic, thermal, and magnetic pressures, $E=\frac{P}{\gamma -1}+\frac{1}{2}\rho {\left|v\right|}^2+\frac{1}{2}{\left|b\right|}^2$,$P_t=P+\frac{1}{2}{\left|b\right|}^2$, where $\gamma$ is the usual gas constant. These equations were solved numerically using a method based on the generalized Lagrange multiplier (GLM) [12].

3. Simulation Results

In comparison to the PIC method, the MHD method offers the primary advantage of high computational efficiency, permitting many comparative analyses to be conducted. In this article, a two-dimensional axisymmetric model is established for the MPDT with Ar as propellants, and the cathode is set to inject a current of 800 A, while the propellant is uniformly injected from the cathode surface at a flow rate of 60 mg/s. The article focuses on the plasma current intensity since it closely matches the experimental image.

3.1. Effect of Cathode Radius on the Thruster

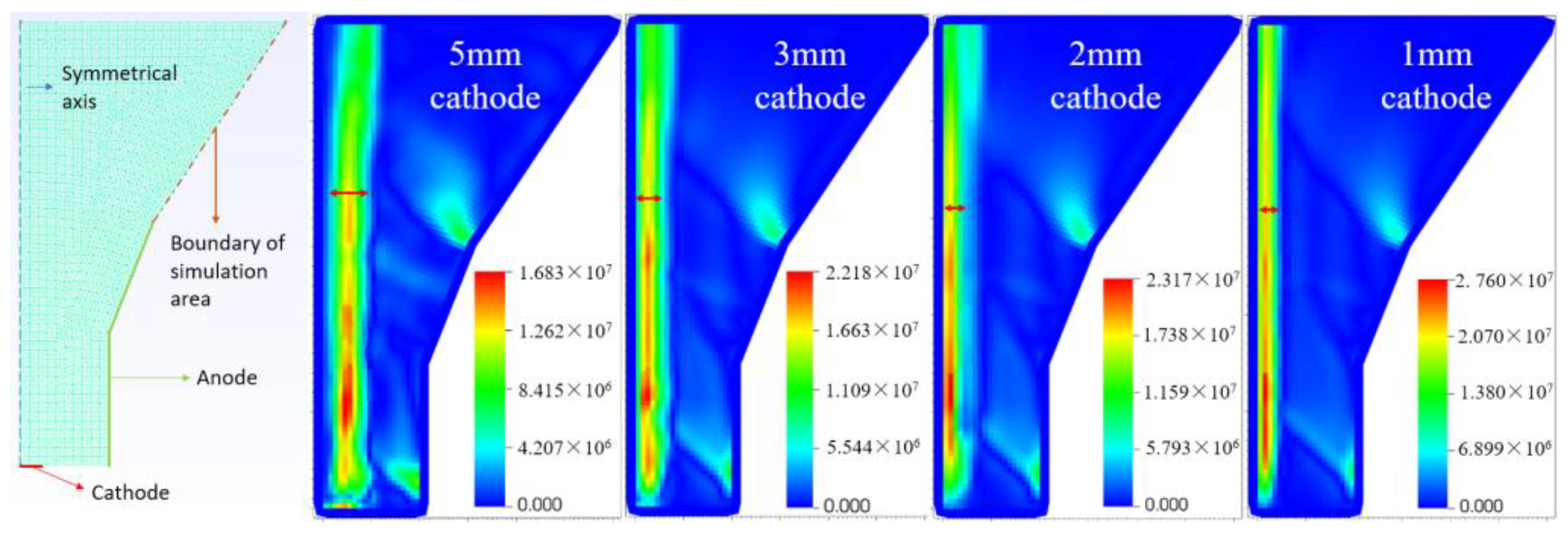
It has been revealed that cathode size has a significant impact on the thruster when models with different cathode sizes are used for simulation. Figure 3 shows the steady-state plume with a cathode radius of 1 mm, 2 mm, 3 mm, and 5 mm, respectively. Comparing the results, it can be observed that the plume is significantly more concentrated, and the peak current intensity is significantly increased as the cathode diameter decreases.

However, since the cathode nozzle will be impacted by a large number of high-energy particles, too small of a cathode radius will adversely affect the cathode lifetime, and a proper balance should be struck between the two.

3.2. Effect of Anode Size on the Thruster

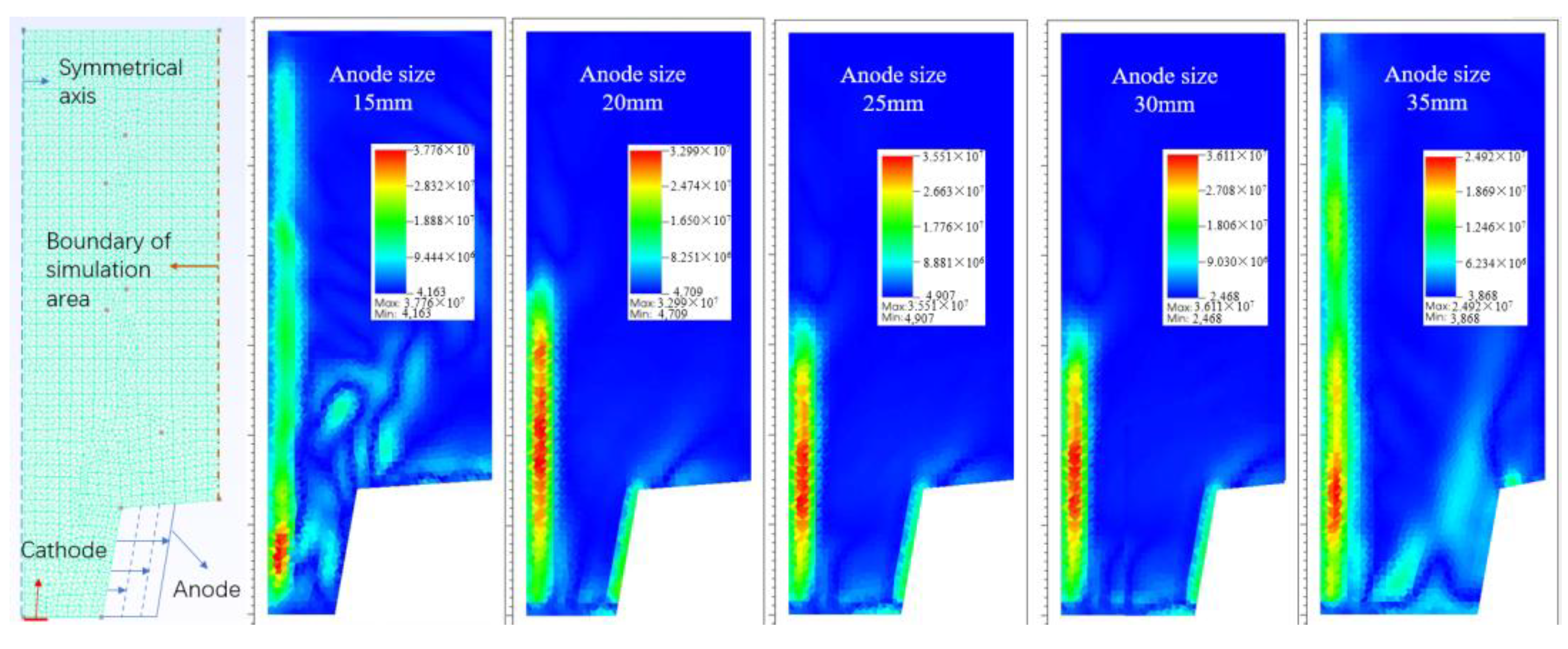
Figure 4 presents the images of the plume as the thruster reaches a steady state for different anode sizes. There was no obvious pattern to be found in this condition. The preliminary analysis suggests that this is the result of a change in the electric field strength between the cathode and anode based on the size of the anode. This phenomenon will be analyzed in detail.

3.3. Effect of Magnetic Field Intensity

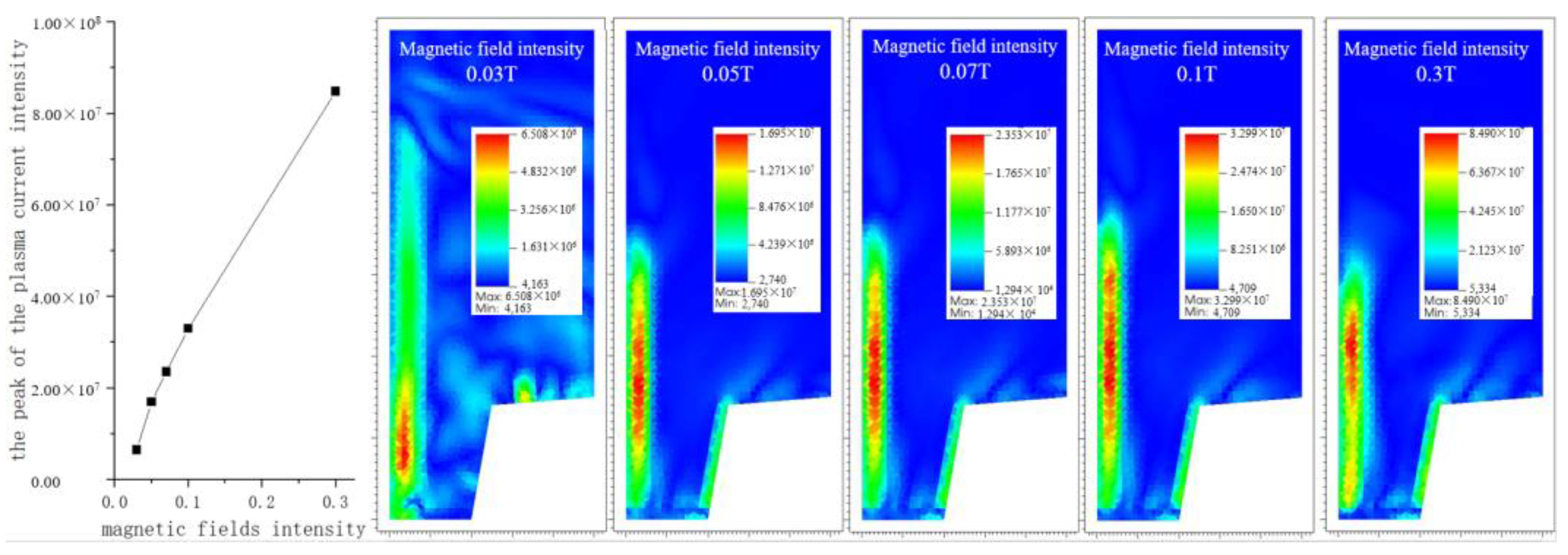
The simulated magnetic field intensity (produced by the external coil) is set as 0.03 T, 0.05 T, 0.07 T, 0.1 T, and 0.3 T, respectively. Comparing the plume images at different magnetic field strengths during the steady operation of MPDT, it is observed that the peak of the plasma current intensity increases with the enhancement of the magnetic field as shown on Figure 5. Accordingly, it is speculated that increasing the magnetic field strength within a specified range can effectively improve the thruster performance.

Since experiments with different cathode sizes require the fabrication of a large number of cathode components, which is costly and time-consuming, the paper focuses on the effect of the magnetic field on the performance of the thruster.

We use argon as a propellant. First, we ionized the argon via a high-voltage arc, and after the plasma was stably generated, a magnetic field was generated by a superconducting coil. We took experimental images with a high-speed camera under different magnetic-field intensities.

Figure 6 illustrates the plasma plume at steady-state moments under varying magnetic field strengths. Since the laboratory diagnostic equipment has not yet been installed, the article analyzes the experimental images from the perspective of plasma emission spectroscopy.

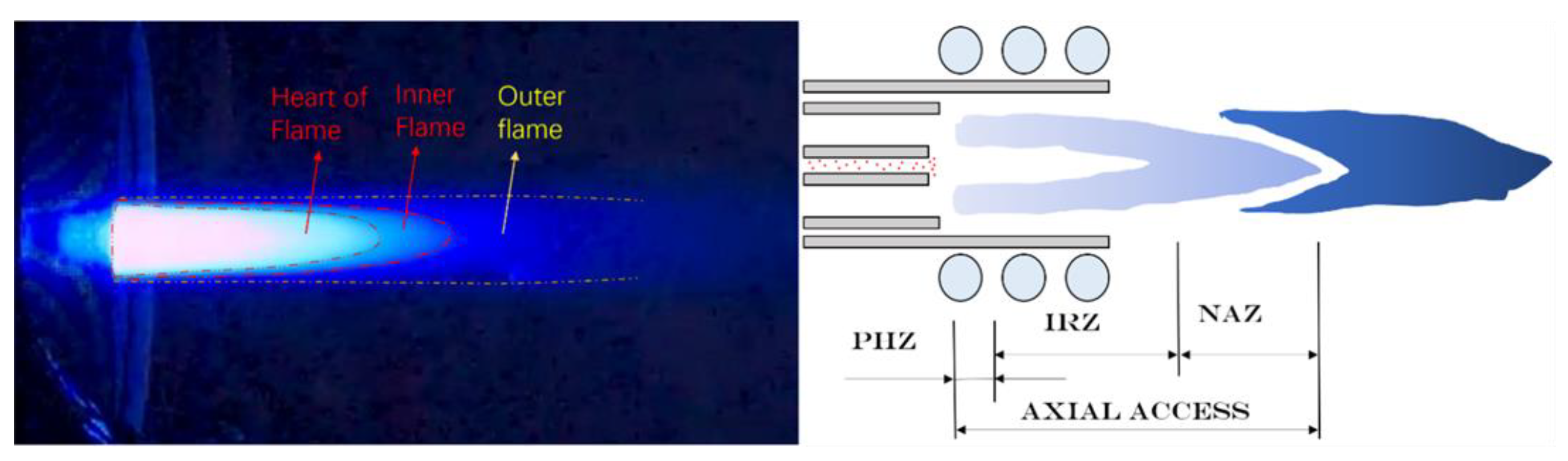
An ICP (Inductive Coupled Plasma Emission Spectrometer) is typically divided into three zones: The preheat zone (PHZ), initial radiation zone (IRZ), and normal analysis zone (NAZ). Accordingly, the plasma plume can be similarly classified based on its brightness color into the flame core, inner flame, and outer flame(Figure 7).

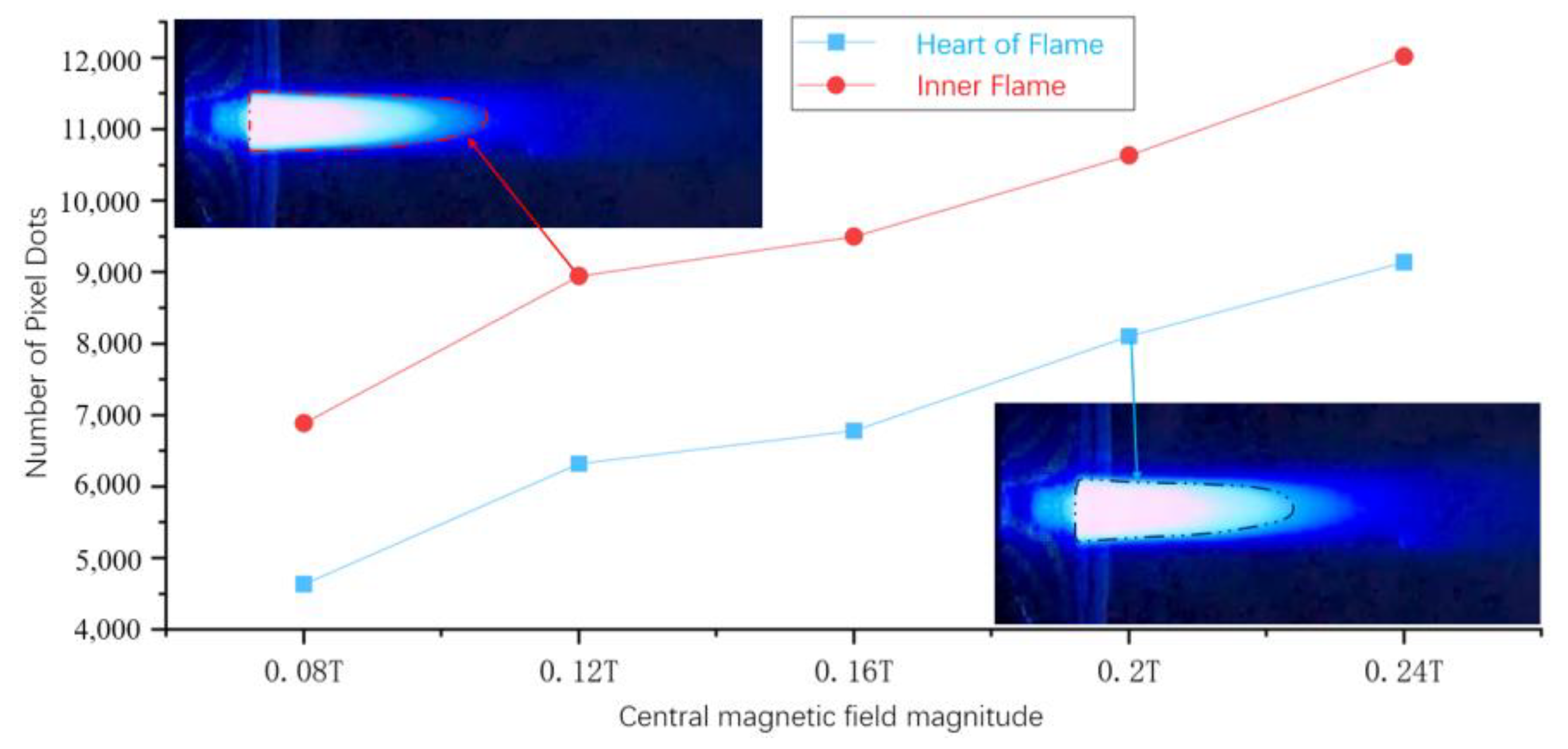
The quantification of the images plays a significant role in the analysis; however, visual observation alone is not sufficient to determine the length of the plume, thus the paper proposed the use of the dimensionless pixel area to characterize the temperature and velocity properties of the plume at different magnetic field strengths.

The area of each zone is dimensionless, and the experiments are taken with the same camera in order to obtain pictures with the same resolution. In this case, the number of pixels can be used instead. Considering that the outer flame boundary is blurred, the research focuses on the flame center and inner flame, as shown in Figure 8, and it can be found that the plume length and area increase with the increase in magnetic field strength.

3.4. Plasma Trend at the Beginning of Thruster Startup

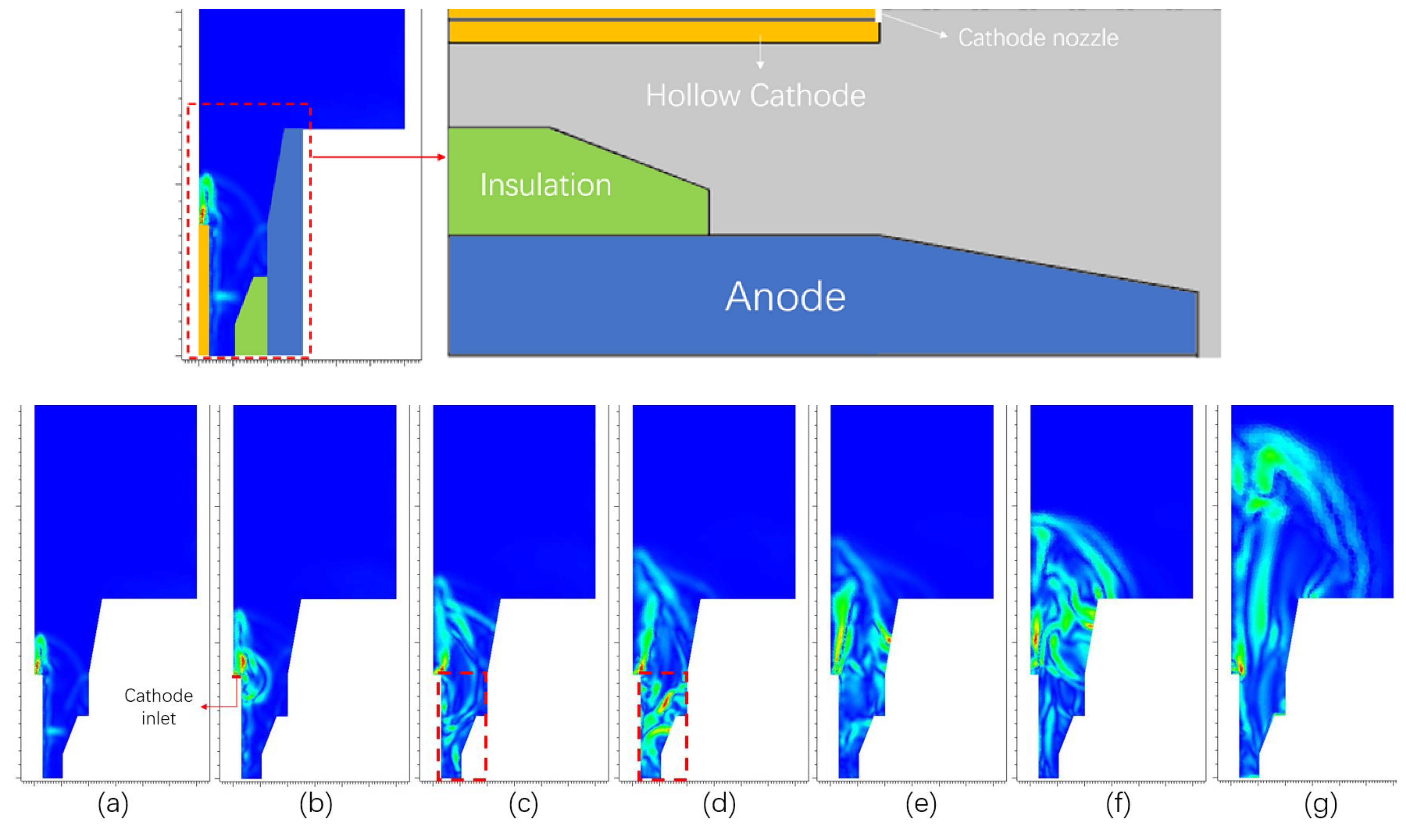
According to the simulation results of the detailed model shown in Figure 9, it can be observed that a strong current appears on the rear side of the cathode nozzle (a–g), gradually spreading outward before concentrating toward the axis.

It can be found that the thruster plume did not spurt out directly backward as an ordinary fluid; rather, it followed a very complex movement, the details of which will be elaborated on in Section 4.

4. Analysis and Discussion

In the current state of MPD research, four acceleration mechanisms are accepted as common explanations: Electrothermal acceleration, self-magnetic acceleration, Hall acceleration, and swirl acceleration [13,14]. Among them, Hall acceleration and vortex acceleration are what distinguish the AF-MPDT from the SF-MPDT.

(1)

Electrothermal acceleration, compared to the traditional chemical thruster, increases propellant enthalpy through the conversion of electrical energy into thermal energy. Following that, the nozzle turns thermal energy into kinetic energy to generate thrust. Electrothermal thrust mainly depends on the propellant flow rate, propellant injection position, pressure inside the nozzle and nozzle area, and other parameters. The thrust can be expressed as:

$$F_{Gas}=k_{Gas}\dot{m}{c}_s$$

(8)

where $c_s$ is the ion acoustic speed and $k_{Gas}$ is a dimensionless coefficient defined as either the angle of the gas flow with respect to the thrust axis or a function of the additional pressure acting on the area of the propellant injection site.

(2)

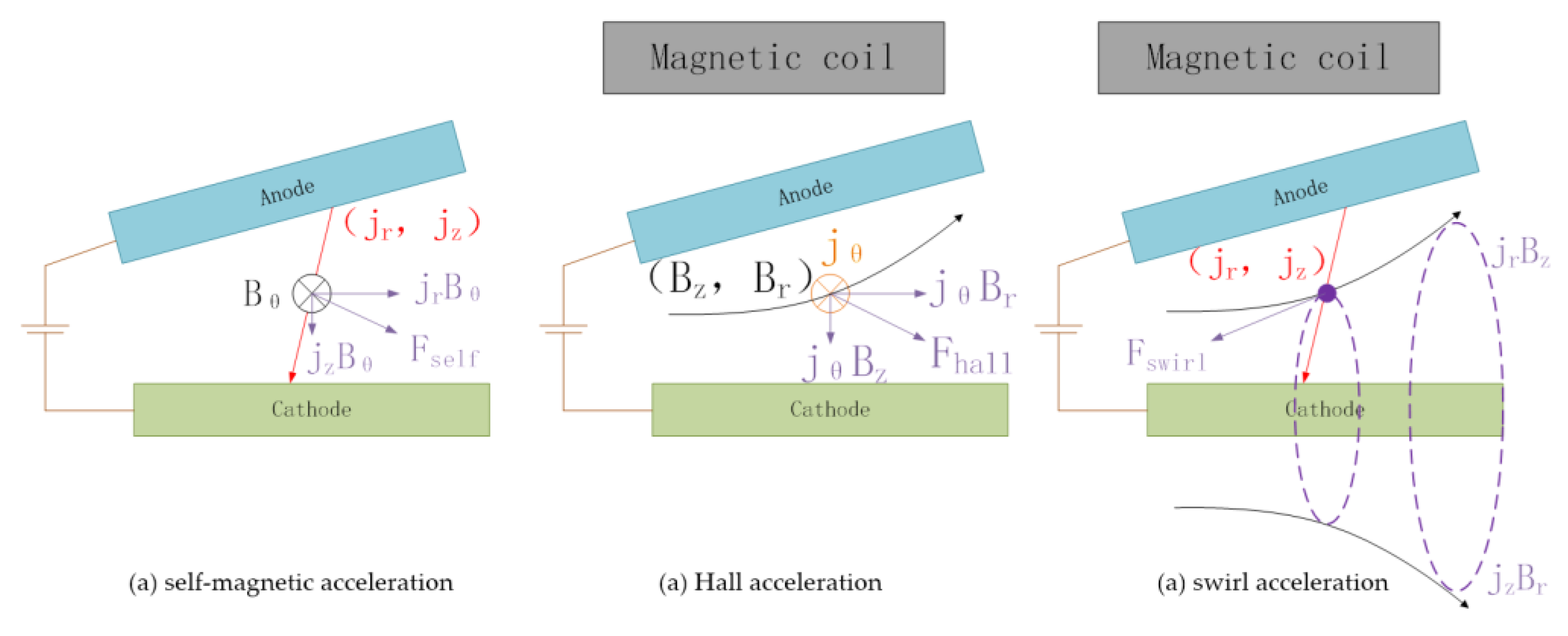
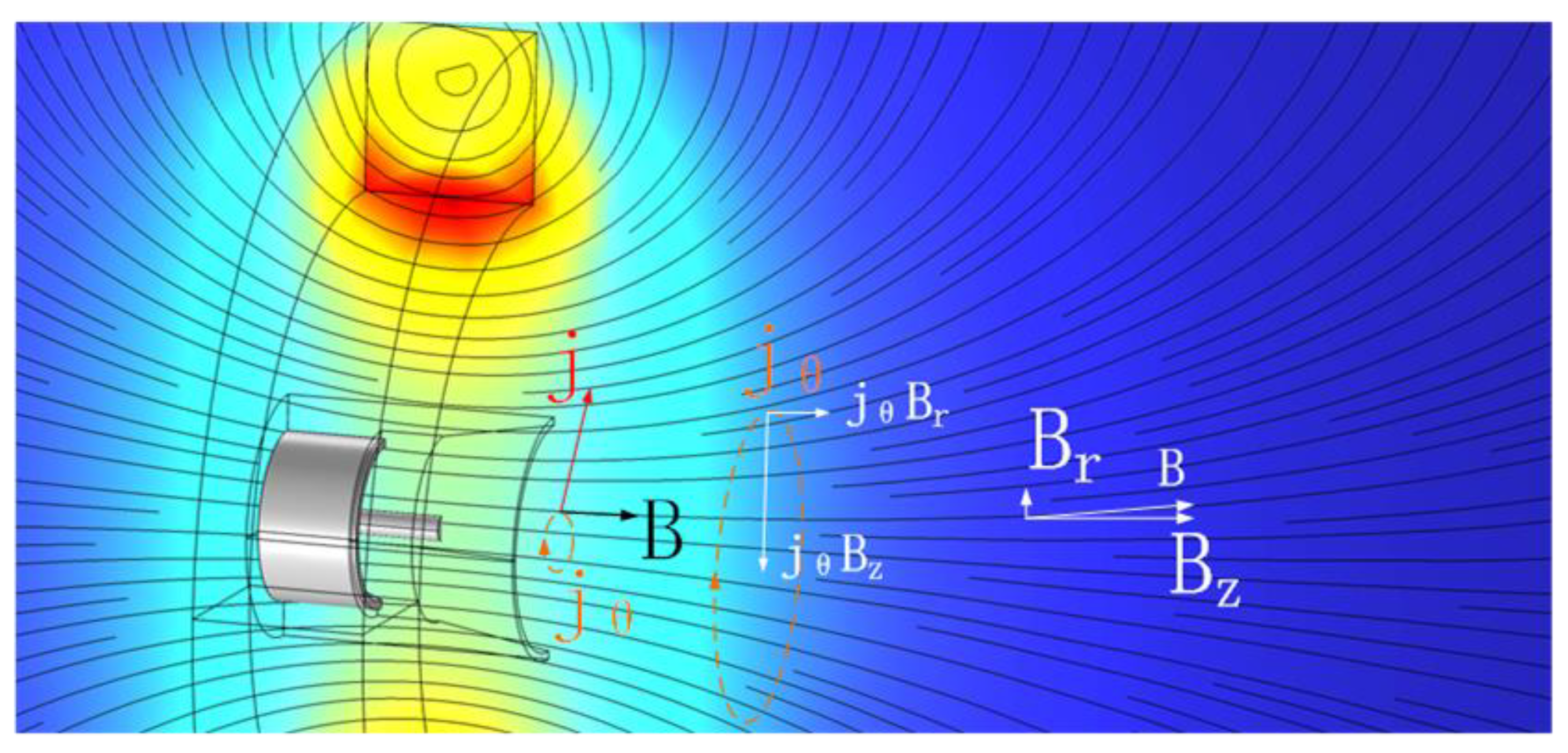
The self-magnetic acceleration mechanism is illustrated in Figure 10a. The circumferential induced magnetic field $B_{\theta }$ generated by the axial component of the current interacts with the current itself to produce the axial force $\left(j_r\times B_{\theta }\right)$ and radial force $\left(j_z\times B_{\theta }\right)$. As $\left(j_r\times B_{\theta }\right)$ accelerates the plasma, $\left(j_z\times B_{\theta }\right)$ compresses it in the radial direction, causing it to have more density near the axis, which generates the ’hrust force indirectly through the pressure difference. Since the additional magnetic field of the AF- MPDT is much larger than the current-induced magnetic field, the contribution of the self-field acceleration mechanism to the thrust is much smaller in the AF-MPDT than in the SF-MPDT.

The self-field thrust can be expressed as:

$$F_{self}=\frac{{\mu }_0{J}^2}{4\pi }\left[\ln \left(\frac{r_a}{r_c}\right)+\frac{3}{4}\right]$$

(9)

where ${\mu }_0$ is the vacuum magnetic permeability, $J$ is the discharge current, $r_c$ is the cathode radius, and $r_a$ is the anode radius.

(3)

For the Hall acceleration, as shown in Figure 10b, the applied magnetic field generated by the electromagnetic coil can be decomposed into an axial magnetic field $B_z$ and a radial magnetic field $B_r$. According to Ohm’s law, a circumferential induced current $j_{\theta }$ will be generated in the plasma. $j_{\theta }$ interacts with the additional magnetic field, which will generate a radial compression force $\left(j_{\theta }\times B_z\right)$ and an axial thrust force $\left(j_{\theta }\times B_r\right)$ similar to the self field acceleration. In contrast to the self-magnetic acceleration mechanism, it is difficult to determine the direction of the force components.

(4)

Swirl acceleration, as shown in Figure 10c, where the current component $\left(j_r,J_z\right)$ interacts with the additional magnetic field $\left(B_z,B_r\right)$, generating an angular electromagnetic force to produce an angular vortex in the plasma, which produces thrust under the magnetic nozzle effect [15].

There are, however, a variety of areas in the discharge chamber that differ in direction and magnitude, so a uniform analysis of the behavior of plasma in the thruster chamber is inappropriate. Meanwhile, since the plasma’s own rotation and flow will also generate magnetic fields and currents as well, multiple physical fields will be superimposed on each other. Given that the process is complex, we can temporarily ignore the small role of plasma’s magnetic acceleration mechanism in favor of focusing on the effects of additional magnetic fields.

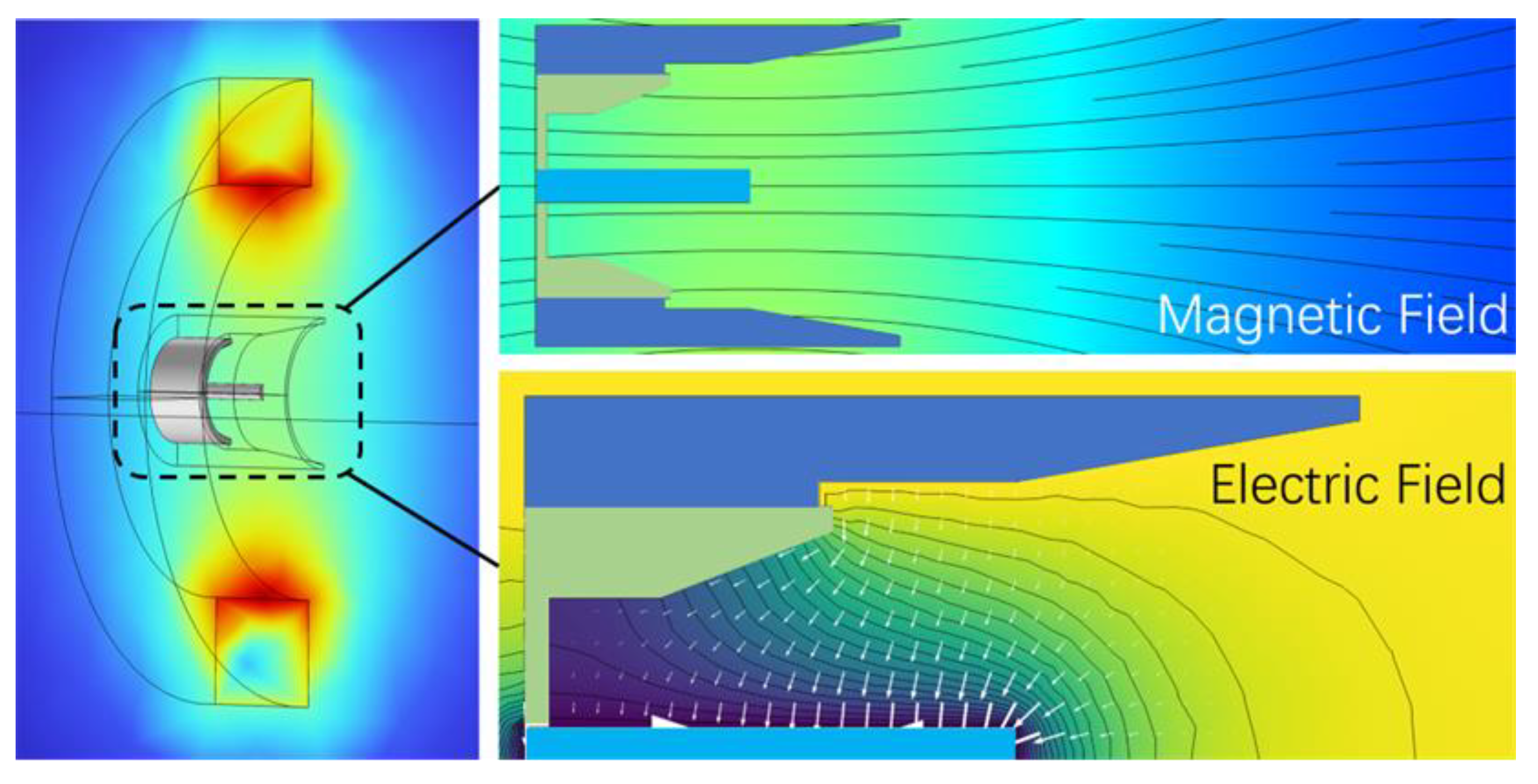
To further investigate the confinement mechanism of the applied magnetic field on the plasma, we also established a three-dimensional electromagnetic field model (Figure 11) to model the electric and magnetic fields inside the MPDT discharge chamber in detail, and after careful observation of the magnetic and electric field lines, it was found that the plasma inside the thruster discharge chamber should not be simply analyzed in a uniform manner.

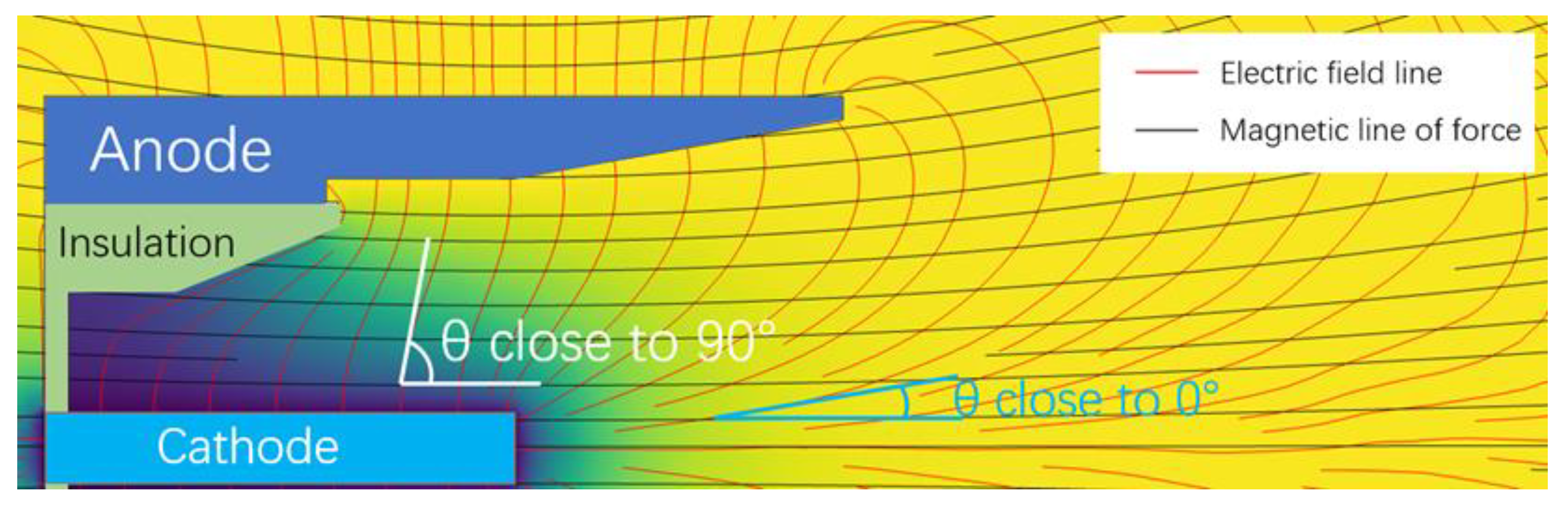
Images of the electric and magnetic fields between the cathode and anode are shown in Figure 12. It is possible to roughly divide the particles into zone A and zone B according to the angle between the electric and magnetic fields (bounded by 45°), and then analyze the motion behavior of the particles in the two zones separately.

Unlike the ordinary magnetic nozzle, the current between the cathode and the anode in the MPDT plays a significant role in the generation of thrust. In the early stage of particle motion, its velocity should be dominated by the electric field. According to the Lorentz force law, it is known that the circumferential current $j_{\theta }$ is composed of the vector product of the electrical field and magnetic field, and the greater the angle, the larger its value. Allowing for the distinction of the discharge chamber based on the angle between the two, as can be observed, the angle between the electric field and the magnetic field in most regions of the A area is even close to 90°, resulting in a large amount of circumferential Lorentz force applied to the plasma, and the circumferential current $j_{\theta }$ is primarily generated in this region. However, in the B region, although the angle between the electric and magnetic fields is close to 45° at the position far from the axis, it is clear from the experimental results that the plasma is mainly concentrated near the axis outside the ionization chamber, which suggests that the circumferential current $j_{\theta }$ formed in the B region is minimal.

In region A, the particle velocity is dominated by the electric field direction, i.e., radial, and this view can be assisted by observing the image of the plasma current intensity change, which can be clearly observed in Figure 9c,d for the radial current. Meanwhile, where magnetic lines are almost completely perpendicular to the current direction, the particle is subjected to circumferential Lorentz force, resulting in circumferential current $j_{\theta }$. As shown in Figure 13, we can divide the magnetic field into axial component $B_z$ and radial component $B_r$, and the circumferential current $j_{\theta }$ generates radial compression force $\left(j_{\theta }\times B_z\right)$ and axial thrust force $\left(j_{\theta }\times B_r\right)$ under the action of each component of the magnetic field.

Considering the B region, instead of conducting a uniform analysis, the particles were divided into α and β: α is the particle directly emitted from the cathode into the B region, and β is the particle entering the B region after completing a series of complex motions in the A region. The biggest difference between the two is the amount of circumferential current $j_{\theta }$. For part α, it is evident from the electric and magnetic field images that the electric and magnetic field angles are almost zero, indicating that there is almost no interaction between the electric and magnetic field forces; part β of the particle already carries a strong circumferential current $j_{\theta }$ as it completed a series of complex motions in region A (described above), which determines a stronger interaction with the magnetic field and thus generates a thrust force.

It should be noted that in the experimental results, the plume is mostly concentrated in the region close to the axis, which is evident in Figure 12 when compared with the experimental images. Based on the observation of the magnetic lines, it is apparent that the radial component of the magnetic field close to the central axis position is almost zero (Figure 13), and the radial components of the magnetic fields near the center of the coil are extremely small, which implies that the force on the particles at the beginning of the ejection is dominated by the radial compression force $\left(j_{\theta }\times B_z\right)$. As the particle gradually moves away from the center of the magnetic coil, the radial component of the magnetic field gradually becomes larger, and at this time, the proportion of the axial thrust force $\left(j_{\theta }\times B_r\right)$ begins to increase. Even if the proportion of the axial thrust force $\left(j_{\theta }\times B_r\right)$ begins to increase as the magnetic field size begins to rapidly decline, its value may not continue to increase. Inferring that the thrust force of MPDT is primarily a result of the pressure difference formed by the radial compression force $\left(j_{\theta }\times B_z\right)$, it is suggested that increasing the potential difference between the cathode and the anode or the strength of the magnetic field will improve the compression force. In addition, it is concluded from the previous section that the particle in the α part should contribute less to the thrust than the particle in the β part because it is almost not subject to the Lorentz force, so the percentage of the particle in the β part should be increased, for example, by appropriately changing the structure of the cathode nozzle, making the propellant flow laterally from the cathode side.

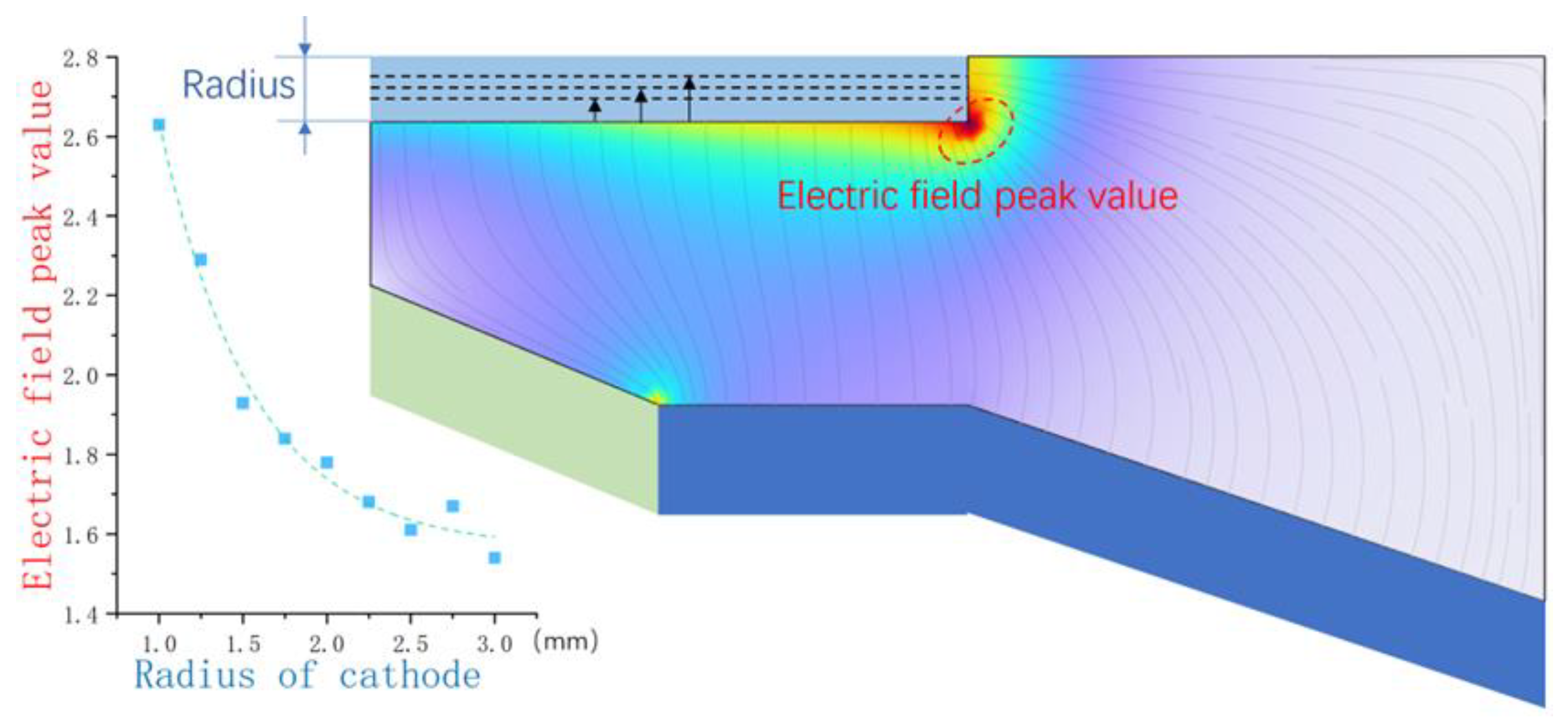
The simulation results in Section 3.1 were re-observed for a different cathode radius with the following conclusions: Many particles are unable to reach the anode due to the binding effect of the magnetic field and tend to rotate near the axis. However, the reduction of the cathode radius increases the electric field strength at the cathode tip, allowing the ions to acquire high velocities at the beginning of their motion, as well as a great value of $j_{\theta }$, which leads to an increase in the radial compression force $\left(j_{\theta }\times B_z\right)$ and the axial thrust force $\left(j_{\theta }\times B_r\right)$. Figure 14 shows how the electric field increases with the reduction of the cathode radius (the electric field peak value in the Figure is dimensionless).

In Section 3.2, a change in the anode radius leads to a large change in the electric field distribution and therefore does not apply to the explanation above.

In Section 3.3, the increase in the magnetic field clearly brings about an increase in the Lorentz force in all directions, thus enhancing the thrust, while the increase in the radial compression force $\left(j_{\theta }\times B_z\right)$ also contributes to the increase in the visible length of the plume.

5. Conclusions

The article presents an ideal magneto-fluid model based on the MHD method, as well as some simulation analyses of AF-MPDT under different working conditions.

However, some phenomena in the simulation results are difficult to explain with previous theories, such as the complex movement of the thruster plume.

Based on the comprehensive comparison and analysis of simulation results and experimental results, we find that the angle between the electric field and the magnetic field is mostly different in each area of the discharge chamber. Therefore, we attempted to understand the MPD propulsion principle in a new way: We partitioned the discharge chamber and then analyzed the particles in each area separately, allowing us to draw the following conclusions:

(1)

The thrust performance can be improved by increasing the electric field strength near the cathode, which boosts the acceleration efficiency of the particles at the beginning of their movement. According to the results of Figure 14, a simple way is to reduce the radius of the cathode. Considering the life of the thruster, the radius of the cathode should be reduced within the allowable range of the cathode’s life.

(2)

The thrust performance can be significantly improved by increasing the magnetic field (the effect may be limited). Due to the limitation of the equipment, we have not tried higher magnetic fields (>0.3 T). However, according to other scholars [16], when B > 0.5 T, the thrust efficiency remains almost constant, which means that the magnetic field has a limited effect on the performance improvement of the thruster.

(3)

The thrust performance can be effectively improved by changing the magnetic field shape (i.e., changing the speed at which the ratio of the axial component to the radial component of the magnetic field changes with the axis direction), but the specific way to change the magnetic field shape need to be further studied.

(4)

According to the inference in Section 4, the performance can be improved by increasing the electric field strength at the cathode tip. Another effective way to do that with a guaranteed cathode life is to change the shape of the cathode (Figure 15).

(5)

The analytical work for MPDT should be carried out via partitioning according to the angle between the magnetic and electric fields. In different regions, the gap between the angles of two fields is even close to 90 degrees (Figure 16), which makes a huge difference in the mechanism of particles subjected to physical fields.