Mass and Force Lumping: An Essential Enhancement to the Intrinsic Beam Finite Element Discretization
Abstract
:1. Introduction
2. Aeroelastic System
2.1. Fully Intrinsic Formulation
2.2. External Forces and Moments
2.2.1. Gravity
2.2.2. Aerodynamics
2.2.3. Thrust
2.3. Attitude and Rotation Matrix
3. Spatial Time Discretization Scheme
3.1. Spatial Finite Element Discretization
3.2. Mass and Force Lumping
3.3. Final Differential-Algebraic Equations
3.4. Time Domain Simulation
4. Linearization and Index Reduction
4.1. Trimming
4.2. Index Reduction
5. Numerical Results
5.1. Trim Results
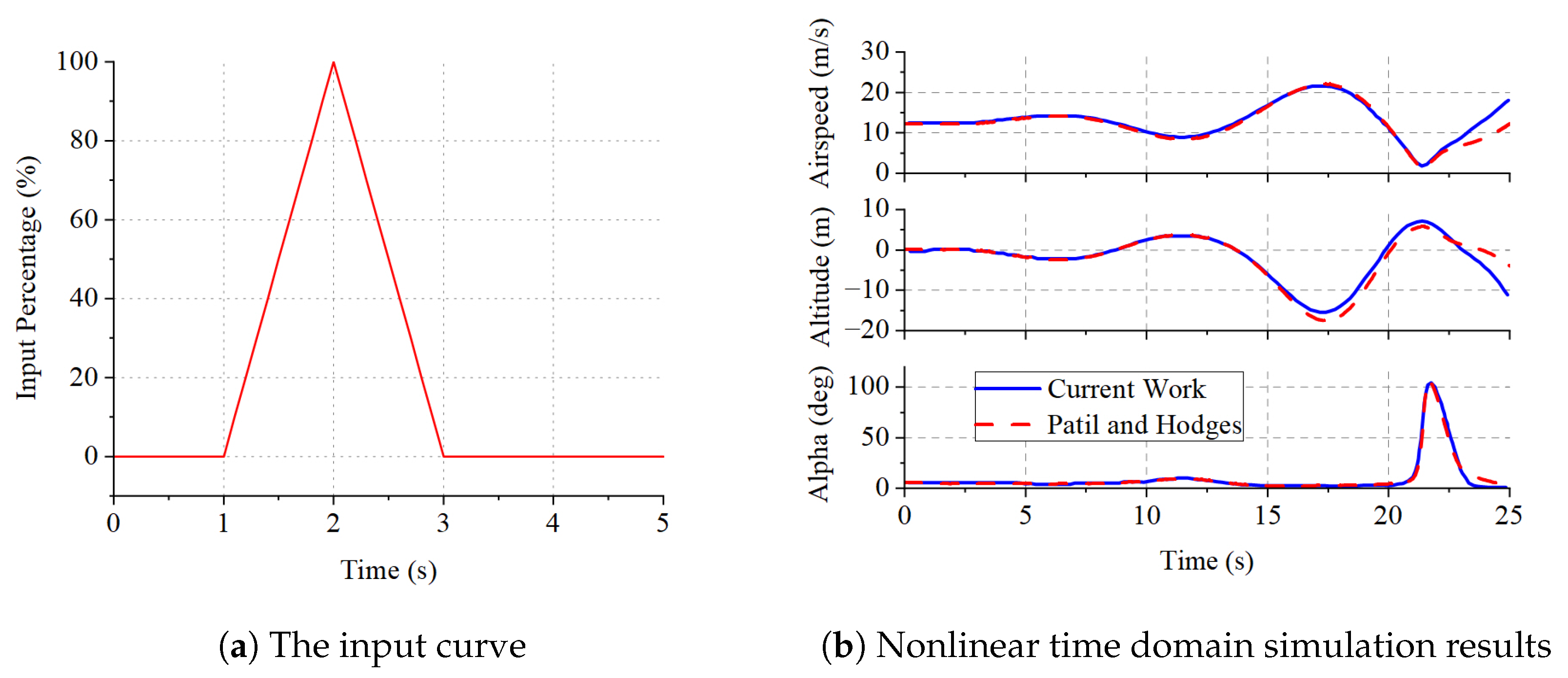
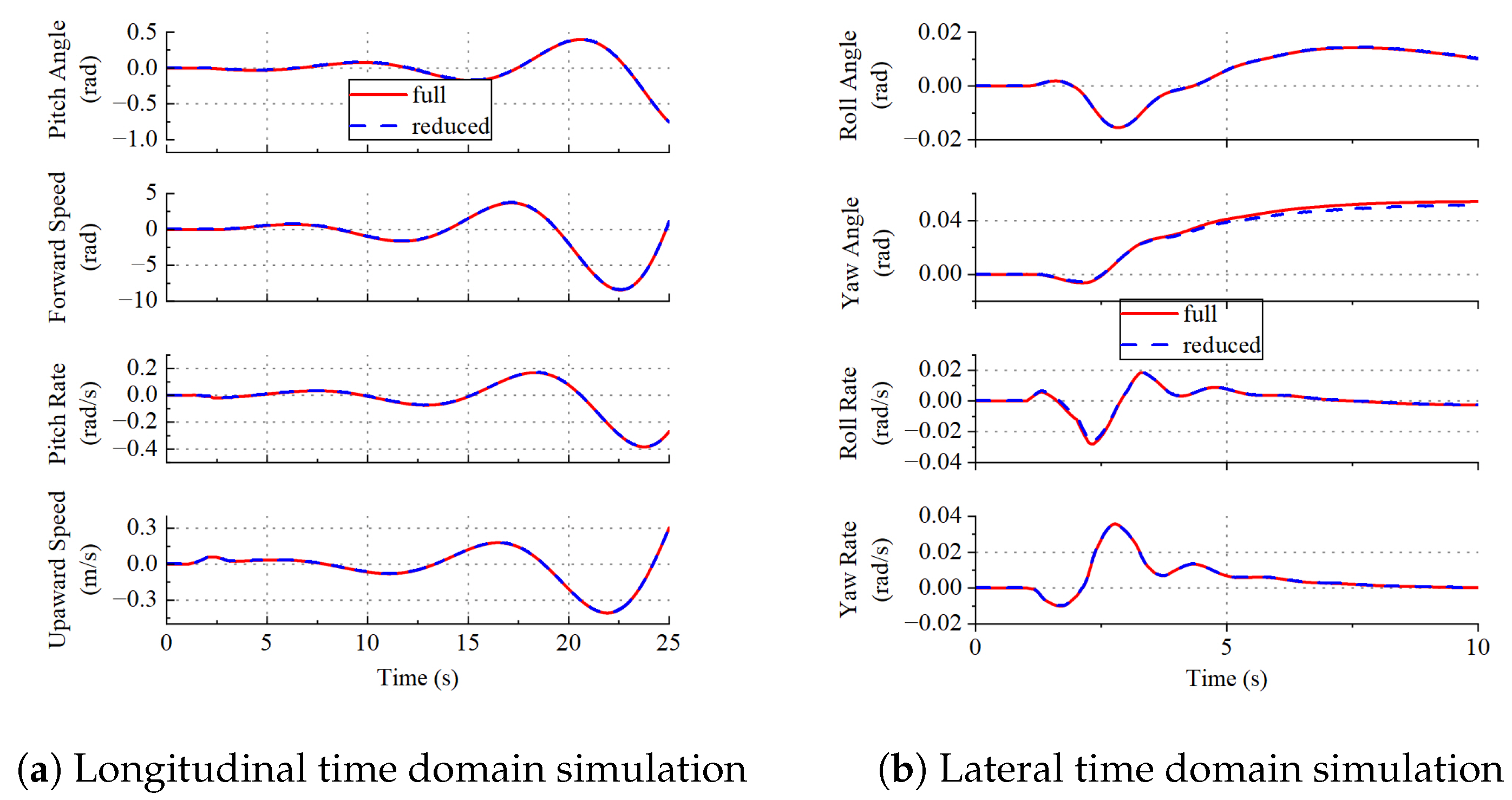
5.2. Nonlinear Time Domain Simulation
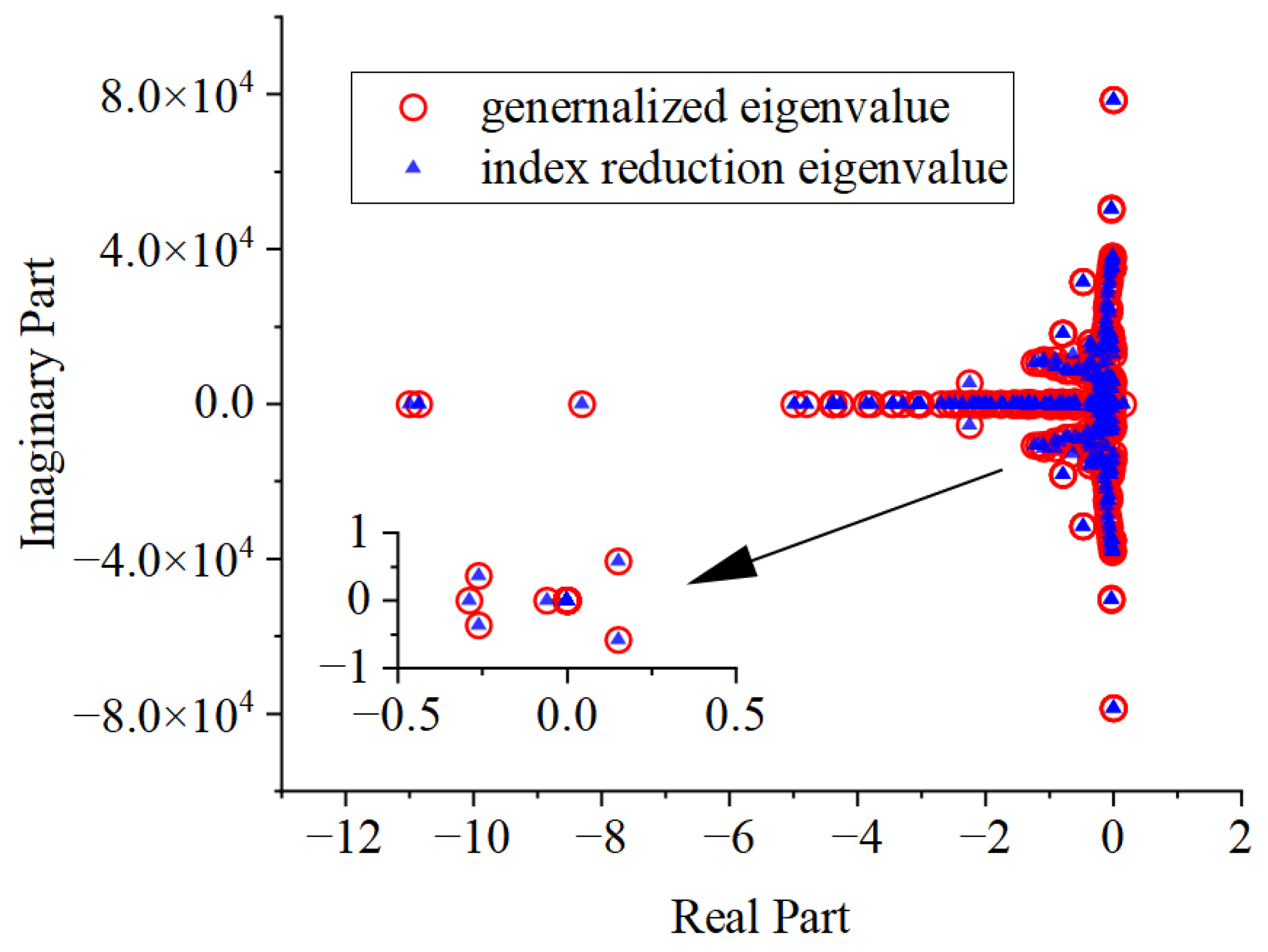
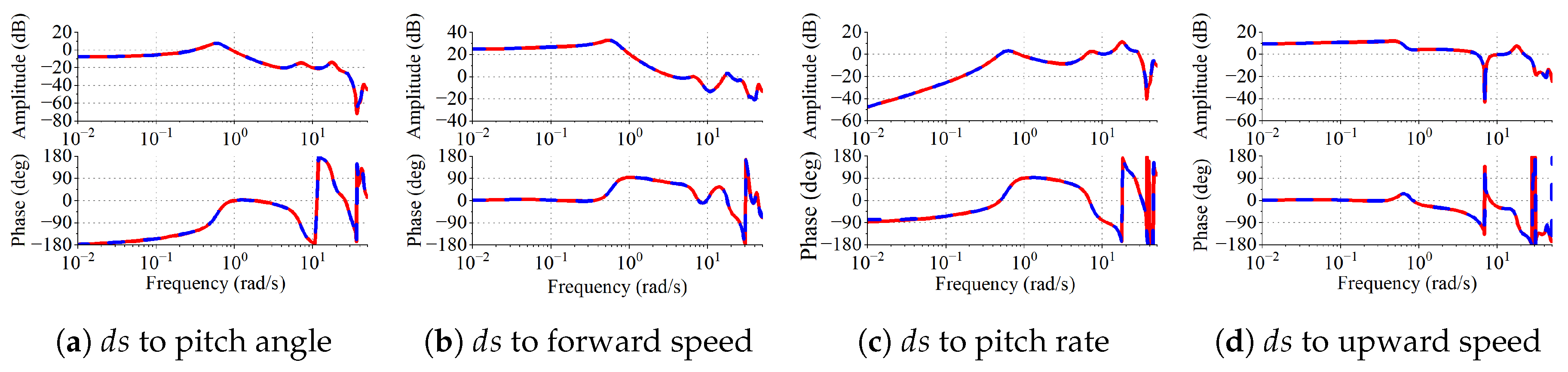
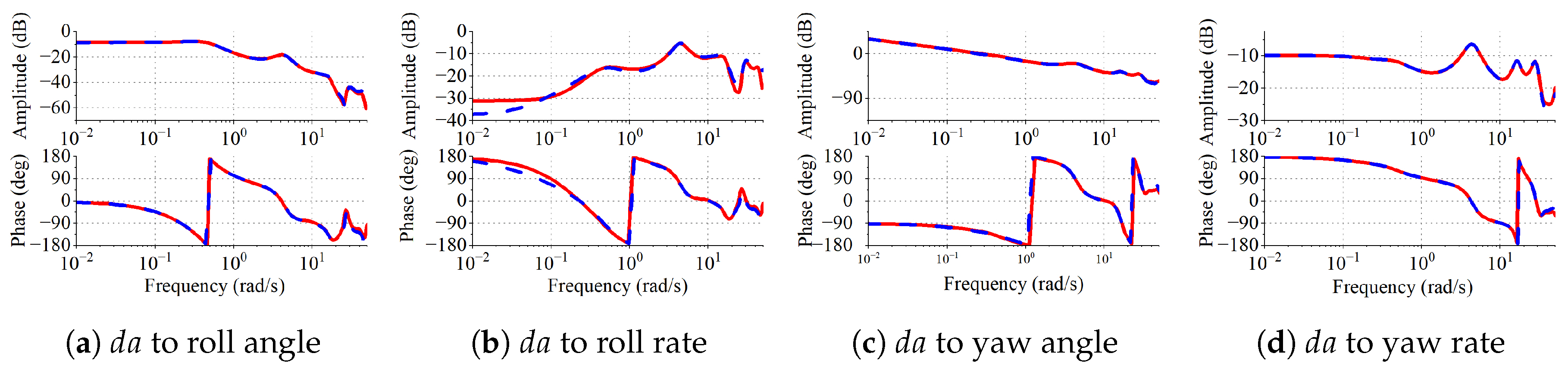
5.3. Linearization and Index Reduction
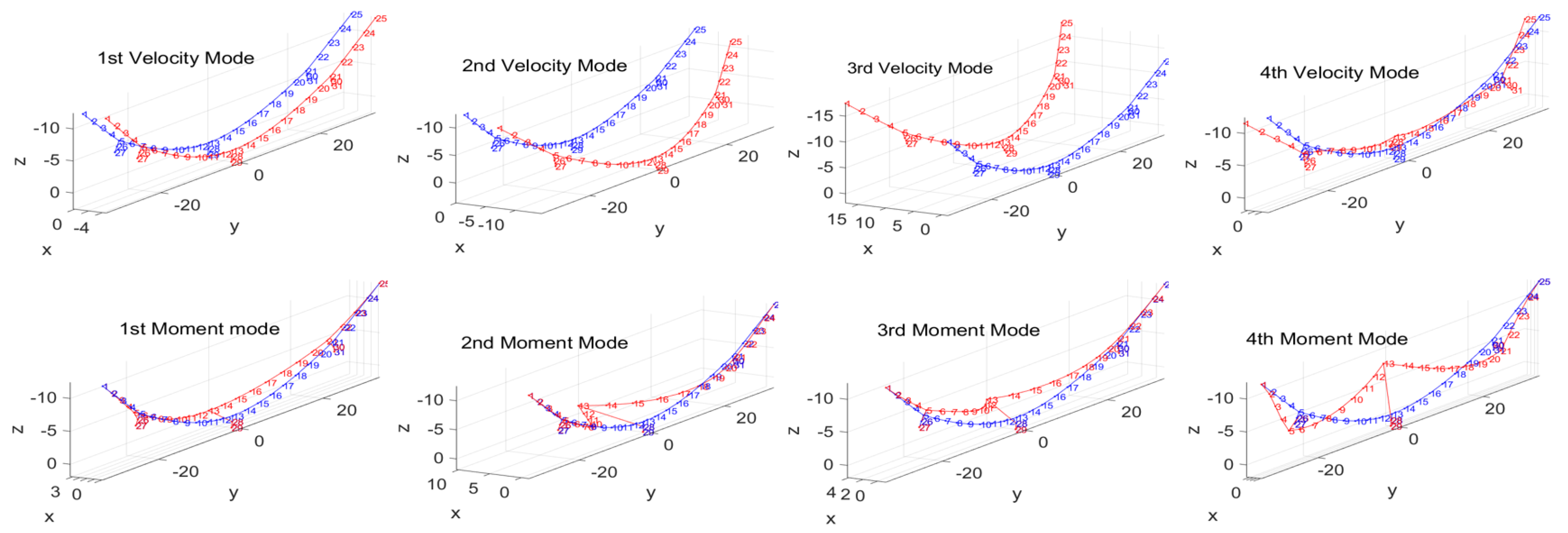
5.4. Model Order Reduction
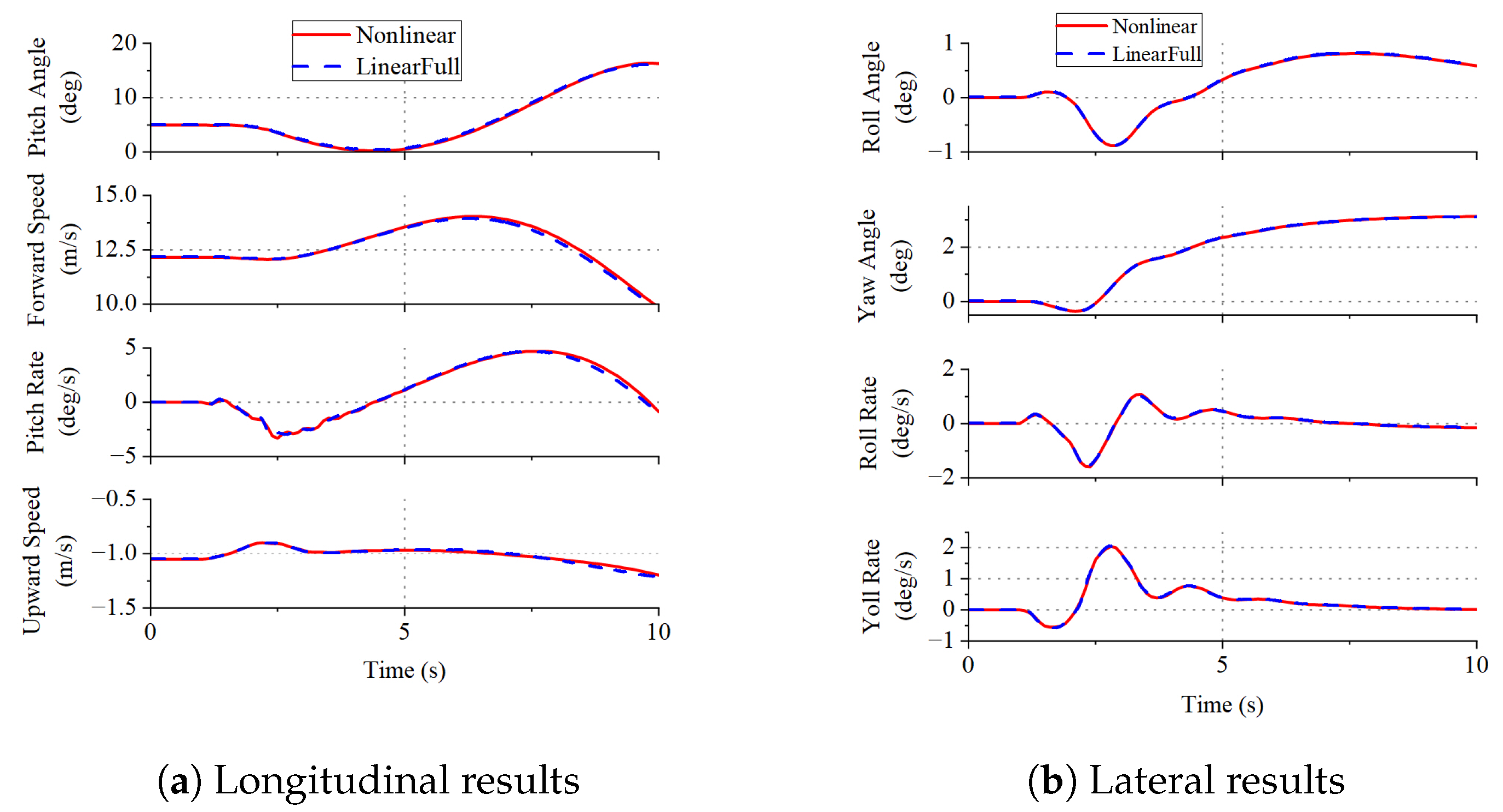
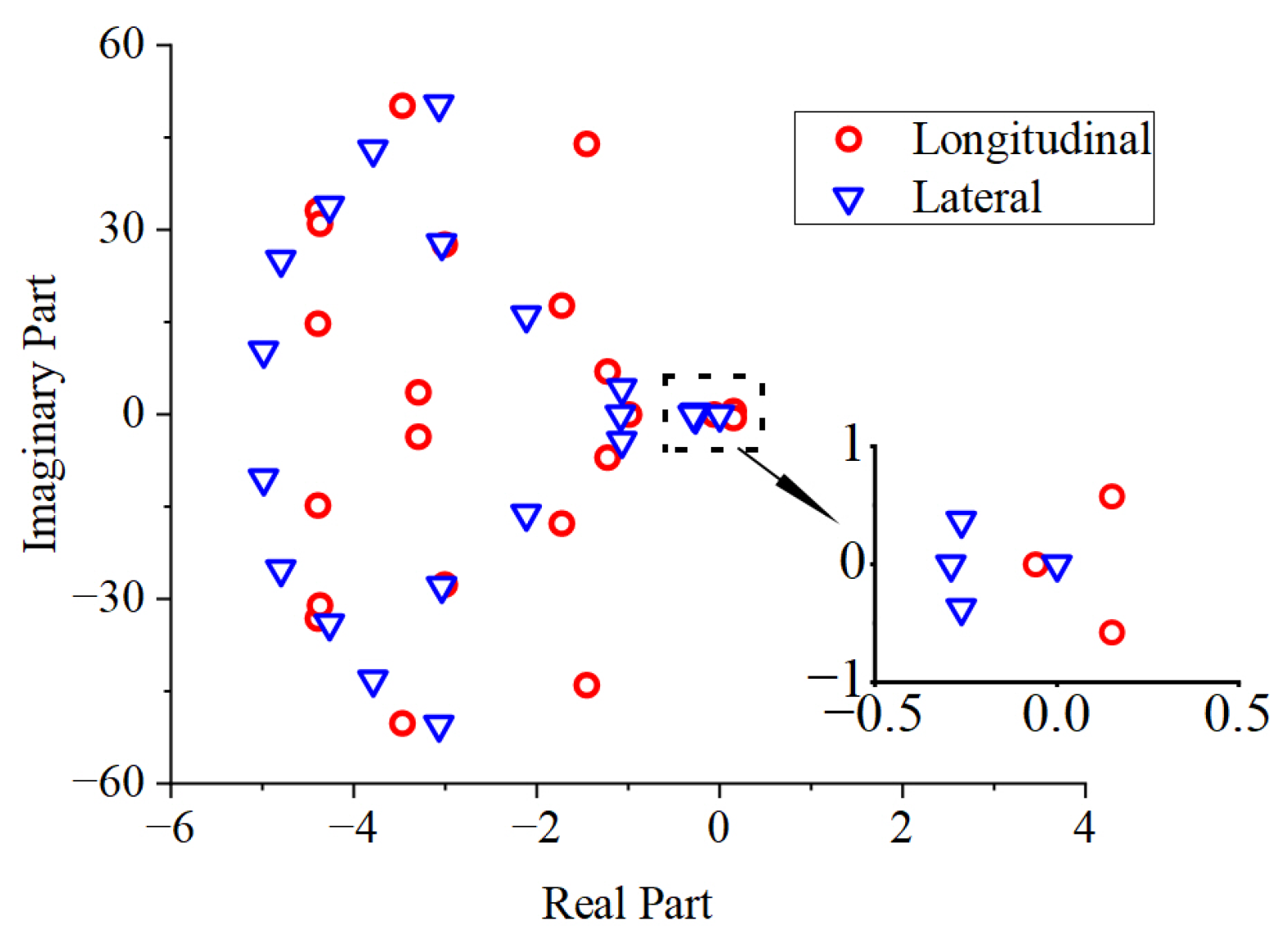
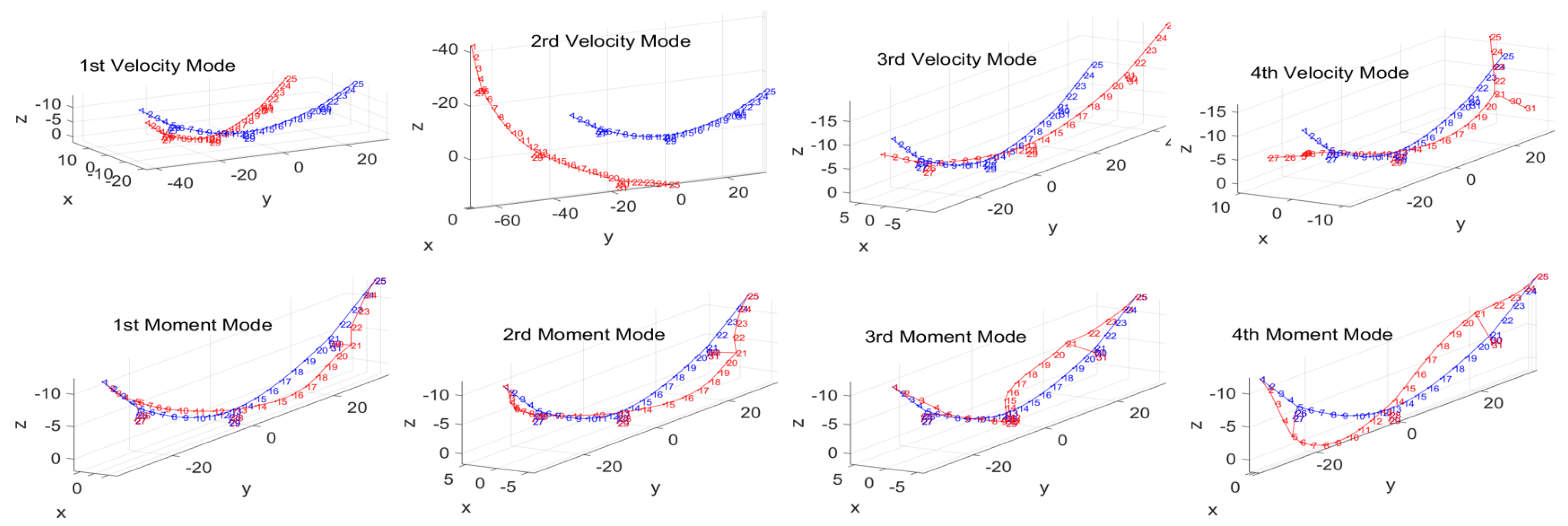
5.5. Analysis of Flight Dynamics
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cesnik, C.E.; Palacios, R.; Reichenbach, E.Y. Reexamined structural design procedures for very flexible aircraft. J. Aircr. 2014, 51, 1580–1591. [Google Scholar] [CrossRef]
- Hodges, D.H. A mixed variational formulation based on exact intrinsic equations for dynamics of moving beams. Int. J. Solids Struct. 1990, 26, 1253–1273. [Google Scholar] [CrossRef]
- Liang, J.; Bai, J.; Sun, Z.; Wang, H.; Zhang, B.; Chang, M. Modeling and analysis of a geometrically nonlinear joined wing under thrust force. J. Sound Vib. 2023, 544, 117369. [Google Scholar] [CrossRef]
- Dehadrai, A.R.; Sharma, I.; Gupta, S.S. Transient planar dynamics of cable-payload systems using geometrically exact beam theory. Int. J. Mech. Sci. 2022, 224, 107271. [Google Scholar] [CrossRef]
- Moravej Barzani, S.H.; Shahverdi, H.; Amoozgar, M. Nonlinear aeroelastic stability analysis of a two-stage axially moving telescopic wing by using fully intrinsic equations. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 3102–3110. [Google Scholar] [CrossRef]
- Chen, L.; Hu, X.; Liu, Y. Space-Time Finite Element Method for Fully Intrinsic Equations of Geometrically Exact Beam. Aerospace 2023, 10, 92. [Google Scholar] [CrossRef]
- Shang, L.; Xia, P.; Hodges, D.H.; Lin, C. Geometrically Exact Beam-Based Aeroelastic Modeling and Solution of Composite Rotor Blades in Forward Flight. J. Am. Helicopter Soc. 2023, 68, 127–142. [Google Scholar] [CrossRef]
- Patuelli, C.; Cestino, E.; Frulla, G. A Beam Finite Element for Static and Dynamic Analysis of Composite and Stiffened Structures with Bending-Torsion Coupling. Aerospace 2023, 10, 142. [Google Scholar] [CrossRef]
- Su, W.; Cesnik, C.E. Dynamic response of highly flexible flying wings. AIAA J. 2011, 49, 324–339. [Google Scholar] [CrossRef]
- Riso, C.; Cesnik, C.E.S. Impact of Low-Order Modeling on Aeroelastic Predictions for Very Flexible Wings. J. Aircr. 2022, 60, 662–687. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H.; Cesnik, C.E. Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft. J. Aircr. 2001, 38, 88–94. [Google Scholar] [CrossRef]
- Moshtaghzadeh, M.; Izadpanahi, E.; Bejan, A.; Mardanpour, P. Evolutionary Aeroelastic Design of Flying-Wing Cross Section. AIAA J. 2022, 60, 913–924. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H. Flight dynamics of highly flexible flying wings. J. Aircr. 2006, 43, 1790–1799. [Google Scholar] [CrossRef]
- Wang, Y.; Wynn, A.; Palacios, R. Nonlinear modal aeroservoelastic analysis framework for flexible aircraft. AIAA J. 2016, 54, 3075–3090. [Google Scholar] [CrossRef]
- Qi, P.; Zhao, X. Flight Control for Very Flexible Aircraft Using Model-Free Adaptive Control. J. Guid. Control. Dyn. 2020, 43, 608–619. [Google Scholar] [CrossRef]
- Afonso, F.; Vale, J.; Oliveira, É.; Lau, F.; Suleman, A. A review on non-linear aeroelasticity of high aspect-ratio wings. Prog. Aerosp. Sci. 2017, 89, 40–57. [Google Scholar] [CrossRef]
- Syed, A.A.; Moshtaghzadeh, M.; Hodges, D.H.; Mardanpour, P. Aeroelasticity of Flying-Wing Aircraft Subject to Morphing: A Stability Study. AIAA J. 2022, 60, 5372–5385. [Google Scholar] [CrossRef]
- Sotoudeh, Z.; Hodges, D.H. Modeling beams with various boundary conditions using fully intrinsic equations. J. Appl. Mech. 2011, 78, 031010. [Google Scholar] [CrossRef]
- Sotoudeh, Z.; Hodges, D.H. Incremental method for structural analysis of joined-wing aircraft. J. Aircr. 2011, 48, 1588–1601. [Google Scholar] [CrossRef]
- Patil, M.J.; Althoff, M. Energy-consistent, Galerkin approach for the nonlinear dynamics of beams using intrinsic equations. J. Vib. Control 2011, 17, 1748–1758. [Google Scholar] [CrossRef]
- Amoozgar, M.; Shahverdi, H.; Nobari, A. Aeroelastic stability of hingeless rotor blades in hover using fully intrinsic equations. AIAA J. 2017, 55, 2450–2460. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y. Differential Quadrature Method for Fully Intrinsic Equations of Geometrically Exact Beams. Aerospace 2022, 9, 596. [Google Scholar] [CrossRef]
- Peters, D.A.; Karunamoorthy, S.; Cao, W.M. Finite state induced flow models. I-Two-dimensional thin airfoil. J. Aircr. 1995, 32, 313–322. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Elastic/reference axis | 25% chord |
| Aerodynamic center | 25% chord |
| Center of gravity | 25% chord |
| N | |
| N | |
| N | |
| m | 8.93 kg/m |
| 4.15 kg·m | |
| 0.69 kg·m | |
| 3.46 kg·m | |
| Wing | 2 |
| Wing | 1 |
| Wing | 0.01 |
| Wing | 0.025 |
| Wing | −0.25 |
| Pod | 5 |
| Pod | 0.02 |
| Pod | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhou, Z. Mass and Force Lumping: An Essential Enhancement to the Intrinsic Beam Finite Element Discretization. Aerospace 2023, 10, 957. https://doi.org/10.3390/aerospace10110957
Wang J, Zhou Z. Mass and Force Lumping: An Essential Enhancement to the Intrinsic Beam Finite Element Discretization. Aerospace. 2023; 10(11):957. https://doi.org/10.3390/aerospace10110957
Chicago/Turabian StyleWang, Jiachen, and Zhou Zhou. 2023. "Mass and Force Lumping: An Essential Enhancement to the Intrinsic Beam Finite Element Discretization" Aerospace 10, no. 11: 957. https://doi.org/10.3390/aerospace10110957
APA StyleWang, J., & Zhou, Z. (2023). Mass and Force Lumping: An Essential Enhancement to the Intrinsic Beam Finite Element Discretization. Aerospace, 10(11), 957. https://doi.org/10.3390/aerospace10110957