Landing Impact Load Analysis and Validation of a Civil Aircraft Nose Landing Gear
Abstract
:1. Introduction
2. Theoretical Model and Tool
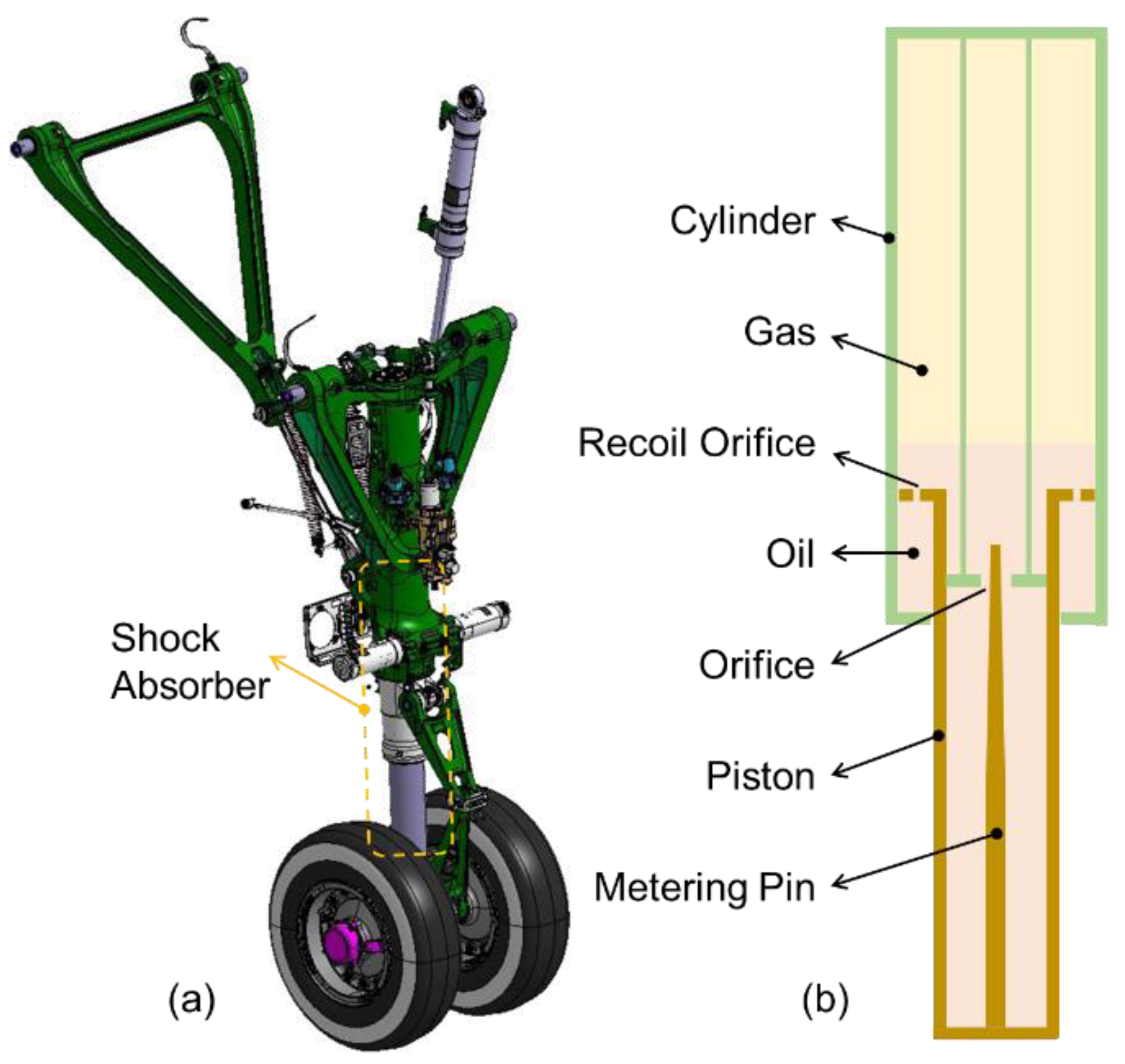
2.1. Landing Gear Structure
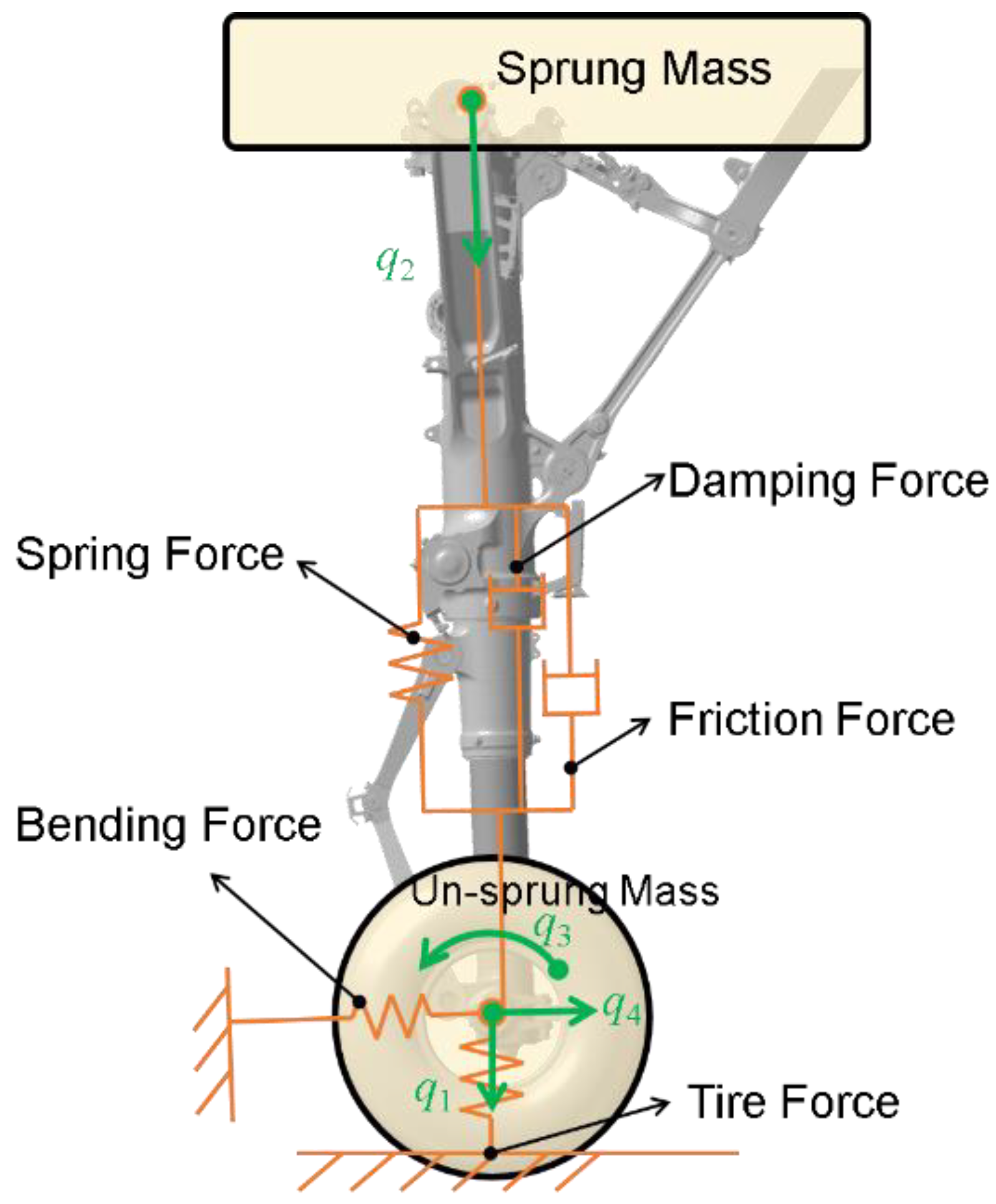
2.2. Landing Dynamic Model
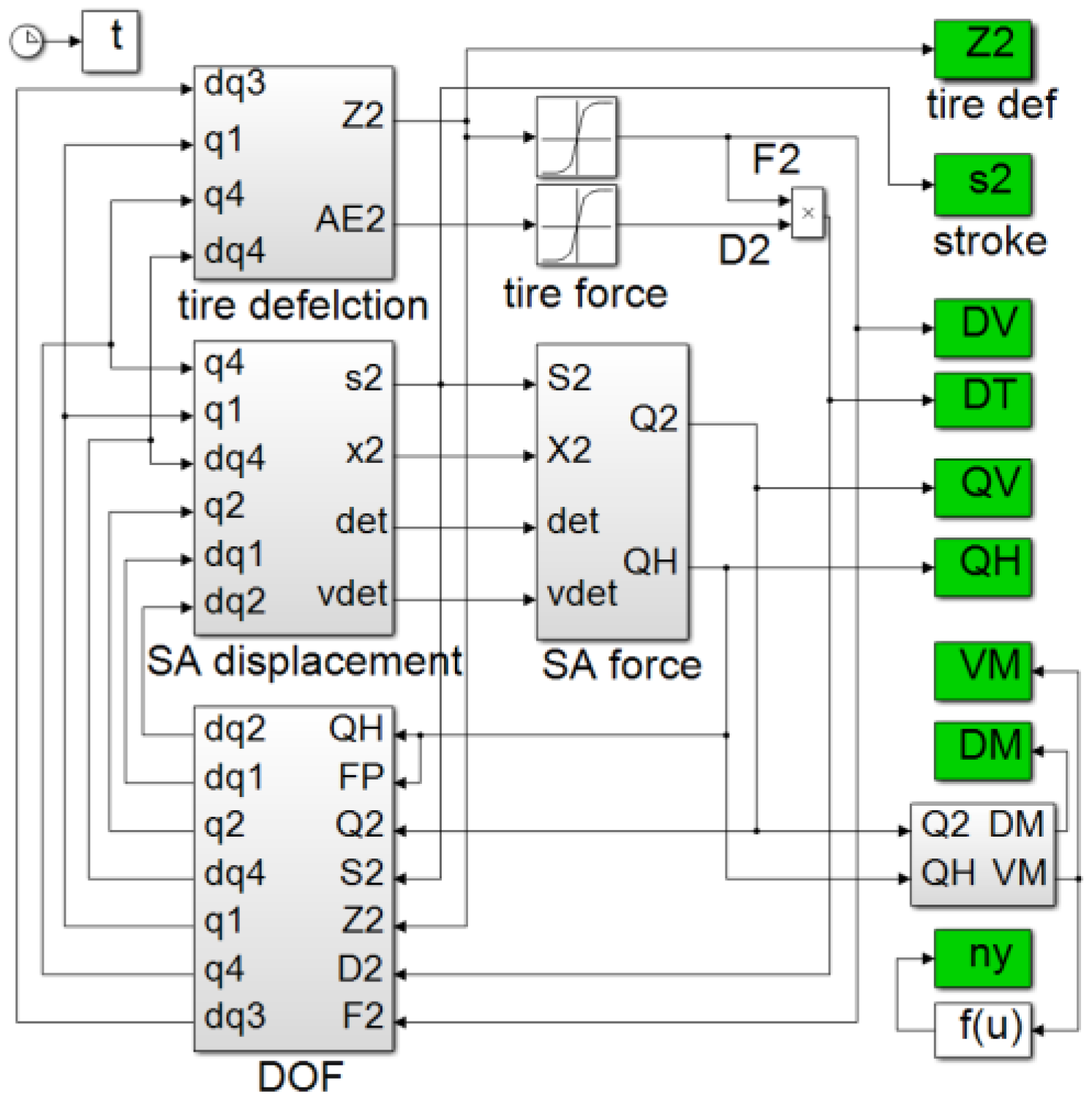
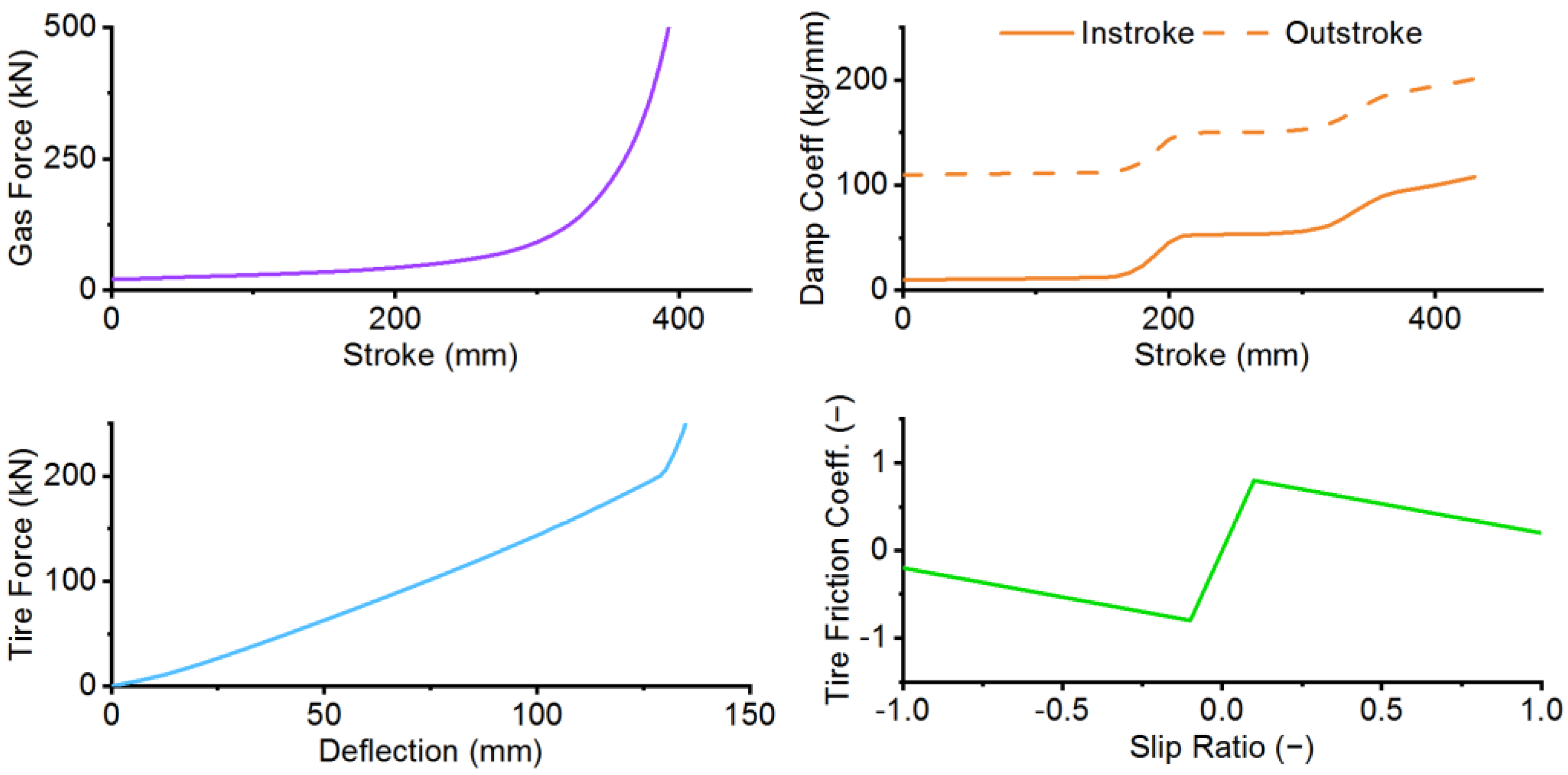
2.3. Landing Analysis Tool
3. Preliminary Analysis
3.1. Analysis Cases
3.2. Performance Verification
3.3. WA and GC Loads
4. Drop Test Validation
4.1. Test Facility and Preparation
4.2. Test Cases
4.3. Processing of Test Results
4.3.1. Parameter Tuning
4.3.2. Load Validation
4.3.3. Performance Validation
5. Conclusions
- The results of the drop test show that the landing simulation analysis model established by the assumption of the two masses (sprung and un-sprung), four degrees of freedom, and a rigid airframe can accurately analyze the landing impact loads.
- Through both the simulation and the test, the difference between the wheel-axle and the ground-contact loads was revealed to be non-negligible.
- If one takes reasonable consideration in the pre-test preparation of the structure’s stiffness and the during-test measurement of the wheel-axle loads, the drop test validation can be accurate and comprehensive, and both the vertical and the longitudinal loads, as well as the wheel-axle and ground-contact loads, can be fully validated.
- The importance of structural flexibility and tire friction modeling, as noted in this paper, should be considered in the current popular dynamic analysis methods based on ADAMS or other software, and the corresponding multi-body modeling methods can be further investigated to accurately analyze longitudinal loads.
- The lateral loads and the detailed attachment point loads may also need to be investigated further via both simulations and tests, including the motion equations for the lateral degrees of freedom, the lateral mechanics model of the tires, and the experimental validation of attachment point loads, especially for main landing gears with more complex asymmetric structures than the nose landing gear.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Currey, N.S.; American Institute of Astronautics. Aircraft Landing Gear Design: Principles and Practices; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1988. [Google Scholar]
- Pritchard, J. Overview of landing gear dynamics. J. Aircr. 2001, 38, 130–137. [Google Scholar] [CrossRef]
- Krüger, W.R.; Morandini, M. Recent developments at the numerical simulation of landing gear dynamics. CEAS Aeronaut. J. 2011, 1, 55–68. [Google Scholar] [CrossRef]
- Zhang, M.; Xiyang, W.; Zimin, Y.; Xiazheng, S. Six-wheel trolley type landing gear ground load analysis study. Xibei Gongye Daxue Xuebao/J. Northwest. Polytech. Univ. 2022, 40, 1090–1099. [Google Scholar] [CrossRef]
- Lernbeiss, R.; Ploechl, M. Simulation model of an aircraft landing gear considering elastic properties of the shock absorber. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2007, 221, 77–86. [Google Scholar] [CrossRef]
- Karam, W.; Maré, J.-C. Advanced model development and validation of landing gear shock struts. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 224, 575–586. [Google Scholar] [CrossRef]
- Haran, A.P.; Sivakumar, S. Mathematical model and vibration analysis of aircraft with active landing gears. J. Vib. Control JVC 2015, 21, 229–245. [Google Scholar]
- Rami, F.; Cezary, G.; Jan, H.S. Adaptable pneumatic shock absorber. J. Vib. Control 2018, 25, 107754631879553. [Google Scholar]
- Gan, S.; Fang, X.; Wei, X. Parametric Analysis on Landing Gear Strut Friction of Light Aircraft for Touchdown Performance. Appl. Sci. 2021, 11, 5445. [Google Scholar] [CrossRef]
- Pecora, R. A Rational Numerical Method for Simulation of Drop-Impact Dynamics of Oleo-Pneumatic Landing Gear. Appl. Sci. 2021, 11, 4136. [Google Scholar] [CrossRef]
- Jiao, F. Oil damping energy loss analysis of landing gear shock absorber. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 3096–3106. [Google Scholar] [CrossRef]
- Baskaran, S.; Sivaprakasam, S. Friction analysis of aircraft landing gears due to landing impact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 274–283. [Google Scholar] [CrossRef]
- Mahjouri, S.; Shabani, R.; Skote, M. Conceptual design of a new experimental setup to simulate aircraft tyre spin-up dynamics. Aircr. Eng. Aerosp. Technol. 2023, 95, 1268–1274. [Google Scholar] [CrossRef]
- McGehee, J.R.; Carden, H.D. Analytical Investigation of the Landing Dynamics of a Large Airplane with a Load-Control System in the Main Landing Gear; TP 1555; NACA: Washington, DC, USA, 1979. [Google Scholar]
- Wei, X.H.; Nie, H. New Method of Attenuating Landing Impact Force on Carrier-based Aircraft Landing Gear. Acta Aeronaut. Astronaut. Sin. 2007, 28, 324. [Google Scholar]
- Stachiw, T.; Khouli, F.; Langlois, R.G.; Afagh, F.F. Landing gear mechanical network synthesis for improving comfort at landing considering aircraft flexibility. J. Aircr. 2021, 58, 1242–1253. [Google Scholar] [CrossRef]
- Kang, B.-H.; Kim, B.-G.; Choi, S.-B. Aircraft landing gear system with magnetorheological shock strut: Performance evaluation via drop test. J. Intell. Mater. Syst. Struct. 2023, 34, 1045389X221147632. [Google Scholar] [CrossRef]
- Suresh, P.; Sura, N.K.; Shankar, K.; Radhakrishnan, G. Synthesis of landing dynamics on land-base high performance aircraft considering multi-variate landing conditions. Mech. Based Des. Struct. Mach. 2023, 51, 3945–3964. [Google Scholar] [CrossRef]
- Monclar, P. Landing gear technology programmes. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2505. [Google Scholar]
- Divakaran, V.; Kumar, G.; Rao, P.S. Aircraft landing gear design and development. Aircr. Land. Gear Des. Dev. 2015, 1, 1–12. [Google Scholar]
- Correia, D.; Ferreira, A. Aircrafts on-ground dynamics models and simulation software: State-of-the-art. Sustainability 2021, 13, 9147. [Google Scholar] [CrossRef]
- Richards, P.W.; Erickson, A. Dynamic Ground Loads Analysis Using Detailed Modeling of Landing Gear and Aircraft Aeroservoelastics. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0759. [Google Scholar]
- McDonald, M.; Richards, P.W.; Walker, M.; Erickson, A.J. Carrier Landing Simulation using Detailed Aircraft and Landing. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 7–11 January 2020; p. 1138. [Google Scholar]
- Zhang, L.; Xue, C.J. A Landing Gear Drop Dynamic Simulation based on the LMS. Virtual. Lab. Appl. Mech. Mater. 2011, 55, 684–687. [Google Scholar] [CrossRef]
- Orlandea, N.V. Multibody systems history of ADAMS. J. Comput. Nonlinear Dyn. 2016, 11, 060301. [Google Scholar] [CrossRef]
- EASA. Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes, CS-25 Amendment 27; European Union Aviation Safety Agency: Cologne, Germany, 2023. [Google Scholar]
- Holmes, G.; Sartor, P.; Reed, S.; Southern, P.; Worden, K.; Cross, E. Prediction of landing gear loads using machine learning techniques. Struct. Health Monit. 2016, 15, 568–582. [Google Scholar] [CrossRef]
- Flugge, W. Landing-Gear Impact; TN 2743; NACA: Washington, DC, USA, 1952. [Google Scholar]
- Caijun, X.; Xiuli, X.; Wengang, Q. Research on the performance of buffer for landing gear based on the drop test. J. Vibroeng. 2012, 14, 794–804. [Google Scholar]
- Norwood, D.S.; Chichester, R.H. Full scale aircraft drop test program for the F-35C carrier variant. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 0459. [Google Scholar]
- Zhang, Z.; Wei, X.; Ye, Q. Heading Load Dynamic Simulation of Landing Gear Test. In Proceedings of the 2018 Asia-Pacific International Symposium on Aerospace Technology (APISAT 2018) 9th, Singapore, 14–19 July 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1469–1476. [Google Scholar]
- Fang, W.; Zhu, L.; Wang, Y. Landing Performance Study for Four Wheels Twin Tandem Landing Gear Based on Drop Test. Aerospace 2022, 9, 334. [Google Scholar] [CrossRef]
- Gao, Z. Aircraft Design Manual: Volume 14, Take-Off and Landing System Design; Aviation Industry Press: Beijing, China, 2001. [Google Scholar]
- Wang, H.; Wu, D.; Wang, F.; Ren, H. A method for determining the horizontal impact load based on the rotational speed of the aircraft’s wheel in a landing gear drop test. Int. J. Crashworthiness 2018, 23, 627–634. [Google Scholar] [CrossRef]
- Son, L.; Bur, M.; Rusli, M. A new concept for UAV landing gear shock vibration control using pre-straining spring momentum exchange impact damper. J. Vib. Control 2018, 24, 1455–1468. [Google Scholar] [CrossRef]
- Chester, D. The equivalent masses at nose landing-gears during landing-impacts and when taxiing over runway perturbations. In Proceedings of the 27th Israel Annual Conference on Aviation and Astronautics, Haifa, Israel, 27–28 February 1985; Volume 27. Collection of Papers. [Google Scholar]
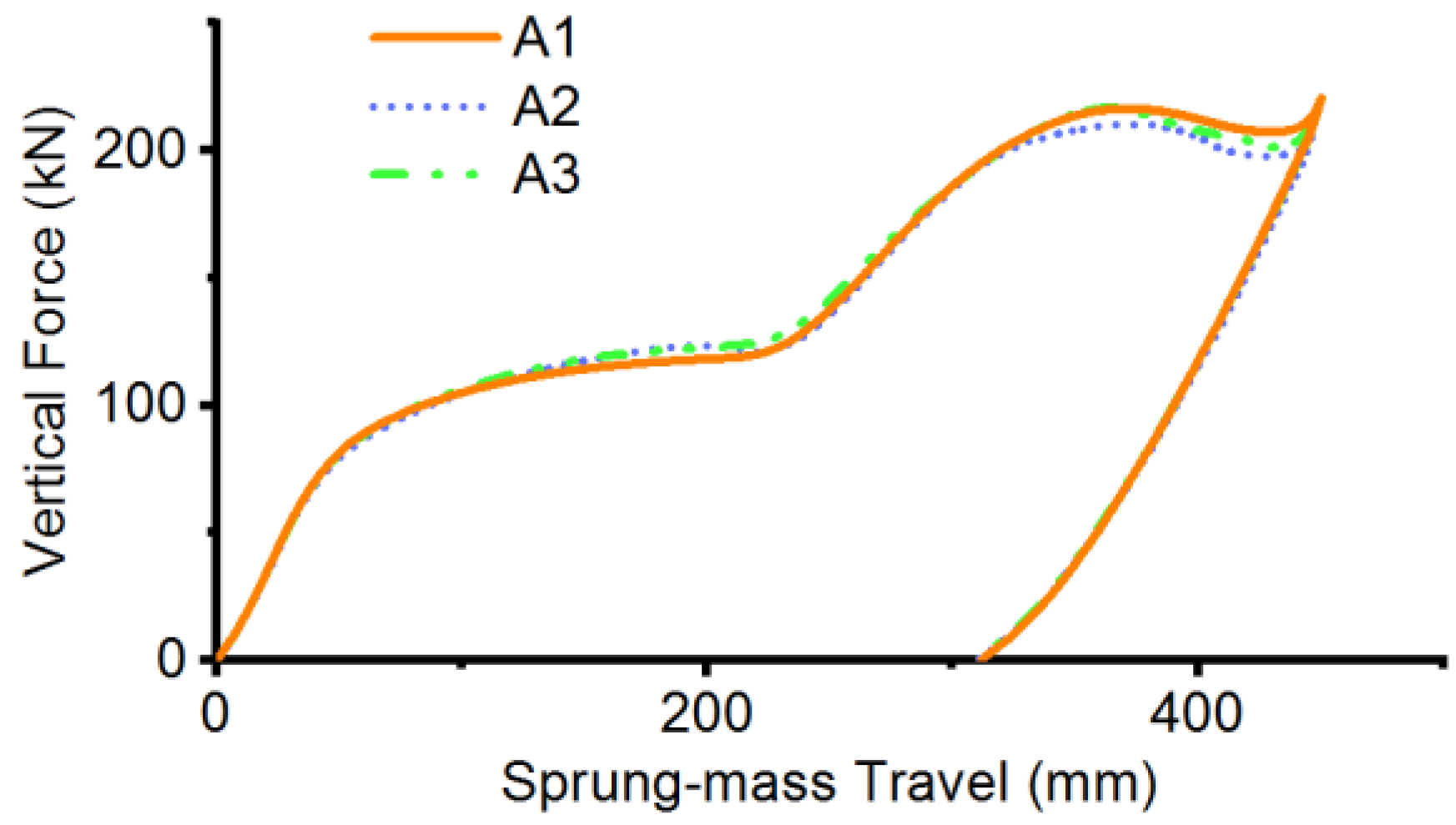
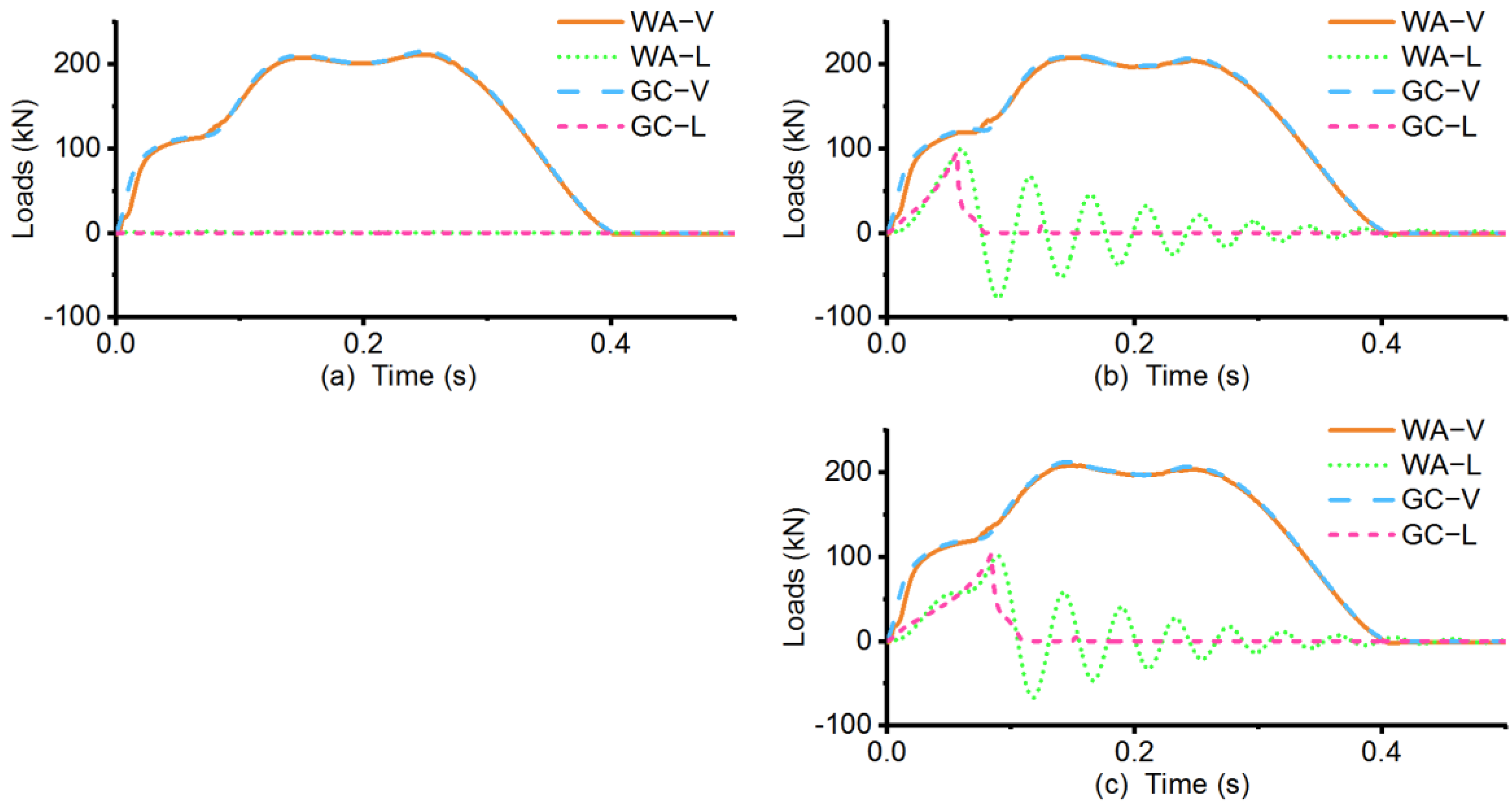


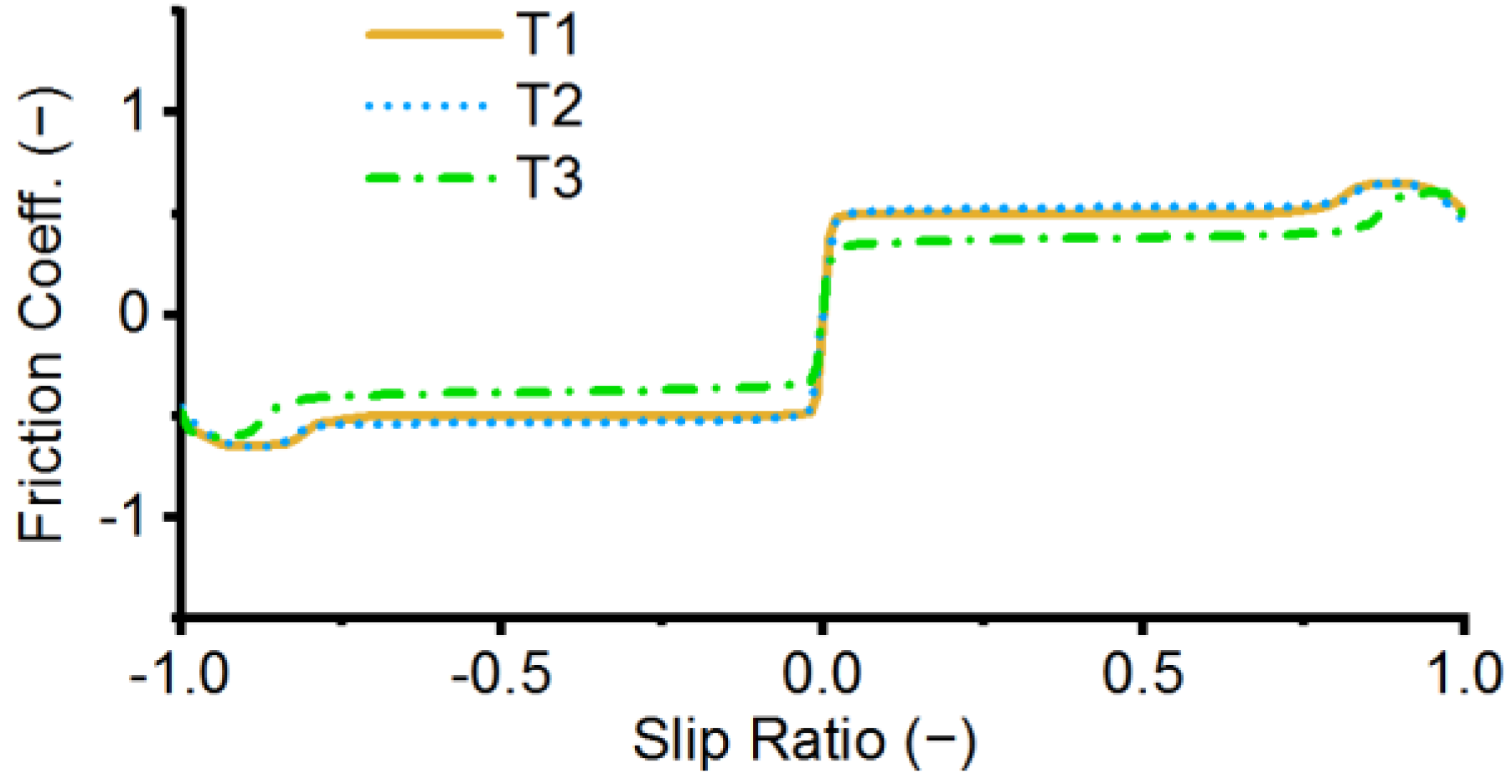
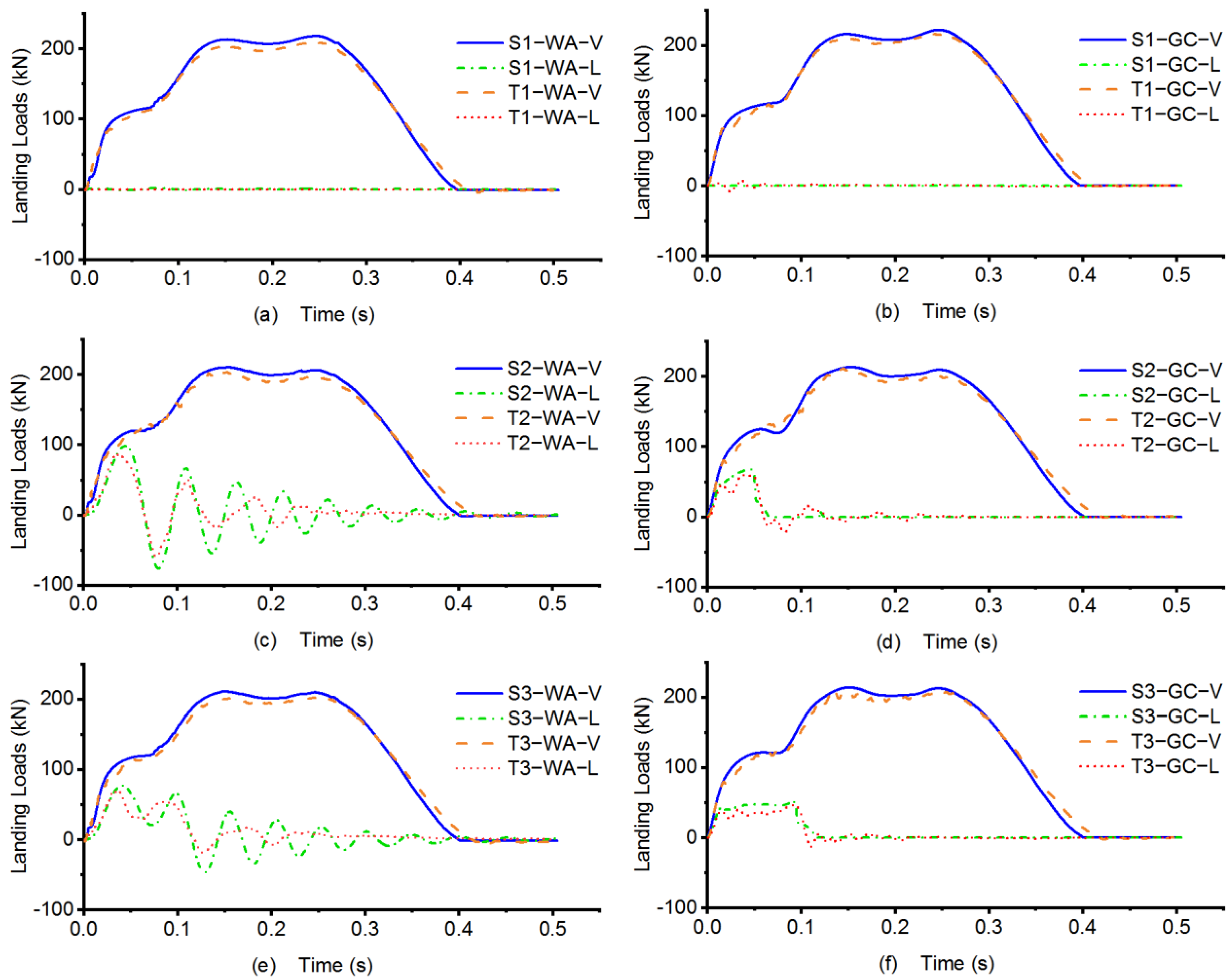
| Preliminary Analysis Case | A1 | A2 | A3 |
|---|---|---|---|
| Reduced mass (kg) | 13,400 | 13,400 | 13,400 |
| Sinking speed (m/s) | 3.05 | 3.05 | 3.05 |
| Longitudinal speed (m/s) | 0 | 58 | 96 |
| Test Case | T1 | T2 | T3 |
|---|---|---|---|
| Reduced Mass (kg) | 13,472 | 13,472 | 13,472 |
| Sinking Speed (m/s) | 3.10 | 3.08 | 3.08 |
| Longitudinal Speed (m/s) | 0 | 58.6 | 96.5 |
| Key Factor | Pre. | T1 | T2 | T3 | Tuned |
|---|---|---|---|---|---|
| Gas polytrophic (−) | 1.1 | 1.13 | 1.05 | 1.12 | 1.08 |
| Oil discharging (−) | 0.8 | 0.82 | 0.84 | 0.79 | 0.8 |
| Bearing friction (−) | 5% | 5% | 9% | 8% | 7% |
| Tire dynamic (−) | 1.08 | 1.04 | 0.97 | 1.07 | 1.08 |
| Performance Index | T1 | T2 | T3 |
|---|---|---|---|
| Load factor (−) | 1.69 | 1.62 | 1.63 |
| Absorption efficiency (−) | 65.9% | 67.8% | 67.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Wang, Y.; Ji, Y. Landing Impact Load Analysis and Validation of a Civil Aircraft Nose Landing Gear. Aerospace 2023, 10, 953. https://doi.org/10.3390/aerospace10110953
Liu W, Wang Y, Ji Y. Landing Impact Load Analysis and Validation of a Civil Aircraft Nose Landing Gear. Aerospace. 2023; 10(11):953. https://doi.org/10.3390/aerospace10110953
Chicago/Turabian StyleLiu, Wenbin, Youshan Wang, and Yuchen Ji. 2023. "Landing Impact Load Analysis and Validation of a Civil Aircraft Nose Landing Gear" Aerospace 10, no. 11: 953. https://doi.org/10.3390/aerospace10110953
APA StyleLiu, W., Wang, Y., & Ji, Y. (2023). Landing Impact Load Analysis and Validation of a Civil Aircraft Nose Landing Gear. Aerospace, 10(11), 953. https://doi.org/10.3390/aerospace10110953







