Coupling Dynamics and Three-Dimensional Trajectory Optimization of an Unmanned Aerial Vehicle Propelled by Electroaerodynamic Thrusters

Abstract

Electroaerodynamic unmanned aerial vehicles (EAD-UAVs) are innovative UAVs that use high-voltage asymmetric electrodes to ionize air molecules and Coulomb force to push these ions to produce thrust. Unlike fixed-wing and rotor UAVs, EAD-UAVs contain no moving surfaces and have the advantages of very low noise, low mechanical fatigue, and no carbon emissions. This paper proposes an EAD-UAV configuration with an orthogonal arrangement of multiple EAD thrusters to adjust the EAD-UAV attitude and flight trajectory through voltage distribution control alone. Based on a one-dimensional dynamic model of an EAD thruster, the attitude–path coupling dynamics of the EAD-UAV were derived. To achieve EAD-UAV flight control for a specified target, the Bezier shaping approach (BSA) was implemented to realize rapid trajectory optimization considering the coupling dynamic constraints. The numerical simulation results indicate that the BSA can quickly procure an optimized flight trajectory that satisfies the dynamic and boundary constraints. Compared with the Gaussian pseudospectral method (GPM), the BSA changes the optimization index of the objective function by nearly 1.14% but demands only nearly 1.95% of the computational time on average. Hence, the improved integrative Bezier shaping approach (IBSA) can overcome the poor convergence issue of the BSA under the continuous acceleration constraint of multi-target flight trajectories.

1. Introduction

Since the first airplane flight took place in 1903, these vehicles have been controlled by moving surfaces such as flaps, propellers, and turbines. Owing to the advantages of good stealth performance, low maintenance difficulty, and low noise, none-control-surface aircrafts (NCSAs) have received a lot of research [1,2,3]. Unmanned aerial vehicles (UAVs) are increasing rapidly in popularity for use in both military and civil applications [4,5,6,7,8], which makes NCS-UAVs an important subject for research on NCSAs. In 2018, the first unmanned aerial vehicle (UAV) without moving surfaces was successfully tested for the first time [9]; it was propelled by an electroaerodynamic (EAD) thruster. The emergence of EAD-UAVs has provided a huge impetus for the development of NCS-UAVs. EAD-UAVs constitute an innovative UAV concept, using high-voltage asymmetric electrodes to ionize air molecules and Coulomb force to push air ions to produce ionic wind, generating thrust. Unlike fixed-wing and rotor UAVs, there are no moving surfaces, such as propellers or turbines, in EAD-UAVs. As solid-state propulsion UAVs, EAD-UAVs have the advantages of very low noise, low mechanical fatigue, and no carbon emissions [10].

EAD propulsion involves generating propulsive forces in air fluid [11,12], which is an approach to handling and moving fluids without the help of moving surfaces, as illustrated in Figure 1. In 1928, Brown proposed a prototype EAD thruster structure, which uses a stack of asymmetric electrodes to generate directional motion in the air under a high voltage of tens of kilovolts [13]. Because EAD-UAVs can fly ultra-silently by generating ionic wind, this innovative UAV concept has garnered increasing research attention and has been employed in several design proposals recently [14,15]. Scholars at the Central Institute of Technology in Paris, France [16] and Yonsei University in Seoul, Korea [17] have studied complex multi-stage stacked propellers, and their research results have proven the possibility of designing complex multi-stage structures to enhance the performance of plasma propellers. Researchers at Sandia National Laboratory in Albuquerque, New Mexico, tested the effects of AC and DC power supplies and positive and negative polarities on propeller performance [18]. In addition to thrust, the thrust-to-power ratio is an important index for measuring the performance of plasma thrusters. Masuyama et al. [19] studied different factors influencing the thrust-to-power ratio and presented a one-dimensional model of the thrust-to-power ratio of plasma thrusters. Monrolin et al. [14] used another index to analyze the performance of plasma thrusters: thrust density. In addition to changing the parameters of single-stage thrusters to improve their performance, this objective can also be achieved through the series parallel connection of multiple thrusters, similar to the series parallel connection of resistors. Series connection means that multiple thrusters are connected at the end and arranged in the same plane; parallel means that the emitters of multiple thrusters are in a single plane, the receivers are in another plane, and the two planes are parallel. Stuetzer et al. [12] considered the effects of parallel and series connections on ion pumps under one-dimensional conditions. Masuyama et al. [19] studied multistage propellers. Colas et al. [16,20,21] conducted series and classification experiments on plasma thrusters and found that the classification structure could produce a greater ion wind velocity. In addition, the feasibility of using EAD devices to generate sufficient propulsion for UAVs has been discussed and questioned [22]. In recent years, considerable progress has been made in lightweight high-pressure generation technology, and the possibility of using plasma propulsion technology to provide the main thrust in UAVs has gradually increased. In 2016, Wynsberghe and Turak proposed using plasma thrusters in stratospheric floating hot air balloons to generate thrust to drive flight [23]. In 2017, Drew and Pister developed and successfully test flew a micro robot propelled by plasma, with a thrust-to-weight ratio of 10 [24]. In 2018, Xu et al. demonstrated that an EAD propulsion system can maintain powered flight by designing and flying a heavier-than-air airplane propelled by an EAD thruster [9]. The investigated EAD-UAV was a fixed-wing airplane with a 5 m wingspan, which was tested 10 times and obtained steady-level flight. The whole power system, including all of the batteries and a pointedly designed ultralight high-voltage (40 kV) power converter, was attached to the body. The actual flight results indicate that traditionally approved limitations in aspects of the thrust-to-power ratio and thrust density [14,15,22], which were once considered to make EAD thrusters unachievable as an approach to airplane propulsion, have been overcome. This research provides a proof of concept for EAD-UAVs, opening up feasibilities for UAVs and aerodynamic devices that are quieter, mechanically simpler, and have no carbon emissions. The unidirectional flight of EAD-UAVs has been proven to be feasible through actual flight experiments. The flight ability of EAD-UAVs has finally been proved through the efforts of many scholars over the years. In 2021, He et al. used EAD thrusters for both the propulsion and yaw control of a blimp, The feasibility of EAD thrusters for attitude control of lighter-than-air aircraft has also been verified [25]. However, attitude and flight trajectory adjustment of heavier-than-air EAD-UAVs without moving surfaces has not been discussed or investigated in depth thus far.

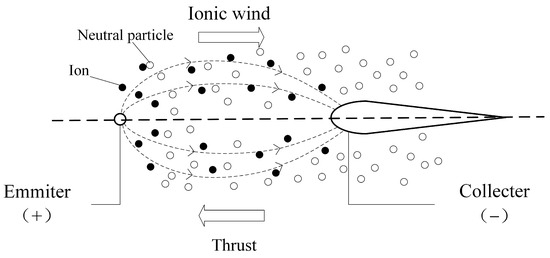
Figure 1. Schematic diagram of the EAD propulsion principle.

This paper proposes a new EAD-UAV configuration with an orthogonal arrangement of multiple EAD thrusters that can adjust the attitude and flight trajectory of an EAD-UAV through voltage distribution control alone. As illustrated in Figure 2, six EAD thrusters are arranged orthogonally under the fixed wing, and their thrusts, F₁–F₆, can be controlled independently by adjusting the voltage. Through the combined control of the EAD thrusters, the desired control torque and propulsive force can be generated within a certain range, which is mainly limited by the maximum voltage. The EAD-UAV in this paper is designed by adding several groups of EAD thrusters for attitude control based on the UAV in [9]. In this paper, the influence of structural change on the aerodynamic characteristics of UAVs is not considered. The airframe parameters are the same as those in [9], the aerodynamic parameters only consider the lift coefficient and drag coefficient, and the lateral force coefficient and aerodynamic moment coefficients are set to 0. It is assumed that the EAD-UAV can track the aircraft deflection angle and track the inclination angle during flight, and the fuselage axis direction is always consistent with the flight speed direction, so the lift coefficient and drag coefficient remain unchanged. The lift of the EAD-UAV comes from the installation angle of the wing. The drag coefficient is estimated according to the drag and flight speed given in [9], and the lift coefficient is estimated according to the lift-drag ratio given in [9]. The six EAD thrusters of the EAD-UAV are assumed to have the same thrust at the same voltage, and the structural parameters of the EAD thrusters are consistent with those in [9]. The thrust of thrusters 3, 4, 5, and 6 has two directions, which are positive to the right and upward, and negative for the opposite. The + and − of F₃, F₄, F₅, and F₆ represent the direction of thrust. The fuselage parameters of the EAD-UAV and the parameters of the EAD propeller are given in Table A1.

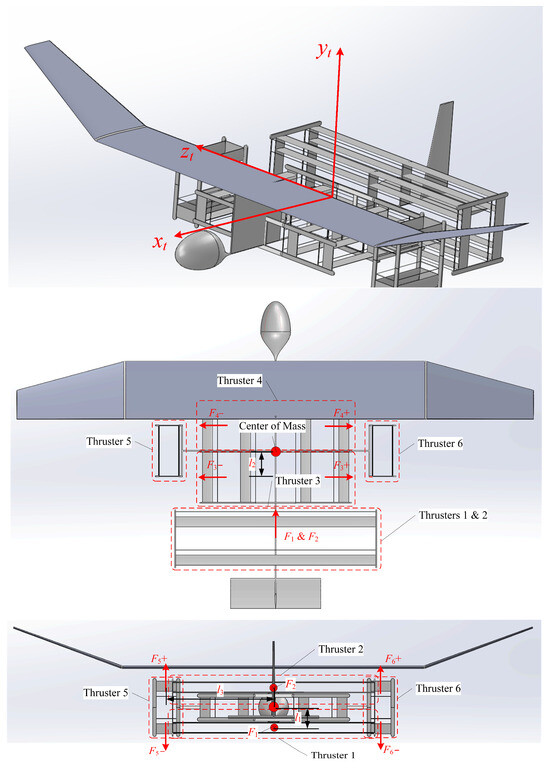
Figure 2. EAD-UAV configuration with an orthogonal arrangement of multiple EAD thrusters.

The EAD-UAV designed in this work performs trajectory and attitude coupling control by adjusting the thruster voltage. A trajectory planned without considering the dynamic constraints may not adhere to the voltage limitations of the thruster. Therefore, in this study, a trajectory optimization method considering dynamic constraints was adopted. Trajectory-optimizing algorithms typically use optimal control theory. Popular numerical solutions to optimal control theory include direct methods (“discrete first and then optimization”) and indirect methods (“optimize first and then discrete”) [26], both of which need to be based on dynamics and require considerable amounts of integral calculations. The pseudospectral method is generally used in direct approaches and works well for numerous aerospace problems [27,28,29]. Recently, many improved pseudospectral methods have been proposed. For instance, Rogowski et al. applied the Chebysev pseudospectral method to create the trajectory of a glider in a vertical plane [30]. Further, Pepy et al. introduced an optimal algorithm based on an indirect shooting method [31]. The geometric method was also employed in optimal control theory. Babel et al. applied the shortest path algorithm to deal with network optimization [32]. They divided trajectories in space into multiple line elements, which could act as the UAV trajectory when connected. However, all UAVs’ speeds were assumed to be constant, so the path length was chosen as the optimization goal. The Pythagorean line graph (PH) method is another impressive geometric method to solve the collaborative path planning problem [33,34,35]. Dynamic constraints are described using geometric differential properties such as curvature and torsion. Although these pure geometric methods have advantages for computational efficiency, they lack consideration of the dynamic characteristics of UAVs. In task allocation when designing numerous UAV trajectories, a practical task planning approach can effectively filter results by applying a pure geometric method. However, this approach may make some tracks difficult to fly. The trajectory generation method based on Bezier curves adopts a combination of geometric and dynamic methods, meaning it can be called a geometric–dynamic method [36]. Further, Petropoulos and Longuski introduced the shape function concept [37], and Jolly et al. used Bezier curves for robot path planning [38]. Bezier curves have been employed to link lines or circles to obtain better curvature smoothness and continuity for UAV trajectories [39,40]. Another similar approach is the B-spline method [41]. In terms of spacecraft trajectory planning, inspired by the shape function concept proposed by Petropoulos et al., Huo et al. applied Bezier curves to the initial three-dimensional trajectory planning of solar sails and proposed a method of quickly generating the minimum-time three-dimensional trajectories of spacecraft propelled by solar sails using feedback control. The simulation results show that, considering the actual characteristics of the thrust vector, this method can design the transfer trajectories of spacecraft propelled by solar sails equipped with the feedback control devices with high accuracy in approximately 1% of the time required by the traditional Gaussian pseudospectral method [42,43,44]. Xiaoliang studied methods of continuous-curvature bounded path planning of fixed-wing UAVs based on Bezier curves [45], and Yu et al. conducted research on the fast generation of the trajectories of multiple UAVs arriving simultaneously based on spatiotemporal Bezier curves [46]. In this study, we investigated the attitude–path coupling dynamics and optimal control of EAD-UAVs via the Bezier shaping approach (BSA).

The rest of this paper is organized as follows. Section 2 presents the EAD-UAV attitude–path coupling dynamics based on the one-dimensional dynamic model of an EAD thruster. Section 3 describes the implementation of the BSA and IBSA to realize rapid trajectory optimization considering the coupling dynamics constraints in order to realize the EAD-UAV flight control for specified targets. Section 4 presents the numerical results within an optimal framework using the proposed approach. Finally, Section 5 summarizes the conclusions.

2. EAD-UAV Attitude–Path Coupling Dynamics

2.1. Reference Frames

Describing different variables in different coordinate systems is necessary to study EAD-UAV flight dynamics more conveniently and to make the expressions of the dynamics equations clearer. Therefore, the coordinate systems used and the conversion relationships between these coordinate systems must be clarified and can be described as follows.

(1)

Ground coordinate system $O_{\mathrm{G}}{x}_{\mathrm{G}}{y}_{\mathrm{G}}{z}_{\mathrm{G}}$

The ground coordinate system, $O_{\mathrm{G}}{x}_{\mathrm{G}}{y}_{\mathrm{G}}{z}_{\mathrm{G}}$, is fixed to the ground, and the original point, $O_{\mathrm{G}}$, is selected as a point joined with the ground according to the application. The $y_{\mathrm{G}}$-axis points perpendicularly upward from the ground, the $x_{\mathrm{G}}$-axis points to the initial course of the EAD-UAV in the horizontal plane, and the $z_{\mathrm{G}}$-axis direction is determined by the right-hand rule. By moving the origin, $O_{\mathrm{G}}$, to coincide with the centroid O of the EAD-UAV, the ground coordinate system, $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$, which is convenient for coordinate system transformation, can be obtained.

(2)

Body coordinate system $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$

The body coordinate system, $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$, is fixed to the EAD-UAV where the origin O is located at its centroid, and the $x_{\mathrm{t}}$-axis points to the head of the EAD-UAV along the direction of the body axis. The $y_{\mathrm{t}}$-axis is located in the longitudinal symmetry plane of the EAD-UAV body, perpendicular to the $x_{\mathrm{t}}$-axis and pointing upwards. The $z_{\mathrm{t}}$-axis is perpendicular to the $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$ plane, and the direction is determined by the right-hand rule.

(3)

Speed coordinate system $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}{z}_{\mathrm{V}}$

The origin O is defined at the center of mass of the EAD-UAV. The $x_{\mathrm{V}}$-axis points in the direction of $V_{\mathrm{U}}$ (the speed of the drone relative to the air). The $y_{\mathrm{V}}$-axis is located in the plane of longitudinal symmetry of the fuselage, perpendicular to the $x_V$-axis and pointing upward. The $z_{\mathrm{V}}$-axis is perpendicular to the $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}$ plane, and the direction is determined by the right-hand rule.

(4)

Track coordinate system $O{x}_{\mathrm{h}}{y}_{\mathrm{h}}{z}_{\mathrm{h}}$

The origin O is defined at the center of mass of the EAD-UAV. The $x_{\mathrm{h}}$-axis points in the direction of $V$ (the speed of the UAV relative to the ground). The $y_{\mathrm{h}}$-axis is perpendicular to the $x_{\mathrm{h}}$-axis, located in the vertical plane of $V$, pointing upward. The $z_{\mathrm{h}}$-axis is perpendicular to the $O{x}_{\mathrm{h}}{y}_{\mathrm{h}}$ plane, and the direction is determined by the right-hand rule.

The transformation matrix, $B_{\mathrm{g}}^{\mathrm{t}}$, from $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$ to $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$ and the transformation matrix, $B_{\mathrm{t}}^{\mathrm{g}}$, from $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$ to $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$ are given by

$$B_{\mathrm{g}}^{\mathrm{t}}={\left(B_{\mathrm{t}}^{\mathrm{g}}\right)}^{\mathrm{T}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \gamma & \sin \gamma \\ 0& -\sin \gamma & \cos \gamma \end{array}\right]\left[\begin{array}{ccc}\cos \vartheta & \sin \vartheta & 0\\ -\sin \vartheta & \cos \vartheta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos \psi & 0& -\sin \psi \\ 0& 1& 0\\ \sin \psi & 0& \cos \psi \end{array}\right],$$

(1)

where the pitch angle, $\vartheta \in \left[-{90}^{\circ },{90}^{\circ }\right]$, is the angle between the $x_{\mathrm{t}}$-axis and the $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}$ plane, the yaw angle, $\psi \in \left[-{180}^{\circ },{180}^{\circ }\right]$, is the angle between the projection of the $x_t$-axis on the $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}$ plane and the $x_{\mathrm{g}}$-axis, and the roll angle, $\gamma \in \left[-{180}^{\circ },{180}^{\circ }\right]$, is the angle between the vertical plane where the $x_{\mathrm{t}}$ axis is located and the $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$ plane as shown in Figure 3.

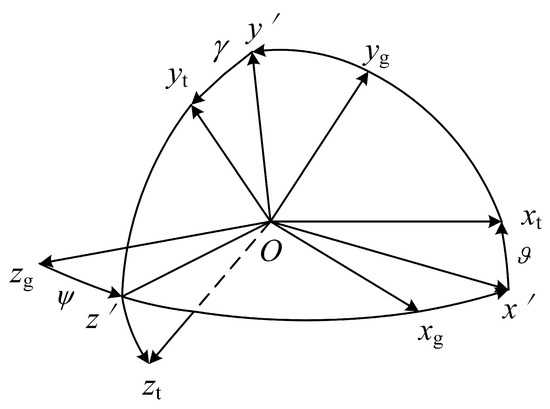
Figure 3. Relationship between $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$ and $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$.

The transformation matrix, $B_{\mathrm{g}}^{\mathrm{h}}$, from $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$ to $O{x}_{\mathrm{h}}{y}_{\mathrm{h}}{z}_{\mathrm{h}}$ and the transformation matrix, $B_{\mathrm{h}}^{\mathrm{g}}$, from $O{x}_{\mathrm{h}}{y}_{\mathrm{h}}{z}_{\mathrm{h}}$ to $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$ are given by

$$B_{\mathrm{g}}^{\mathrm{h}}={\left(B_{\mathrm{h}}^{\mathrm{g}}\right)}^{\mathrm{T}}=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos {\psi }_V& 0& -\sin {\psi }_V\\ 0& 1& 0\\ \sin {\psi }_V& 0& \cos {\psi }_V\end{array}\right],$$

(2)

where the track deflection angle, ${\psi }_V\in \left[-{180}^{\circ },{180}^{\circ }\right]$, is the angle between the projection line of the $x_{\mathrm{h}}$-axis on the $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}$ plane and the $x_g$-axis and the track inclination angle, $\theta \in \left[-{90}^{\circ },{90}^{\circ }\right]$, is the angle between the $x_{\mathrm{h}}$-axis and the $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}$ plane as shown in Figure 4.

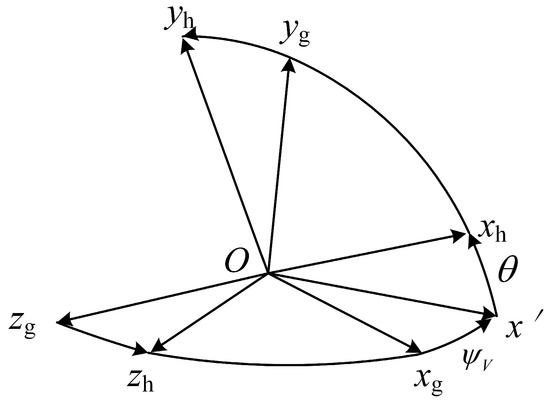
Figure 4. Relationship between $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$ and $O{x}_{\mathrm{h}}{y}_{\mathrm{h}}{z}_{\mathrm{h}}$.

The transformation matrix, $B_{\mathrm{V}}^{\mathrm{t}}$, from $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}{z}_{\mathrm{V}}$ to $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$ and the transformation matrix, $B_{\mathrm{t}}^{\mathrm{V}}$, from $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$ to $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}{z}_{\mathrm{V}}$ are given by

$$B_{\mathrm{V}}^{\mathrm{t}}={\left(B_{\mathrm{t}}^{\mathrm{V}}\right)}^{\mathrm{T}}=\left[\begin{array}{ccc}\cos \alpha & \sin \alpha & 0\\ -\sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos \beta & 0& -\sin \beta \\ 0& 1& 0\\ \sin \beta & 0& \cos \beta \end{array}\right],$$

(3)

where the angle of attack, $\alpha \in \left[-{90}^{\circ },{90}^{\circ }\right]$, is the angle between the projection of the $x_{\mathrm{V}}$-axis on the $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$ plane and the $x_{\mathrm{t}}$-axis and the sideslip angle, $\beta \in \left[-{180}^{\circ },{180}^{\circ }\right]$, is the angle between the $x_{\mathrm{V}}$-axis and the $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$ plane as shown in Figure 5.

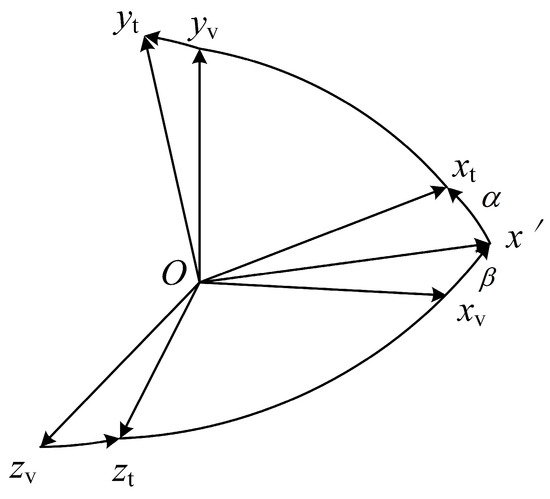
Figure 5. Relationship between $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}{z}_{\mathrm{V}}$ and $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$.

2.2. Forces and Torques Acting on EAD-UAVs

The mechanical environments that EAD-UAVs face during flight are very complex. As a compromise between modeling accuracy and computational cost, only the following main forces and torques were considered in this study.

(1)

Aerodynamic forces

The directions of the aerodynamic forces acting on the EAD-UAV are described in $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}{z}_{\mathrm{V}}$, where the aerodynamic forces can be decomposed into three components of drag (X), lift (Y), and lateral force (Z) along the three coordinate axes of $O{x}_{\mathrm{V}}{y}_{\mathrm{V}}{z}_{\mathrm{V}}$. The main factors influencing the aerodynamic forces are the dynamic pressure of the incoming flow, $q_{\mathrm{V}}$, and the characteristic area of the EAD-UAV, $S$. The relationships between the aerodynamic forces and influencing factors are given by

$$\left\{\begin{array}{l}X=C_X{q}_{\mathrm{V}}S\\ Y=C_Y{q}_{\mathrm{V}}S\\ Z=C_Z{q}_{\mathrm{V}}S\\ q_{\mathrm{V}}=\frac{1}{2}\rho V_{\mathrm{U}}^2\end{array}\right.,$$

(4)

where $C_X$, $C_Y$, and $C_Z$ are the dimensionless drag coefficient, lift coefficient, and lateral force coefficient, respectively, and $\rho$ is the air density.

(2)

Aerodynamic torques

The aerodynamic torques acting on an EAD-UAV affect its flight attitude and can be decomposed into three components: roll torque ($M_x$), yaw torque ($M_y$), and pitch torque ($M_z$) relative to the three coordinate axes of $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$. In addition to the dynamic pressure and characteristic area, the characteristic lengths of the EAD-UAV are the main factors influencing the aerodynamic torques. The relationships between the aerodynamic torques and influencing factors are given by

$$\left\{\begin{array}{l}{M}_x=C_{mx}{q}_{\mathrm{V}}S{l}_{\mathrm{c}}\\ M_y=C_{my}{q}_{\mathrm{V}}S{l}_{\mathrm{c}}\\ M_z=C_{mz}{q}_{\mathrm{V}}S{l}_z\end{array}\right.,$$

(5)

where $l_{\mathrm{c}}$ is the lateral characteristic length, $l_z$ is the longitudinal characteristic length, and $C_{mx}$, $C_{my}$, and $C_{mz}$ are the dimensionless roll, yaw, and pitch moment coefficients, respectively.

(3)

EAD forces and torques

Unlike traditional fixed-wing UAVs, EAD-UAVs have no moving parts, which means they have lower mechanical fatigue, longer service lives, and lower flight noise. Therefore, the control torques cannot be obtained through the deflection of the rudder surface. In order to control the attitude of an EAD-UAV, it is necessary to control the thrust distribution by adjusting the voltage distribution in different areas of the six sets of thrusters installed orthogonally, so as to generate control torque and realize attitude control of the EAD-UAV. The $x_{\mathrm{t}}$-directional thrust, $P_x$, and pitch torque, $M_{z\mathrm{EAD}}$, are generated by $O{z}_{\mathrm{t}}{x}_{\mathrm{t}}$ plane-symmetric EAD thrusters 1 and 2. The $z_{\mathrm{t}}$-directional thrust, $P_z$, and yaw torque, $M_{y\mathrm{EAD}}$, are generated by $O{y}_{\mathrm{t}}{z}_{\mathrm{t}}$ plane-symmetric EAD thrusters 3 and 4. Finally, the $y_{\mathrm{t}}$-directional thrust, $P_y$, and roll torque, $M_{x\mathrm{EAD}}$, are generated by $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$ plane-symmetric EAD thrusters 5 and 6. The EAD thrusts and steering torques can be expressed in the form shown in Equation (6) using the thrusts of the six sets of EAD thrusters:

$$\left\{\begin{array}{l}{P}_x=F_1+F_2\\ P_y=F_5+F_6\\ P_z=F_3+F_4\\ M_{x\mathrm{EAD}}=\left(F_5-F_6\right)l_3\\ M_{y\mathrm{EAD}}=\left(F_3-F_4\right)l_2\\ M_{z\mathrm{EAD}}=\left(F_1-F_2\right)l_1\end{array}\right.,$$

(6)

where $l_1$ is the distance between the projection of the thrust center of thruster 1 (or thruster 2) on the $O{y}_{\mathrm{t}}{z}_{\mathrm{t}}$ plane and the center of mass, $l_2$ is the distance between the projection of the thrust center of thruster 3 (or thruster 4) on the $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$ plane and the centroid, and $l_3$ is the distance between the projection of the thrust center of thruster 5 (or thruster 6) on the $O{z}_{\mathrm{t}}{x}_{\mathrm{t}}$ plane and the center of mass, as shown in Figure 2.

2.3. Dynamic Equations of EAD-UAVs

(1)

Dynamic equation of the motion of the center of mass of an EAD-UAV

In order to analyze the change law of an EAD-UAV track conveniently, the dynamic vector equation of the motion of the centroid can be projected into the track coordinate system as

$$m\left[\begin{array}{c}\dot{V}\\ V\dot{\theta }\\ -V{\dot{\psi }}_V\cos \theta \end{array}\right]=B_{\mathrm{g}}^{\mathrm{h}}{B}_{\mathrm{t}}^{\mathrm{g}}\left(\left[\begin{array}{c}{P}_x\\ P_y\\ P_z\end{array}\right]+B_{\mathrm{V}}^{\mathrm{t}}\left[\begin{array}{c}-X\\ Y\\ Z\end{array}\right]\right)+B_{\mathrm{g}}^{\mathrm{h}}\left[\begin{array}{c}0\\ -mg\\ 0\end{array}\right],$$

(7)

(2)

Dynamic equation of an EAD-UAV rotating around the centroid

The dynamic vector equation of an EAD-UAV rotating around the centroid can be projected into the body coordinate system as

$$\left[\begin{array}{c}{J}_x{\dot{\omega }}_x-J_{xy}{\dot{\omega }}_y+\left(J_z-J_y\right){\omega }_z{\omega }_y+J_{xy}{\omega }_x{\omega }_z\\ J_y{\dot{\omega }}_y-J_{xy}{\dot{\omega }}_x+\left(J_x-J_z\right){\omega }_x{\omega }_z-J_{xy}{\omega }_z{\omega }_y\\ J_z{\dot{\omega }}_z+\left(J_y-J_x\right){\omega }_x{\omega }_y+J_{xy}\left({\omega }_y^2-{\omega }_x^2\right)\end{array}\right]=\left[\begin{array}{c}{M}_x+M_{x\mathrm{EAD}}\\ M_y+M_{y\mathrm{EAD}}\\ M_z+M_{z\mathrm{EAD}}\end{array}\right],$$

(8)

where ${\omega }_x$, ${\omega }_y$, and ${\omega }_z$ are the angular velocities of the EAD-UAV rotating around each axis of $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$; $J_x$, $J_y$, and $J_z$ are the moments of inertia of the EAD-UAV relative to each axis of the body coordinate system; and $J_{xy}$ is the inertial product of the EAD-UAV with respect to the $x_{\mathrm{t}}$- and $y_{\mathrm{t}}$-axes. Because the EAD-UAV is symmetrical on the longitudinal symmetry plane, $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}$, and there is no symmetry deviation, $J_{yz}=J_{zx}=0$.

(3)

Kinematic equation of the motion of the center of mass of an EAD-UAV

According to the relationship between flight speed and position, the kinematic equation of the center of mass of an EAD-UAV in $O_{\mathrm{G}}{x}_{\mathrm{G}}{y}_{\mathrm{G}}{z}_{\mathrm{G}}$ is given by

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=B_{\mathrm{h}}^{\mathrm{g}}\left[\begin{array}{c}V\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}V\cos \theta \cos {\psi }_V\\ V\sin \theta \\ -V\cos \theta \sin {\psi }_V\end{array}\right].$$

(9)

(4)

Kinematic equation of an EAD-UAV rotating about its center of mass

In order to obtain the attitude information of an EAD-UAV in the air, it is necessary to establish a kinematic equation describing an EAD-UAV relative to $O{x}_{\mathrm{g}}{y}_{\mathrm{g}}{z}_{\mathrm{g}}$; its form is

$$\left[\begin{array}{c}\dot{\vartheta }\\ \dot{\psi }\\ \dot{\gamma }\end{array}\right]=\left[\begin{array}{c}{\omega }_y\sin \gamma +{\omega }_z\cos \gamma \\ \frac{1}{\cos \vartheta }\left({\omega }_y\cos \gamma -{\omega }_z\sin \gamma \right)\\ {\omega }_x-\tan \vartheta \left({\omega }_y\cos \gamma -{\omega }_z\sin \gamma \right)\end{array}\right].$$

(10)

(5)

Supplementary equations

When flying an EAD-UAV in non-calm atmosphere conditions, the effect of the wind speed on the flight must be considered. The relationship among the speed of the EAD-UAV relative to the ground, $V$, speed of the relative airflow, $V_{\mathrm{U}}$, and wind speed, $V_{\mathrm{W}}$, is

$$V=V_{\mathrm{U}}+V_{\mathrm{W}},$$

(11)

where $V_{\mathrm{U}}$ can be expressed as shown in Equation (12); $V_{\mathrm{U}x\mathrm{t}}$, $V_{\mathrm{U}y\mathrm{t}}$, and $V_{\mathrm{U}z\mathrm{t}}$ are the $V_{\mathrm{U}}$-components of the three coordinate axes in $O{x}_{\mathrm{t}}{y}_{\mathrm{t}}{z}_{\mathrm{t}}$; and $V_{\mathrm{W}x}$, $V_{\mathrm{W}y}$, and $V_{\mathrm{Wz}}$ are the $V_{\mathrm{W}}$-components of the three coordinate axes in $O_{\mathrm{G}}{x}_{\mathrm{G}}{y}_{\mathrm{G}}{z}_{\mathrm{G}}$:

$$\left[\begin{array}{c}{V}_{\mathrm{U}x\mathrm{t}}\\ V_{\mathrm{U}y\mathrm{t}}\\ V_{\mathrm{U}y\mathrm{t}}\end{array}\right]=B_{\mathrm{g}}^{\mathrm{t}}\left(B_{\mathrm{h}}^{\mathrm{g}}\left[\begin{array}{c}V\\ 0\\ 0\end{array}\right]-\left[\begin{array}{c}{V}_{\mathrm{W}x}\\ V_{\mathrm{W}y}\\ V_{\mathrm{Wz}}\end{array}\right]\right).$$

(12)

The angle of attack $\alpha$ and sideslip angle $\beta$ of an EAD-UAV can be expressed as

$$\left\{\begin{array}{l}\tan \alpha =-V_{\mathrm{U}y\mathrm{t}}/V_{\mathrm{U}x\mathrm{t}}\\ \sin \beta =V_{\mathrm{U}z\mathrm{t}}/V_{\mathrm{U}}\\ V_{\mathrm{U}}=\sqrt{V_{\mathrm{U}x\mathrm{t}}^2+V_{\mathrm{U}y\mathrm{t}}^2+V_{\mathrm{U}z\mathrm{t}}^2}\end{array}\right.,$$

(13)

(6)

Relationship between the thrust and voltage of an EAD thruster

In the one-dimensional model of an EAD thruster cited from [15], its thrust is given by

$$F=\frac{Id}{\mu }=\frac{CU\left(U-U_0\right)d}{\mu },$$

(14)

where I is the current of the EAD thruster; $C$ is a constant related to the EAD thruster structure and ion mobility, $\mu$; $U$ is the applied voltage; $U_0$ is the initial voltage of the EAD thruster when corona discharge occurs; and $d$ is the distance between the emitter electrode and collector electrode of the EAD thruster electrode pair. $C$ can be expressed as Equation (15), cited from [14],

$$C=\frac{C_{0}l\mu {\epsilon }_0}{d^2},$$

(15)

where $l$ is the electrode length of the EAD thruster and ${\epsilon }_0$ is the vacuum permittivity. The dimensionless constant, $C_0$, is estimated based on the relevant data in [9].

$U_0$ can be determined applying Equation (15), cited from [47], by approximating the situation in this paper to the form of parallel wires,

$$U_0=E_p{r}_c\ln \left(\frac{d}{r_c}\right).$$

(16)

Here, $E_p$ is the intensity of the corona inception electric field at which the corona discharge phenomenon occurs, which can be calculated by utilizing Equation (17), cited from [48], and $r_c$ is the radius of the emitter electrode in centimeters,

$$E_p=E_0\delta \epsilon \left(1+\frac{0.308}{\sqrt{\delta r_c}}\right).$$

(17)

Here, $E_0$ is the electric field strength corresponding to air breakdown (for air, $E_0$ = 31 kV/cm) $\delta$ is the relative atmospheric density, and $\epsilon$ is the smoothness of the electrode surface; in this paper, $\epsilon =1$.

(7)

Coupling dynamic equation of an EAD-UAV

The dynamic equation of an EAD-UAV can be expressed in the form of $\dot{\mathit{x}}=f(\mathit{x},\mathit{u})$, where $\mathit{x}={\left[x,y,z,\vartheta ,\psi ,\gamma ,{\omega }_x,{\omega }_y,{\omega }_z,V,\theta ,{\psi }_V\right]}^{\mathrm{T}}$ is the state variable vector and $\mathit{u}={\left[U_1,U_2,U_3,U_4,U_5,U_6\right]}^{\mathrm{T}}$ is the control variable vector.

According to the above equations, the position–attitude coupling dynamic equation of the EAD-UAV can be obtained, as shown in Equation (18). The coupled control of the position and attitude of the EAD-UAV can be achieved by adjusting the voltages of the six EAD thrusters.

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\\ \dot{\vartheta }\\ \dot{\psi }\\ \dot{\gamma }\\ {\dot{\omega }}_x\\ {\dot{\omega }}_y\\ {\dot{\omega }}_z\\ \dot{V}\\ \dot{\theta }\\ {\dot{\psi }}_V\end{array}\right]=\left[\begin{array}{c}V\cos \theta \cos {\psi }_V\\ V\sin \theta \\ -V\cos \theta \sin {\psi }_V\\ {\omega }_y\sin \gamma +{\omega }_z\cos \gamma \\ \frac{1}{\cos \vartheta }\left({\omega }_y\cos \gamma -{\omega }_z\sin \gamma \right)\\ {\omega }_x-\tan \vartheta \left({\omega }_y\cos \gamma -{\omega }_z\sin \gamma \right)\\ \frac{-J_{xy}{}^2{\omega }_y{\omega }_z+\left(\left(J_x+J_y-J_z\right){\omega }_x{\omega }_z-\left(F_3\left(\mathit{u}\right)-F_4\left(\mathit{u}\right)\right)l_2-M_y\right)J_{xy}-\left(\left(J_y-J_z\right){\omega }_y{\omega }_z+\left(F_5\left(\mathit{u}\right)-F_6\left(\mathit{u}\right)\right)l_3+M_x\right)J_y}{-J_x{J}_y+J_{xy}{}^2}\\ \frac{J_{xy}{}^2{\omega }_x{\omega }_z+\left(-\left(J_x-J_y+J_z\right){\omega }_y{\omega }_z-\left(F_5\left(\mathit{u}\right)-F_6\left(\mathit{u}\right)\right)l_3-M_x\right)J_{xy}-\left(-\left(J_x+J_z\right){\omega }_x{\omega }_z+\left(F_3\left(\mathit{u}\right)-F_4\left(\mathit{u}\right)\right)l_2+M_y\right)J_x}{-J_x{J}_y+J_{xy}{}^2}\\ \frac{J_{xy}{\omega }_x{}^2+\left(J_x-J_y\right){\omega }_x{\omega }_y-J_{xy}{\omega }_y{}^2+\left(F_1\left(\mathit{u}\right)-F_2\left(\mathit{u}\right)\right)l_1+M_z}{J_z}\\ \frac{\left(A_4-A_5-A_6\cos \psi -A_7\right)\cos \theta -\left(A_3\sin \vartheta -A_1\cos \vartheta \cos \gamma +A_2\cos \vartheta \sin \gamma +G\right)\sin \theta }{m}\\ \frac{\left(-A_4+A_5+A_6\cos {\psi }_V+A_7\right)\sin \theta -\left(A_3\sin \vartheta -A_1\cos \vartheta \cos \gamma +A_2\cos \vartheta \sin \gamma +G\right)\cos \theta }{mV}\\ \frac{\left(\left(-A_2\cos \gamma -A_1\sin \gamma \right)\cos \psi +A_8\sin \psi \right)\cos {\psi }_V-\left(A_8\cos \psi +\left(A_2\cos \gamma +\sin \gamma A_1\right)\sin \psi \right)\sin {\psi }_V}{mV\cos \theta }\end{array}\right],$$

(18)

where

$$\left\{\begin{array}{l}{A}_1=\left(Z\sin \beta +X\cos \beta \right)\sin \alpha +Y\cos \alpha +F_5\left(\mathit{u}\right)+F_6\left(\mathit{u}\right)\\ A_2=Z\cos \beta -X\sin \beta +F_3\left(\mathit{u}\right)+F_4\left(\mathit{u}\right)\\ A_3=Z\sin \beta \cos \alpha +X\cos \alpha \cos \beta -Y\sin \alpha -F_1\left(\mathit{u}\right)-F_2\left(\mathit{u}\right)\\ A_4=\left(-A_1\cos \gamma +A_2\sin \gamma \right)\left(\cos \psi \cos {\psi }_V+\sin \psi \sin {\psi }_V\right)\sin \vartheta \\ A_5=A_2\left(\cos \psi \sin {\psi }_V-\sin \psi \cos {\psi }_V\right)\cos \gamma \\ A_6=A_3\cos \vartheta \cos \psi -A_1\sin \gamma \sin \psi \\ A_7=\left(A_1\sin \gamma \cos \psi +A_3\sin \psi \cos \vartheta \right)\sin {\psi }_V\\ A_8=\left(-A_1\cos \gamma +A_2\sin \gamma \right)\sin \vartheta -A_3\cos \vartheta \\ F_i(\mathit{u})=\frac{C{U}_i\left(U_i-U_0\right)d}{\mu },\left(i=1,2,3,4,5,6\right)\end{array}\right.$$

3. Trajectory Optimization Using the Integrative Bezier Shaping Approach (IBSA)

3.1. Optimization Problem

This paper describes the trajectory planning problem of multi-point exploration using an EAD-UAV. The EAD-UAV leaves the starting point of the flight trajectory at moment $T^{\left(0\right)}$ and reaches the first target point at moment $T^{\left(1\right)}$. Then, the EAD-UAV arrives at the k-th objective at moment $T^{\left(k\right)}$, where the superscript k = [1, N] is the parameter and corresponds to the k-th segment of the trajectory (that is, the trajectory between the (k–1)-th objective and the k-th objective). The optimal EAD-UAV control law can be obtained by taking the minimum total flight time of the flight trajectory of an EAD-UAV flying over the N targets as the optimization objective, that is, the voltage distribution of the six EAD thrusters at each moment, $\mathit{u}={\left[\begin{array}{ccc}{U}_1& U_2& \begin{array}{cccc}{U}_3& U_4& U_5& U_6\end{array}\end{array}\right]}^{\mathrm{T}}$. Therefore, the objective function of the optimization problem can be expressed as

$$J_T={\displaystyle \sum _{k=1}^N\Delta T^{\left(k\right)}},$$

(19)

where $\Delta T^{\left(k\right)}=T^{\left(k\right)}-T^{\left(k-1\right)}$ is the flight time from the (k–1)-th objective to the k-th objective. The flight times $\Delta T^{\left(k\right)},\hspace{1em}k=[1,N]$ are chosen as the optimization variables in the process of solving.

EAD-UAV has high voltage requirements, which places high demands on batteries, so minimum energy consumption is also a reasonable optimization objective. The objective function for minimum energy consumption can be expressed as:

$$J_{Energy}={\displaystyle \sum _{k=1}^N{\displaystyle \sum _{j=1}^{m-1}{\displaystyle \sum _{i=1}^6{U}_i\left(j\right)I_i}}\left(j\right)\Delta T^{\left(k\right)}\left(j\right)},$$

(20)

where $\Delta T^{\left(k\right)}\left(j\right)$ is the time interval between the j-th point and the (j + 1)-th point after discretizing the time between $T^{\left(k-1\right)}$ and $T^{\left(k\right)}$ into m points, while $P_{power}=U_i\left(j\right)I_i\left(j\right)$ is the power of the i-th thruster at the j-th point. $P_{average}=\frac{J_{Energy}}{\Delta T^{\left(k\right)}}$ is the average power of the k-th trajectory. The average power can be used to evaluate the battery performance requirements of EAD-UAV.

For the multi-point continuous optimization problem of EAD-UAV trajectories, besides the boundary constraints at moments $T^{\left(0\right)}$ and $T^{\left(N\right)}$, the boundary constraints of the k-th trajectory at moment $T^{\left(k\right)}, k=[1,N-1]$ should be considered. The position, velocity, track angles, and attitude angles of the EAD-UAV in the ground coordinate system at $T^{\left(0\right)}$ and $T^{\left(N\right)}$ and the triaxial angular velocity in the body coordinate system at $T^{\left(0\right)}$ and $T^{\left(N\right)}$ are known quantities; the boundary constraints at moments $T^{\left(0\right)}$ and $T^{\left(N\right)}$ are given by

$$\left\{\begin{array}{l}\mathit{x}\left(T^{\left(0\right)}\right)=\left[\begin{array}{cccc}x\left(T^{\left(0\right)}\right)& y\left(T^{\left(0\right)}\right)& z\left(T^{\left(0\right)}\right)& \begin{array}{ccc}V\left(T^{\left(0\right)}\right)& \theta \left(T^{\left(0\right)}\right)& {\psi }_V\left(T^{\left(0\right)}\right)\end{array}\end{array}\right.\\ \begin{array}{cccccc} & & & & & \begin{array}{cccc}\vartheta \left(T^{\left(0\right)}\right)& \psi \left(T^{\left(0\right)}\right)& \gamma \left(T^{\left(0\right)}\right)& \begin{array}{ccc}{\omega }_x\left(T^{\left(0\right)}\right)& {\omega }_y\left(T^{\left(0\right)}\right)& {\left.{\omega }_z\left(T^{\left(0\right)}\right)\right]}^{\mathrm{T}}\end{array}\end{array}\end{array}\\ \mathit{x}\left(T^{\left(N\right)}\right)=\left[\begin{array}{cccc}x\left(T^{\left(N\right)}\right)& y\left(T^{\left(N\right)}\right)& z\left(T^{\left(N\right)}\right)& \begin{array}{ccc}V\left(T^{\left(N\right)}\right)& \theta \left(T^{\left(N\right)}\right)& {\psi }_V\left(T^{\left(N\right)}\right)\end{array}\end{array}\right.\\ \begin{array}{cccccc} & & & & & \begin{array}{cccc}\vartheta \left(T^{\left(N\right)}\right)& \psi \left(T^{\left(N\right)}\right)& \gamma \left(T^{\left(N\right)}\right)& \begin{array}{ccc}{\omega }_x\left(T^{\left(N\right)}\right)& {\omega }_y\left(T^{\left(N\right)}\right)& {\left.{\omega }_z\left(T^{\left(N\right)}\right)\right]}^{\mathrm{T}}\end{array}\end{array}\end{array}\end{array}\right.,$$

(21)

where $\mathit{x}$ is the state vector of the EAD-UAV.

At moment $T^{\left(k\right)}, k=[1,N-1]$, the positions are known quantities as boundary constraints. Therefore, the boundary constraints are given by

$$\left\{\begin{array}{l}x\left(T^{\left(k\right)}\right)=x^{\left(k\right)}\left(T^{\left(k\right)}\right)\\ y\left(T^{\left(k\right)}\right)=y^{\left(k\right)}\left(T^{\left(k\right)}\right)\\ z\left(T^{\left(k\right)}\right)=z^{\left(k\right)}\left(T^{\left(k\right)}\right)\end{array}\right.,$$

(22)

where $x^{\left(k\right)}\left(T^{\left(k\right)}\right)$, $y^{\left(k\right)}\left(T^{\left(k\right)}\right)$, and $z^{\left(k\right)}\left(T^{\left(k\right)}\right)$ are the three-axis positions of the k-th objective at time $T^{\left(k\right)}$, $k=[1,N-1]$.

Furthermore, although there are no boundary constraints for the velocity, acceleration, attitude angle, or angular velocity at the intermediate points, these quantities also need to be continuous for the EAD-UAV trajectory to be continuous.

3.2. Bezier State Approximation

Among the state variables in the EAD-UAV dynamics equation, ${\omega }_x,{\omega }_y,{\omega }_z,V,\theta ,{\psi }_V$ can be expressed as follows by using $x,y,z,\vartheta ,\psi ,\gamma$ and their first derivatives:

$$\left[\begin{array}{l}{\omega }_x\\ {\omega }_y\\ {\omega }_z\\ V\\ \theta \\ {\psi }_V\end{array}\right]=\left[\begin{array}{c}\dot{\gamma }+\dot{\psi }\cos \vartheta \tan \vartheta \\ \dot{\vartheta }\sin \gamma +\dot{\psi }\cos \gamma \cos \vartheta \\ \dot{\vartheta }\cos \gamma -\dot{\psi }\sin \gamma \cos \vartheta \\ \sqrt{{\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2}\\ \arcsin \left(\frac{\dot{y}}{V}\right)\\ \arctan \left(-\frac{\dot{z}}{\dot{x}}\right)\end{array}\right].$$

(23)

Therefore, all state variables and their first derivatives can be represented by $x,y,z,\vartheta ,\psi ,\gamma$ and their first and second derivatives.

According to the EAD-UAV dynamic equation, the thrusts $F_1$–$F_6$ of the six EAD thrusters can be determined and expressed as follows by using $x,y,z,\vartheta ,\psi ,\gamma$ and their first and second derivatives:

$$\left\{\begin{array}{l}{F}_1=\frac{m{l}_1\left(B_1-B_2\right)\cos \left(\vartheta \right)+B_3+B_4+B_5}{2l_1}\\ F_2=\frac{m{l}_1\left(B_1-B_2\right)\cos \left(\vartheta \right)+B_3+B_4-B_5}{2l_1}\\ F_3=\frac{m{l}_2\left({\Gamma }_1-{\Gamma }_2\right)\cos \left(\theta \right)-{\Gamma }_3+{\Gamma }_4+{\Gamma }_5}{2l_2}\\ F_4=\frac{m{l}_2\left({\Gamma }_1-{\Gamma }_2\right)\cos \left(\theta \right)-{\Gamma }_3+{\Gamma }_4-{\Gamma }_5}{2l_2}\\ F_5=\frac{l_3\left({\Delta }_1-{\Delta }_2\right)\cos \left(\gamma \right)-{\Delta }_3+{\Delta }_4+{\Delta }_5}{2l_3}\\ F_6=\frac{l_3\left({\Delta }_1-{\Delta }_2\right)\cos \left(\gamma \right)-{\Delta }_3+{\Delta }_4-{\Delta }_5}{2l_3}\end{array}\right.,$$

(24)

where

$$\left\{\begin{array}{l}{B}_1=\left(\left({\psi }_V\sin \left(\psi \right)V+\dot{V}\cos \left(\psi \right)\right)\cos \left({\psi }_V\right)+\sin \left({\psi }_V\right)\left(-{\dot{\psi }}_V\cos \left(\psi \right)V+\dot{V}\sin \left(\psi \right)\right)\right)\cos \left(\theta \right)\\ B_2=\dot{\theta }\sin \left(\theta \right)V\left(\cos \left(\psi \right)\cos \left({\psi }_V\right)+\sin \left(\psi \right)\sin \left({\psi }_V\right)\right)\\ B_3=l_{1}V\vartheta m\cos \left(\theta \right)\sin \left(\vartheta \right)+l_1\left(\dot{V}\sin \left(\theta \right)m+G\right)\sin \left(\vartheta \right)\\ B_4=l_1\left(Z\sin \left(\beta \right)+X\cos \left(\beta \right)\right)\cos \left(\alpha \right)-Y{l}_1\sin \left(\alpha \right)\\ B_5=-J_{xy}{\omega }_x^2-{\omega }_y\left(J_x-J_y\right){\omega }_x+J_{xy}{\omega }_y^2+J_z{\dot{\omega }}_z-M_z\\ {\Gamma }_1=\left(\left(\left({\dot{\psi }}_V\sin \left(\psi \right)V+\dot{V}\cos \left(\psi \right)\right)\cos \left({\psi }_V\right)+\sin \left({\psi }_V\right)\left(-{\dot{\psi }}_V\cos \left(\psi \right)V+\dot{V}\sin \left(\psi \right)\right)\right)\sin \left(\vartheta \right)-\dot{\vartheta }\cos \left(\vartheta \right)V\right)\sin \left(\gamma \right)\\ {\Gamma }_2=\left(\left({\dot{\psi }}_V\cos \left(\psi \right)V-\dot{V}\sin \left(\psi \right)\right)\cos \left({\psi }_V\right)+\sin \left({\psi }_V\right)\left({\dot{\psi }}_V\sin \left(\psi \right)V+\dot{V}\cos \left(\psi \right)\right)\right)\cos \left(\gamma \right)\\ {\Gamma }_3=\left(\dot{\theta }\sin \left(\theta \right)Vm\left(\cos \left(\psi \right)\cos \left({\psi }_V\right)+\sin \left(\psi \right)\sin \left({\psi }_V\right)\right)\sin \left(\vartheta \right)+\cos \left(\vartheta \right)\left(\dot{V}\sin \left(\theta \right)m+G\right)\right)l_2\sin \left(\gamma \right)\\ {\Gamma }_4=\dot{\theta }\sin \left(\theta \right)Vm{l}_2\left(\cos \left(\psi \right)\sin \left({\psi }_V\right)-\cos \left({\psi }_V\right)\sin \left(\psi \right)\right)\cos \left(\gamma \right)-Z{l}_2\cos \left(\beta \right)+X{l}_2\sin \left(\beta \right)\\ {\Gamma }_5=\left(-{\omega }_y{J}_{xy}+{\omega }_x\left(J_x-J_z\right)\right){\omega }_z-J_{xy}{\dot{\omega }}_x+J_y{\dot{\omega }}_y-M_y\\ {\Delta }_1=m\left(\left(\left({\dot{\psi }}_V\sin \left(\psi \right)V+\dot{V}\cos \left(\psi \right)\right)\cos \left({\psi }_V\right)+\sin \left({\psi }_V\right)\left(-{\dot{\psi }}_V\cos \left(\psi \right)V+\dot{V}\sin \left(\psi \right)\right)\right)\sin \left(\vartheta \right)-\dot{\theta }\cos \left(\vartheta \right)V\right)\cos \left(\theta \right)\\ {\Delta }_2=\dot{\theta }\sin \left(\theta \right)Vm\left(\cos \left(\psi \right)\cos \left({\psi }_V\right)+\sin \left(\psi \right)\sin \left({\psi }_V\right)\right)\sin \left(\vartheta \right)-\cos \left(\vartheta \right)\left(\dot{V}\sin \left(\theta \right)m+G\right)\\ {\Delta }_3=m{l}_3\sin \left(\gamma \right)\left(\left({\dot{\psi }}_V\cos \left(\psi \right)V-\dot{V}\sin \left(\psi \right)\right)\cos \left({\psi }_V\right)+\sin \left({\psi }_V\right)\left({\dot{\psi }}_V\sin \left(\psi \right)V+\dot{V}\cos \left(\psi \right)\right)\right)\cos \left(\theta \right)\\ {\Delta }_4=l_3\dot{\theta }\sin \left(\theta \right)Vm\left(\cos \left(\psi \right)\sin \left({\psi }_V\right)-\cos \left({\psi }_V\right)\sin \left(\psi \right)\right)\sin \left(\gamma \right)-l_3\left(Z\sin \left(\beta \right)+X\cos \left(\beta \right)\right)\sin \left(\alpha \right)-Y{l}_3\cos \left(\alpha \right)\\ {\Delta }_5=\left({\omega }_x{J}_{xy}-{\omega }_y\left(J_y-J_z\right)\right){\omega }_z-J_{xy}{\dot{\omega }}_y+J_x{\dot{\omega }}_x-M_x\end{array}\right.$$

It can be seen from Equation (14) that after corona discharge occurs (that is, when the applied voltage is greater than the corona initiation voltage), the thrust of the EAD thruster increases monotonically with increasing voltage, so the applied voltage, $U$, can be given by Equation (24) in the form of a function of the EAD thrust, $F$. Therefore, the control variables of the dynamic equation of an EAD-UAV can be expressed by using $x,y,z,\vartheta ,\psi ,\gamma$ and their first and second derivatives.

$$U=\frac{C^{\prime }{U}_0+\sqrt{C^{\prime }\left(C^{\prime }{U}_0^2+4F\right)}}{2C^{\prime }},$$

(25)

Here, $C^{\prime }$ is given by

$$C^{\prime }=\frac{Cd}{\mu }.$$

(26)

Therefore, the whole EAD-UAV dynamic equation can be expressed by using $x,y,z,\vartheta ,\psi ,\gamma$ and their first and second derivatives.

Concerning the k-th trajectory, the approximations of the six-degree-of-freedom position can be expanded in the time domain by applying a Bezier curve function:

$$\begin{array}{l}{x}^{(k)}(\tau )={\displaystyle {\displaystyle \sum }_{j=0}^{n_x^{(k)}}}{B}_{x,j}^{(k)}(\tau )P_{x,j}^{(k)}\\ y^{(k)}(\tau )={\displaystyle {\displaystyle \sum }_{j=0}^{n_y^{(k)}}}{B}_{y,j}^{(k)}(\tau )P_{y,j}^{(k)}\\ z^{(k)}(\tau )={\displaystyle {\displaystyle \sum }_{j=0}^{n_z^{(k)}}}{B}_{z,j}^{(k)}(\tau )P_{z,j}^{(k)}\\ {\vartheta }^{(k)}(\tau )={\displaystyle {\displaystyle \sum }_{j=0}^{n_{\vartheta }^{(k)}}}{B}_{\vartheta ,j}^{(k)}(\tau )P_{\vartheta ,j}^{(k)}\\ {\psi }^{(k)}(\tau )={\displaystyle {\displaystyle \sum }_{j=0}^{n_{\psi }^{(k)}}}{B}_{\psi ,j}^{(k)}(\tau )P_{\psi ,j}^{(k)}\\ {\gamma }^{(k)}(\tau )={\displaystyle {\displaystyle \sum }_{j=0}^{n_{\gamma }^{(k)}}}{B}_{\gamma ,j}^{(k)}(\tau )P_{\gamma ,j}^{(k)}\end{array},$$

(27)

where $0\le \tau =t/\Delta T^{(k)}\le 1$ is the self-defined scaled time parameter; $t$ and $\Delta T^{(k)}$ are the actual time and total flight time duration in the k-th segment of trajectory, respectively; $n_x^{(k)}$, $n_y^{(k)}$, $n_z^{(k)}$, $n_{\vartheta }^{(k)}$, $n_{\psi }^{(k)}$, and $n_{\gamma }^{(k)}$ are the orders of the Bezier curve function for each of the six degrees; and $P_{x,j}^{(k)}(j\in [0,n_x^{(k)}])$, $P_{y,j}^{(k)}(j\in [0,n_y^{(k)}])$, $P_{z,j}^{(k)}(j\in [0,n_z^{(k)}])$, $P_{\vartheta ,j}^{(k)}(j\in [0,n_{\vartheta }^{(k)}])$, $P_{\psi ,j}^{(k)}(j\in [0,n_{\psi }^{(k)}])$, and $P_{\gamma ,j}^{(k)}(j\in [0,n_{\psi }^{(k)}])$ are the Bezier coefficients. $B_{x,j}^{(k)}(\tau )$, $B_{y,j}^{(k)}(\tau )$, $B_{z,j}^{(k)}(\tau )$, $B_{\vartheta ,j}^{(k)}(\tau )$, $B_{\psi ,j}^{(k)}(\tau )$, and $B_{\gamma ,j}^{(k)}(\tau )$ are the Bezier basis functions for the coordinate approximations and are given by

$$\begin{array}{l}{B}_{x,j}^{(k)}(\tau )=\frac{n_x^{(k)}!}{j!\left(n_x^{(k)}-j\right)!}{\tau }^j{(1-\tau )}^{n_x^{(k)}-j}\hspace{1em}\hspace{1em}j\in [0,n_x^{(k)}]\\ B_{y,j}^{(k)}(\tau )=\frac{n_y^{(k)}!}{j!\left(n_y^{(k)}-j\right)!}{\tau }^j{(1-\tau )}^{n_y^{(k)}-j}\hspace{1em}\hspace{1em}j\in [0,n_y^{(k)}]\\ B_{z,j}^{(k)}(\tau )=\frac{n_z^{(k)}!}{j!\left(n_z^{(k)}-j\right)!}{\tau }^j{(1-\tau )}^{n_z^{(k)}-j}\hspace{1em}\hspace{1em}j\in [0,n_z^{(k)}]\\ B_{\vartheta ,j}^{(k)}(\tau )=\frac{n_{\vartheta }^{(k)}!}{j!\left(n_{\vartheta }^{(k)}-j\right)!}{\tau }^j{(1-\tau )}^{n_{\vartheta }^{(k)}-j}\hspace{1em}\hspace{1em}j\in [0,n_{\vartheta }^{(k)}]\\ B_{\psi ,j}^{(k)}(\tau )=\frac{n_{\psi }^{(k)}!}{j!\left(n_{\psi }^{(k)}-j\right)!}{\tau }^j{(1-\tau )}^{n_{\psi }^{(k)}-j}\hspace{1em}\hspace{1em}j\in [0,n_{\psi }^{(k)}]\\ B_{\gamma ,j}^{(k)}(\tau )=\frac{n_{\gamma }^{(k)}!}{j!\left(n_{\gamma }^{(k)}-j\right)!}{\tau }^j{(1-\tau )}^{n_{\gamma }^{(k)}-j}\hspace{1em}\hspace{1em}j\in [0,n_{\gamma }^{(k)}]\end{array},$$

(28)

In order to avoid repetition, individually, the procedure of an approximation for coordinate x is presented in this paper, and the other five degrees can be handled in an analogical manner. According to Equation (27), the first and second τ-derivatives of the degree x can be written as

$$\left\{\begin{array}{l}{x}^{(k){}^{\prime }}(\tau )={\displaystyle \sum _{j=0}^{n_x^{(k)}}{B}_{x,j}^{(k){}^{\prime }}(\tau )P_{x,j}^{(k)}}\\ x^{(k){}^{″}}(\tau )={\displaystyle \sum _{j=0}^{n_x^{(k)}}{B}_{x,j}^{(k){}^{″}}(\tau )P_{x,j}^{(k)}}\end{array}\right.,$$

(29)

where the superscript ′ represents the derivative with respect to the parameter τ and $B_{x,j}^{(k){}^{\prime }}(\tau )$ and $B_{x,j}^{(k){}^{″}}(\tau )$ are the first and second τ-derivatives of the Bezier basis function for the degree x approximation in the k-th interplanetary trajectory, respectively. According to Equation (28), one can obtain

$$\begin{array}{l}{B}_{x,j}^{(k){}^{\prime }}(\tau )=\left\{\begin{array}{cc}-n_x^{(k)}{(1-\tau )}^{n_x^{(k)}-1}& j=0\\ \frac{n_x^{(k)}!}{(j-1)!\left(n_x^{(k)}-j\right)!}{\tau }^{j-1}{(1-\tau )}^{n_x^{(k)}-j}-\frac{n_x^{(k)}!}{j!\left(n_x^{(k)}-j-1\right)!}{\tau }^j{(1-\tau )}^{n_x^{(k)}-j-1}& j\in [1,n_x^{(k)}-1]\\ n_x^{(k)}{\tau }^{n_x^{(k)}-1}& j=n_x^{(k)}\end{array}\right.\\ B_{x,j}^{(k){}^{″}}(\tau )=\left\{\begin{array}{cc}{n}_x^{(k)}\left(n_x^{(k)}-1\right){(1-\tau )}^{n_x^{(k)}-2}& j=0\\ n_x^{(k)}\left(n_x^{(k)}-1\right)\left(n_x^{(k)}-2\right)\tau {(1-\tau )}^{n_x^{(k)}-3}-2n_x^{(k)}\left(n_x^{(k)}-1\right){(1-\tau )}^{n_x^{(k)}-2}& j=1\\ \frac{n_x^{(k)}!}{(j-2)!\left(n_x^{(k)}-j\right)!}{\tau }^{j-2}{(1-\tau )}^{n_x^{(k)}-j}-2\frac{n_x^{(k)}!}{(j-1)!\left(n_x^{(k)}-j-1\right)!}{\tau }^{j-1}{(1-\tau )}^{n_x^{(k)}-j-1}+\frac{n_x^{(k)}!}{j!\left(n_x^{(k)}-j-2\right)!}{\tau }^j{(1-\tau )}^{n_x^{(k)}-j-2}& j\in [2,n_x^{(k)}-2]\\ n_x^{(k)}\left(n_x^{(k)}-1\right)\left(n_x^{(k)}-2\right){\tau }^{n_x^{(k)}-3}(1-\tau )-2n_x^{(k)}\left(n_x^{(k)}-1\right){\tau }^{n_x^{(k)}-2}& j=n_x^{(k)}-1\\ n_x^{(k)}\left(n_x^{(k)}-1\right){\tau }^{n_x^{(k)}-2}& j=n_x^{(k)}\end{array}\right.\end{array},$$

(30)

By substituting $\tau =0$ and $\tau =1$ into Equations (29) and (30), interesting characteristics of the Bezier basis function at the boundary can be obtained, as follows:

$$\begin{array}{ll}{B}_{x,j}^{(k)}(\tau =0)=\left\{\begin{array}{ll}1& j=0\\ 0& j\in [1,n_x^{(k)}]\end{array}\right.& B_{x,j}^{(k)}(\tau =1)=\left\{\begin{array}{ll}0& j\in [0,n_x^{(k)}-1]\\ 1& j=n_x^{(k)}\end{array}\right.\\ B_{x,j}^{(k){}^{\prime }}(\tau =0)=\left\{\begin{array}{ll}-n_x^{(k)}& j=0\\ n_x^{(k)}& j=1\\ 0& j\in [2,n_x^{(k)}]\end{array}\right.& B_{x,j}^{(k){}^{\prime }}(\tau =1)=\left\{\begin{array}{ll}0& j\in [0,n_x^{(k)}-2]\\ -n_x^{(k)}& j=n_x^{(k)}-1\\ n_x^{(k)}& j=n_x^{(k)}\end{array}\right.\\ B_{x,j}^{(k){}^{″}}(\tau =0)=\left\{\begin{array}{ll}{n}_x^{(k)}\left(n_x^{(k)}-1\right)& j=0\\ -2n_x^{(k)}\left(n_x^{(k)}-1\right)& j=1\\ n_x^{(k)}\left(n_x^{(k)}-1\right)& j=2\\ 0& j\in [3,n_x^{(k)}]\end{array}\right.& B_{x,j}^{(k){}^{″}}(\tau =1)=\left\{\begin{array}{ll}0& j\in [0,n_x^{(k)}-3]\\ n_x^{(k)}\left(n_x^{(k)}-1\right)& j=n_x^{(k)}-2\\ -2n_x^{(k)}\left(n_x^{(k)}-1\right)& j=n_x^{(k)}-1\\ n_x^{(k)}\left(n_x^{(k)}-1\right)& j=n_x^{(k)}\end{array}\right.\end{array},$$

(31)

According to Equations (27), (29) and (31), the relationships between the boundary constraints of the k-th segment of the trajectory and the Bezier coefficient can be found, as shown in Equation (32):

$$\begin{array}{ccc}\hfill x\left(T^{(k-1)}\right)& =& x^{(k)}(\tau =0)=P_{x,0}^{(k)}\hfill \\ \hfill x\left(T^{(k)}\right)& =& x^{(k)}(\tau =1)=P_{x,n_x^{(k)}}^{(k)}\hfill \\ \hfill \Delta T^{(k)}\dot{x}\left(T^{(k-1)}\right)& =& x^{{}^{\prime }(k)}(\tau =0)=n_x^{(k)}\left(P_{x,1}^{(k)}-P_{x,0}^{(k)}\right)\hfill \\ \hfill \Delta T^{(k)}\dot{x}\left(T^{(k)}\right)& =& x^{{}^{\prime }(k)}(\tau =1)=n_x^{(k)}\left(P_{x,n_x^{(k)}}^{(k)}-P_{x,n_x^{(k)}-1}^{(k)}\right)\hfill \\ \hfill {\left(\Delta T^{(k)}\right)}^2\ddot{x}\left(T^{(k-1)}\right)& =& x^{{}^{″}(k)}(\tau =0)=n_x^{(k)}\left(n_x^{(k)}-1\right)\left(P_{x,0}^{(k)}+P_{x,2}^{(k)}-2P_{x,1}^{(k)}\right)\hfill \\ \hfill {\left(\Delta T^{(k)}\right)}^2\ddot{x}\left(T^{(k)}\right)& =& x^{{}^{″}(k)}(\tau =1)=n_x^{(k)}\left(n_x^{(k)}-1\right)\left(P_{x,n_x^{(k)}}^{(k)}+P_{x,n_x^{(k)}-2}^{(k)}-2P_{x,n_x^{(k)}-1}^{(k)}\right)\hfill \end{array},$$

(32)

where the superscript ^· represents the derivative of the actual time, t, from which one can obtain the Bezier representation of x and its first and second derivatives at the start time $T^{(k-1)}$ and end time $T^{(k)}$ of the k-th segment of the trajectory.

Hence, it was ensured that the approximate EAD-UAV flight trajectory naturally met the boundary constraints in aspects of position, velocity, and acceleration at the boundary time ($T^{(k-1)}$ and $T^{(k)}$) of the k-th segment by determining Bezier coefficients $P_{x,0}^{(k)}$, $P_{x,1}^{(k)}$, $P_{x,2}^{(k)}$, $P_{x,n_x^{(k)}-2}^{(k)}$, $P_{x,n_x^{(k)}-1}^{(k)}$, and $P_{x,n_x^{(k)}}^{(k)}$ as

$$\begin{array}{lll}\hfill P_{x,0}^{(k)}& =& x\left(T^{(k-1)}\right)\hfill \\ \hfill P_{x,1}^{(k)}& =& x\left(T^{(k-1)}\right)+\Delta T^{(k)}\dot{x}\left(T^{(k-1)}\right)/n_x^{(k)}\hfill \\ \hfill P_{x,2}^{(k)}& =& x\left(T^{(k-1)}\right)+2\Delta T^{(k)}\dot{x}\left(T^{(k-1)}\right)/n_x^{(k)}+{\left(\Delta T^{(k)}\right)}^2\ddot{x}\left(T^{(k-1)}\right)/\left(n_x^{(k)}\left(n_x^{(k)}-1\right)\right)\hfill \\ \hfill P_{x,n_x^{(k)}-2}^{(k)}& =& x\left(T^{(k)}\right)-2\Delta T^{(k)}\dot{x}\left(T^{(k)}\right)/n_x^{(k)}+{\left(\Delta T^{(k)}\right)}^2\ddot{x}\left(T^{(k)}\right)/\left(n_x^{(k)}\left(n_x^{(k)}-1\right)\right)\hfill \\ \hfill P_{x,n_x^{(k)}-1}^{(k)}& =& x\left(T^{(k)}\right)-\Delta T^{(k)}\dot{x}\left(T^{(k)}\right)/n_x^{(k)}\hfill \\ \hfill P_{x,n_x^{(k)}}^{(k)}& =& x\left(T^{(k)}\right)\hfill \end{array},$$

(33)

This characteristic is fairly beneficial for dealing with fast trajectory optimization; instead of concerning boundary constraints, only the dynamic constraints and optimization performance index must be considered during the optimization procedure. In order to deal with the acceleration continuity of an EAD-UAV in multi-target trajectory optimization, the relationship between the second derivative of the coordinate approximations ($\ddot{x}\left(T^{(k-1)}\right)$, $\ddot{x}\left(T^{(k)}\right)$) and the coefficients ($P_{x,2}^{(k)},\hspace{1em}{P}_{x,n_x^{(k)}-2}^{(k)}$) is determined, which is different from the single-target trajectory optimization problem.

3.3. Nonlinear Programming Problem (NLP)

The essential problem is to obtain a practical trajectory within the capabilities of the EAD thrusters in all segments of EAD-UAV flight. Thus, it is essential to assess the motion of each trajectory at selected discretized points. Legendre–Gauss (LG) distribution, defined as the roots of the $m^{(k)}$th-degree Legendre polynomial, was selected as the discrete mode of discretized points in this paper and is given by

$${\tau }_1=0<{\tau }_2<\cdots <{\tau }_{m^{(k)}-1}<{\tau }_{m^{(k)}}=1,$$

(34)

The discrete six-degree-of-freedom position and attitude coordinates can be expressed in the form of matrix products. For example, x can be expressed as

$$\begin{array}{c}{[x^{(k)}]}_{m^{(k)}\times 1}={[B_x^{(k)}]}_{m^{(k)}\times (n_x^{(k)}+1)}{[P_x^{(k)}]}_{(n_x^{(k)}+1)\times 1}\\ {[x^{(k){}^{\prime }}]}_{m^{(k)}\times 1}={[B_x^{(k){}^{\prime }}]}_{m^{(k)}\times (n_x^{(k)}+1)}{[P_x^{(k)}]}_{(n_x^{(k)}+1)\times 1}\\ {[x^{(k){}^{″}}]}_{m^{(k)}\times 1}={[B_x^{(k){}^{″}}]}_{m^{(k)}\times (n_x^{(k)}+1)}{[P_x^{(k)}]}_{(n_x^{(k)}+1)\times 1}\end{array},$$

(35)

where ${[P_x^{(k)}]}_{(n_x^{(k)}+1)\times 1}={[\begin{array}{ccccc}{P}_{x,0}^{(k)}& P_{x,1}^{(k)}& \cdots & P_{x,n_x^{(k)}-1}^{(k)}& P_{\rho ,n_x^{(k)}}^{(k)}\end{array}]}^T$ is a column vector composed of known and unknown Bezier coefficients and $P_{x,0}^{(k)},\hspace{1em}{P}_{x,1}^{(k)},\hspace{1em}{P}_{x,2}^{(k)},\hspace{1em}{P}_{x,n_x^{(k)}-2}^{(k)},\hspace{1em}{P}_{x,n_x^{(k)}-1}^{(k)},\hspace{1em}{P}_{x,n_x^{(k)}}^{(k)}$ are determined by the boundary constraints. At the middle target point of the trajectory, the boundary condition is only the position of the target point. Considering the continuity of velocity and acceleration, $P_{x,0}^{(k)},\hspace{1em}{P}_{x,1}^{(k)},\hspace{1em}{P}_{x,2}^{(k)}$ can be determined according to

$$\left\{\begin{array}{l}{P}_{x,0}^{(k)}=P_{x,n_x^{(k-1)}}^{(k-1)}\\ P_{x,1}^{(k)}=\left(1+\frac{\Delta T^{(k)}}{\Delta T^{(k-1)}}\right)P_{x,n_x^{(k-1)}}^{(k-1)}-\frac{\Delta T^{(k)}}{\Delta T^{(k-1)}}{P}_{x,n_x^{(k-1)}-1}^{(k-1)}\\ P_{x,2}^{(k)}={\left(1+\frac{\Delta T^{(k)}}{\Delta T^{(k-1)}}\right)}^2{P}_{x,n_x^{(k-1)}}^{(k-1)}-2\frac{\Delta T^{(k)}}{\Delta T^{(k-1)}}\left(1+\frac{\Delta T^{(k)}}{\Delta T^{(k-1)}}\right)P_{x,n_x^{(k-1)}-1}^{(k-1)}+{\left(\frac{\Delta T^{(k)}}{\Delta T^{(k-1)}}\right)}^2{P}_{x,n_x^{(k-1)}-2}^{(k-1)}\end{array}\right.,$$

(36)

By substituting discretized points, ${[\tau ]}_{m^{(k)}\times 1}$, into the coordinate approximations and their τ-derivatives, matrices ${[B_x^{(k)}]}_{m^{(k)}\times (n_x^{(k)}+1)}$, ${[B_x^{(k){}^{\prime }}]}_{m^{(k)}\times (n_x^{(k)}+1)}$, and ${[B_x^{(k){}^{″}}]}_{m^{(k)}\times (n_x^{(k)}+1)}$ can be expressed as follows:

$$\begin{array}{c}{[B_x^{(k)}]}_{m^{(k)}\times (n_x^{(k)}+1)}=\left[\begin{array}{ccc}{B}_{x,0}^{(k)}({\tau }_1)& \cdots & B_{x,n_x^{(k)}}^{(k)}({\tau }_1)\\ ⋮& \ddots & ⋮\\ B_{x,0}^{(k)}({\tau }_{m^{(k)}})& \cdots & B_{x,n_x^{(k)}}^{(k)}({\tau }_{m^{(k)}})\end{array}\right]\\ {[B_x^{(k){}^{\prime }}]}_{m^{(k)}\times (n_x^{(k)}+1)}=\left[\begin{array}{ccc}{B}_{x,0}^{(k){}^{\prime }}({\tau }_1)& \cdots & B_{x,n_x^{(k)}}^{(k){}^{\prime }}({\tau }_1)\\ ⋮& \ddots & ⋮\\ B_{x,0}^{(k){}^{\prime }}({\tau }_{m^{(k)}})& \cdots & B_{x,n_x^{(k)}}^{(k){}^{\prime }}({\tau }_{m^{(k)}})\end{array}\right]\\ {[B_x^{(k){}^{″}}]}_{m^{(k)}\times (n_x^{(k)}+1)}=\left[\begin{array}{ccc}{B}_{x,0}^{(k){}^{″}}({\tau }_1)& \cdots & B_{x,n_x^{(k)}}^{(k){}^{″}}({\tau }_1)\\ ⋮& \ddots & ⋮\\ B_{x,0}^{(k){}^{″}}({\tau }_{m^{(k)}})& \cdots & B_{x,n_x^{(k)}}^{(k){}^{″}}({\tau }_{m^{(k)}})\end{array}\right]\end{array},$$

(37)

It is worth noting that when the number of discretized points, $m^{(k)}$, and the order of the Bezier curve, $n_x^{(k)}$, are determined, ${[B_x^{(k)}]}_{m^{(k)}\times (n_x^{(k)}+1)}$, ${[B_x^{(k){}^{\prime }}]}_{m^{(k)}\times (n_x^{(k)}+1)}$, and ${[B_x^{(k){}^{\prime }}]}_{m^{(k)}\times (n_x^{(k)}+1)}$ will be determined and become constant matrices. Thus, without the need for repeating calculation of the basis function matrices, the computational efficiency of the trajectory optimization greatly improves.

By using the six-degree-of-freedom coordinates in matrix form and their first and second $\tau$-derivatives, the voltages of the six groups of plasma thrusters can be expressed in the form of the following discretization matrix:

$$\begin{array}{r}{[U_i^{(k)}]}_{m^{(k)}\times 1}=U_i^{(k)}\left(\begin{array}{l}{[x^{(k)}]}_{m^{(k)}\times 1},{[y^{(k)}]}_{m^{(k)}\times 1},{[z^{(k)}]}_{m^{(k)}\times 1},{[{\vartheta }^{(k)}]}_{m^{(k)}\times 1},{[{\psi }^{(k)}]}_{m^{(k)}\times 1},{[{\gamma }^{(k)}]}_{m^{(k)}\times 1},\\ {[x^{(k){}^{\prime }}]}_{m^{(k)}\times 1},{[y^{(k){}^{\prime }}]}_{m^{(k)}\times 1},{[z^{(k){}^{\prime }}]}_{m^{(k)}\times 1},{[{\vartheta }^{(k){}^{\prime }}]}_{m^{(k)}\times 1}{[{\psi }^{(k){}^{\prime }}]}_{m^{(k)}\times 1},{[{\gamma }^{(k){}^{\prime }}]}_{m^{(k)}\times 1},\\ {[x^{(k){}^{″}}]}_{m^{(k)}\times 1},{[y^{(k){}^{″}}]}_{m^{(k)}\times 1},{[z^{(k){}^{″}}]}_{m^{(k)}\times 1},{[{\vartheta }^{(k){}^{″}}]}_{m^{(k)}\times 1},{[{\psi }^{(k){}^{″}}]}_{m^{(k)}\times 1},{[{\gamma }^{(k){}^{″}}]}_{m^{(k)}\times 1}\end{array}\right),\\ (i=1,2,3,4,5,6)\end{array},$$

(38)

When the EAD thruster is working, the voltage, $U$, must be greater than the corona voltage, $U_0$. However, if the voltage is higher than the breakdown voltage, spark discharge will occur and the thruster will fail. Thus, the voltage of the thruster needs to satisfy the constraint $U_0\le U_i\le U_{\max },(i=1,2,3,4,5,6)$. It is assumed that the drag coefficient, $C_X$, and lift coefficient, $C_Y$, remain unchanged during the flight of the EAD-UAV, so the angle of attack and sideslip angle are limited to a relatively small range, between $\alpha \in [-1^{\circ },1^{\circ }]$ and $\beta \in [-1^{\circ },1^{\circ }]$. Combined with the objective function shown in Equation (22), the N-segment trajectory optimization problem can be converted into a nonlinear programming problem (NLP) expressed as:

$$\begin{array}{l}\underset{[X_x^{(k)}],[X_y^{(k)}],[X_z^{(k)}],[X_{\vartheta }^{(k)}],[X_{\psi }^{(k)}],[X_{\gamma }^{(k)}],\Delta T^{(k)}}{\min }\hspace{1em}{\displaystyle \sum _{k=1}^N\Delta T^{(k)}}\\ \begin{array}{cc}\mathrm{s}.\mathrm{t}.& \hspace{1em}\hspace{1em}{U}_0\le U_i\le U_{\max },(i=1,2,3,4,5,6)\\ & \begin{array}{c}{\alpha }_{\min }\le \alpha \le {\alpha }_{\max }\\ {\beta }_{\min }\le \beta \le {\beta }_{\max }\end{array}\end{array}\end{array},$$

(39)

where $[X_x^{(k)}],[X_y^{(k)}],[X_z^{(k)}],[X_{\vartheta }^{(k)}],[X_{\psi }^{(k)}],[X_{\gamma }^{(k)}]$ are the unknown parts of the Bezier coefficients $\left[P_x^{(k)}\right],\hspace{1em}\left[P_y^{(k)}\right],\hspace{1em}\left[P_z^{(k)}\right],\left[P_{\vartheta }^{(k)}\right],\hspace{1em}\left[P_{\psi }^{(k)}\right],\hspace{1em}\left[P_{\gamma }^{(k)}\right]$, which need to be optimized to satisfy the dynamic constraints and obtain the optimal parameters.

The NLP whose optimization objective is minimum energy consumption can be expressed as:

$$\begin{array}{l}\underset{[X_x^{(k)}],[X_y^{(k)}],[X_z^{(k)}],[X_{\vartheta }^{(k)}],[X_{\psi }^{(k)}],[X_{\gamma }^{(k)}],\Delta T^{(k)}}{\min }\hspace{1em}{\displaystyle \sum _{k=1}^N{\displaystyle \sum _{j=1}^{m-1}{\displaystyle \sum _{i=1}^6{U}_i(j)I_i}}(j)\Delta T^{(k)}(j)}\\ \begin{array}{cc}\mathrm{s}.\mathrm{t}.& \begin{array}{cc}& \end{array}\hspace{1em}{U}_0\le U_i\le U_{\max },(i=1,2,3,4,5,6)\\ & \begin{array}{c}{\alpha }_{\min }\le \alpha \le {\alpha }_{\max }\\ {\beta }_{\min }\le \beta \le {\beta }_{\max }\end{array}\end{array}\end{array}$$

(40)

4. Numerical Results

An EAD-UAV was applied in two flight scenarios in this study: single- and multi-target continuous optimal flight control. The position and attitude parameters of the EAD-UAV at the starting and target points are given in Table A2 and Table A3. In the single-target optimal flight scenario, two numerical simulations for time–optimal trajectory optimization were conducted and the optimized results achieved by the BSA were used as feasible initial value estimations of the Gaussian pseudospectral method (GPM). The BSA is cited from [49] and the GPM is cited from [50]. Optimization for optimal trajectory of energy consumption was conducted using BSA, the results were compared with those obtained in time–optimal trajectory optimization. In the multi-target optimal flight control scenario, to demonstrate the practicability of the IBSA, a series of numerical simulations were conducted, and the results were compared with those obtained using the traditional BSA, which converts the optimization problem of multi-target EAD-UAV flight trajectory into multiple independently solved NLP problems. In the trajectory optimization problems using the IBSA and BSA, the Bezier orders and the number of LG points were chosen as $n_x^{(k)}=n_y^{(k)}=n_z^{(k)}=n_{\vartheta }^{(k)}=n_{\psi }^{(k)}=n_{\gamma }^{(k)}=6$ and $m^{(k)}=50$. The interior-point method was employed to solve the converted NLP problem because of the absence of equality constraints. In the trajectory optimization problems using the GPM, the SQP algorithm was applied to solve the NLP problem, and the numbers of LG points were chosen to be 70. The interior-point method and the SQP algorithm were implemented by using the fmincon MATLAB function. All numerical simulations were performed on a Ryzen R7-5800H CPU 3.5 GHz with Windows 11 and run on MATLAB R2020a.

4.1. Single-Target Optimal Flight Control

To verify the practicability of the EAD-UAV, we conducted two numerical simulations for the time optimal single-target flight control of the BSA and GPM under different maximum voltages, U_max. Optimal single-target trajectories of the EAD-UAV with U_max = 80 kV were designed by the BSA and GPM and are shown in Figure 6. The mass of the EAD-UAV was 2.6 kg, and when U₀ = 7.7 kV and U_max = 80 kV, the maximum thrust of each EAD thruster, F_max, was 14.4184 N. Except for the boundary constraints between the start and target, there were no constraints on the speed and attitude of the EAD-UAV, only on the U_max of the EAD thruster. It can be seen from Figure 7 that the attitude angles of the EAD-UAV are within reasonable ranges during flight. As can be seen from Figure 8, the angle of attack and sideslip angle of the EAD-UAV are within the limited range, which satisfies the assumption that the lift coefficient and drag coefficient are constant. Figure 9 and Figure 10 reveal that the thrust of the EAD thruster always satisfies the maximum voltage constraint during flight, indicating that the dynamic model of the EAD-UAV is reasonable and that the BSA can fully satisfy the dynamic constraints. It can be seen from Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 that the BSA and GPM optimization results are very similar. The flight time of the optimal trajectory based on the BSA is 192.5029 s, and the calculation time is 0.7824 s. Meanwhile, the flight time of the optimal trajectory obtained through GPM is 189.8874 s, and the calculation time is 49.3636 s. The difference between the BSA and GPM results is 1.38%, and the calculation time of the BSA is only 1.58% of that of GPM. Thus, the BSA has considerable advantages in trajectory planning. In the figures, the +/− of U and F represent the thrust direction, + indicates that the EAD thruster generates the right or upward thrust, and − indicates the opposite meaning.

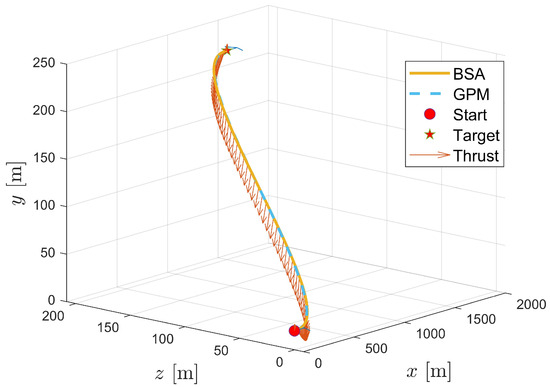
Figure 6. Optimal single-target trajectory of an EAD-UAV for J = J_T with U_max = 80 kV.

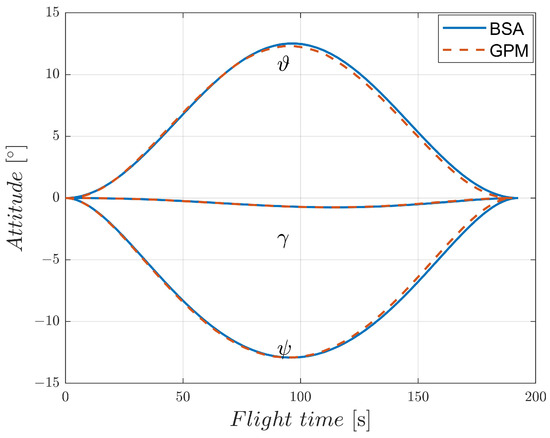
Figure 7. Attitude of the EAD-UAV in the single-target optimal trajectory for J = J_T with U_max = 80 kV.

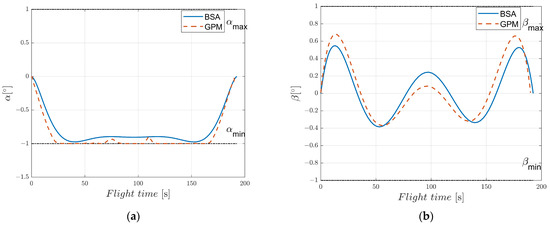
Figure 8. Angle of attack and sideslip angle of EAD-UAV in the single-target optimal trajectory for J = J_T with U_max = 80 kV. (a) Angle of attack, (b) sideslip angle.

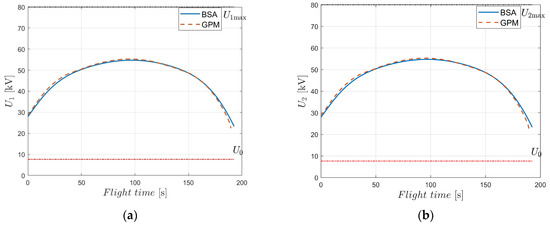
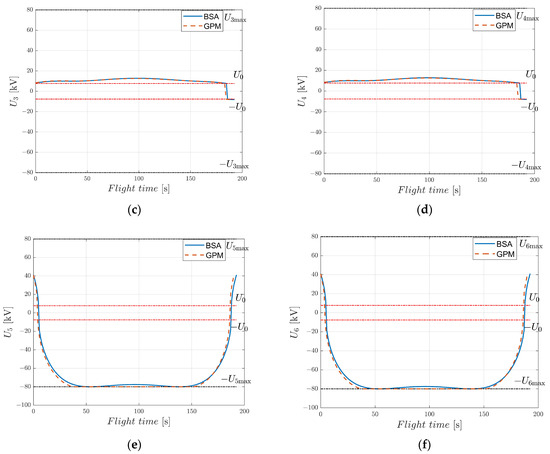
Figure 9. Voltages of EAD-UAV thrusters with single-target optimal trajectories for J = J_T obtained using U_max = 80 kV. (a) Voltage of thruster 1, (b) voltage of thruster 2, (c) voltage of thruster 3, (d) voltage of thruster 4, (e) voltage of thruster 5, (f) voltage of thruster 6.

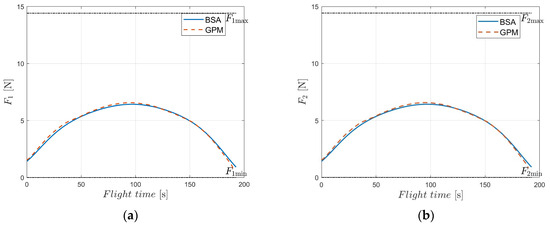
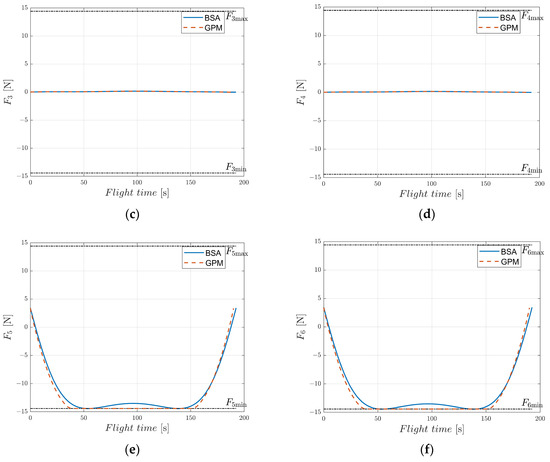
Figure 10. Thrusts of EAD-UAV thrusters with single-target optimal trajectories for J = J_T obtained using U_max = 80 kV. (a) Thrust of thruster 1, (b) thrust of thruster 2, (c) thrust of thruster 3, (d) thrust of thruster 4, (e) thrust of thruster 5, (f) thrust of thruster 6.

Table A4 presents the flight times obtained from the numerical simulations of the trajectory optimization using the BSA and GPM when U_max was in the range of [50:2:80] kV. With increasing U_max, the flight time decreases. A larger U_max makes the EAD-UAV have a higher flight speed and greater maneuverability. This result is in agreement with the expectations. When the voltage is higher than 50 kV and the thrust is higher than 5.2735 N, the simulation can converge to get the optimal trajectory. This level of thrust is similar to that in [9], and we can optimize the EAD thruster to reach this level, which shows that it is feasible to use BSA to optimize the trajectory of an EAD-UAV. The average deviation between the flight times of the optimal trajectories obtained by the BSA and GPM is 1.14%, and the average calculation time of the BSA is only 1.95% of that of GPM, which shows that the BSA has obvious advantages in terms of calculation efficiency and that the calculation accuracy is not much different from that of GPM.

To verify the battery performance requirements of EAD-UAV, we conducted a numerical simulation to optimize the trajectory under different voltages for the optimal energy consumption using BSA. Optimal single-target trajectories of the EAD-UAV with U_max = 60 kV and U_max = 80 kV designed by the BSA are shown in Figure 11. It can be seen from Figure 12 that the attitude angles of the EAD-UAV are within reasonable ranges during flight. As can be seen from Figure 13, the angle of attack and sideslip angle of the EAD-UAV are within the limited range. Figure 14 and Figure 15 reveal that the thrust of the EAD thruster always satisfies the maximum voltage constraint during flight. The maximum thrust during flight is only 4.2 N, which is similar to that in [9]. This level of thrust is expected to be achieved by improving the EAD thruster. It can be seen from Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 that the trajectory and other indexes under different voltages are very close, indicating that the voltage required for flight under the optimal energy consumption is relatively low. As shown in Table A5, the flight time, energy consumption, and average power of the flight trajectory with the optimal energy consumption were basically the same when U_max was in the range of [60:2:80], indicating that applied voltage was much lower than U_max to reduce energy consumption, leading to relatively lower battery performance requirements. The UAV power in [9] is 600 W, and the average power of the EAD-UAV under the optimal energy consumption is 1.4 kW. Considering that the EAD-UAV has more thrusters, the higher power is reasonable. Battery performance can be optimized based on the UAV in [9] to achieve this level of power. In the case of optimal time, the thrusters tend to increase the power as much as possible to reduce the flight time. The average power was 4~8 times that in the case of the optimal energy consumption, reducing the flight time by 18–28%. When U_max was in the range of [60:2:80], the average power reached 5~11 kW, which is very demanding for the battery, meaning it may be difficult to find a qualified power supply. The energy consumption taking minimum energy consumption as the optimization objective is 106.6640 W·h, much less than that in the case of optimal time, which can be used as a reference for the selection of battery capacities of EAD-UAVs in the design of power supply systems. The energy consumption taking time as the optimization objective is 323.9982~589.3262 W·h, which is 3~5.5 times that in the case of the optimal energy consumption. Although higher energy consumption can achieve rapid transfer between targets, larger energy consumption requires greater battery capacity. This will lead to greater battery weight, which will pose a greater challenge to the design of the EAD-UAV, considering its low thrust. Therefore, balancing the energy consumption and flight time is very important when optimizing the flight trajectory of EAD-UAVs.

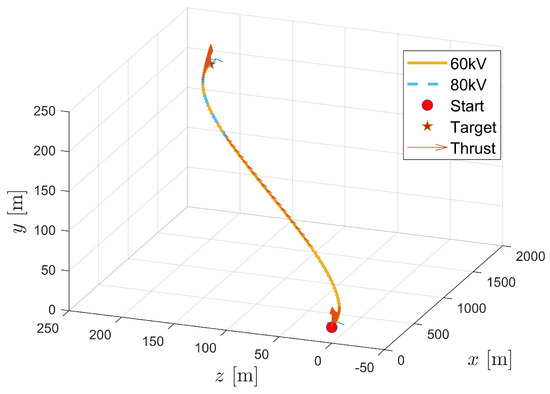
Figure 11. Optimal single-target trajectory of an EAD-UAV for J = J_Energy with U_max = 60 kV and U_max = 80 kV.

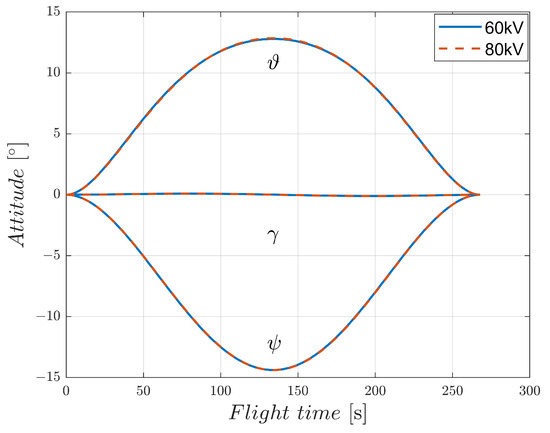
Figure 12. Attitude of the EAD-UAV in the single-target optimal trajectory for J = J_Energy with U_max = 60 kV and U_max = 80 kV.

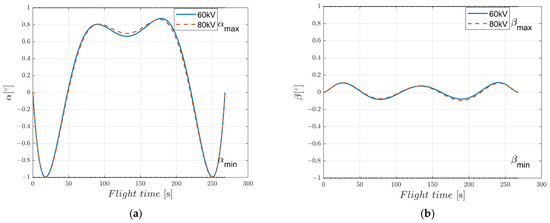
Figure 13. Angle of attack and sideslip angle of EAD-UAV in the single-target optimal trajectory for J = J_Energy with U_max = 60 kV and U_max = 80 kV. (a) Angle of attack, (b) sideslip angle.

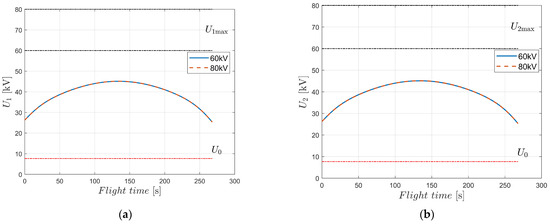
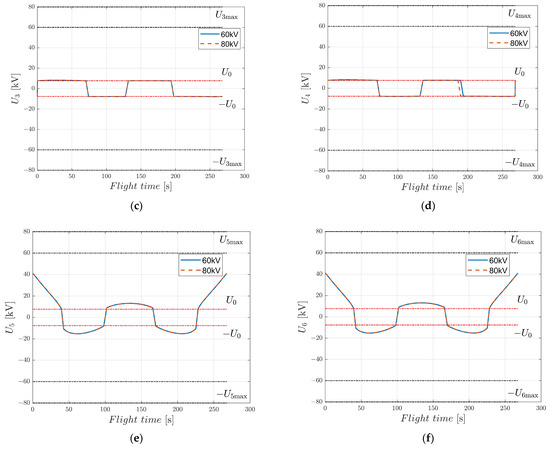
Figure 14. Voltages of EAD-UAV thrusters with single-target optimal trajectories for J = J_Energy obtained using U_max = 60 kV and U_max = 80 kV. (a) Voltage of thruster 1, (b) voltage of thruster 2, (c) voltage of thruster 3, (d) voltage of thruster 4, (e) voltage of thruster 5, (f) voltage of thruster 6.

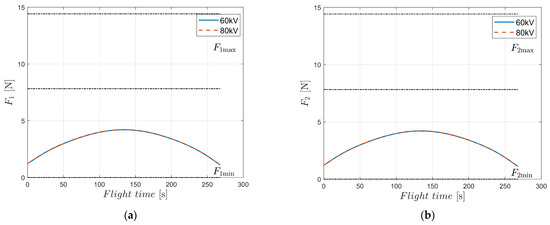
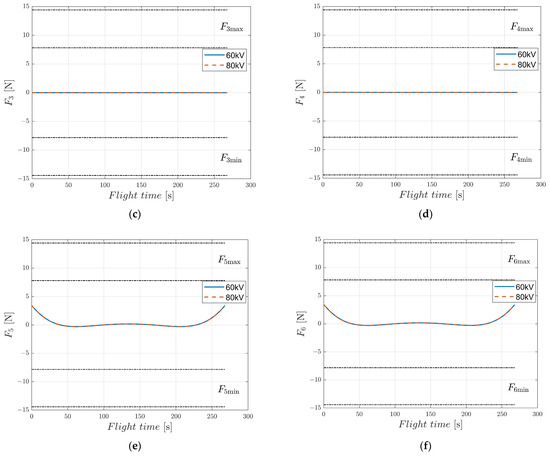
Figure 15. Thrusts of EAD-UAV thrusters with single-target optimal trajectories for J = J_Energy obtained using U_max = 60 kV and U_max = 80 kV. (a) Thrust of thruster 1, (b) thrust of thruster 2, (c) thrust of thruster 3, (d) thrust of thruster 4, (e) thrust of thruster 5, (f) thrust of thruster 6.

4.2. Multi-Target Continuous Optimal Flight Control

To demonstrate the feasibility of the EAD-UAV and computational efficiency of the IBSA in multi-target continuous flight trajectory optimization, we analyzed the continuous trajectory optimization problem involving an EAD-UAV passing through three targets from the start. The IBSA and BSA were used for trajectory optimization. The acceleration continuity problem at the target point of the IBSA was taken as the constraint in the overall trajectory planning. The BSA performed subsection optimization of the three-stage trajectory and added the acceleration continuity constraint at the trajectory connection. The optimal flight path obtained using the IBSA when the maximum voltage of the EAD thruster was 80 kV is shown in Figure 16. There is a smooth transition at the connection of the three-segment trajectory, and the flight trajectory is a smooth curve. It can be seen from Figure 17 and Figure 18 that the velocity and acceleration of the EAD-UAV are continuous, indicating that the IBSA satisfies the constraints of the second-order continuity of the flight trajectory. It can be seen from Figure 19 that the attitude angles of the EAD-UAV obtained using IBSA are also continuous and within a reasonable range. As can be seen from Figure 20, the angle of attack and sideslip angle of the EAD-UAV are within the limited range. It can be seen from Figure 21 and Figure 22 that the flight trajectory obtained by IBSA optimization also satisfies the EAD thruster voltage and thrust constraints. The flight path determined by trajectory optimization using the IBSA is a second-order continuous curve; the flight time from the start to target 1 is 62.8919 s, that from target 1 to target 2 is 60.1779 s, and that from target 2 to target 3 is 62.7654 s; the calculation time of the optimization process is 6.3757 s.

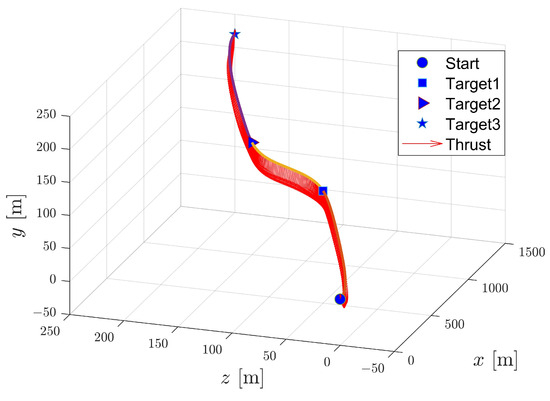
Figure 16. Thrusts of EAD-UAV thrusters with multi-target optimal trajectory obtained using U_max = 80 kV.

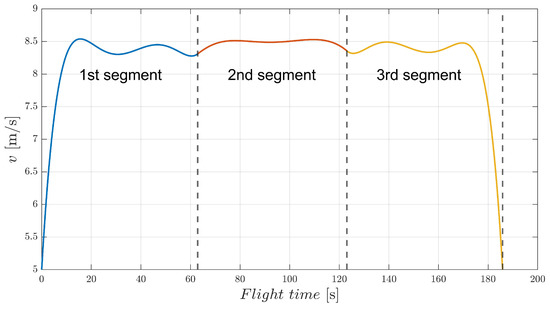
Figure 17. Velocity of an EAD-UAV with the multi-target optimal trajectory obtained using U_max = 80 kV.

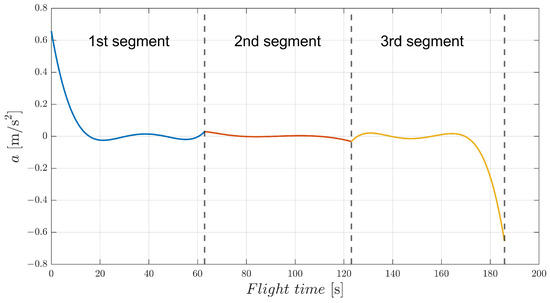
Figure 18. Acceleration of an EAD-UAV with the multi-target optimal trajectory obtained using U_max = 80 kV.

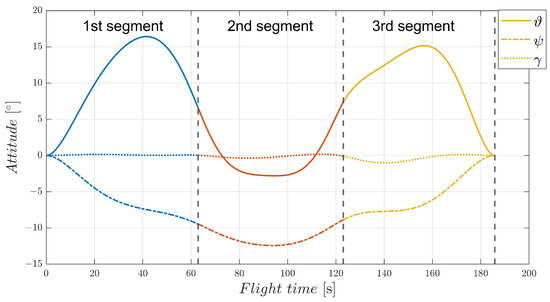
Figure 19. Attitude of an EAD-UAV with the multi-target optimal trajectory obtained using U_max = 80 kV.

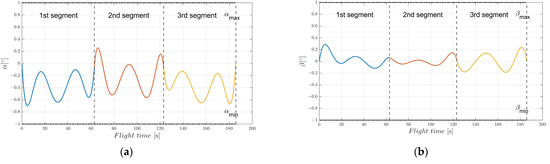
Figure 20. Angle of attack and sideslip angle of EAD-UAV in the multi-target optimal trajectory with U_max = 80 kV. (a) Angle of attack, (b) sideslip angle.

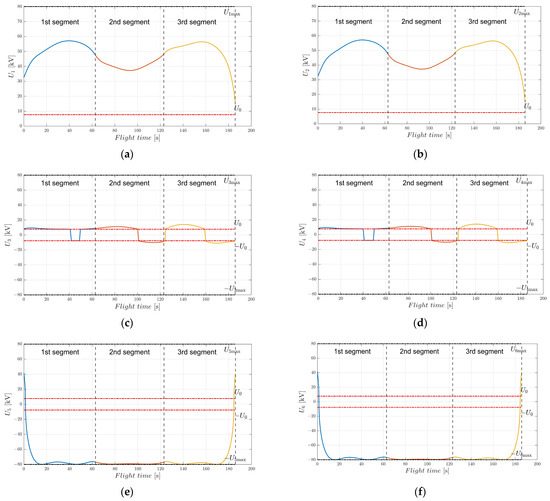
Figure 21. Voltages of EAD-UAV thrusters with multi-target optimal trajectory obtained using U_max = 80 kV. (a) Voltage of thruster 1, (b) voltage of thruster 2, (c) voltage of thruster 3, (d) voltage of thruster 4, (e) voltage of thruster 5, (f) voltage of thruster 6.

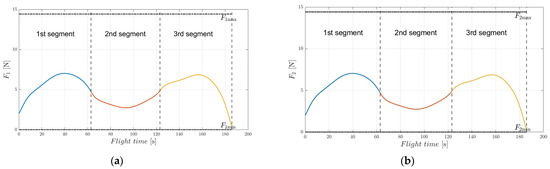
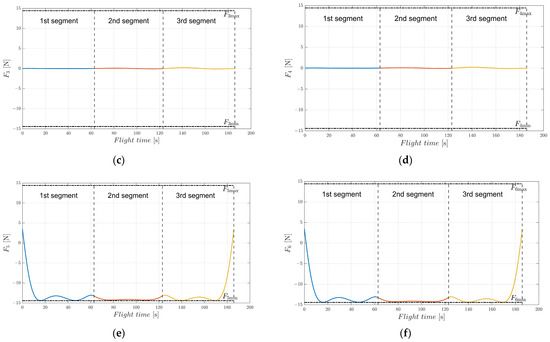
Figure 22. Thrusts of EAD-UAV thrusters for multi-target optimal trajectory with U_max = 80 kV. (a) Thrust of thruster 1, (b) thrust of thruster 2, (c) thrust of thruster 3, (d) thrust of thruster 4, (e) thrust of thruster 5, (f) thrust of thruster 6.

Table A6 lists the flight times resulting from the mathematical simulation of the IBSA and BSA trajectory planning when U_max = [50:2:80] kV. The IBSA results are convergent within this range, which shows that the flight trajectory can be controlled by adjusting only the EAD-UAV voltage. With increasing U_max, the flight time decreases. A larger U_max makes the EAD-UAV have a higher flight speed and greater maneuverability. This result is in agreement with the expectations. The simulation using IBSA can converge to obtain the optimal trajectory with a U_max higher than 50 kV and a thrust limit higher than 5.2735 N. This indicates that the trajectory optimization of the EAD-UAV using IBSA can be realized with a thrust level similar to that in [9], which shows the feasibility of IBSA. As the BSA does not consider the subsequent optimization process when optimizing the trajectory of the current segment, it will leave a relatively poor initial value for the subsequent trajectory optimization problem, and the dynamic model of the EAD-UAV is relatively complex. Therefore, when using the BSA for trajectory optimization, only the first segment or first two segments of the three-segment flight trajectory converge, and the third segment flight trajectory diverges.

5. Conclusions

This paper presented the configuration of an EAD-UAV and the derivation of its attitude–path coupling dynamic equation. Based on this dynamic equation, the BSA method was used to optimize the three-dimensional flight trajectory between two points, and an IBSA algorithm was proposed to deal with the optimization of the multi-target flight trajectory rapidly when concerning the continuity of acceleration. The relationships among the boundary constraints, intermediate constraints, and Bezier basis function coefficients were deduced, and the continuous multi-target trajectory optimization problem was transformed into a single NLP problem that naturally satisfied the boundary condition and intermediate constraints. For the BSA used in the single-target scenario and IBSA, the simulation can converge with a U_max higher than 50 kV and a thrust limit higher than 5.2735 N. This level of thrust is similar to that in [9], and we can optimize the EAD thruster to reach this level, which indicates the feasibility of the BSA in single-target scenarios and IBSA for trajectory optimization of the EAD-UAV. The simulation showed that using the BSA to optimize the 3D trajectory of an EAD-UAV yielded results 1.14% different from the optimized performance index of GPM and a calculation time that was only 1.95% of that of GPM. Using the minimum energy consumption as the optimization goal, the average power was 1.4 kW, which is achievable. In the case of optimal time, the average power was four to eight times that in the case of the optimal energy consumption, leading to very high requirements for the battery. Therefore, balancing the energy consumption and flight time is very important when optimizing the flight trajectory of an EAD-UAV. Hence, the IBSA can overcome the poor convergence issue of the BSA under the continuous acceleration constraint for multi-target flight trajectories. For the EAD-UAV with the coupled dynamics, the IBSA can rapidly produce 3D trajectory optimization results.