Robust Constrained Multi-Objective Guidance of Supersonic Transport Landing Using Evolutionary Algorithm and Polynomial Chaos
Abstract
:1. Introduction
2. Robust Constrained Multi-Objective Trajectory Optimization
2.1. Problem Formulation
2.2. Reformulation to a Deterministic Problem
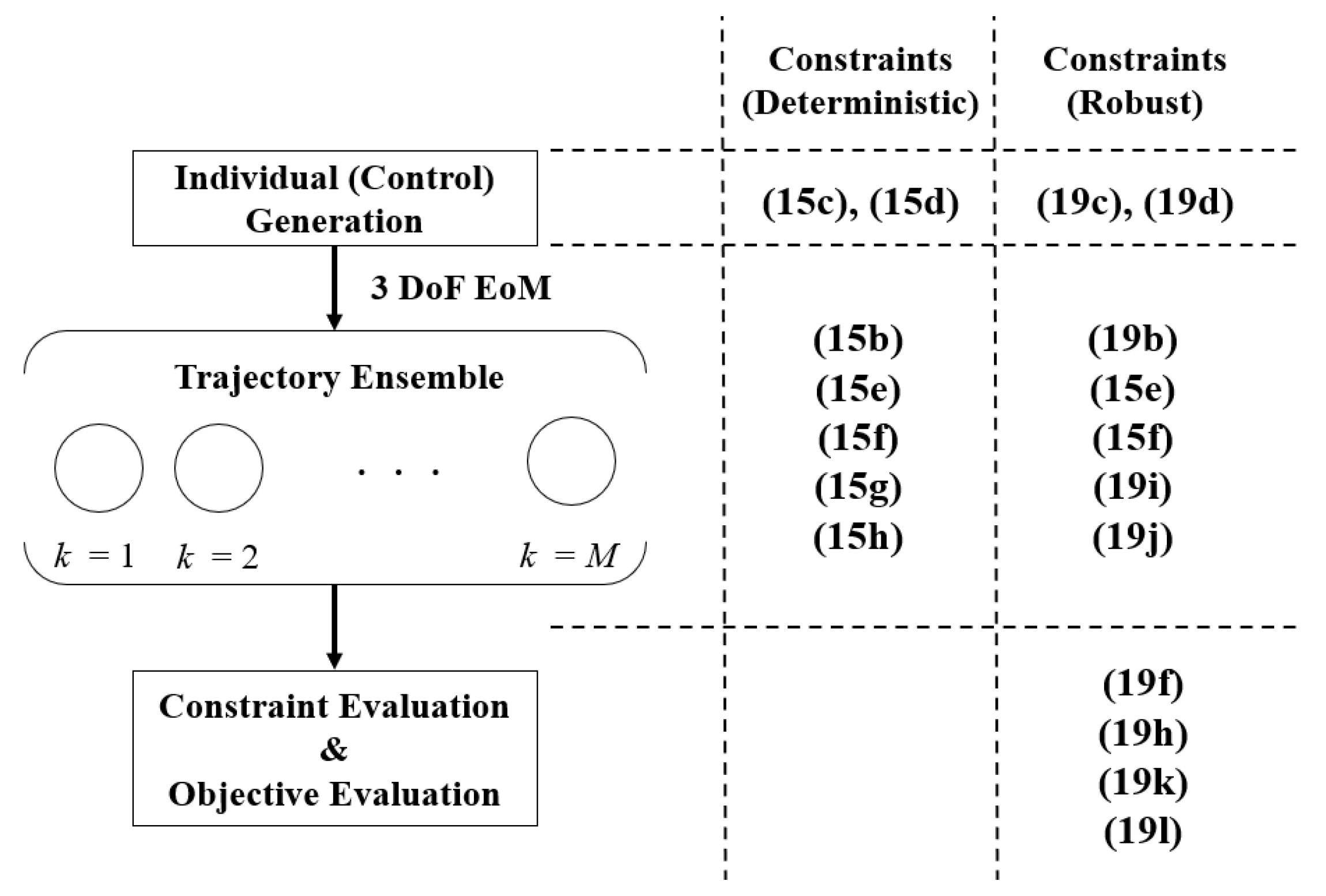
2.3. Global Optimization Method: Integration into the Constrained MOEA
3. SST Landing Trajectory Optimization
3.1. Deterministic Formulation
3.2. Robust Formulation with Wind Uncertainty
3.3. Implementation
4. Results and Analysis
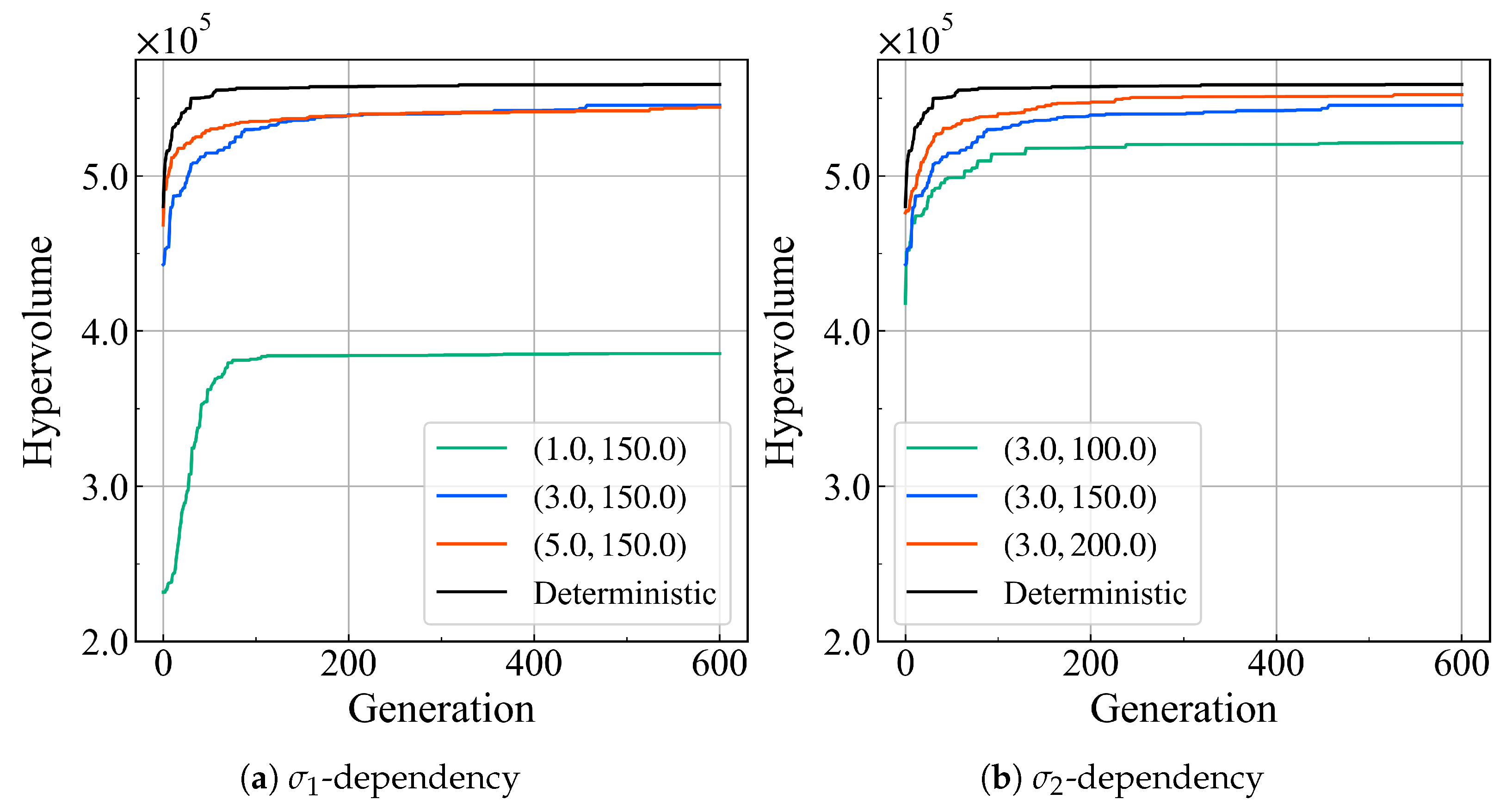
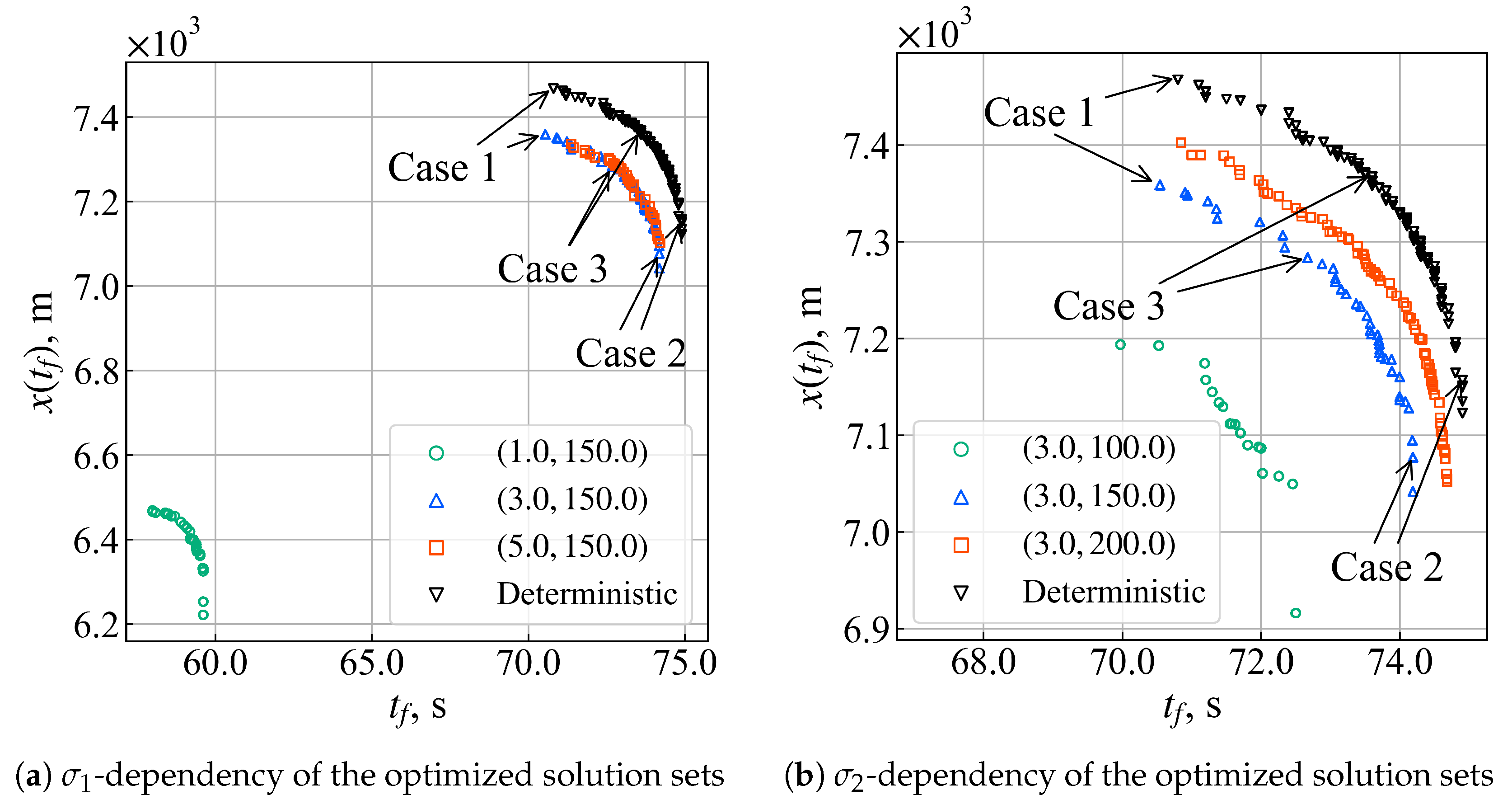
4.1. Non-Inferior Solutions Sets
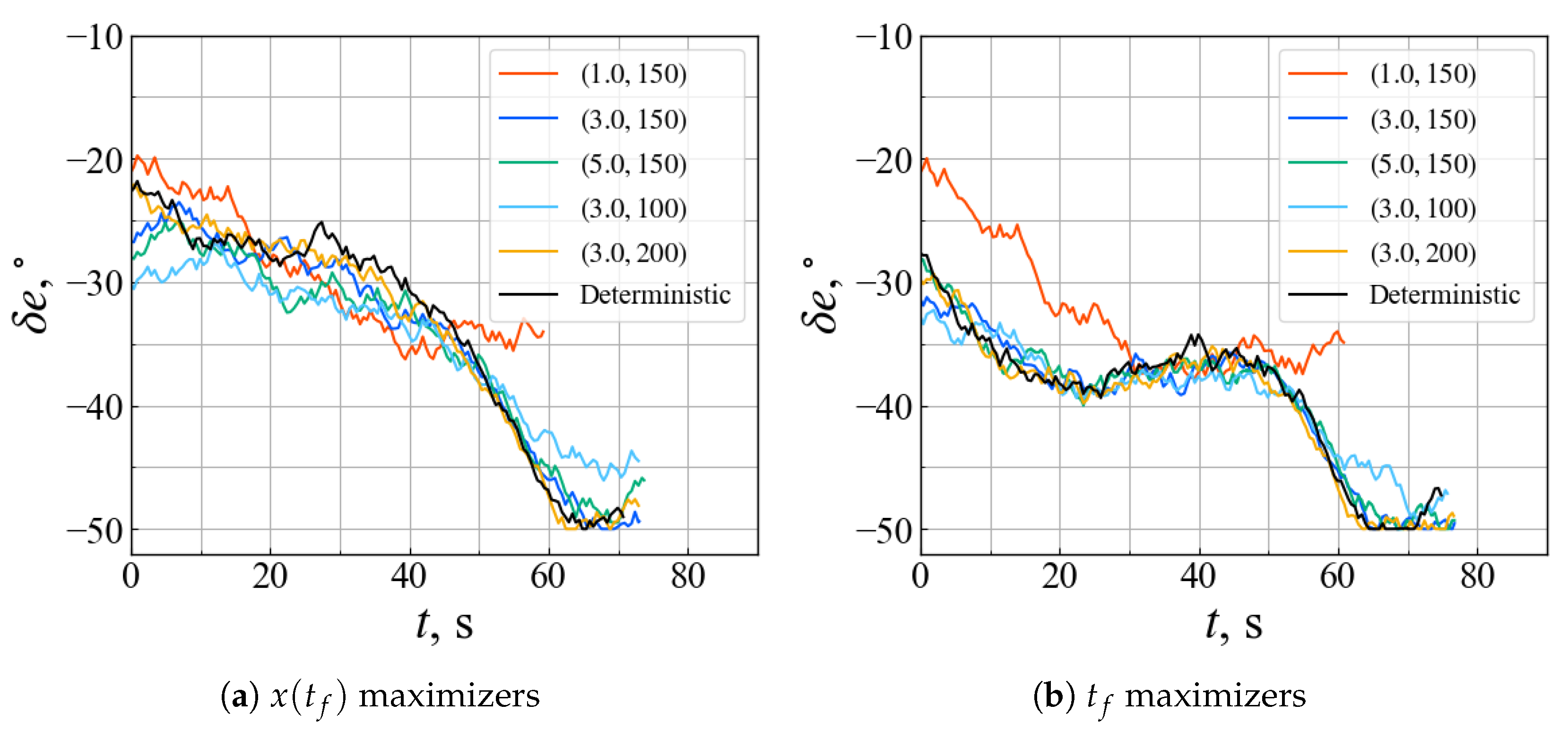
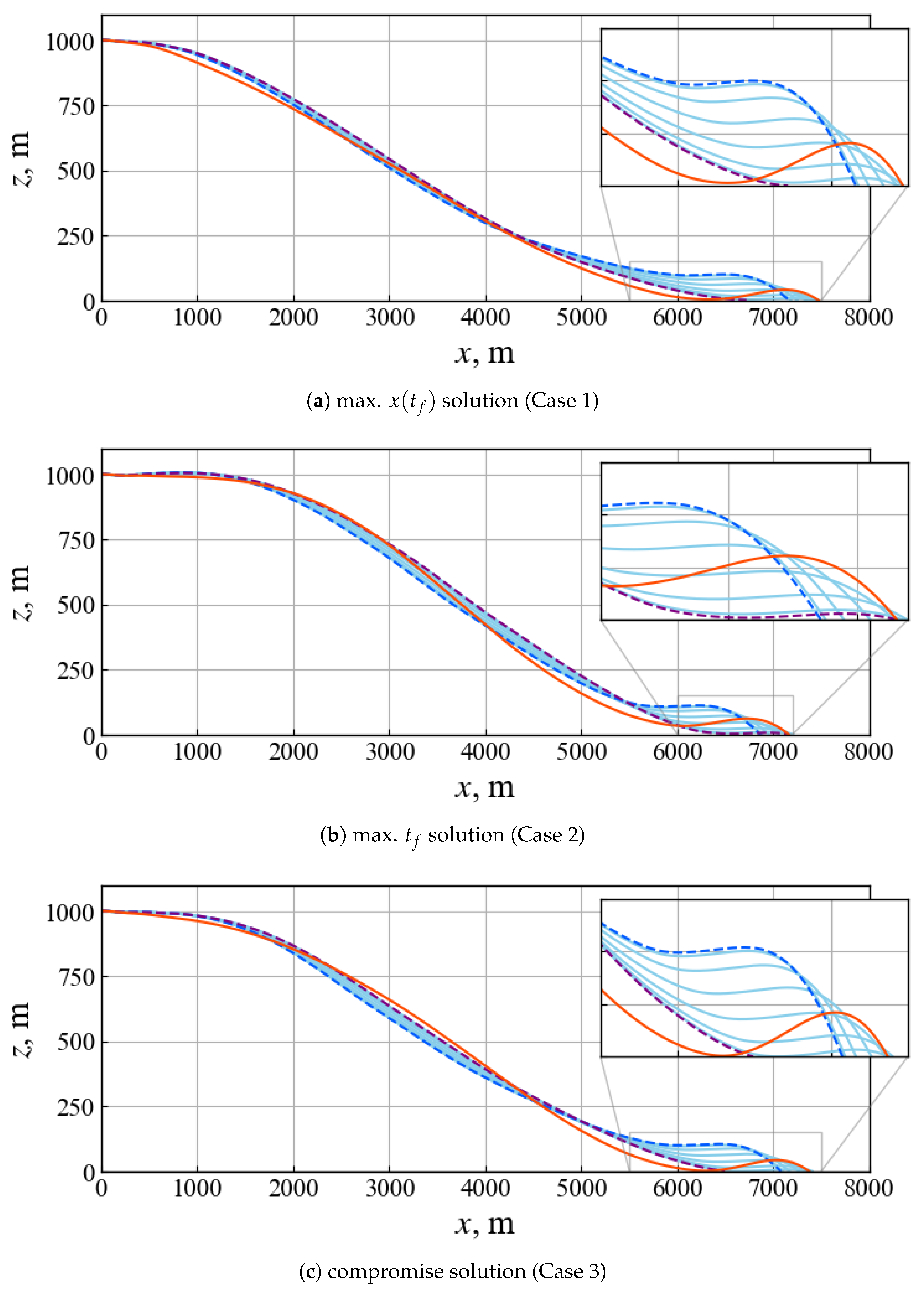
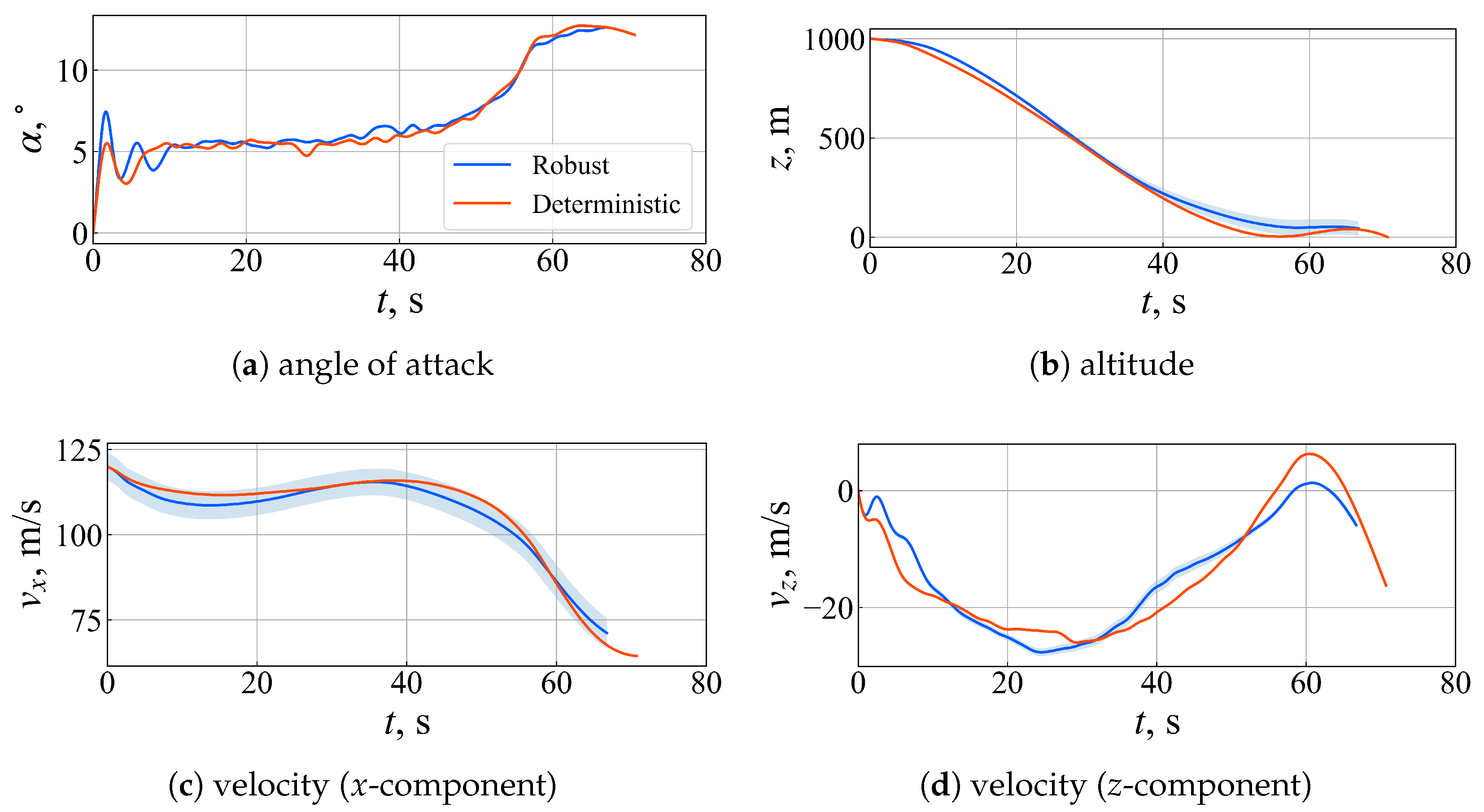
4.2. Comparisons of Representative Trajectories from Non-Inferior Solutions Set
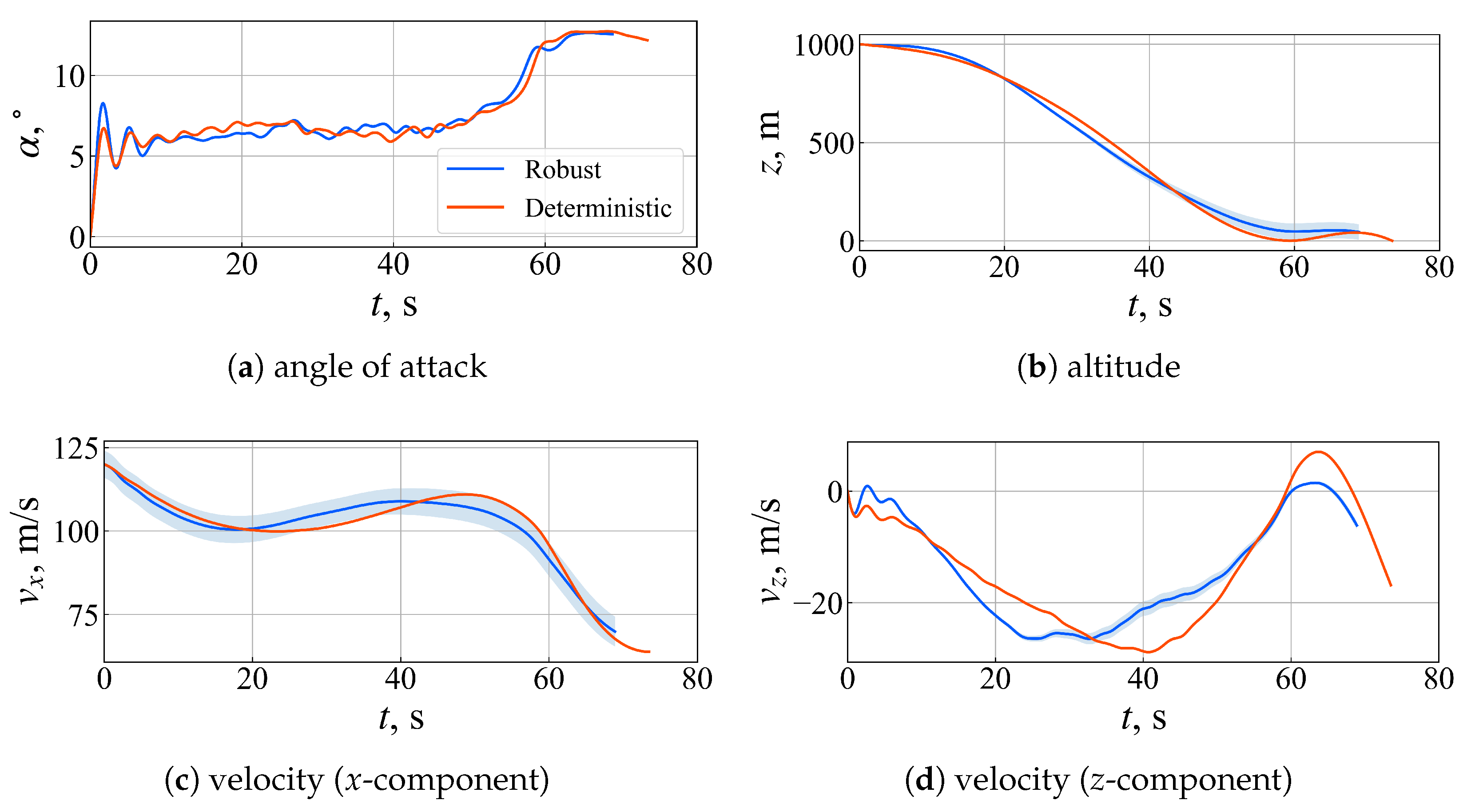
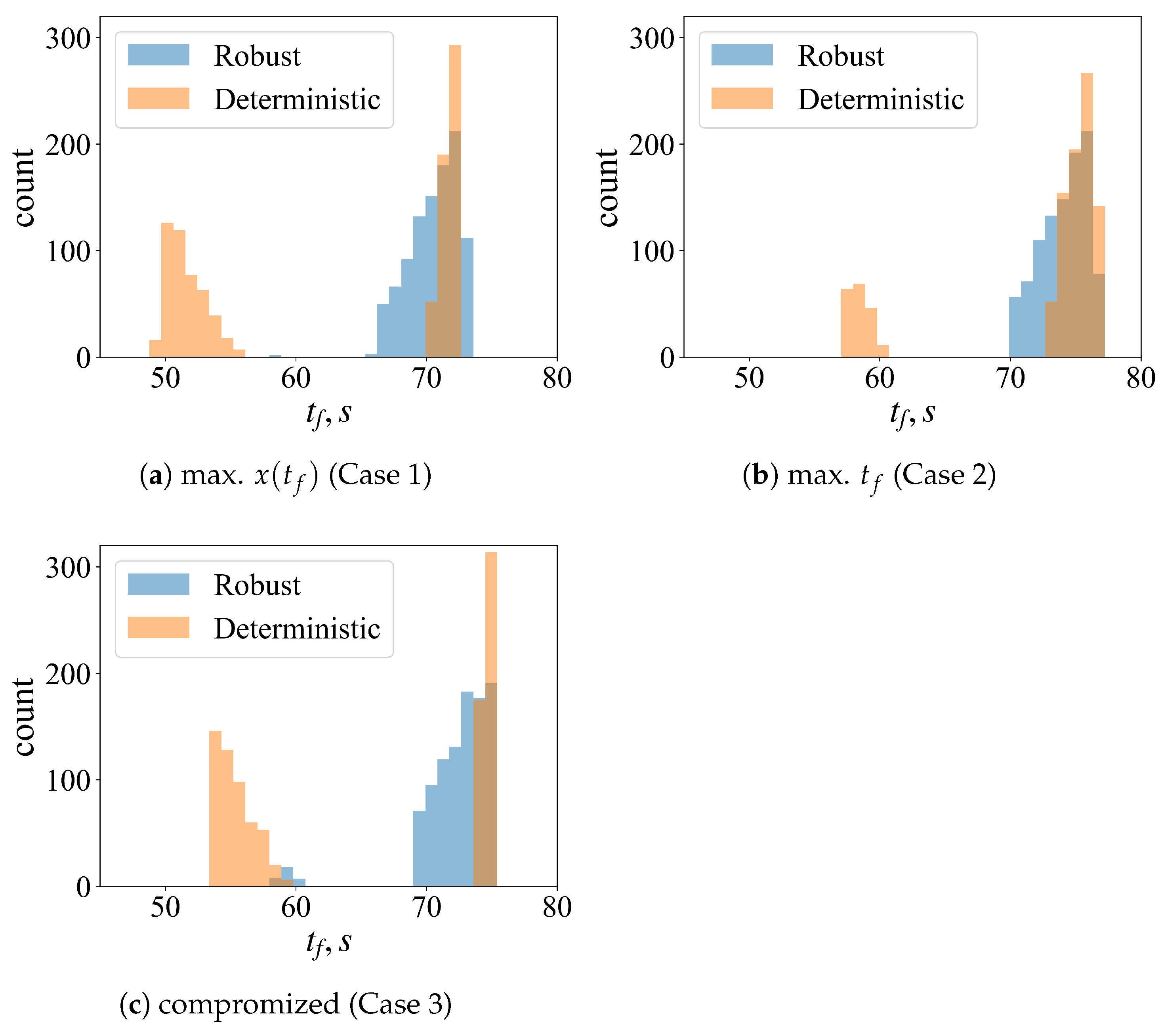
4.3. Validation of the Robust Control Law
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| speed of sound | |
| CDO | continuous descent operation |
| EoM | equations of motion |
| dynamics | |
| inequality constraint | |
| g | gravitational acceleration |
| equality constraint function | |
| moment of inertia (around y-axis) | |
| objective function | |
| l | number of quadrature points |
| mean aerodynamic chord length | |
| M | number of sampled trajectories for an ensemble |
| m | aircraft mass |
| Mach number | |
| MC | Monte-Carlo (simulation) |
| MOEA | multi-objective evolutionary algorithm |
| N | number of objective functions |
| NLP | nonlinear programming |
| ODE | Ordinary differential equation |
| p | approximation order of polynomial chaos expansion |
| PCE | Polynomial chaos expansion |
| q | number of uncertain parameters |
| reference surface area | |
| SST | supersonic transport |
| pitching torque | |
| t | time |
| control variables | |
| v | velocity |
| w | weight function |
| X | aerodynamics force (x-component) |
| state variables | |
| x | flight range |
| Z | aerodynamic force (z-component) |
| z | alight altitude |
| angle of attack | |
| Kronecker’s delta | |
| elevator deflection angle | |
| flight angle | |
| mean | |
| variance | |
| orthogonal basis function | |
| probabilistic parameters | |
| probability density function | |
| atmospheric density | |
| angular velocity |
References
- Ericsson, L.E. Pitch rate effects on delta wing vortex breakdown. J. Aircr. 1996, 33, 639–642. [Google Scholar] [CrossRef]
- Razak, K.; Snyder, M., Jr. A Review of the Planform Effects on the Low-Speed Aerodynamic Characteristics of Triangular and Modified Triangular Wings; Technical Report; NASA: Cleveland, OH, USA, 1966. [Google Scholar]
- Pourtakdoust, S.H.; Kiani, M.; Hassanpour, A. Optimal trajectory planning for flight through microburst wind shears. Aerosp. Sci. Technol. 2011, 15, 567–576. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Lygeros, J. Sequential Monte Carlo methods for multi-aircraft trajectory prediction in air traffic management. Int. J. Adapt. Control Signal Process. 2010, 24, 830–849. [Google Scholar] [CrossRef]
- Lecchini Visintini, A.; Glover, W.; Lygeros, J.; Maciejowski, J. Monte Carlo Optimization for Conflict Resolution in Air Traffic Control. IEEE Trans. Intell. Transp. Syst. 2006, 7, 470–482. [Google Scholar] [CrossRef]
- Markley, F.L.; Carpenter, J.R. Generalized linear covariance analysis. J. Astronaut. Sci. 2009, 57, 233–260. [Google Scholar] [CrossRef]
- Geller, D. Linear Covariance Techniques for Orbital Rendezvous Analysis and Autonomous Onboard Mission Planning. J. Guid. Control. Dyn. 2006, 29, 1404–1414. [Google Scholar] [CrossRef]
- Saunders, B. Optimal Trajectory Design under Uncertainty. Master’s Thesis, Department of Aeronautics and Astronautics, MIT, Cambridge, MA, USA, 2012. [Google Scholar]
- Tang, G.; Luo, Y.; Li, H. Optimal robust linearized impulsive rendezvous, Aerospace Science Technology. Aerosp. Sci. Technol. 2007, 11, 314–325. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 60, 897–936. [Google Scholar] [CrossRef]
- Eldred, M.; Webster, C.; Constantine, P. Evaluation of Non-Intrusive Approaches for Wiener-Askey Generalized Polynomial Chaos. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, USA, 7–10 April 2008; AIAA: Reston, VA, USA, 2008. [Google Scholar] [CrossRef]
- Li, X.; Nair, P.; Zhang, Z.; Gao, L.; Gao, C. Aircraft Robust Trajectory Optimization Using Nonintrusive Polynomial Chaos. J. Aircr. 2014, 51, 1592–1603. [Google Scholar] [CrossRef]
- Matsuno, Y.; Tsuchiya, T.; Wei, J.; Hwang, I.; Matayoshi, N. Stochastic optimal control for aircraft conflict resolution under wind uncertainty. Neural Comput. Appl. 2015, 43, 77–88. [Google Scholar] [CrossRef]
- Fisher, J.; Bhattacharya, R. Optimal trajectory generation with probabilistic system uncertainty using polynomial chaos. J. Dyn. Syst. Meas. Control 2011, 133, 014501. [Google Scholar] [CrossRef]
- Xiong, F.; Xiong, Y.; Xue, B. Trajectory Optimization under Uncertainty based on Polynomial Chaos Expansion. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015; AIAA: Reston, VA, USA, 2015; p. 1761. [Google Scholar] [CrossRef]
- Casado, E.; Civita, M.L.; Vilaplana, M.; McGookin, E.W. Quantification of aircraft trajectory prediction uncertainty using polynomial chaos expansions. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017; pp. 1–11. [Google Scholar] [CrossRef]
- Wang, F.; Yang, S.; Xiong, F.; Lin, Q.; Song, J. Robust trajectory optimization using polynomial chaos and convex optimization. Aerosp. Sci. Technol. 2019, 92, 314–325. [Google Scholar] [CrossRef]
- Nakka, Y.K.; Chung, S. Trajectory optimization for chance-constrained nonlinear stochastic systems. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control, Nice, France, 11–13 December 2019; IEEE: New York, NY, USA, 2019; pp. 3811–3818. [Google Scholar] [CrossRef]
- Gambier, A.; Badreddin, E. Multi-objective Optimal Control: An Overview. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 170–175. [Google Scholar] [CrossRef]
- Mueller, R. Multi-Objective Optimization of an Aircraft Trajectory between Cities using an Inverse Model Approach. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4489. [Google Scholar]
- Hartjes, S.; Visser, H. Efficient trajectory parameterization for environmental optimization of departure flight paths using a genetic algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 1115–1123. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Hartjes, S.; Geijselaers, L.; Visser, H.; Curran, R. Optimization of noise abatement aircraft terminal routes using a multi-objective evolutionary algorithm based on decomposition. Transp. Res. Procedia 2018, 29, 157–168. [Google Scholar] [CrossRef]
- Kanazaki, M.; Othman, N.B. Time-series optimization methodology and knowledge discovery of descend trajectory for civil aircraft. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; IEEE: New York, NY, USA, 2016; pp. 893–900. [Google Scholar]
- Kanazaki, M.; Setoguchi, N.; Saisyo, R. Evolutionary Algorithm Applied to Time-Series Landing Flight Path and Control Optimization of Supersonic Transport. Neural Comput. Appl. 2021, 35, 1211–1223. [Google Scholar] [CrossRef]
- Marto, S.; Vasile, M. Many-Objective Robust Trajectory Optimisation Under Epistemic Uncertainty and Imprecision. Acta Astronaut. 2022, 191, 99–124. [Google Scholar] [CrossRef]
- Luo, Y.; Tang, G.; Lei, Y. Optimal Multi-Objective Linearized Impulsive Rendezvous. J. Guid. Control. Dyn. 2007, 30, 383–389. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, Z.; Li, H. Robust optimization of nonlinear impulsive rendezvous with uncertainty. Sci. China Phys. Mech. Astron. 2014, 57, 731–740. [Google Scholar] [CrossRef]
- Yang, Z.; Luo, Y.z.; Zhang, J. Robust Planning of Nonlinear Rendezvous with Uncertainty. J. Guid. Control. Dyn. 2017, 40, 1954–1967. [Google Scholar] [CrossRef]
- González-Arribas, D.; Sanjurjo-Rivo, M.; Soler, M. Multiobjective Optimisation of Aircraft Trajectories Under Wind Uncertainty Using GPU Parallelism and Genetic Algorithms. In Evolutionary and Deterministic Methods for Design Optimization and Control with Applications to Industrial and Societal Problems; Andrés-Pérez, E., González, L., Periaux, J., Gauger, N., Quagliarella, D., Giannakoglou, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 453–466. [Google Scholar]
- Levine, J.; Blaney, D.; Connemey, J.; Greeley, R.; Head III, J.; Hoffman, J.; Jakosky, B.; McKay, C.; Sotin, C.; Summers, M. Science from a Mars airplane: The aerial regional-scale environmental survey (ARES) of Mars. In Proceedings of the 2nd AIAA “Unmanned Unlimited” Conf. and Workshop & Exhibit, San Diego, CA, USA, 15–18 September 2003; p. 6576. [Google Scholar]
- Hall, J.L.; Cameron, J.; Pauken, M.; Izraelevitz, J.; Dominguez, M.W.; Wehage, K.T. Altitude-controlled light gas balloons for Venus and Titan exploration. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3194. [Google Scholar]
- Toyoda, T.; Kanazaki, M. Trajectory Optimization for Space Debris Re-entry Considering Land Security by Evolutionary Algorithm. In Proceedings of the 34th International Symposium on Space Technology and Science (ISTS), Fukuoka, Japan, 3–9 June 2023. [Google Scholar]
- Takubo, Y.; Kanazaki, M. Robust Constrained Multi-objective Evolutionary Algorithm based on Polynomial Chaos Expansion for Trajectory Optimization. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; IEEE: New York, NY, USA, 2022; pp. 1–9. [Google Scholar]
- Bryson, A.E. Applied Optimal Control: Optimization, Estimation, and Control; Routledge: Milton Park, UK, 2018. [Google Scholar]
- González-Arribas, D.; Soler, M.; Sanjurjo-Rivo, M. Robust Aircraft Trajectory Planning Under Wind Uncertainty Using Optimal Control. J. Guid. Control. Dyn. 2018, 41, 673–688. [Google Scholar] [CrossRef]
- Mühlpfordt, T.; Roald, L.; Hagenmeyer, V.; Faulwasser, T.; Misra, S. Chance-Constrained AC Optimal Power Flow: A Polynomial Chaos Approach. IEEE Trans. Power Syst. 2019, 34, 4806–4816. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Kwak, D.; Miyata, K.; Noguchi, M.; Sunada, Y.; Rinoie, K. Experimental investigation of high lift device for SST. In The National Aerospace Laboratory Technical Report; NAL TR-1450; National Aerospace Laboratory(NAL): Tokyo, Japan, 2002. (In Japanese) [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1988, 13, 455–492. [Google Scholar] [CrossRef]
- Code of Federal Regulations, Title 14, Part 121.195. 2023. Available online: https://www.ecfr.gov/current/title-14/chapter-I/subchapter-G/part-121 (accessed on 24 October 2023).
- Matsuno, Y.; Tsuchiya, T.; Matayoshi, N. Near-Optimal Control for Aircraft Conflict Resolution in the Presence of Uncertainty. J. Guid. Control. Dyn. 2016, 39, 326–338. [Google Scholar] [CrossRef]



| SST Configuration | Value |
|---|---|
| 15,000 | |
| 319,900 | |
| Physical parameter | |
| Parameter | Range | Interval |
|---|---|---|
| Values | ||
|---|---|---|
| Conservative | 1.0 | 100.0 |
| Baseline | 3.0 | 150.0 |
| Relaxed | 5.0 | 200.0 |
| Solution Points | Case | ||||
|---|---|---|---|---|---|
| max. (Case 1) | Determinisitc Robust | 62.37 70.53 | 10.11 1.89 | 6720.98 7355.46 | 686.74 99.52 |
| max. (Case 2) | Determinisitc Robust | 72.07 74.08 | 6.693 1.80 | 6895.32 7081.88 | 402.39 102.98 |
| Compromise (Case 3) | Determinisitc Robust | 64.79 72.29 | 9.71 2.93 | 6610.21 7257.44 | 623.49 166.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takubo, Y.; Kanazaki, M. Robust Constrained Multi-Objective Guidance of Supersonic Transport Landing Using Evolutionary Algorithm and Polynomial Chaos. Aerospace 2023, 10, 929. https://doi.org/10.3390/aerospace10110929
Takubo Y, Kanazaki M. Robust Constrained Multi-Objective Guidance of Supersonic Transport Landing Using Evolutionary Algorithm and Polynomial Chaos. Aerospace. 2023; 10(11):929. https://doi.org/10.3390/aerospace10110929
Chicago/Turabian StyleTakubo, Yuji, and Masahiro Kanazaki. 2023. "Robust Constrained Multi-Objective Guidance of Supersonic Transport Landing Using Evolutionary Algorithm and Polynomial Chaos" Aerospace 10, no. 11: 929. https://doi.org/10.3390/aerospace10110929
APA StyleTakubo, Y., & Kanazaki, M. (2023). Robust Constrained Multi-Objective Guidance of Supersonic Transport Landing Using Evolutionary Algorithm and Polynomial Chaos. Aerospace, 10(11), 929. https://doi.org/10.3390/aerospace10110929






