Electromagnetic Performance Analysis of Inhomogeneous Radome Walls Considering Temperature and Ablation

Abstract

The radome is an important component of the aircraft seeker. The radome of high-speed aircraft usually has ablation, which affects the electromagnetic performance of the radome. Therefore, it is important to study the electromagnetic performance of the radome wall during high-temperature ablation. However, most existing studies mainly consider the influence of temperature and ignore structural changes caused by ablation. To solve the above problems, this paper studies the influence of ablation on the electromagnetic performance of inhomogeneous radome walls (IRW) by considering the structure parameters, thermal expansion characteristics, and dielectric parameters during the ablation. The two typical types of IRW design methods are analyzed, the parameters calculation method in the ablation process is proposed, and the influence of ablation on the two types of IRW is studied. The results give the electromagnetic changing characteristics of the IRW under different ablation conditions. The contribution of this work is to lay a solid theoretical foundation for improving the performance of the radome in the ablation process, which is of great significance.

1. Introduction

The radome is an important part of the aircraft seeker, which protects the antenna array from the external harsh environment [1,2,3]. During the high-speed flight of aircraft, the airflow in front of the radome head is compressed, which generates a lot of heat. The rising temperature may result in ablation [4]. Temperature and ablation directly affect the electromagnetic performance of the radome, so it is important to study the electromagnetic performance of the radome under high temperature and ablation conditions.

In studies of the electromagnetic performance of different radome walls at room temperature, P. S. Mohammed Yazeen and R. U. Nair proposed the seven-layer inhomogeneous streamline airborne radome and the half-wave hybrid variable-thickness radome (hy-VTR), respectively. The electromagnetic performance of those radomes was analyzed, and the results verified the proposed radome has better electromagnetic performance than the traditional constant thickness radome (CTR) [5,6]. W. Xu introduced the novel concept of average incidence angle and proposed a thickness optimization design method for a half-wave streamlined airborne radome. The method can optimize the boresight error and transmission loss using particle swarm optimization (PSO), which helps apply variable thickness design to streamlined airborne radome [7,8]. R. U. Nair proposed an inhomogeneous planar layer (IPL) design method for airborne applications of radome, and the results showed the proposed method has good electromagnetic characteristics such as high transmission and low reflection [9,10]. To utilize the advantages of variable thickness radome and multilayer radome, Z. Wang designed a variable-thickness streamlined radome for airborne application using a genetic algorithm (GA). During the design process, the parameters of a monolithic variable thickness radome are taken as the initial value of iterations. The results show that the proposed design method simplifies the design variables and provides the foundation for the mechanical design of radome [11]. F. Ghiasvand thoroughly investigated the electromagnetic characteristics of the inhomogeneous planar radome, gave closed-form expressions of the transmission and reflection coefficients, and proposed the radome design procedures [12]. Some works systematically compared the BSE, TL, and other electromagnetic properties of the conventional CTR and variable thickness radome (VTR), and analyzed the effects of bandwidth, coating layer, and thickness tolerance on the electromagnetic properties of the radome [13,14].

In studies of the electromagnetic performance of different radome walls in high-temperature ablation environments, J. Zhou studied nitride-based continuous fiber-reinforced ceramic matrix composites (CFCMCs) in the application of high-temperature airborne radomes, and gave specific recommendations for radome preparation [15]. A. Nag analyzed the advantages and disadvantages of ceramic materials for high-temperature environment radome, including high-purity alumina, pyroceram, slip-cast fused-silica, etc. [16]. Silicon nitride (Si₃N₄) ceramics have been widely used in radome under high-temperature environments due to their excellent high-temperature resistance and good mechanical and dielectric properties [17,18,19]. The graded radome is mostly made of Si₃N₄, and the porosity is used to control the dielectric constant of the material. F. Chen analyzed the relationship between flight speed, radome temperature, and flight height, and studied the design method of graded radome under high temperatures. The results verified the superiority of graded porous radome in broadband radome applications [20]. L. Zhou proposed an analytical calculation method for one-dimensional steady heat conduction in a radome, analyzed the thermal stress distribution of the lamination affected by temperature, and studied the electromagnetic performance of a radome with graded porous structure at high-temperature conditions [21]. A. Parameswaran designed a new inhomogeneous planar variable thickness radome. The influence of the thermal expansion coefficient on the radome wall thickness was considered in the design stage and the electromagnetic performance of the radome was analyzed via the ray tracing method. The results show that this type of radome has good electromagnetic performance in different high-temperature environments [22]. H. S. Sonalikar built the multilayer radome model with an ablative layer and coating layer, and the transmission coefficients, insertion phase shift, and other parameters of the radome at high temperatures were analyzed [23,24].

The above studies have made outstanding contributions to the radome field. However, most existing studies of the radome in a high-temperature environment do not fully consider the influence of high-temperature ablation on electromagnetic parameters, which could cause obvious performance degradation of the radome in a high-temperature environment. To solve the above problems, the electromagnetic performance of inhomogeneous radome walls (IRW) is studied by considering the thermal protect layers peeled off, dielectric parameters (dielectric constant and dielectric loss) changing, and thermal expansion. Firstly, the design methods of multilayer radome walls and graded radome walls are given and analyzed. Secondly, the calculation method of radome parameters in the ablation process is proposed. Finally, the influence of temperature and ablation on the electromagnetic performance of radome walls is analyzed in detail.

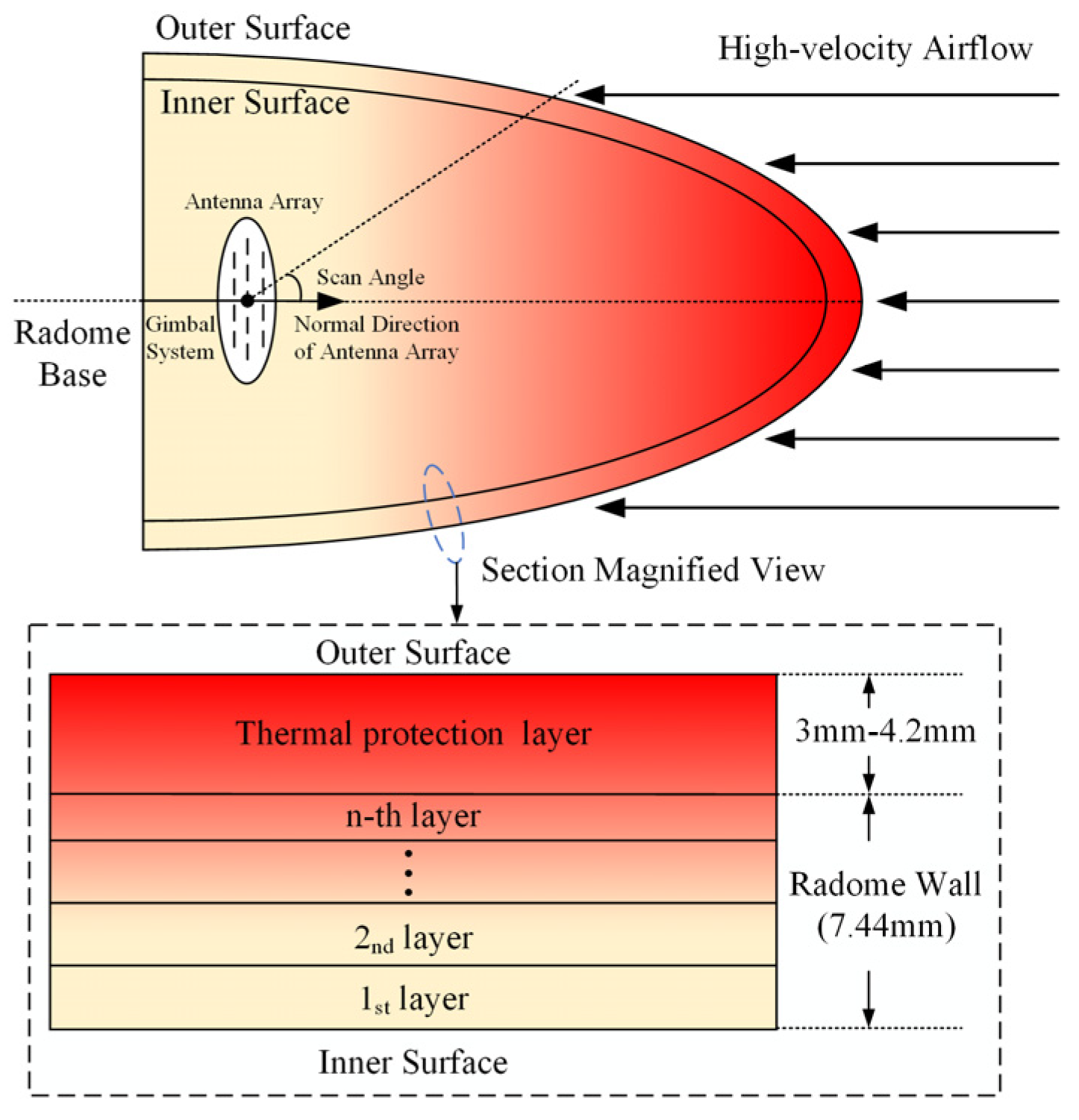
2. Theoretical Basis of IRW

The theoretical basis of IRW mainly includes design methods and transmission parameters calculation methods. The typical tangent oval radome in high-temperature environments is shown in Figure 1.

The antenna array is connected to the radome base through a gimbal system. During the high-speed flying process, the airflow in front of the radome head is compressed, which generates a large amount of heat and might cause ablation. The radome wall is mainly divided into single-layer solid walls (thin wall, half-wave wall), multilayer walls (A-sandwich, B-sandwich, C-sandwich, multilayer), and the graded wall. The thin walls and half-wave walls are mainly the determined frequency applications. Multilayer walls and graded walls often have better performance and are good for simulating radomes in a high-temperature environment. Therefore, this paper focuses on those two types of IRW structures.

2.1. Design for Typical IRW

The design of the radome wall mainly refers to determining the thickness, number of layers, and dielectric parameters (dielectric constant and dielectric loss) of each layer. The existing design methods mainly include method A for multilayer radome walls and method B for graded radome walls.

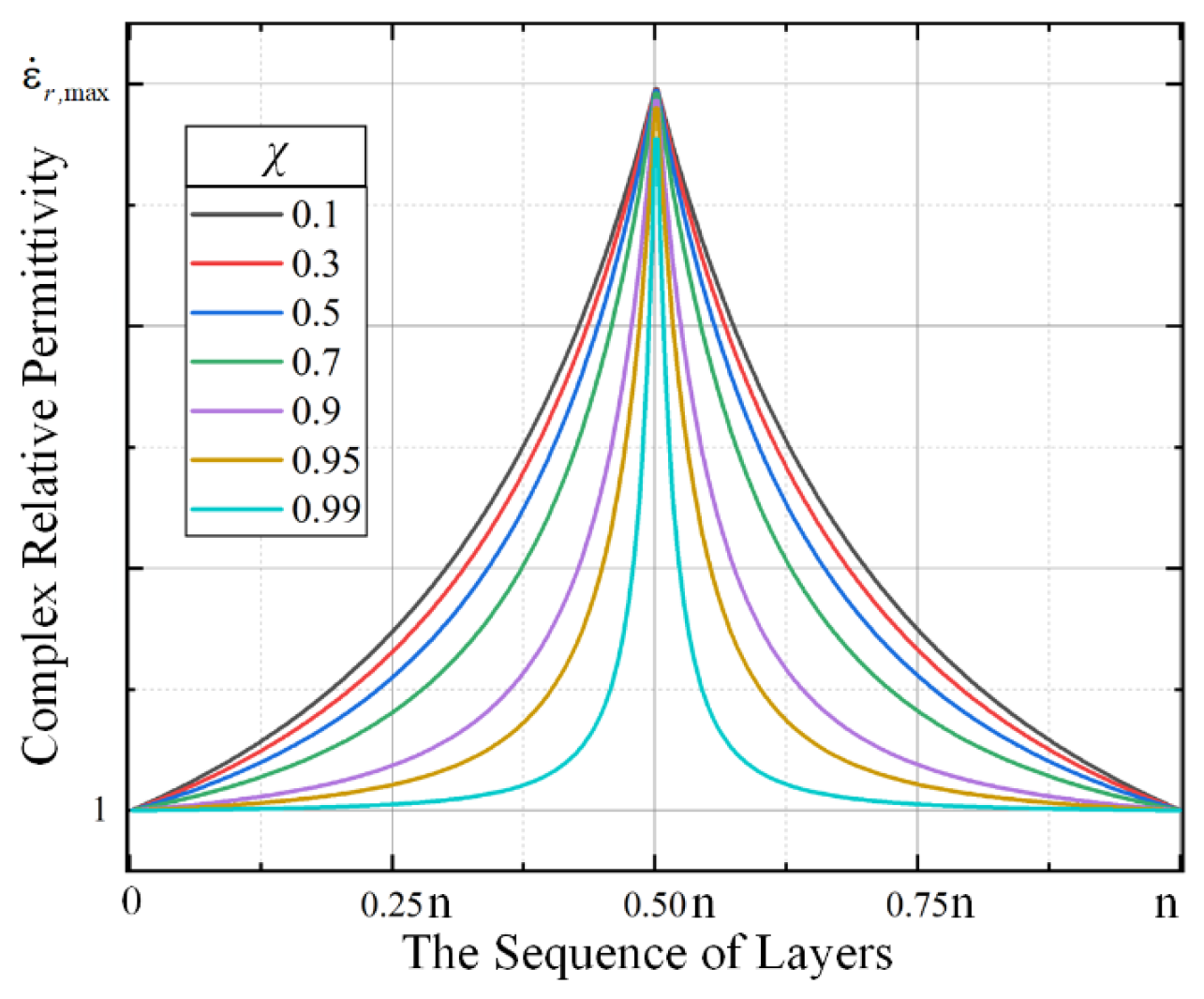
2.1.1. Method A

Based on Maxwell equations and wave equations, method A for determining the complex permittivity of multilayer radome walls is given in Equation (1) [25]. Where method A is widely used in inhomogeneous radome wall design [9]:

$${\dot{\mathrm{\epsilon }}}_r\left(r\right)=\mathrm{\chi }+\left(\frac{b^2}{{\left[a\left|0.5d-r\right|+1\right]}^2}\right)$$

(1)

where r is the distance from one wall surface, ${\dot{\mathrm{\epsilon }}}_r\left(r\right)$ is the relative permittivity, d is the thickness of the radome wall (the thickness sum of each wall layer), and $\mathrm{\chi }$ is the curvature coefficient within [0, 1). The coefficients a and b in (1) are:

$$\left\{\begin{array}{cc}a& =\frac{\left\{-1+{\left[\left({\dot{\mathrm{\epsilon }}}_{r,\max }-\mathrm{\chi }\right)/(1-\mathrm{\chi })\right]}^{1/2}\right\}}{0.5d}\\ b& ={\left({\dot{\mathrm{\epsilon }}}_{r,\max }-\mathrm{\chi }\right)}^{1/2}\end{array}\right.$$

(2)

where ${\dot{\mathrm{\epsilon }}}_{r,\max }$ is the maximum of the relative permittivity. Assuming that the thickness of the i-th layer of the radome wall is $d_i$, relative permittivity can be determined using the integral average value in the i-th layer based on Equations (1) and (2). Therefore, the relative permittivity ${\dot{\mathrm{\epsilon }}}_{r,i}$ of the i-th layer is:

$${\dot{\mathrm{\epsilon }}}_{r,i}=\frac{1}{d_i}{\displaystyle {\int }_{{\displaystyle \sum _{j=1}^{i-1}{d}_j}}^{{\displaystyle \sum _{j=1}^i{d}_j}}{\dot{\mathrm{\epsilon }}}_r\left(r\right)}dr$$

(3)

The results of method A are related to the curvature coefficient $\mathrm{\chi }$. To simplify the calculation, it is assumed that the number of layers is n, and the thickness of each layer is equal. It should be noted that the number of layers is often a predetermined parameter. When the n is determined, the dielectric constant of each layer can be determined using Equations (1)–(3). The relative permittivity of each layer with different curvature coefficients $\mathrm{\chi }$ is shown in Figure 2.

Figure 2 shows that the radome wall designed using method A has a symmetric relative permittivity distribution. The relative permittivity increases gradually from one wall surface to the maximum at the middle layer and then decreases gradually.

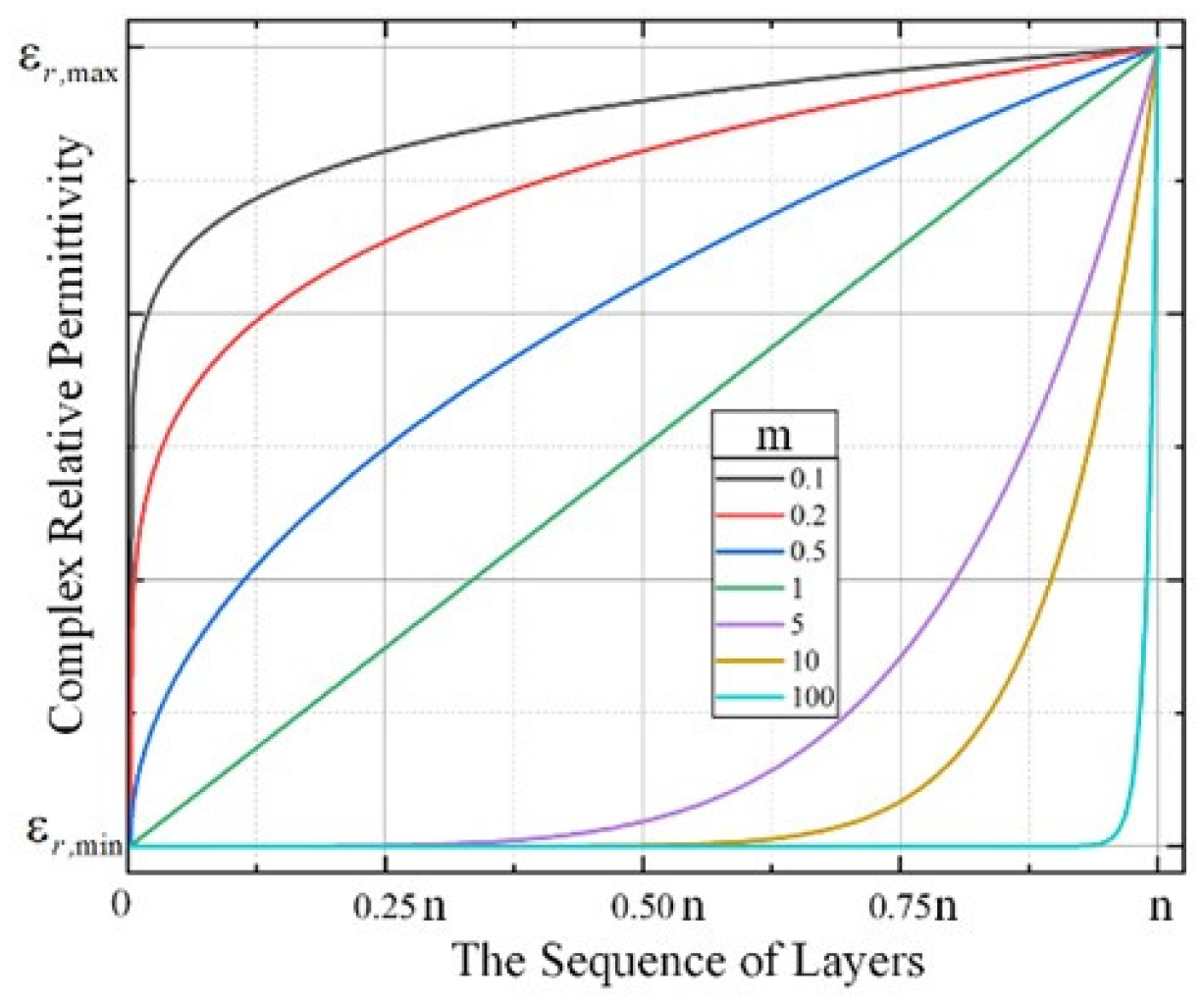
2.1.2. Method B

The multilayer walls of the radome are usually made of foam, glass fiber, etc. [21]. Thermal stress between the layers with different materials can easily cause new problems during the ablation process. Therefore, graded radome walls are often used to alleviate the thermal stress problems between different layers. Graded radome walls are often made of Si₃N₄ ceramics. To solve the problem of the high dielectric constant of dense Si₃N₄ ceramics, the porous method is often used [26]. The dielectric constant of graded radome walls is usually within two to eight when changing the porosity of each layer [20]. It should be noted that each layer of the radome walls in this way has the same material with different porosity. Method B for determining the dielectric constant of graded radome walls is:

$${\mathrm{\epsilon }}_{r,i}={\mathrm{\epsilon }}_{r,\min }+\left({\mathrm{\epsilon }}_{r,\max }-{\mathrm{\epsilon }}_{r,\min }\right){\left(\frac{i-1}{n-1}\right)}^m$$

(4)

where n is the number of layers, ${\mathrm{\epsilon }}_{r,\min }$ and ${\mathrm{\epsilon }}_{r,\max }$ are the relative dielectric constant of the innermost layer (the first layer) and the outermost layer (the n-th layer), I is the i-th layer ($i=1,2,\cdots ,n$), and m is the gradient coefficient. The dielectric constant ${\mathrm{\epsilon }}_{r,i}$ of each layer of graded radome under different gradient coefficients m is shown in Figure 3.

Figure 3 shows that the radome wall designed using method B has an increasing dielectric constant from the innermost layer to the outermost layer. It should be noted that the dielectric loss is not given in method B. The dielectric loss of graded radome walls is mainly within 0.006 [20,26].

2.2. Parameters Calculation of IRW

A local small element of the tangent oval radome wall can be regarded as a planar wall with negligible curvature. The wall of a multilayer radome and a graded radome can be equivalent to multilayer planar walls in the analysis process.

The propagation of the electromagnetic wave in each layer can be expressed using a uniform transmission line equation. The performance of IRW can be solved using the cascade matrix of the transmission line equations. The transmission line matrix of the non-uniform radome walls is:

$$\left[\begin{array}{l}A B\\ C D\end{array}\right]={\displaystyle \prod _{i=1}^n\left[\begin{array}{l}{A}_i B_i\\ C_i D_i\end{array}\right]}$$

(5)

where n is the number of the radome wall layers. $A_i$, $B_i$, $C_i$ and $D_i$ are the coefficients of the i-th layer wall:

$$\left\{\begin{array}{l}{A}_i=D_i=\mathit{cosh}\left(j\cdot {\gamma }_i{d}_i\right)\\ B_i=Z_{ci}\cdot \mathit{sinh}\left(j\cdot {\gamma }_i{d}_i\right)\\ C_i=\left(\frac{1}{Z_{ci}}\right)\cdot \mathit{sinh}\left(j\cdot {\gamma }_i{d}_i\right)\\ {\gamma }_i=k_0\cdot \sqrt{{\dot{\mathrm{\epsilon }}}_{r,i}-{\mathit{sin}}^2\left({\theta }_0\right)}\end{array}\right.$$

(6)

where ${\dot{\mathrm{\epsilon }}}_{r,i}$ is the relative permittivity of the i-th layer, ${\theta }_0$ is the incidence angle, and $k_0$ is the vacuum wave number. It is approximately considered that the radome material is non-magnetic, and the equivalent characteristic impedance of the i-th layer under different polarization are:

$$\left\{\begin{array}{l}{Z}_{ci,pa}=\frac{\sqrt{{\dot{\mathrm{\epsilon }}}_{r,i}-{\mathit{sin}}^2\left({\theta }_0\right)}}{{\dot{\mathrm{\epsilon }}}_{r,i}\cdot \mathit{cos}\left({\theta }_0\right)} \\ Z_{ci,pe}=\frac{\mathit{cos}\left({\theta }_0\right)}{\sqrt{{\dot{\mathrm{\epsilon }}}_{r,i}-{\mathit{sin}}^2\left({\theta }_0\right)}}\end{array}\right.$$

(7)

where $Z_{ci,pa}$ and $Z_{ci,pe}$ are the characteristic impedance of parallel polarization and perpendicular polarization, respectively. The normalized matrix coefficients A, B, C, and D can be obtained using Equations (6) and (7) into Equation (5). The reflection coefficient and transmission coefficient of radome walls are:

$$\left\{\begin{array}{l}T=\frac{2}{A+B+C+D}=\left|T_0\right|e^{-j{\mathrm{\phi }}_t}\\ R=\frac{A+B-C-D}{A+B+C+D}=\left|R_0\right|e^{-j{\mathrm{\phi }}_r}\end{array}\right.$$

(8)

The power transmission coefficient (PTC) is ${\left|T_0\right|}^2$, and the power reflection coefficient (PRC) is ${\left|R_0\right|}^2$. It should be noted that the higher the PTC and the lower the PRC, the better the electromagnetic performance of the radome walls.

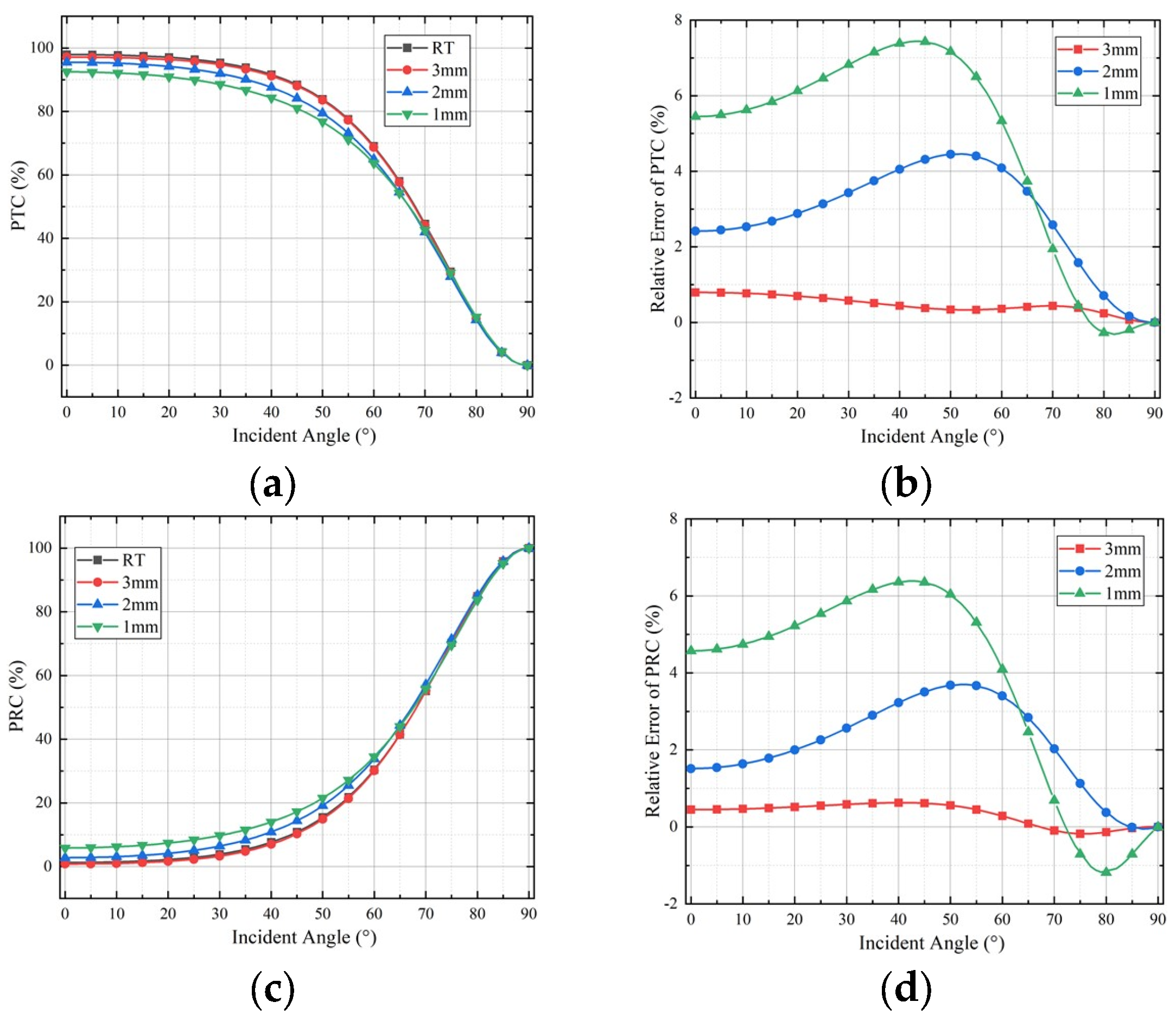
3. Analysis of IRW Using Two Methods

X-band is a commonly used frequency band for airborne radome. This section mainly focuses on how to choose the dielectric constant of each layer and the number of layers. Different frequencies will cause different total thicknesses of radome walls; to eliminate the influence of that, this section mainly discusses the performance of radomes with different designs at 10 GHz. The incidence angle is 0° to 90°, and the polarization modes are parallel polarization and perpendicular polarization. The wall thickness at 10 GHz can be calculated as 7.44 mm using the half-wave wall design method [9]. Therefore, the thickness sum of all radome wall layers is taken as 7.44 mm using the aforementioned design methods (method A and method B). To simplify the calculation, the equal thickness design is adopted in subsequent analysis.

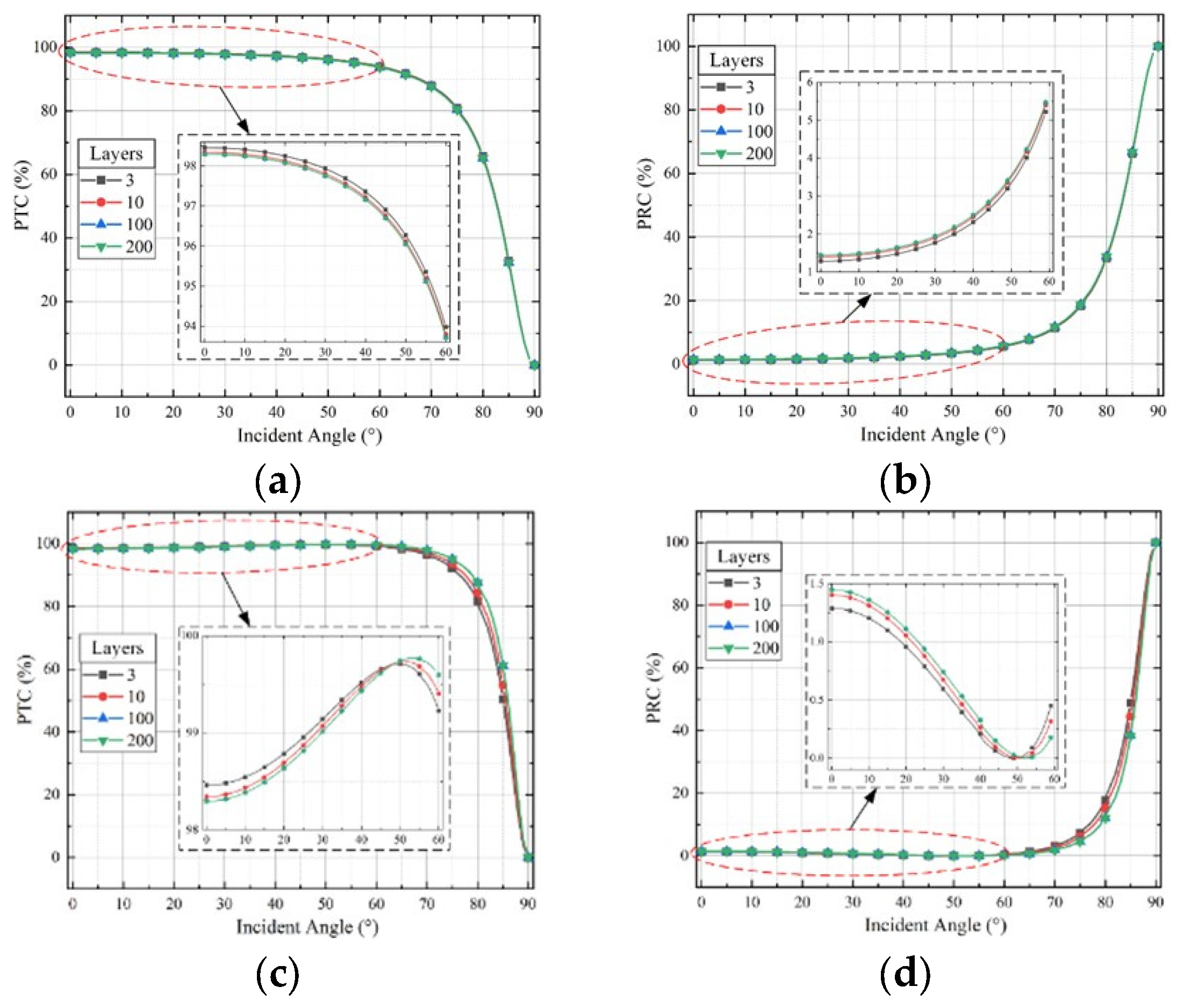
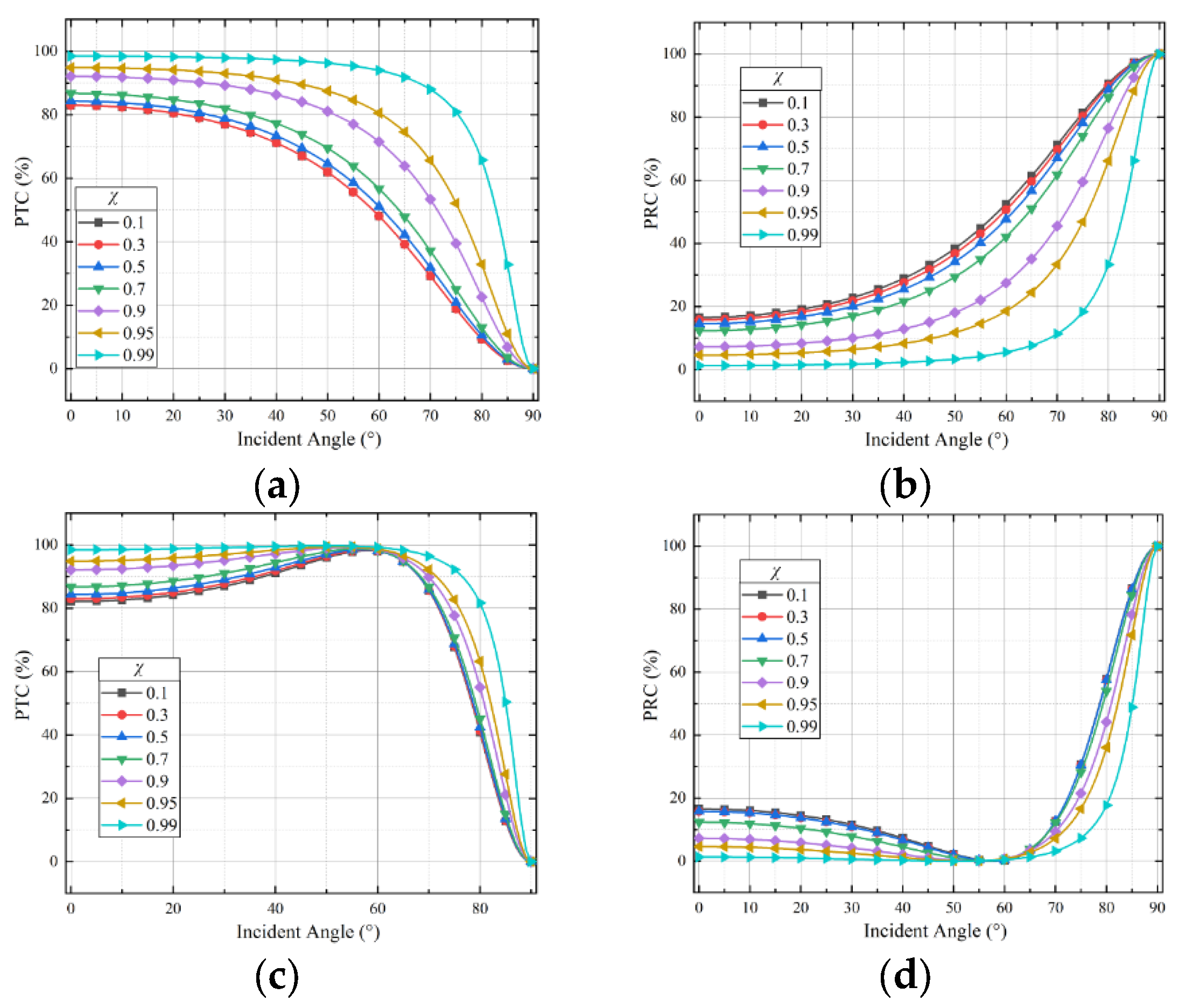
3.1. Results of Method A

Method A is mainly used in multilayer radome walls. The minimum dielectric constant of multilayer radome walls is close to the air dielectric constant. Therefore, the maximum dielectric constant is 4.0 and the minimum dielectric constant is 1.0, while the maximum dielectric loss is 0.015 and the minimum dielectric loss is 0 [9]. Method A is mainly affected by the curvature factor $\mathrm{\chi }$ and the number of wall layers n. When $\mathrm{\chi }$ is 0.99, the control variable method is adopted to calculate the PTC and PRC of radome walls with different layers, as shown in Figure 4.

Figure 4 shows that the PTC decreases with increasing incident angle, while the PRC increases with increasing incident angle. The PTC and PRC have a good performance within 0 to 60 degrees of the incidence angle. Additionally, increasing the number of radome wall layers has a very limited effect on the improvement of radome performance in method A. When the number of wall layers increases from 3 to 200, the PTC and PRC only change within 0.5%. Therefore, radome walls with three layers are chosen to further analyze the influence of the curvature factor $\mathrm{\chi }$ on electromagnetic performance, as shown in Figure 5.

Figure 5 shows that the greater the curvature coefficient $\mathrm{\chi }$, the better the performance of the radome. The larger $\mathrm{\chi }$ means the larger thickness of the low dielectric constant material close to the innermost and outermost of the wall surface. Since the minimum dielectric constant is one, the lowest dielectric constant materials can be regarded as air. Therefore, the larger $\mathrm{\chi }$ also means the thinner the radome wall. On the premise of ensuring other requirements, it is recommended that actual radome manufacturing should choose the larger curvature coefficient $\mathrm{\chi }$. Since $\mathrm{\chi }$ is within [0, 1), the closer $\mathrm{\chi }$ is to one, the better performance of radome walls can be obtained.

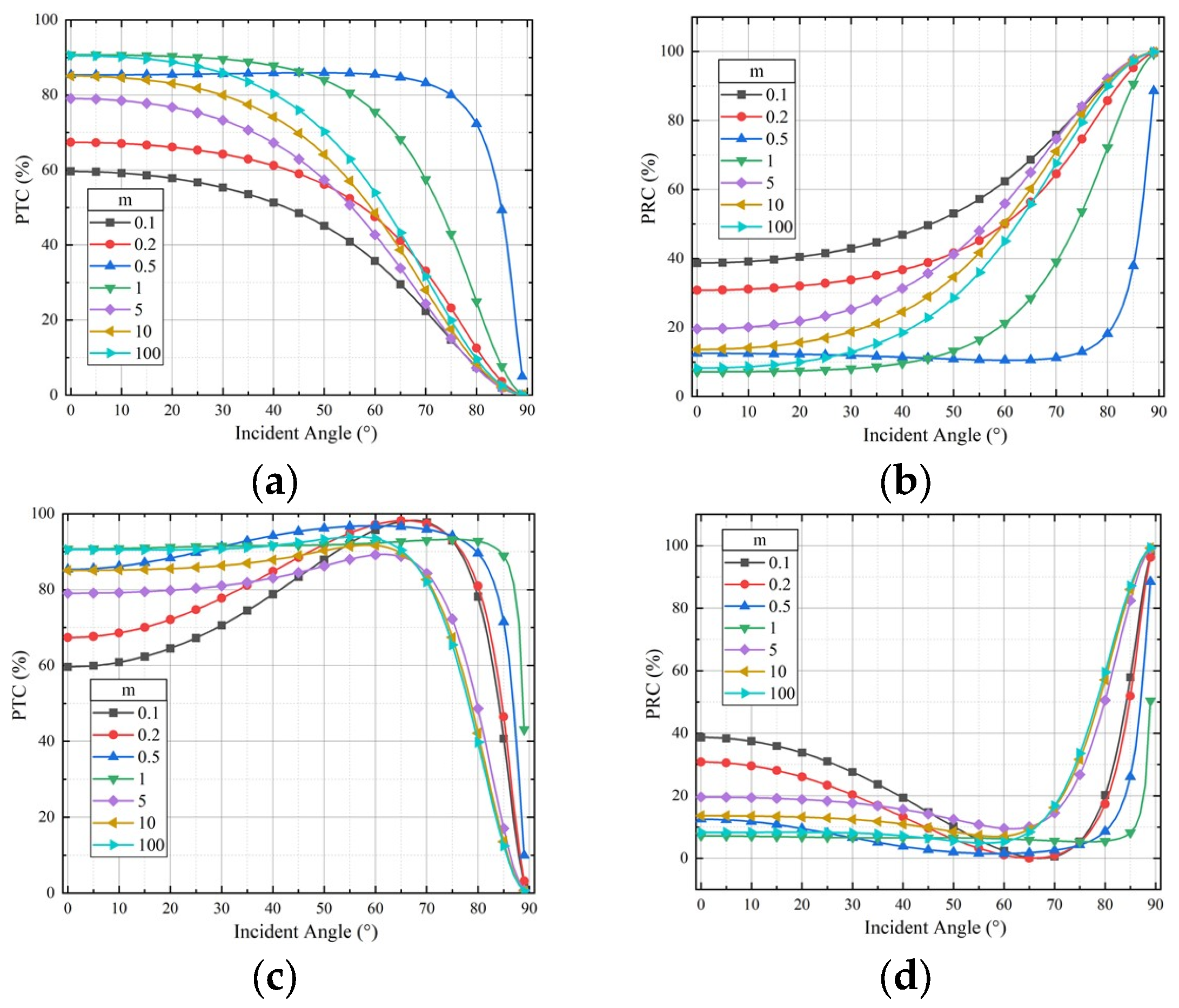
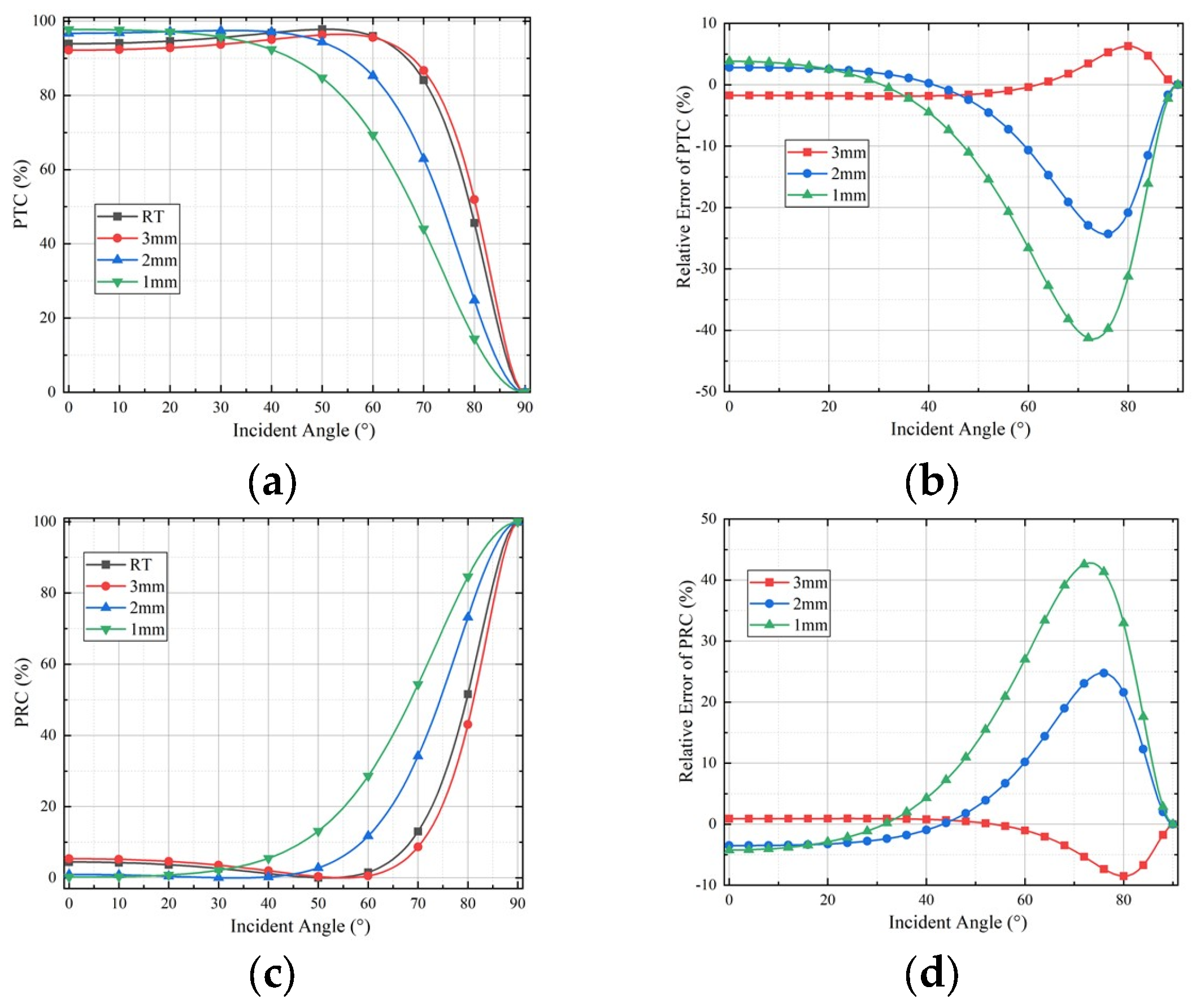
3.2. Results of Method B

Method B is used for designing the graded radome. The graded radome walls are mainly made of Si₃N₄ ceramics. The dielectric constant of most Si₃N₄ with different porosity is within two to eight [11]. It is assumed that the maximum and minimum dielectric constant are eight and two, respectively, and the dielectric loss is 0.004. Similarly, when the gradient coefficient is one, the equal thickness design is adopted to analyze the PTC and PRC of graded radome walls with different layers, as shown in Figure 6.

Figure 6 indicates that the PTC decreases and PRC increases with increasing incident angle. The PTC and PRC have good performance in the range of 0° to 60° incidence angle. The performance of the radome is improved significantly by increasing n of the radome wall within 10 layers. When the number of layers is greater than 10, the performance improvement in this way is very limited. The PTC of the ten-layer wall at a 60° incidence angle in both polarization modes is greater than that of the three-layer wall by about 5%. However, when the number of radome wall layers increases from 10 to 200, the PTC and PRC only change within 0.54%. Therefore, ten-layer graded radome walls are chosen to further analyze the influence of the gradient factor m on electromagnetic performance, as shown in Figure 7.

Figure 7 indicates that the PTC of the radome increases and the PRC decreases when coefficient m increases from 0.1 to 1. When m increases from 1 to 5, the performance of the radome degrades, and when m increases from 5 to 100, the performance of the radome improves. When m is 100, the PTC and PRC of the 0° to 20° incidence angle of the radome are close to the value when m is 1, but the PTC and PRC of most other incidence angles are relatively poorer. Figure 3 shows that m is far greater than 1 and the greater the thickness of the material with a low dielectric constant (greater porous ratio), the less conducive to ensuring the mechanical reliability of the radome. On the other hand, the gradient coefficient m is far less than 1 (approaching 0), and the performance is too poor. Therefore, it is recommended that radome manufacturing should make the gradient coefficient m in the range of 1 to 10.

4. Parameters Calculation of IRW in the Ablation Process

In the high-temperature ablation process of the radome wall, there are three main influencing factors: 1. The ablation would result in a change in the surface structure of the radome wall; 2. High temperature would cause the change of dielectric constant and dielectric loss of the radome wall; 3. The temperature would cause thermal expansion of the radome wall. Among them, the ablation can be approximated to the reduction in the thickness of the surface ablation protective material, as shown in Figure 1. The subsequent analysis in this section focuses on the temperature distribution of the radome wall and the parameters changing caused by high temperatures.

4.1. Temperature Distribution of IRW

The radome temperature distribution of high-speed aircraft is shown in Figure 1. The high-speed airflow is compressed in front of the radome, which generates a lot of heat. The rising temperature may cause ablation on the surface of the radome. The highest temperature area where the ablation is most likely to occur is usually at the head of the radome. The temperature is transferred to the radome basis along the tangential direction of the radome wall; at the same time, the temperature is also transferred from the outer surface to the inner surface along the normal direction of the radome wall. Therefore, the temperature is divided into tangential temperature and normal temperature in this section.

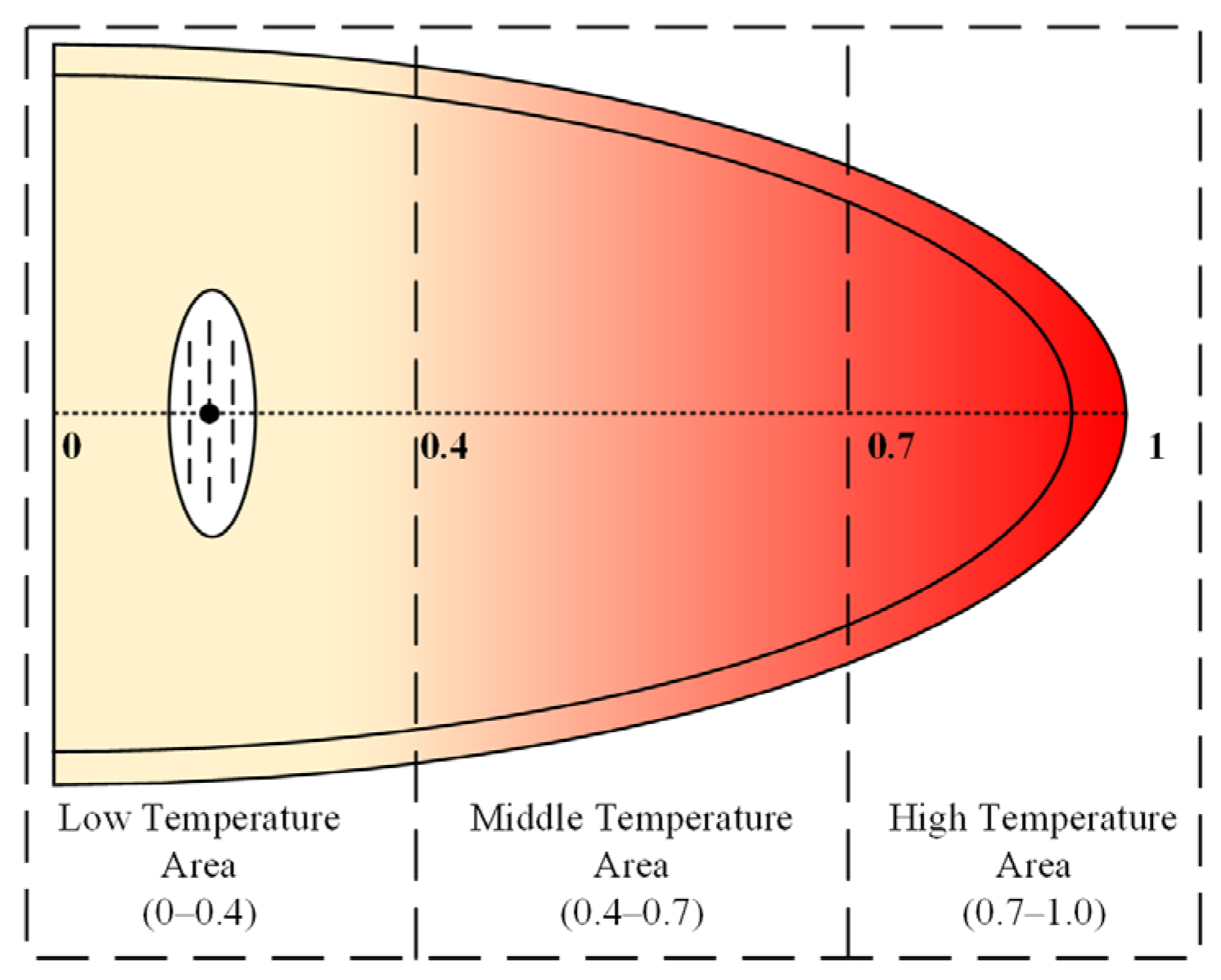
4.1.1. Tangential Temperature Distribution

In the tangential temperature distribution of radome walls, the temperature distribution at the innermost and outermost layer of the walls is analyzed, and the temperature in the radome walls can be ignored. According to the temperature of the inner and outer surfaces of the radome wall in Ref. [22], the fitting method is used to obtain the temperature as follows:

$$\left\{\begin{array}{l}{T}_{\mathrm{in}}\left(x\right)=\left(T_{\mathrm{in},\max }-T_{\mathrm{in},\min }\right)\cdot \left[0.005e^{5.32\cdot x}+0.0822e^{0.1926\cdot x}\right]\\ T_{\mathrm{out}}\left(x\right)=\left(T_{\mathrm{out},\max }-T_{\mathrm{out},\min }\right)\cdot \left[0.1694e^{1.645\cdot x}+0.0026e^{4.77\cdot x}\right]\end{array}\right.$$

(9)

where $T_{\mathrm{in}}\left(x\right)$ and $T_{\mathrm{out}}\left(x\right)$ are the temperature distribution of the inner and outer surfaces of the radome wall, $T_{\mathrm{in},\max }$ and $T_{\mathrm{in},\min }$ are the maximum and minimum temperature of the inner surfaces, and $T_{\mathrm{out},\max }$ and $T_{\mathrm{out},\min }$ are the maximum and minimum temperature of the outer surfaces. x is the unit length of the radome walls as shown Figure 8, where the radome can be roughly divided into a low-temperature zone (x is 0 to 0.4), a middle-temperature zone (x is 0.4 to 7), and a high-temperature zone (x is 0.7 to 1).

4.1.2. Normal Temperature Distribution

The multilayer radome and the graded radome both contain a multilayer structure. Equation (9) can only calculate the temperature of the innermost and outermost surface at a certain location x₀. For a certain location, the temperature difference between the innermost place and the outermost place usually does not exceed 600 °C. Although the normal temperature distribution might be non-linear, since the temperature difference is not large, the errors between linear assumption temperature and real non-linear temperature do not have much influence on the dielectric constant. Therefore, the linear temperature assumption is adopted in subsequent analysis, which means that the normal temperature of the radome wall is linearly distributed to the thickness, and the temperature of each layer can be approximately considered as the integral average of a linearly distributed equation based on $T_{\mathrm{in}}\left(x_0\right)$ and $T_{\mathrm{out}}\left(x_0\right)$, as follows:

$$T_{\mathrm{i}}=T_{\mathrm{in}}\left(x_0\right)+\frac{\left[T_{\mathrm{out}}\left(x_0\right)-T_{\mathrm{in}}\left(x_0\right)\right]}{{\displaystyle \sum _{j=1}^n{d}_j}}\frac{{\left({\displaystyle \sum _{j=1}^i{d}_j}\right)}^2-{\left({\displaystyle \sum _{j=1}^{i-1}{d}_j}\right)}^2}{2d_i}$$

(10)

where, $T_{\mathrm{i}}$ is the average temperature of the i-th layer, d_j is the thickness of the j-th layer, and n is the total number of layers.

4.2. Dielectric Parameters of IRW Affected by High Temperatures

During the ablation of radome walls, the dielectric constant and dielectric loss of radome walls usually increase to a certain extent when the temperature rises. In most situations, the dielectric loss will increase more significantly. However, there are many types of radome materials and the temperature sensitivity of the dielectric constant and dielectric loss of materials is different, so it is difficult to quantitatively analyze them. Based on the data in Refs. [11,20,24], it is assumed that the relative complex permittivity increases by 3% and the dielectric loss of materials increases by 100% when the radome wall temperature increases by 600 °C [27].

4.3. Thermal Expansion of IRW Affected by High Temperatures

The increase in temperature and the ablation will change the structural parameters of materials. The ablation will make the thermal protection layer fall off, and the high temperature will cause certain thermal expansion of materials. The linear thermal expansion coefficient is:

$$\mathsf{\alpha }=\frac{1}{d_i}\frac{d_i^{\prime }-d_i}{\left(\Delta T+274.15\right)}$$

(11)

where $\mathsf{\alpha }$ is the thermal expansion coefficient and the unit is 1/K, $d_i$ is the thickness of the i-th layer wall before ablation, $d_i^{\prime }$ is the thickness of the i-th layer wall after ablation, and $\Delta T$ is the absolute value of temperature difference before and after ablation and the unit is °C. Equation (11) can be simplified as:

$$d_i^{\prime }=d_i\left(1+\mathsf{\alpha }\left(\Delta T+274.15\right)\right)$$

(12)

The thermal expansion coefficient of most radome materials is in the range of $\left(2.5~4.0\right)\times {10}^{-6}/\mathrm{K}$ [28,29,30]. Therefore, $\mathsf{\alpha }$ is taken as $4.0\times {10}^{-6}$ in the subsequent analysis.

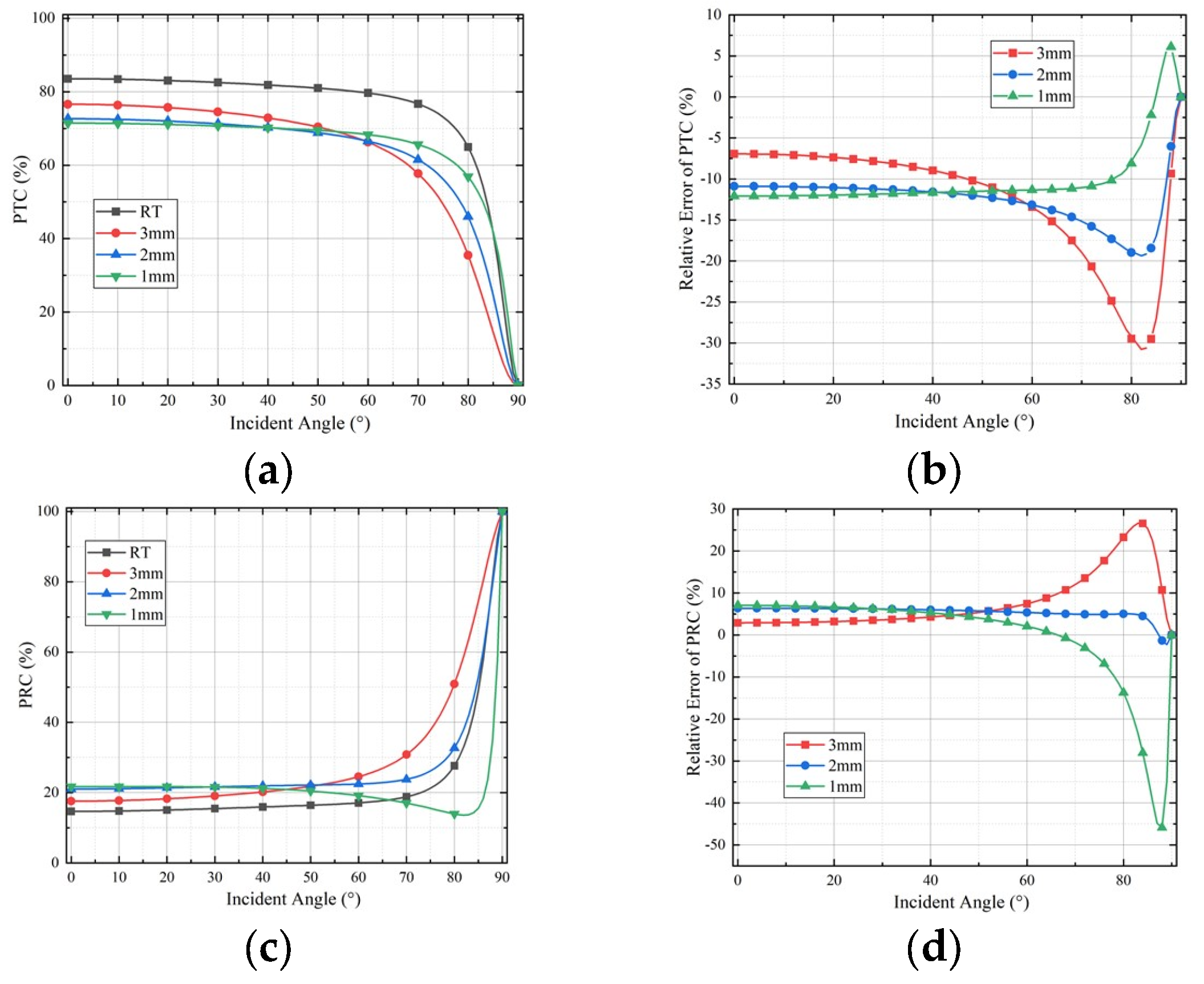
5. Discussion

This section mainly discusses the influence of temperature and ablation on two typical types of IRW: multilayer radome walls (MRW) and graded radome walls (GRW).

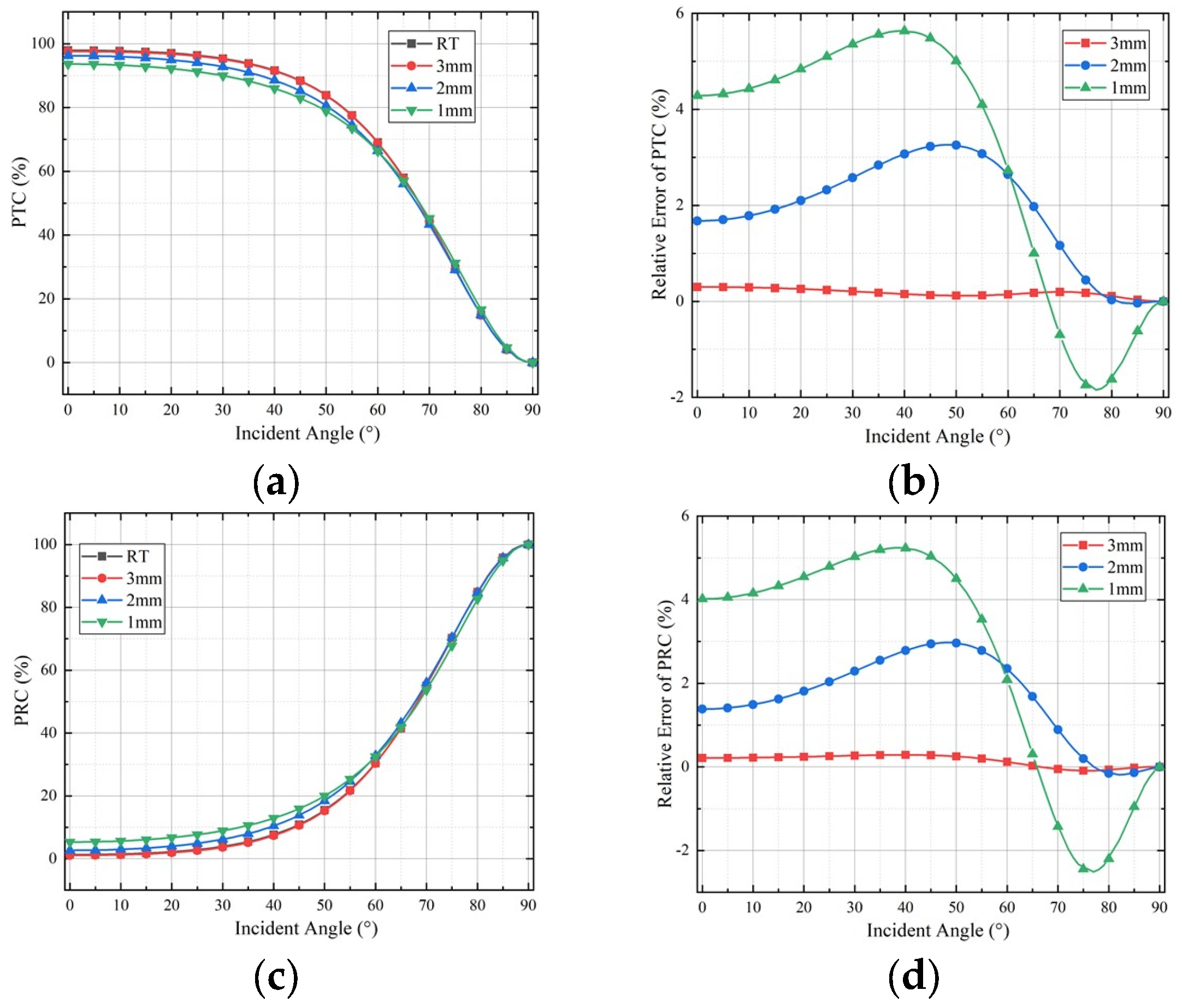
5.1. The Influence of Temperature and Ablation on MRW

The multilayer radome wall is designed using method A and the working frequency is 10 GHz. In addition, $\mathrm{\chi }$ is 0.9, the number of layers is three, and the thickness sum of all layers is still 7.44 mm, which is calculated using the half-wave wall design method [9]. The thickness of each layer is 2.48 mm because of the equal-thickness design. The thermal protection layer is generally 3 mm to 4.2 mm, and is taken as 3 mm in this section. The relative dielectric constant and dielectric loss of the thermal protection layer are 2.33 and 0.0012, respectively [23]. It should be noted that the dielectric constant and loss of the thermal protection layer are assumed to be constant during the ablation process, and different ablation degrees are approximately equivalent to the ablation layer with different thicknesses.

When the flight speed is within Mach 3, the outer surface temperature of the radome wall is often within 800 °C. When the flight speed is Mach 3 to Mach 5, the outer surface temperature is about 800 to 1200 °C. When the flight speed is greater than Mach 5, the outer surface temperature of the radome wall is about 1200 to 1800 °C. Ablation usually occurs at higher temperatures, so this paper focuses on the case above Mach 5, assuming that $T_{\mathrm{out},\max }$ is 1800 °C and $T_{\mathrm{in},\max }$ is 1300 °C. To ensure the normal operation of the antenna array, the temperature near the antenna array should not be too high in that case. Therefore, $T_{\mathrm{out},\min }$ and $T_{\mathrm{in},\min }$ are taken as 121.1 °C and 37.7 °C based on Ref. [22]. The middle-temperature and high-temperature areas in Figure 7 are studied. First, selecting a location x = 0.6 in the middle-temperature zone, $T_{\mathrm{in}}\left(0.6\right)$ and $T_{\mathrm{out}}\left(0.6\right)$ are calculated as 270.2 °C and 839.5 °C, respectively, using Equation (9). The parameters of the ablated radome wall are calculated using Equation (12), as shown in

Table 1. Parameters of three-layer radome walls before and after ablation at x = 0.6.

i	AT (°C)	Thickness (mm)		${\mathit{\epsilon }}_{\mathit{r},\mathit{i}}$		$\mathit{t}\mathit{a}\mathit{n}\mathit{\delta }$ (10−3)
		BA	AA	BA	AA	BA	AA
1	337.82	2.480	2.486	1.12	1.14	0.5	0.78
2	473.05	2.480	2.487	2.13	2.18	7.1	12.70
3	608.29	2.480	2.489	1.12	1.15	0.5	1.01

, where BA represents before ablation, AA represents after ablation, AT is the average temperature, i is the i-th layers, ${\mathrm{\epsilon }}_{r,i}$ is the dielectric constant, and $\mathit{tan}\mathrm{\delta }$ is dielectric loss. ${\mathrm{\epsilon }}_{r,i}$ and $\mathit{tan}\mathrm{\delta }$ can be determined based on Section 3.1 and Section 4.2.

According to the parameters in Table 1, the thickness (3 mm, 2 mm, 1 mm) of the thermal protection layer is equivalent to the ablation degree. The PTC and PRC under different ablation degrees are calculated as shown in Figure 8 and Figure 9. Where RT is the room temperature, the relative error is the PTC or PRC in different ablation cases (3 mm, 2 mm, 1 mm) minus the PTC or PRC in the RT environment. It should be noted that the peeling of the thermal protection layer means ablation (2 mm, 1 mm). “RT” and “3 mm” both have a 3 mm thermal protection layer but work at different temperatures.

The curves of “RT” and “3 mm” in Figure 9 show that the influence of temperature on the PTC and PRC can be almost ignored and the relative error is less than 1%. In this situation affected by rising temperature, only the dielectric constant, dielectric loss, layer thickness changes, and the thermal protection layer remain the same. When the thermal protection layer peeled off from the initial 3 mm to 1 mm due to ablation, the maximum decrease in the PTC was about 5.4% (91.4% to 86%) and the PRC increased by about 5.6% (6.8% to 12.4%). Therefore, the influence of the thermal protective layer peeling caused by the ablation is greater than the influence of the change of dielectric constant, dielectric loss, and thickness expansion caused by rising temperature.

Another location, x = 0.9, in the high-temperature zone is chosen, and $T_{\mathrm{in}}\left(0.9\right)$ and $T_{\mathrm{out}}\left(0.9\right)$ are calculated as 881.7 °C and 1569.5 °C, respectively, using Equation (9). Similar to the calculation process of Table 1, the parameters of the ablated radome wall are calculated as shown in

Table 2. Parameters of three-layer radome walls before and after ablation at x = 0.9.

i	AT (°C)	Thickness (mm)		${\mathit{\epsilon }}_{\mathit{r},\mathit{i}}$		$\mathit{t}\mathit{a}\mathit{n}\mathit{\delta }$ (10−3)
		BA	AA	BA	AA	BA	AA
1	963.1	2.480	2.492	1.12	1.17	0.5	1.30
2	1126.0	2.480	2.494	2.13	2.25	7.1	20.42
3	1288.9	2.480	2.496	1.12	1.19	0.5	1.57

.

Similarly, the PTC and PRC with different thermal protective layer thicknesses (3 mm, 2 mm, 1 mm) are calculated as shown in Figure 10 based on Table 2.

The “RT” and “3 mm” curves in Figure 10 indicate that the dielectric constant, dielectric loss, and thermal expansion of the thickness caused by temperature have a negligible influence on the PTC and PRC (less than 1%). When the thermal protection layer peeled off from the initial 3 mm to 1 mm due to ablation, the maximum decrease in the PTC is about 7.1% (88.1% to 81%) and the PRC increased by about 7% (9.5% to 16.5%). It can be seen from Figure 9 and Figure 10 that the higher the temperature is, the more serious the ablation is, the more the thermal protection layer peels off, and the more significant the radome wall degradation.

5.2. The Influence of Temperature and Ablation on GRW

Similarly, the working frequency is 9.4 GHz, $T_{\mathrm{out},\max }$ and $T_{\mathrm{in},\max }$ are 1800 °C and 1300 °C, and $T_{\mathrm{out},\min }$ and $T_{\mathrm{in},\min }$ are 121.1 °C and 37.7 °C. The location x = 0.6 in the middle-temperature area and the location x = 0.9 in the high-temperature area are studied. The parameters of graded radome walls at x = 0.6 and x = 0.9 at room temperature correspond to S3 and S1 of Table IV in Ref. [11]. $T_{\mathrm{out}}\left(0.6\right)$ and $T_{\mathrm{in}}\left(0.6\right)$ are still 839.5 °C and 270.2 °C. Similar to the calculation process of Table 1, the graded radome wall parameters at x = 0.6 after ablation are calculated as shown in

Table 3. Parameters of GRW before and after ablation at x = 0.6.

i	AT (°C)	Thickness (mm)		${\mathit{\epsilon }}_{\mathit{r},\mathit{i}}$		$\mathit{t}\mathit{a}\mathit{n}\mathit{\delta }$ (10−3)
		BA	AA	BA	AA	BA	AA
1	311.4	1.250	1.256	2.50	2.54	4	6.08
2	392.9	1.220	1.226	2.60	2.65		6.62
3	470.4	1.130	1.136	2.90	2.97		7.14
4	542.3	1.050	1.056	3.30	3.39		7.62
5	608.3	0.950	0.956	3.90	4.02		8.06
6	668.0	0.860	0.866	4.70	4.86		8.45
7	722.1	0.780	0.785	5.70	5.91		8.81
8	771.6	0.720	0.725	6.80	7.06		9.14
9	817.4	0.670	0.675	8.00	8.33		9.45

.

The thickness of the thermal protective layer is equivalent to the ablation degree. The PTC and PRC under different ablation degrees are calculated based on Table 3 as shown in Figure 11, where the relative error is the PTC or PRC in different ablation cases (3 mm, 2 mm, 1 mm) minus the PTC or PRC in the RT environment.

“RT” and “3 mm” curves in Figure 11 show that the PTC and PRC of graded radome walls change very little with rising temperature. When the incident angle increases from 0° to 50°, the relative error of PTC and PRC are within 2% and 1%, respectively. When the thermal protection layer peeled off from the initial 3 mm to 1 mm due to ablation, the PTC within 30° increases by about 4% and the PRC within 30° decreases by about 3%, which means a slight improvement in transmission performance. The design parameters in Ref. [10] might not consider the thermal protection layer. However, when the incident angle is larger than 30° in ablation processes, the transmission performance of the ablated radome will be significantly degraded. The maximum PTC drop and maximum PRC rise in the “2 mm” and “1 mm” curves are both over 20%. Compared to the three-layer radome walls in Figure 9, the graded radome walls are more easily affected by temperature and ablation, especially in high incident areas. The reason may be that graded radome has more layers and each layer would be affected by temperature. Therefore, more variables of layers are introduced in graded radome walls, which means graded radome’s performance at high temperatures is more difficult to control.

$T_{\mathrm{in}}\left(0.9\right)$ and $T_{\mathrm{out}}\left(0.9\right)$ are still 881.7 °C and 1569.5 °C. Similar to Table 1, Table 2 and Table 3, the graded radome wall parameters at x = 0.9 after ablation are calculated as shown in

Table 4. Parameters of GRW before and after ablation at x = 0.9.

i	AT (°C)	Thickness (mm)		${\mathit{\epsilon }}_{\mathit{r},\mathit{i}}$		$\mathit{t}\mathit{a}\mathit{n}\mathit{\delta }$ (10−3)
		BA	AA	BA	AA	BA	AA
1	932.3	1.310	1.316	2.50	2.62	4	10.22
2	1032.0	1.270	1.276	2.60	2.73		10.88
3	1126.7	1.180	1.186	2.90	3.06		11.51
4	1214.0	1.080	1.086	3.30	3.50		16.09
5	1293.6	0.980	0.986	3.90	4.16		16.62
6	1365.5	0.880	0.885	4.70	5.03		17.10
7	1430.0	0.790	0.795	5.70	6.11		17.53
8	1488.7	0.730	0.735	6.80	7.31		17.92
9	1543.2	0.680	0.684	8.00	8.62		18.29

.

The thickness of the thermal protective layer is equivalent to the ablation degree. The PTC and PRC under different ablation degrees are calculated based on Table 4 as shown in Figure 12.

“RT” and “3 mm” curves in Figure 12 show that the PTC and PRC are affected by temperature, which means the degradation of transmission performance. When the incident angle is 0°, the PTC decreases from 83.5% to 76.6%, and the PRC increases from 14.7% to 17.6%. In addition, when the thermal protection layer is peeled from 3 mm to 1 mm, the transmission performance of the radome is further degraded. The maximum rise in PTC and the maximum drop in PRC are about 4%. Comparing Figure 11 to Figure 12, the PTC and PRC change is much more significant in the high-temperature area (x = 0.9). Therefore, the high temperature and ablation will cause the degradation of transmission performance. In those conditions in the low-incident area (the incident angle is less than 30°), changes to the PTC and PRC are not as obvious as those to the PTC and PRC in the high-incident area (the incident angle is larger than 60°).

6. Conclusions

This paper has analyzed the electromagnetic performance of two typical radome walls (multilayer walls and graded walls) and given the optimal design for different radome walls. In addition, considering dielectric parameters changing, thermal expansion, and thermal protection layers peeling because of temperature and ablation, the electromagnetic performance of radome under different ablation conditions has been analyzed. The main results are:

(1) Increasing the number of radome layers cannot significantly improve the electromagnetic performance of multilayer radome walls and graded radome walls. Based on improving the transmission performance, a larger $\mathrm{\chi }$ should be chosen, and multilayer radome walls designed using method A are recommended not to exceed three layers and graded radome walls designed using method B are suggested not to exceed ten layers. In addition, the curvature coefficient $\mathrm{\chi }$ of method A should be close to 1, and the gradient coefficient m of method B should be in the range of 1 to 10.

(2) The electromagnetic performance of the traditional three-layer radome is mainly affected by thermal protection layers peeled by ablation rather than temperature. In contrast, temperature and ablation both have significant influence on the electromagnetic performance of graded radome, especially in high-incident areas. Therefore, the electromagnetic performance degradation of graded radome affected by high-temperature ablation in the high-incident area should be fully considered in the design stage. In general, the graded radomes are more easily influenced by high-temperature ablation than traditional three-layer radomes. As such, the higher the temperature, the more obvious the performance degradation of the radome wall.

In conclusion, this work can lay a foundation for improving the electromagnetic performance of the radome and the guidance ability of the radar seeker with the radome during the ablation process, and encourage further studies into the influence of a high-temperature environment on frequency selective surfaces (FSS) radomes.

In general, this work is a preliminary study about the electromagnetic performance of radomes affected by high temperature and ablation. In the future work, more verification work will be carried out, including preparation and electromagnetic testing of different types of radome walls and full-size radome, high-temperature wind tunnel test for radome, etc.