Earth-Venus Mission Analysis via Weak Capture and Nonlinear Orbit Control

Abstract

Exploration of Venus is recently driven by the interest of the scientific community in understanding the evolution of Earth-size planets, and is leading the implementation of missions that can benefit from new design techniques and technology. In this work, we investigate the possibility to implement a microsatellite exploration mission to Venus, taking advantage of (i) weak capture, and (ii) nonlinear orbit control. This research considers the case of a microsatellite, equipped with a high-thrust and a low-thrust propulsion system, and placed in a highly elliptical Earth orbit, not specifically designed for the Earth-Venus mission of interest. In particular, to minimize the propellant mass, phase (i) of the mission was designed to inject the microsatellite into a low-energy capture around Venus, at the end of the interplanetary arc. The low-energy capture is designed in the dynamical framework of the circular restricted 3-body problem associated with the Sun-Venus system. Modeling the problem with the use of the Hamiltonian formalism, capture trajectories can be characterized based on their state while transiting in the equilibrium region about the collinear libration point L1. Low-energy capture orbits are identified that require the minimum velocity change to be established. These results are obtained using the General Mission Analysis Tool, which implements planetary ephemeris. After completing the ballistic capture, phase (ii) of the mission starts, and it is aimed at driving the microsatellite toward the operational orbit about Venus. The transfer maneuver is based on the use of low-thrust propulsion and nonlinear orbit control. Convergence toward the desired operational orbit is investigated and is proven analytically using the Lyapunov stability theory, in conjunction with the LaSalle invariance principle, under certain conditions related to the orbit perturbing accelerations and the low-thrust magnitude. The numerical results prove that the mission profile at hand, combining low-energy capture and low-thrust nonlinear orbit control, represents a viable and effective strategy for microsatellite missions to Venus.

1. Introduction

The exploration of Venus has captivated scientists and space enthusiasts since the beginning of the space age. In 1962, the Mariner II probe performed a close flyby of Venus, collecting crucial atmospheric data and marking the first successful interplanetary mission [1,2]. Following this, the Venera program accomplished noteworthy achievements, including the first impact on another celestial body (Venera 3, 1965) and successful atmospheric entry (Venera 4, 1967). Subsequently, the program achieved data transmission (Venera 7, 1970) and imagery capture (Venera 9, 1975) from the surface of Venus [3,4]. These early missions were primarily dedicated to the landing of probes on the Venusian surface, and it took 13 years after Mariner II for the deployment of the first orbiter, Venera 9.

Starting from the late 70’s and through the 80’s, the interest in comprehending Venus’s surface and atmosphere prompted the development of orbiters. Data from the Pioneer Venus 1–2 spacecraft (1978) allowed producing the first topographical map of Venus surface and provided atmospheric data within an altitude range of 10 to 50 km [5]. These results were later improved by Magellan (1989), offering a high-resolution synthetic aperture radar map of the Venusian surface with details down to 120 and 300 m [6]. Furthermore, Venus Express (2005) generated a temperature map of the planet’s southern hemisphere and collected information to study the upper atmosphere [7].

To date, the only spacecraft orbiting Venus is Akatsuki (2010), operated by JAXA, dedicated to investigate Venus’s climate. However, a renewed interest in the planet’s evolution and human space exploration is leading the design of novel mission architectures [8,9,10,11]. In this context, Haibin et al. explored the feasibility of fast low-energy halo-to-halo transfers to reduce fuel consumption and flight time with respect to traditional solutions [12]. Zubko et al. proposed the use of resonant orbits to expand landing areas and ensure landing in the desired region [13,14]. This approach could even be extended to transfer an orbiter from Earth to Venus using a free-impulse flyby of an asteroid [15]. Heiligers et al. studied the application of solar sails to maintain pole-sitters at Venus, enabling continuous planetary polar observation [16]. Girija et al. expanded the use of aerocapture at Venus, demonstrating its effectiveness in deploying satellites in low-altitude circular orbits with different inclinations [17]. The problem of rideshare launches to Venus was also addressed by Graham et al., who combined patched perturbed Sims–Flanagan trajectories and low-thrust propulsion to design an Earth-Venus trajectory which concludes in a weak capture around the arrival planet [18]. Additionally, in the broader context of space exploration, the choice of a nominal space telescope orbit around the Sun-Venus L2 libration point has been discussed by Shirobokov et al., emphasizing its appeal for observing potentially hazardous asteroids approaching Earth from the daytime side of the sky [19].

In this work, we develop an Earth-Venus mission which leverages the use of traditional high-energy interplanetary transfers, low-energy captures and nonlinear orbit control for low-thrust propulsion to inject a spacecraft into any desired orbit at Venus. Low-energy trajectories are special solutions of the restricted 3-body problem, whose applications were extensively investigated in the past decades [20,21,22,23,24,25]. Their use in the design of an Earth-Venus transfer, though attractive because it leads to savings in the total delta-V (propellant mass) required [26,27], has a major drawback in the longer transfer time. The combined use of high- and low-energy trajectory, developed here, allows preserving the saving in propellant mass while limiting the increase in the transit time [28]. Nonlinear orbit control, implemented through an original feedback control law, and low-thrust propulsion allow maneuvering the spacecraft from the capture orbit to the target one [29].Two target orbits, originally selected for the Venus Flagship Mission by the Goddard Space Flight Center, are considered in this study: (i) an elliptic orbit with semilatus rectum of 12,075.7 km, eccentricity of 0.9011 and inclination of 90${}^{\circ }$, and (ii) a circular orbit with the same inclination and altitude of 300 km [30].

The paper is organized as follows. The mathematical model of the dynamical frameworks are presented in Section 2. Nonlinear orbit control is developed in Section 3. Section 4 provides an overview of the mission profile and a description of the Earth-Venus interplanetary arc. The low-energy capture at Venus and the orbit injection are discussed in Section 5, including also applications on the above-mentioned test cases. Final remarks are reported in Section 6.

2. Orbit Dynamics

The Earth-Venus mission profile presented in this research is developed using two dynamical frameworks that represent different limit cases of the general N-body problem. The perturbed restricted two-body problem (R2BP), discussed in Section 2.2, is employed when the spacecraft dynamics evolves under the dominating effect of a single (central) celestial body. This applies to the interplanetary transfer arc, where the Sun serves as the central body. Additionally, in the final phase where nonlinear control is applied, Venus acts as the central body.

When the gravitational attraction of the Sun and Venus are comparable, the spacecraft dynamics is investigated in the more general dynamical framework of the restricted 3-body problem. This circumstance occurs as the spacecraft evolves inside the equilibrium region surrounding the libration point L1 of the Sun-Venus system, as detailed in Section 2.3. Given that Venus’s orbit is nearly circular, the CR3BP proves very adequate for preliminary analysis.

2.1. Reference Frames

In this paper, the orbit dynamics of the perturbed two-body problem is described using three distinct reference frames: the Local-Vertical Local-Horizontal (LVLH) frame, the J2000 Earth-Centered Inertial (ECI) frame and the Venus-Centered Inertial (VCI) frame. The LVLH frame, a non-inertial reference, has its origin at the center of mass $O_b$ of the spacecraft, while the ECI and VCI frames have their origins at the centers of mass of Earth and Venus, respectively. The LVLH frame is defined by three axes: $\widehat{r}$, representing the local-vertical direction pointing from the center of mass of the planet to $O_b$; $\widehat{h}$, which aligns with the angular momentum of the spacecraft’s orbit; and $\widehat{\theta }$, completing the orthogonal reference frame. In the VCI frame, denoted as $\left({\widehat{g}}_1,{\widehat{g}}_2,{\widehat{g}}_3\right)$, the third unit vector is aligned with the planet’s rotational axis, pointing above the plane of the Ecliptic. ${\widehat{g}}_1$ is defined as ${\widehat{h}}_3\times {\widehat{g}}_3/|{\widehat{h}}_3\times {\widehat{g}}_3|$, where ${\widehat{h}}_3$ is orthogonal to the Ecliptic plane. ${\widehat{g}}_2$ is derived by taking the cross product of ${\widehat{g}}_3$ and ${\widehat{g}}_1$, ensuring that both axes lie within the Venusian equatorial plane. Another useful reference frame, rotating together with the spacecraft, is associated with $(\widehat{r},\widehat{E},\widehat{N})$, where $\widehat{E}$ and $\widehat{N}$ are aligned with the local East and North directions, respectively (varying depending on the orbiting planet). This frame introduces the angles $\xi$ (absolute longitude), $\varphi$ (latitude), and $\zeta$ (heading). These angles establish the relationship between the ECI or VCI frame and the ($\widehat{r}$, $\widehat{E}$, $\widehat{N}$)-frame, as well as the ($\widehat{r}$, $\widehat{\theta }$, $\widehat{h}$)-frame. To illustrate this concept, let’s consider the VCI frame:

$${\left[\begin{array}{ccc}\widehat{r}& \widehat{\theta }& \widehat{h}\end{array}\right]}^T={\mathbf{R}}_1\left(\zeta \right){\left[\begin{array}{ccc}\widehat{r}& \widehat{E}& \widehat{N}\end{array}\right]}^T={\mathbf{R}}_1\left(\zeta \right){\mathbf{R}}_2(-\varphi ){\mathbf{R}}_3\left(\xi \right){\left[\begin{array}{ccc}{\widehat{g}}_1& {\widehat{g}}_2& {\widehat{g}}_3\end{array}\right]}^T$$

(1)

where ${\mathbf{R}}_j\left(\chi \right)$ denotes the matrix associated with the elementary counterclockwise rotation by an angle $\chi$ about axis j. Moreover, an additional relation between the VCI (or ECI) frame and the ($\widehat{r}$, $\widehat{\theta }$, $\widehat{h}$)-frame can be written in terms of Keplerian orbit elements:

$${\left[\begin{array}{ccc}\widehat{r}& \widehat{\theta }& \widehat{h}\end{array}\right]}^T={\mathbf{R}}_3(\omega +\theta ){\mathbf{R}}_1\left(i\right){\mathbf{R}}_3(\Omega ){\left[\begin{array}{ccc}{\widehat{g}}_1& {\widehat{g}}_2& {\widehat{g}}_3\end{array}\right]}^T$$

(2)

reminding that $(a,e,\Omega ,\omega ,i,\theta )$ correspond to the semi-major axis, eccentricity, right ascension of the ascending node (RAAN), argument of pericenter, inclination, and true anomaly, respectively.

2.2. Perturbed Two-Body Problem

The R2BP describes the motion of a negligible mass $\tilde{m}$ (i.e., the spacecraft) under the gravitational attraction of a central body of mass $m_1\gg \tilde{m}$. The spacecraft dynamics is expressed in the LVLH frame. To avoid singularities in the dynamic equations of motion, the modified equinoctial elements are employed. These elements are defined as follows [31]:

$$\left\{\begin{array}{c}{x}_1=a(1-e^2)\hfill \\ x_2=ecos(\Omega +\omega )\hfill \\ x_3=esin(\Omega +\omega )\hfill \\ x_4=tan\frac{i}{2}cos\Omega \hfill \\ x_5=tan\frac{i}{2}sin\Omega \hfill \\ x_6=\Omega +\omega +\theta \hfill \end{array}\right.$$

(3)

Using the modified equinoctial elements, the following form of the dynamic equations of motion is obtained [29]:

$$\left\{\begin{array}{c}\dot{\mathit{z}}=\sqrt{\frac{x_1}{\mu }}\mathit{G}(\mathit{z},x_6)\mathit{a}\hfill \\ {\dot{x}}_6=\sqrt{\frac{\mu }{x_1^3}}{\left(1+x_{2}cos{x}_6+x_{3}sin{x}_6\right)}^2+\sqrt{\frac{x_1}{\mu }}\frac{x_{4}sin{x}_6-x_{5}cos{x}_6}{1+x_{2}cos{x}_6+x_{3}sin{x}_6}{a}_h\hfill \end{array}\right.$$

(4)

where the dot sign indicates the derivative in time and $\mathit{z}:={[x_1,x_2,x_3,x_4,x_5]}^T$,

$$\mathit{G}(\mathit{z},x_6)=\left[\begin{array}{ccc}0& \frac{2}{x_1}\eta & 0\\ sin{x}_6& \frac{\left(\eta +1\right)cos{x}_6+x_3}{\eta }& -\frac{x_{4}sin{x}_6-x_{5}cos{x}_6}{\eta }{x}_3\\ -cos{x}_6& \frac{\left(\eta +1\right)sin{x}_6+x_3}{\eta }& -\frac{x_{4}sin{x}_6-x_{5}cos{x}_6}{\eta }{x}_2\\ 0& 0& \frac{1+x_4^2+x_5^2}{2\eta }cos{x}_6\\ 0& 0& \frac{1+x_4^2+x_5^2}{2\eta }sin{x}_6\end{array}\right]$$

(5)

$$\eta =1+x_{2}cos{x}_6+x_{3}sin{x}_6$$

(6)

and $\mathit{a}={[a_r,a_{\theta },a_h]}^T$ is the net acceleration acting onto the satellite, given by the sum of the thrust acceleration $\left({\mathit{a}}_{\mathit{T}}\right)$ and the acceleration due to orbital perturbations $\left({\mathit{a}}_{\mathit{P}}\right)$.

The thrust acceleration acting onto the spacecraft during an orbital maneuver is determined by the ratio of the thrust force $\mathit{T}$ to the spacecraft mass $\tilde{m}$. As the mass decreases during the propelled phases, we introduce the variable $x_7=\tilde{m}/{\tilde{m}}_0$, representing the mass ratio, where ${\tilde{m}}_0$ is the initial mass of the spacecraft. We can add another differential equation to Equations (4) to express the rate of change of $\tilde{m}$, given by

$${\dot{x}}_7=-\frac{u_T}{c},\mathrm{with}{u}_T=\left|{\mathit{u}}_{\mathit{T}}\right|\in \left[0,u_T^{(max)}\right]$$

(7)

where ${\mathit{u}}_{\mathit{T}}$ denotes the ratio of $\mathit{T}$ to ${\tilde{m}}_0$, and c is the effective exhaust velocity of the propulsion system. Equation (7) allows us to rearrange the expression for the thrust acceleration as

$${\mathit{a}}_{\mathit{T}}=\frac{{\mathit{u}}_{\mathit{T}}}{x_7}$$

(8)

In the analysis of the Venus arc, our model includes two significant perturbing factors: the non-spherical nature of Venus’s gravitational field and the gravitational influence exerted by a third celestial body, namely, the Sun. The former perturbations are modeled through the spherical harmonic expansion of the gravitational potential (per unit mass). This expansion is expressed in terms of Legendre polynomials, $P_{lm}$

$$U=\frac{\mu }{r}\{1-\sum _{l=2}^{\infty }{\left({\displaystyle \frac{R_V}{r}}\right)}^l{J}_l{P}_{l0}\left(sin\varphi \right)+\sum _{l=2}^{\infty }\sum _{m=1}^l{\left(\frac{R_V}{r}\right)}^l{J}_{lm}{P}_{lm}\left(sin\varphi \right)cos\left[m({\lambda }_g-{\lambda }_{lm})\right]\}$$

(9)

where $R_V$ represents Venus’s equatorial radius, $\varphi$ denotes the spacecraft’s latitude, and ${\lambda }_g$ its geographical longitude, measured from Venus’s prime meridian [32]. The corresponding sidereal time, denoted as ${\theta }_G$, is measured counterclockwise from ${\widehat{g}}_3$, which allows to express the satellite’s geographical longitude as ${\lambda }_g=\xi -{\theta }_G$. In this study, we consider all harmonics up to $l=m=15$ for the analysis of Venus [33]. The coefficients associated with these harmonics are denoted as $J_{lm}$ and ${\lambda }_{lm}$ in Equation (9).

Within the $\left(\widehat{r},\widehat{E},\widehat{N}\right)$-frame, the gravitational acceleration acting upon the spacecraft on Venus is obtained as

$$\mathit{g}=\nabla U\mathrm{where}\nabla =\widehat{r}{\displaystyle \frac{\partial r}{\partial r}}+{\displaystyle \frac{\widehat{E}}{rcos\varphi }}{\displaystyle \frac{\partial }{\partial {\lambda }_g}}+{\displaystyle \frac{\widehat{N}}{r}}{\displaystyle \frac{\partial }{\partial \varphi }}$$

(10)

The preceding equation, in conjunction with Equation (9), allows the calculation of the three components of acceleration, namely, $(g_r,g_{\theta },g_h)$, in the LVLH frame.

Additionally, the contribution of the Sun is accounted for as a third-body acceleration [34]

$${\mathbf{a}}^{\left(3B\right)}=-{\mu }_P\left\{\frac{{\mathbf{r}}_{\mathbf{P}}}{r_P^3}+\frac{\mathbf{r}-{\mathbf{r}}_{\mathbf{P}}}{{\left[\left(\mathbf{r}-{\mathbf{r}}_{\mathbf{P}}\right)·\left(\mathbf{r}-{\mathbf{r}}_{\mathbf{P}}\right)\right]}^{\frac{3}{2}}}\right\}$$

(11)

where ${\mu }_P$ and ${\mathbf{r}}_{\mathbf{P}}$ respectively represent the gravitational parameter of the perturbing body ($m_P$) and the position vector of $m_P$ relative to $\tilde{m}$.

To summarize, during the interplanetary arc and the transfer from the capture orbit to the target one, the spacecraft dynamics is modeled using Equations (4) and (7). The total acceleration acting on the spacecraft is the sum of Equations (8)–(11).

2.3. Circular Restricted 3-Body Problem

The CR3BP describes the motion of a body of negligible mass $\tilde{m}$ under the gravitational attraction of two celestial bodies with masses $m_1>m_2\gg \tilde{m}$, moving along circular orbits about their common center of mass O [35]. In this work, the negligible mass $\tilde{m}$ represents the spacecraft and the primaries are the Sun ($m_1$) and Venus ($m_2$). Because the primaries rotate at a constant rate $\omega$ around O, the motion of the satellite can be conveniently described in a rotating, or synodic, coordinate system centered in O, with axes $\widehat{x}$ pointing from $m_1$ to $m_2$, $\widehat{z}$ orthogonal to the orbital plane of the primaries and $\widehat{y}$ completing the rectangular frame. The dynamic equations governing the motion in the CR3BP are

$$\left\{\begin{array}{c}\dot{x}=u\hfill \\ \dot{y}=v\hfill \\ \dot{z}=w\hfill \\ \dot{u}=2v+x-{\displaystyle \frac{1-\mu }{r_1^3}}(x+\mu )-{\displaystyle \frac{\mu }{r_2^3}}(x-1+\mu )\hfill \\ \dot{v}=-2u+y-{\displaystyle \frac{1-\mu }{r_1^3}}y-{\displaystyle \frac{\mu }{r_2^3}}y\hfill \\ \dot{w}=-{\displaystyle \frac{1-\mu }{r_1^3}}z-{\displaystyle \frac{\mu }{r_2^3}}z\hfill \end{array}\right.$$

(12)

where $\mu =\frac{m_2}{m_1+m_2}$, $(x,y,z)$ and $(u,v,w)$ are, respectively, the spacecraft position and velocity coordinates in the synodic frame, and $r_i$ indicates the distance between the spacecraft and the i-th primary. It shall be noted that the set of Equations (12) is dimensionless, and the corresponding dimensional values can be obtained by using the units of distance and time expressed as

$$\left\{\begin{array}{c}DU=r_{12}\hfill \\ TU=\frac{1}{\omega }\hfill \end{array}\right.$$

(13)

where $r_{12}$ is the (constant) distance between the primaries.

The CR3BP admits 5 equilibrium points $\left(L_i\right)$, also named the Lagrange or libration points, and one integral of motion, the Jacobi constant [36]:

$$C=-({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)+(x^2+y^2)+2\left({\displaystyle \frac{1-\mu }{r_1}}+{\displaystyle \frac{\mu }{r_2}}\right)$$

(14)

Indicating by $C_1$ the value of the Jacobi constant calculated at $L_1$, the libration point laying on $\widehat{x}$ at $-\mu <x_{L_1}<1-\mu$, it can be proved that the spacecraft can transit between the two primaries if and only if $C<C_1$ [37]. This condition is pivotal to characterize low-energy trajectories considered in this work, as detailed hereafter.

Recalling that the Hamiltonian function of the CR3BP is by definition $H=-C/2$, the system of Equations (12) can be rearranged in the form of Hamilton’s equations:

$$\left\{\begin{array}{c}\dot{\mathit{q}}={\displaystyle \frac{\partial H}{\partial \mathit{p}}}\hfill \\ \dot{\mathit{p}}=-{\displaystyle \frac{\partial H}{\partial \mathit{q}}}\hfill \end{array}\right.$$

(15)

These equations can be linearized around the $L_1$ equilibrium point by expanding the Hamiltonian H as a power series and keeping terms up to second order. The corresponding Hamiltonian position and conjugate momenta are defined as $\mathit{q}={\left[x-x_{L_1},y,z\right]}^T$ and $\mathit{p}={\left[u-y,v+x-x_{L_1},w\right]}^T$, respectively. The quadratic Hamiltonian function can be written as:

$$H_2=\frac{1}{2}(p_1^2+p_2^2+p_3^2+2p_1{q}_2-2p_2{q}_1)-\frac{K}{2}(2q_1^2-q_2^2-q_3^2)=h$$

(16)

with $K=\frac{1-\mu }{|x_{L_1}{+\mu |}^2}+\frac{\mu }{|x_{L_1}{+\mu -1|}^2}$. In virtue of the linearization, this function satisfies the relation $H_2=\frac{1}{2}\left(C_1-C\right)=h$, where h is an arbitrarily small constant named “energy level”.

The linear dynamical system obtained applying Equation (16) to Equation (15) has one real $\left(\rho \right)$ and two complex $(i{\lambda }_1,i{\lambda }_2)$ eigenvalues. Based on Morse’s lemma, $H_2$ can be rearranged as the sum of three local integrals of motion, each associated with one of the three eigenspaces mentioned above. This new form of H can be derived by applying a canonical transformation by Siegel and Moser ${[\mathit{\sigma },\mathit{\tau }]}^T={\mathit{T}}_N{[\mathit{q},\mathit{p}]}^T$, producing [38]:

$${\widehat{H}}_2=\rho {\sigma }_1{\tau }_1+\frac{{\lambda }_1}{2}({\sigma }_2^2+{\tau }_2^2)+\frac{{\lambda }_2}{2}({\sigma }_3^2+{\tau }_3^2)=h$$

(17)

with ${\sigma }_1,{\tau }_1\in \mathbb{R}$ and ${\sigma }_i,{\tau }_i\in \mathbb{C},i=2,3$. The long-term behavior of low-energy trajectories and their osculating orbital elements can be characterized by their topological location inside the phase space surrounding the libration point $L_1$, which is referred to as the “equilibrium region” and is defined by the following set of equations [39,40]:

$$\left\{\begin{array}{c}\rho {\sigma }_1{\tau }_1+\frac{{\lambda }_1}{2}({\sigma }_2^2+{\tau }_2^2)+\frac{{\lambda }_2}{2}({\sigma }_3^2+{\tau }_3^2)=h\hfill \\ |{\sigma }_1-{\tau }_1|\le ϵ\hfill \end{array}\right.$$

(18)

where $ϵ$ is an arbitrarily small constant. It is worth to clarify here that the second of Equations (18) indicates that the spacecraft moves close to the equilibrium point. In fact, if this condition is not verified, ${\widehat{H}}_2$ does not provide an accurate description of the system dynamics. Figure 1 shows a projection of the equilibrium region onto the $[{\sigma }_1,{\tau }_1]$ plane with boundaries represented by the green dashed hyperbola (${\sigma }_1{\tau }_1=h/\rho$) and the green straight lines $|{\sigma }_1-{\tau }_1|=ϵ$. In the same figure, the flow associated to some classes of trajectories is represented:

• ${\sigma }_1{\tau }_1>0$ (solid black hyperbola), transit trajectories which cross the equilibrium region multiple times (i.e., evolve alternately around one of the primaries)
• ${\sigma }_1{\tau }_1<0$ (dashed black hyperbola), bouncing trajectories which may enter but never cross the equilibrium region (they evolve around only one of the two primaries)
• ${\sigma }_1={\tau }_1=0$, quasi-periodic orbits that evolve only within the equilibrium region
• ${\sigma }_1=0$ (blue line) or ${\tau }_1=0$ (red line), trajectories asymptotic to or from the quasiperiodic orbits.

Moreover, as stated by Conley, trajectories close to asymptotic ones (${\sigma }_1\to 0$ or ${\tau }_1\to 0$) represent long-term capture orbits, which evolve around either primary indefinitely over time after crossing the equilibrium region once [39].

For the sake of clarity, the capture condition is henceforth expressed in terms of position and velocity coordinates in the synodic frame, which are obtained by applying the inverse of the Siegel-Moser canonical transformation, followed by the conversion from Hamiltonian to position space variables [41]:

$$\left(1+2{\gamma }^2\right)(x-x_{L_1})+\left(1-{\gamma }^2\right)y+\rho v_x-{\rho }_y\to 0$$

(19)

with ${\gamma }^2=\left(-\frac{\mu }{|x_{L_1}{+\mu -1|}^3}-\frac{1-\mu }{|x_{L_1}{+\mu |}^3}\right)$ and $\alpha =-2\rho /\left({\rho }^2+{\gamma }^2-1\right)$.

The reader shall note that these properties are preserved also in the presence of a fourth body introducing a small gravitational perturbation or if the motion of the primaries is slightly elliptical [42,43]. Consequently, the CR3BP model is not only adequate, but also acceptably accurate to design low-energy captures in the Sun-Venus system if further perturbations are not considered.

3. Nonlinear Orbit Control

We present a nonlinear feedback orbit control law for the guidance of a spacecraft toward some desired conditions. These are specified in terms of modified equinoctial elements, as a function of $\mathit{z}$ only, in the following target set:

$$\mathit{\psi }\left(\mathit{z}\right)=\mathbf{0}$$

(20)

where $\mathit{\psi }$ is a nonlinear vector function, such that $dim\left(\mathit{\psi }\right)\le 5$ (at most one condition can be imposed for each orbital element contained in $\mathit{z}$).

The feedback control law is constructed using the direct method of Lyapunov, which provides sufficient conditions for stability and avoids linearization around a reference solution [44]. The following candidate Lyapunov function is introduced:

$$V=\frac{1}{2}{\mathit{\psi }}^T\mathbf{K}\mathit{\psi }$$

(21)

where $\mathbf{K}$ is a diagonal matrix with positive constant elements (representing weight coefficients selected a priori based on the application) and it is positive definite. It is easily recognized that $V\ge 0$, with $V=0$ if and only if $\mathit{\psi }=\mathbf{0}$ (i.e., if the target state is reached), making it a definite positive function. Additional conditions must be satisfied for V to be a valid Lyapunov function. First, we introduce the following auxiliary vector:

$$\mathit{b}:={\mathbf{G}}^T{\left({\displaystyle \frac{\partial \mathit{\psi }}{\partial \mathit{z}}}\right)}^T\mathbf{K}\mathit{\psi }$$

(22)

Two propositions establish the conditions for V to serve as a Lyapunov function and lead to the identification of a saturated feedback law.

Proposition 1.

If ψ and $\left(\partial \mathit{\psi }/\partial \mathit{z}\right)$ are continuous, $\left|\mathit{b}\right|>0$ unless $\mathit{\psi }=\mathbf{0}$, and $u_T^{(max)}\ge x_7\left|\mathit{b}+{\mathit{a}}_{\mathit{P}}\right|$, then the feedback control law

$${\mathit{u}}_{\mathit{T}}=-x_7\left(\mathit{b}+{\mathit{a}}_{\mathit{P}}\right)$$

(23)

leads a dynamical system governed by Equations (4) and (7) to converge asymptotically to the target set associated with Equation (20).

Indeed, the proposed control law ensures that $\dot{V}=-{\mathit{b}}^T\mathit{b}=-{\left|\mathit{b}\right|}^2\le 0$ with $\dot{V}=0\iff \mathit{b}=\mathbf{0}$, which corresponds to the attracting set. Therefore, it establishes the candidate function (21) as a valid Lyapunov function [44]. As a result, the control law (23) drives the dynamical system to asymptotically converge to the target state defined by (20). This control law incorporates feedback from the spacecraft state in all its terms, except for the weight matrix. By leveraging the information provided by the state variables, the control law dynamically adjusts the direction and magnitude of thrust at each iteration, enabling the achievement of the desired orbital conditions. However, the physical feasibility of the control lies in ensuring that the magnitude of ${\mathit{u}}_{\mathit{T}}$ does not exceed $u_T^{(max)}$. Consequently, the condition $x_7\left|\mathit{b}+{\mathit{a}}_{\mathit{P}}\right|\le u_T^{(max)}$ must be satisfied to ensure control feasibility. In cases where this constraint is violated, an alternative feedback control law can be employed, which operates in a saturated manner by applying maximum thrust.

Proposition 2.

If ψ and $\left(\partial \mathit{\psi }/\partial \mathit{z}\right)$ are continuous, $\left|\mathit{b}\right|>0$ unless $\mathit{\psi }=\mathbf{0}$, and $u_T^{(max)}<x_7\left|\mathit{b}+{\mathit{a}}_{\mathit{P}}\right|$ and ${\mathit{b}}^T{\mathit{a}}_{\mathit{P}}\le 0$, then the feedback control law

$${\mathit{u}}_{\mathit{T}}=-u_T^{(max)}\frac{\mathit{b}+{\mathit{a}}_{\mathit{P}}}{\left|\mathit{b}+{\mathit{a}}_{\mathit{P}}\right|}$$

(24)

leads a dynamical system governed by Equations (4) and (7) to converge asymptotically to the target set associated with Equation (20).

It can be shown that for the given control law, $\dot{V}\le 0$ if ${\mathit{b}}^T{\mathit{a}}_{\mathit{P}}<0$, while no conclusions can be drawn if ${\mathit{b}}^T{\mathit{a}}_{\mathit{P}}>0$ [45]. The sign of this term generally varies over time and relies on the specific time-evolution of the dynamical system. Consequently, an additional sufficient condition is necessary to ensure that $\dot{V}<0$ even when ${\mathit{b}}^T{\mathit{a}}_{\mathit{P}}>0$.

Proposition 3.

If ψ and $\left(\partial \mathit{\psi }/\partial \mathit{z}\right)$ are continuous, $\left|\mathit{b}\right|>0$ unless $\mathit{\psi }=\mathbf{0}$, and $x_7\left|{\mathit{a}}_{\mathit{P}}\right|<u_T^{(max)}<x_7\left|\mathit{b}+{\mathit{a}}_{\mathit{P}}\right|$, then the feedback control law in Equation (24) leads a dynamical system governed by Equations (4) and (7) to converge asymptotically to the target set associated with Equation (20).

Proposition 3 provides a valuable sufficient condition with a clear interpretation: if the magnitude of the thrust acceleration, $u_T^{(max)}/x_7$, exceeds the perturbation acceleration magnitude, $\left|{\mathit{a}}_{\mathit{P}}\right|$, then $\dot{V}<0$ unless $\mathit{b}=\mathbf{0}$.

The two feedback laws presented in Equations (23) and (24) can be combined into a single expression:

$${\mathit{u}}_{\mathit{T}}=-u_T^{(max)}\frac{x_7\left(\mathit{b}+{\mathit{a}}_{\mathit{P}}\right)}{max\left\{u_T^{(max)},\left|x_7\left(\mathit{b}+{\mathit{a}}_{\mathit{P}}\right)\right|\right\}}$$

(25)

This control law can be implemented using steerable and throttleable propulsive thrust, where both the magnitude and direction can vary over time.

Propositions 1–3 establish sufficient conditions for Lyapunov stability. Consequently, the asymptotic convergence is not necessarily compromised if $\dot{V}$ becomes positive within limited time intervals.

Nonlinear Control for Semi-Major Axis, Eccentricity, and Inclination

With the newly defined control law, we aim to achieve a specific target state identified by the following orbit elements: semi-major axis, eccentricity, and inclination. This implies that the other orbital elements are left free and can take any value within their respective ranges. The desired conditions, denoted with the subscript d, can be expressed by the following equations:

$$x_1=p_d{x}_2^2+x_3^2=e_d^2{x}_4^2+x_5^2={tan}^2{\displaystyle \frac{i_d}{2}}$$

(26)

where $p_d=a_d\left(1-e_d^2\right)$ and $e_d<1$. We define the vector that represents the target set as:

$$\mathit{\psi }=\left[\begin{array}{c}{x}_1-p_d\\ x_2^2+x_3^2-e_d^2\\ x_4^2+x_5^2-{tan}^2{\displaystyle \frac{i_d}{2}}\end{array}\right]$$

(27)

We analytically derive the components $\left\{b_1,b_2,b_3\right\}$ of the vector $\mathit{b}$ to be used in the control law (25):

$$b_1=-2k_2\sqrt{{\displaystyle \frac{x_1}{\mu }}}\left(x_{3}cos{x}_6-x_{2}sin{x}_6\right)\left(x_2^2+x_3^2-e_d^2\right)$$

(28)

$$b_2={\displaystyle \frac{2}{\eta }}\sqrt{{\displaystyle \frac{x_1}{\mu }}}\left\{k_1{x}_1\left(x_1-p_d\right)+k_2\left(x_2^2+x_3^2-e_d^2\right)\left[{\eta }^2+x_2^2+x_3^2-1\right]\right\}$$

(29)

$$b_3={\displaystyle \frac{k_3}{\eta }}\sqrt{{\displaystyle \frac{x_1}{\mu }}}\left(x_{4}cos{x}_6+x_{5}sin{x}_6\right)\left(x_4^2+x_5^2-{tan}^2{\displaystyle \frac{i_d}{2}}\right)\left(x_4^2+x_5^2+1\right)$$

(30)

where $k_i$$\left(i=1,2,3\right)$ represent the elements of the diagonal matrix $\mathbf{K}$.

We proceed with the identification of the attracting set, collecting all the dynamical states that satisfy $\dot{V}=0\iff \mathit{b}=\mathbf{0}$. This set includes the target set since $\mathit{\psi }=\mathbf{0}$ implies $\mathit{b}=\mathbf{0}$. However, the reverse is not guaranteed. As a matter of fact, considering the definition of $\mathit{b}$, it includes the term $\mathit{\psi }$ among its factors: if this term is zero, then $\mathit{b}=\mathbf{0}$. However, it is possible for $\mathit{b}$ to cancel out due to other terms. This implies that $\dot{V}=0$ but $V\ne 0$, resulting in the non-attainment of the target state. Hence, it is possible to reach the attracting set without reaching the target set ($\mathit{b}=\mathbf{0}$, $\mathit{\psi }\ne \mathbf{0}$), leading to the settling of the Lyapunov function at a nonzero steady-state value, thereby achieving a different condition than the desired target.

In our case, the attracting set includes the following subsets [46]:

1.

$x_1=0$ (rectilinear trajectories);

2.

$x_1=p_d$, $x_2^2+x_3^2=e_d^2$, and $x_4=x_5=0$ (equatorial elliptical orbits with semilatus rectum $p_d$ and eccentricity $e_d$);

3.

$x_1=p_d$, $x_2^2+x_3^2=0$, and $x_4^2+x_5^2={tan}^2{\displaystyle \frac{i_d}{2}}$ (circular orbits with radius $p_d$ and inclination $i_d$);

4.

$x_1=p_d$, $x_2^2+x_3^2=0$, and $x_4^2+x_5^2=0$ (circular equatorial orbits with radius $p_d$);

5.

$x_1=p_d$, $x_2^2+x_3^2=e_d^2$, and $x_4^2+x_5^2={tan}^2{\displaystyle \frac{i_d}{2}}$ (target set).

The application of LaSalle’s invariance principle allows ruling out subset 1.

Given the continuity of $\mathit{\psi }$ and $\dot{V}<0$ (except within the attracting set, denoted as A), the condition $V\left(\mathit{z}\right)<V\left({\mathit{z}}_0\right)$, where ${\mathit{z}}_0$ represents the evaluation of $\mathit{z}$ at the initial time, defines a compact set C. To apply LaSalle’s principle, we seek the invariant set within the intersection of A and C. The invariant set comprises dynamical states within the attracting set of $\mathit{z}$ that remain unchanged when $\mathit{a}\equiv \mathbf{0}$. Consequently, once the invariant set is reached, $\mathit{b}\equiv \mathbf{0}$ at subsequent times, implying $\dot{\mathit{b}}\equiv \mathbf{0}$ while $\mathit{a}\equiv \mathbf{0}$. In this specific scenario, when $\mathit{a}\equiv \mathbf{0}$, the time derivatives of the three components of $\mathit{b}$ can be expressed as

$${\dot{b}}_j=\frac{\partial b_j}{\partial x_6}\sqrt{\frac{\mu }{x_1^3}}{\eta }^2\left(j=1,2,3\right)$$

(31)

An examination of ${\dot{b}}_j(j=1,2,3)$ reveals that subset 1 ($x_1=0$) does not belong to the invariant set, thereby ruling out convergence toward rectilinear trajectories. On the other hand, subsets 2 and 5 constitute the invariant set for the given problem [46].

It should be noted that convergence toward subsets 2 through 5 is purely theoretical, as demonstrated in [46], with the interesting practical consequence that the dynamical system under consideration exhibits global convergence toward the desired operational conditions when the control law (25) is adopted.

4. Interplanetary Transfer

The mission begins at the satellite deployment on a Trans-Lunar Injection (TLI) trajectory, chosen to be compatible with currently available rideshare opportunities, with orbit parameters summarized in

Table 1. Orbit parameters for the spacecraft at deployment in the ECI reference frame.

Parameter	Symbol [Unit]	Value
Semi-major axis	a [km]	216,500
Eccentricity	e	0.969
Inclination	i [deg]	57 or 123
Release Altitude	h [km]	70,000

. Depending on mission requirements, the orbital inclination can be either 57${}^{\circ }$ or the supplementary 123${}^{\circ }$ (retrograde launch), while the right ascension of the ascending node and the argument of perigee can be freely chosen.

After being released from the launcher, the spacecraft undergoes a first three-dimensional impulsive maneuver at the apogee to increase its energy and adjust the inclination, which is necessary for the spacecraft to be on the right trajectory toward Venus. The perigee altitude is raised to 1000 km, a value chosen to minimize the energy losses by thrusting as close as possible to the attracting body (Earth) [34], while avoiding crossing the Low Earth Orbit region. The selection of 1000 km, although arbitrary, appears reasonable and serves as a mission constraint. Subsequently, at the perigee, another critical impulsive maneuver called Trans-Venus Injection (TVI) is executed. With this maneuver, the spacecraft is transferred to a hyperbolic orbit, reaching Venus at a pericenter altitude of 300 km. Upon reaching Venus, the mission explores two distinct scenarios to achieve capture around the planet and the attainment of the target orbits, with the goal of minimizing the total propellant usage:

1.

The first scenario, named “APO”, achieves this objective by first targeting a specific “optimal apocenter” altitude for the initial capture around Venus and then employing nonlinear low-thrust control to reach the desired target orbit.

2.

The second scenario, labelled as “L1”, focuses on the use of low-energy captures designed in the equilibrium region about $L_1$.

These scenarios will be comprehensively discussed in Section 5.

The preliminary interplanetary trajectory from Earth to Venus is designed using the patched conics method, which simplifies calculations in a multi-body environment while ensuring accuracy [34]. This method divides the trajectory into three arcs: a hyperbolic departure trajectory from Earth, an elliptical heliocentric transfer arc, and a hyperbolic arrival trajectory to Venus. The first and third arcs are considered within the sphere of influence of the respective planet, with the Sun acting as the only attracting body beyond these regions in the second arc. To determine the velocities at departure and arrival, the hyperbolic excess velocities $v_{{\infty }_1}$ and $v_{{\infty }_2}$ are calculated. $v_{{\infty }_1}$ represents the excess velocity at departure relative to Earth, while $v_{{\infty }_2}$ corresponds to the velocity at arrival at Venus. These velocities are obtained by subtracting the velocities of Earth and Venus from the departing and arriving velocities in the heliocentric frame, respectively. Specifically, we have:

$$v_{{\infty }_1}=\left|{\mathit{v}}_{\mathbf{1}}-{\mathit{v}}_{\mathit{E}}\right|$$

(32)

$$v_{{\infty }_2}=\left|{\mathit{v}}_{\mathbf{2}}-{\mathit{v}}_{\mathit{v}}\right|$$

(33)

Here, ${\mathit{v}}_{\mathbf{1}}$ and ${\mathit{v}}_{\mathbf{2}}$ represent the departing and arriving velocities, while ${\mathit{v}}_{\mathit{E}}$ and ${\mathit{v}}_{\mathit{v}}$ denote the velocities of Earth and Venus, respectively.

The mission timeline is set between 2029 and 2033, aligning with the launch periods of notable future missions such as VERITAS, EnVision, DAVINCI+, Venera-D, and the Venus Flagship Mission [10,47,48,49,50]. To analyze the optimal launch opportunities, porkchop plots are generated for the years 2029–2033, covering each day of the year with a flight duration (ToF, Time of Flight) ranging from 100 to 200 days. This range for the ToF is chosen based on the consideration of a “short” journey to Venus, although more fuel efficient longer duration solutions may exist. By examining the results of the porkchop plots, launch opportunities that align with the available propulsion capabilities can be identified. These plots depict contour lines of the hyperbolic excess velocity ($v_{\infty }$) in relation to combinations of departure and arrival dates. They are generated by solving the Lambert’s problem for all possible combinations of departure and arrival dates within specified intervals. The algorithm outputs the initial and final velocities of the spacecraft, ${\mathit{v}}_{\mathbf{1}}$ and ${\mathit{v}}_{\mathbf{2}}$, along the transfer heliocentric trajectory. Then the two hyperbolic excess velocities ($v_{{\infty }_1}$ and $v_{{\infty }_2}$) are calculated using Equations (32) and (33). The DE405 ephemerides are used for the positions and velocities of the two planets.

To systematically search for the optimal heliocentric transfer, the sum of the hyperbolic excess velocities is minimized:

$$v_{\infty }^{\mathrm{TOT}}:=v_{{\infty }_1}+v_{{\infty }_2}$$

(34)

The desired solution corresponds to the best combination of departure date and corresponding time of flight which minimizes $v_{\infty }^{\mathrm{TOT}}$. This overall minimization reduces the propulsion effort required for departure from Earth and orbital insertion around Venus, resulting in propellant savings.

An exhaustive investigation is conducted to find the minimum value of $v_{\infty }^{\mathrm{TOT}}$, with the porkchop plots generated using MATLAB. The obtained solution is presented in

Table 2. Solutions minimizing $v_{\infty }^{\mathrm{TOT}}$ for the years 2029, 2031, and 2032. All times are given in UTC.

Departure		Arrival		ToF	${\mathit{v}}_{{\mathit{\infty }}_1}$	${\mathit{v}}_{{\mathit{\infty }}_2}$	${\mathit{v}}_{\mathit{\infty }}^{\mathbf{TOT}}$
Date		Date		(Days)	(km/s)	(km/s)	(km/s)
25 October 2029	05:00	3 April 2030	19:24	160.6	2.8098	4.8299	7.6397
23 May 2031	16:00	26 October 2031	13:36	155.9	2.5632	3.8096	6.3728
6 December 2032	05:00	12 May 2033	17:00	157.5	3.1757	2.7201	5.8958

.

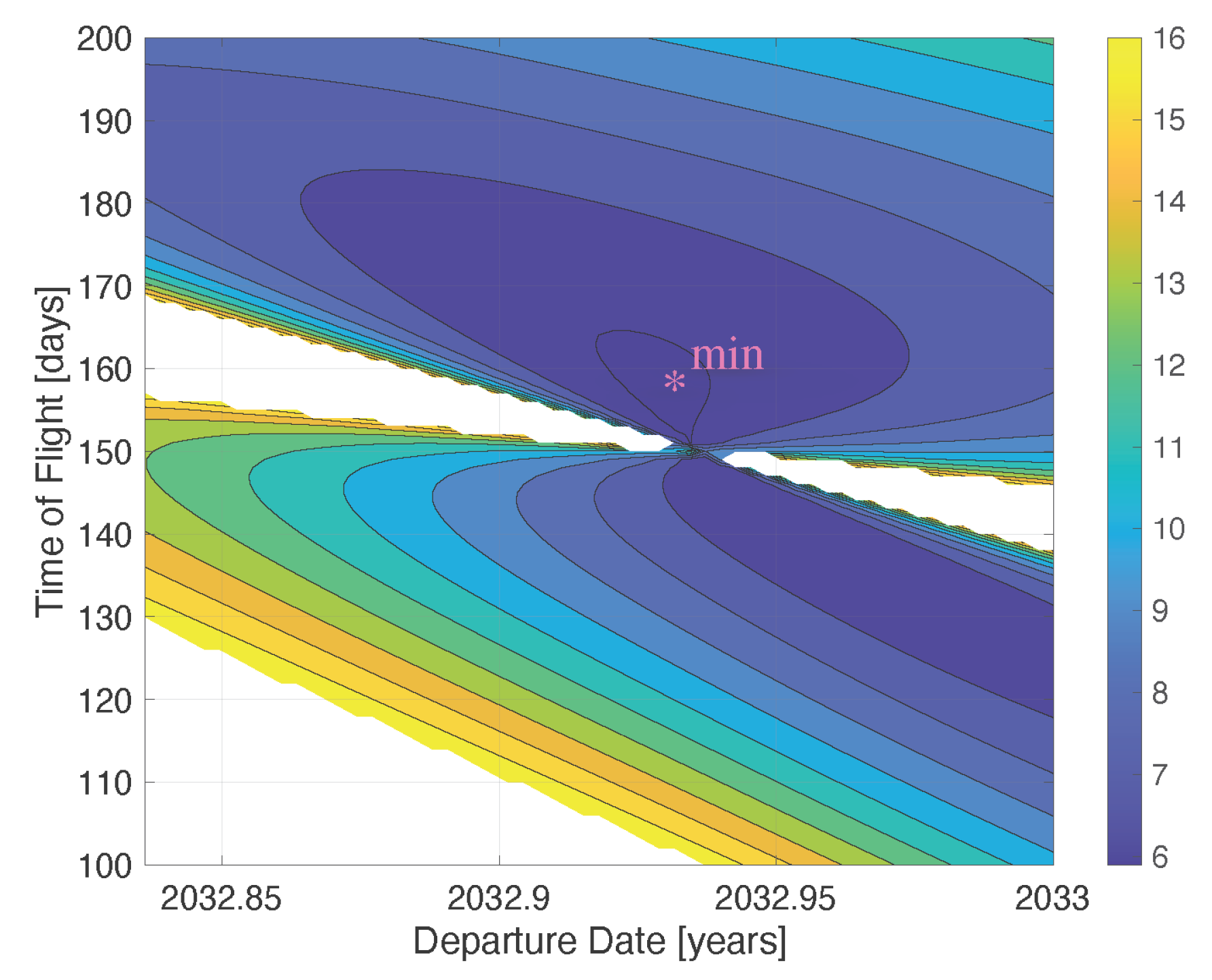
The porkchop plots, displayed in Figure 2 and Figure 3, provide a visual representation of the transfer options for the years 2029 to 2033, with a specific focus on 2032. The optimal solution corresponds to a departure on 6 December 2032, and an arrival 158 days later on 13 May 2033. The resulting $v_{\infty }^{\mathrm{TOT}}$ is calculated as $3.1757\mathrm{km}/\mathrm{s}+2.7201\mathrm{km}/\mathrm{s}=5.8958$ km/s. Notably, this solution is located in the same region as the minimum arrival hyperbolic excess velocity at Venus, rather than the departure from Earth. The trajectory corresponding to this optimal solution, obtained using the Lambert problem solver algorithm, is depicted in Figure 4. This trajectory serves as the baseline for the mission and is reproduced using the General Mission Analysis Tool (GMAT) propagator [51], in a high-fidelity framework.

During our investigation, we explored alternative trajectories and discovered a more advantageous solution that involved multiple revolutions. This alternative solution, with a departure on 5 June 2032, and arrival on 31 August 2033, resulted in a total $v_{\infty }$ of 5.6163 km/s. Compared to the previously identified optimal solution, this alternative solution offered a reduction of 280 m/s in total $v_{\infty }$, but at the expense of a 452-day travel duration, nearly three times longer.

Table 3. Numerical results for the Hohmann transfer from Earth to Venus, using JPL data [52].

Parameter	Symbol [Unit]	Value
Departure v-infinity	$v_{{\infty }_1}$ [km/s]	2.4991
Arrival v-infinity	$v_{{\infty }_2}$ [km/s]	2.7109
Time of Flight	ToF [days]	146.04
Synodic period	${\tau }_{\mathrm{syn}}$ [days]	584

presents the main parameters of the Hohmann transfer for reference, which can serve only as a comparative case (because it assumes coplanar circular orbits of Earth and Venus). Taking into account the trade-off between energy savings and extended travel durations, we selected the shorter optimal solution as the reference for our mission.

The initial reference solution involves departing from Earth on 6 December 2032, at 05:00 UTC, and arriving at Venus on 12 May 2033, at 17:00 UTC. It’s important to note that these dates do not consider the dynamics inside the spheres of influence or perturbations. In the following sections, we will address these factors by employing GMAT for the propagation.

The mission profile outlined at the beginning of Section 4 is designed using backward propagation, from the Venus arrival date, which allows for a more detailed specification of arrival conditions and enhances flexibility during the Earth departure phase. The spacecraft’s arrival at Venus is set to 12 May 2033, at 17:00 UTC. The trajectory is hyperbolic, characterized by a pericenter altitude of 300 km and an excess velocity $v_{{\infty }_2}=2.7201$ km/s ($C_3=7.3989$ km${}^2$/s${}^2$), as determined from the porkchop plots. By employing a Target sequence in GMAT, the orientation of the hyperbola at Venus is determined, enabling backward propagation to achieve an Earth return with an altitude of 1000 km from the hyperbolic perigee. The dynamical model for this phase includes the Sun, Venus, Earth, and the Moon as point masses, while disregarding other perturbations. It is worth noting that multiple combinations of parameters exist that yield the same $v_{{\infty }_1}$, resulting in hyperbolas that share energy and asymptote direction. To further optimize the mission, additional conditions can be imposed, such as matching the initial inclination to the one of the TLI trajectory, thereby eliminating the need for costly plane change maneuvers.

In the APO strategy, the spacecraft is transferred to the TVI trajectory on 5 December 2032, at 14:40 UTC, which is approximately 14 h earlier than the solution derived from the porkchop plots. This indicates that the solution obtained in GMAT, which considers accurate propagation, deviates by less than a day compared to the Lambert algorithm. Moreover, the $v_{{\infty }_1}$ obtained in GMAT is 3.1651 km/s, closely matching the reference value of 3.1757 km/s, with a difference of approximately 11 m/s. These results can be considered satisfactory.

On the other hand, the L1 strategy requires one or more deep space maneuvers (DSMs), within the interplanetary arc, to adjust the angles $\left\{i,\Omega ,\omega \right\}$ of the arrival hyperbolic trajectory at Venus so that the spacecraft can be later injected into the equilibrium region about $L_1$, as detailed in Section 5.2. To determine the necessary DSM, a new Target sequence is created in GMAT, focusing on finding the maneuver components in the Vertical-Normal-Binormal (VNB) reference frame [51]. This DSM, like the other maneuvers, is considered impulsive. In interplanetary missions, corrective maneuvers typically involve modest impulses of tens of m/s. Analytical studies have shown that applying an infinitesimal impulse at an infinite distance from the attracting body can modify the eccentricity of a hyperbolic trajectory without changing its energy [53]. This insight is valuable as it allows for the adjustment of the pericenter radius through small impulses at significant distances, without introducing substantial energy variations to the trajectory.

In this particular case, a single corrective impulse, represented as $\Delta {\mathit{V}}_{\mathit{c}}$, is sufficient. The timing of the maneuver is a parameter that can be adjusted to minimize the magnitude of the delta-v and reduce propellant consumption. By iteratively modifying the application position in GMAT and calculating the corresponding delta-v magnitude, it is possible to approximate the region where the minimum occurs. Figure 5 provides a visualization of some of these results. The magnitude of the corrective delta-v is plotted as a function of the days before arrival at Venus pericenter. The results indicate a decreasing trend until reaching a minimum value at approximately 60 days prior to arrival ($\Delta V_c=\left|\Delta {\mathit{V}}_{\mathit{c}}\right|=16.9$ m/s at −60 days). Beyond this point, the magnitude of the delta-v starts to increase.

Further investigation leads to the determination of the optimal solution. Utilizing the Yukon optimizer, a slightly different solution is obtained with a delta-v magnitude of 16.8 m/s at −59.98 days. This final solution, achieved by adjusting the corrective impulse, ensures an inclination close to 123${}^{\circ }$ at the perigee, enabling the utilization of the retrograde TLI trajectory. The components of the corrective impulse are listed in

Table 4. Velocity components of $\Delta {\mathit{V}}_{\mathit{c}}$ in the VNB reference frame.

Components (m/s)			Magnitude (m/s)
$\widehat{\mathit{v}}$	$\widehat{\mathit{n}}$	$\widehat{\mathit{b}}$
$5.9$	$14.8$	$-5.4$	$16.8$

.

Finally, for both the APO and L1 strategies, the angles $\left\{i,\Omega ,\omega \right\}$ that identify the orientation of the hyperbola are presented in

Table 5. Orientation angles of the arrival hyperbola at Venus in the VCI reference frame for APO and L1 scenarios.

Scenario	i	$\mathbf{\Omega }$	$\mathit{\omega }$
APO	67.3338${}^{\circ }$	352.4962${}^{\circ }$	342.7342${}^{\circ }$
L1	49.8824${}^{\circ }$	185.4746${}^{\circ }$	137.0611${}^{\circ }$

in the VCI frame.

4.1. Impulsive Maneuvers in the Geocentric Arc and Propellant Consumption Analysis

Two maneuvers are performed in Earth’s orbit to transition from the Trans-Lunar Injection trajectory (specified in Table 1) to a hyperbolic departure from Earth. The first maneuver, $\Delta V_1$, occurs at apogee and aims to increase the radius at perigee. It is typically a three-dimensional maneuver, with an out-of-plane correction if necessary. The second maneuver, $\Delta V_2$, takes place at perigee and is executed along the velocity vector to enter the desired hyperbolic orbit with a perigee altitude of 1000 km. Figure 6 depicts a representation of this phase, starting from the spacecraft’s orbital insertion after launch.

According to Kepler’s theory, the $\Delta V_2$ value can be calculated as

$$\Delta V_2=v_P^{+}-v_P^{-}=\sqrt{v_{{\infty }_1}^2+\frac{2{\mu }_E}{r_P}}-\sqrt{\frac{{\mu }_E}{a_{-}}\frac{1-e_{-}}{1+e_{-}}}=560\mathrm{m}/\mathrm{s}$$

(35)

In the above equation, the subscript P denotes the perigee, while the subscripts + and − represent the values after and before the maneuver. This value serves as a reference for refinement in GMAT, where the dynamic model incorporates Earth’s gravitational contribution, considering spherical harmonics up to the 4th degree and order, as well as perturbations from the Sun and Moon.

Using GMAT, the magnitude of $\Delta V_1$ is determined to be $7.7$ m/s. The individual components in the VNB reference frame are reported in

Table 6. Velocity components of $\Delta {\mathit{V}}_{\mathbf{1}}$ in the VNB reference frame for the APO and L1 scenarios.

Scenario	Components (m/s)			Magnitude (m/s)
	$\widehat{\mathit{v}}$	$\widehat{\mathit{n}}$	$\widehat{\mathit{b}}$
APO	7.6585	$-0.0764$	$-3.7229\times {10}^{-4}$	7.6589
L1	24.2227	5.5241	0.0307	24.8447

.

The magnitude of $\Delta V_2$ obtained through GMAT’s Target sequence is very close to the predicted value, measuring $557.5$ m/s. The overall delta-v budget in Earth’s orbit, $\Delta V_E$, is the sum of $\Delta V_1$ and $\Delta V_2$, amounting to $565.2$ m/s.

To estimate the propellant required for these maneuvers, we apply the Tsiolkovsky equation with an effective exhaust velocity of $c_{HT}=3000$ m/s. This allows us to calculate the mass ratio $x_{7_f}$, representing the final mass (${\tilde{m}}_f$) of the spacecraft after all maneuvers, relative to its initial mass (${\tilde{m}}_0$). After applying the equation to the total delta-v, $\Delta V_E$, we find a final mass ratio of $0.8283$ or $82.83\%$, indicating that only $17.17\%$ of the propellant has been consumed compared to the probe’s initial mass.

For the L1 strategy, the magnitude of the delta-v values are $\left|\Delta V_1\right|=24.9$ m/s (at apogee) and $\Delta V_2=565.6$ m/s (at perigee), respectively. The components of $\Delta V_1$ in the VNB reference frame are detailed in Table 6. In this case, the total delta-v in Earth’s orbit, $\Delta V_E$, includes the two delta-v values in the geocentric arc and the corrective delta-v. The sum is $\Delta V_E=\Delta V_1+\Delta V_2+\Delta V_c=607.3$ m/s. The final mass ratio is determined to be $0.8167$ or $81.67\%$, indicating a propellant consumption of $18.33\%$ before entering Venus’s sphere of influence.

4.2. Comparative Analysis of Mission Profiles

It is beneficial to compare the two mission profiles designed so far.

For the “APO” scenarios, the trajectory follows the following sequence:

1.

Launch and insertion into a direct TLI trajectory on November 24, 2032, at 1:03 UTC.

2.

Application of a three-dimensional impulsive maneuver $\Delta {\mathit{V}}_{\mathbf{1}}$ at apogee to lower the pericenter altitude and slightly change the inclination (magnitude of 7.7 m/s).

3.

Application of an impulsive maneuver $\Delta V_2$ at perigee in the direction of velocity for insertion into the departure hyperbola (magnitude of 560 m/s).

4.

Ballistic interplanetary arc until arrival at Venus with a pericenter altitude of 300 km and a velocity of 10.473 km/s.

For the “L1” scenario, the sequence presents some differences:

1.

Launch and insertion into a retrograde TLI trajectory on 23 November 2032, at 21:17 UTC.

2.

Application of a three-dimensional impulsive maneuver $\Delta {\mathit{V}}_{\mathbf{1}}$ at apogee to lower the pericenter altitude and slightly change the inclination (magnitude of 24.9 m/s).

3.

Application of an impulsive maneuver $\Delta V_2$ at perigee in the direction of velocity for insertion into the departure hyperbola (magnitude of 565.6 m/s).

4.

Interplanetary arc with an intermediate corrective impulse $\Delta {\mathit{V}}_{\mathit{c}}$ (magnitude of 16.8 m/s).

5.

Arrival at Venus with a pericenter altitude of 300 km and corresponding velocity of 10.473 km/s.

5. Capture and Orbit Injection at Venus

Upon reaching the 300 km pericenter along the hyperbolic orbit on 12 May 2033, at 17:00, the spacecraft can employ various strategies to achieve the desired orbits around Venus. In the subsequent paragraphs, we present comprehensive descriptions of these strategies for both target orbits. Each scenario involves a Venus Orbit Insertion (VOI) maneuver at the pericenter to decelerate the spacecraft, with the magnitude of deceleration tailored to the specific strategy. Chemical propulsion is employed for the high-thrust phase, while electric propulsion is used for the low-thrust phase, following the control law (25) to achieve the target orbit parameters, including semi-latus rectum, eccentricity, and inclination. The performance parameters for the low-thrust system are:

$$c_{LT}=30\mathrm{km}/\mathrm{s}{u}_T^{(max)}=5\times {10}^{-5}{g}_0$$

Here, $c_{LT}$ represents the effective exhaust velocity for low-thrust propulsion (LT), and $u_T^{(max)}$ represents the maximum thrust acceleration relative to the spacecraft’s initial mass (${\tilde{m}}_0$) at launch. The values selected are of the same order of magnitude as those of Busek BIT-3 ion thrusters [54]. To consider the maximum propulsive acceleration relative to the initial mass ${\tilde{m}}_i$ during the low-thrust control phase, normalization of $u_T^{(max)}$ by the corresponding mass ratio $x_{7_i}={\tilde{m}}_i/{\tilde{m}}_0$ is necessary.

5.1. Capture in Highly Elliptic Orbit and Low-Thrust Orbit Injection

The first scenario (named “APO”) involves the impulsive application of the VOI maneuver at the pericenter of the inbound hyperbolic trajectory toward Venus, followed by a low-thrust orbital control phase. The VOI maneuver, performed using chemical propulsion in the opposite direction of the spacecraft’s velocity, reduces the spacecraft’s energy and inserts it into an elliptical capture orbit around Venus.

For this scenario, three different strategies are considered, indicated as “APO.A,” “APO.B,” and “APO.C.” Each strategy is analyzed twice: for the final elliptical orbit and for the final circular orbit. The magnitude of the impulsive delta-v at the pericenter associated to the VOI, denoted as $\Delta V_3$, varies case by case based on the strategy and the target orbit. It is optimized to minimize the overall propellant consumption, considering both chemical and electric propulsion. Depending on the magnitude of $\Delta V_3$, the spacecraft is inserted into an elliptical orbit with varying eccentricities (same pericenter radius and different apocenter radii). Increasing the magnitude of $\Delta V_3$ reduces the apocenter radius of the elliptical orbit, while decreasing the impulsive maneuver intensity results in a more energetic elliptical orbit with a higher apocenter altitude. At first glance, the latter case may seem more advantageous as it allows for initial propellant savings followed by the low-thrust phase. However, due to the non-linearity of the control law, reducing $\Delta V_3$ does not necessarily reduce the overall propellant consumption since the low-thrust phase may require higher consumption. If it were the case, the minimum value of $\Delta V_3$ would be sought, which would subsequently allow for the successful application of the non-linear low-thrust control. This delta-v might not be the minimum for inserting into an elliptical orbit, which means reducing the velocity just below the escape velocity. In fact, Equation (25) can work in some cases even when applied to a hyperbolic orbit if the available thrust levels are sufficient [55]. Since the intensity of the impulsive maneuver cannot be determined in advance, the value of $\Delta V_3$ is sought to maximize the resulting mass ratio once the target orbit is reached.

To conduct this search, the insertion into an elliptical orbit with apocenter radius equal to the radius of Venus’s Sphere of Influence (SOI) is taken as a reference: $r_A\equiv r_{SOI}=0.616\times {10}^6$ km (using the Laplace definition). A very high apocenter allows for significant savings in maneuver costs. The corresponding delta-v, denoted as $\Delta V_{SOI}$, is calculated using Keplerian theory:

$$\left|\Delta V_{SOI}\right|=v_P^{-}-v_P^{+}=\underset{10.47318\mathrm{km}/\mathrm{s}}{\underbrace{\sqrt{v_{{\infty }_2}^2+{\displaystyle \frac{2{\mu }_V}{r_P}}}}}-\underset{10.06204\mathrm{km}/\mathrm{s}}{\underbrace{\sqrt{{\displaystyle \frac{{\mu }_V}{a_{SOI}}}{\displaystyle \frac{1+e_{SOI}}{1-e_{SOI}}}}}}=411.1\mathrm{m}/\mathrm{s}$$

(36)

where $v_P^{-}$ represents the velocity at the pericenter before the maneuver (on the hyperbola), and $v_P^{+}$ the velocity just after the maneuver (on the ellipse). The pericenter radius is calculated as: $r_P=R_V+h_P$, with $R_V=6051.8$ km [56]. The result in (36) is confirmed in GMAT.

The optimization process involves searching for the optimal value of $\Delta V_3$ in the vicinity of $\Delta V_{SOI}$. Once the maneuver is applied, the low-thrust orbital control phase begins, aiming to reach the two target orbits using different strategies for each. The numerical iteration proceeds as follows:

• Determine the braking $\Delta V_3$ (applied along $-\widehat{v}$).
• Calculate $x_{7_i}=x_{7_0}{e}^{-\Delta V_3/c_{HT}}$ (Tsiolkovsky’s law), with $x_{7_0}$ determined in Section 4 based on $\Delta V_E$. This value serves as the initial value for the mass ratio $x_7$ and helps establish the maximum thrust acceleration: $u_T^{(max)}=5\times {10}^{-5}{g}_0/x_{7_i}$.
• Propagate the spacecraft’s motion while applying low-thrust control: numerically integrate the dynamic Equations (4)–(7) using the control law (25) to determine ${\mathit{u}}_{\mathit{T}}$, inserted in (8). Gravitational perturbations related to spherical harmonics (up to degree and order 15) and the third body (the Sun) are taken into account using the Expressions (9)–(11), respectively. The initial conditions utilize the equinoctial elements corresponding to the starting state (dependent on the control activation point based on the strategy) and $x_{7_i}$ for the mass ratio. The propagation continues until the desired target orbit is reached (although this may not always occur).
• Identify the final mass ratio $x_{7_f}$ after integration.

This iterative process is repeated for a series of $\Delta V_3$ values to determine the one that maximizes the final mass ratio.

For each control gain, namely $k_1$, $k_2$, and $k_3$, an initial range is manually defined. These intervals serve as a starting point for the Particle Swarm Optimization (PSO) process. Within these ranges, the particles in the swarm can explore and move. The results obtained from PSO can be further refined by using MATLAB’s fminsearch routine. The optimization of weights is performed for each strategy using a reference case that applies $\Delta V_{SOI}$, and then these optimized weights are used for all considered $\Delta V_3$ values.

Since the exact time required to reach the target state is unknown in advance, the propagation is initiated for a predetermined number of days considered sufficient to achieve the objective. If needed, the propagation can be restarted for a longer duration. A stopping condition is also implemented: the numerical integration is halted when $V<{10}^{-16}$, which implies $\mathit{\psi }=\mathbf{0}$, related to MATLAB’s machine precision [57]. When the weights are well-optimized, this condition is easily met. However, if the weights are not fully optimized, the propagation continues for the entire planned duration. It is important to note that even if the stopping condition is not met, it does not necessarily mean that the target conditions (such as obtaining $V\approx 0$) are not reached. It simply suggests that the used weights may not be fully optimized yet.

In our study, we explore various cases based on the moment of ignition for electric propulsion, referred to as APO.A, APO.B, and APO.C strategies. These strategies aim to achieve the target orbit with the highest possible mass ratio while considering realistic mission scenarios and limitations.

The APO.A strategy assumes the immediate activation of low-thrust nonlinear control right after the application of $\Delta V_3$. By initiating propulsion effects starting from the pericenter, this strategy allows us to analyze the impact of thrust on the trajectory. However, it is important to note that APO.A is not practically implementable as it assumes an instantaneous application of the VOI maneuver and immediate activation of the electric thruster right after.

In order to introduce more realism, the APO.B strategy incorporates a time delay of one hour between the impulsive application of $\Delta V_3$ and the activation of low-thrust control. This delay simulates the scenario where spacecraft state control can be performed and the two maneuvers can be temporally separated.

For the APO.C strategy, the low-thrust control is applied after propagating the spacecraft for an entire orbit until reaching the new pericenter. This approach ensures that the pericenter does not end up inside the planet with a negative altitude, which can be caused by significant third-body perturbations. In fact, solutions that result in a return to Venus with an altitude lower than 200 km are disregarded, as atmospheric perturbations become highly significant and potentially destructive.

The analysis begins with the examination of the elliptical target orbit with dimensions $300\times \mathrm{116,108.4}$ km. The desired orbital parameters expressed in the VCI reference frame are:

$$p_d=\mathrm{12,075.715}\mathrm{km},e_d=0.9011,i_d=90{}^{\circ }$$

(37)

The comprehensive results for all strategies and target orbits can be found in

Table 7. Results for APO and L1 strategies with elliptical and circular target orbits.

Target Orbit	Strategy	Scenario
		APO		L1
		Mass Ratio	Time of Flight	Mass Ratio	Time of Flight
Elliptical	A	68.05%	17.77 days	64.65%	30.14 days
	B	68.04%	16.87 days	65.82%	24.31 days
	C	68.12%	10.31 days	65.82%	24.31 days
Circular	A	55.40%	83 days	53.13%	88 days
	B	54.49%	92 days	55.63%	75 days
	C	56.10%	86 days	55.71%	75 days

, which provides the final mass ratio and the associated time of flight during the low-thrust control phase.

For the APO strategies, each time a range for $\Delta V_3$ is explored for the optimization. For example, for APO.A, $\Delta V_3\in \left[\Delta V_{SOI}-40\mathrm{m}/\mathrm{s},\Delta V_{SOI}+100\mathrm{m}/\mathrm{s}\right]$ is analyzed. The results of this analysis, with the $\Delta V_3$ interval discretized into 200 points, are depicted in Figure 7.

The maximum final mass ratio achieved is 67.91%, corresponding to $\Delta V_3$ = 438.7 m/s. The reference $\Delta V_{SOI}$ position, corresponding to a final mass ratio of 67.68%, is marked by a gray dashed vertical line. Further optimization in the vicinity of this solution leads to convergence to the target state after 17.77 days with a final mass ratio of 68.05%. Instantaneously applying $\Delta V_3=$ 438.7 m/s corresponds to $r_A=$ 400,384.4 km. However, due to the gravitational effect of the Sun perturbing the trajectory, propagating to the apocenter yields a radius of 396,877.6 km. The temporal behaviors of controlled orbital parameters and the mass ratio are shown in Figure 8.

By propagating beyond the necessary time to reach the target state, a change in the slope of the mass ratio can be observed. The absolute value of the slope decreases as the orbit tracking phase is completed, and the maintenance phase begins to compensate the gravitational effects related to spherical harmonics and the third body. For instance, by maintaining control for an entire year, the mass ratio decreases to 67.03%, resulting in an approximate 1% of mass depletion.

Similar results are obtained for the APO.B and APO.C strategies. The most favorable solution is provided by the APO.C strategy, with a higher final mass ratio of 68.12%. It also corresponds to the shortest time of flight, approximately 10 days.

The objective now is to achieve a circular orbit with an altitude of 300 km. The same principles discussed for the elliptical target orbit apply here as well. The desired orbital elements in the VCI reference frame are:

$$p_d=6351.8\mathrm{km},e_d=0,i_d=90{}^{\circ }$$

(38)

The three strategies are investigated again to minimize propellant consumption. The results are presented in Table 7. Once again, the optimal solution aligns with strategy APO.C, with a mass ratio of 56.10% achieved in 86 days, this time with $\Delta V_3<\Delta V_{SOI}$. The trajectory undergoes significant deformation due to the gravitational effect of the Sun, as evident in the violet portion of Figure 9.

Numerous revolutions around the planet are completed, as often happens in low-thrust applications. The orbit gradually reduces its semimajor axis, eliminating eccentricity at an altitude of 300 km. The corresponding temporal variations of the relevant orbital parameters are presented in Figure 10. At approximately 86 days, a change in slope is observed in the mass ratio, marking the beginning of the orbit’s station-keeping phase.

5.2. Low-Energy Capture and Low-Thrust Orbit Injection

In this scenario the spacecraft is transferred from the hyperbolic trajectory (interplanetary arc) to a long-term capture orbit by a two-impulse maneuver. The first maneuver is provided during the Venus flyby, at the pericenter, and allows injecting the spacecraft into the equilibrium region surrounding $L_1$ of the Sun-Venus system. This is achieved providing a $\Delta V_3$ that reduces the energy level from the high value of the interplanetary trajectory $h\gg 0$ to a lower $h>0$ compatible with the models described in Section 2.3. The corresponding $\Delta V_3$ is lower compared to the previously discussed cases in Section 5.1, as $L_1$ lies outside Venus’s sphere of influence.

At the entrance into the equilibrium region, the spacecraft dynamical state is characterized by $h>0$, ${\sigma }_1>0$ and ${\tau }_1>0$, therefore a second maneuver $(\Delta V_{L_1})$ is performed to establish the long-term capture condition given by Equation (19) (${\sigma }_1\to 0$).

In this study, energy levels of the order $h={10}^{-4}$ inside the equilibrium region are considered and the following capture conditions are computed: $x-x_{L_1}=4.91\times {10}^5$ km, $y=1.98\times {10}^5$ km and $u=-0.120$ km/s. Then a target sequence in GMAT allows determining the hyperbola’s orientation angles at flyby (see i, $\Omega$, and $\omega$ in Table 5) and $\Delta V_3=$ 387.9 m/s, applied opposite to the spacecraft’s velocity. From these data, the value $\Delta V_{L_1}=$ 51 m/s is finally determined. Figure 11 shows the obtained trajectory.

This is a low-energy trajectory that is “trapped” by the planet’s gravitational field for a relatively long period. During this period, low-thrust control is activated, allowing the spacecraft to reach the desired target orbit.

The total delta-v from the start of the mission, entirely associated with chemical propulsion, is calculated as $\Delta V_{HT}=\Delta V_E+\Delta V_3+\Delta V_{L_1}=$ 1041.5 m/s. This corresponds to a mass ratio $x_{7_i}=$ 70.67%.

Various cases are explored based on the moment of ignition for electric propulsion, identified as “L1.A,” “L1.B,” and “L1.C.” The objective remains to minimize the overall propellant consumption. In the L1.A strategy, low-thrust control is activated one hour after applying $\Delta V_{L_1}$ within the equilibrium region. In the L1.B strategy, control is activated at the first pericenter (expected to be reached on 2 November 2033) at an altitude of 219,818 km, which already possesses an inclination of approximately 90${}^{\circ }$. Since the trajectory constructed for this scenario with weak capture involves numerous revolutions around the planet, this behavior can be utilized to identify other potential points for low-thrust application over the years. Specifically, reference is made to the subsequent pericenters and apocenters after the first one. Using the same weights as in the L1.B strategy, we examine whether convergence to the target state is achievable at these points.

The attainment of the target elliptical and circular orbits, with orbital elements defined in (37) and (38), is now examined. The results are presented in Table 7. The optimal solution for the elliptical target orbit is achieved by activating thrust from the first pericenter at Venus, using strategy L1.B. The trajectory is shown in Figure 12.

In this case, the inclination at pericenter is already 90${}^{\circ }$, which provides an advantage. Further exploration using the L1.C strategy for subsequent pericenters and apocenters reveals results depicted in Figure 13. The optimal solution corresponds to activating control at the first pericenter, resulting in a final mass ratio of 65.82%.

The L1 strategy offers flexible low-thrust control activation for achieving the desired orbit. Real-time adaptability is enabled by a feedback control law, which has been demonstrated to consistently converge to the target state. To validate its effectiveness, simulations are conducted considering temporary propulsion system failure. The L1.B strategy, identified as the most fuel-saving, involves activating low-thrust control at pericenter for $N_1$ days, followed by a temporary propulsion failure lasting $N_2$ days. For elliptical orbits, the resulting mass ratio and total flight time vary with $N_1$ and $N_2$, as shown in Figure 14. A range of $N_1\in \left[0,30\right]$ and $N_2\in \left[0,100\right]$ is explored, encompassing all scenarios, including delayed control activation ($N_1=0$). Convergence is achieved in all 3000 cases, with higher mass ratio values when the failure occurs within the first 10 days after reaching Venus’s pericenter. The total flight time increases with $N_2$. On average, the mass ratio is 64.26%, with a standard deviation of 0.61%, and the average total flight time is 82.08 days, with a standard deviation of 29.50 days. Figure 15 displays overlaid profiles for the controlled orbital parameters.

Moving on to achieving a circular orbit, the L1 strategies yield optimal results by initiating low-thrust control once the spacecraft enters orbit around Venus. In this scenario, a slightly superior outcome is attained at the pericenter reached on 19 December 2034, corresponding to a mass ratio of 55.71% compared to 55.70% at the initial pericenter on 2 November 2033. Multiple opportunities exist for implementing low thrust during the capture phase around the planet.

5.3. Discussion of Results

The analysis of different strategies for achieving orbits around Venus has revealed significant findings, demonstrating the effectiveness of both APO and L1 strategies. These strategies combine impulsive maneuvers with chemical propulsion and subsequent low-thrust control using electric propulsion.

For the elliptical target orbit, the APO.C strategy stood out as the most fuel efficient solution, resulting in a final mass ratio of 68.12% achieved within a short time of 10.31 days. In the L1 scenario, the L1.B strategy emerged as the one with the highest final mass ratio of 65.82% and a total flight time of 24.31 days. However, when comparing these results with a traditional strategy that relies solely on optimized impulsive chemical propulsion, with a final mass ratio around 67%, the proposed strategies offer little or no advantage in terms of propellant savings.

For the circular target orbit, the APO strategies achieved mass ratios ranging from approximately 54% to 56%, with the APO.C strategy performing slightly better than the others. On the other hand, the L1 strategies demonstrated favorable outcomes, with the L1.B strategy standing out with a mass ratio of 55.71% and the shortest total flight time of 75 days. When contrasting these outcomes with a specific case with only chemical propulsion, resulting in a mass ratio of approximately 27%, the superiority of the proposed APO and L1 strategies becomes even more evident. These strategies deliver mass ratios that are approximately twice the values with impulsive injection, leading to a substantial enhancement in efficiency and performance. The comparison clearly demonstrates the superiority of the proposed approaches over traditional methods, emphasizing their significant advantage in achieving circular target orbits around Venus.

Furthermore, the analysis considered the impact of temporary propulsion system failure on the L1.B strategy. Simulations demonstrated that convergence to the target state was still attainable in all cases, with the mass ratios deviating only slightly from the nominal case. This highlights the robustness and adaptability of the proposed strategies in real mission scenarios.

6. Concluding Remarks

We developed a novel mission profile to transfer a spacecraft from a highly elliptic Earth orbit to a target orbit around Venus. This study, verified by means of numerical integration, includes a novel approach that (i) combines traditional high-energy interplanetary trajectories with low-energy ones, to transfer the spacecraft into a weak capture orbit at Venus, and (ii) implements a novel nonlinear orbit control using low-thrust propulsion, to inject the spacecraft into the desired final orbit. This mission profile benefits from the use of low-energy arcs and low-thrust propulsion to reduce the propellant mass required for maneuvers, while still allowing for short transfer times, only marginally longer than Earth-Venus transfers designed using a traditional approach.

Two different scenarios were investigated, named as APO and L1. In the APO scenario, an impulsive maneuver performed at the first Venus flyby injects the spacecraft into a highly elliptic orbit and then nonlinear orbit control, implemented by a low-thrust propulsion system, allows transferring it into the desired target orbit. In the L1 scenario, the spacecraft is initially injected into the equilibrium region surrounding Sun-Venus $L_1$. From here, it is sequentially transferred to a weak capture trajectory and finally, by means of nonlinear orbit control and low-thrust propulsion, into the target orbit.

To evaluate the feasibility of these two options, we performed numerical studies in GMAT and MATLAB, considering departure dates for Venus missions planned between 2028 and 2033. If compared to a traditional (impulsive) strategy, the proposed mission profiles result in significant savings in the propellant mass. Specifically, the propellant usage reduces from the 73% to the 44% for the APO strategy and to the 45% for the L1 strategy, considering a circular target orbit around Venus. Even-though the L1 scenario requires an additional mid-course interplanetary maneuver (DSM) and is less favorable with respect to the APO scenario, it enhances the mission flexibility and reliability, since the low-thrust propulsion system can be actuated at any apocenter or pericenter of the low-energy capture orbit ensuring successful injection into the target orbit.

Furthermore, our research proves that delaying the injection into the low-energy capture trajectory from the beginning of the interplanetary arc to its end can lead to savings in the total transfer time. While low-energy transfers from Earth to Venus can take up to 300% more time than traditional ones, the L1 scenario demonstrates a better outcome, with only a 56% increase in total transfer time.

In conclusion, the proposed novel mission profiles, leveraging low-energy trajectories and low-thrust propulsion, offer significant propellant savings and improved mission efficiency, making them promising candidates for future interplanetary missions from Earth to Venus.