Abstract
A formation flying control algorithm using the Lorentz force for Low Earth Orbits to achieve a trajectory with required shape and size is proposed in the paper. The Lorentz force is produced as a result of interaction between the Earth’s magnetic field and an electrically charged spacecraft. Achievement of the required trajectories represents a challenge since the control in three-dimensional space is a scalar value of the satellite’s charge. A Lyapunov-based control algorithm is developed for elimination of the initial relative drift after the launch. It also aims at reaching a required amplitudes for close relative trajectories for in-plane and out-of-plane motion. Due to the absence of full controllability, the algorithm is incapable of correcting all the parameters of the relative trajectory such as in-plane and out-of-plane phase angles. The proposed control allows to converge to the trajectory with required shape and size, though with some oscillating errors in the vicinity of the required trajectory parameters. Numerical simulation of the relative motion is used to study performance of the control algorithm for one case of one controlled satellite and two cases of five controlled satellites forming a nested ellipses and train formations. The convergence time and final trajectory accuracy are evaluated for different control parameters and orbits using Monte Carlo approach.
1. Introduction
A satellite formation flying is defined as a set of satellites moving in close relative trajectories that can control their relative position and/or relative velocities, keeping close distances and solving a common problem. This type of distributed space systems has multiple applications such as spatial measurement of magnetosphere parameters [1], monitor clouds [2,3], lightning study and localization [4], gravitational waves detection [5], image demonstration in the sky [6,7] and many others. In order to achieve required bounded relative motion of the satellites in the formation, a control is required. The control force could be applied by the onboard propulsion as in [8,9,10], or by using environmental forces such as aerodynamic drag [11], solar radiation pressure [12], electrostatic [13,14] or electromagnetic forces [15]. The control approaches that do not utilize thrusters are the most attractive since they do not require a propellant. However, each of them has constraints and can be applied only for some range of orbit heights [16].
This paper considers application of Lorenz force for the relative motion control in satellite formation flying. A charged particle moving in the Earth’s magnetic field accelerates in a direction perpendicular to its velocity vector and the local magnetic field vector due to the Lorentz force [17]. The first works about the Lorentz force effects on charged bodies were conducted by Schaffer and Burns who developed a model explaining the influence of the plasma environment on the dynamics of charged dust particles orbiting Jupiter and Saturn [18]. These studies proved that the orbital motion and dynamics are greatly influenced by the Lorentz force and that this force along with gravity effects, lunar perturbations, and solar radiation pressure are responsible for the existence of gaps in both Jupiter’s and Saturn’s ring resonances. Following the work developed by Schaffer and Burns, Peck conducted a series of studies proposing the implementation of the Lorentz force for the development of a propellantless satellite technology using the proposed Lorentz Augmented Orbit (LAO) system [17]. He presented a possible design for LAO system configurations and showed that LAO systems can be used for drag compensation, formation flying control, orbital inclination control and nodal precession control. Although LAO system configurations are not based on the electrodynamic tethers, the effect on the orbital dynamics of both systems are similar. For a LAO spacecraft, the body acts as a point charge which moves relatively to the planet magnetic field, the moving charge represents the electrical current similar to the one flowing in the electrodynamic tethers [19].
The Lorentz force applications have been widely studied in the literature. Analytical expressions for orbital perturbations due to Lorentz force are developed in [20]. Many papers are devoted to orbital control of a single satellite for drag compensation in Low Earth Orbit (LEO), as in [21,22]. In [23], the Lorentz force time-optimal transfer trajectory in Jovian magnetic field is designed. A set of papers consider the application of Lorentz force for attitude passive [24] and active control [25,26]. Fault-tolerant sliding mode satellite attitude stabilization control algorithm using magneto-Coulombic torquers is proposed in [27]. Stabilization of a programmed rotation mode for a satellite with electrodynamic attitude control system is considered in [28]. The most frequent application of Lorentz force in the literature is the satellite formation flying control. Bounded relative orbital motion in the presence of the Lorentz force and J2 perturbations are studied analytically and numerically in [29] for the cases when the chief satellite is in circular or elliptical orbit and the deputy satellite is charged. An approximate analytical solution for the motion of charged spacecraft is derived in [30], where it is indicated that Lorenz force mainly affects the satellite along-track position and changes the orbital plane. Lorenz force-based control approaches can be classified into two main areas: optimal trajectory generation and closed-loop controllers. The control strategy for the Lorenz force-based rendezvous and reconfiguration are developed in [31]. For transfer problem in satellite formation flying, sequential quadratic programming is proposed in [32]. Another approach for the transfer problem using the energy-optimal open-loop trajectories is developed in [33]. In addition, the authors of this paper propose the closed-loop integral sliding-mode controller and compare two control approaches. In several papers, Lorentz force is combined with another actuation. For example, in [34], the rendezvous problem is solved using hybrid system based on aerodynamic and Lorentz forces, the energy-optimal trajectory is calculated considering constrains on the electrostatic charge value and aerodynamic plates angular velocity. The literature review revealed that the problem of achieving the required closed relative trajectory in satellite formation flying using Lorentz force has not been studied. Since there is no full controllability in 3D relative space using Lorentz force, the in-plane and out-of-plane phase angles remain uncontrolled. The purpose of the paper is to develop a Lyapunov-based control algorithm using Lorenz force only in order to achieve the required trajectory of the defined size and shape.
The structure of the rest of the paper is as follows. In Section 2, the problem statement is formulated, and the motion equations are presented. In Section 3, the control algorithm is derived and its implementation using Lorenz force is described. In Section 4, the proposed algorithm is applied to control a group of two or five satellites. In the last Section, the results of the work are summarized.
2. Problem Statement and Motion Equations
The problem statement of this work is as follows. Several satellites equipped with charging capable devices are considered to be in LEO. The Earth’s magnetic field is modeled as the tilted dipole model. The satellites are considered to be point masses; their attitude motion is not considered throughout the paper. Due to the influence of the Debye shielding in LEO orbits, intersatellite and Earth satellite electrostatic interaction is neglected. For simulation of controlled motion, the second harmonic of the geopotential J2 is taken into account as the only environmental perturbation. Control force affecting the satellite is
where is satellite charge, and are the satellite radius vector and velocity in Earth-centered inertial reference frame, is the Earth angular velocity, is Earth magnetic induction vector. Hence, there is no full controllability of the translational relative motion. The control law should firstly eliminate the relative drift between the satellites, and secondly provide the necessary relative orbit size. The phase angles for the in-plane and out-of-plane relative motion remain uncontrolled. To achieve this goal, a Lyapunov-based control algorithm is developed.
It is also necessary to study the performance of the developed algorithm depending on a variety of factors, such as charging capacity maximum value, orbital height, and the variation of the initial conditions. Monte Carlo simulation method is used to evaluate the influence of these parameters on the convergence time or the accuracy of the control algorithm.
2.1. Motion Equations
The Clohessy–Wiltshire equations (CW) are utilized to describe the relative motion of two arbitrarily chosen satellites within the formation [35], expressed in the rotating Local-Vertical/Local-Horizontal reference frame (LVLH) designated as (Figure 1). Its origin is located at a reference point moving along a circular orbit with radius at an orbital angular velocity . The z-axis points towards the radial direction, the y-axis is aligned with orbital angular momentum and the x-axis completes the right-handed orthogonal frame. These linear ordinary differential equations of motion can be solved analytically. Note that CW equations are the linearized ones, so we can use them only when the relative distance between the satellites is several orders of magnitude smaller than the orbit radius.
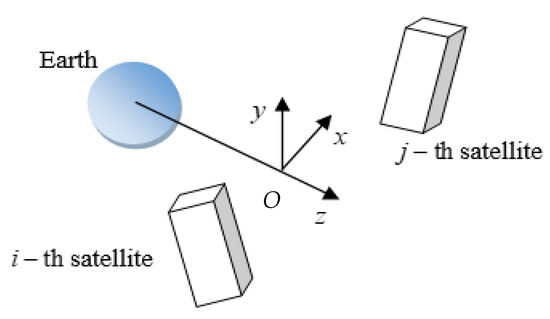
Figure 1.
LVLH reference frame.
Let and be the vectors of the i-th and j-th satellites in the LVLH reference frame, where is the number of the satellites in the formation. Then, the components of the relative position vector .
Consider the controlled motion equations of the formation flying, and assume that each i-th satellite is equipped with a motion control system able to produce the acceleration . Hence, the relative motion of two i-th and j-th satellites in the LVLH reference frame are as follows:
where is the difference of the two control accelerations written in LVLH frame. Its solution in case of can be written as follows [36]:
where the parameters are the motion parameters which depend on the initial conditions. is the parameter that describes the drift between the satellites. If it equals zero, then the relative motion is finite, i.e., the satellites do not fly away from each other. In this case, the relative motion in orbital plane Oxz corresponds to the ellipse, shifted along transversal at , with semimajor and semiminor axes equal to , respectively. Out-of-plane motion is described by oscillation with a given amplitude . Further, we will consider these elements as osculating ones, which would lead to the following differential equations of controlled motion:
Using these equations, a control algorithm for achieving required relative trajectory parameters is to be developed.
2.2. Lorentz Force
This paper aims for the development of a formation flying control algorithm using Lorentz force. Consider a set of aspects of its application.
Any charged particle with non-zero velocity would be accelerated by magnetic field. This effect is called the Lorentz force [19] and can be described by (1). For the charged particles interaction, an important factor is the Debye shielding effect, which can be quantified by the Debye length as a measure of the electrostatic net effect of a charge and the distance in which it persists. For the LEO, the measured Debye length values are small (∼= 1 cm) due to plasma surroundings, which leads to the superiority of the Lorentz force over the Coulomb force [19]. Note that Debye length increases with height. In addition, the satellite velocity with respect to the geomagnetic field decreases with height. Hence, at sufficiently high orbits, the Coulomb’s force (which corresponds to the interaction between the charges) would prevail over the Lorenz force. However, at LEO, the Lorenz force-based control is more beneficial.
In the design of LAO capable systems, the most important parameter is the maximal acceleration value due to Lorentz force, which is proportional to the q/m ratio. In addition, the charge losses rate to the environment is another aspect affecting the LAO system design. From studies [17,19], the best achieved design for a LAO spacecraft is based on the surface of a conducting sphere. However, this shape preludes charge concentrations, which could lead to arcing and discharge into the plasma. To counter this phenomenon, the authors propose to use a surrounding conducting sphere, therefore establishing a Faraday cage that would completely protect the interior components from electrical discharge.
There are several models for the simulation of the Earth’s magnetic field, and each of them has different accuracy and numerical complexity. In our paper, the Tilted Dipole Geomagnetic Model is used [29]. According to this model, the Earth’s magnetic induction vector in Earth-centred inertial reference frame is as follows:
where is the Earth’s magnetic dipole moment value, is the unit vector along the satellite radius vector, is the distance from the Earth’s centre of mass, is the unit vector along the Earth dipole vector, which is not coincident with the Earth rotation axis. The Earth magnetic dipole vector can be expressed in Earth Centred Inertial reference frame as follows:
where is the angle between the magnetic south pole and geocentric north pole, and , where is the Greenwich’s longitude at and ◦/s is the Earth’s angular rotation rate.
3. Control Algorithm
The main goal of this paper is to develop the control law which is able to provide the required size and shape of the relative orbit. Size and shape here are defined as parameters , so there are no restrictions imposed on the satellite phase in relative orbit. The direct Lyapunov method is applied for the development of the control algorithm [37]. Consider the following deviation from the desired motion:
where the desired relative orbit ellipse is defined by the parameters, and parameter represents the current trajectory parameter values (here and after we omit index at and ). The control application should provide convergence of all to zero. Since formation flying requires closed relative orbits, is always set to be zero.
Note that Lorenz force is actually rather small, so the control law is constructed in two stages. Firstly, it is necessary to eliminate the initial drift between the satellites. On the second stage, the necessary relative geometry is provided.
3.1. Lyapunov-Based Control
3.1.1. Relative Drift and Relative Shift Control
In order to set the relative drift and the relative shift to zero, the following Lyapunov function candidate is proposed for the first stage as in [36]:
Deriving the function with time and substituting some of the terms for the simplifications result in the following:
According to the Barbashin–Krasovsky theorem [38], to achieve and obtain the global asymptotic stability at point with and , the following control acceleration can be applied:
where and are positive control parameters.
3.1.2. In-Plane and Out-of-Plane Amplitudes Control
After reaching the desired values for and inside the convergence zone, the algorithm starts a second stage in order to achieve both the in-plane and out-of-plane required trajectory amplitude values. Thus, the following Lyapunov function is used:
Its time derivative is
Consider the following control vector:
If this control is substituted into the derivative of Lyapunov function, one can obtain
The term could be positive, but after the first control stage its value will be much smaller than the sum of the first three terms in this equation. Therefore, it is assumed that this term rather insignificantly impacts the Lyapunov function derivative. In addition, we can consider two motion modes: when the drift and/or shift is too large, the satellite utilizes control law (2), otherwise (3) is used.
It should be noted that the calculated control may not be possible to implement considering the system’s charging capacity limits. Henceforth, it is required to take into account the implementation restrictions during the controlled motion simulation. This important issue is addressed in the next section.
3.2. Control Implementation Using Lorenz Force
In accordance with (1), the Lorenz force direction is defined by current satellite velocity and local magnetic field direction. Hence, the only control input is the satellite charge. However, during Lyapunov control derivation, we have used two (Control (2)) or three (Control (3)) independent control inputs. It means that in general case, the exact required value of control cannot be obtained. Let us consider the following values:
where is the satellite mass, are the control acceleration components defined in the previous section, and are the Lorentz force vector components in the LVLH reference frame. Introduced correspond to the charge value that is necessary to provide the required torque along a given axis. Ideally, it must be the same value for each axis, but in reality, they will be different. We suggest to use the following value for the satellite charge:
Although this way we cannot guarantee convergence of motion to the desired one, simulations show that this approach is viable.
During the charge calculation, we must also take into account restrictions on its maximum value . It is done in the following way:
In addition, the charge cannot be changed too fast, i.e.,
where is the maximum speed of the change in satellite charge, is simulation time step. Hence, the resulting charge value is
Note that considered control strategy is suggested for the case when there are only two satellites in a group. In case of multiple satellites for centralized leader–followers configuration, the described control approach can be applied as it is without any modification.
4. Results of Numerical Study
Consider a set of satellites in Low Earth Orbit. In this section, a performance of the proposed algorithm for two satellite formation flying case and for swarm relative motion is studied depending on the capabilities of the onboard charging device, required relative trajectory, orbital height and inclination. All the simulation parameters values are listed in Table 1.

Table 1.
Simulation parameters.
The control parameters are chosen to obtain the best performance of the algorithm considering the convergence and the constants errors. The scheme of the simulation is presented in Figure 2. First, according to the initial conditions, the satellite motion is simulated according to the orbital dynamics taking into account the J2 perturbation and Lorenz force control. The orbital state radius vectors and velocities are converted to the relative state vector in LVLH reference frame. Using the relative state vectors, the current relative orbit parameters are calculated, which define the calculated control by (2) or (3) depending on the control stage. The control component values are used for the parameter calculations according to (4). The resulting satellite charge value is provided by (5). It is modified by (6) and (8) in case the charge exceeds the constrain on the maximum value or on the maximal speed if the charge changes. The final value of the charge is used for the Lorenz force calculation by (1) and its vector is an input in the orbital motion simulation for the next simulation step.
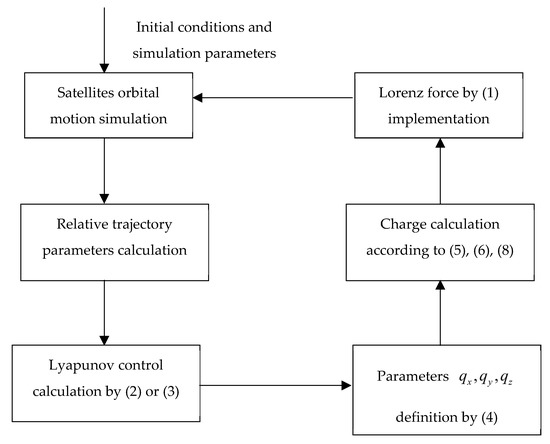
Figure 2.
Scheme of controlled motion simulation.
4.1. Free Motion of Two Satellites
Consider two satellites’ formation motion with random initial conditions defined above. No control is applied to the satellites. The resulted relative trajectory after simulation is presented in Figure 3. Since the relative drift does not equal zero after the launch, relative trajectory is not closed, and the satellites are flying apart. It means that without control, it is impossible to obtain close relative trajectories during the whole time of the mission. Even if initially the relative drift is zero, the perturbations lead to gradual drift increase.
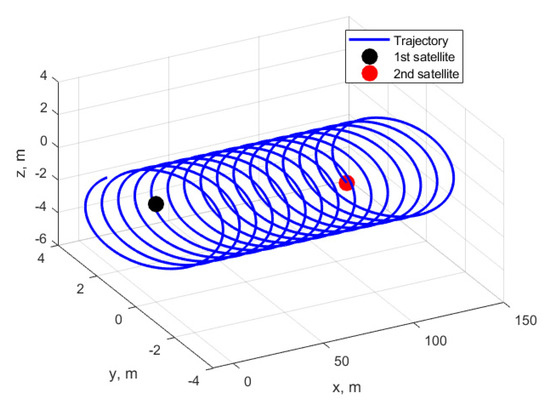
Figure 3.
Relative trajectories of the two satellites’ free relative motion.
4.2. Case of Study of One Controlled Satellite
Consider an application of the proposed control algorithm for the same initial conditions as described for the example of free relative motion. One of the satellites is considered passively moving along the orbit, the other is controlled using the proposed control algorithm based on Lorentz force. The time of the controlled motion simulation is 5 days. Figure 4 presents an example of the relative motion. It can be seen that there was an initial drift that was stopped by the first stage of the algorithm. When the parameters defining the relative drift and relative shift and entered the vicinity of the required values, the second stage was started to change the in-plane and out-of-plane trajectory amplitudes. Figure 5, Figure 6, Figure 7 and Figure 8 show the values of the controlled motion and the required ones. From the plots, it can be concluded that the first stage of the algorithm required approximately 15 h, then the relative shift and relative drift reached the required values. The second stage also lasted for approximately 15 h; during this period, the trajectory amplitudes level to the vicinity of the required values. Starting from 30 h from the simulation beginning, the trajectory can be considered as converged to the trajectory with desired shape and size. It can be seen that at time of approximately 60 h, the value of the relative shift deviated more than the threshold value of 2.5 m, and the control temporarily returned at the first stage till the returned to the acceptable vicinity of the required value. The control errors caused by the constrains of the value and direction Lorenz force result in errors in trajectory parameters during the station keeping of the required trajectory. The maximum deviation of the relative drift is approximately 0.05 m, and for the relative shift it is approximately 3 m. The errors in the amplitudes and are no more than 1 m.
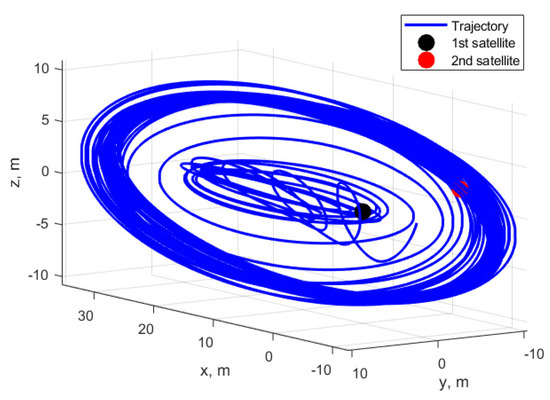
Figure 4.
Relative trajectory under control.
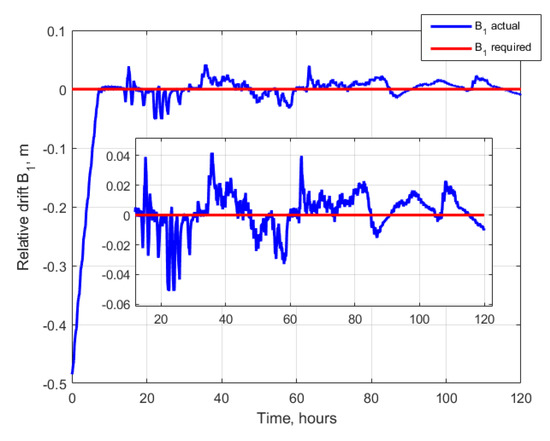
Figure 5.
Relative drift.
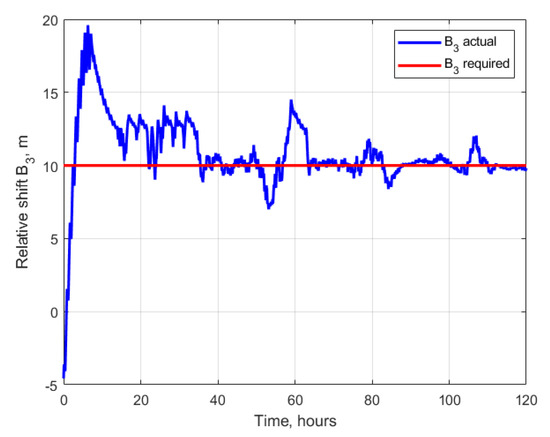
Figure 6.
Relative shift.
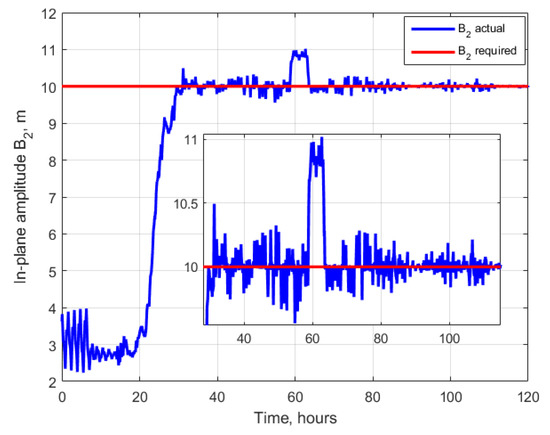
Figure 7.
In-plane amplitude.
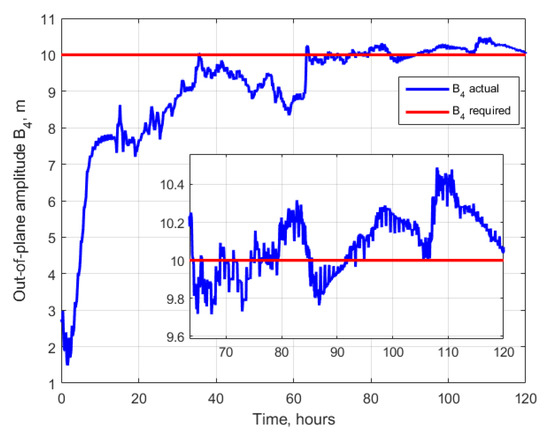
Figure 8.
Out-of-plane amplitude.
The value of the implemented charge of the satellite during the control is presented in Figure 9 and Figure 10. It can be seen that the value of the charge is limited by 10 µC. In zoomed Figure 10, the continuous change in the charge is demonstrated. The speed of charging is also limited. Even if the calculated value of the charge changes the sign, it takes time to reach the required value. In such a way, the delays in the system are simulated and the limitation of the charging devices are taken into account. The peak values of the charge after convergence can be explained by the fact that at the orbital position close to the pole, the component of the Lorentz force on the normal vector to the orbital plane has the smallest value, which leads to a high value of parameter twice an orbit. The limitation on the maximum value prevents the unfeasibly high value of the charge, and it does not lead to trajectory divergence.
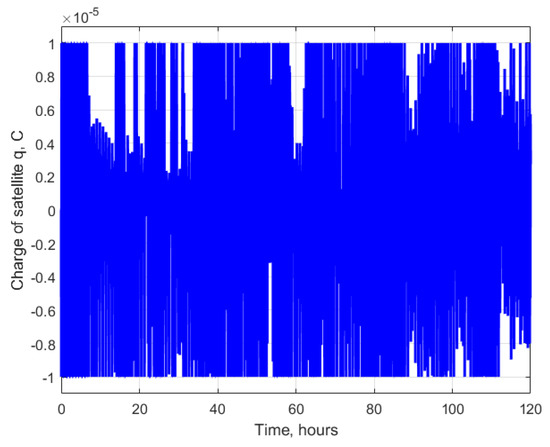
Figure 9.
Satellite charge.
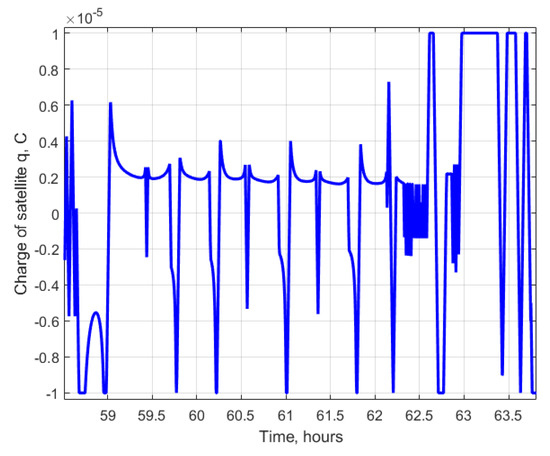
Figure 10.
Satellite charge (zoomed).
The calculated control values according to the Lyapunov-based control algorithm are presented in Figure 11. The sudden high values for the required control along x direction are caused by transition to the second stage of the algorithm—the deviation of the amplitude was quite large and it required a large control. Though the implemented control through Lorenz force differs significantly from the calculated control (see Figure 12), the motion still converges to the desired one. The value of the Lorenz force in the along-track direction is of one order smaller than the other components. Nevertheless, it was enough for drift stopping and for convergence to the required shift value. Since the only control parameter in case of Lorenz force is the charge, during implementation, the implementation errors are inevitable. The direction of the Lorenz force is determined by the velocity vector and local magnetic field vector. By choosing the charge value, only the most significant component of the required control vector is to be partly implemented, while the other components are to be implemented with large errors, although due to magnetic field vector rotation in the LVLH reference frame along the orbit, the errors of implementation are averaging and the trajectory is converging to the required one. From Figure 12, one can also note a sinusoidal behavior of the peaks of Lorenz forces with a period of about 24 h. It can be explained by the rotational motion of the tilted Earth’s magnetic dipole that causes the slight change in the possible direction of the Lorenz force.
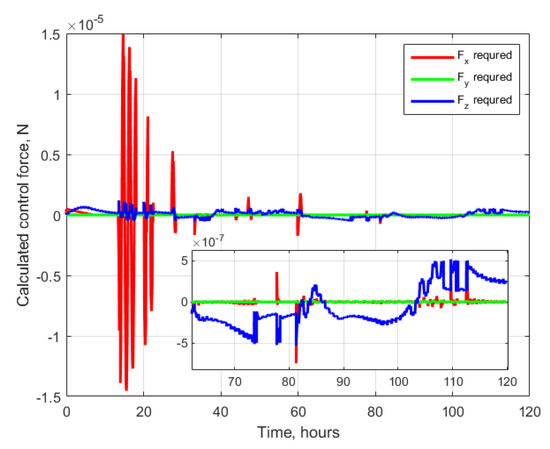
Figure 11.
Calculated control values.
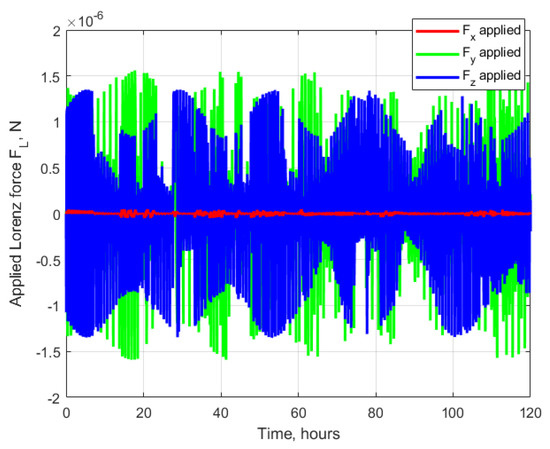
Figure 12.
Applied Lorenz force.
The performance of the control algorithm strongly depends on a set of parameters including the initial conditions. Using Monte Carlo simulations with random initial conditions described in Table 1, the convergence time and the errors of the obtained trajectory parameters are studied.
The convergence time depends on the initial relative drift value. For each random maximal initial relative drift, 50 numerical simulations were performed. The time of the convergence is defined at a time moment when all the parameters are in a certain vicinity of the required values. Figure 13 demonstrates the box-plots of the results of the simulations. Inside the box, there are 50 % of the simulation results, below and under the box are 25 % of the results, and the red line is a median value. One can observe that the more significant the initial drift, the larger the convergence time.
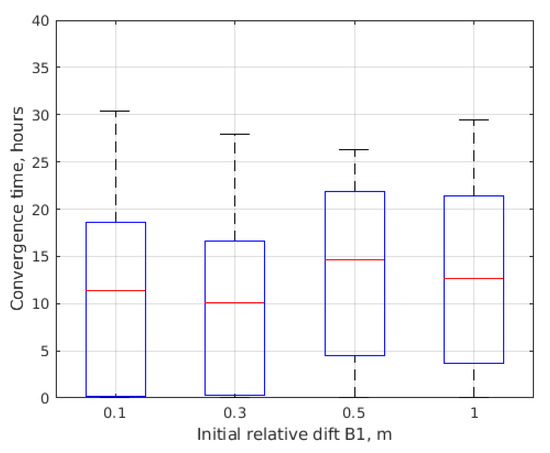
Figure 13.
Convergence time depending on initial drift .
From the Monte Carlo simulation results, it can be concluded that there is no sensible dependence of the errors in the trajectory parameters on the initial relative drift value. The errors on the relative drift are no more than 2 m, the errors in are below 0.5 m. The most significant errors are in out-of-plane amplitudes and they amount to approximately several meters.
The algorithm performance dependence on the maximum possible charge value is also studied. The Monte Carlo simulations for different maximum charge values are carried out. The convergence time boxplot is presented in Figure 14. It can be seen that the convergence time reduces significantly with larger values of the maximum charge . It can be explained by the increased value of the implemented control force resulting in faster approaching the required trajectory. According to Figure 14, at some initial conditions, the convergence could require considerable time: up to 30 h even for the maximum charge value of , though the median value of the simulation results are approximately 2 h for the considered example.
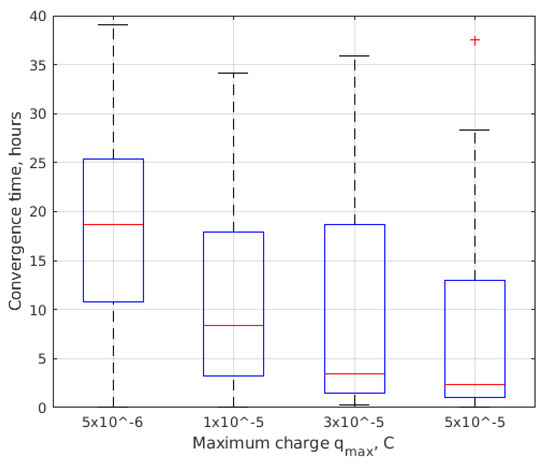
Figure 14.
Convergence time depending on maximal charge value .
It is a quite interesting result that after the convergence the errors in relative drift and relative shift are of the same order for each of the maximum charge value as presented in Figure 15, Figure 16, Figure 17 and Figure 18. However, the errors in the in-plane and out-of-plane amplitudes and strongly depend on the charge value. The higher the , the larger the mean value of the error and its variance. At , the errors in the amplitudes are not acceptable, the mean error in exceeds 10 m, and in it is almost at 5 m; at some initial conditions, the errors are even larger. This effect can be explained by the errors in control implementation using Lorenz force. The required control vector is implemented only partially due to direction and value constrains of the Lorenz force. Such an implementation described in previous chapter inevitably leads to disturbances caused by control errors. The larger the , the higher the level of this disturbance. From the Figure 15, Figure 16, Figure 17 and Figure 18, it can be concluded that this effect of enlarging disturbance causes the increasing value of the error only in and constants.
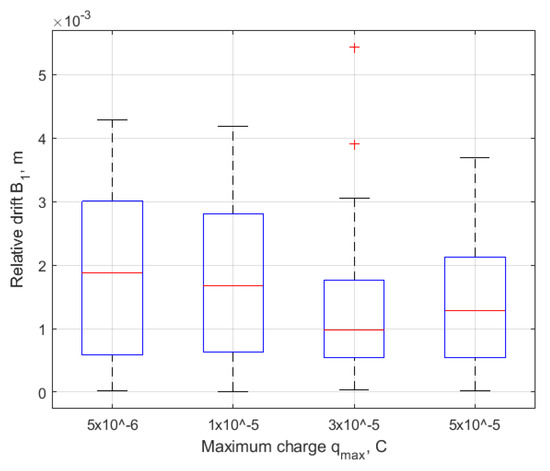
Figure 15.
Mean error in after convergence.
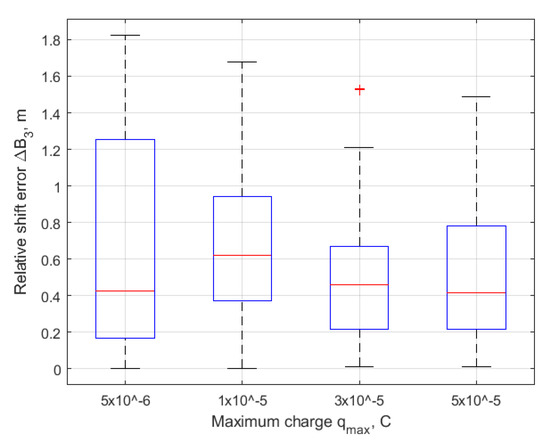
Figure 16.
Mean error in after convergence.

Figure 17.
Mean error in after convergence.
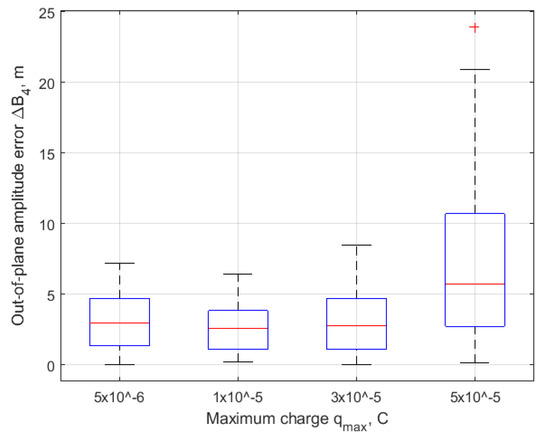
Figure 18.
Mean error in after convergence.
Since the control is based on the Lorenz force which is the result of the cross product of the local magnetic field and the velocity, the controllability of this system depends on variation of magnetic field, i.e., its direction must change over time in the LVLH frame. However, if the satellite is in equatorial orbit, the geomagnetic field vector is almost constant during the orbital motion. These constraints on the geomagnetic field vector direction could influence the control algorithm performance. The Monte Carlo simulations were performed for the fixed parameters presented in Table 1 and different values of the orbit inclination.
For the equatorial orbit, the proposed Lorenz force control is not working as follows from the simulation results. It is caused by the almost fixed geomagnetic field vector along the orbit and as a result the only direction of the Lorenz force. The control algorithm started to achieve the required trajectory beginning from approximately 30 deg of inclination.
Figure 19 presents the results of the convergence time for three values of inclination: 30, 51.7 and 90 deg. The convergence time is shorter for the polar orbit since the geomagnetic field vector rotates almost in the orbital plane and more control force directions are available along the orbit.
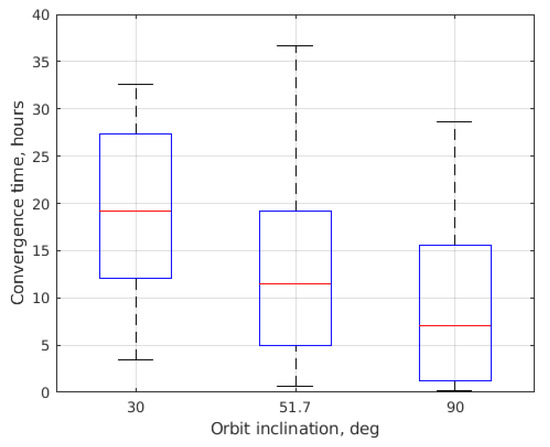
Figure 19.
Convergence time depending on orbit inclination.
Figure 20, Figure 21, Figure 22 and Figure 23 present the results of Monte Carlo simulations—the errors in the trajectory parameters after convergence. Errors in are almost the same after the convergence. The relative shift error is less for the polar orbit and amounts to approximately 0.25 m. The error in in-plane amplitude decreases dramatically with increasing the inclination. The behavior of the out-of-plane amplitude is almost opposite, though the values of the errors do not exceed 10 m in the worst case.
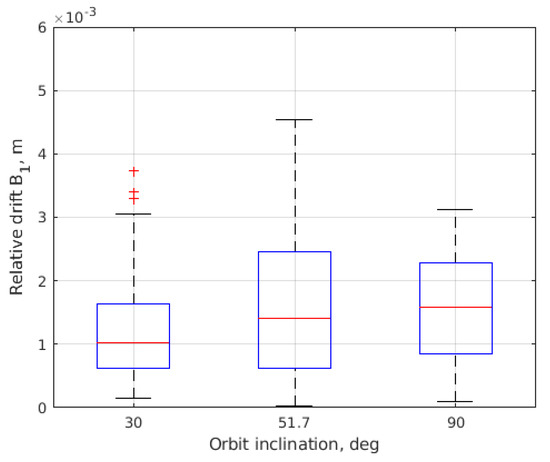
Figure 20.
Mean error in after convergence.
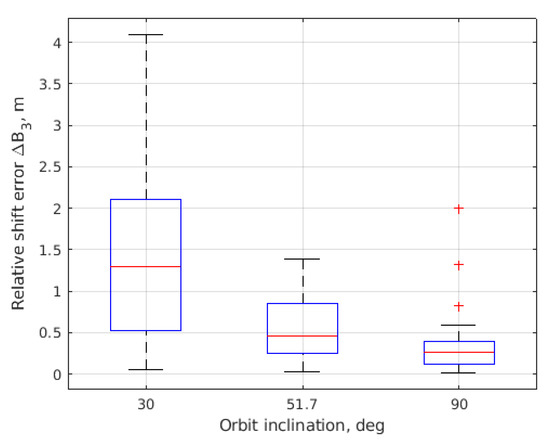
Figure 21.
Mean error in after convergence.
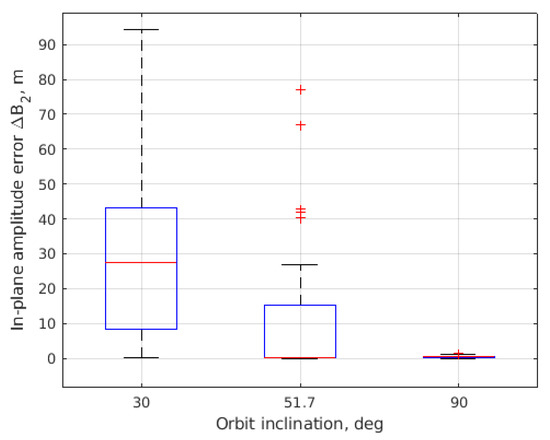
Figure 22.
Mean error in B2 after convergence.
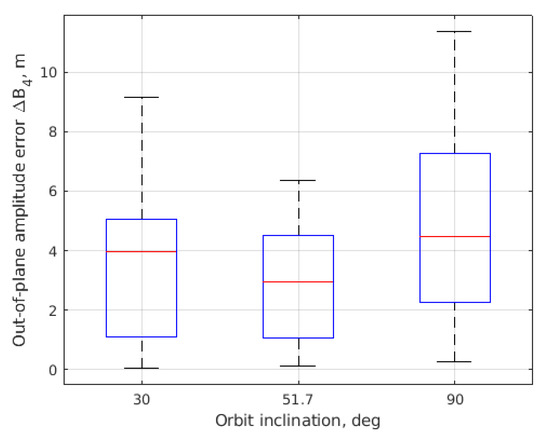
Figure 23.
Mean error in after convergence.
4.3. Cases of Satellites Swarm
The proposed control can be applied for the formation flying consisting of various numbers of satellites. A swarm of satellites can be used as a spatial distributed measurement system in LEO. Consider the two examples of distributed swarm of nanosatellites controlled using the proposed control algorithm. First example is a formation consisting of N satellites with required zero drift and shift relative to the virtual central satellite but different size of the in-plane amplitude. Such a configuration could be useful for construction of the spatial measurement system in space. Second example is a train formation when all the satellite are distributed with the same relative distance in the along-track direction.
4.3.1. Nested Ellipses
Consider a formation flying consisting of five satellites. The number of satellites could be larger and the algorithm performance would be the same, though the resulting relative trajectory will be difficult to present. That is why, in the case of the study, only five satellites are considered. The initial conditions are the same as in Table 1, except for the required trajectory constants. The required drift and shift are zero for all the satellites , . The out-of-plane amplitude is also constant, and . In order to construct the spatially distributed system, the required in-plane amplitudes differ by 10 m for each satellite. Therefore, after the convergence, the satellite trajectories are located along the nested ellipses of different size. Figure 24 shows the example of the relative trajectories of five satellites during the 120 h of simulation, and Figure 25 presents the resulting trajectories after convergence. As one can observe, the algorithm successfully achieved the trajectory of the required size of the ellipses nested inside each other. Figure 26 and Figure 27 present the relative drift and shift which are in the vicinity of the required zero value. Figure 28 shows the convergence of the in-plane amplitudes to the required values. The larger the amplitude, the longer time is required to achieve its vicinity. For the 5th satellite, almost 100 h were required to achieve to the required value of 40 m. The errors in out-of-plane amplitudes are up to 4 m after convergence as one can observe in Figure 29.
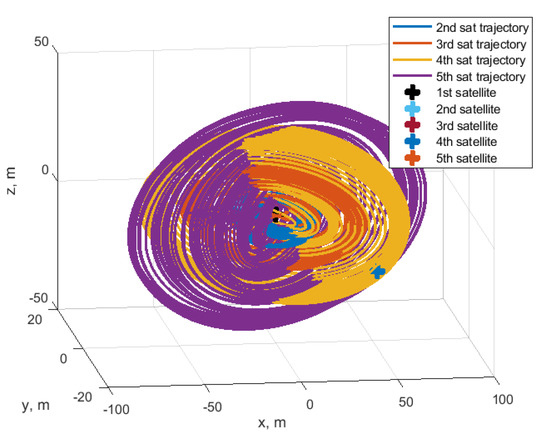
Figure 24.
Relative trajectories.
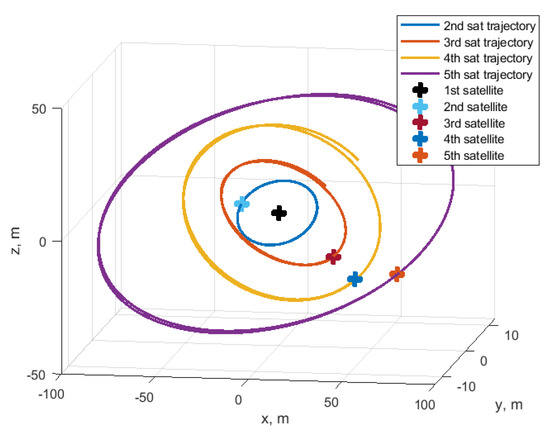
Figure 25.
Relative trajectories during the last 2 h of simulation.
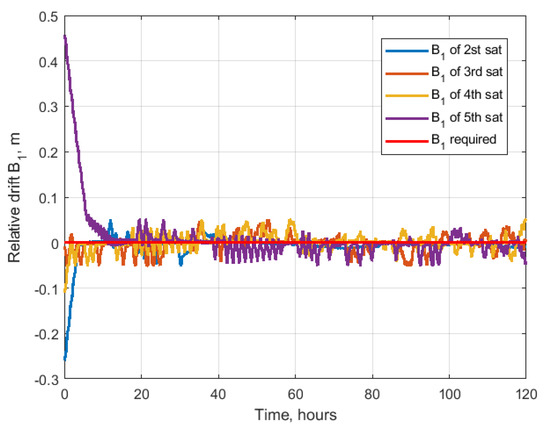
Figure 26.
Relative drift.
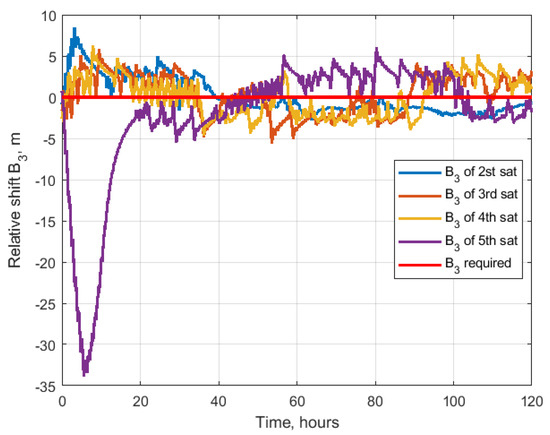
Figure 27.
Relative shift.
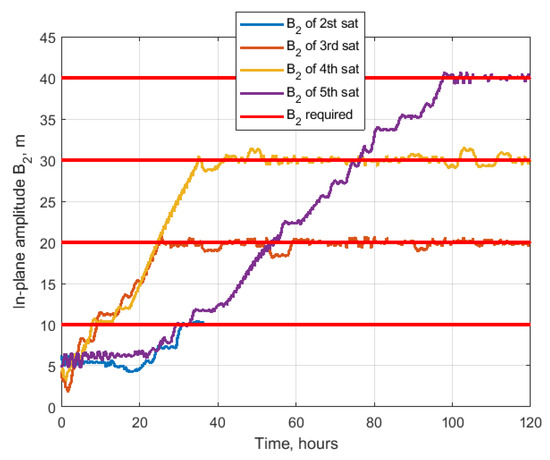
Figure 28.
In-plane amplitude.
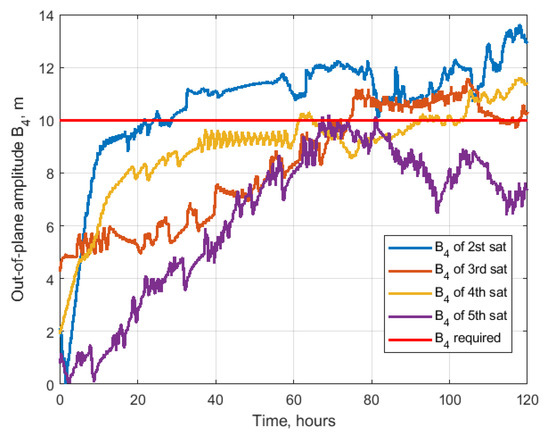
Figure 29.
Out-of-plane amplitude.
In the presented example, the control was implemented using centralized approach when all the satellites follow the motion of the chief satellite; in this case, it is the first satellite that is in the center of the nested ellipses. Since the phases of the satellites are not controllable, the positions of the satellites on the ellipses are random and the planes of the ellipses do not coincide.
4.3.2. Train Formation
The train formation is used when the uniformly distributed measurements along the same orbit are required for the mission. To achieve such a configuration using the proposed control law, the required shift values should be different and the other parameters should tend to zero. Consider a formation consisting of five satellites; all the simulation parameters are the same as those of the previous example. In this case, the control can be implemented using decentralized approach. Each satellite tries to achieve the required value of the shift relative to the neighbour satellite with smallest positive value of . Figure 30 shows the example of the relative trajectories of five satellites during the 120 h of simulation, and Figure 31 presents the resulting trajectories after convergence. As one can observe, after a time, all the satellites are lined up in along-track direction with separation of 10 m. The out-of-plane amplitudes are of about 5 m in the end of simulation, and in-plane amplitudes are all around zero except for the second satellite whose value is approximately 0.8 m.
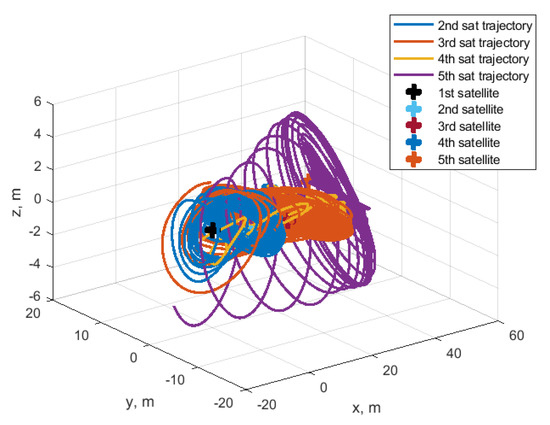
Figure 30.
Relative trajectories.
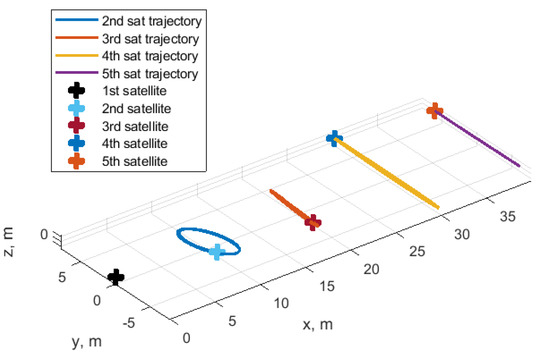
Figure 31.
Relative trajectories during the last 2 h of simulation.
Figure 32, Figure 33, Figure 34 and Figure 35 present the values of the parameters . The relative drift is close to zero value. However, the relative shifts are all at the required values with 10 m of difference. In the train configuration, the amplitudes should converge to zero. The in-plane amplitudes are almost all converged to zero after 160 h of simulation, but the out-of-plane convergence is even slower. After 160 h of simulation, there is the error of several meters. Figure 36 demonstrates the charges of the satellites. All the values do not exceed the maximum value, and after the convergence, the values rarely achieve this constraint.
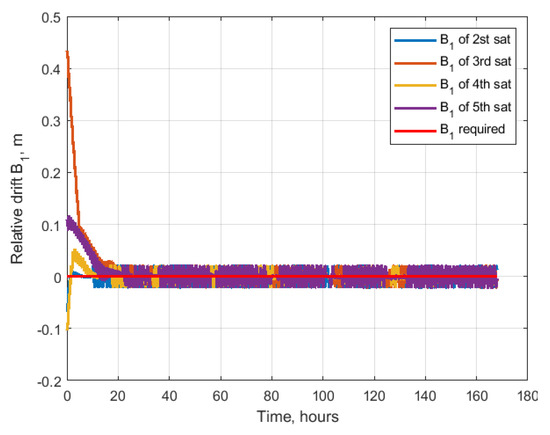
Figure 32.
Relative drift.
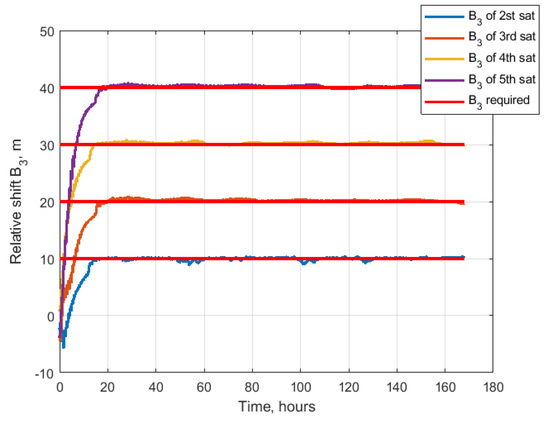
Figure 33.
Relative shift.
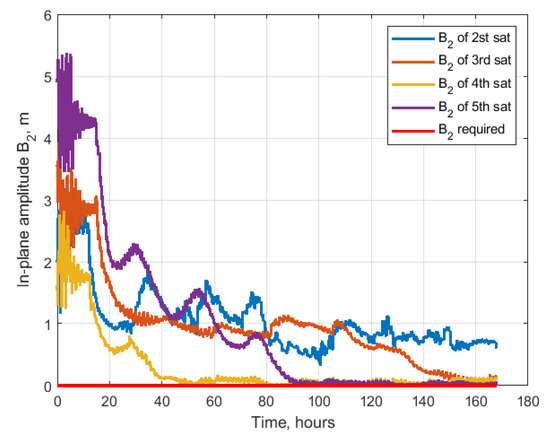
Figure 34.
In-plane amplitude.
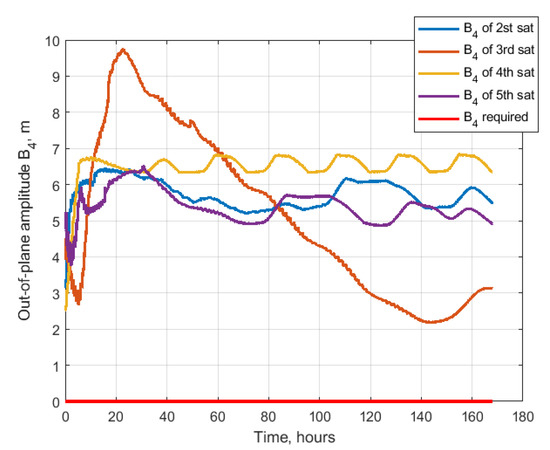
Figure 35.
Out-of-plane amplitude.
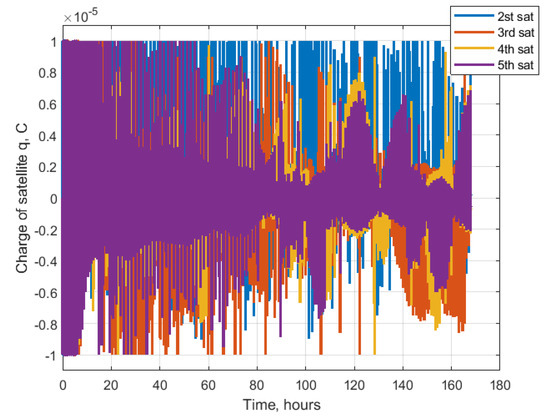
Figure 36.
Charges of the satellites.
Thus, the examples of the proposed algorithm application for the construction and maintenance of the two configurations consisting of multiple satellites demonstrate the performance of the algorithm. All the trajectories converged to the required ones with final error of several meters.
5. Conclusions
A control algorithm based on the Lorenz force application is developed for the solution of the problems of the construction and maintenance of the small satellites’ formation flying relative motion. For application of the Lorenz force, the onboard charging device capable to provide the required charge in satellite is considered. Since the Lorenz force direction is limited along the orbit and it is determined by the local geomagnetic filed and orbital velocity, only four of six elements of state vector are controllable. In terms of relative trajectory parameters, the proposed Lyapunov-based control is aimed to achieve the required relative drift, relative shift and in-plane and out-of-plane amplitudes. The in-plane and out-of-plane phases are considered as uncontrollable. Thus, the required relative configuration, size and shape can be achieved by the proposed control. The numerical study showed that the best algorithm performance could be achieved at near polar orbit. The initial conditions and the maximum possible charge affect the convergence time as well as the trajectory errors after the convergence. The errors in out-of-plane amplitude are the worst among the errors of the other parameters and could exceed several meters. The results of the application of the proposed algorithm are demonstrated in three cases: the case of one controlled satellite in two satellites’ formation flying, and the two examples of multiple satellites’ formation flying in nested ellipses and train configurations. In all study cases, the control algorithm successfully achieved the required trajectories with final errors of several meters. The proposed Lorenz force-based control is promising for the application onboard small satellites since it does not require any fuel consumption.
Author Contributions
Analysis of obtained results, D.I.; numerical simulation study, G.A.; control algorithm development, Y.M.; supervision, M.O.; problem statement formulation, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Moscow Center of Fundamental and Applied Mathematics, Agreement with the Ministry of Science and Higher Education of the Russian Federation, No. 075-15-2022-283, and by the Portuguese Foundation for Science and Technologies via the Centre for Mechanical and Aerospace Science and Technologies, C-MAST, POCI-01-0145-FEDER-007718.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
| LAO | Lorentz Augmented Orbit |
| LEO | Low Earth Orbit |
| CW | Clohessy–Wiltshire equations |
| LVLH | Local-Vertical/Local-Horizontal reference frame |
| Lorentz-force vector | |
| Satellite radius vector in Earth-centered inertial reference frame | |
| Satellite velocity in Earth-centered inertial reference frame | |
| Satellite charge | |
| Earth angular velocity | |
| Earth magnetic induction vector | |
| Radius of circular orbit | |
| Orbital angular velocity | |
| Vectors of the i-th satellite in the LVLH reference frame | |
| Relative position vector in the LVLH reference frame | |
| Control acceleration applied to i-th satellite | |
| Difference of the two control accelerations written in LVLH frame | |
| Relative motion parameters | |
| Earth magnetic dipole moment value | |
| Unit vector along the Earth’s dipole vector | |
| Distance from the Earth’s center of mass | |
| Unit vector along the satellite radius vector | |
| Angle between the magnetic south pole and geocentric north pole | |
| Latitude angle | |
| Greenwich’s longitude at initial time | |
| Deviation of motion parameters from the desired motion | |
| Desired motion parameters | |
| Lyapunov function | |
| Positive control parameters | |
| Parameters for control implementation | |
| Satellite mass | |
| Lorentz force vector components | |
| Value of the satellite charge | |
| Maximum value of the satellite charge | |
| Speed of the change in the satellite charge | |
| Simulation time step |
References
- Guzmán, J.J.; Edery, A. Mission design for the MMS tetrahedron formation. IEEE Aerosp. Conf. Proc. 2004, 1, 533–540. [Google Scholar] [CrossRef]
- Tzabari, M.; Holodovsky, V.; Shubi, O.; Eytan, E.; Altaratz, O.; Koren, I.; Aumann, A.; Schilling, K.; Schechner, Y.Y. CloudCT 3D volumetric tomography: Considerations for imager preference, comparing visible light, short-wave infrared, and polarized imagers. Proc. SPIE Polariz. Sci. Remote Sens. X 2021, 11833, 19–26. [Google Scholar] [CrossRef]
- Dauner, J.; Elsner, L.; Ruf, O.; Borrmann, D.; Scharnagl, J.; Schilling, K. Visual servoing for coordinated precise attitude control in the TOM small satellite formation. Acta Astronaut. 2022, 202, 760–771. [Google Scholar] [CrossRef]
- Mashtakov, Y.; Ovchinnikov, M.; Ivanov, D.; Roldugin, D.; Shestakov, S.; Klimov, P.; Iyudin, A.; Svertilov, S.; Pansyrnyi, O.; Churilo, I. Nanosatellites triangle formation flying for terrestrial gamma-ray flashes and transient luminous events study. In Proceedings of the International Astronautical Congress, IAC, 15 October 2020; International Astronautical Federation (IAF): Paris, France, 2020. [Google Scholar]
- Joffre, E.; Wealthy, D.; Fernandez, I.; Trenkel, C.; Voigt, P.; Ziegler, T.; Martens, W. LISA: Heliocentric formation design for the laser interferometer space antenna mission. Adv. Sp. Res. 2020, 67, 3868–3879. [Google Scholar] [CrossRef]
- Biktimirov, S.; Belyj, G.; Pritykin, D. Satellite Formation Flying for Space Advertising: From Technically Feasible to Economically Viable. Aerospace 2022, 9, 419. [Google Scholar] [CrossRef]
- Biktimirov, S.; Ivanov, D.; Pritykin, D. A satellite formation to display pixel images from the sky: Mission design and control algorithms. Adv. Sp. Res. 2022, 69, 4026–4044. [Google Scholar] [CrossRef]
- Kramer, A.; Bangert, P.; Schilling, K. UWE-4: First Electric Propulsion on a 1U CubeSat—In-Orbit Experiments and Characterization. Aerospace 2020, 7, 98. [Google Scholar] [CrossRef]
- Scharnagl, J.; Haber, R.; Dombrovski, V.; Schilling, K. NetSat—Challenges and lessons learned of a formation of 4 nano-satellites. Acta Astronaut. 2022, 201, 580–591. [Google Scholar] [CrossRef]
- Kahr, E.; Roth, N.; Montenbruck, O.; Risi, B.; Zee, R.E. GPS relative navigation for the CanX-4 and CanX-5 formation-flying nanosatellites. J. Spacecr. Rockets 2018, 55, 1545–1558. [Google Scholar] [CrossRef]
- Leonard, C.L.; Hollister, W.M.; Bergmann, E. V Orbital formationkeeping with differential drag. J. Guid. Control. Dyn. 1989, 12, 108–113. [Google Scholar] [CrossRef]
- Johnson, L.; Whorton, M.; Heaton, A.; Pinson, R.; Laue, G.; Adams, C. NanoSail-D: A solar sail demonstration mission. Acta Astronaut. 2011, 68, 571–575. [Google Scholar] [CrossRef]
- Hogan, E.A.; Schaub, H. Collinear invariant shapes for three-spacecraft Coulomb formations. Acta Astronaut. 2012, 72, 78–89. [Google Scholar] [CrossRef]
- Saaj, C.M.; Lappas, V.; Schaub, H.; Izzo, D. Hybrid propulsion system for formation flying using electrostatic forces. Aerosp. Sci. Technol. 2010, 14, 348–355. [Google Scholar] [CrossRef]
- Kwon, D.W. Propellantless formation flight applications using electromagnetic satellite formations. Acta Astronaut. 2010, 67, 1189–1201. [Google Scholar] [CrossRef]
- Ivanov, D.; Ovchinnikov, M. Constellations and formation flying. In Cubesat Handbook; Academic Press: Cambridge, MA, USA, 2021; pp. 135–146. [Google Scholar]
- Peck, M.A. Prospects and challenges for lorentz-augmented orbits. Collect. Tech. Pap.-AIAA Guid. Navig. Control Conf. 2005, 3, 1631–1646. [Google Scholar] [CrossRef]
- Schaffer, L.; Burns, J.A. Charged dust in planetary magnetospheres: Hamiltonian dynamics and numerical simulations for highly charged grains. J. Geophys. Res. Sp. Phys. 1994, 99, 17211–17223. [Google Scholar] [CrossRef]
- Saaj, C.M.; Lappas, V.; Richie, D.; Peck, M.; Streetman, B.; Schaub, H.; Izzo, D. Electrostatic Forces for Satellite Swarm Navigation and Reconfiguration; European Space Agency: Paris, France, 2006.
- Paul, S.N.; Frueh, C. Analytical expressions for orbital perturbations due to Lorentz force. Acta Astronaut. 2021, 182, 466–485. [Google Scholar] [CrossRef]
- Huang, X.; Yan, Y.; Zhou, Y. Dynamics and control of spacecraft hovering using the geomagnetic Lorentz force. Adv. Sp. Res. 2014, 53, 518–531. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Y.; Zhu, Z.; Deng, Y.; Zhao, Y. A new design of drag-free and attitude control based on non-contact satellite. ISA Trans. 2019, 88, 62–72. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, S.; Li, J. Lorentz force time-optimal transfer trajectory design in Jovian magnetic field. Adv. Sp. Res. 2015, 55, 1061–1073. [Google Scholar] [CrossRef]
- Yamakawa, H.; Hachiyama, S.; Bando, M. Attitude dynamics of a pendulum-shaped charged satellite. Acta Astronaut. 2012, 70, 77–84. [Google Scholar] [CrossRef]
- Abdel-Aziz, Y.A.; Shoaib, M. Attitude dynamics and control of spacecraft using geomagnetic Lorentz force. Res. Astron. Astrophys. 2014, 15, 127–144. [Google Scholar] [CrossRef][Green Version]
- Kalenova, V.I.; Morozov, V.M. Novel approach to attitude stabilization of satellite using geomagnetic Lorentz forces. Aerosp. Sci. Technol. 2020, 106, 106105. [Google Scholar] [CrossRef]
- Prabhat, H.; Mukherjee, B.K.; Giri, D.K.; Sinha, M. Fault-tolerant sliding mode satellite attitude stabilization using magneto-Coulombic torquers. Aerosp. Sci. Technol. 2022, 121, 107316. [Google Scholar] [CrossRef]
- Aleksandrov, A.Y.; Aleksandrova, E.B.; Tikhonov, A.A. Stabilization of a programmed rotation mode for a satellite with electrodynamic attitude control system. Adv. Sp. Res. 2018, 62, 142–151. [Google Scholar] [CrossRef]
- Peng, C.; Gao, Y. Lorentz-force-perturbed orbits with application to J2-invariant formation. Acta Astronaut. 2012, 77, 12–28. [Google Scholar] [CrossRef]
- Pollock, G.E.; Gangestad, J.W.; Longuski, J.M. Analytical solutions for the relative motion of spacecraft subject to Lorentz-force perturbations. Acta Astronaut. 2011, 68, 204–217. [Google Scholar] [CrossRef]
- Yamakawa, H.; Bando, M.; Yano, K.; Tsujii, S. Spacecraft relative dynamics under the influence of geomagnetic lorentz force. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar] [CrossRef]
- Tsujii, S.; Bando, M.; Yamakawa, H. Spacecraft Formation Flying Dynamics and Control Using the Geomagnetic Lorentz Force. J. Guid. Control. Dyn. 2013, 36, 136–148. [Google Scholar] [CrossRef]
- Huang, X.; Yan, Y.; Zhou, Y. Optimal spacecraft formation establishment and reconfiguration propelled by the geomagnetic Lorentz force. Adv. Sp. Res. 2014, 54, 2318–2335. [Google Scholar] [CrossRef]
- Sun, R.; Shan, A.; Zhang, C.; Jia, Q. Optimal spacecraft rendezvous using the combination of aerodynamic force and Lorentz force. Adv. Sp. Res. 2021, 67, 3583–3597. [Google Scholar] [CrossRef]
- Hill, G.W. Researches in Lunar Theory. Am. J. Math. 1878, 1, 5–26. [Google Scholar] [CrossRef]
- Mashtakov, Y.; Ovchinnikov, M.; Petrova, T.; Tkachev, S. Two-satellite formation flying control by cell-structured solar sail. Acta Astronaut. 2020, 170, 592–600. [Google Scholar] [CrossRef]
- Merkin, D.R. Introduction to the Theory of Stability; Springer: New York, NY, USA, 1997. [Google Scholar]
- Barbashin, E.A. On construction of Lyapunov functions for non-linear systems. In Proceedings of the Proc. First Congr. IFAK, Moscow, Russia; 1961; pp. 742–751. Available online: https://dl.acm.org/doi/abs/10.1016/j.automatica.2022.110411 (accessed on 28 November 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).