Numerical Investigations of Precise Wind Field in Main Landing Area during the Landing Phase of “Shen Zhou” Series Spacecraft Mission
Abstract
1. Introduction
2. Case Description and Methodology
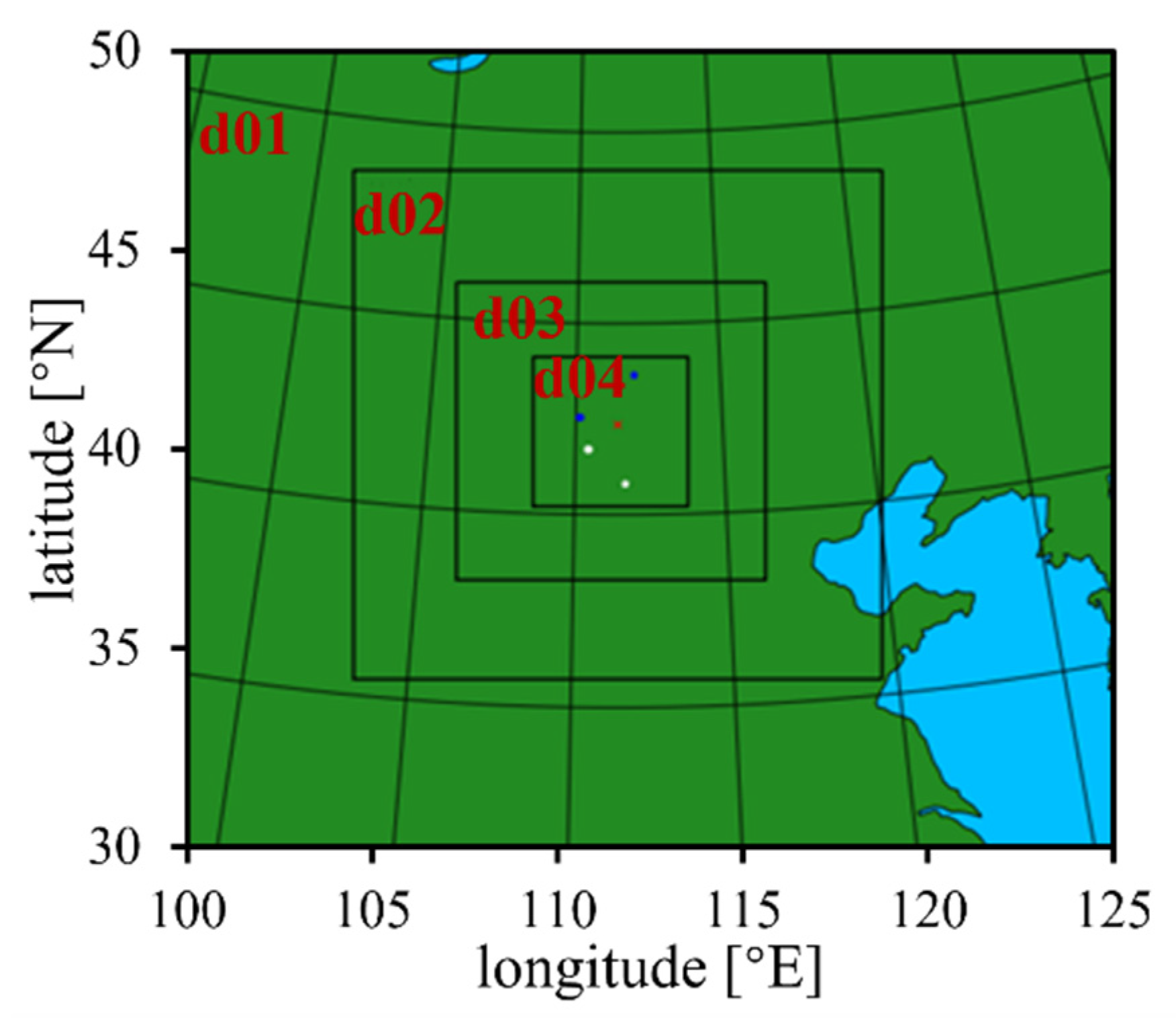
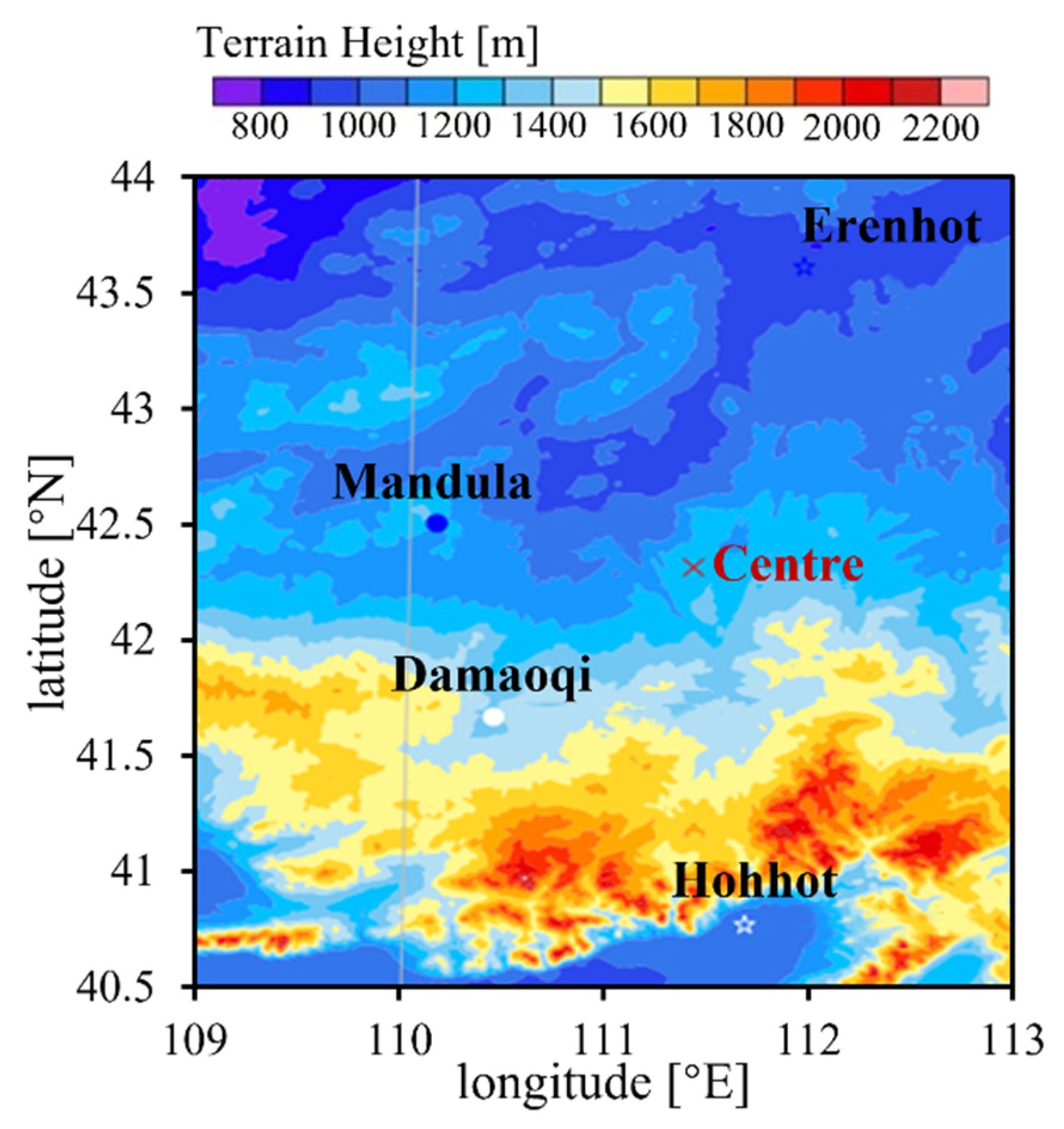
2.1. Target Area
2.2. The WRF Model
2.3. Case Setup
2.4. In Situ Datasets
3. Results and Discussion
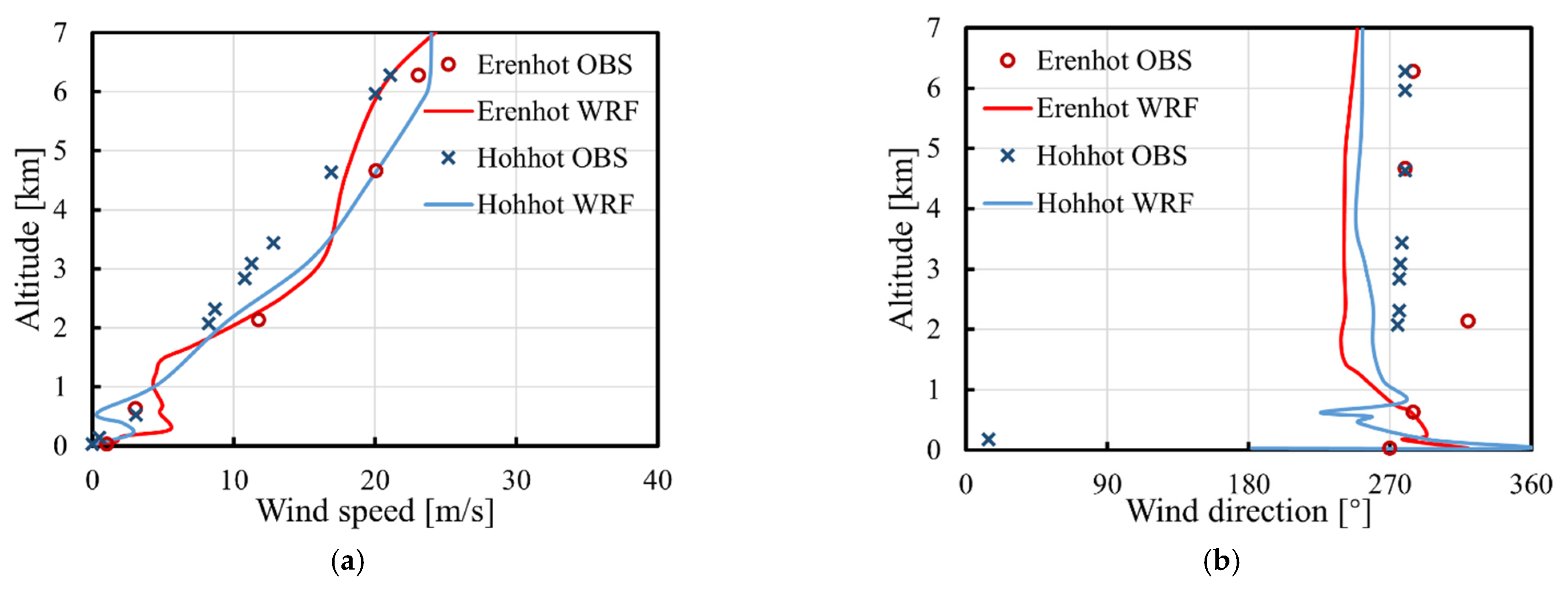
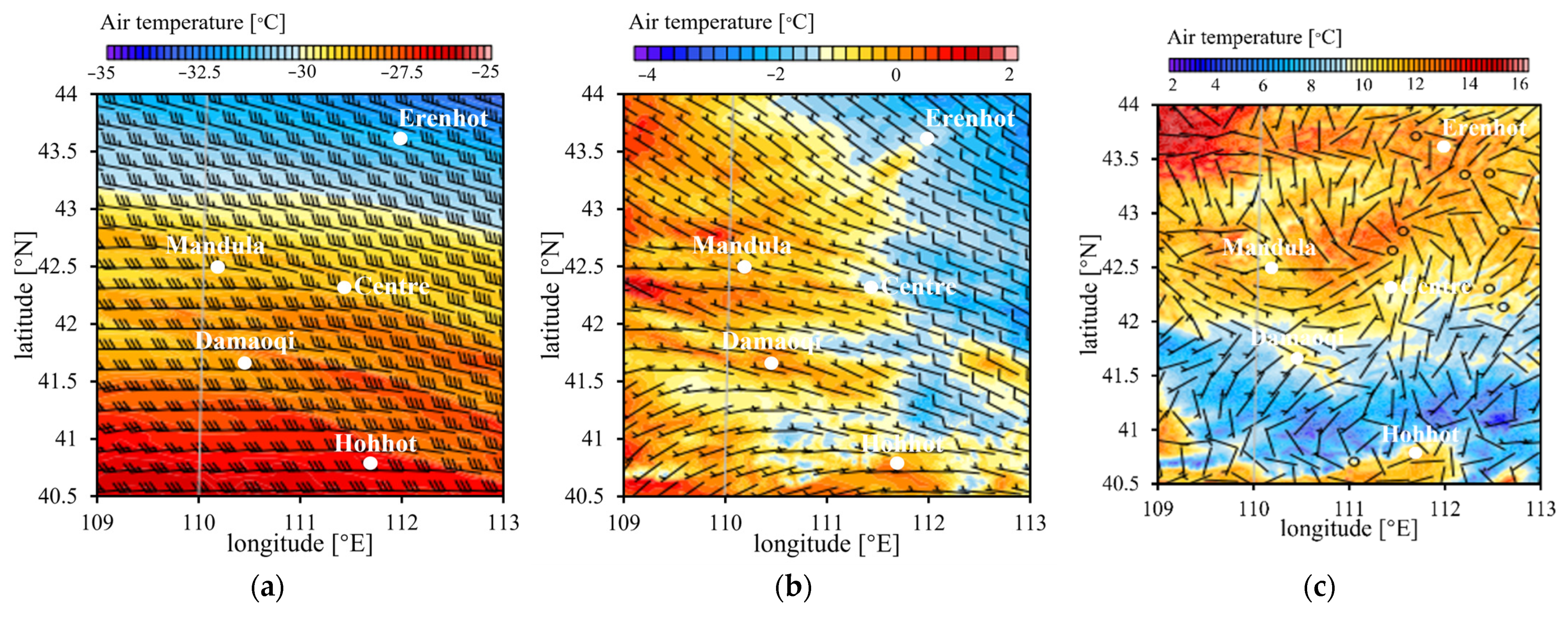
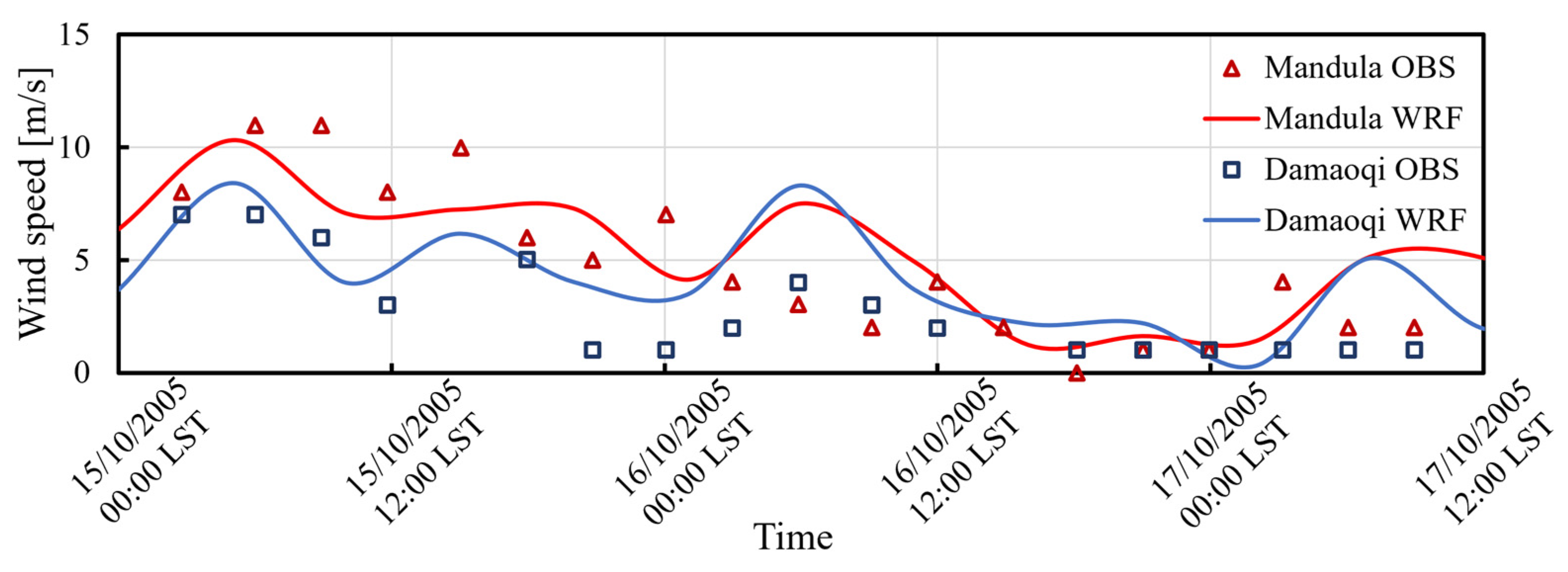
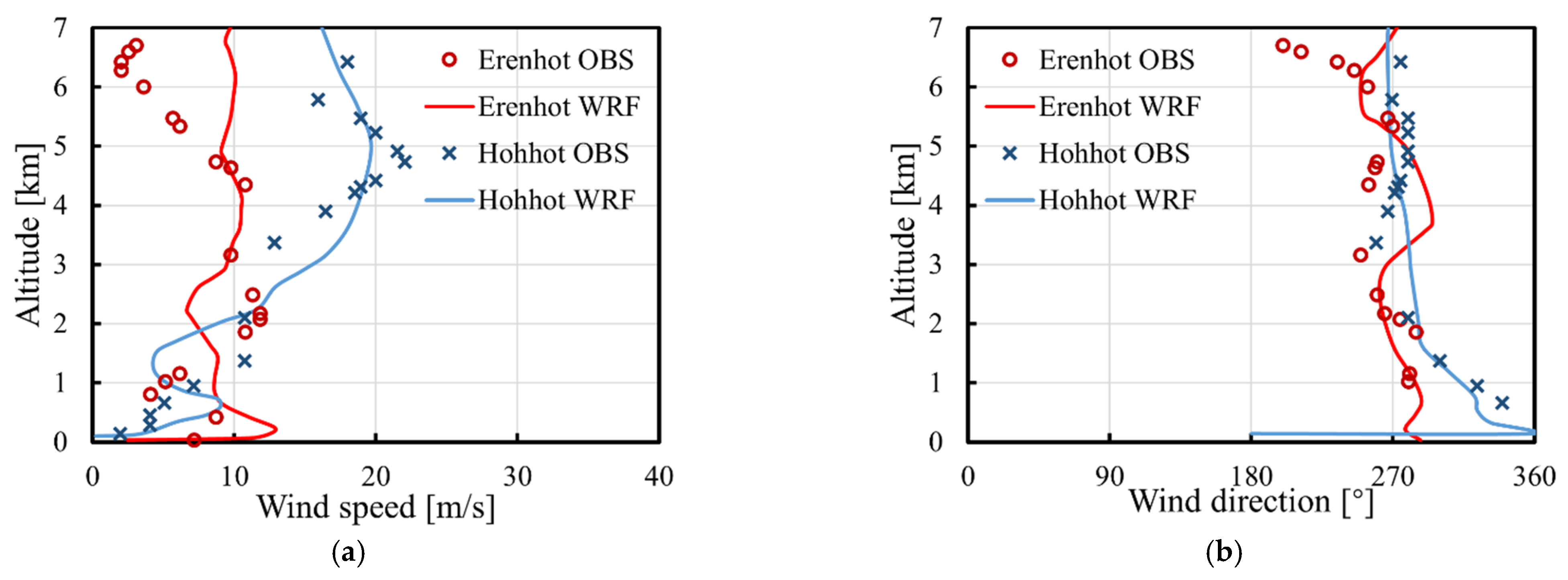
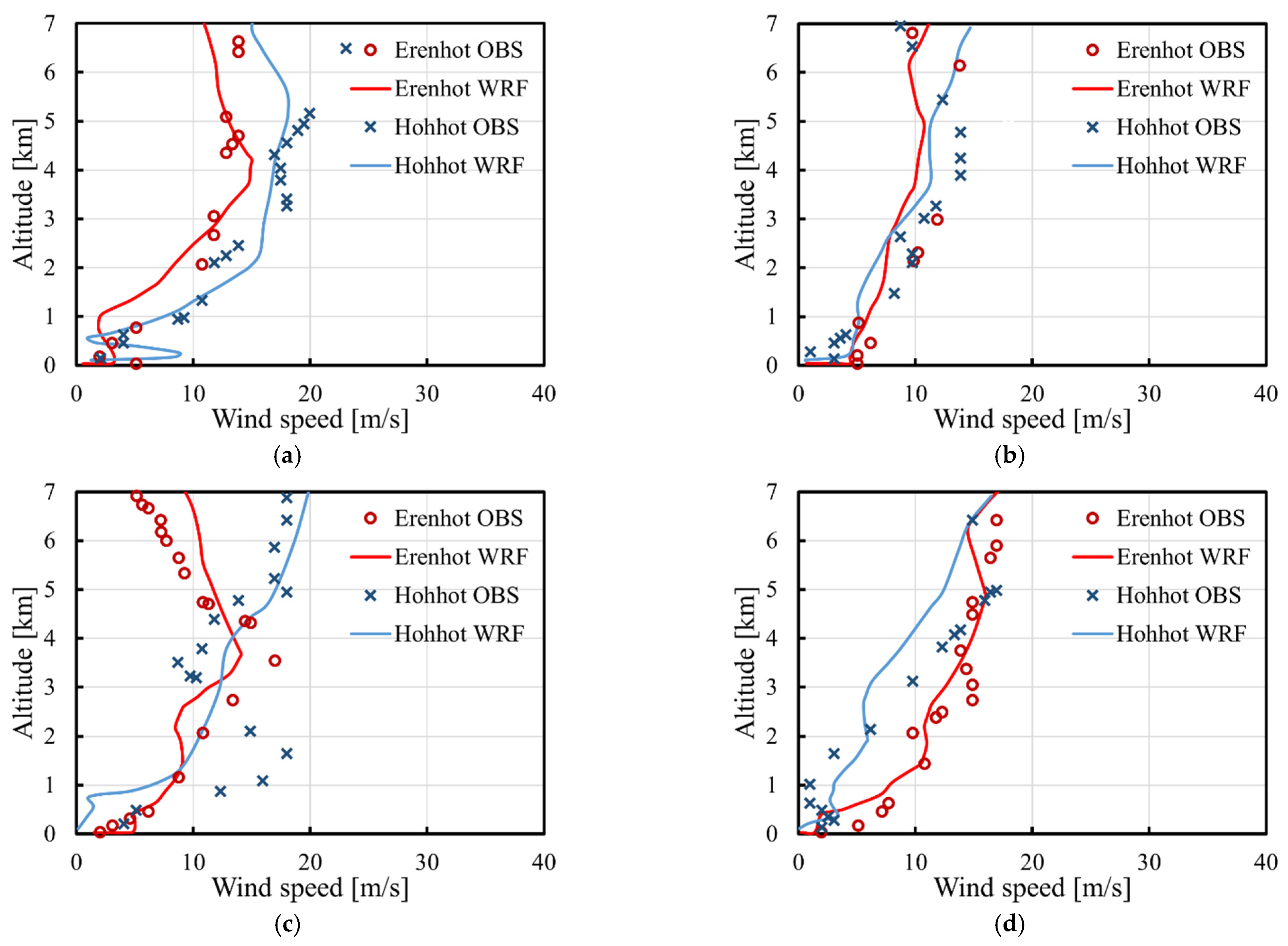
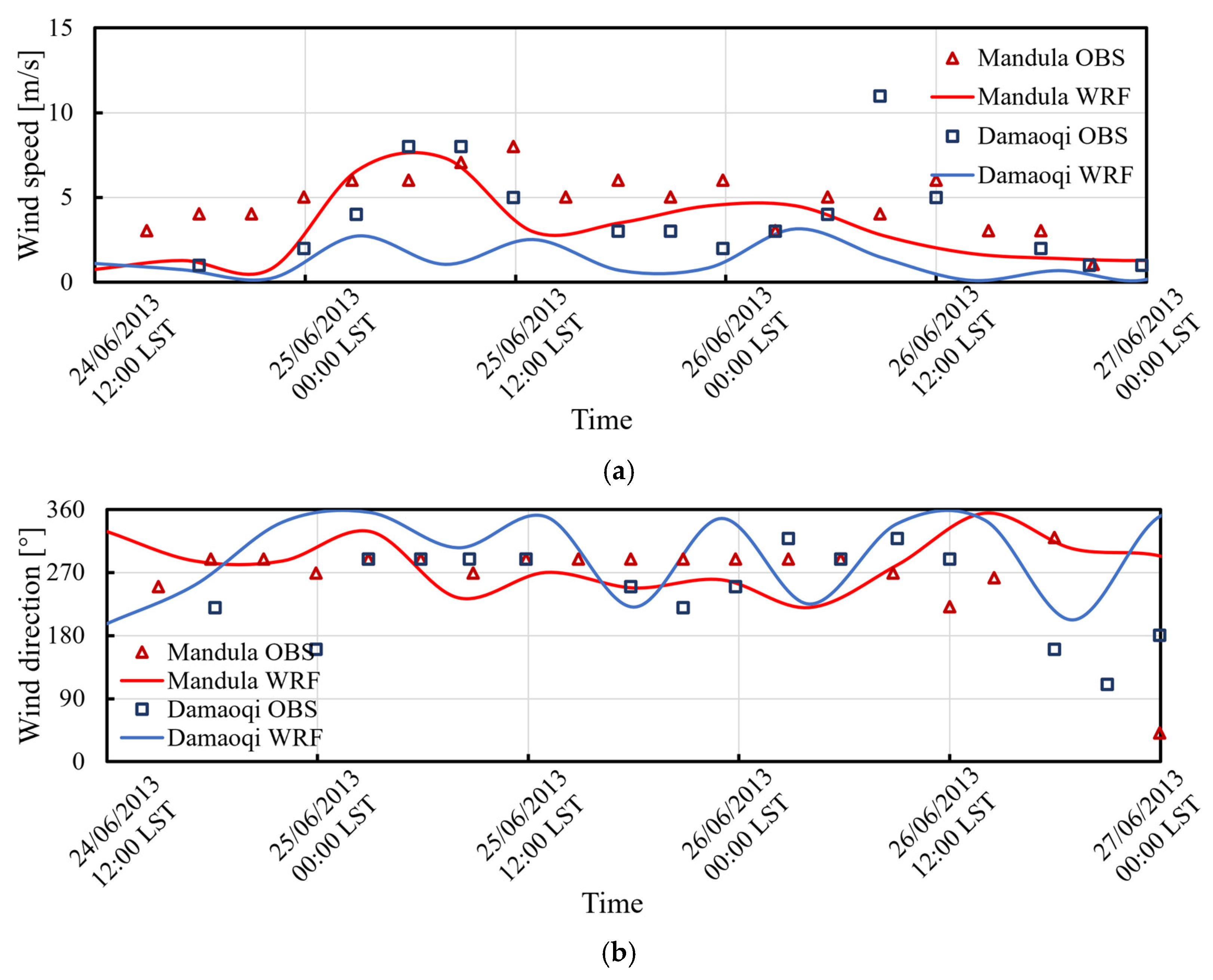
3.1. “Shen Zhou 6” Case
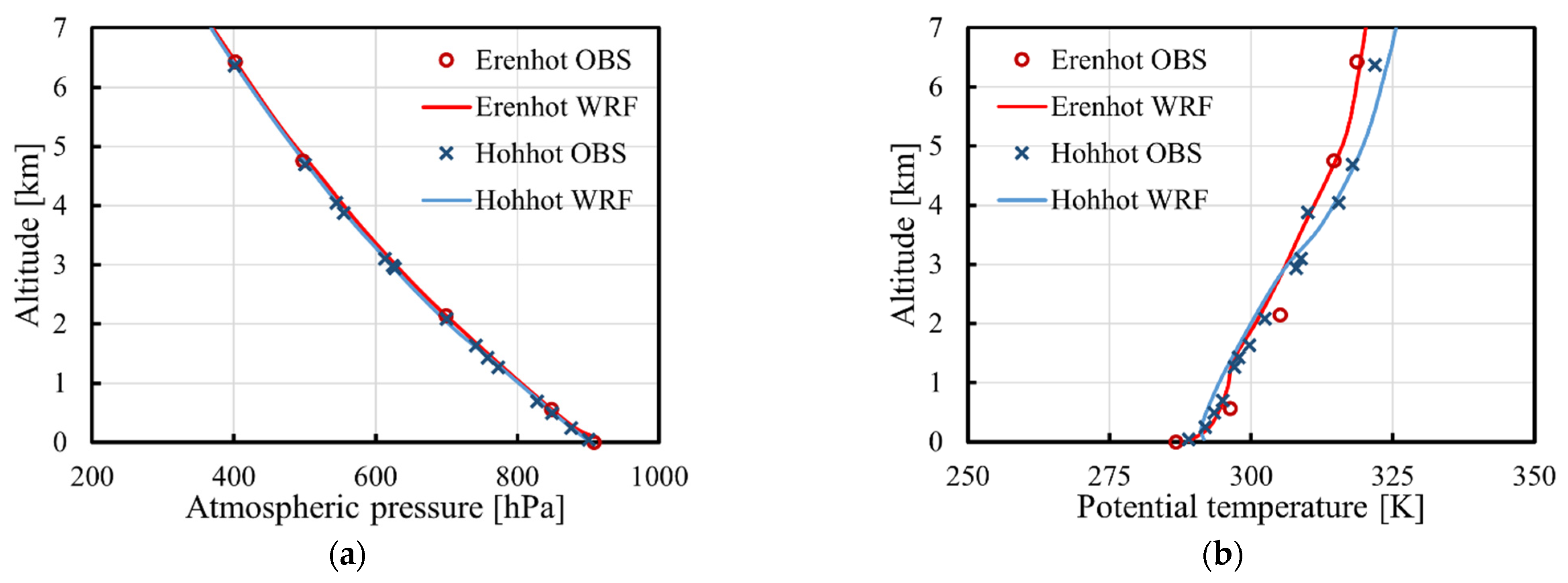
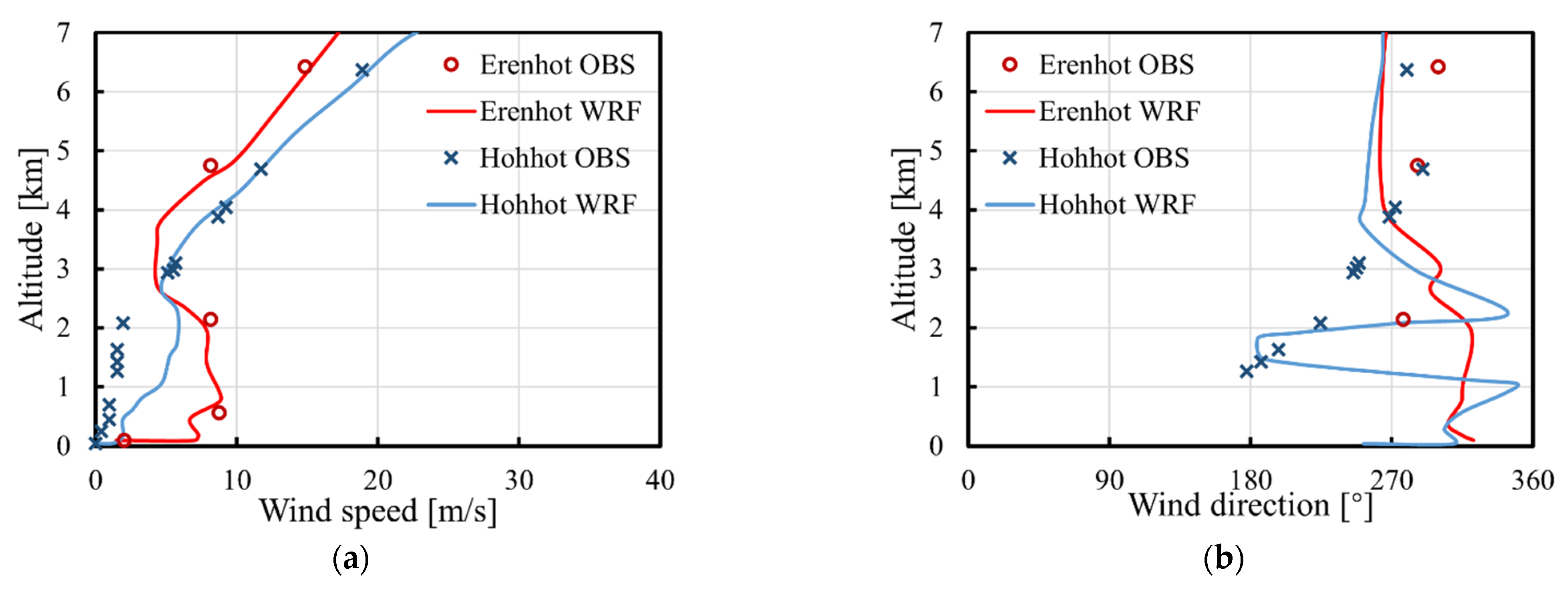
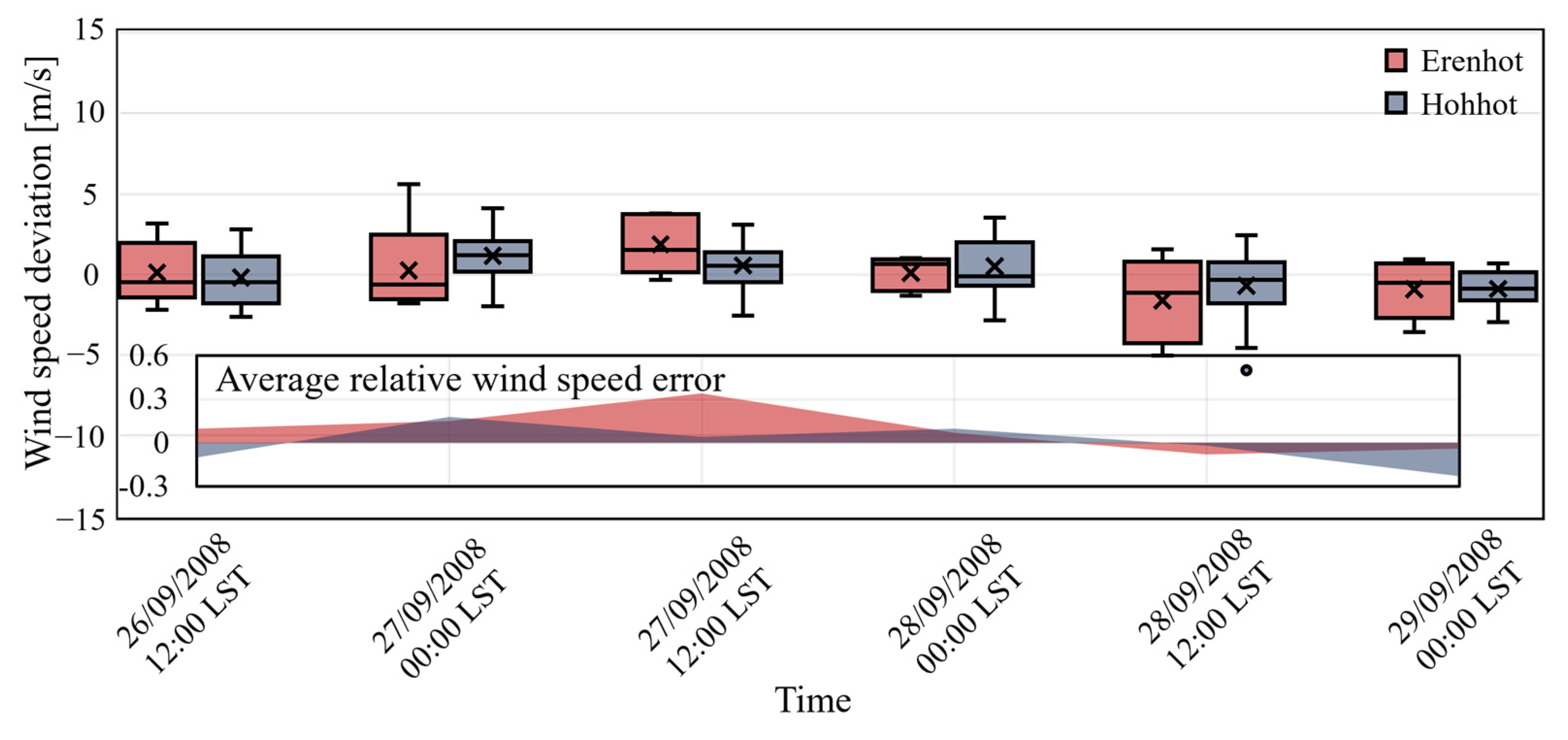
3.2. “Shen Zhou 7” Case
3.3. “Shen Zhou 10” Case
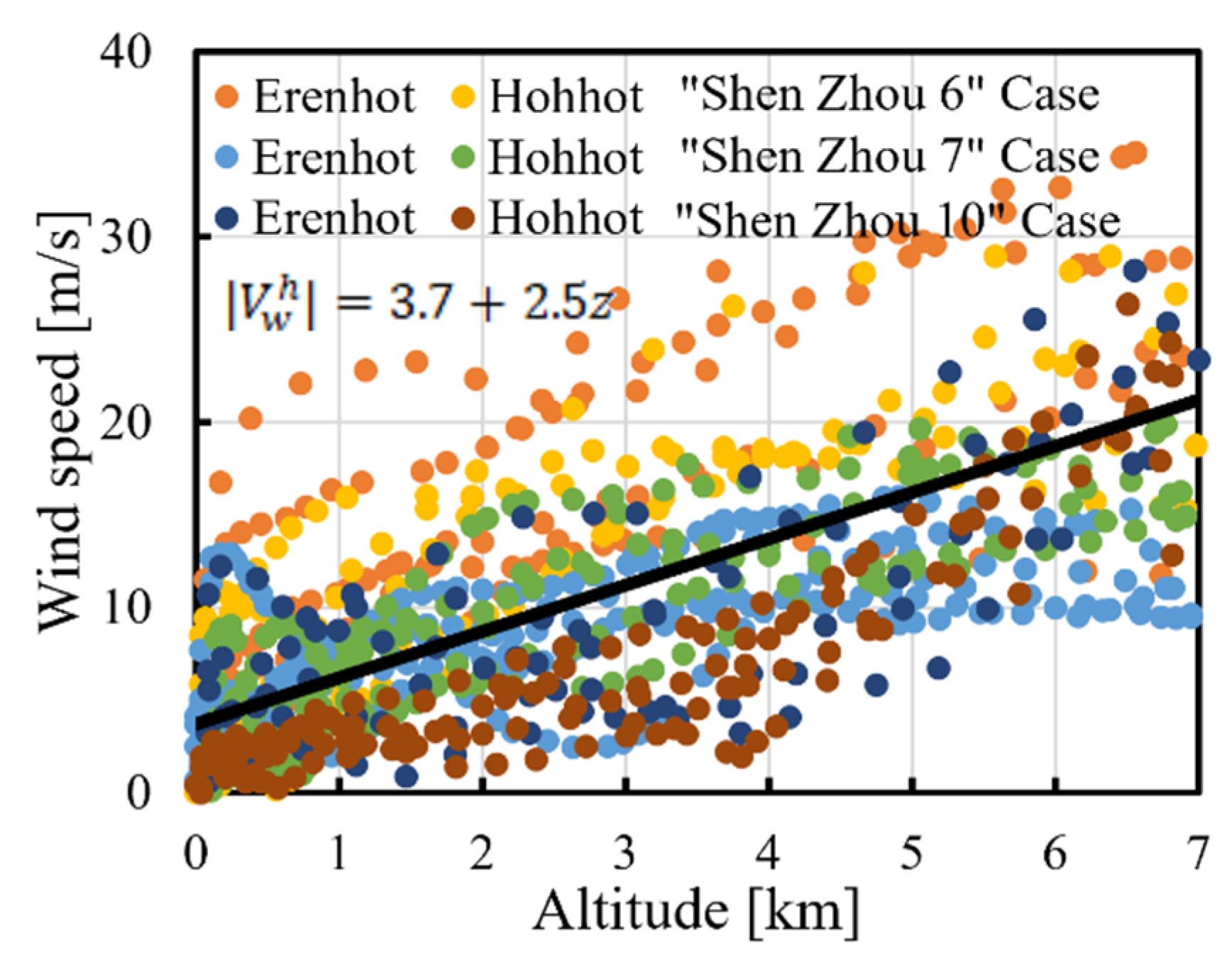
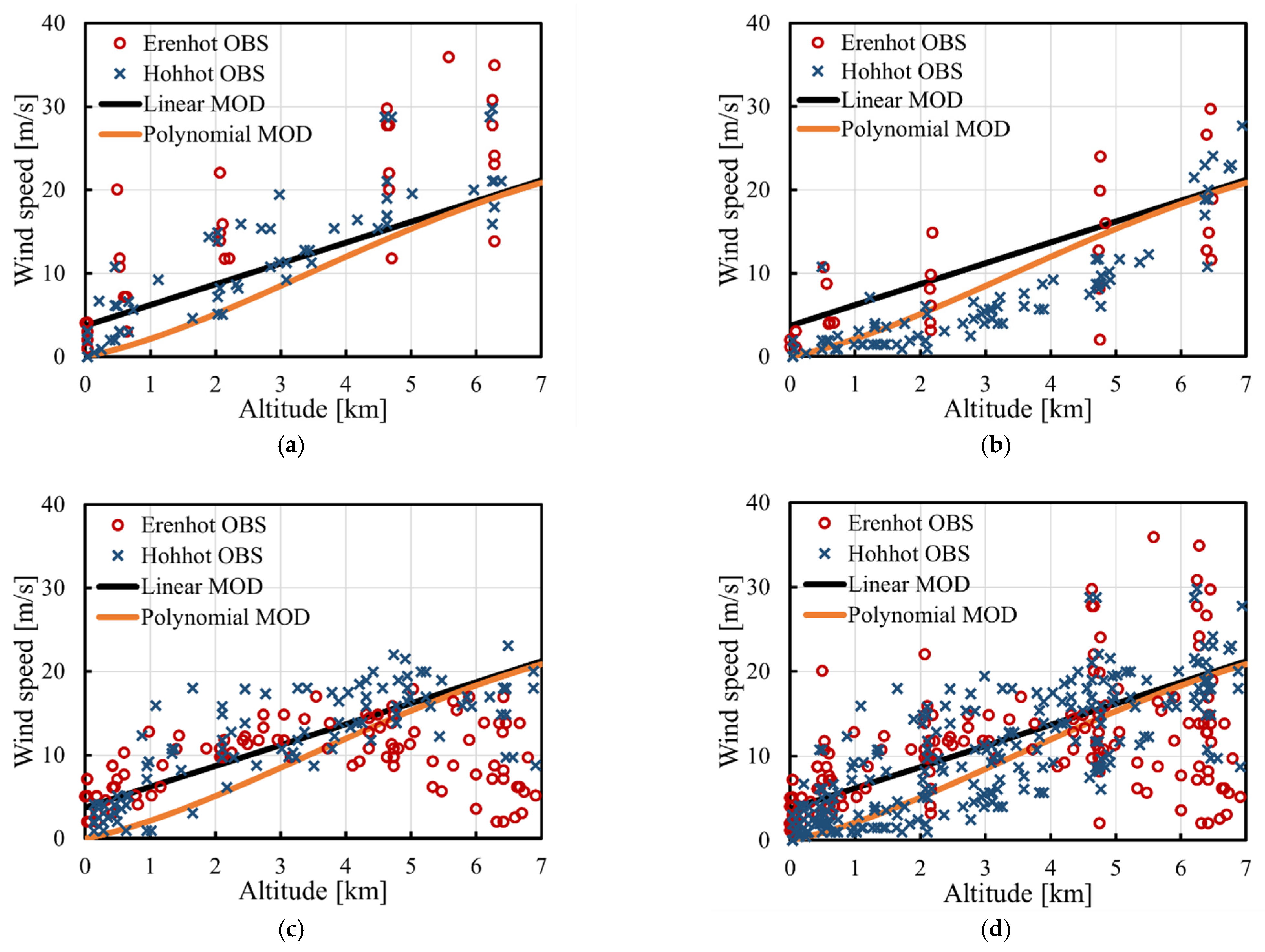
4. Engineering Wind Model
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fortier, L.J. An Application of a Proposed Airdrop Planning System; Massachusetts Institute of Technology: Cambridge, MA, USA, 2004. [Google Scholar]
- Cinnamon, A. Improving Airdrop Precision Through Error Budget Analysis. In Proceedings of the Interservice/Industry Training, Simulation, and Education Conference, Orlando, FL, USA, 28 November–2 December 2016. [Google Scholar]
- Hasager, C.B.; Astrup, P.; Zhu, R.; Chang, R.; Badger, M.; Hahmann, A.N.J.R.S. Quarter-century offshore winds from SSM/I and WRF in the North Sea and South China Sea. Remote Sens. 2016, 8, 769. [Google Scholar] [CrossRef]
- Hasager, C.B.; Hahmann, A.N.; Ahsbahs, T.; Karagali, I.; Sile, T.; Badger, M.; Mann, J.J.W.E.S. Europe’s offshore winds assessed with synthetic aperture radar, ASCAT and WRF. Wind. Energy Sci. 2020, 5, 375–390. [Google Scholar] [CrossRef]
- Sward, J.; Ault, T.; Zhang, K.J.E. Spatial biases revealed by LiDAR in a multiphysics WRF ensemble designed for offshore wind. Energy 2023, 262, 125346. [Google Scholar] [CrossRef]
- Yuan, H.; Du, J.; Hou, J.J.J.o.t.M.S. The numerical simulation of wind fields in main landing-area by model WRF in the phase of “Shen Zhou 6” spacecraft mission. Sci. Meteorol. Sin. 2008, 28, 56–61. [Google Scholar]
- Guo, Z.; Miao, Q.; Wang, S.; Li, H.J.S.C.E.S. Prediction of the trajectory of the manned spacecraft SHENZHOU-7 deploying a parachute based on a fine wind field. Sci. China Earth Sci. 2011, 54, 1413–1429. [Google Scholar] [CrossRef]
- Magelinski, T. Uncertainty and Inaccuracy of Airdrop Modeling. Baccalaureate Thesis, Virginia Polytechnic and State University, Blacksburg, VA, USA, May 2017. [Google Scholar]
- Cañadillas, B.; Beckenbauer, M.; Trujillo, J.J.; Dörenkämper, M.; Foreman, R.; Neumann, T.; Lampert, A.J.W.E.S. Offshore wind farm cluster wakes as observed by long-range-scanning wind lidar measurements and mesoscale modeling. Wind. Energy Sci. 2022, 7, 1241–1262. [Google Scholar] [CrossRef]
- Kale, B.; Buckingham, S.; van Beeck, J.; Cuerva-Tejero, A.J.R.E. Implementation of a generalized actuator disk model into WRF v4. 3: A validation study for a real-scale wind turbine. Renew. Energy 2022, 197, 810–827. [Google Scholar] [CrossRef]
- Beal, T.R. Digital simulation of atmospheric turbulence for Dryden and von Karman models. J. Guid. Control. Dyn. 1993, 16, 132–138. [Google Scholar] [CrossRef]
- Vishniak, A. Simulation of the payload-parachute-wing system flight dynamics. In Proceedings of the Aerospace Design Conference, Melbourne, Australia, 13–15 September 1993; p. 1250. [Google Scholar]
- Cao, K. A Study of Fundamental Heat Transfer Behavior at Near-Space Altitudes; The University of Alabama: Tuscaloosa, AL, USA, 2008. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D. A Description of the Advanced Research WRF Model Version 4; National Center for Atmospheric Research: Boulder, CO, USA, 2019; Volume 145, p. 145. [Google Scholar]
- Kleczek, M.A.; Steeneveld, G.-J.; Holtslag, A.A.J.B.-L.M. Evaluation of the weather research and forecasting mesoscale model for GABLS3: Impact of boundary-layer schemes, boundary conditions and spin-up. Bound. Layer Meteorol. 2014, 152, 213–243. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Vincent, C.L.; Peña, A.; Lange, J.; Hasager, C.B. Wind climate estimation using WRF model output: Method and model sensitivities over the sea. Int. J. Climatol. 2015, 35, 3422–3439. [Google Scholar] [CrossRef]
- Hassim, M.; Lane, T.; Grabowski, W. Physics. The diurnal cycle of rainfall over New Guinea in convection-permitting WRF simulations. Atmos. Chem. Phys. 2016, 16, 161–175. [Google Scholar] [CrossRef]
- Short, C.J.; Petch, J. Reducing the spin-up of a regional NWP system without data assimilation. Q. J. R. Meteorol. Soc. 2022, 148, 1623–1643. [Google Scholar] [CrossRef]
- Bowden, J.H.; Otte, T.L.; Nolte, C.G.; Otte, M.J. Examining interior grid nudging techniques using two-way nesting in the WRF model for regional climate modeling. J. Clim. 2012, 25, 2805–2823. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.J. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Kokaly, R.; Clark, R.; Swayze, G.; Livo, K.; Hoefen, T.; Pearson, N.; Wise, R.; Benzel, W.; Lowers, H.; Driscoll, R.J. Usgs Spectral Library Version 7 Data: Us Geological Survey Data Release; United States Geological Survey (USGS): Reston, VA, USA, 2017.
- Hong, S.-Y.; Lim, J.-O.J. The WRF single-moment 6-class microphysics scheme (WSM6). Asia-Pac. J. Atmos. Sci. 2006, 42, 129–151. [Google Scholar]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Dudhia, J.; Santos-Alamillos, F.J.; Pozo-Vázquez, D. Surface clear-sky shortwave radiative closure intercomparisons in the Weather Research and Forecasting model. J. Geophys. Res. Atmos. 2013, 118, 9901–9913. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Hari Prasad, K.; Venkata Srinivas, C.; Venkateswara Naidu, C.; Baskaran, R.; Venkatraman, B. Assessment of surface layer parameterizations in ARW using micro-meteorological observations from a tropical station. Meteorol. Appl. 2016, 23, 191–208. [Google Scholar] [CrossRef]
- Janjic, Z.I. The surface layer in the NCEP Eta Model. In Proceedings of the Eleventh Conference on Numerical Weather Prediction, Norfolk, VA, USA, 19–23 August 1996; American Meteorological Society: Boston, MA, USA; pp. 354–355. [Google Scholar]
- Janić, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model; National Centers for Environmental Prediction (U.S.): College Park, MD, USA, 2001.
- LeMone, M.A.; Tewari, M.; Chen, F.; Alfieri, J.G.; Niyogi, D. Evaluation of the Noah land surface model using data from a fair-weather IHOP_2002 day with heterogeneous surface fluxes. Mon. Weather. Rev. 2008, 136, 4915–4941. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. Convective parameterization for mesoscale models: The Kain-Fritsch scheme. In The Representation of Cumulus Convection in Numerical Models; Springer: Berlin/Heidelberg, Germany, 1993; pp. 165–170. [Google Scholar]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Albiñana Burdiel, C. Design and Testing of a Parachute Recovery System for a Sounding Rocket Experiment; Universitat Politècnica de València: Valencia, Spain, 2022. [Google Scholar]




| Physical Process | Parameterization Scheme |
|---|---|
| Microphysics | WSM6 (WRF Single-moment 6-class) [22] |
| Longwave radiation | RRTM (Rapid Radiative Transfer Model) [23] |
| Shortwave radiation | Dudhia [24,25] |
| Surface layer | Eta similarity (Monin-Obukhov) [26,27,28] |
| Land surface | Noah [29] |
| PBL physics | MYNN (Mellor-Yamada-Nakanishi-Niino) 2.5 level TKE [30] |
| Cumulus physics | Kain-Fritsch (new Eta) [31,32] |
| Station Name | Station No. | Longitude [°E] | Latitude [°N] | Altitude [m] |
|---|---|---|---|---|
| Mandula | 53,149 | 42.533 | 110.133 | 1223 |
| Damaoqi | 53,352 | 41.700 | 110.433 | 1377 |
| Erenhot | 53,068 | 43.650 | 112.000 | 996 |
| Hohhot | 53,463 | 40.810 | 111.680 | 1065 |
| Time [LST] | Wind Speed [m/s] | Time [LST] | Wind Speed [m/s] | ||||
|---|---|---|---|---|---|---|---|
| Maximum Deviation | Minimum Deviation | Average Deviation | Maximum Deviation | Minimum Deviation | Average Deviation | ||
| Erenhot | Hohhot | ||||||
| 15—00:00 | 3.84 | −2.05 | 1.82 | 15—00:00 | 3.87 | −1.41 | 0.95 |
| 15—12:00 | 3.45 | −0.71 | 0.59 | 15—12:00 | 2.62 | 0.88 | 1.18 |
| 16—00:00 | 3.57 | −2.26 | 0.74 | 16—00:00 | 9.09 | −0.92 | 3.04 |
| 16—12:00 | 0.92 | −2.44 | −1.06 | 16—12:00 | 3.01 | 5.63 | 3.83 |
| 17—00:00 | −2.17 | 1.86 | −0.85 | 17—00:00 | −2.64 | 3.87 | 1.87 |
| 17—12:00 | −1.98 | 2.52 | 0.13 | 17—12:00 | −1.37 | 3.79 | 1.25 |
| Time [LST] | Wind Speed [m/s] | Time [LST] | Wind Speed [m/s] | ||||
|---|---|---|---|---|---|---|---|
| Maximum Deviation | Minimum Deviation | Average Deviation | Maximum Deviation | Minimum Deviation | Average Deviation | ||
| Erenhot | Hohhot | ||||||
| 26—12:00 | 3.17 | −2.17 | 0.12 | 26—12:00 | 2.82 | −2.65 | −0.20 |
| 27—00:00 | 5.61 | −1.80 | 0.26 | 27—00:00 | 4.13 | −1.99 | 1.17 |
| 27—12:00 | 3.75 | −0.33 | 1.86 | 27—12:00 | 3.11 | −2.57 | 0.56 |
| 28—00:00 | 0.95 | −1.30 | 0.10 | 28—00:00 | 3.54 | −2.86 | 0.50 |
| 28—12:00 | 1.55 | −5.03 | −1.61 | 28—12:00 | 2.45 | −4.54 | −0.70 |
| 29—00:00 | 0.95 | −3.59 | −0.91 | 29—00:00 | 0.67 | −2.94 | −0.90 |
| Layer Name | Altitude Range | No. | Altitude [m] | Relative Wind Speed Error [%] |
|---|---|---|---|---|
| Free atmosphere layer | 2 km–7 km | 1 | 6717.23 | 3.29 |
| 2 | 3817.23 | 3.30 | ||
| 3 | 2087.23 | 4.51 | ||
| Ekman layer | 100 m–2 km | 4 | 1019.23 | −5.32 |
| Surface layer | surface–100 m | 5 | 12.23 | 6.17 |
| The average absolute value of relative wind speed error [%] | 4.52 | |||
| Time [LST] | Wind Speed [m/s] | Time [LST] | Wind Speed [m/s] | ||||
|---|---|---|---|---|---|---|---|
| Maximum Deviation | Minimum Deviation | Average Deviation | Maximum Deviation | Minimum Deviation | Average Deviation | ||
| Erenhot | Hohhot | ||||||
| 24—12:00 | 1.83 | −3.23 | −0.83 | 24—12:00 | 2.88 | −1.79 | −0.62 |
| 25—00:00 | 4.46 | −3.65 | 0.87 | 25—00:00 | 3.89 | −8.39 | −0.96 |
| 25—12:00 | 7.94 | −5.13 | 1.83 | 25—12:00 | 4.69 | −6.48 | 0.00 |
| 26—00:00 | 6.99 | −6.62 | 0.09 | 26—00:00 | 0.41 | −6.57 | −2.42 |
| 26—12:00 | 1.05 | −7.37 | −2.77 | 26—12:00 | 6.03 | −2.57 | 0.06 |
| 27—00:00 | 1.05 | −4.73 | −1.66 | 27—00:00 | 2.17 | −4.56 | −1.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Ma, G.; Tian, L.; Zhao, N.; Lu, X. Numerical Investigations of Precise Wind Field in Main Landing Area during the Landing Phase of “Shen Zhou” Series Spacecraft Mission. Aerospace 2023, 10, 37. https://doi.org/10.3390/aerospace10010037
Song Y, Ma G, Tian L, Zhao N, Lu X. Numerical Investigations of Precise Wind Field in Main Landing Area during the Landing Phase of “Shen Zhou” Series Spacecraft Mission. Aerospace. 2023; 10(1):37. https://doi.org/10.3390/aerospace10010037
Chicago/Turabian StyleSong, Yilei, Guolin Ma, Linlin Tian, Ning Zhao, and Xiyun Lu. 2023. "Numerical Investigations of Precise Wind Field in Main Landing Area during the Landing Phase of “Shen Zhou” Series Spacecraft Mission" Aerospace 10, no. 1: 37. https://doi.org/10.3390/aerospace10010037
APA StyleSong, Y., Ma, G., Tian, L., Zhao, N., & Lu, X. (2023). Numerical Investigations of Precise Wind Field in Main Landing Area during the Landing Phase of “Shen Zhou” Series Spacecraft Mission. Aerospace, 10(1), 37. https://doi.org/10.3390/aerospace10010037







