Experimental Proof of Concept of a Noncircular Rotating Detonation Engine (RDE) for Propulsion Applications
Abstract
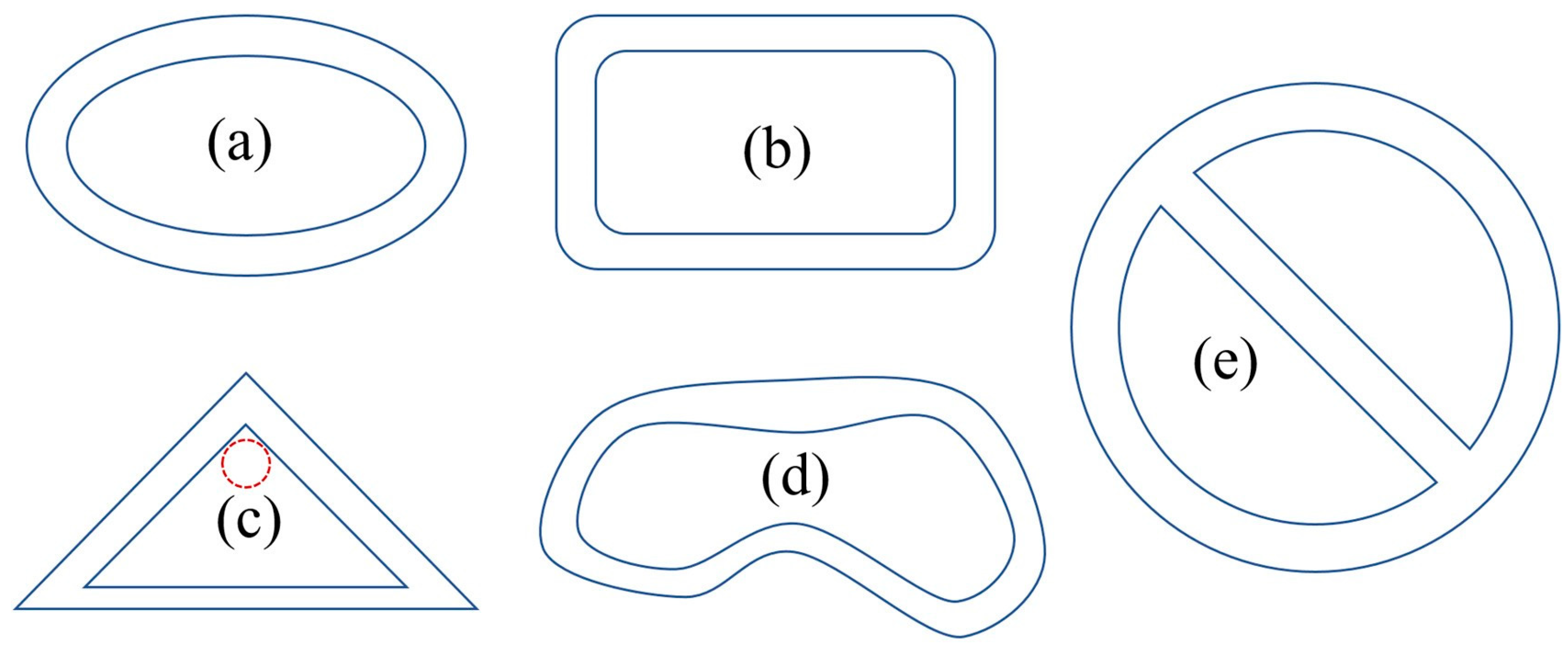
1. Introduction
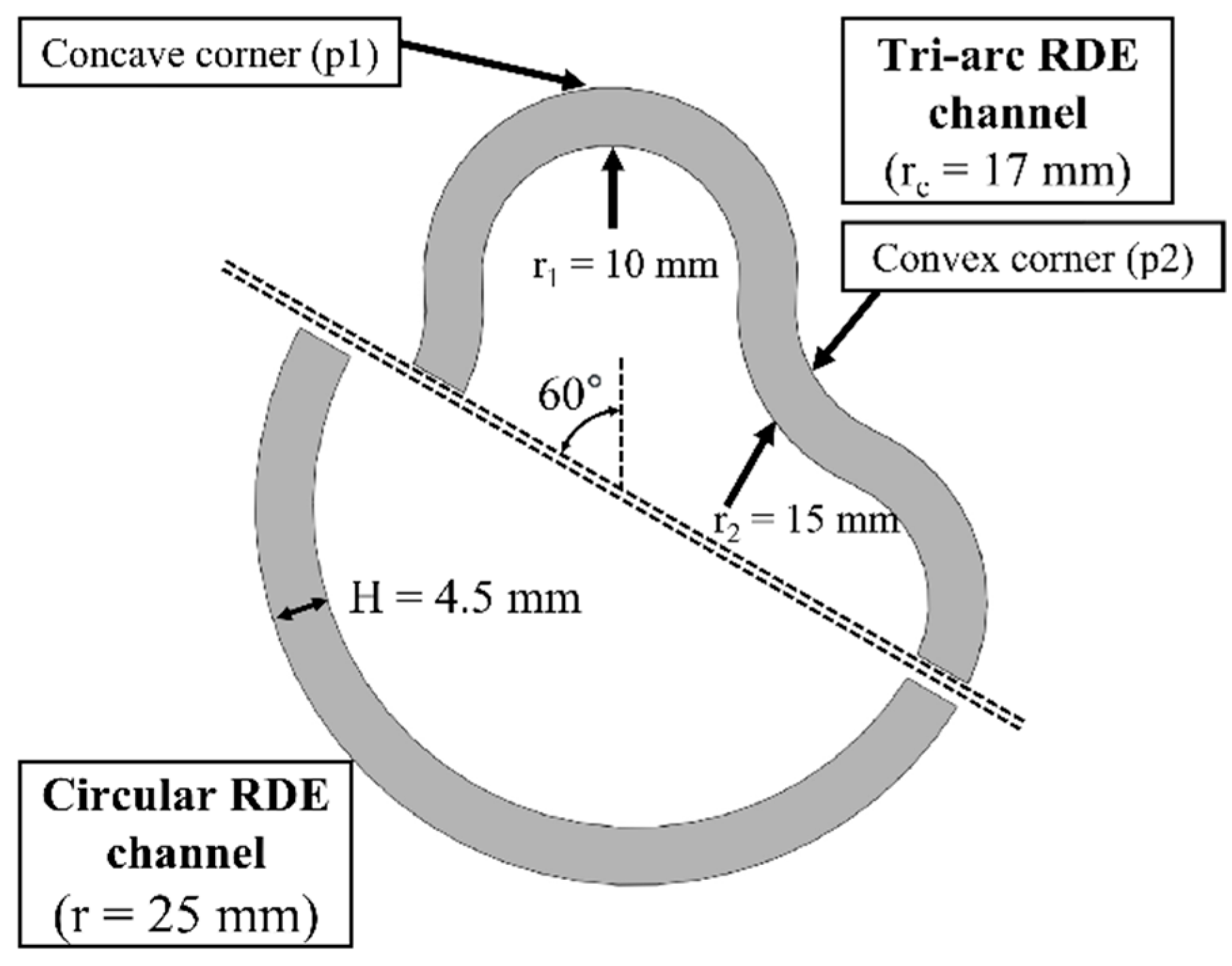
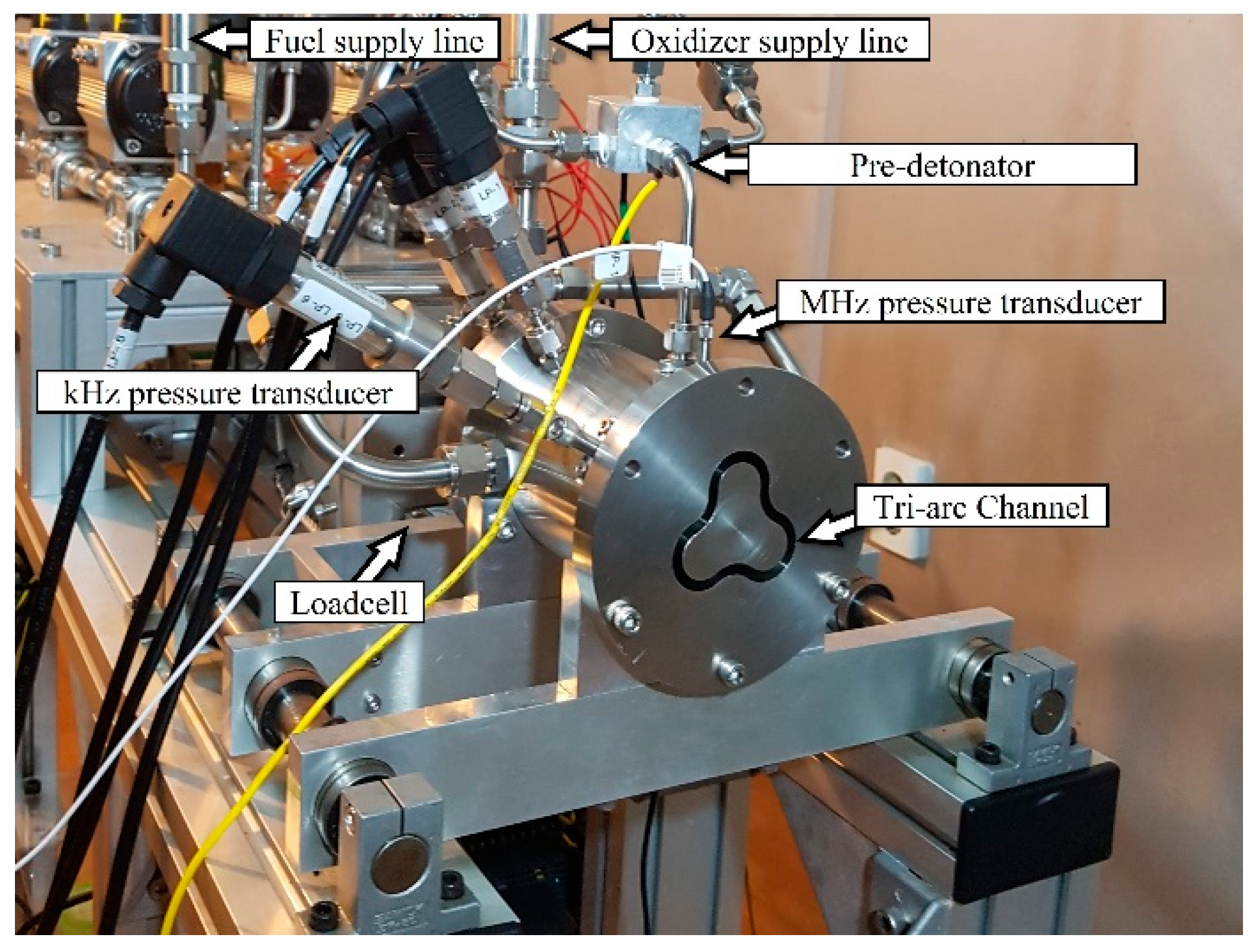
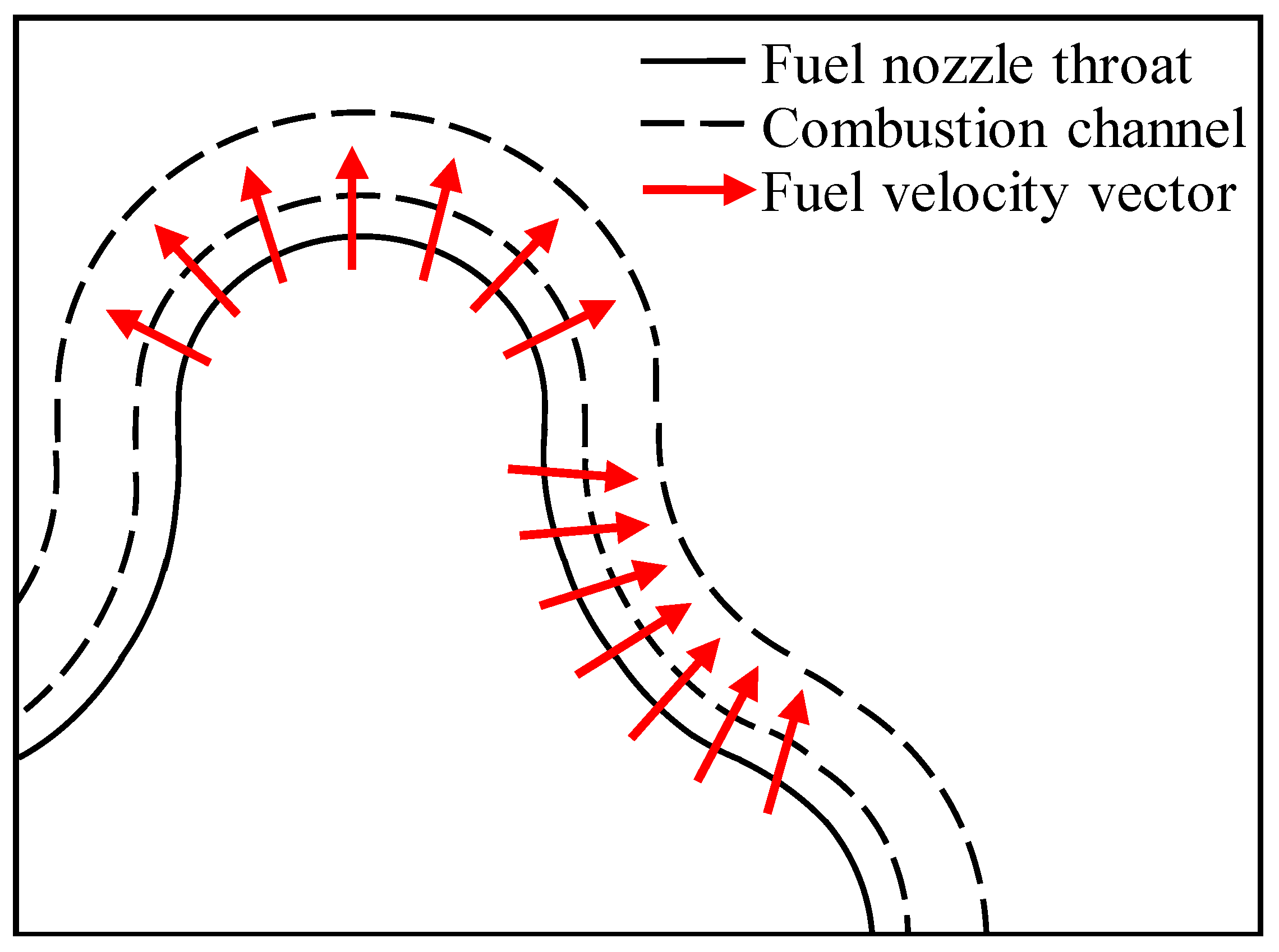
2. Experimental Setup
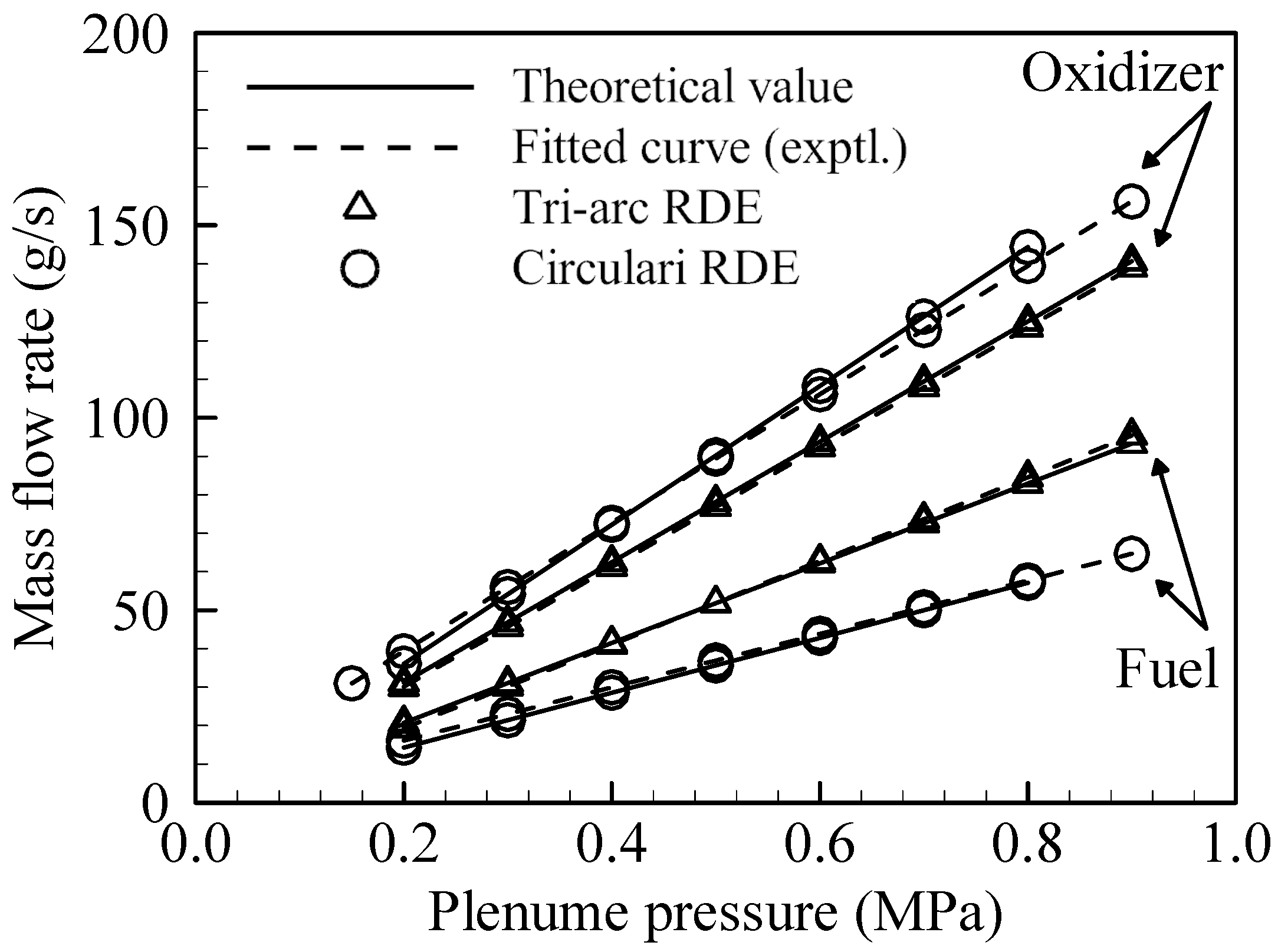
3. Mass Flow Rate Calibration
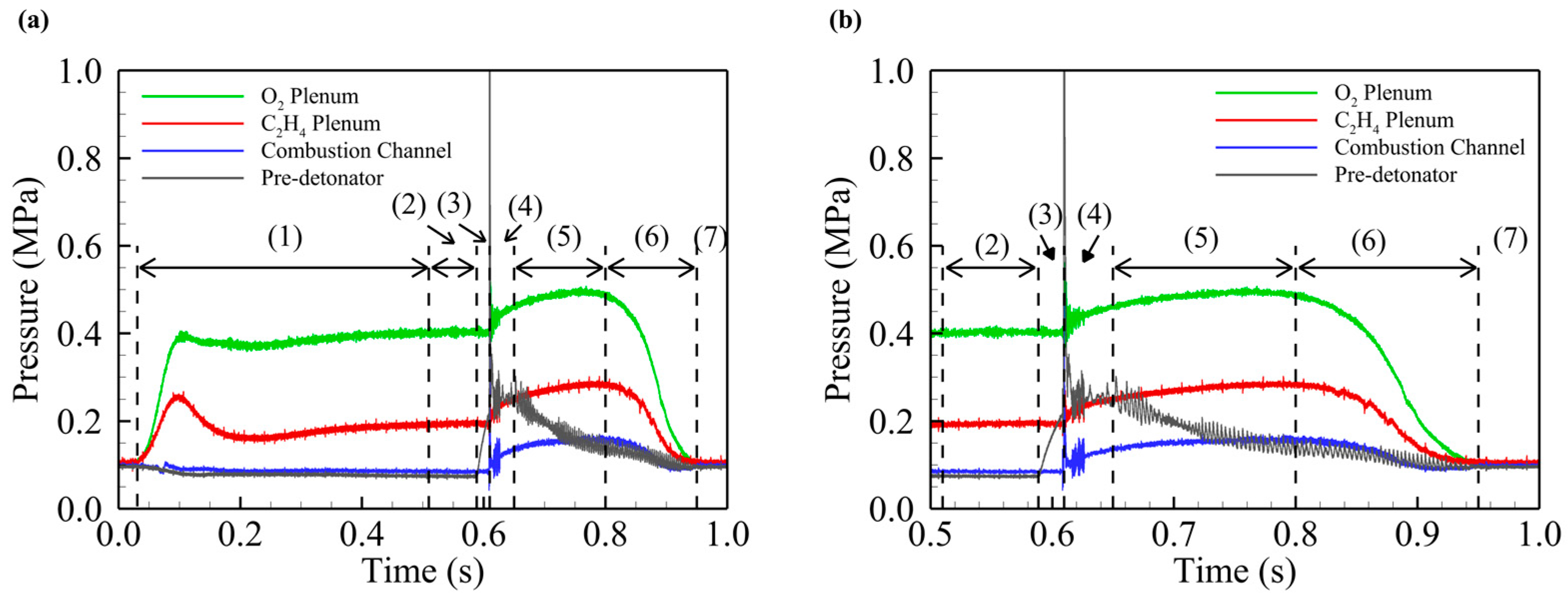
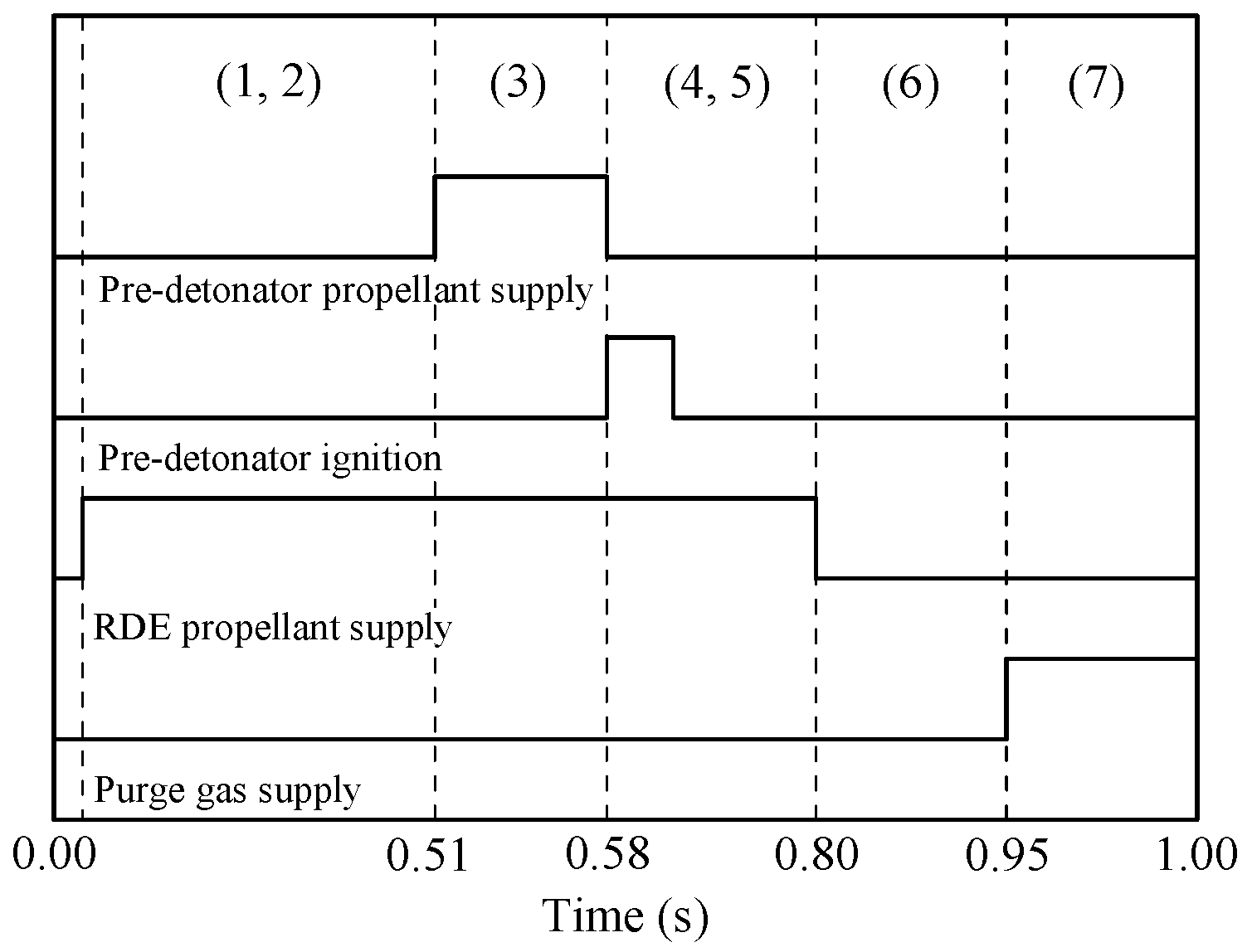
4. Experimental Procedure
5. Operational Characteristics
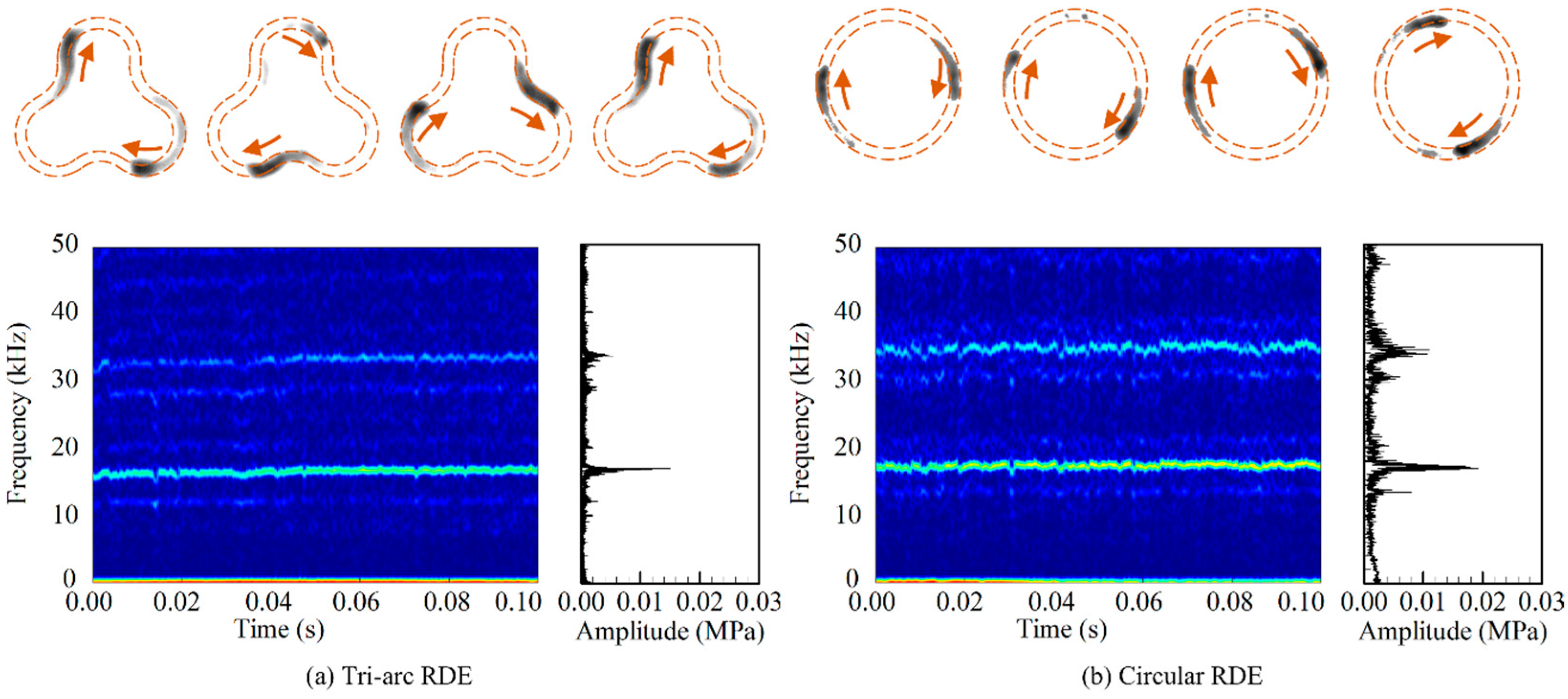
5.1. Operational Characteristics at Reference Mass Flow Rate
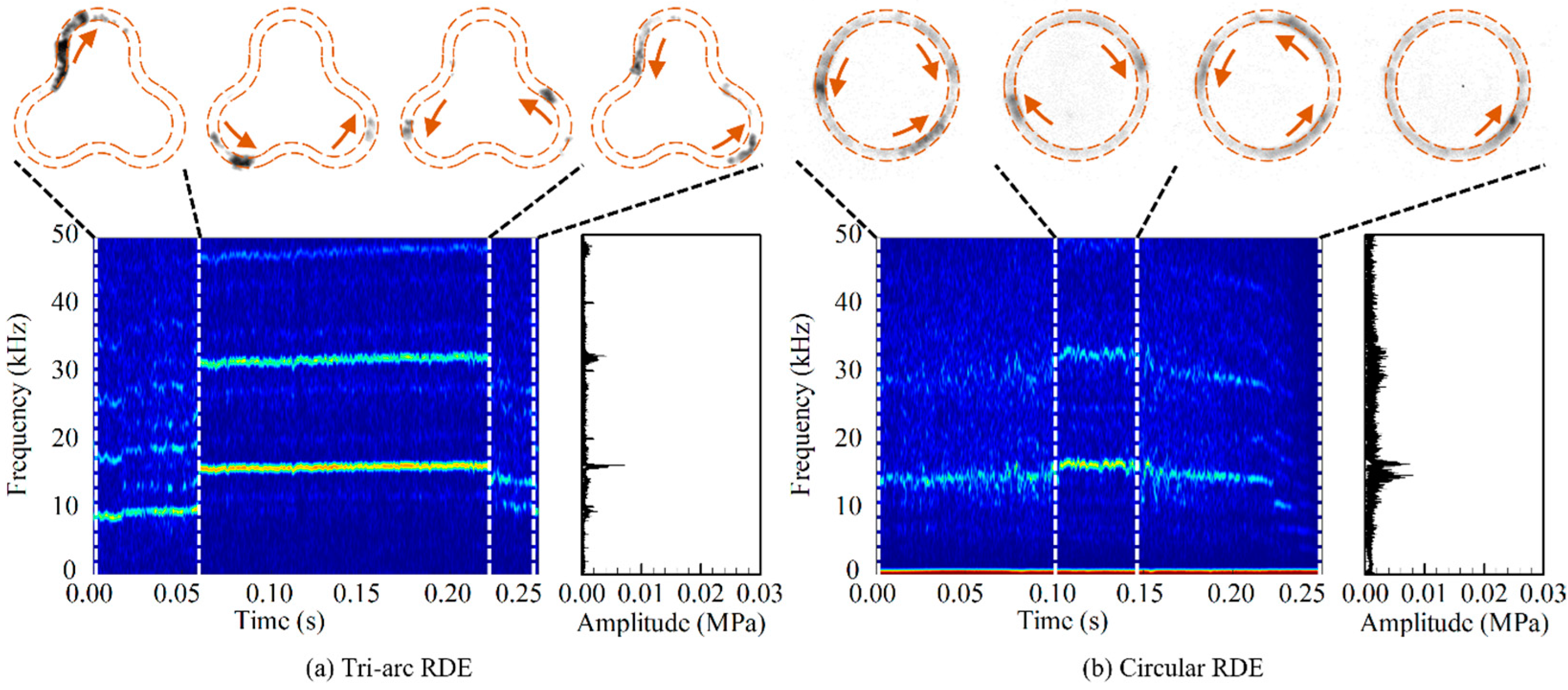
5.2. Operational Characteristics at Low Mass Flow Rate
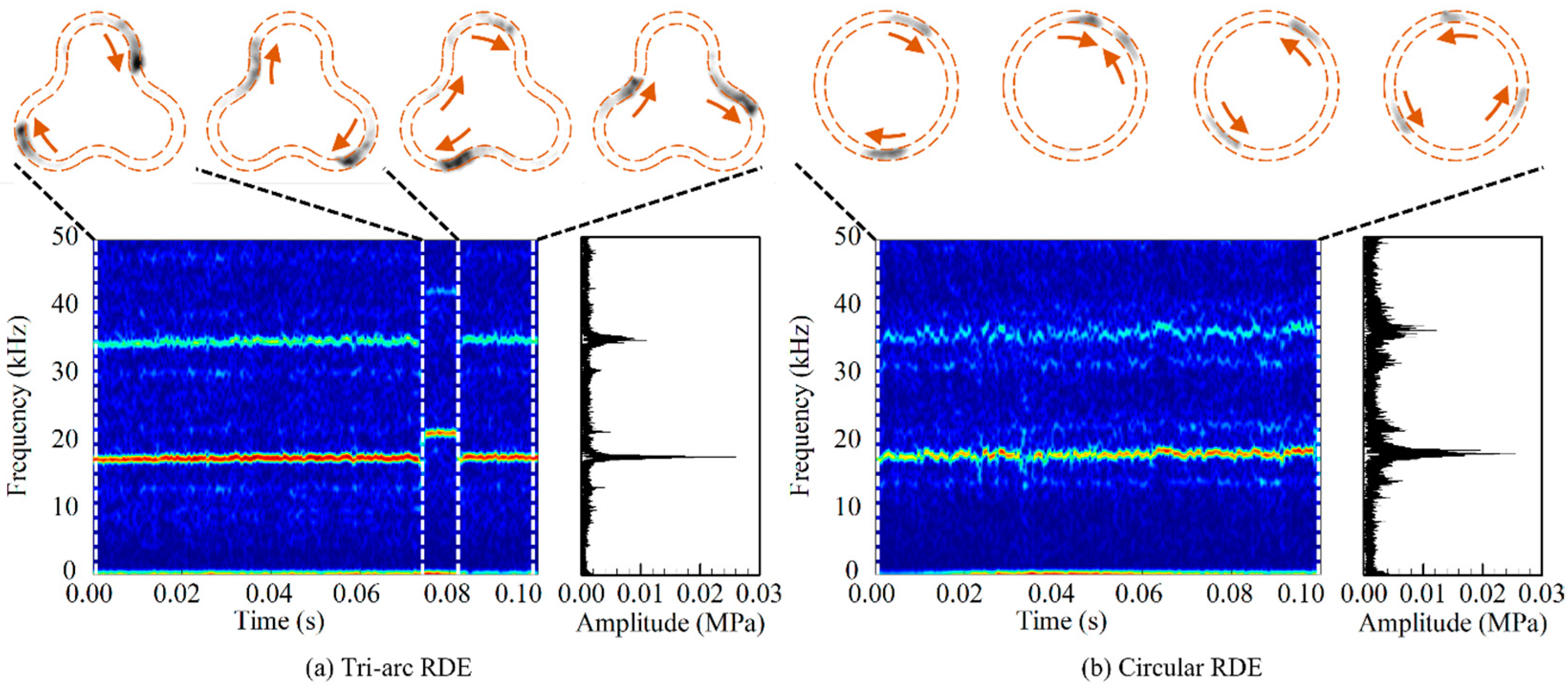
5.3. Operational Characteristics at High Mass Flow Rate
6. Wall Pressure Characteristics
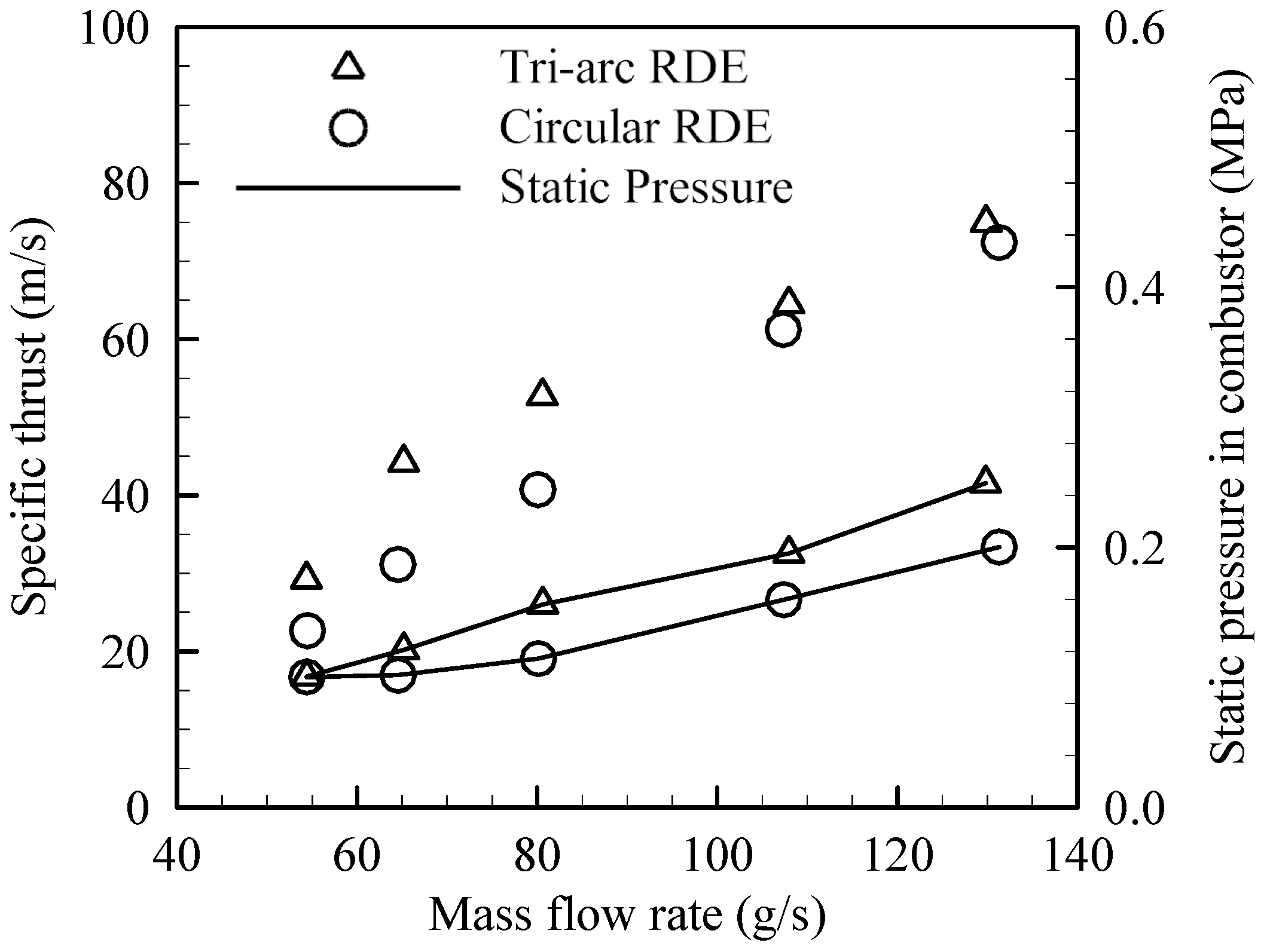
7. Thrust Performance
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nejaamtheen, M.N.; Kim, T.Y.; Pavalavanni, P.K.; Ryu, J.; Choi, J.-Y. Effects of the dimensionless radius of an annulus on the detonation propagation characteristics in circular and non-circular rotating detonation engines. Shock Waves 2021, 31, 703–715. [Google Scholar] [CrossRef]
- Le Naour, B.; Falempin, F.H.; Coulon, K. MBDA R&T Effort Regarding Continuous Detonation Wave Engine for Propulsion—Status in 2016. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 March 2017. [Google Scholar] [CrossRef]
- Gawahara, K.; Nakayama, H.; Kasahara, J.; Matsuoka, K.; Tomioka, S.; Hiraiwa, T.; Matsuo, A.; Funaki, I. Detonation engine development for reaction control systems of a spacecraft. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013. [Google Scholar]
- Wen, H.; Xie, Q.; Wang, B. Propagation behaviors of rotating detonation in an obround combustor. Combust. Flame 2019, 210, 389–398. [Google Scholar] [CrossRef]
- Peng, H.; Liu, W.; Liu, S. Ethylene Continuous Rotating Detonation in optically accessible racetrack-like combustor. Combust. Sci. Technol. 2018, 191, 676–695. [Google Scholar] [CrossRef]
- Feleo, A.; Chacon, F.; White, L.W.; Gamba, M. Evaluation of OH Emission for Determining Operation of a Rotating Detonation Engine. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Chacon, F.; Gamba, M. Study of Parasitic Combustion in an Optically Accessible Continuous Wave Rotating Detonation Engine. In Proceedings of the 2019 AIAA Scitech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Chacon, F.; Gamba, M. OH PLIF Visualization of an Optically Accessible Rotating Detonation Combustor. In Proceedings of the 2019 AIAA Propulsion and Energy Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Chacon, F.; Gamba, M. Development of an optically accessible continuous wave Rotating Detonation Engine. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Sosa, J.; Ahmed, K.A.; Fievisohn, R.; Hoke, J.; Ombrello, T.; Schauer, F. Supersonic driven detonation dynamics for rotating detonation engines. Int. J. Hydrogen Energy 2019, 44, 7596–7606. [Google Scholar] [CrossRef]
- Lee, S.-H.; Cho, D.-R.; Choi, J.-Y. Numerical Analysis of Detonation Wave Propagation Characteristics in Annular Channels. J. KSPE 2008, 12, 26–37. [Google Scholar]
- Kudo, Y.; Nagura, Y.; Kasahara, J.; Sasamoto, Y.; Matsuo, A. Oblique detonation waves stabilized in rectangular-cross-section bent tubes. Proc. Combust. Inst. 2011, 33, 2319–2326. [Google Scholar] [CrossRef]
- Nakayama, H.; Moriya, T.; Kasahara, J.; Matsuo, A.; Sasamoto, Y.; Funaki, I. Stable detonation wave propagation in rectangular-cross-section curved channels. Combust. Flame 2012, 159, 859–869. [Google Scholar] [CrossRef]
- Nakayama, H.; Kasahara, J.; Matsuo, A.; Funaki, I. Front shock behavior of stable curved detonation waves in rectangular-cross-section curved channels. Proc. Combust. Inst. 2013, 34, 1939–1947. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Nakayama, Y.; Matsuo, A.; Nakayama, H.; Kasahara, J. Numerical Investigations on Detonation Propagation in a Two-Dimensional Cured Channel. Combust. Sci. Tech. 2014, 186, 1662–1679. [Google Scholar] [CrossRef]
- Pan, Z.; Qi, J.; Pan, J.; Zhang, P.; Zhu, Y.; Gui, M. Fabrication of a helical detonation channel: Effect of initial pressure on the detonation propagation modes of ethylene/oxygen mixtures. Combust. Flame 2018, 192, 1–9. [Google Scholar] [CrossRef]
- Pan, Z.; Chen, K.; Qi, J.; Zhang, P.; Zhu, Y.; Pan, J.; Gui, M. The propagation characteristics of curved detonation wave: Experiments in helical channels. Proc. Combust. Inst. 2019, 37, 3585–3592. [Google Scholar] [CrossRef]
- Xia, Z.; Ma, H.; Zhuo, C.; Zhou, C. Propagation process of H2/air rotating detonation wave and influence factors in plane-radial structure. Int. J. Hydrogen Energy 2018, 43, 4609–4622. [Google Scholar] [CrossRef]
- Kawasaki, A.; Inakawa, T.; Kasahara, J.; Goto, K.; Matsuoka, K.; Matsuo, A.; Funaki, I. Critical condition of inner cylinder radius for sustaining rotating detonation waves in rotating detonation engine thruster. Proc. Combust. Inst. 2018, 37, 3461–3469. [Google Scholar] [CrossRef]
- Katta, V.R.; Cho, K.Y.; Hoke, J.L.; Codoni, J.R.; Schauer, F.R.; Roquemore, W.M. Effect of increasing channel width on the structure of rotating detonation wave. Proc. Combust. Inst. 2019, 37, 3575–3583. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, J.-P. Numerical investigation of shock wave reflections near the head ends of rotating detonation engines. Shock. Waves 2013, 23, 461–472. [Google Scholar] [CrossRef]
- Zhao, N.; Meng, Q.; Zheng, H.; Li, Z.; Deng, F. Numerical study of the influence of annular width on the rotating detonation wave in a non-premixed combustor. Aerosp. Sci. Technol. 2020, 100, 105825. [Google Scholar] [CrossRef]
- Wang, Y. Rotating detonation in a combustor of trapezoidal cross section for the hydrogen–air mixture. Int. J. Hydrogen Energy 2016, 41, 5605–5616. [Google Scholar] [CrossRef]
- Han, H.-S.; Lee, E.; Choi, J.-Y. An Experimental Investigation of C2H4/GO2 Rocket-type Rotating Detonation Engine with Circular Chamber. Energies 2021, 14, 1381. [Google Scholar] [CrossRef]
- Hansmetzger, S.; Zitoun, R.; Vidal, P. Detonation Regimes in a Small-scale RDE. In Proceedings of the 26th International Colloquium on the Dynamics of Explosions and Reactive Systems, Boston, MA, USA, 30 July–4 August 2017. [Google Scholar]
- Wolanski, P. Rotating Detonation Wave Stability. In Proceedings of the 23rd International Colloquium on the Dynamics of Explosions and Reactive Systems, Irvine, CA, USA, 23–29 July 2011. [Google Scholar]
- Choi, J.Y.; Ma, F.H.; Yang, V. Some numerical issues on simulation of detonation cell structures. Combust. Explos. Shock. Waves 2008, 44, 560–578. [Google Scholar] [CrossRef]
- Choi, J.; Jeung, I.-S.; Yoon, Y. Computational fluid dynamics algorithms for unsteady shock-induced combustion, Part 1: Validation. AIAA J. 2000, 38, 1179–1187. [Google Scholar] [CrossRef]
- Choi, J.; Jeung, I.-S.; Yoon, Y. Computational fluid dynamics algorithms for unsteady shock-induced combustion, Part 2: Comparison. AIAA J. 2000, 38, 1188–1195. [Google Scholar] [CrossRef]
- Choi, J.; Unnikrishnan, U.; Hwang, W.; Jeong, S.; Han, S.; Kim, K.; Yang, V. Effect of fuel temperature on flame characteristics of supersonic turbulent combustion. Fuel 2022, 329, 125310. [Google Scholar] [CrossRef]


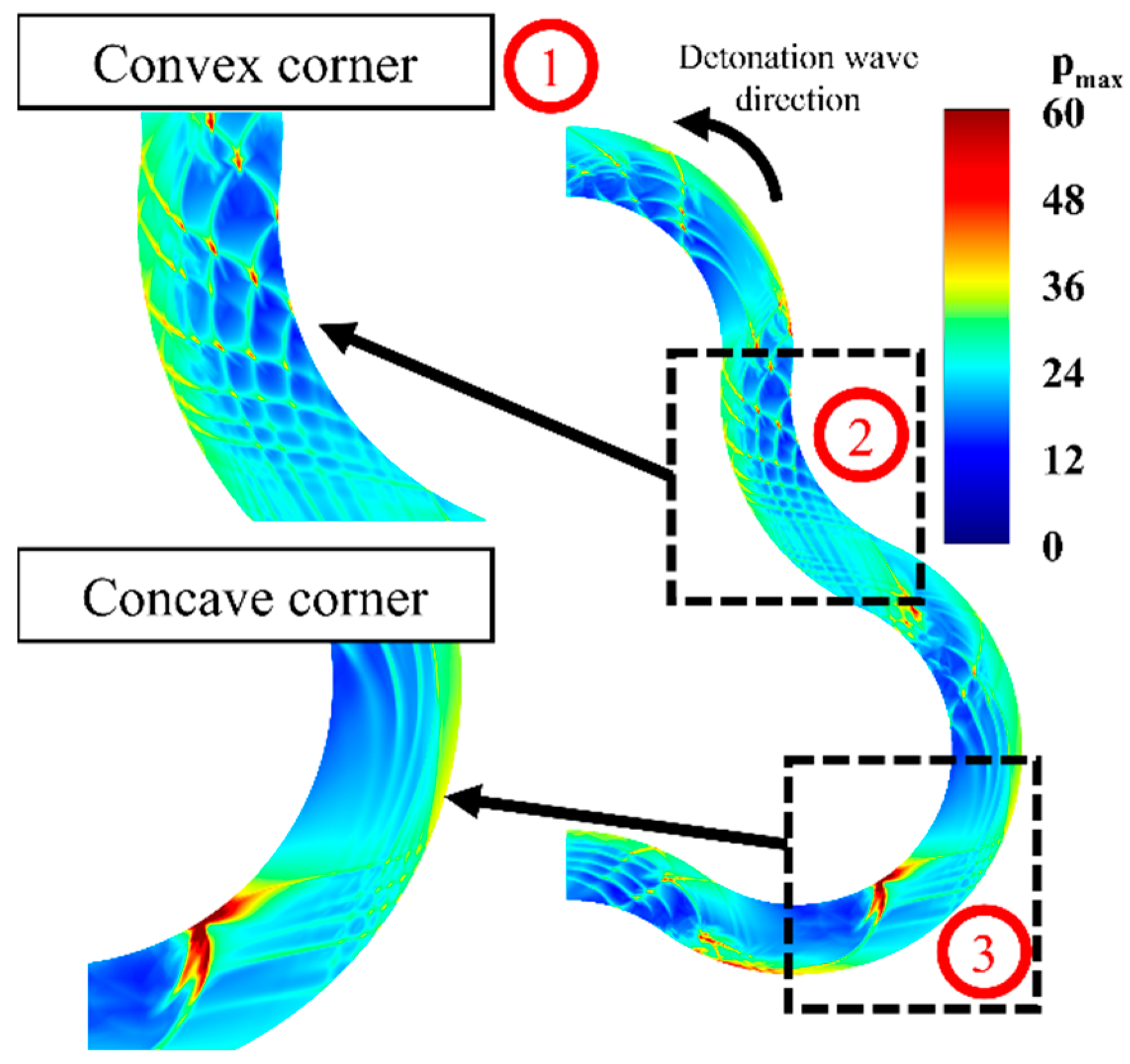
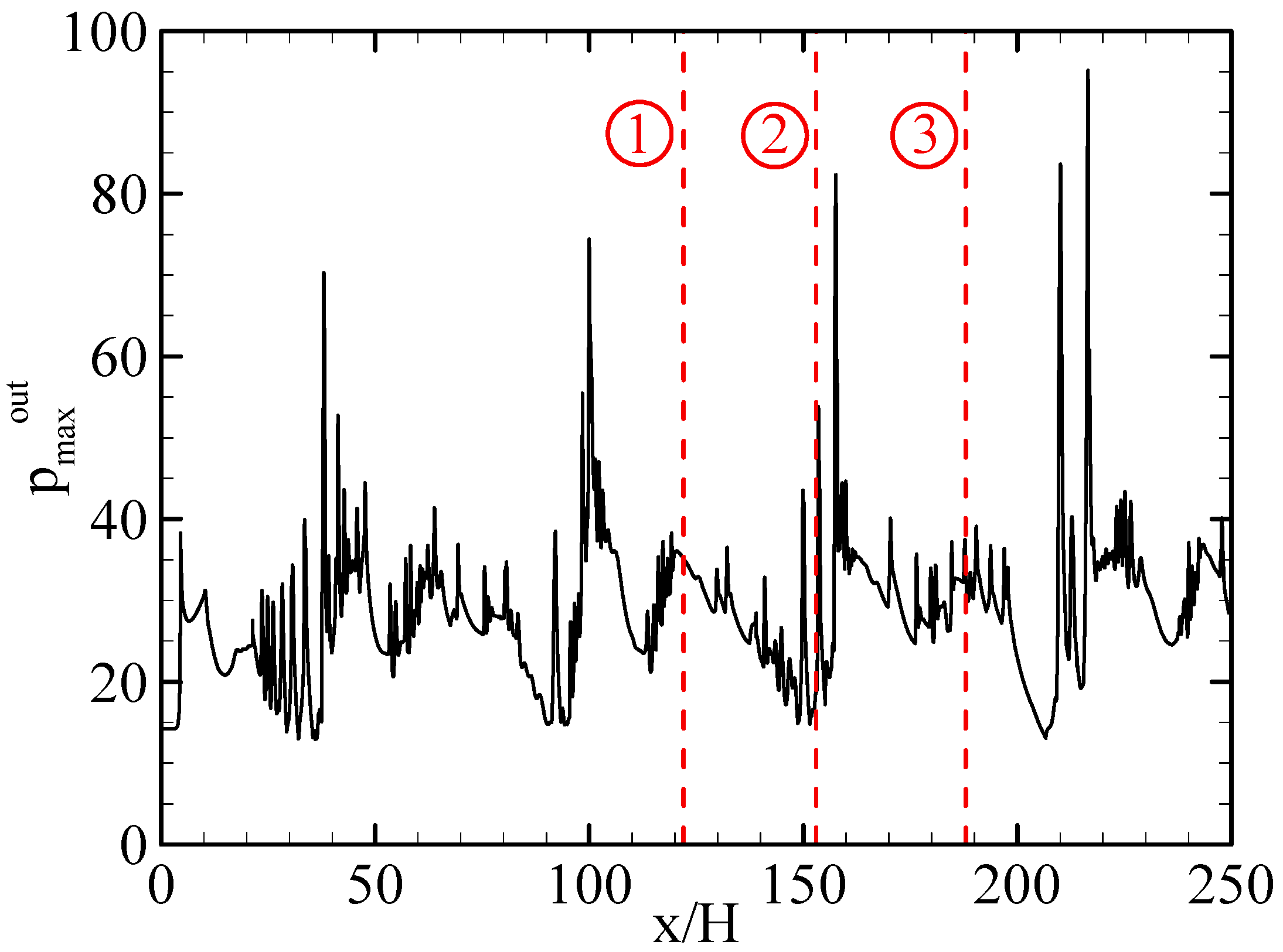
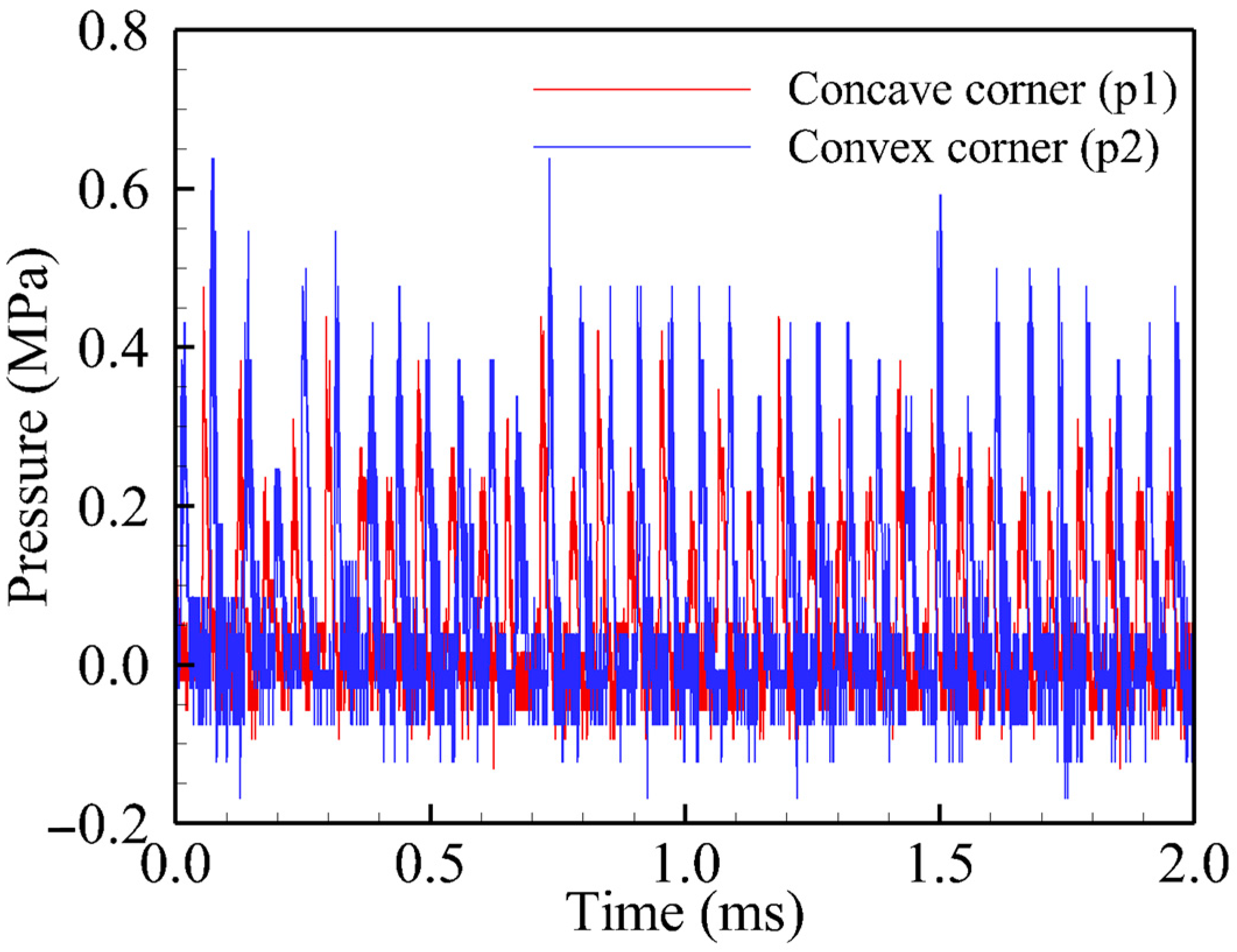
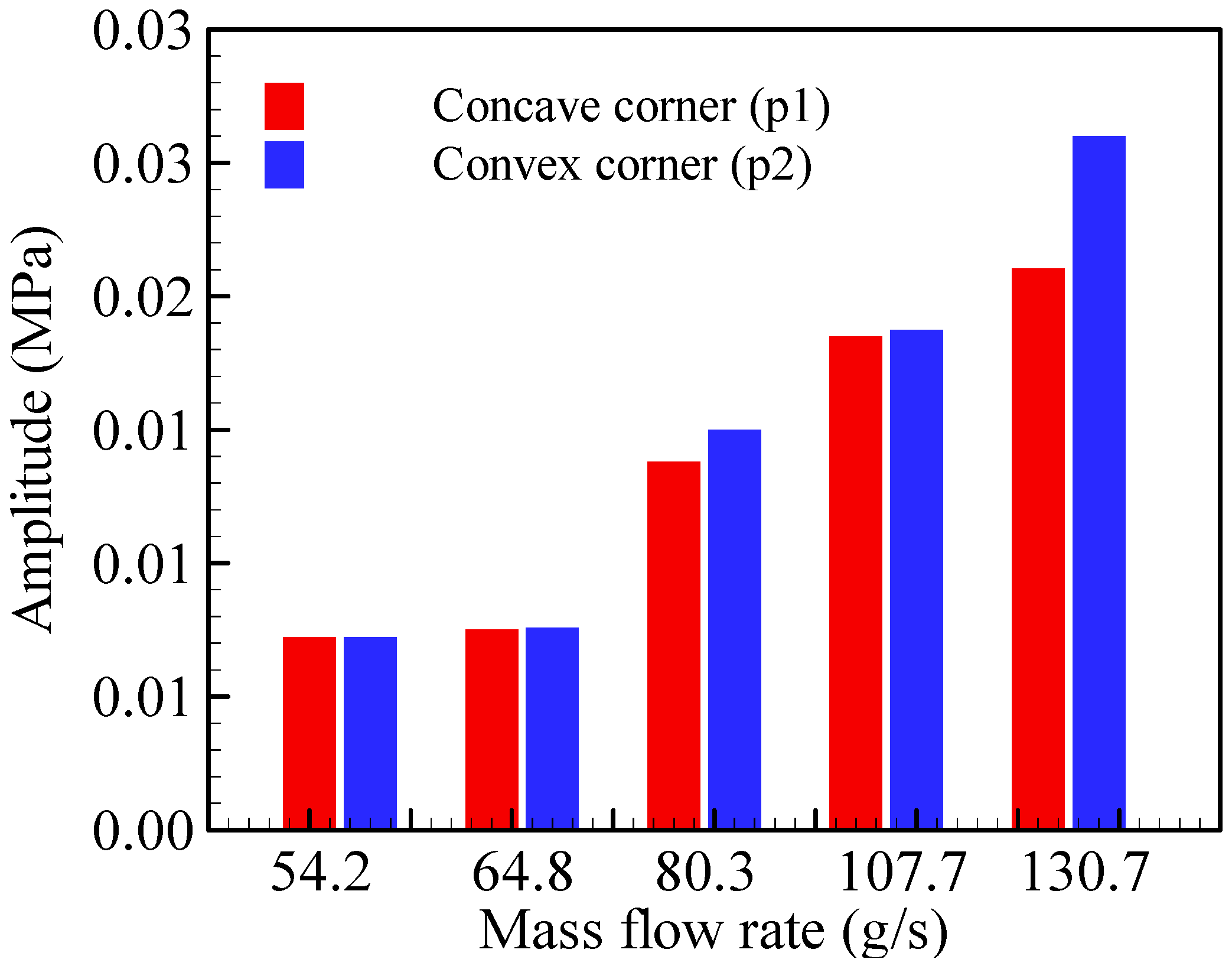
| Combustor Length (mm) | Slot Width (mm) | Cross-Sectional Area (mm2) | r/H | ||||
|---|---|---|---|---|---|---|---|
| Fuel Slot | Oxidizer Slot | Fuel Slot | Oxidizer Slot | Combustor | |||
| Tri-arc RDE | 75.00 | 0.34 | 0.40 | 46.80 | 63.30 | 771.4 | 3.55–6.50 |
| Circular RDE | 75.00 | 0.30 | 0.46 | 47.10 | 72.80 | 758.7 | 6.06 |
| Hansmetzger [25] | 90 | 0.3 | 0.5 | 47.12 | 79.33 | 1885.00 | 3.5 |
| (g/s) | Φ | RDE Type | Stability | Dominant Frequency (kHz) | Velocity Deficit (m/s) |
|---|---|---|---|---|---|
| 64.8 0.32 | 1.03 0.001 | Tri-arc | Stable | 16.71 | 844.40 |
| Circular | Stable, temporarily unstable | 16.88 | 826.96 | ||
| 80.3 0.20 | 1.04 0.001 | Tri-arc | Stable | 16.72 | 843.47 |
| Circular | Stable | 17.60 | 760.16 | ||
| 107.7 0.71 | 1.04 0.008 | Tri-arc | Stable | 17.78 | 745.24 |
| Circular | Stable | 17.70 | 750.88 |
| Description | Value | |
|---|---|---|
| Specific heat ratio | Unburned gas | 1.602 |
| Burned gas | 1.288 | |
| Dimensionless heat addition | 24.2 | |
| Dimensionless activation energy | 32.46 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Ryu, J.-H.; Lee, E.-S.; Han, H.-S.; Choi, J.-Y. Experimental Proof of Concept of a Noncircular Rotating Detonation Engine (RDE) for Propulsion Applications. Aerospace 2023, 10, 27. https://doi.org/10.3390/aerospace10010027
Lee J-H, Ryu J-H, Lee E-S, Han H-S, Choi J-Y. Experimental Proof of Concept of a Noncircular Rotating Detonation Engine (RDE) for Propulsion Applications. Aerospace. 2023; 10(1):27. https://doi.org/10.3390/aerospace10010027
Chicago/Turabian StyleLee, Jae-Hyuk, Jae-Hoon Ryu, Eun-Sung Lee, Hyung-Seok Han, and Jeong-Yeol Choi. 2023. "Experimental Proof of Concept of a Noncircular Rotating Detonation Engine (RDE) for Propulsion Applications" Aerospace 10, no. 1: 27. https://doi.org/10.3390/aerospace10010027
APA StyleLee, J.-H., Ryu, J.-H., Lee, E.-S., Han, H.-S., & Choi, J.-Y. (2023). Experimental Proof of Concept of a Noncircular Rotating Detonation Engine (RDE) for Propulsion Applications. Aerospace, 10(1), 27. https://doi.org/10.3390/aerospace10010027







