Abstract
Multi-stage disc rotor assembly is an important part of the aero-engine rotor manufacturing process. To solve the problem that excessive unbalance of assembly affects the vibration of the whole machine, this paper presents an optimization method for aero-engine rotor assembly balance based on an improved Harris Hawk algorithm. Firstly, the assembly sequence model of the single-stage disc blade and the phase assembly model of a multi-stage disc of the engine rotor is established. Secondly, by using the initial population generation based on dynamic opposing learning and the escape energy function of the non-linear logarithmic convergence factor, the search mechanism of the whale optimization algorithm is introduced in the global exploration, and the adaptive weight strategy and mutation strategy of the genetic algorithm is introduced in the development to improve the algorithm. Then, the effectiveness of the algorithm is verified by experiments and compared with particle swarm optimization, genetic algorithm, and Harris Hawk algorithm, the unbalance of the optimal blade assembly sequence is reduced by 91.75%, 99.82%, and 83.39%, respectively. The algorithm comparison and analysis are carried out for all disc-blade assembly optimization of the rotor. The optimal unbalance of the improved Harris Hawk optimization algorithm is reduced by 79.71%, 99.48%, and 54.92% on average. The unbalance of the algorithm in this paper is the best. Finally, the improved Harris Hawk algorithm is used to find the best assembly phase, and the optimized unbalanced force and moment are reduced by 84.22% and 98.05%, respectively. The results of this study prove that the improved Harris Hawk algorithm for aero-engine rotor assembly balance optimization can effectively reduce the unbalance of rotor disc blade assembly and rotor unbalance and provide a powerful solution for solving engine vibration.
1. Introduction
Assembly is very important in the manufacturing process of products, and its results have a significant impact on the final performance and quality of products [1]. The assembly quality of aero-engines is an important factor to ensure the overall performance of aero-engines. According to statistics, the number of engine failures caused by vibration accounts for 50% to 60% of the total number of engine failures [2]. The unbalance force caused by excessive rotor unbalance is the main factor causing vibration during the operation of an aero-engine [3]. The unbalance of the rotor will not only cause vibration but also cause airflow exciting force. Under certain conditions, it may cause rotor instability, which will adversely affect the normal operation of the entire engine. The aero-engine rotor is composed of multi-stage discs and blades. In the process of the rotor assembly, the assembly sequence of blades affects the balance quality of the assembled disc, while the assembly phase angle of multi-stage discs affects the overall balance quality of the rotor. These two factors are important factors affecting the balancing quality of the rotor [4].
The assembly sequence of the aero-engine rotor blade set not only directly determines the static balance quality of the rotor, but also indirectly affects the dynamic balance quality of the rotor. To ensure the balanced mass of the rotor, the gravity moment of the blades must be equally distributed so that the centrifugal forces in all directions can be offset as far as possible and the residual unbalance can be kept as close as possible to the minimum. Under ideal conditions, if the moments of gravity of the rotor blades are equal, then the residual imbalance of the rotor is zero, but the actual processing conditions of the blades are unable to achieve the ideal conditions. To minimize residual imbalance, the blade assembly sequence must be optimized. To solve the engineering optimization problem of assembly sequence planning, researchers have introduced some optimization algorithms into actual engineering assembly-optimization, such as particle swarm optimization, ant colony algorithm, genetic algorithm, and simulated annealing algorithm [5]. Liu et al. [6], for NP-hard characteristics of assembly sequence planning and low efficiency in solving relatively optimal assembly sequences, used an improved simulated annealing algorithm to solve the optimization problem of the rotor blade assembly sequence. The effectiveness of the improved simulated annealing algorithm is verified by the assembly of turbine rotor blades. Zhao et al. [7] proposed a small-world network-based genetic algorithm to solve the problem of assembly sequence optimization for rotor blades. The proposed method consists of a standard genetic algorithm and NW small-world network. An experiment was carried out on the assembly of turbine rotor blades to verify the effectiveness of the algorithm. Lili Li et al. [8], while aiming at the problems of the multi-adjustable rotor blades of aero-engine blower with a low success rate of assembly, used the improved simulated annealing algorithm to optimize the assembly sequence of rotating blades, which greatly reduced the residual unbalance of blades and helped to reduce the number of assembly adjustments of blades. Li et al. [9], aiming at the optimization of rotor blade assembly sequence, adopted the improved simulated annealing algorithm to plan the assembly sequence of the blade with the restriction of gravity moment difference of diagonal blade, which provided an optimized assembly sequence for the rotor blade assembly. Zhu et al. [10], aiming at the problem of large unbalanced value in moving vane assembly, based on the brief analysis of moving vane assembly and weighing principle, put forward an intelligent optimization method for moving vane installation sequencing, by combining the global optimization and fast convergence of the genetic algorithm. Pitsoulis et al. [11] proposed a heuristic algorithm to solve NP-Hard combinatorial optimization problems in turbine engine manufacturing and maintenance. Wang et al. [12] improved the non-dominant sequencing genetic algorithm and introduced the controlling elite and dynamic congestion distance, which showed a good performance in dealing with multi-objective optimization problems of wind turbines. However, the blade matching problem is a combinatorial optimization problem, and the difficulty of solving the matching problem increases geometrically with the number of rotor stages and components. Therefore, it is difficult to find the optimal solution of the problem with traditional methods, and it is easy to fall into the local optimum.
The assembly phase angle of the multi-stage disc affects the overall balancing quality of the rotor, and the excessive initial unbalance of the multi-stage disc rotor after assembly will bring difficulties to the subsequent balancing process. At the same time, greater vibration will occur when the rotor fails, so it is very important to control the initial unevenness during an assembly. Many scholars have studied this problem. Tu et al. [13] proposed an efficient method to solve the optimal stacking assembly scheme based on geometric algebraic theory and combined it with a multi-objective optimization method. The non-dominant sequencing genetic algorithm was used to solve the multi-objective optimization problem of the rotor assembly, and the effectiveness of the method was verified by experiments. Zhang et al. [14] carried out phase optimization by predicting the assembly eccentricity of rotor parts with the intelligent algorithm, and optimized different phases with particle swarm optimization to meet the requirements of the coaxial of the aero-engine high-pressure rotor assembly, which verified the effectiveness of the method. Chen et al. [15] proposed an assembly method based on the dual-objective synchronous optimization of coaxial and imbalance, which was used to predict the coaxial and imbalance of multistage rotors. The genetic algorithm was used to achieve the synchronous optimization of coaxial and imbalance of multistage rotors. The effectiveness of the optimization method was verified by experiments conducted by Zhang et al. [16]. Zhang et al. [17] proposed a hybrid evolutionary algorithm. This algorithm is the combination of the ant colony algorithm and SA algorithm to reduce the problem of falling into the local optimal solution. Chen et al. [18] predicted the best assembly angle of the rotor at each stage in the pre-assembly process, put forward an optimization method for multi-stage rotor assembly of the aero-engine, solved the best assembly angle of the rotor at each stage by genetic algorithm, and verified by experiments that the optimization method could achieve synchronous optimization of coaxial and imbalance. Wang et al. [19] proposed an optimization model for the coaxial error of multi-stage rotors. With coaxial error as the optimization objective, the best assembly angle of each rotor was obtained. Chen et al. [20] pointed out that the assembly datum of unbalanced optimization should not be equal to that of geometric eccentricity error optimization, and proposed an unbalanced optimization method based on the orientation change axis. Sun et al. [21] proposed an assembly optimization method for the dual objectives of the concentricity and imbalance of multi-stage rotors, which enables concentricity and imbalance to approach their optimum solutions as close as possible at the same time. Li et al. [22] further improved the optimization of rotor balance by genetic algorithm to optimize the angle installation position of discs at all levels. Chen et al. [23] proposed a multi-stage rotor assembly optimization method for aero-engines based on a genetic algorithm and constructed a dual-objective fitness function based on coaxial and imbalance. It was verified by experiments that the proposed assembly optimization method can achieve synchronous optimization of coaxial and imbalance in the pre-assembly process of the aero-engine. The relevant research at home and abroad has improved the balance of the rotor to a certain extent, but the calculation method is complex. In addition, when the number of rotor stages is large, the manufacturer faces a large workload. The balance of the rotor cannot be monitored during the assembly process, and it is easy to carry out multiple installations and tests.
The assembly planning problem is NP-hard. The complexity of searching for the optimal planning increases with the size of the possible assembly sequence space searched exhaustively, and it is difficult to obtain relatively optimal planning in a short time. This challenge has become one of the important driving forces for the study of assembly planning optimization [24]. The meta heuristic algorithm first randomly generates multiple candidate solutions in the problem-solve space, and then improves these solutions in the iterative process. Finally, the best candidate solution for improvement is introduced as the solution to the problem. Said et al. [25] established a multi-attribute optimization method for sustainable aviation fuel production process using the multi-objective response surface method. Sharma et al. [26] proposed a response surface method to optimize the performance and emission parameters of mixed-fuel diesel engines. Hendricks et al. [27] proposed an effective analysis method to optimize the gas engine cycle, and realized the design optimization of some new concepts. At present, scholars have solved assembly planning problems through different optimization algorithms, such as Ant Colony Optimization (ACO) [27], Genetic Simulated Annealing Algorithm (GSAA) [28], Genetic Algorithm (GA) [29], Immune Algorithm (IA) [30], Sparrow Search Algorithm (SSA) [31], Grey Wolf Optimization Algorithm (GWO) [32], and Flower Pollination Algorithm (IFPA) [33]. These algorithms have a common feature: the search step has two stages: exploration (diversification) and development (enhancement). In the search phase, the algorithm should use the randomization operator as much as possible to explore different regions of the feature space. The exploitation phase is usually carried out after the exploration phase. The algorithm focuses on the feature space of the solution with better adjacent quality, and strengthens the local area search-process. A good optimizer should be able to achieve a reasonable and fine balance between exploration and development trends. Otherwise, the possibility of falling into local optimal (LO) and premature convergence defects increases. Table 1 lists the performance of the optimization algorithm.

Table 1.
An overview of important research in the field of optimization methods.
Table 1.
An overview of important research in the field of optimization methods.
| Reference | Algorithm | Advantages and Disadvantages of Algorithm |
|---|---|---|
| Literature [27] | ACO | The fast convergence speed and low diversity of the population are not conducive to improving the global optimization ability of the algorithm. |
| Literature [29] | GA | Fast and random search capability, with potential parallelism, so the search speed of the algorithm is relatively slow |
| Literature [30] | IA | Immune algorithm has the advantages of adaptability, randomness, parallelism, global convergence, population diversity |
| Literature [31] | SSA | The algorithm has fast convergence speed and strong global search ability. |
| Literature [32] | GWO | It has the characteristics of strong convergence, few parameters and easy realization. |
| Literature [33] | IFPA | It is easy to fall into local optimum, and the convergence speed is slow in the later stage |
The above method can solve the optimization problem in the rotor assembly stage to a certain extent, but does not consider the influence of the initial unbalance of the disk on the assembly stage, and the optimization result has errors. According to the analysis of the research status of the above-mentioned optimization methods for aero-engine rotor assembly, there are problems that the vane-sequencing optimization method does not consider the initial static imbalance of the disc, and the influence of the vane-sequencing optimization of the multi-disc is not considered in the rotor multi-disc assembly optimization. In this paper, an assembly optimization method for the multi-stage rotor of an aero-engine based on an improved Harris Hawk algorithm is proposed. The improved Harris Hawk algorithm uses initial population generation based on dynamic opposing learning and improved escape from energy function. In the global exploration, the exploration mechanism of the whale optimization algorithm is introduced to expand the search space, and the adaptive weight strategy is introduced in the development to improve the optimization efficiency and convergence speed of the algorithm. Before entering the next iteration, the mutation in the genetic algorithm is used to avoid a premature algorithm. For the assembly optimization of the aero-engine rotor, the assembly process is as follows: Firstly, with the restriction of diagonal mass-moment difference, the single-stage blade, and the disc assembly model is established, and the optimal assembly sequence is found by using an improved Harris Hawk algorithm. Then, the assembly sequence of the remaining single-stage blade and the corresponding disc is completed by repeated operations. Finally, in multi-stage disc assembly, based on the imbalance of multiple discs, the multi-stage disc rotor assembly model is established, and the optimal assembly phase is found by using an improved Harris Hawk algorithm, and the optimal imbalance force and the corresponding assembly phase of the multi-stage disc are obtained. This paper takes an aero-engine rotor as an example to verify the effectiveness of the algorithm and obtain the optimal assembly sequence. At the same time, the performance of the algorithm is analyzed and compared with particle swarm optimization, the genetic algorithm, and the Harris Hawk algorithm. It is found that the improved Harris Hawk optimization algorithm is superior to other algorithms in convergence speed and optimization. The flow chart is shown in Figure 1, which briefly describes the process.
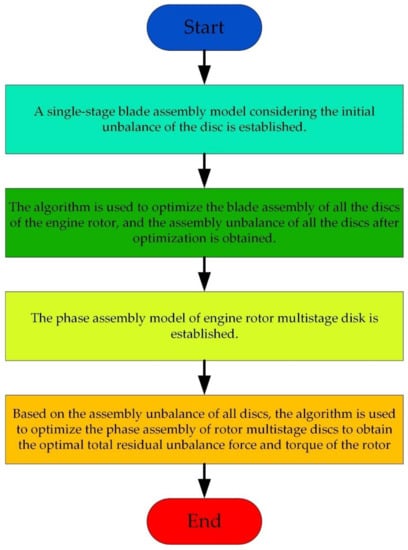
Figure 1.
Flow chart of engine rotor assembly optimization.
2. Single Stage Disc and Blade Optimization Model
The objective of single-stage blade assembly sequence-planning is to ensure that the design values are not exceeded thereby ensuring that the rotor blades are assembled in the planned assembly sequence and that the rotor static balance meets the design requirements. Because all blades rotate at the same angular velocity, the minimum residual imbalance is a vector and the minimum of the mass moment of all blades relative to the axis of rotation. The residual imbalance is a calculated method shown in Equations (1)–(4):
where, is the component of gravity moment in direction and direction respectively; is the moment of gravity of blade ; is the angle between the gravity moment vector of the blade and the positive direction of axis , is the residual unbalance, is the angle between the residual unbalance vector and the positive direction of axis .
Figure 2 shows the position representation and initial unbalance vector distance , showing the solution method of residual unbalance .
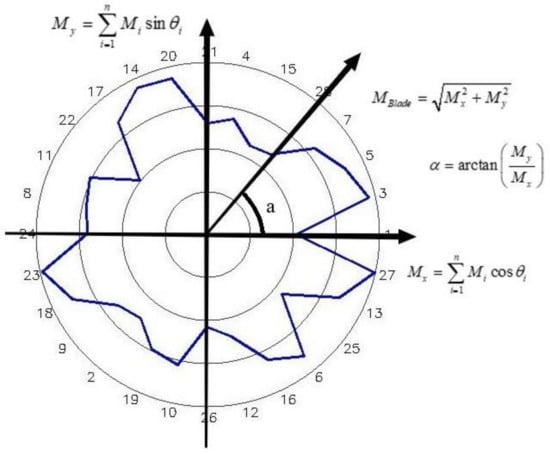
Figure 2.
Remaining unbalance of blade.
To make the rotor run more stably, the deviation range of the blade groups should be controlled to avoid too much difference of mass moment between the same group of blades. According to the enterprise design regulations, the difference in the mass moment between the diagonal position of the blades on both blades must not exceed the specified value. Therefore, the constraint conditions for blade assembly in this paper are shown in Equation (5):
where is the upper limit of the mass moment difference at the diagonal position of the blade at a certain level.
Ideally, the discs are symmetrical. In fact, the discs are asymmetric due to machining errors. Before optimizing the assembly sequence of the blades, we should consider both the unbalance of the mass moment of the blades and the initial unbalance of the disc. The objective of our assembly sequence optimization is to achieve the minimum unbalance when the blades are assembled on the disc. Figure 3 shows the effect of the initial disc imbalance on the assembled disc imbalance. The disc mass moment affects the minimum imbalance of the optimum assembled blade sequence. How to obtain the minimum imbalance of the entire blade disc is the next problem to be solved. As can be seen from Figure 3, considering the eccentric mass moment of the disc, the minimum imbalance is shown in Equations (6)–(8):
where is the mass moment of the disc, is the angle between the vector and the positive direction of the axis, and is the angle between the residual unbalance vector and the positive direction of the axis.
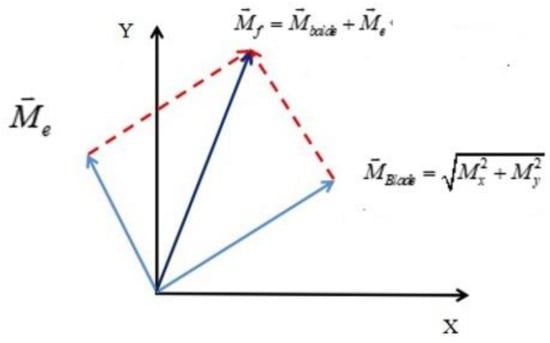
Figure 3.
The initial unbalance of the disc influences optimum unbalance in the blade assembly.
Then the optimization objective function for the assembly sequence optimization of discs and blades are shown in Equation (9).
3. Optimum Assembly Model of Multi-Stage Disc Rotor
The single-stage blade and disc optimization model established can calculate the residual imbalance after each stage of disc and blade assembly, while the total imbalance generated by the aero-engine rotor is the result of the accumulation of residual imbalance after all blade assembly. When the rotor rotates at high speed, these residual imbalances produce large imbalance forces and moments, which can seriously affect engine performance, as shown in Figure 4. Take the five-stage disc blade as an example. After each stage of the blade assembly, unbalanced blade groups are superimposed on the plane. In the actual assembly process, changing the assembly phase angle of the blades can effectively adjust the overall imbalance of multi-stage blades after assembly, so it is necessary to consider the influence of the blade assembly phase on the overall imbalance of the rotor.
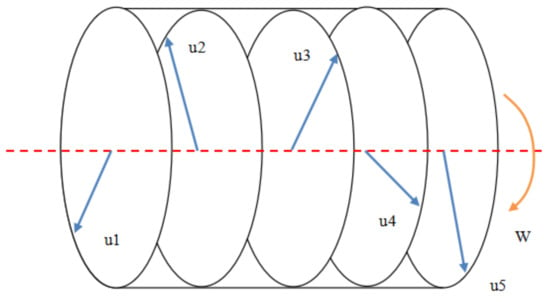
Figure 4.
Five-stage disc rotor assembly imbalance.
The sum of the initial unbalance of each stage disc and the unbalance after blade assembly is . Due to the unbalance moment, a deformation force is generated at the journal position of the engine rotor, thus the position of the journal force in the rotor is recorded.
In addition, the distance coordinates of the force points between the other discs and blade groups are defined as . The direction of unbalance of each stage disc and blade is taken as a design variable, and the component of unbalance force on axis and axis is expressed as Equations (10) and (11).
where is the component of the unbalanced force on the axis; is the component of the unbalanced force on the axis. is the number of fan blade stages.
The moment of the unbalanced force around the and axes is expressed as Equations (12) and (13).
where is the moment of the unbalanced force around the axis; is the moment when an unbalanced force is applied around the axis.
Multi-stage phase optimization aims to minimize unbalance after the assembly of multi-stage blades, which means that the unbalance forces and moments are minimized. Therefore, the objective function of the multi-stage vane phase optimization model is Equations (14) and (15).
where is the weight coefficient.
4. Harris Hawk Optimization Algorithm
Heidari et al. [34] proposed the HHO model method based on the Harris Hawk’s hunting strategy and operator structure of grey wolf optimization and divided the Harris Hawk algorithm into two stages of exploration and development.
4.1. Exploration Phase
When , the Harris Hawk randomly inhabits the search space and searches for prey through two strategies, balancing the probability of using the strategy with a random number . The mathematical expression is Equation (16).
where and are Harris Hawk locations at iterations and , are random Harris Hawk locations at iterations , are random numbers evenly distributed in [0, 1] intervals, and are prey rabbit locations (current iteration optimum), and Harris Hawk center locations, and are upper and lower bounds of the range of values. Formula (16) describes the exploratory behavior of the HHO algorithm when the prey escapes energy , where E decreases with iteration, the formula is as Equations (17) and (18).
where is the maximum number of iterations, is the current iteration step, is the initial energy value, and take the random number that is evenly distributed between [1, 1].
4.2. Development Phase
When indicates that the Harris Eagle has found the direction of the prey, the HHO algorithm performs the development behavior. The “surprise” hunting behavior of the Haris hawk can be divided into four strategies by comparing its absolute energy value with its random number of 0.5.
4.2.1. Soft Surrounding
When and , The prey still has enough energy and tries to escape through some random misleading jumps, but it cannot escape in the end. the Harris Hawk performs a hard encirclement strategy. Harris Hawk implemented a hard encirclement strategy rule such as Equation (19).
Whereas is a random number within [0, 1], represents the jumping ability of the prey. The value varies randomly during each iteration to simulate the nature of the prey’s motion.
4.2.2. Hard Surrounding
When and , The prey is very tired and its escape energy is very low. In addition, Harris’s eagle almost did not encircle the target, and finally carried out a surprise attack. Harris Hawk implemented a hard encirclement strategy rule such as Equation (20).
4.2.3. Progressive Rapid Subduction Soft Surrounding
When and , because the prey still has a large jumping ability , the Harris Hawk initiates a fast dive soft surprise. If the attack fails ( fitness does not improve), a random walk is performed and if it fails, it returns to its original location. The formula is as Equations (21)–(23).
In the formula, is the fitness function, is the problem dimension, is the dimensional random vector and is the Levy flight function expression. is a Levy flight function and is calculated using the formula in [33] as Equation (24).
where and are random values within (0,1).
4.2.4. Progressive Rapid Subduction Hard Surrounding
When and , because the prey still has a large jumping ability , the Harris Hawk initiates a fast dive hard surprise. If the attack fails ( fitness does not improve), a random walk is performed and if it fails, it returns to its original location. The formula is as Equations (25)–(27).
5. Improved Discrete Harris Hawk Algorithm
HHO achieves the transition from global search to local search based on the decay of the prey energy. The exploration process mainly relies on the best individual information and does not communicate with other individuals, which leads to the decline in population diversity and a slow convergence rate. As the number of iterations increases, the energy of the prey decreases and enters the local development stage. Four different strategies are adopted according to the energy of the prey and the probability of escape.
Figure 5 shows all stages of the improved HHO algorithm, which are described in the following sections.
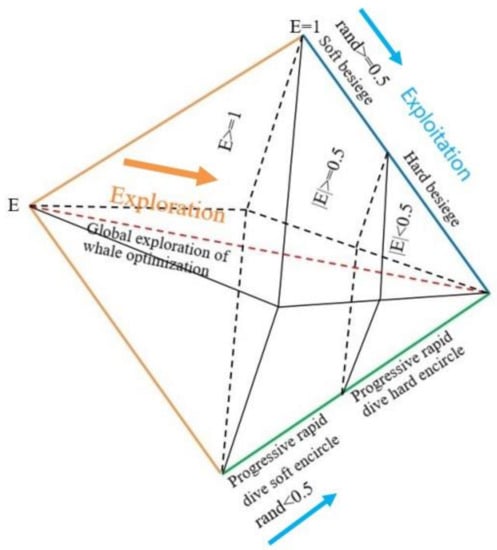
Figure 5.
Different stages of improving the Harris Hawk optimization algorithm.
5.1. Initial Population Generation of Dynamic Opposing Learning
In the meta-heuristic optimization algorithms, population initialization is often generated randomly in the search space, which can only guarantee the dispersion of the population in the search space but cannot guarantee the quality of the initial solution. However, the research shows that the quality of initialization will directly affect the convergence speed and accuracy of the algorithm. The randomly generated solutions do not consider whether these solutions satisfy the constraints. An anti-inverse learning method is introduced, which can significantly improve the performance of the algorithm.
Assuming is the solution vector of dimension, the inverse solution is calculated as Equation (28).
where represents the initialization population generated randomly; and is the lower and upper limits of variable , respectively.
First, the algorithm generates the original initial population and the reverse initial population respectively, and then combines the two populations into a new population . Calculate the fitness value of the new population, and make full competition within the population by using greedy strategy, select the best individuals as the initialization population. Through this method, the population can approach the optimal solution faster, thus improving the convergence speed of the algorithm.
5.2. The Improved Escape Energy Function
For a group intelligence optimization algorithm, how to better balance its exploration and development ability is particularly important. At the early stage of algorithm evolution, strong global exploration capability is required to maintain the diversity of the population, while at the later stage of algorithm iteration, better development capability is required to ensure that the algorithm can be developed locally. For the HHO algorithm, the escape energy of prey is an important parameter in the transition from the exploration stage to the development stage of the algorithm. It is used to control the balance between the exploration and development stages. Based on the improved method of convergence factor in reference [35]. In this paper, a nonlinear logarithmic convergence factor escape energy function such as Equation (28).
where is the natural constant, is the current iteration, is the maximum iteration number, and is the initial escape energy. The rate of reduction is faster in the early stage and slower in the later stage. Due to the excellent population diversity of the HHO algorithm in the early iteration period, strong local development capability is required in the later iteration period.
5.3. Discrete Exploration for Whale Optimization
The introduction of a whale optimization algorithm [36] to search for a prey strategy increases diversity and solves the problem that the algorithm has poor global exploration capability. The improved global pollination method is shown by Equations (30)–(32):
where is a weight vector, decreases from 2 linear to 0; is a random number in [0, 1]. is a randomly selected individual from the iteration population and is a random number of [−1, 1] distributions.
To enable exploratory development to deal with discrete problems, the following discrete rules are set.
- (1)
- A new assembly sequence is obtained by subtracting assembly sequence from . Considering that the result will be negative, the absolute value is adopted. The calculation formula is as Equation (33).
- (2)
- Array multiplication, corresponding value multiplication, the rules are as follows:
The constraint conditions for blade assembly in this paper are as Equation (34).
- (3)
- Arrays are added and corresponding values are added according to the following rules as Equation (35).
- (4)
- is an -dimensional integer array randomly generated by Levy distribution. The values of the array are generated by the Formula (24). The characteristics of LF are that it generates a small number in most of the time and suddenly jumps to a very large number randomly, thus mimicking the Levy flight behavior of birds. is an -dimensional array of numbers 0 and 1 that are generated.
The following example shows the modified discrete global exploration rule and illustrates the above discretization process:
In the obtained assembly sequence, there are more than the maximum number of blades, duplicate values and missing values, and the assembly sequence needs to meet the constraints, so the final assembly sequence needs to be repaired, the repair steps are as follows:
- (1)
- Statistically identify the values in the array that exceed the maximum number of blades and repeat the values, and change these values to 0. At the same time, record the missing values and the number of values in the sequence.
- (2)
- The missing value is randomly filled into the position of 0 in the array to get a new sequence.
- (3)
- To satisfy the constraints and generate the optimal sequence which meets the conditions, the assembly sequence is updated. The update rule is to exchange the blades which do not meet the conditions randomly until the conditional output is met.
The new assembly sequence after all repairs is as follows:
5.4. Discrete Development Method of Adaptive Weighting
Inspired by particle swarm optimization (PSO), an inertia weight varying with the number of iterations is added to the position update of the Harris Hawk. In the early stage of the algorithm search, the effect of the optimal Harris Hawk position on current individual position adjustment is weakened and the search area of the algorithm in the early stage is enlarged. As the number of iterations increases, when the inertia weight is small, the later search ability of the algorithm is strong, and a fine search can be carried out around the optimal solution. According to the change of update times in the Harris Hawk optimization algorithm, the adaptive inertia weight composed of iterations is as Equations (36) and (37):
The adaptive inertia weight has a property of non-linear change between [0, 1]. Because of the change characteristics of function between , the weight is small at the beginning of the algorithm, but the change speed is slightly faster. At the later stage of the algorithm, the value is large, but the change speed will be slow down, which can fully guarantee the convergence of the algorithm.
5.4.1. Discrete Soft Surrounding
When and , the Harris Hawk performs a soft encirclement strategy. Such as Equation (38).
Whereas is a random number within [0, 1], represents the jumping ability of the prey. The value varies randomly during each iteration to simulate the nature of the prey’s motion.
Discrete processing in global exploration rules is used to apply it to local development rules. The following example illustrates the modified local development rules and procedure flow.
The repair strategy in the improved global exploration rule is adopted to repair the defects. The new assembly sequence after all the repairs is as follows:
5.4.2. Discrete Hard Surrounding
When and B, the Harris Hawk performs a hard encirclement strategy. Such as Equation (39).
Discrete processing in global exploration rule is used to apply it to discrete hard surrounding rule. The following example illustrates the modified local pollination rules and procedure.
The repair strategy in the improved global exploration rule is adopted to repair the defects. The new assembly sequence after all the repairs is as follows:
5.4.3. Discrete Progressive Rapid Subduction Soft Surrounding
When and , because the prey still has a large jumping ability , the Harris Hawk initiates a fast dive soft surprise. If the attack fails ( fitness does not improve), a random walk is performed and if it fails, it returns to its original location. The formula is as Equations (40)–(42).
In the formula, is the fitness function, is the problem dimension, is the dimensional random vector and is the Levy flight function expression.
The discretization treatment in the global exploration rule is applied to the local pollination rule. The following example illustrates the modified local pollination rule and procedure flow.
The repair strategy in the improved global exploration rule is adopted to repair the defects. The new assembly sequence after all the repairs is as follows:
5.4.4. Discrete Progressive Rapid Subduction Hard Surrounding
When and , because the prey still has a large jumping ability , the Harris Hawk initiates a fast dive hard surprise. If the attack fails ( fitness does not improve), a random walk is performed and if it fails, it returns to its original location. The formula is as Equations (43)–(45).
The discretization treatment in the global exploration rule is applied to the local pollination rule. The process is the same as that in Section 5.4.3, where is the randomly selected individual in the iteration.
5.5. Genetic Operator Variation
It is known from the construction of HHO that the HHO algorithm will produce the phenomenon that the updated individual will fall into the local optimum during the iteration process, which will affect the optimization ability of HHO. In this paper, the idea of mutation in the genetic algorithm is used to expand the population search space by mutation variation before the algorithm enters the next iteration, which can make the algorithm jump out of local optimum, maintain the diversity of the population, and increase the ability of optimization.
The adaptive variation probability makes the variation probability increase with the number of iterations, which helps the Harris Hawk individual avoid being trapped by the local optimum at the later stage of iteration and improves the convergence accuracy of the algorithm. such as Equation (46).
The probability of variation varies nonlinearly during the iteration process and slows down the increase of the probability of variation at the later stage of iteration to avoid large oscillations and converge the population. The rules for improvement are as follows:
Calculate the variation probability of the variation operator. If the probability is less than the variation probability, randomly select two different locations, exchange their values, and repeat the exchange five times to complete the variation. Otherwise, skip.
5.6. Improving the Procedure of Harris Hawk Algorithm Implementation
Based on the above improvements, an improved Harris Hawk optimization algorithm is proposed, which has the following steps:
Step 1: Initialization of parameters, determination of population , dimension (part number) , the maximum number of iterations ;
Step 2: Initial population generation is carried out based on dynamic opposing learning and greedy strategy, and fitness value of individual population is calculated, optimum fitness value and corresponding assembly sequence are saved;
Step 3: Calculate the escape energy by Formula (29). If goes to step 4, no, go to step 5;
Step 4: Global exploration, updating individual population according to Formula (30);
Step 5: Local development, if goes to Step 6, no, then goes to Step 11;
Step 6: If goes to step 7, no, go to step 9;
Step 7: Calculate Y according to the Formula (44). If is updated to Y, turn to Step 12. No, turn to Step 8;
Step 8: Calculate Z according to the Formula (45). If is updated to Step 12 of Z, no, do not update Step 12 of Z;
Step 9: Calculate Y according to the Formula (41). If is updated to Y, turn to Step 12. No, turn to Step 10;
Step 10: Calculate Z according to the Formula (42). If is updated to Step 12 of Z, no, do not update Step 12 of Z;
Step 11: If is updated according to Formula (39), no, according to Formula (38);
Step 12: If carries out genetic variation, no, skip;
Step 13: Are all population individuals updated? No, go to Step 3;
Step 14: Calculate the fitness value of individuals who update the population, find the optimum fitness value and corresponding solution in the updated population, and update the optimum fitness value and corresponding is assembly sequence;
Step 15: To determine whether the end condition is met, yes, output the optimum value and the corresponding solution and exit the program, no, go to Step 3.
The flow chart for improving the Harris Hawk optimization algorithm is shown in Figure 6.
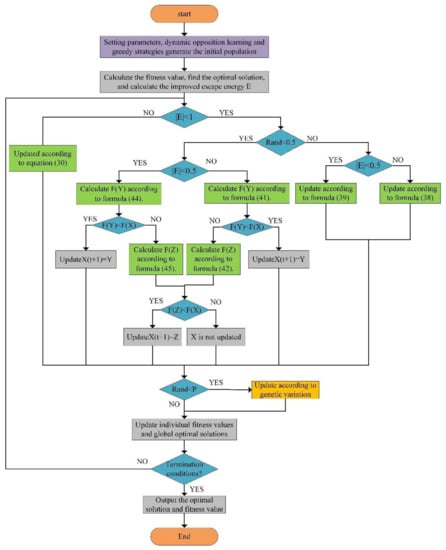
Figure 6.
Improved flow chart for Harris Hawk algorithm.
6. Instance Validation
In this paper, the assembly of rotor blades of a certain stage fan of an aero-engine is taken as an example for verification. To verify the effectiveness of the algorithm, we use C++ programming on Visual Studio 2017 software to implement the algorithm in this paper. The operating environment is CPU frequency 2.9 GHz, memory 16 GB, Windows10 64bit operating system.
6.1. Single Stage Disc and Single Stage Blade Assembly
The assembly sequence of a stage blade of an aero-engine is optimized. The blades are numbered from minimum to maximum according to the mass moment data. The blade data are shown in Table 2.

Table 2.
Blade data.
For the simulation run of the algorithm in this paper, the parameters are set as follows: initial population m = 100, 500 iterations. Figure 7 shows the convergence diagram of the improved pollination algorithm in 500 iterations.
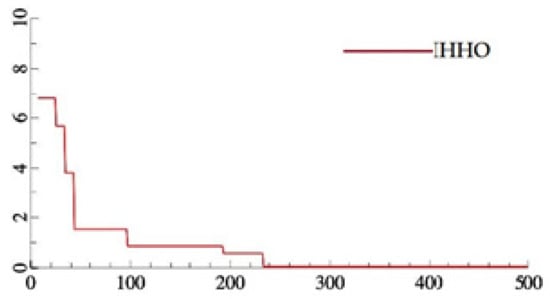
Figure 7.
Iterative Graph of Improved Harris Hawk Optimization Algorithm.
For general or unreasonable sorting, the rotor unbalance can reach 6000 g·mm or more. According to Figure 6, we can see that the imbalance becomes smaller and smaller as the number of iterations of the algorithm increases, and the minimum imbalance is 0.0517 g·mm when the number of iterations reaches 234. The corresponding sorting results are shown in Table 3, and the corresponding assembly sequence diagram is shown in Figure 8.

Table 3.
Optimum blade assembly sequence found by IHHO.
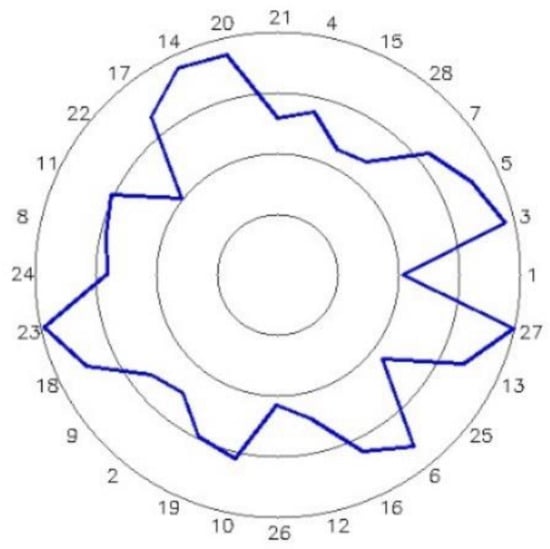
Figure 8.
Installation drawing of optimal blade assembly sequence searched by IHHO.
The improved Harris Hawk algorithm is compared with the particle swarm optimization algorithm, genetic algorithm, and basic Harris Hawk algorithm. The above algorithms have been independently simulated for 200 iterations. Table 4 lists the optimal sequence of aero-engine single-stage blade assembly obtained by the four algorithms, and gives the unbalance calculated by the optimal assembly sequence. The convergence graphs of average fitness and global optimal fitness of the four algorithms are shown in Figure 9 and Figure 10, and the assembly sequence is shown in Figure 11.

Table 4.
Optimum blade assembly sequence and unbalance data for each algorithm.
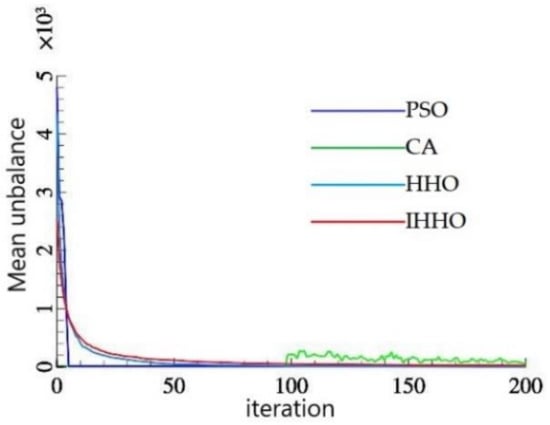
Figure 9.
IHHO average unbalance iteration chart.
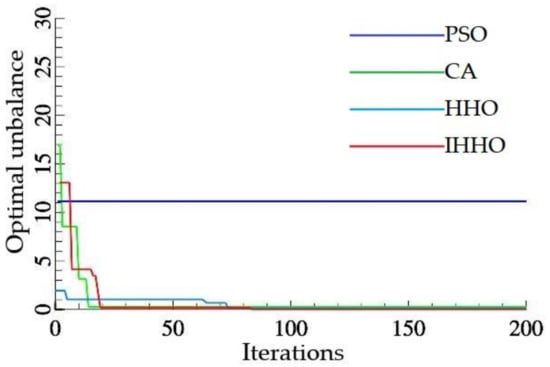
Figure 10.
IHHO optimal unbalance iteration chart.
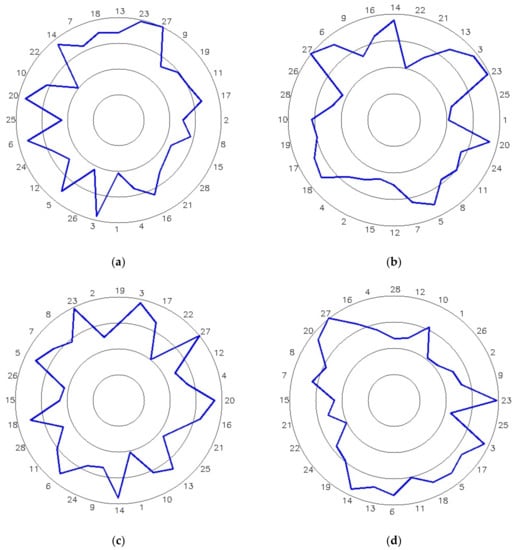
Figure 11.
Blade mass moment arrangement under 4 optimization algorithms: (a) PSO; (b) CA; (c) HHO; (d) IHHO.
Through the comparative analysis of the data in Table 3, it can be found that the minimum unbalance of the optimal assembly sequence given by the improved Harris Hawk algorithm proposed in this paper is 0.024, which is 91.75% lower than the particle swarm optimization algorithm, 99.82% lower than the genetic algorithm, and 83.39% lower than the Harris Hawk algorithm. By comparing the global optimal fitness convergence graph of the algorithm, it is found that the improved eagle algorithm is obviously superior to the other three algorithms. First, the optimal assembly sequence found by the improved Harris Hawk algorithm has the lowest unbalance and the fastest convergence speed in the early stage of the algorithm. Compared with PSO and GA algorithms, IHHO and HHO iterations converge faster, and IHHO finds a better fitness value than HHO, that is, IHHO finds a better assembly sequence. This shows that the performance of the IHHO algorithm proposed in this paper is better than the other three algorithms.
6.2. Rotor Multistage Disc Phase Assembly
The blade data of the first, second, third, fourth, and fifth stages of an aero-engine rotor were used as an example to verify the optimization effect of this algorithm applied to the phase assembly of rotor multistage discs. The blade data of each stage are shown in Table 5.

Table 5.
Blade data of all rotors.
Particle swarm optimization, genetic algorithm, HHO optimization algorithm, and IHHO optimization algorithm are used for blade assembly optimization of each stage of rotor. The results are shown in Table 6.

Table 6.
Comparisons of optimization algorithms for rotor blade assembly at various stages.
Analysis
Table 5 compares the results of the improved Harris Hawk optimization algorithm with particle swarm optimization, genetic algorithm, and the original Harris Hawk optimization algorithm. The optimal imbalance of improved Harris Hawk optimization algorithm is reduced by 79.71%, 99.48%, and 54.92%, respectively. The IHHO proposed in this paper is much lower than other algorithms in finding the optimal sequence and is obviously superior to the other three algorithms in finding the optimal solution.
The assembly sequence table (counterclockwise) of the first stage, second stage, third stage, fourth stage, and fifth stage disc blades optimized by the improved Harris Hawk algorithm is shown in Table 7. The phase angle of the multistage blade assembly is optimized by improving Harris Hawk algorithm, and the total residual unbalance force, The optimized blade layout obtained by improving Harris Hawk algorithm is shown in Figure 12.

Table 7.
Improve the IHHO assembly sequence of each stage of disc blades.
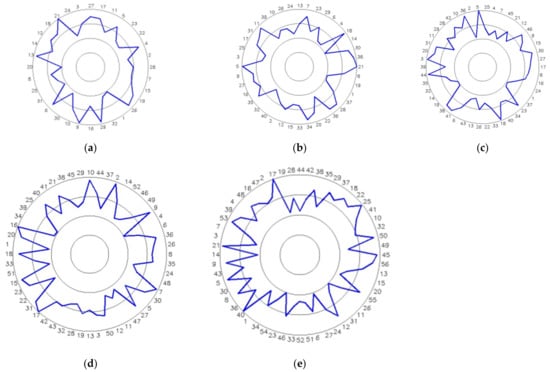
Figure 12.
Assembly sequence of engine rotor disc blades at each stage: (a) First stage disc blade assembly sequence; (b) Assembly sequence of the second stage disc blade; (c) Assembly sequence of the third stage disc blade; (d) Assembly sequence of fourth stage disc blade. (e) Assembly sequence of fifth stage disc blade.
After the blade layout of each stage is completed, the assembly phase angle between discs of each stage is optimized by improving the Harris Hawk algorithm. The residual unbalanced force vectors of discs at all levels are superposed to make the residual unbalanced force and torque of the whole rotor meet the requirements. Unbalanced moment and blade assembly phase angle before and after optimization are compared, as shown in Table 8.

Table 8.
IHHO-optimized aero-engine rotor assembly phase angle.
By analyzing the data in Table 8, before optimization, the greatest residual unbalance force calculated by using the phase angle of the first-, second-, third-, and fifth-stage blade sets is 0.1058, and the unbalance moment is 0.6348. The optimal installation angle of the first stage blade group after IHHO optimization is 247° relative to the disk, the second stage blade group is 92° relative to the disk, the third stage blade group is 261° relative to the disk, the fourth stage blade group is 0° relative to the disk, the greatest residual unbalanced force is 0.0167, which is 84.22% lower than that before optimization, and the unbalanced moment is 0.0124, which is 98.05% lower than that before optimization. As shown above, it is workable to optimize the phase angle of multistage disk blade assembly by using the improved Harris Hawk algorithm.
7. Conclusions
In this paper, we propose a discrete improved Harris Hawk optimization algorithm to optimize the imbalance of engine rotor assembly. The improved Harris Hawk optimization algorithm adopts the initial population generation based on dynamic anti-vertical learning and the improved escape from energy function and introduces the exploration mechanism of the whale optimization algorithm in the global exploration to expand the search space. The adaptive weight strategy is introduced in the development to improve the optimization efficiency and convergence speed of the algorithm. Before entering the next iteration, the mutation in the genetic algorithm is used to avoid premature algorithm. First, based on the mass moment of a single blade, the diagonal mass moment difference is introduced as a constraint to establishing a single-stage blade and disk assembly model. The improved Harris Hawk algorithm is used to find the optimal assembly sequence, and repeated operations are performed to complete the assembly sequence of the remaining single-stage blades and corresponding disks. For the assembly of the engine rotor, based on the imbalance amount of multiple disc blades after assembly obtained by the improved algorithm in this paper, a multi-stage disc rotor assembly model is established. The improved Harris Eagle optimization algorithm is used to find the optimal assembly phase, and the optimal unbalanced force and the assembly phase of the multi-stage disc corresponding to the unbalanced force distance are obtained. The main results of this study are as follows:
- For the optimization of single stage disc and blade assembly unbalance, the improved Harris Hawk optimization algorithm is compared with the particle swarm optimization, the genetic algorithm, and the Harris Hawk optimization algorithm, and the unbalance of the optimal blade assembly sequence is reduced by 91.75%, 99.82%, and 83.39%, respectively;
- For the assembly of each stage disc blade of the engine rotor, the results of the improved Harris Hawk optimization algorithm, particle swarm optimization algorithm, genetic algorithm, and Harris Hawk optimization algorithm are compared and analyzed. The optimal unbalance of the improved Harris Hawk optimization algorithm is reduced by 79.71%, 99.48%, and 54.92%, respectively. The proposed IHHO algorithm is obviously superior to the other three algorithms in finding the optimal solution;
- The phase angle of the multistage blade assembly is optimized by improving the Harris Hawk optimization algorithm. The total residual unbalanced force, unbalanced torque, and blade assembly phase angle of each stage before and after optimization are compared. The optimized assembly phase angles are 247°, 92°, 261°, 0°, 115°. The total residual unbalanced force and moment of assembly are 0.0167 and 0.0124, and the total residual unbalanced force and moment of assembly after optimization are 84.22% and 98.05% lower than those before optimization.
This research is effective in developing an improved Harris Hawk optimization algorithm to improve the assembly quality of aero-engine rotor and blade. In order to improve the assembly quality in the future work, the assembly optimization model will be improved in the future, and more realistic factors will be considered. In the future, it is planned to test the assembly optimization method developed in this study in the actual aero-engine assembly, and compare it with the method in engineering, so as to adapt to the aero-engine rotor assembly in the enterprise in the future.
Author Contributions
Conceptualization, B.Z. and H.L.; methodology, B.Z.; software, D.S.; validation, B.Z., Y.Y. and H.L.; formal analysis, S.L.; investigation, H.L. and B.Z.; resources, H.L.; data curation, S.L. and B.Z.; writing—original draft preparation, B.Z.; writing—review and editing, H.L.; visualization, B.Z.; supervision, H.L.; project administration, H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Jiangxi Natural Science Foundation (No. 20201BBE51002).
Data Availability Statement
Not applicable.
Acknowledgments
Thanks to Liu Shun processed the experimental data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.M.; Zhang, M.W.; Sun, C.Z.; Hu, M.; Chen, D.Y.; Liu, Z.W.; Tan, J.B. A method to minimize stage-by-stage initial unbalance in the aero engine assembly of multistage rotors. Aerosp. Sci. Technol. 2019, 85, 270–276. [Google Scholar] [CrossRef]
- Chen, D. Research on Vibration Suppression Method of Aero-Engine Rotor Based on Stack Assembly Optimization. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Lin, Z. Research on Rotor Assembly Method Based on Axial Compression; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- Zhang, H.; Wang, M.; Li, Z.; Zhou, J.; Zhang, K.; Ma, X.; Wang, M. Semi-Physical Simulation of Fan Rotor Assembly Process Optimization for Unbalance Based on Reinforcement Learning. Aerospace 2022, 9, 342. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Ab, R.M.F.F.; Ghazalli, Z. Optimization of assembly sequence planning using soft computing approaches: A review. Arch. Comput. Methods. Eng. 2019, 26, 461–474. [Google Scholar] [CrossRef]
- Liu, L.K.; LI, L.L. Optimization of Assembly Sequence Planning of Turbine Low-pressure Rotor Blades Based on the Improved Simulated Annealing Algorithm. J. Phys. Conf. Ser. 2021, 1939, 012098. [Google Scholar]
- Zhao, L.P.; Li, B.H.; Chen, H.R.; Zhao, L.P. An assembly sequence optimization oriented small world networks genetic algorithm and case study. Assem. Autom. 2018, 38, 387–397. [Google Scholar] [CrossRef]
- Li, L.L.; Chen, K.; Gao, J.M.; Liu, J.K. Research on Optimizing Selection and Optimizing Matching Technologies of Aeroengine Fan Rotor Blades. Shock Vib. 2021, 2021, 5595535. [Google Scholar] [CrossRef]
- Li, L.L.; Chen, K.; Gao, J.M.; Liu, J.K.; Gao, Z.Y.; Dai, H.W. Research on optimizing-assembly and optimizing-adjustment technologies of aero-engine fan rotor blades. Adv. Eng. Inform. 2022, 51, 101506. [Google Scholar] [CrossRef]
- Zhu, M.Y.; Li, M.Q.; Wen, X.; Li, D.Y. Intelligent optimization of turbine rotor blade assembly sequence. J. Aerosp. Power. 2017, 32, 2536–2543. [Google Scholar]
- Pitsoulis, L.S.; Pardalos, P.M.; Hearn, D.W. Approximate solutions to the turbine balancing problem. Eur. J. Oper. Res. 2001, 130, 147–155. [Google Scholar] [CrossRef]
- Wang, L.; Wang, T.G.; Luo, W.Y. Improved non-dominated sorting genetic algorithm (NSGA)-II in multi-objective optimization studies of wind turbine blades. Appl. Math. Mech. Engl. Ed. 2011, 32, 739–748. [Google Scholar] [CrossRef]
- Tu, J.B.; Li, Z.; Ge, H.T.; Liu, L.; Liu, H.H. Multi-objective optimization of rotor-stack assembly based on geometric algebra theory. Acta Aeronaut. Astronaut. Sin. 2021, 42, 395–405. [Google Scholar]
- Zhang, Z.H.; Guo, J.K.; Hong, J.; Sun, Y.H. Application study intelligent algorithms for prediction and phase optimization of assembly eccentricity of aero-engine high pressure rotor. J. Xi’an Jiaotong Univ. 2021, 55, 47–54. [Google Scholar]
- Chen, Y.; Cui, J.; Sun, X. A Vibration Suppression Method for the Multistage Rotor of an Aero-Engine Based on Assembly Optimization. Machines 2021, 9, 189. [Google Scholar] [CrossRef]
- Zhang, Y.; He, L.; Yang, J.; Wang, J.; Zhu, G. Vibration control of tie rod rotors with optimization of unbalanced force and unbalanced moment. IEEE Access 2020, 8, 66578–66587. [Google Scholar] [CrossRef]
- Zhao, B.; Yuan, Q.; Li, P. Improvement of the vibration performance of rod-fastened rotor by multi optimization on the distribution of original bending and unbalance. J. Mech. Sci. Technol. 2020, 34, 83–95. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, J.; Sun, X. An Assembly Method for the Multistage Rotor of An Aero-Engine Based on the Dual Objective Synchronous Optimization for the Coaxality and Unbalance. Aerospace 2021, 8, 94. [Google Scholar] [CrossRef]
- Wang, L.; Sun, C.; Tan, J.; Zhao, B.; Wan, G. Improvement of location and orientation tolerances propagation control in cylindrical components assembly using stack-build assembly technique. Assem. Autom. 2015, 35, 358–366. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, J.; Sun, X. An unbalance optimization method for a multi-Stage rotor based on an assembly error propagation model. Appl. Sci. 2021, 11, 887. [Google Scholar] [CrossRef]
- Sun, C.Z.; Liu, Z.W.; Liu, Y.M.; Wang, X.M.; Tan, J.B. An adjustment method of geometry and mass centers for precision rotors assembly. IEEE Access 2019, 7, 169992–170002. [Google Scholar] [CrossRef]
- Zhi, L.L.; Ying, W. Optimum Design for Balance in Multi-Disk Rotor Installation Based on Genetic Algorithm. J. Vib. Meas. Diagn. 2008, 28, 4. [Google Scholar]
- Chen, Y.; Cui, J.W.; Sun, X.; Cui, S.H. Research on multistage rotor assembly optimization methods for aeroengine based on the genetic algorithm. Complexity 2021, 2021, 8847690. [Google Scholar] [CrossRef]
- Wang, H.; Rong, Y.; Xiang, D. Mechanical assembly planning using ant colony optimization. Comput. Aided Des. 2014, 47, 59–71. [Google Scholar] [CrossRef]
- Said, Z.; Nguyen, T.H.; Sharma, P.; Li, C.; Ali, H.M.; Ahmed, S.F.; Van, D.N.; Truong, T.H. Multi-attribute optimization of sustainable aviation fuel production-process from microalgae source. Fuel 2022, 324, 124759. [Google Scholar] [CrossRef]
- Sharma, P.; Le, M.P.; Chhillar, A.; Said, Z.; Deepanraj, B.; Cao, D.N.; Bandh, S.A.; Hoang, A.T. Using response surface methodology approach for optimizing performance and emission parameters of diesel engine powered with ternary blend of Solketal-biodiesel-diesel. Sustain. Energy Technol. Assess. 2022, 52, 102343. [Google Scholar] [CrossRef]
- Hendricks, E.S.; Gray, J.S. pyCycle: A Tool for Efficient Optimization of Gas Turbine Engine Cycles. Aerospace 2019, 6, 87. [Google Scholar] [CrossRef]
- Shan, H.B.; Zhou, S.H.; Sun, Z.H. Research on assembly sequence planning based on genetic simulated annealing algorithm and ant colony optimization algorithm. Assem. Autom. 2009, 29, 249–256. [Google Scholar] [CrossRef]
- Chen, S.F.; Liu, Y.J. An adaptive genetic assembly-sequence planner. Int. J. Comput. Integr. Manuf. 2001, 14, 489–500. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Liu, H.J.; Li, L.Y. Research on a kind of assembly sequence planning based on immune algorithm and particle swarm optimization algorithm. Int. J. Adv. Manuf. Technol. 2014, 71, 795–808. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, Y. Discrete sparrow search algorithm for symmetric traveling salesman problem. Appl. Soft Comput. 2022, 118, 108469. [Google Scholar] [CrossRef]
- Ab Rashid, M.F.F. A hybrid Ant-Wolf Algorithm to optimize assembly sequence planning problem. Assem. Autom. 2017, 37, 238–248. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, H.Y.; Song, H.Q.; Liu, S.; Yang, Y.C.; Sang, D.D. Overall planning of aero-engine assembly based on improved pollination Algorithm. J. Aerosp. Power. 2022, 37, 1–12. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Guo, W.; Xu, P.; Dai, F.; Zhao, F.; Wu, M. Improved Harris hawks optimization algorithm based on random unscented sigma point mutation strategy. Appl. Soft Comput. 2021, 113, 108012. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).