Numerical Study of Unstable Shock-Induced Combustion with Different Chemical Kinetics and Investigation of the Instability Using Modal Decomposition Technique
Abstract
1. Introduction
2. Numerical Modeling
2.1. Governing Equations
2.2. Numerical Methods
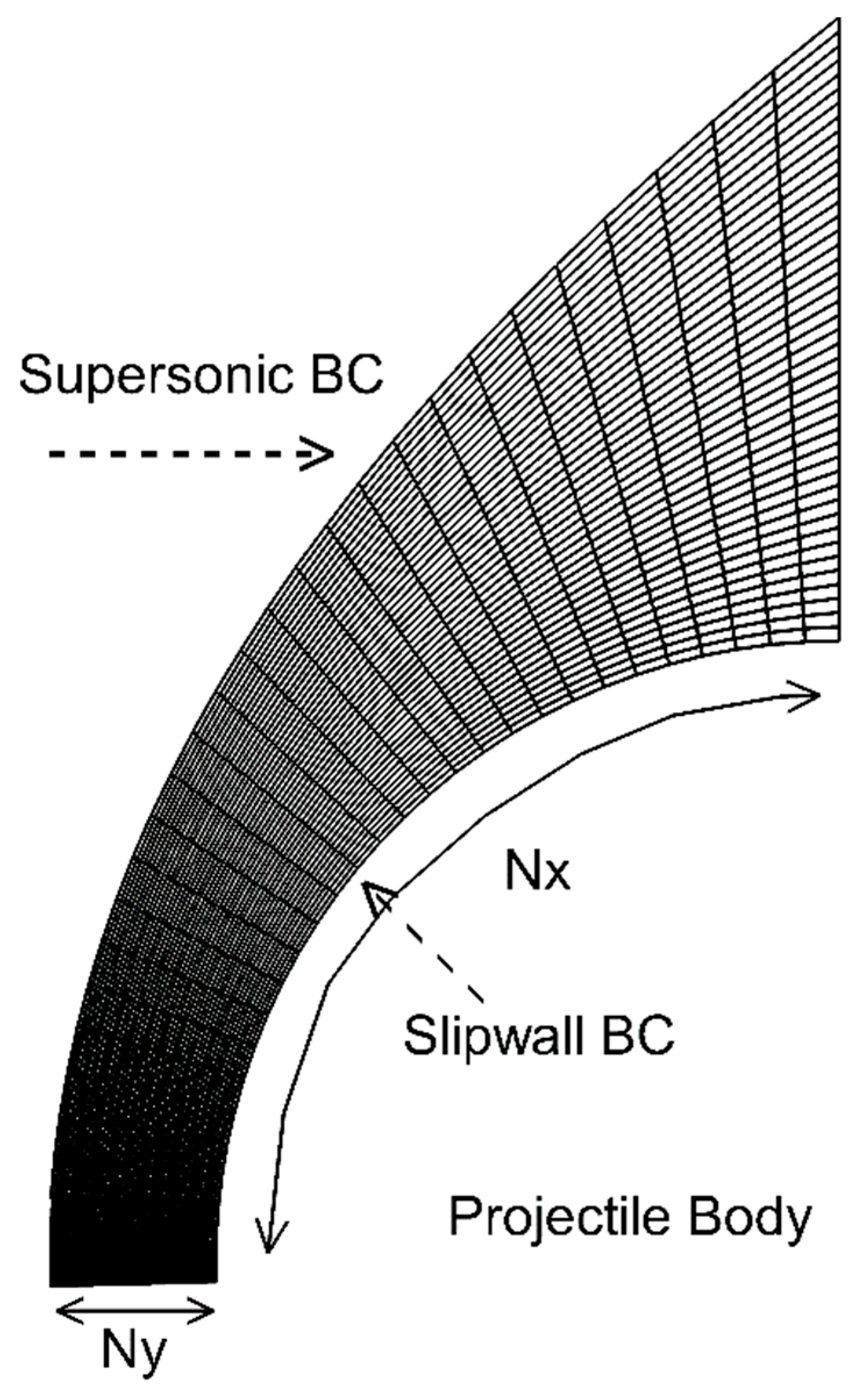
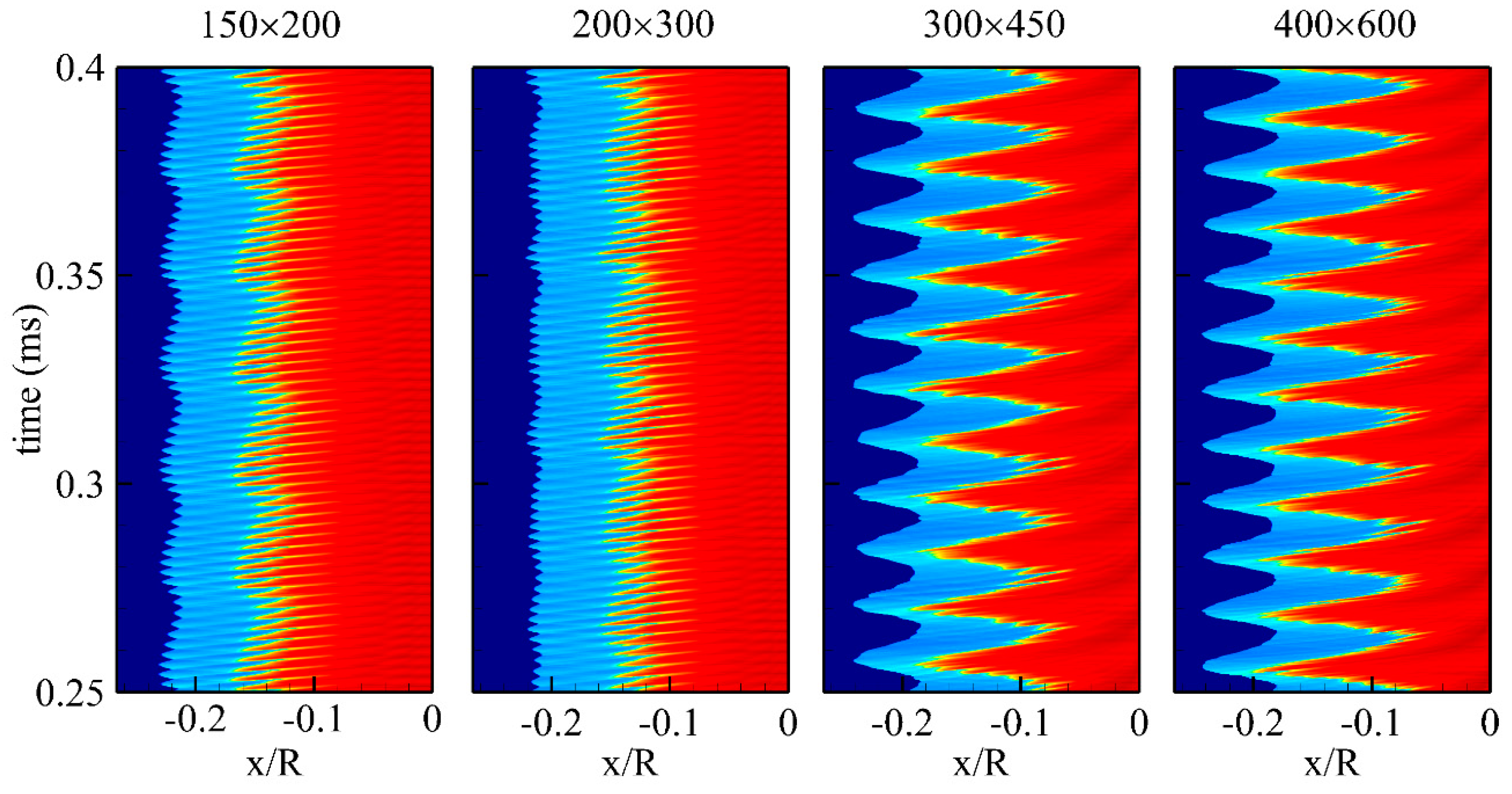
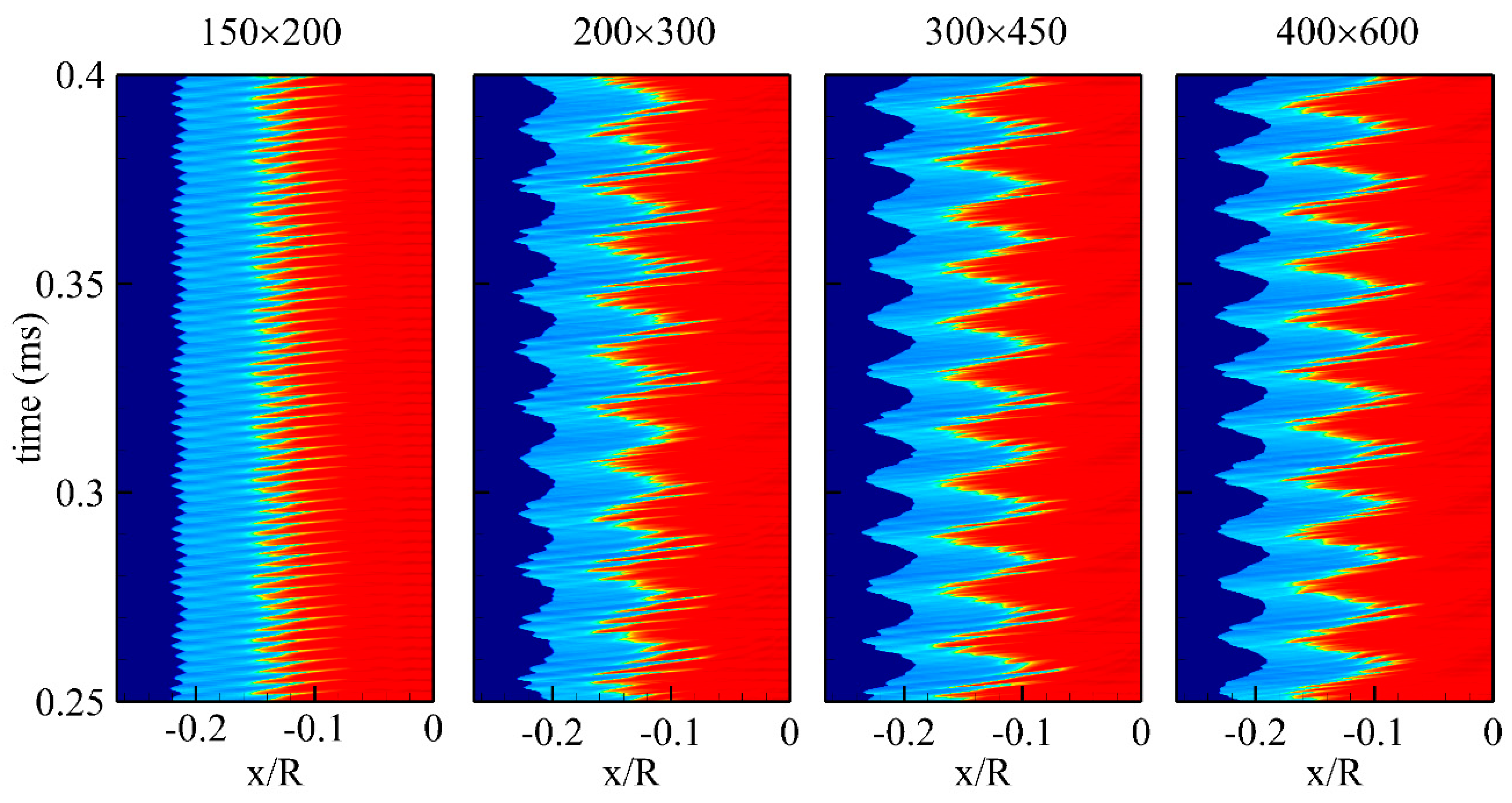
2.3. Numerical Setup
3. Numerical Simulation of Shock-Induced Combustion Using Different Chemical Kinetic Mechanisms
3.1. Hydrogen–Air Combustion Mechanisms
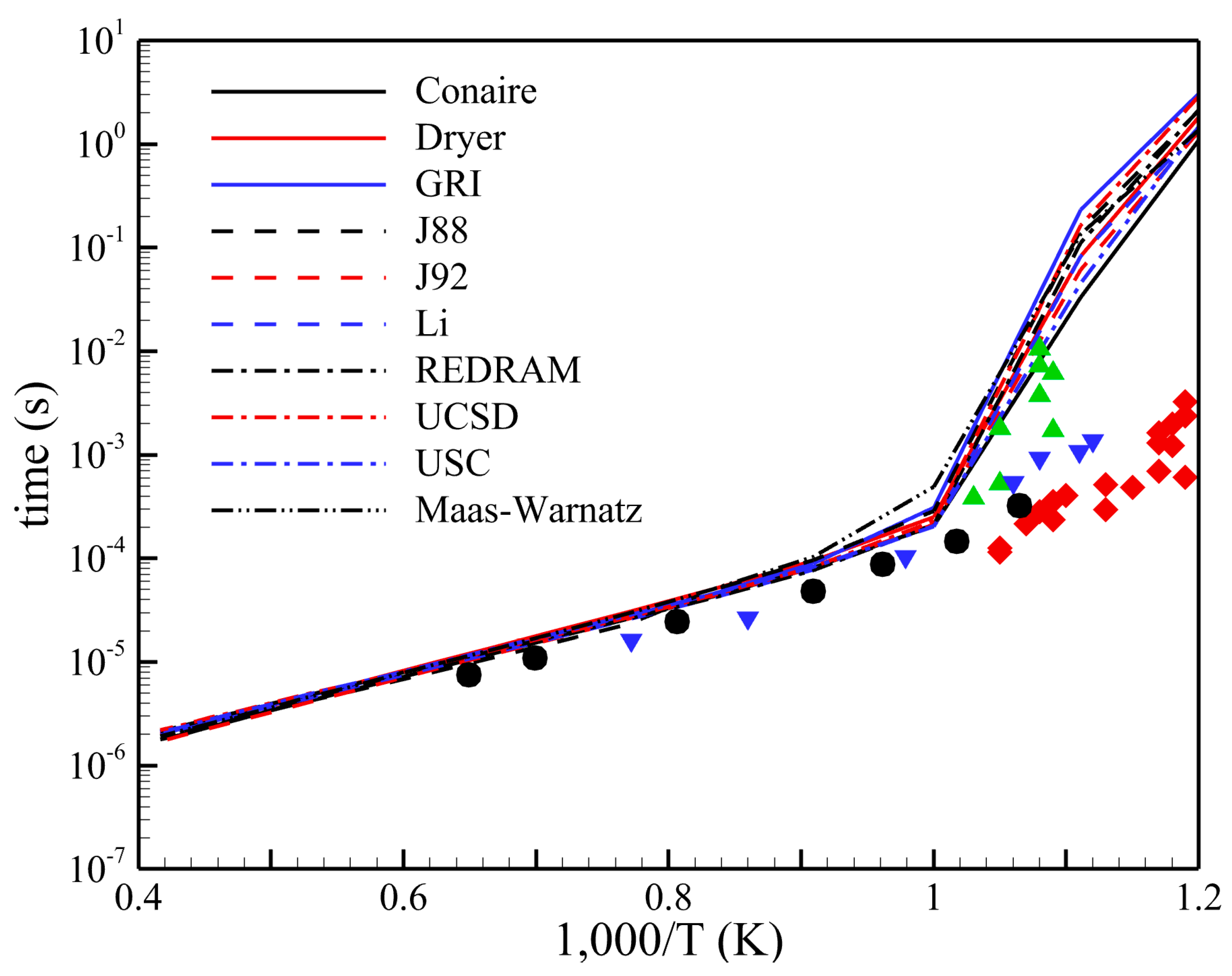
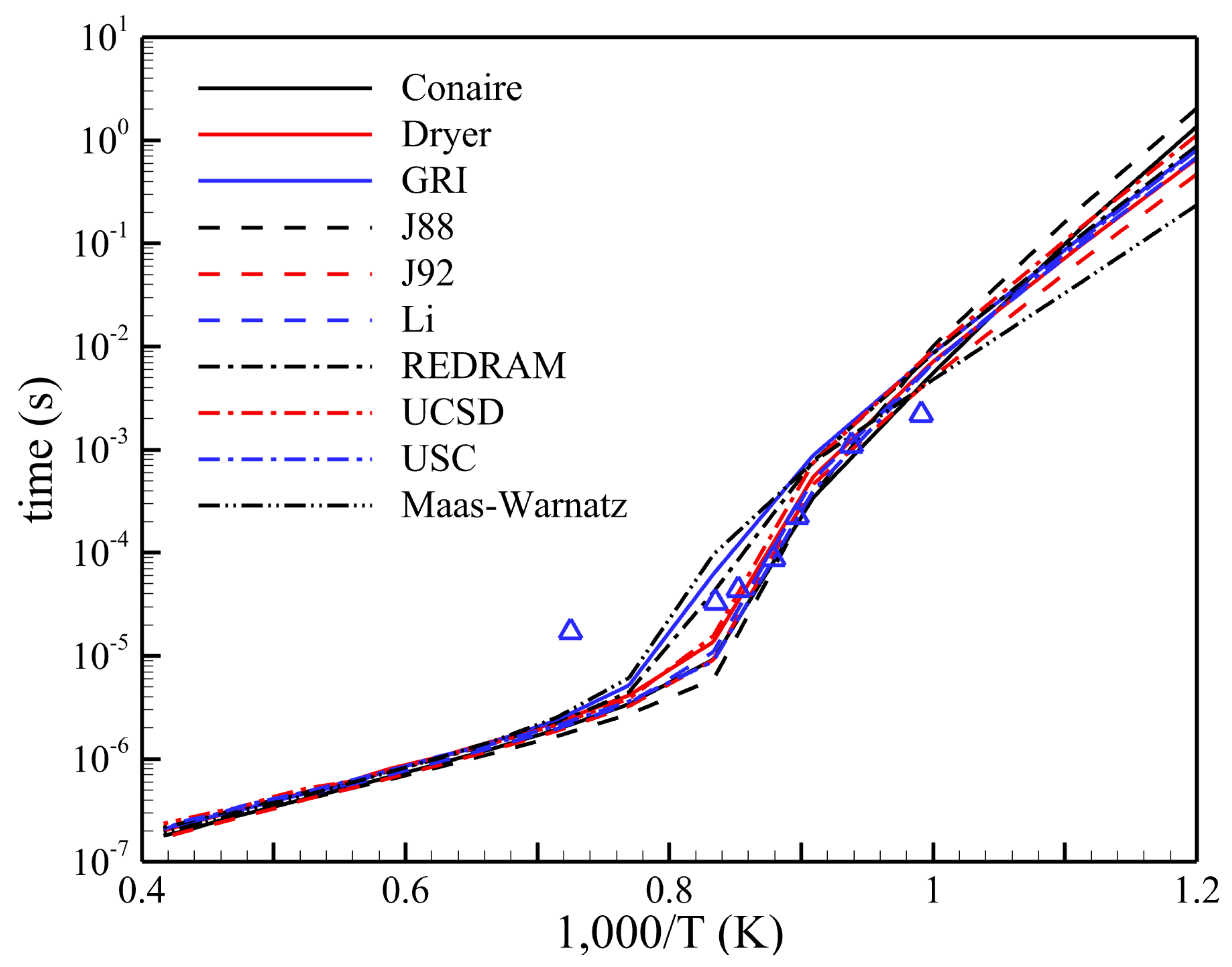
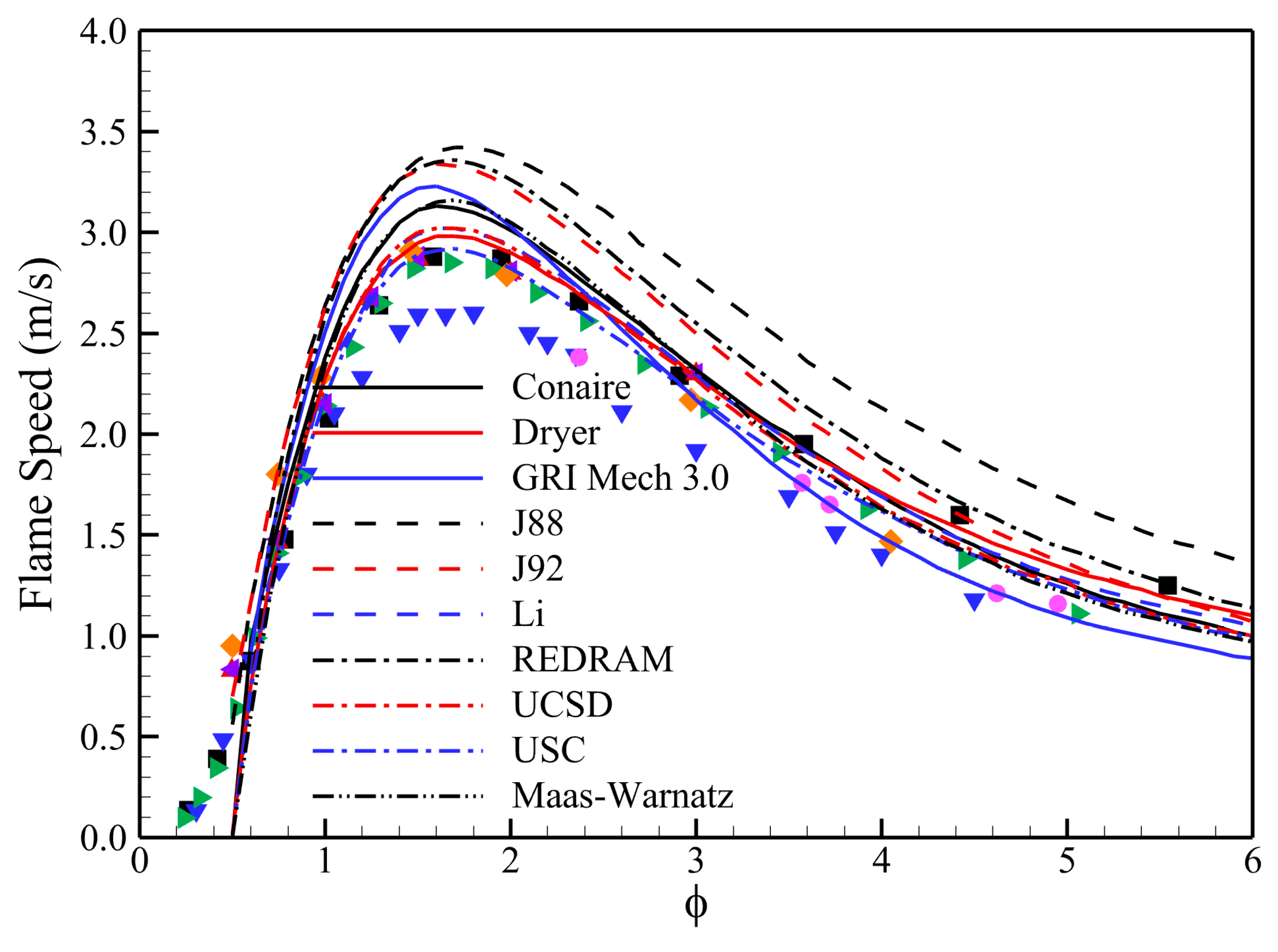
3.2. Comparison of Ignition Delay Time and Laminar Flame Speed
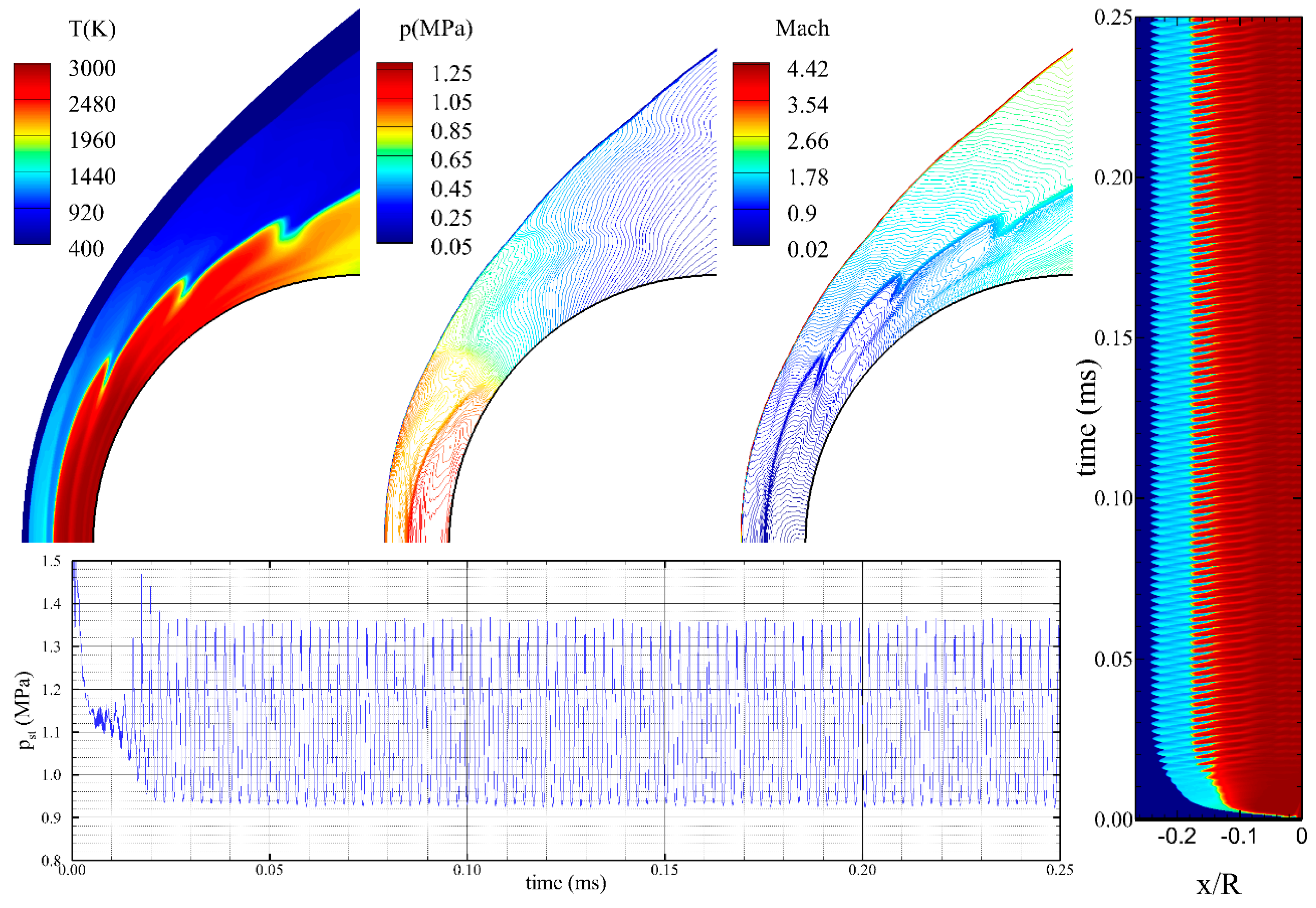
3.3. Comparison of the Mechanisms for SIC Flow Field
4. DMD Analysis of the Shock-Induced Combustion Instability
4.1. Description of Modal Decomposition Analysis
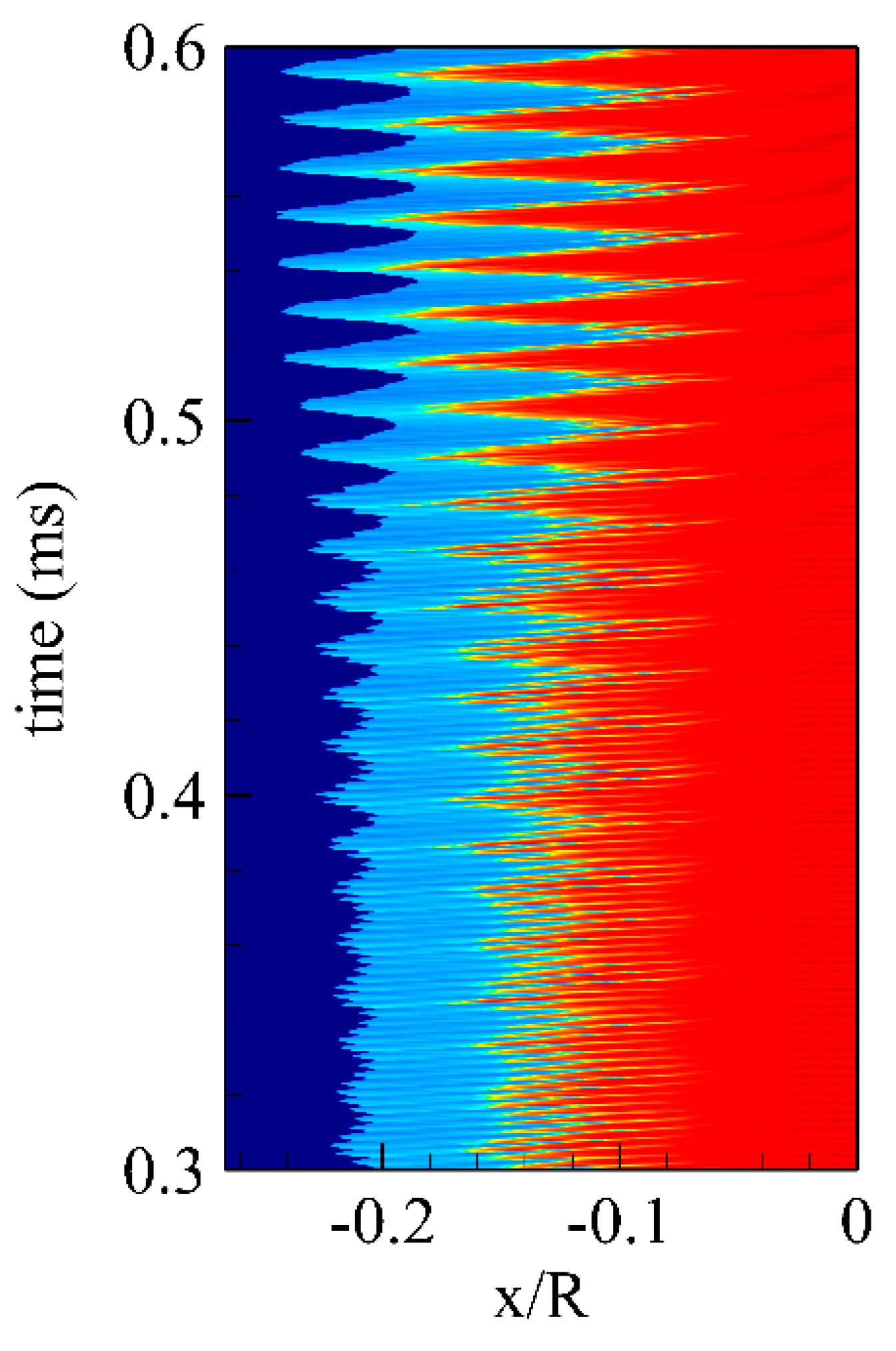
4.2. Time-Sequencing of the Snapshots
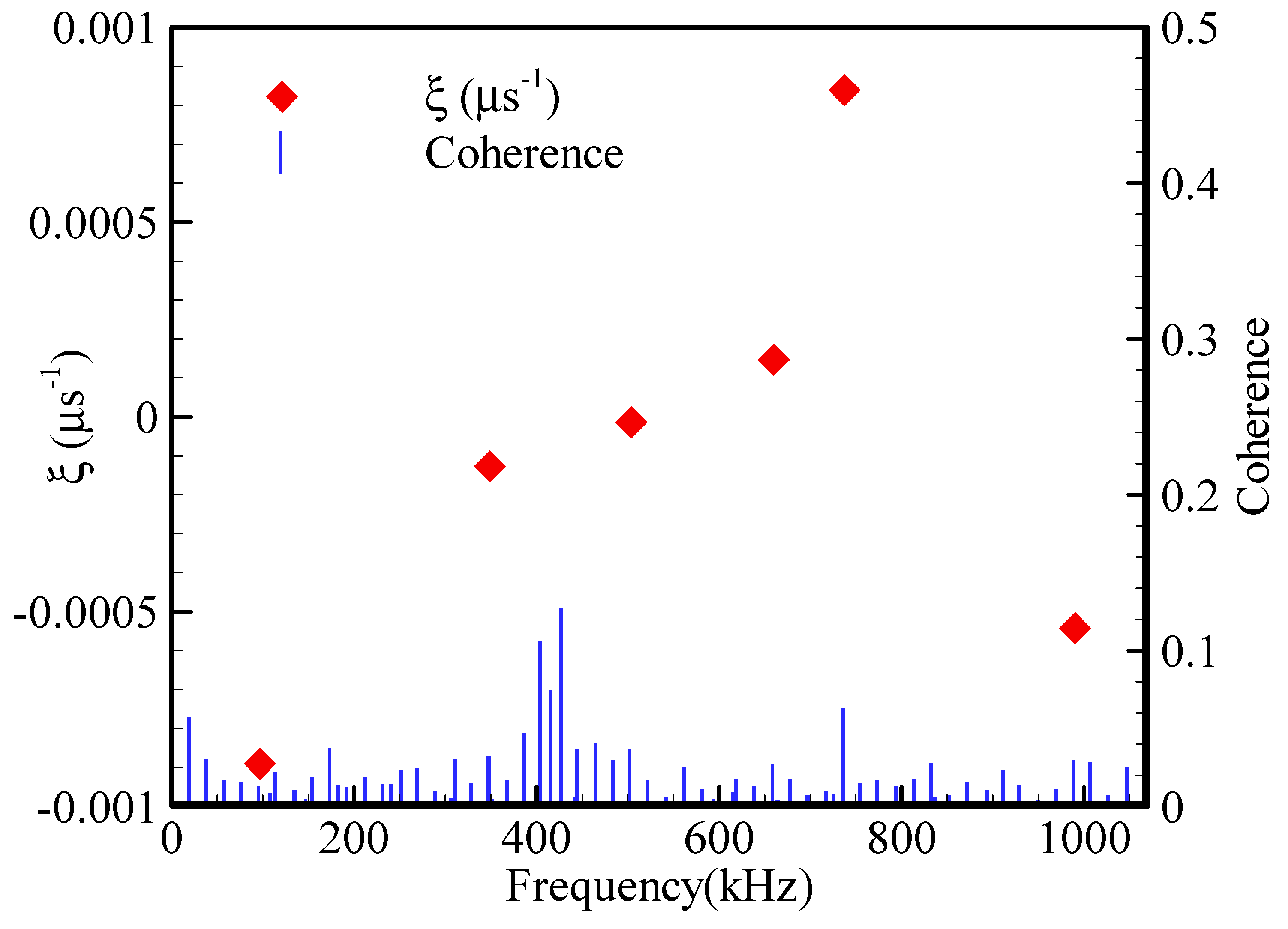
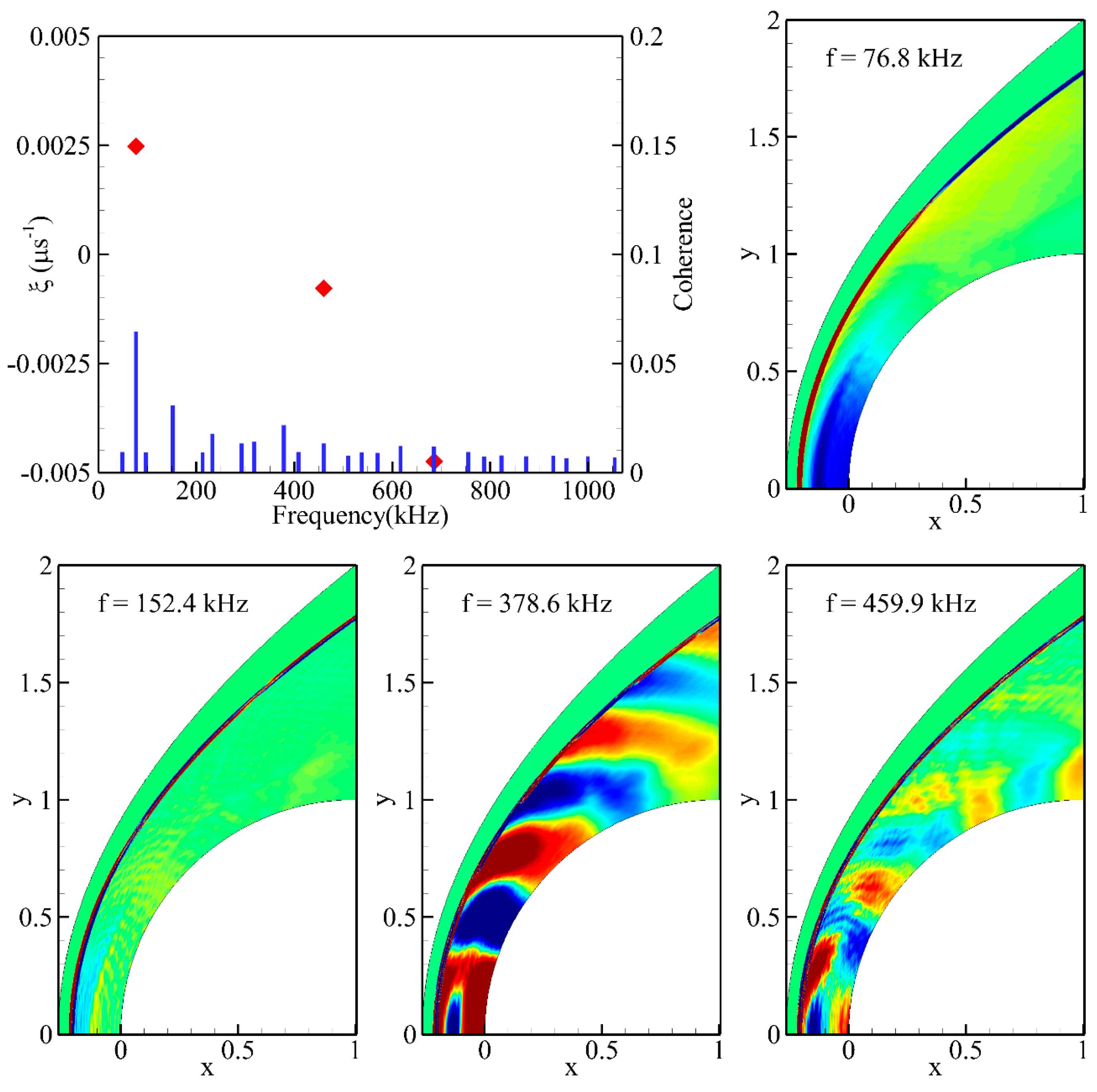
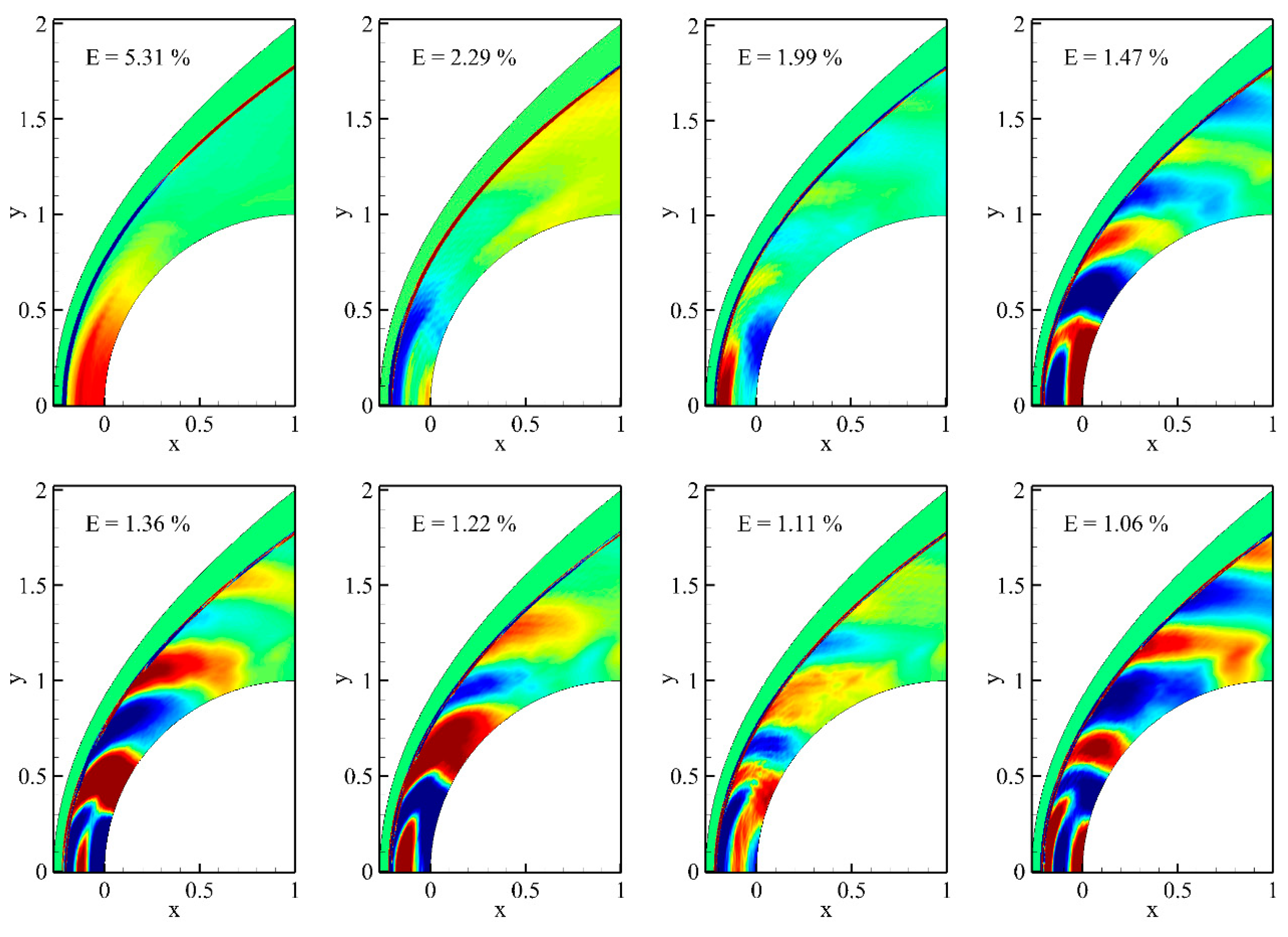
4.3. Ranking of the Modes
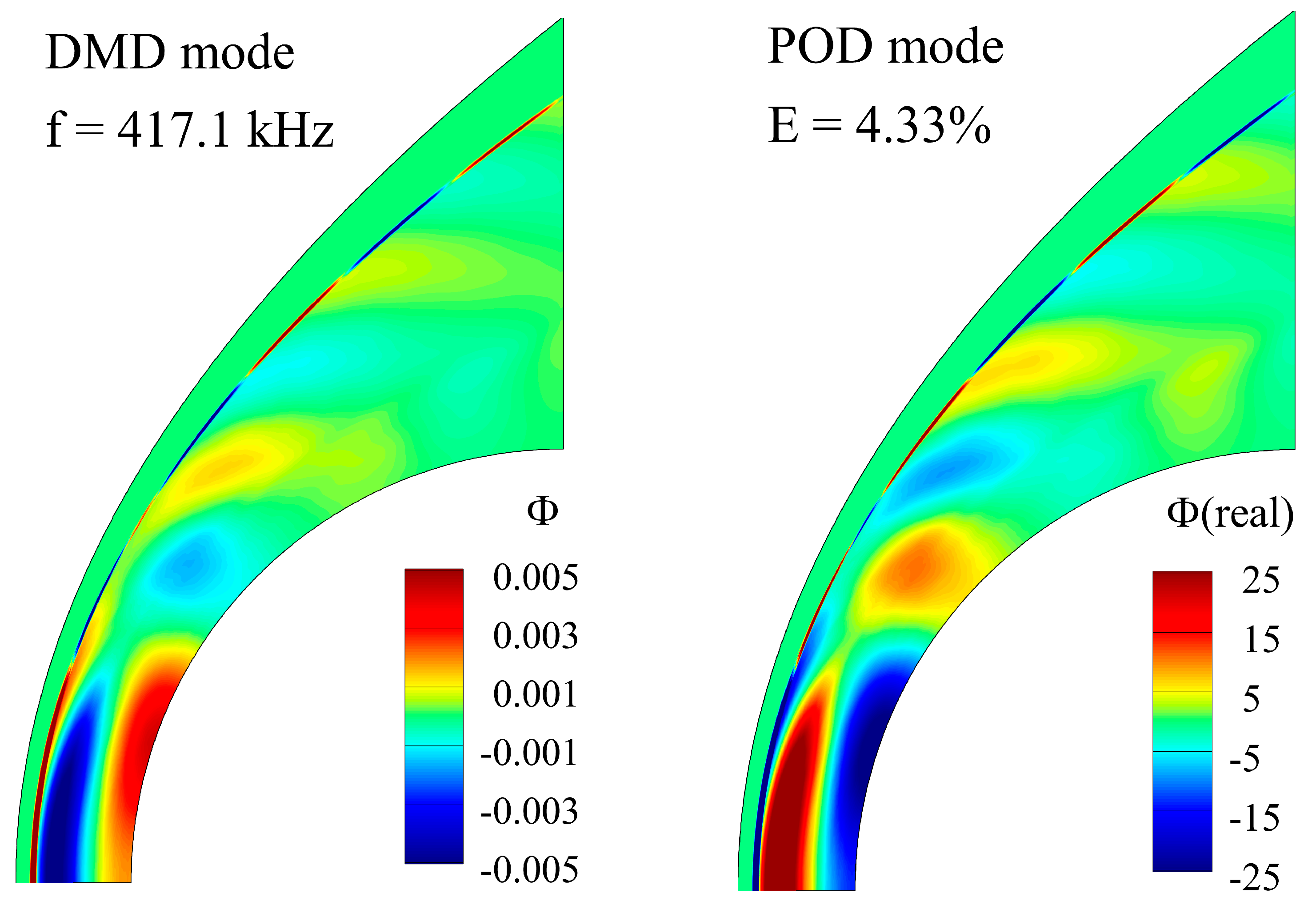
4.4. Modal Decomposition of the Flow Field with Regular Oscillation
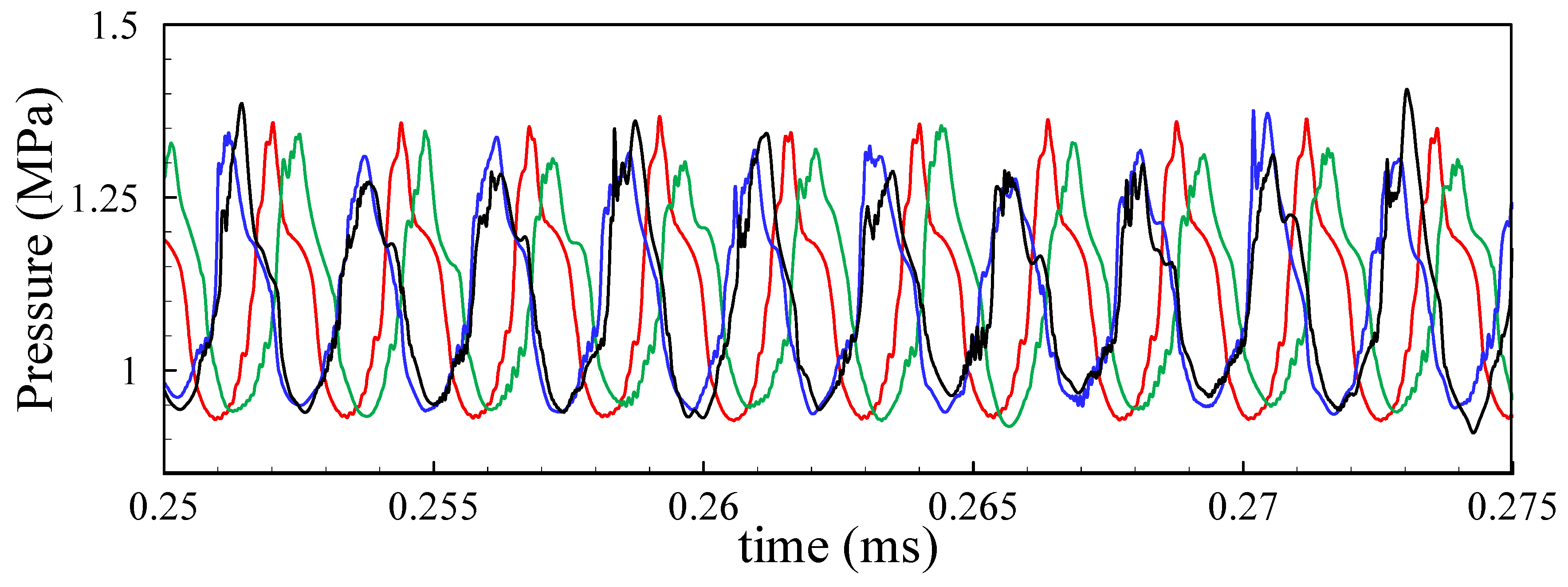
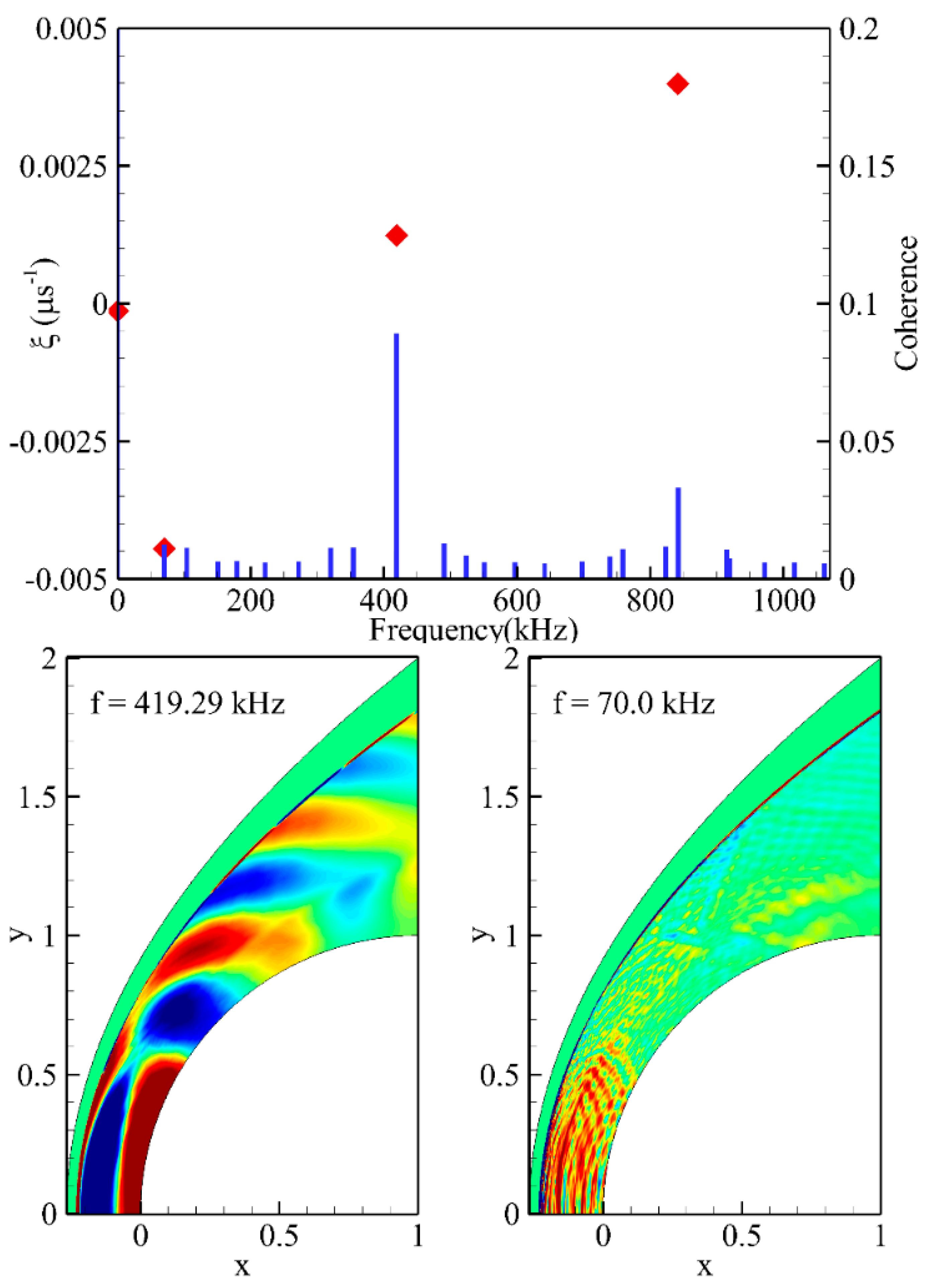
4.5. Modal Decomposition of the Flow Field with Instability Phenomena
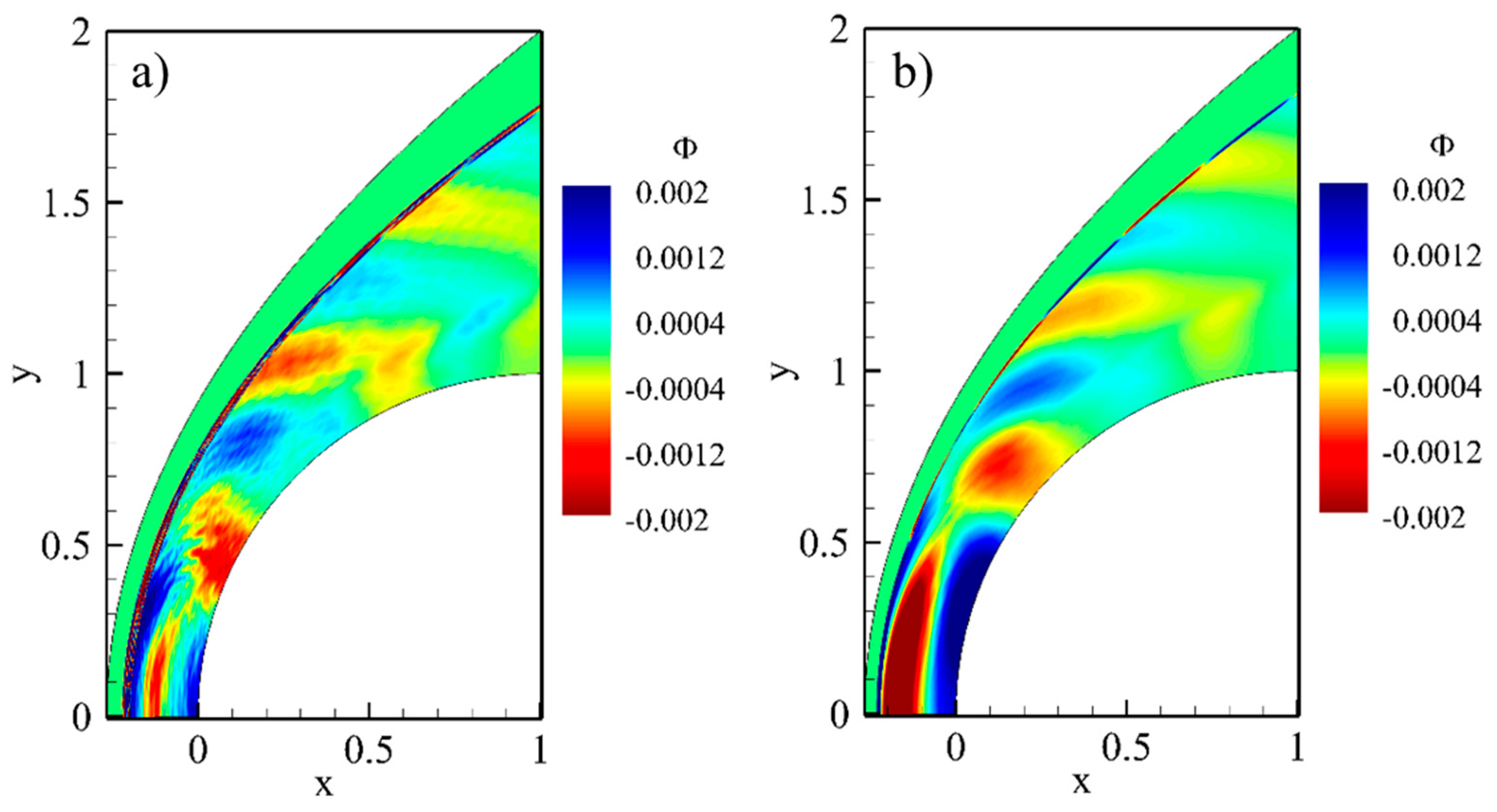
4.6. Coherent Structure of the Experimental Modes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruegg, F.W.; Dorsey, W.W. A missile technique for the study of detonation waves. J. Res. Natl. Bur. Stand. C 1962, 66, 51–58. [Google Scholar] [CrossRef]
- Behrens, H.; Struth, W.; Wecken, F. Studies of hypervelocity firings into mixtures of hydrogen with air or with oxygen. Symp. Combust. 1965, 10, 245–252. [Google Scholar] [CrossRef]
- Chernyi, G. Supersonic flow past bodies with formation of detonation and combustion fronts. Acta Astronaut. 1968, 13, 467–480. [Google Scholar]
- McVey, J.B. Mechanism of Instabilities of Exothermic Hypersonic Blunt-Body Flows. Combust. Sci. Technol. 1971, 3, 63–76. [Google Scholar] [CrossRef]
- Alpert, R.L.; Toong, T.Y. Periodicity in exothermic hypersonic flows about blunt projectiles. Acta Astronaut. 1972, 17, 539–560. [Google Scholar]
- Toong, T.Y. Instabilities in reacting flows. Acta Astronaut. 1974, 1, 317–344. [Google Scholar] [CrossRef]
- Lehr, H.F. Experiments on Shock-Induced Combustion. Acta Astronaut. 1972, 17, 589–597. [Google Scholar]
- Kailasanath, K. Review of propulsion applications of detonation waves. AIAA J. 2000, 38, 1698–1708. [Google Scholar] [CrossRef]
- Nejaamtheen, M.N.; Kim, J.-M.; Choi, J.-Y. Review on the research progresses in rotating detonation engine. In Detonation Control for Propulsion: Pulse Detonation and Rotating Detonation Engines; Springer: Berlin/Heidelberg, Germany, 2018; pp. 109–159. [Google Scholar]
- Anand, V.; Gutmark, E. Rotating detonation combustors and their similarities to rocket instabilities. Prog. Energy Combust. Sci. 2019, 73, 182–234. [Google Scholar] [CrossRef]
- Yungster, S.; Eberhardt, S.; Bruckner, A.P. Numerical simulation of hypervelocity projectiles in detonable gases. AIAA J. 1991, 29, 187–199. [Google Scholar] [CrossRef]
- Yungster, S.; Radhakrishnan, K. A fully implicit time accurate method for hypersonic combustion: Application to shock-induced combustion instability. Shock Waves 1996, 5, 293–303. [Google Scholar] [CrossRef]
- Wilson, G.J.; Sussman, M.A. Computation of unsteady shock-induced combustion using logarithmic species conservation equations. AIAA J. 1993, 31, 294–301. [Google Scholar] [CrossRef]
- Matsuo, A.; Fujiwara, T. Numerical investigation of oscillatory instability in shock-induced combustion around a blunt body. AIAA J. 1993, 31, 1835–1841. [Google Scholar] [CrossRef]
- Matsuo, A.; Fujii, K. Computational study of large-disturbance oscillations in unsteady supersonic combustion around projectiles. AIAA J. 1995, 33, 1828–1835. [Google Scholar] [CrossRef]
- Matsuo, A.; Fujii, K.; Fujiwara, T. Flow features of shock-induced combustion around projectile traveling at hypervelocities. AIAA J. 1995, 33, 1056–1063. [Google Scholar] [CrossRef]
- Choi, J.-Y.; Jeung, I.-S.; Yoon, Y. Computational fluid dynamics algorithms for unsteady shock-induced combustion, part 1: Validation. AIAA J. 2000, 38, 1179–1187. [Google Scholar] [CrossRef]
- Choi, J.-Y.; Jeung, I.-S.; Yoon, Y. Computational fluid dynamics algorithms for unsteady shock-induced combustion, part 2: Comparison. AIAA J. 2000, 38, 1188–1195. [Google Scholar] [CrossRef]
- Jachimowski, C.J. Analytical Study of the Hydrogen-Air Reaction Mechanism with Application to Scramjet Combustion; NASA Technical Paper No. 2791; NASA: Washington, DC, USA, 1988. [Google Scholar]
- Jachimowski, C.J. An Analysis of Combustion Studies in Shock Expansion Tunnels and Reflected Shock Tunnels; NASA Technical Paper No. 3224; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Clutter, J.K.; Mikolaitis, D.W.; Shyy, W. Reaction mechanism requirements in shock-induced combustion simulations. Proc. Combust. Inst. 2000, 28, 663–669. [Google Scholar] [CrossRef]
- Pavalavanni, P.K.; Kim, K.-S.; Oh, S.; Choi, J.-Y. Numerical comparison of hydrogen-air reaction mechanisms for unsteady shock-induced combustion applications. J. Mech. Sci. Technol. 2015, 29, 893–898. [Google Scholar]
- Olm, C.; Zsély, I.G.; Pálvölgyi, R.; Varga, T.; Nagy, T.; Curran, H.J.; Turányi, T. Comparison of the performance of several recent hydrogen combustion mechanisms. Combust. Flame 2014, 161, 2219–2234. [Google Scholar] [CrossRef]
- Ströhle, J.; Myhrvold, T. An evaluation of detailed reaction mechanisms for hydrogen combustion under gas turbine conditions. Int. J. Hydrog. Energy 2007, 32, 125–135. [Google Scholar] [CrossRef]
- GRI-Mech 3.0. Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html (accessed on 27 December 2022).
- Maas, U.; Warnatz, J. Ignition processes in hydrogen-oxygen mixtures. Combust. Flame 1988, 74, 53–69. [Google Scholar] [CrossRef]
- Conaire, M.Ó.; Curran, H.J.; Simmie, J.M.; Pitz, W.J.; Westbrook, C.K. A comprehensive modeling study of hydrogen oxidation. Int. J. Chem. Kinet. 2004, 37, 603–622. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Kazakov, A.; Dryer, F.L. An updated comprehensive kinetic model of hydrogen combustion. Int. J. Chem. Kinet. 2004, 36, 566–575. [Google Scholar] [CrossRef]
- Petersen, E.L.; Hanson, R.K. Reduced Kinetics Mechanisms for Ram Accelerator Combustion. J. Propuls. Power 1999, 15, 591–600. [Google Scholar] [CrossRef]
- Burke, M.P.; Chaos, M.; Ju, Y.; Dryer, F.L.; Klippenstein, S.J. Comprehensive H2/O2 kinetic model for high-pressure combustion. Int. J. Chem. Kinet. 2012, 44, 444–474. [Google Scholar] [CrossRef]
- USC Mech Version II. High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds. Available online: http://ignis.usc.edu/USC_Mech_II.htm (accessed on 27 December 2022).
- Williams, F.A.; Seshadri, K.; Cattolica, R. Chemical-Kinetic Mechanisms for Combustion Applications. Available online: http://combustion.ucsd.edu (accessed on 27 December 2022).
- MECHMOD v. 1.4: Program for the Transformation of Kinetic Mechanisms. Available online: http://www.chem.leeds.ac.uk/Combustion/Combustion.html (accessed on 27 December 2022).
- RESPECTH. Available online: http://respecth.chem.elte.hu/respecth/index.php (accessed on 27 December 2022).
- Kao, S.; Shepherd, J. Numerical solution methods for control volume explosions and ZND detonation structure. GALCIT Rep. 2006, 7, 1–46. [Google Scholar]
- Kéromnès, A.; Metcalfe, W.K.; Heufer, K.A.; Donohoe, N.; Das, A.K.; Sung, C.-J.; Herzler, J.; Naumann, C.; Griebel, P.; Mathieu, O.; et al. An experimental and detailed chemical kinetic modeling study of hydrogen and syngas mixture oxidation at elevated pressures. Combust. Flame 2013, 160, 995–1011. [Google Scholar] [CrossRef]
- JovanoviĆ, M.R.; Bamieh, B. Componentwise energy amplification in channel flows. J. Fluid Mech. 2005, 534, 145–183. [Google Scholar] [CrossRef]
- Schmid, P.J. Nonmodal Stability Theory. Annu. Rev. Fluid Mech. 2006, 39, 129–162. [Google Scholar] [CrossRef]
- Bagheri, S. Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 2013, 726, 596–623. [Google Scholar] [CrossRef]
- Jeong, S.-M.; Choi, J.-Y. Combined Diagnostic Analysis of Dynamic Combustion Characteristics in a Scramjet Engine. Energies 2020, 13, 4029. [Google Scholar] [CrossRef]
- Quinlan, J.M. Investigation of Driving Mechanisms of Combustion Instabilities in Liquid Rocket Engines Via the Dynamic Mode Decomposition. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 10 August 2015. [Google Scholar]
- Hwang, W.-S.; Sung, B.-K.; Han, W.; Huh, K.Y.; Lee, B.J.; Han, H.S.; Sohn, C.H.; Choi, J.-Y. Real-Gas-Flamelet-Model-Based Numerical Simulation and Combustion Instability Analysis of a GH2/LOX Rocket Combustor with Multiple Injectors. Energies 2021, 14, 419. [Google Scholar] [CrossRef]
- Richecoeur, F.; Hakim, L.; Renaud, A.; Zimmer, L. DMD algorithms for experimental data processing in combustion. In Proceedings of the CTR Summer Program, Los Angeles, CA, USA, 14 December 2012. [Google Scholar]
- Torregrosa, A.J.; Broatch, A.; García-Tíscar, J.; Gomez-Soriano, J. Modal decomposition of the unsteady flow field in compression-ignited combustion chambers. Combust. Flame 2018, 188, 469–482. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Pavalavanni, P.K.; Sohn, C.H.; Lee, B.J.; Choi, J.-Y. Revisiting unsteady shock-induced combustion with modern analysis techniques. Proc. Combust. Inst. 2019, 37, 3637–3644. [Google Scholar] [CrossRef]

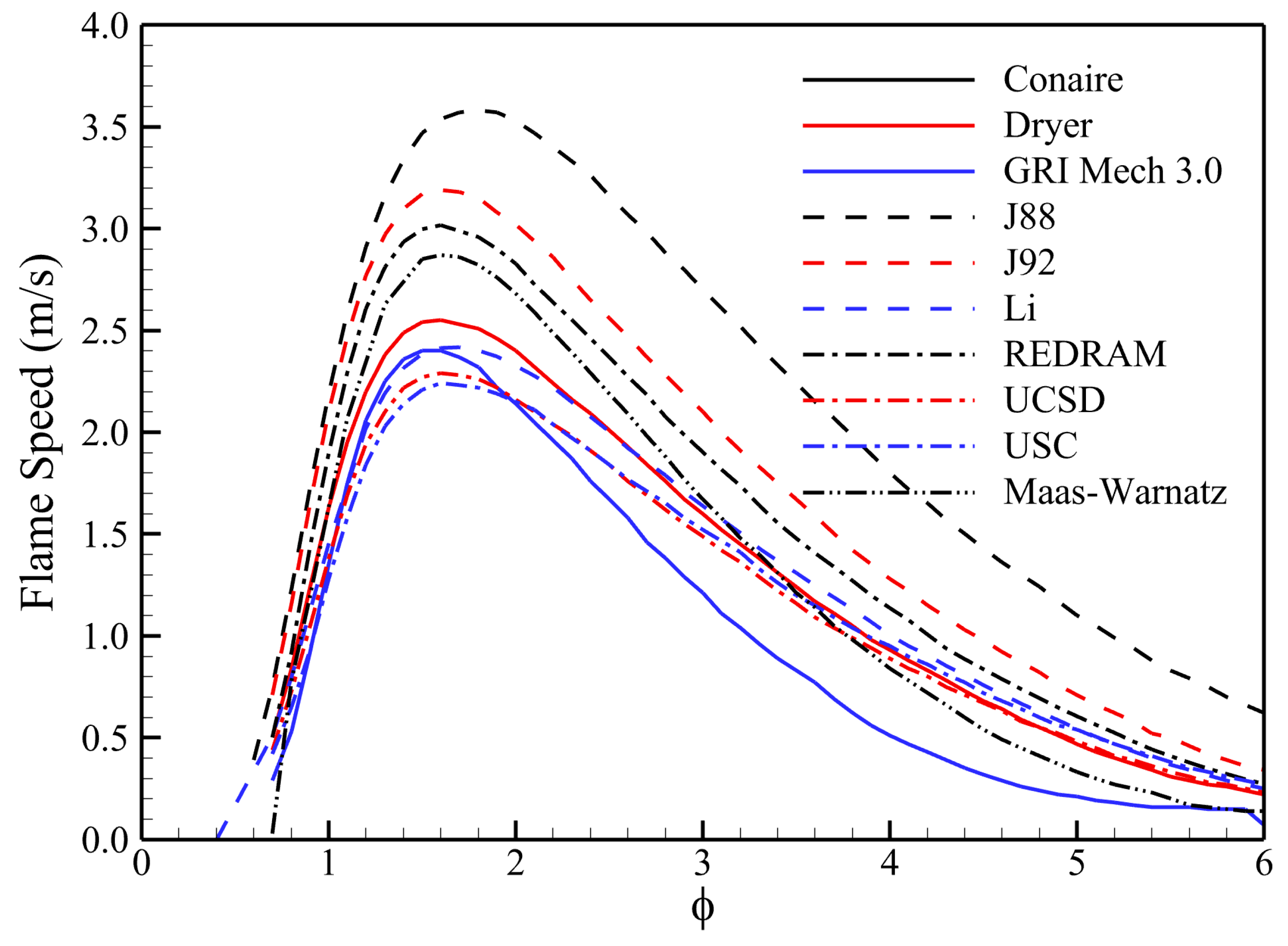

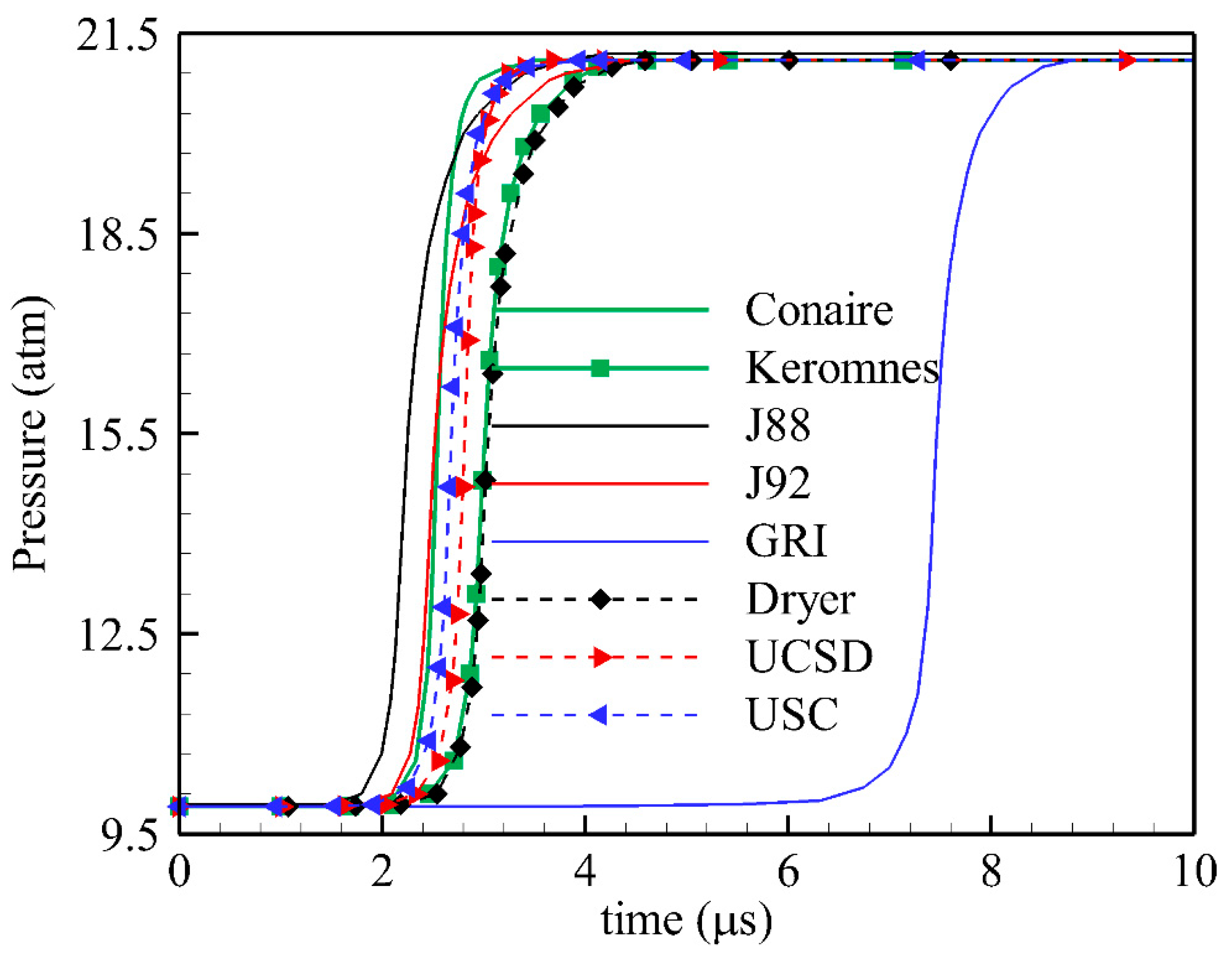

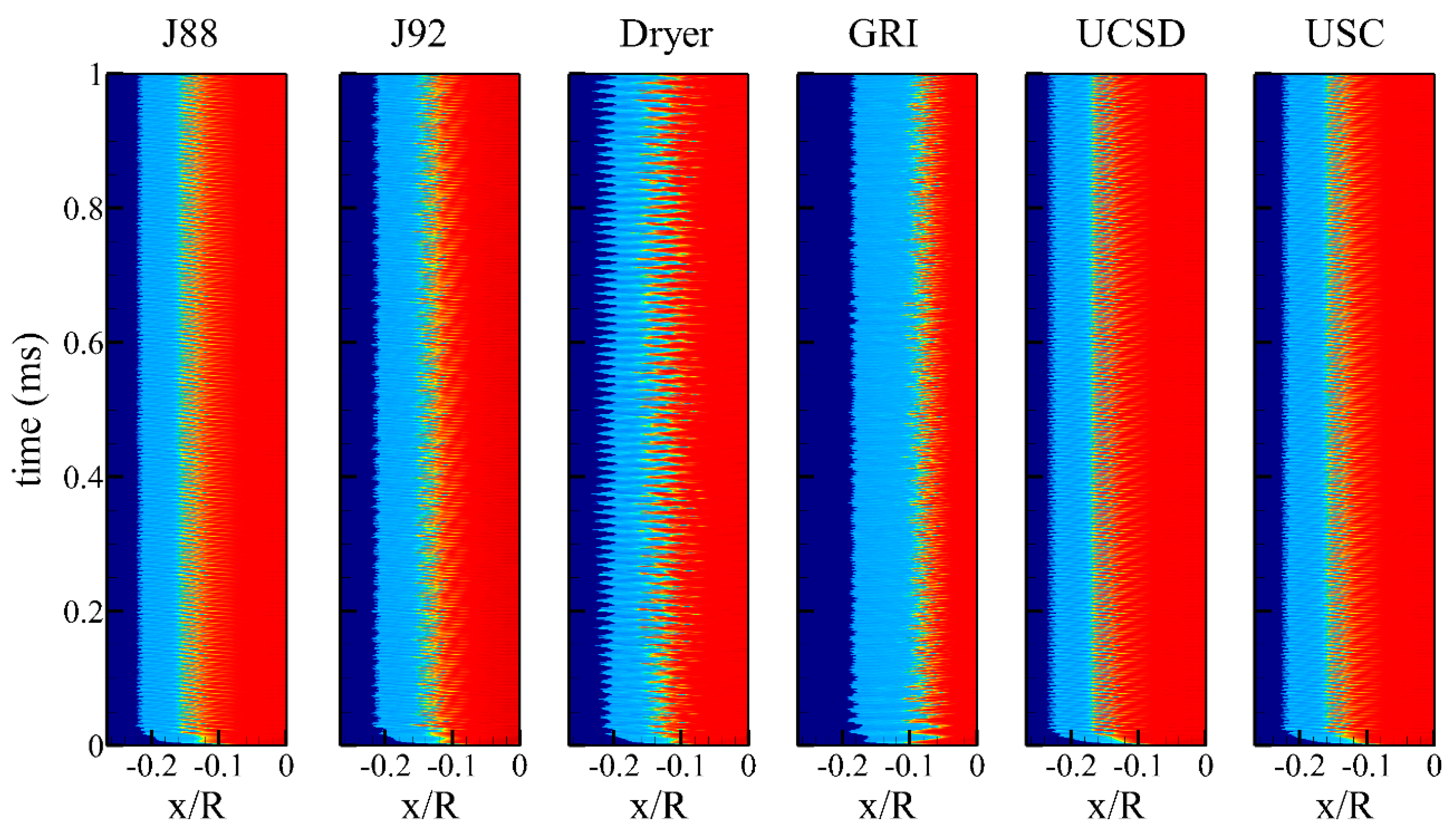
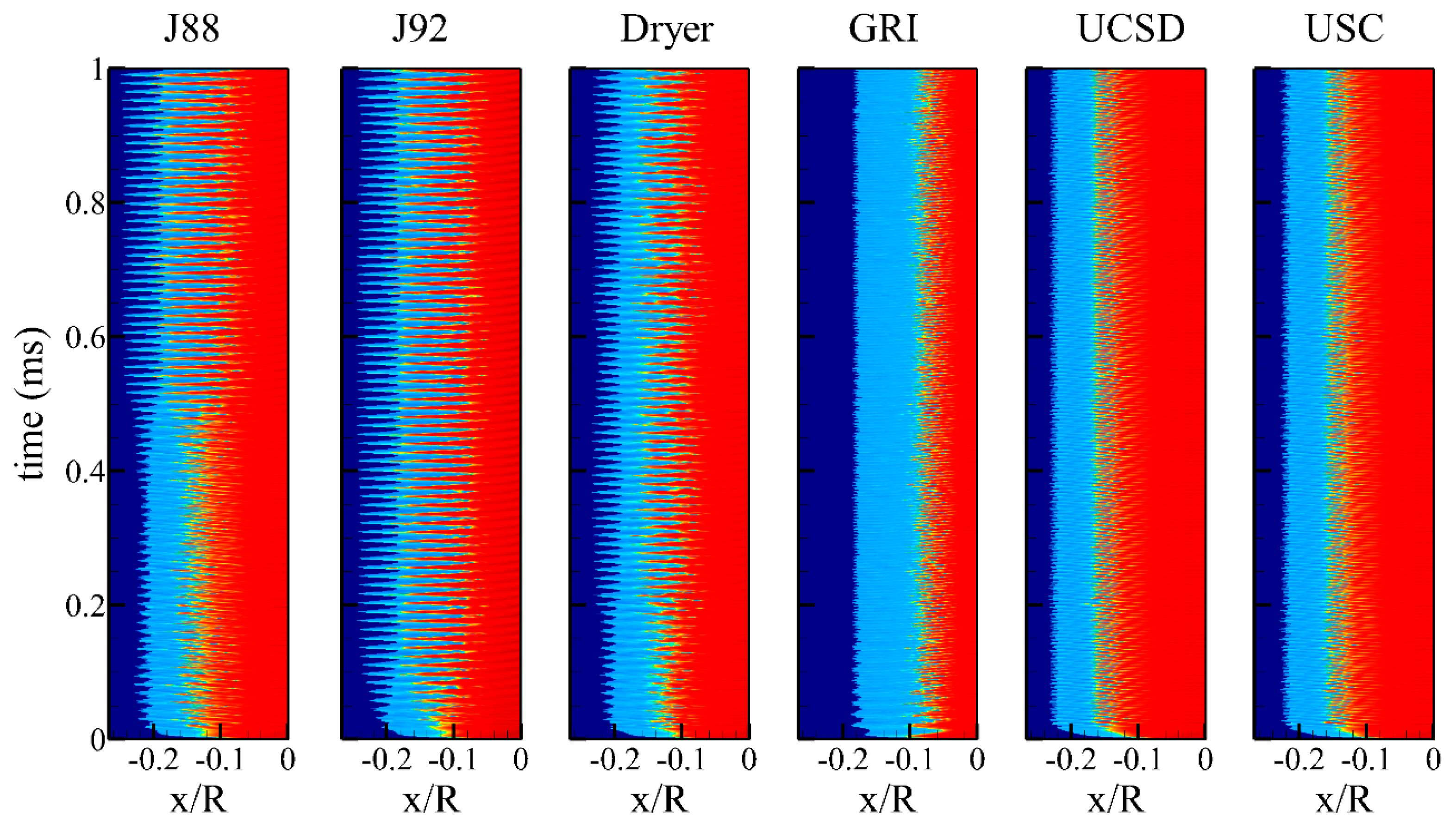


| Reaction Mechanism | Ignition Delay (μs) |
|---|---|
| Conaire | 2.537 |
| Kéromnès | 2.983 |
| Jachimowski 88 | 2.194 |
| Jachimowski 92 | 2.466 |
| GRI Mech 3.0 | 7.444 |
| Dryer | 3.005 |
| UCSD | 2.811 |
| USC | 2.676 |
| Reaction Mechanism | 150 × 200 | 200 × 300 | 300 × 450 | 400 × 600 |
|---|---|---|---|---|
| Jachimowski (1988) | 430.2 | 444.6 | 428.1 | 75.0/330.0 |
| Jachimowski (1992) | 408.4/41.0 | 416.7 | 76.2/513 | 72.2/360.0 |
| Dryer | 397.2 | 80.0/413.8 | 79.0/351 | 74.9/335.0 |
| GRI Mech 3.0 | 226.0 | 230.35 | 220.5 | 208.5 |
| UCSD | 416.5 | 431.3 | 415.4 | 409.4 |
| USC | 416.7 | 427.0 | 411.1 | 398.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavalavanni, P.K.; Jo, M.-S.; Kim, J.-E.; Choi, J.-Y. Numerical Study of Unstable Shock-Induced Combustion with Different Chemical Kinetics and Investigation of the Instability Using Modal Decomposition Technique. Aerospace 2023, 10, 292. https://doi.org/10.3390/aerospace10030292
Pavalavanni PK, Jo M-S, Kim J-E, Choi J-Y. Numerical Study of Unstable Shock-Induced Combustion with Different Chemical Kinetics and Investigation of the Instability Using Modal Decomposition Technique. Aerospace. 2023; 10(3):292. https://doi.org/10.3390/aerospace10030292
Chicago/Turabian StylePavalavanni, Pradeep Kumar, Min-Seon Jo, Jae-Eun Kim, and Jeong-Yeol Choi. 2023. "Numerical Study of Unstable Shock-Induced Combustion with Different Chemical Kinetics and Investigation of the Instability Using Modal Decomposition Technique" Aerospace 10, no. 3: 292. https://doi.org/10.3390/aerospace10030292
APA StylePavalavanni, P. K., Jo, M.-S., Kim, J.-E., & Choi, J.-Y. (2023). Numerical Study of Unstable Shock-Induced Combustion with Different Chemical Kinetics and Investigation of the Instability Using Modal Decomposition Technique. Aerospace, 10(3), 292. https://doi.org/10.3390/aerospace10030292







