Experimental and Numerical Studies on the Effect of Airflow Separation Suppression on Aerodynamic Performance of a Ducted Coaxial Propeller in Hovering
Abstract
1. Introduction
2. Methods
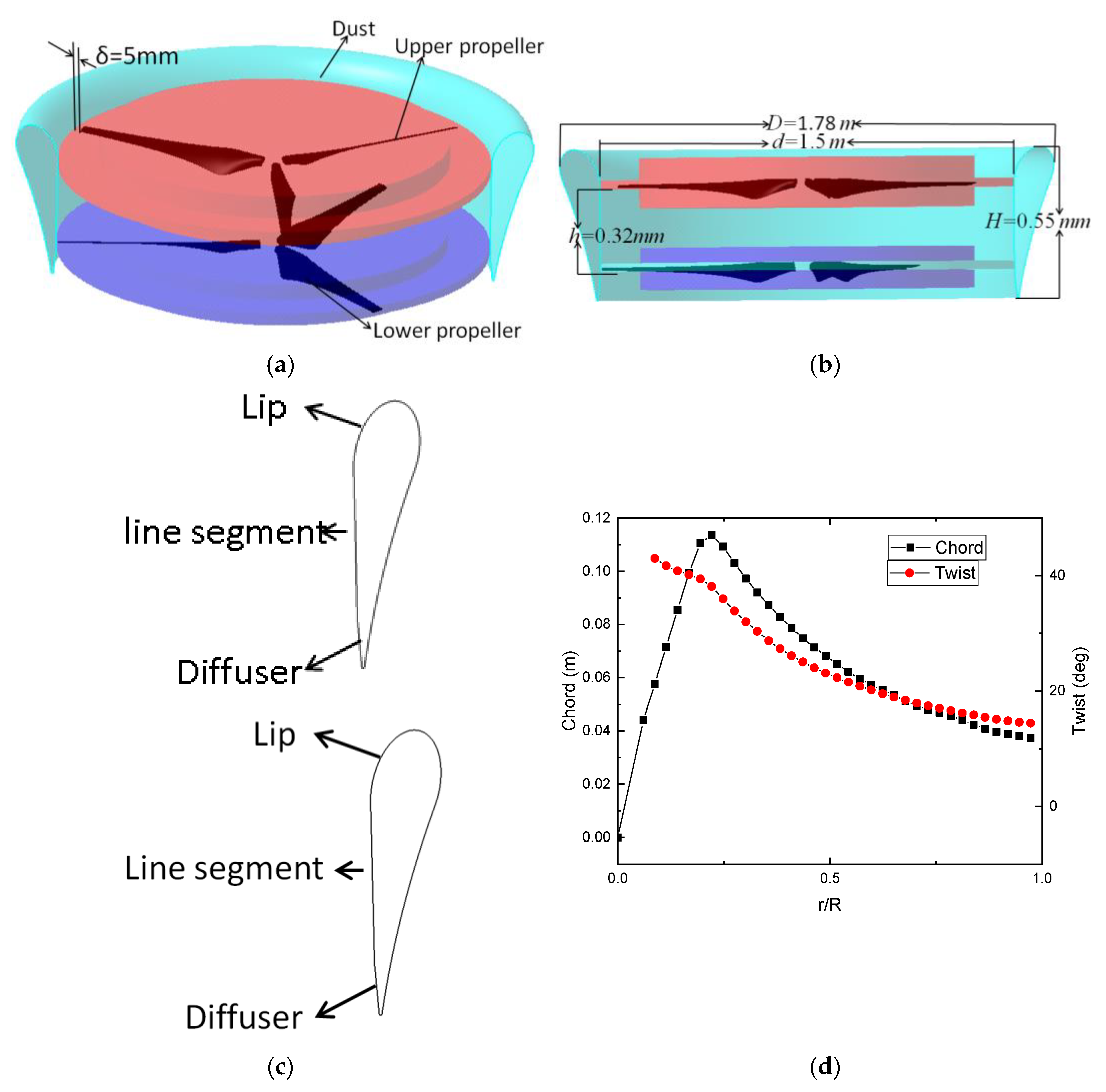
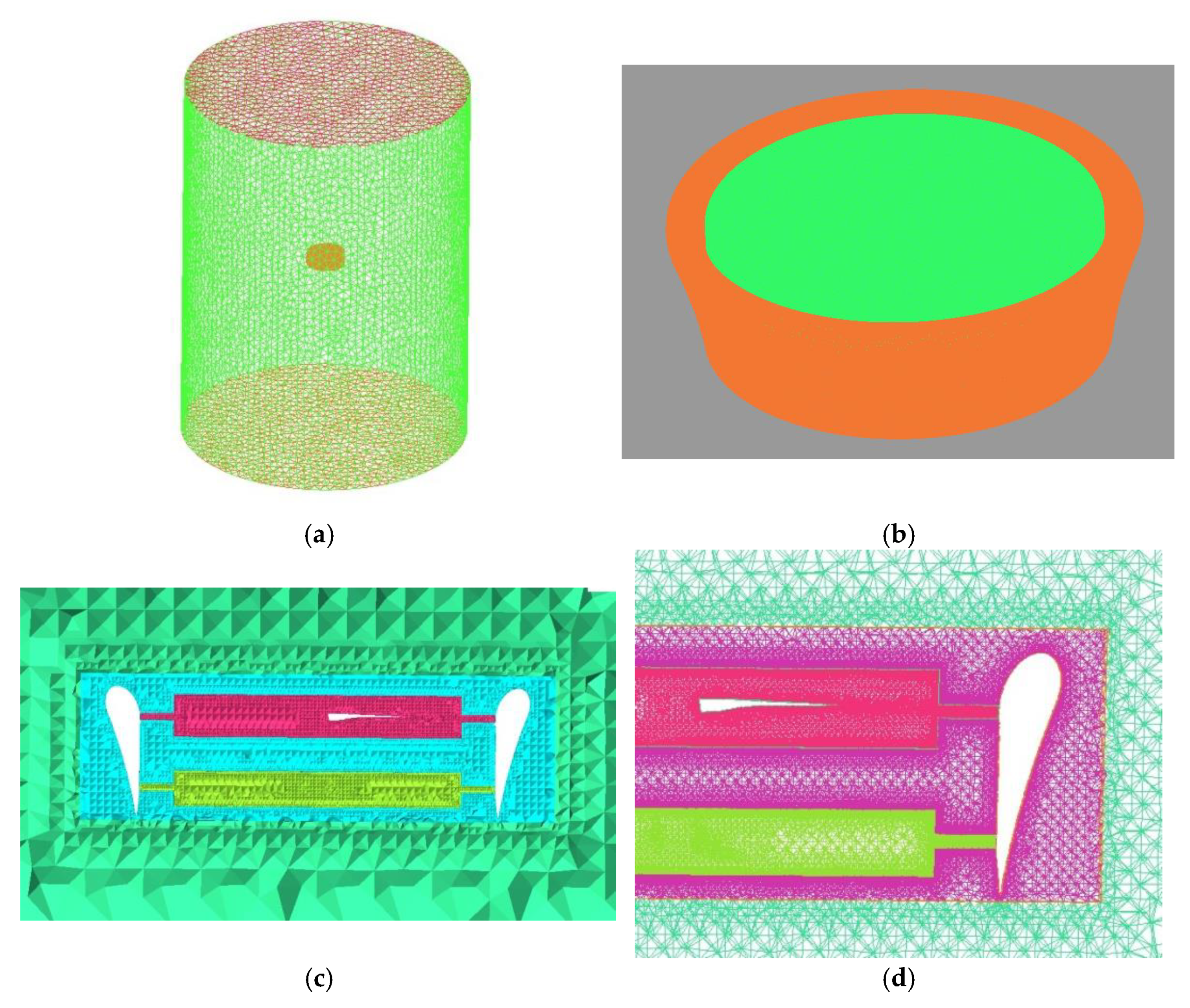
2.1. System Description
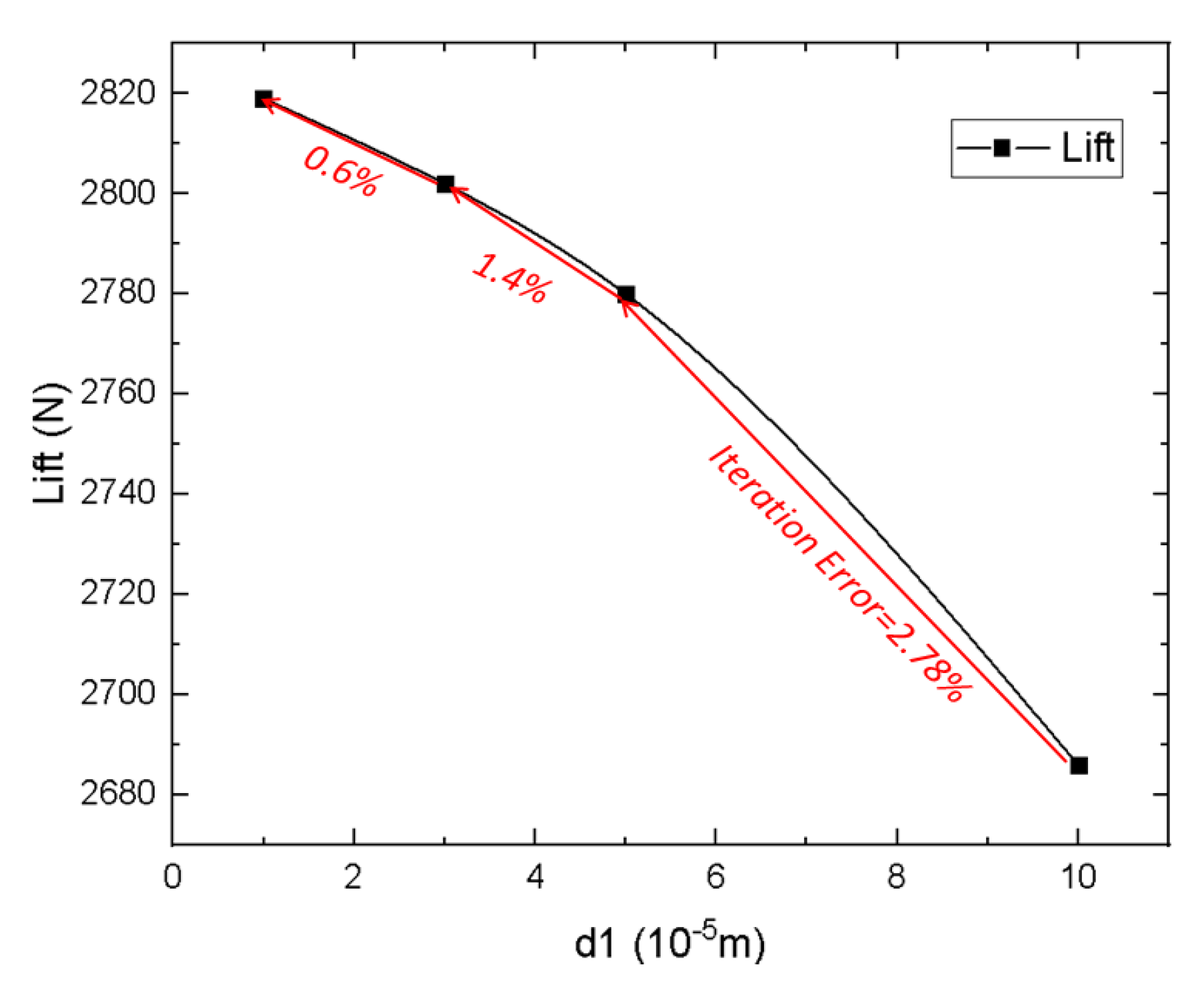
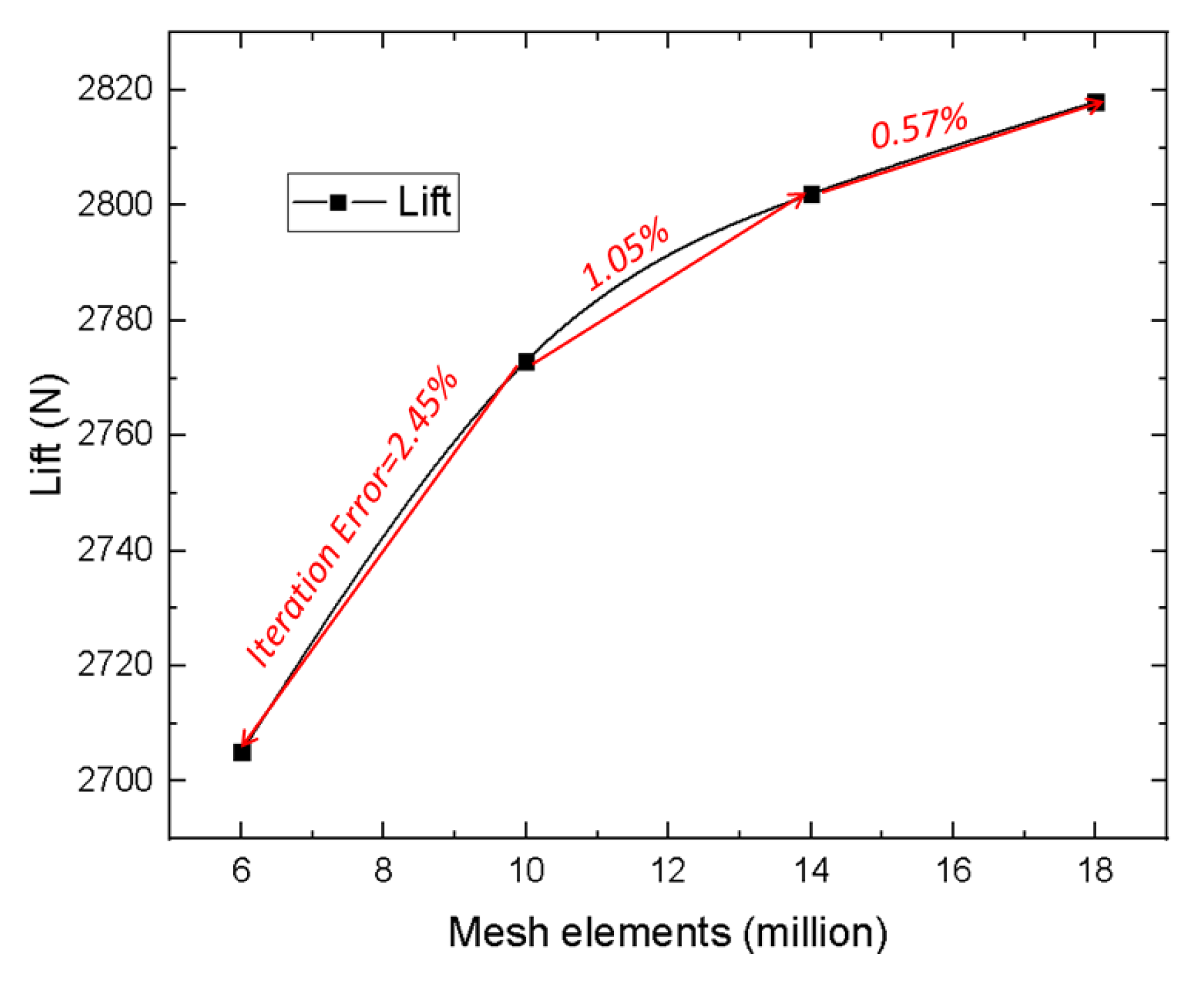
2.2. Grid Refinement
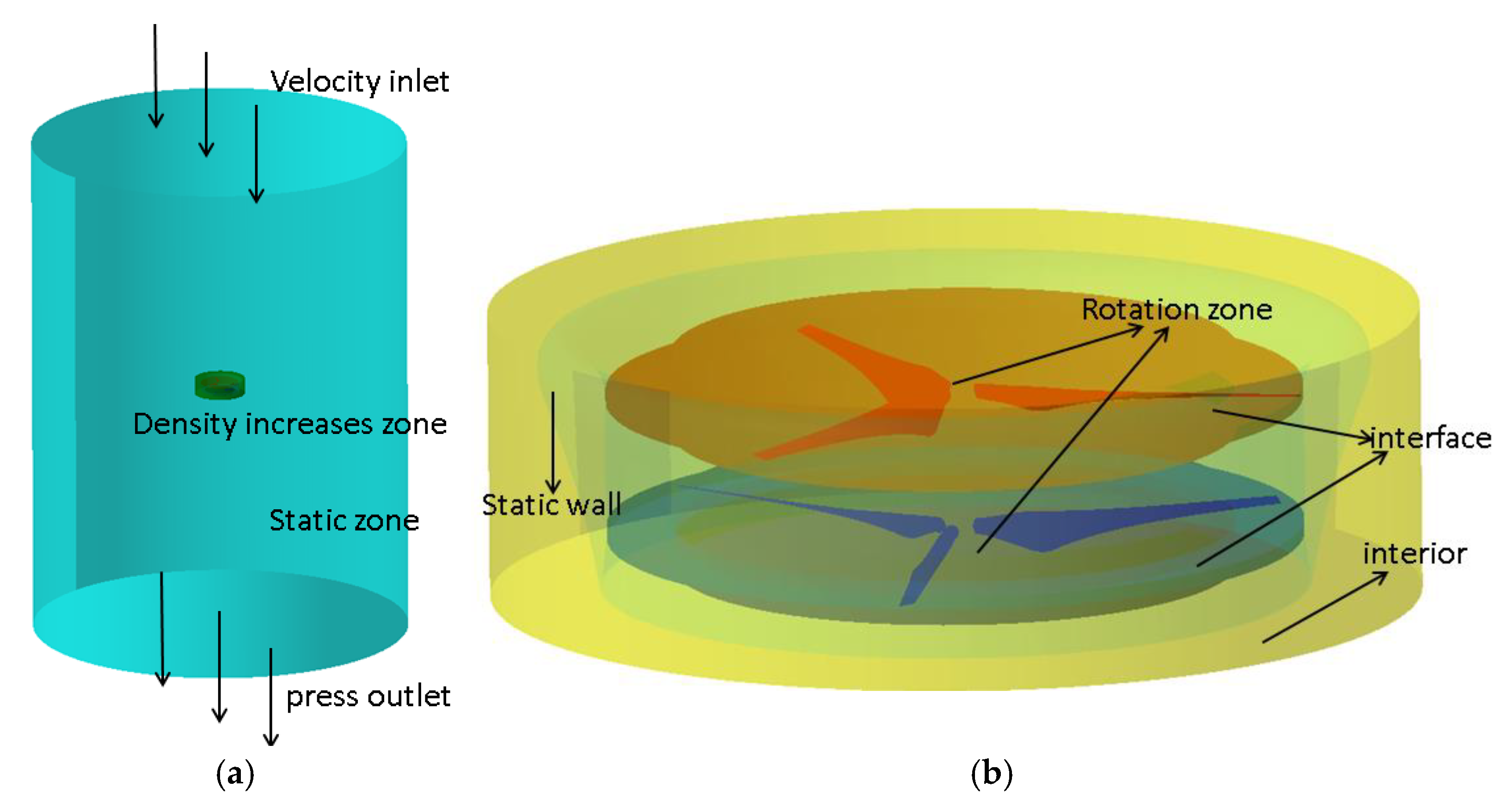
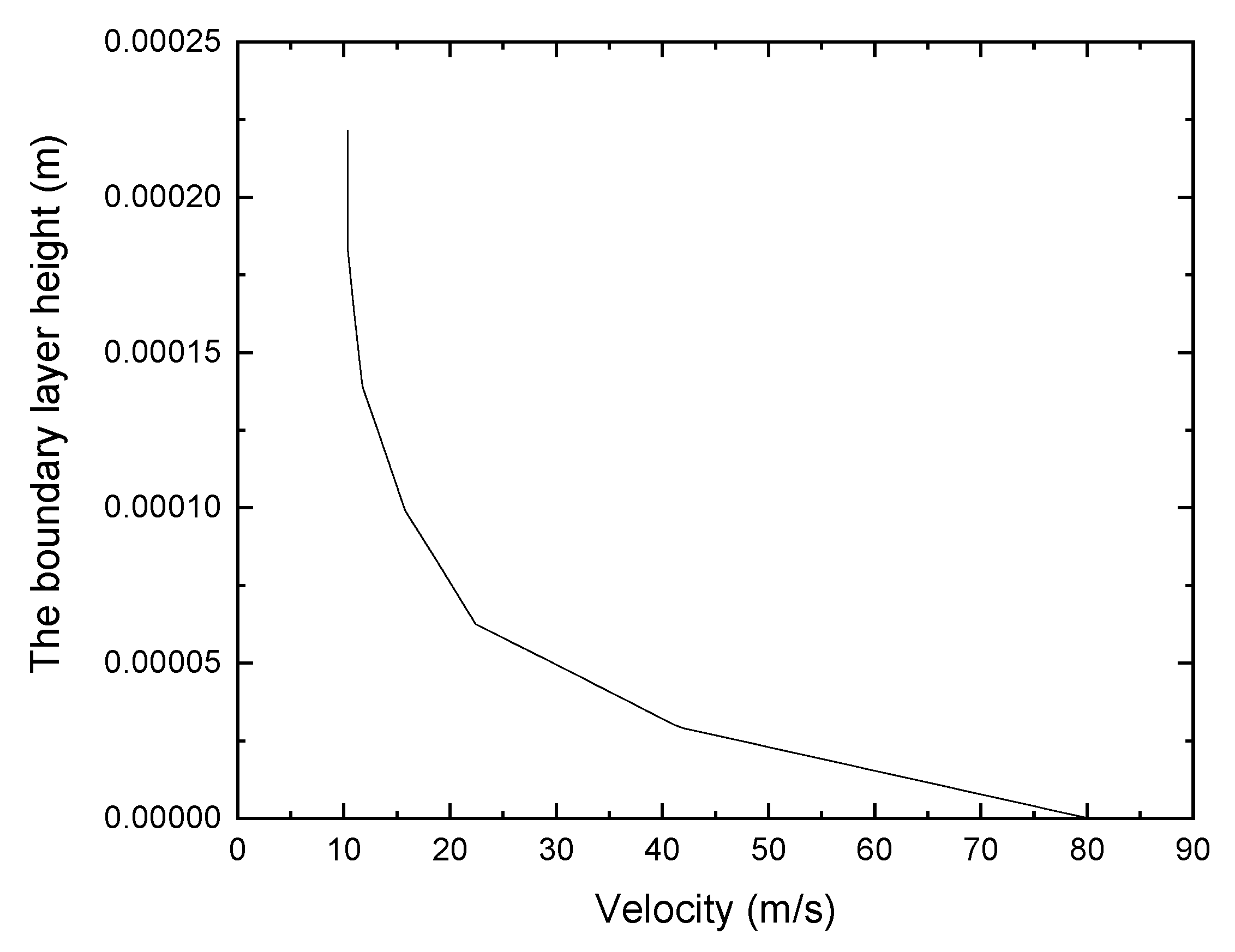
2.3. Numerical Methods
3. Experiment and Validation
3.1. Experiment Setup
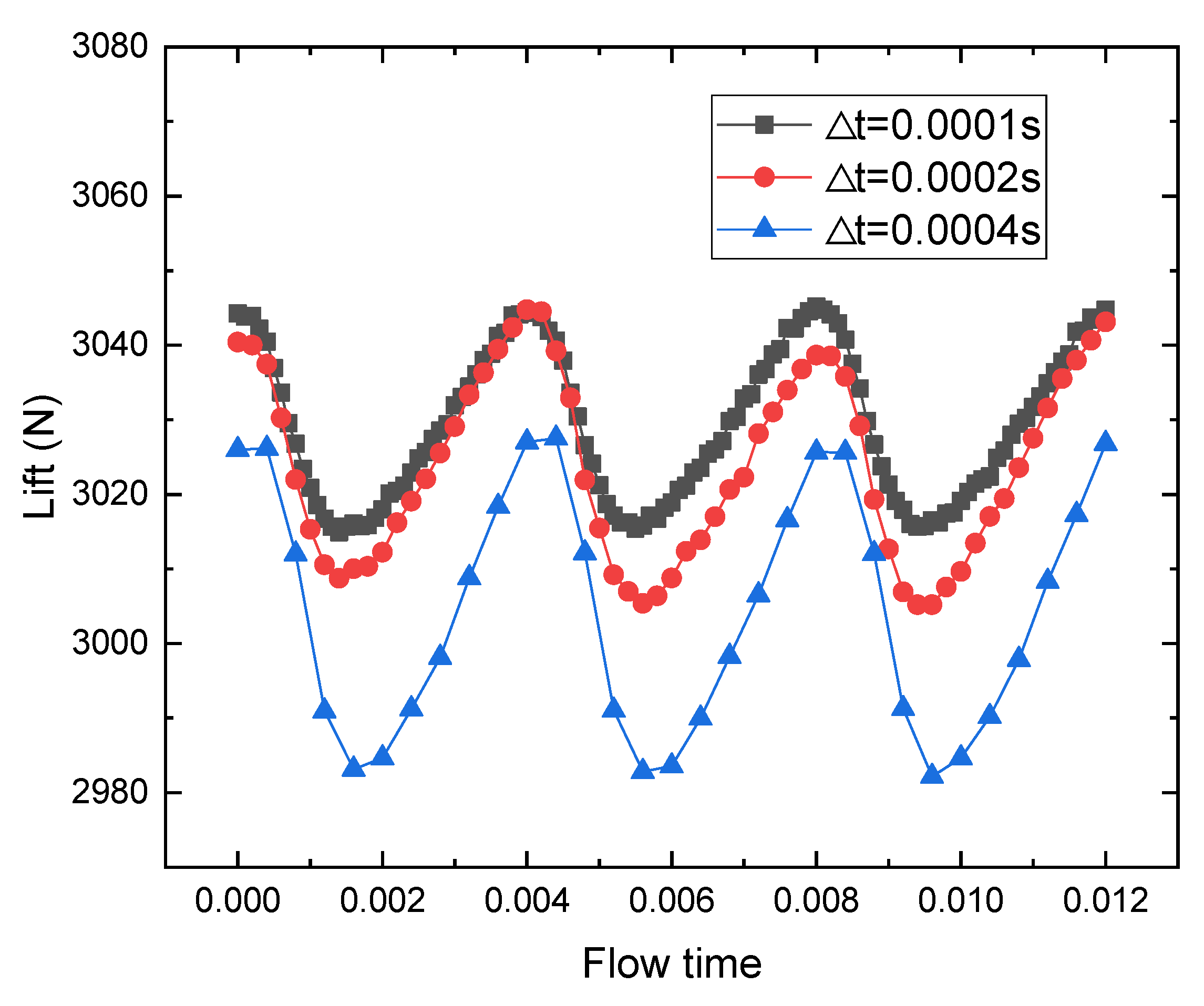
3.2. Time-Step Sensitivity Test
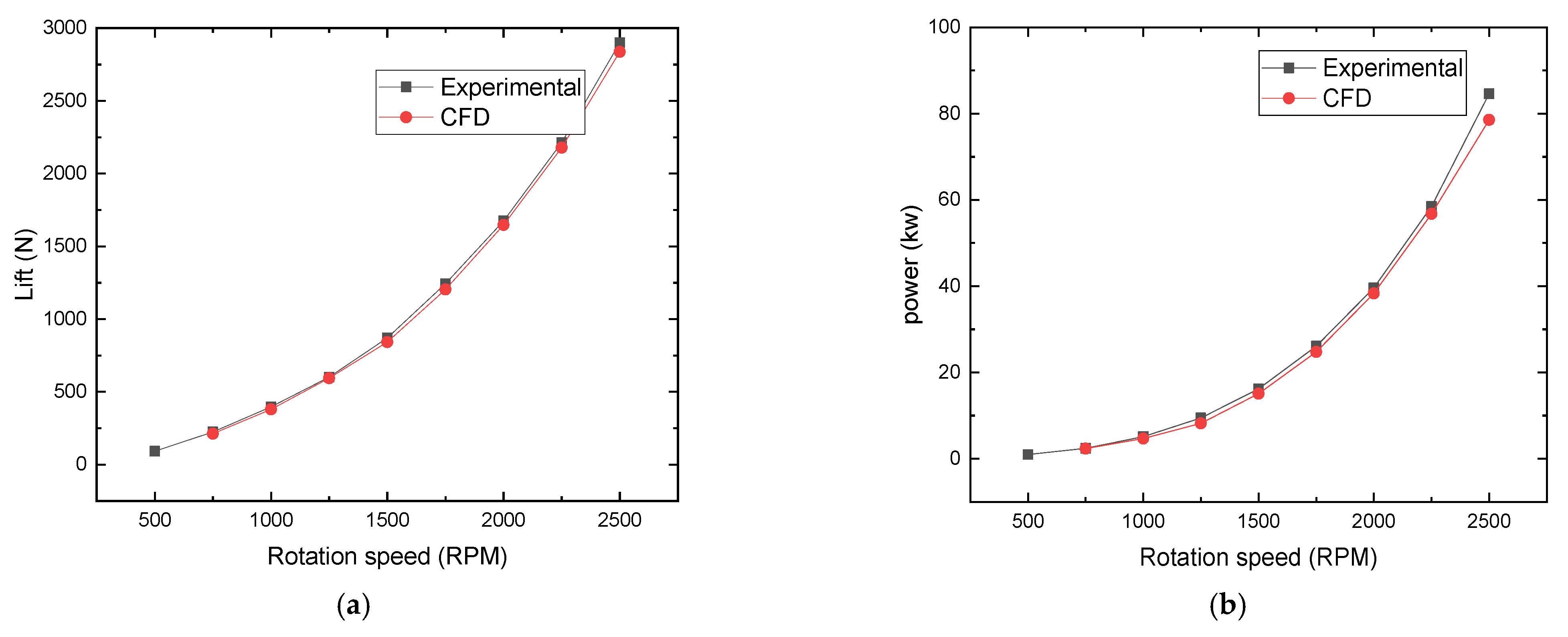
3.3. Method Validation
4. Analysis and Discussion on Airflow Separation of DCP
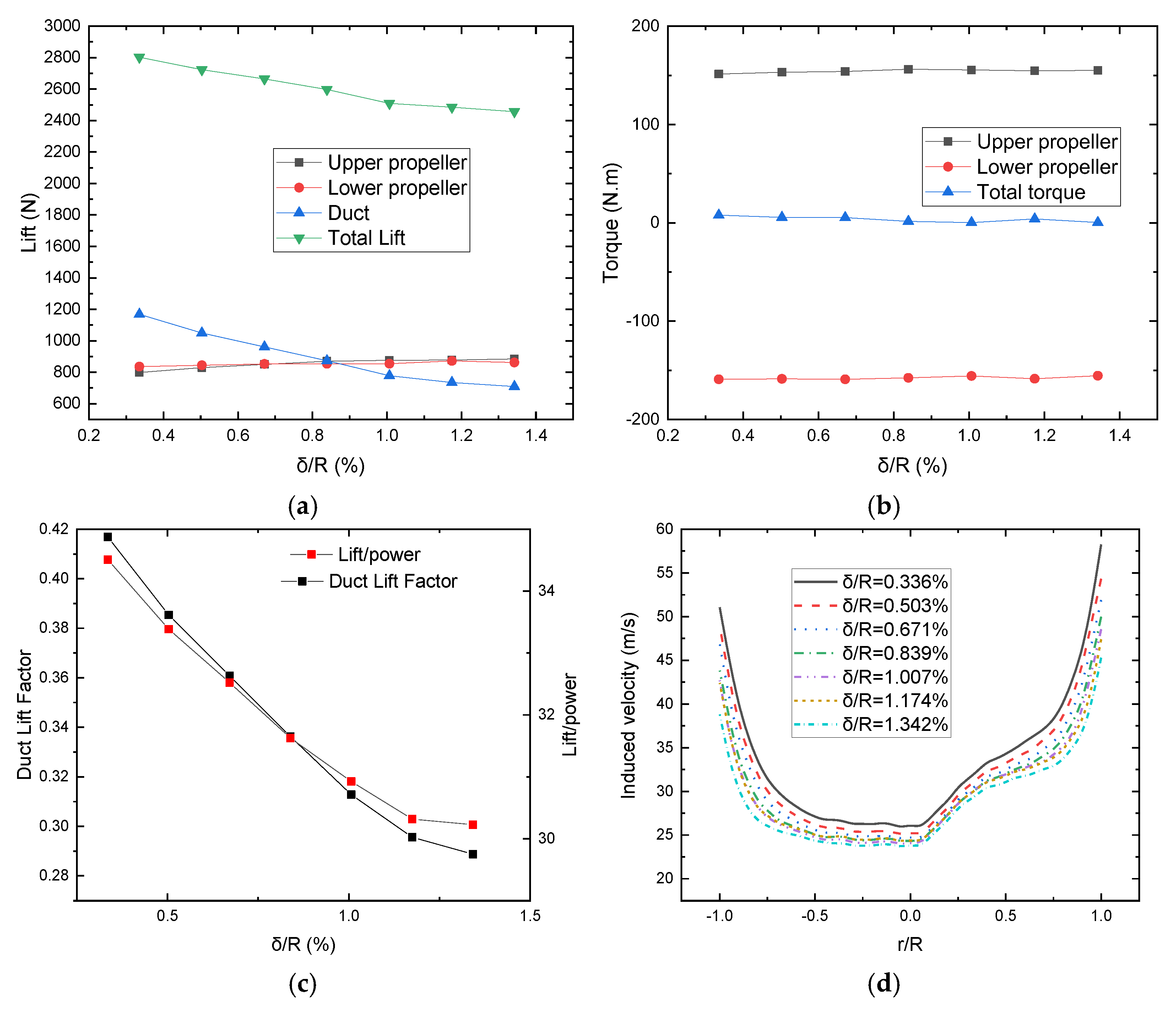
4.1. Influence of Tip Clearance on Aerodynamic Characteristics
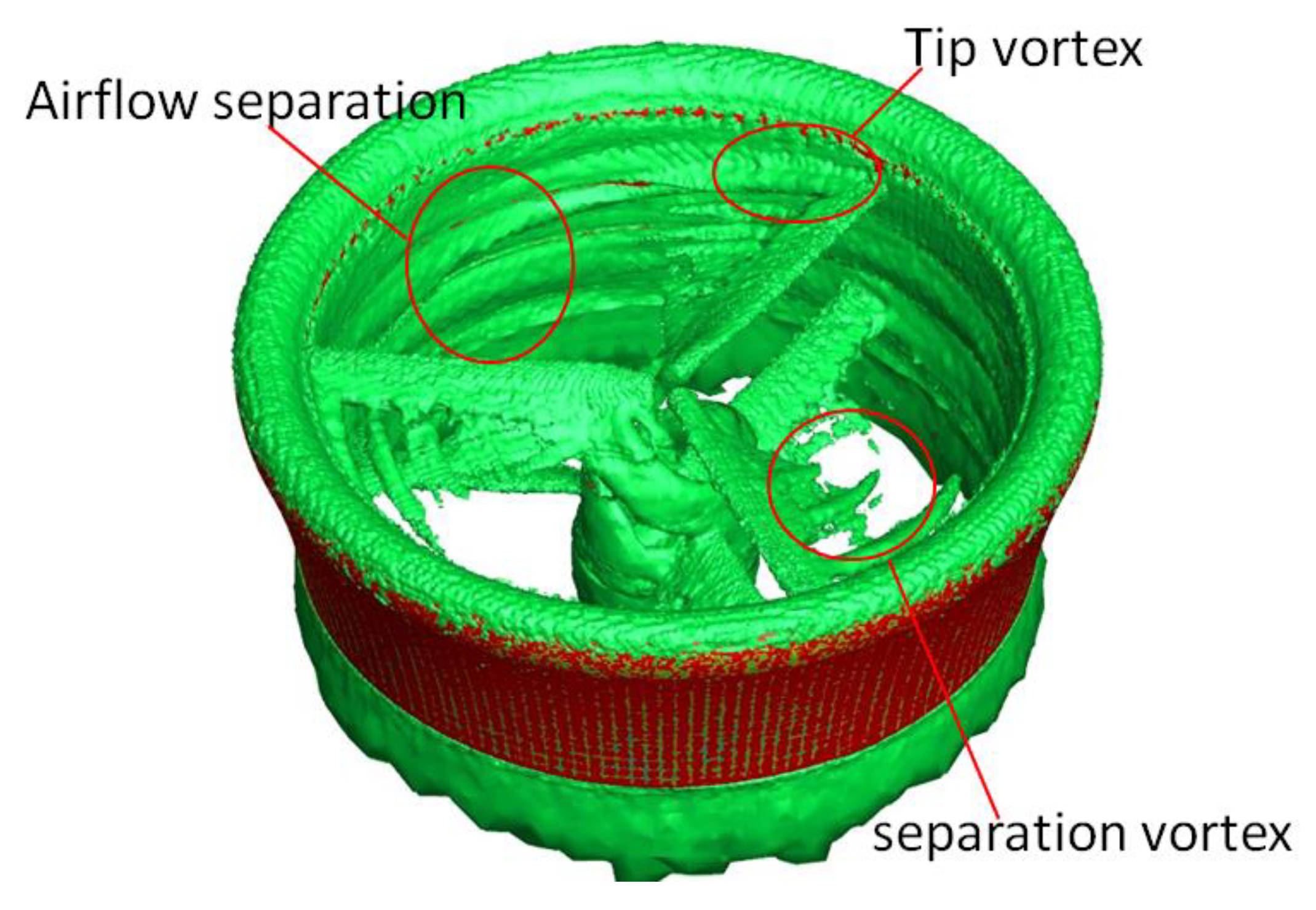
4.2. Phenomenon and Mechanisms of Airflow Separation
4.3. Suppression of DCP Airflow Separation
5. Conclusions
- (1)
- The effect of tip clearance on the aerodynamic performance of the DCP is relatively significant. When the tip clearance ratio increases from 0.336% to 1.342%, the total lift and aerodynamic efficiency both decrease by about 11.3%. The effects mainly lie in the formation of the tip vortex, airflow separation in the straight section, and diffusion section of the inner wall of the duct. Firstly, the tip vortex and airflow separation increase energy dissipation; secondly, the vortex blocks the inner wall of the duct, reduces the effective inner diameter, and decreases the airflow through the duct; finally, the role of the duct is weakened, and the wake is contracted, which increases the induced velocity and thus the induced power loss.
- (2)
- The mechanism of airflow separation in the straight section and the diffusion outlet of the duct: when the tip vortex in the duct moves downward along the inner wall with the axial airflow, airflow separation occurs, induced by the viscous effect of the duct wall and the contraction of the wake together, which blocks the inner wall area of the duct, reducing the effective inner diameter and lowering the airflow through the duct. As for the diffusion port below the lower propeller, airflow separation is more likely to occur due to flow expansion and the reverse pressure gradient at the port, resulting in air backflow, which directly leads to airflow separation at the duct diffusion port. Therefore, airflow separation is more likely to occur in the diffusion port than in the straight section for the DCP.
- (3)
- Adding the VRR to the inner wall diffusion section of the duct can effectively suppress the occurrence of the tip vortex and airflow separation and improve the airflow flow quality inside the duct, thus improving aerodynamic efficiency by 5.1%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Φ | Generalized flux |
| ρ | Air density |
| V | Velocity vector |
| ΓΦ | Diffusion coefficient |
| Sϕ | Source term |
| V0 | Free flow velocity |
| R | Radius of the rotor |
| νh | Induced velocity |
| y+ | Dimensionless wall distance |
| LNewmesh | Lift of the new grid |
| LOldmesh | Lift of the last grid |
| PCFD | CFD power |
| Ptext | Text power |
| UAM | Urban air mobility |
| eVTOL | Electrically driven vertical take-off and landing |
| DCP | Ducted coaxial propeller |
| VRR | Vortex restrain ring |
| FCP | Free coaxial propeller |
| DSP | Ducted single propeller |
| CFD | Computational fluid dynamics |
| ESC | Electronic stability controller |
| SST | Shear stress transport |
References
- Pavel, M.D. Understanding the control characteristics of electric vertical take-off and landing (eVTOL) aircraft for urban air mobility. Aerosp. Sci. Technol. 2022, 125, 107143. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J.; Lee, J. Holding area conceptual design and validation for various urban air mobility (Uam) operations: A case study in seoul–gyungin area. Appl. Sci. 2021, 11, 10707. [Google Scholar] [CrossRef]
- Polaczyk, N.; Trombino, E.; Wei, P.; Mitici, M. A Review of Current Technology and Research in Urban On-Demand Air Mobility Applications. In Proceedings of the 8th Biennial Autonomous VTOL Technical Meeting and 6th Annual Electric VTOL Symposium, Washington, DC, USA, 28 January–1 February 2019; pp. 333–343. [Google Scholar]
- Alex, Z.; Davide, A. Aerodynamic interaction between tandem overlapping propellers in eVTOL airplane mode flight condition. Aerosp. Sci. Technol. 2022, 124, 510–521. [Google Scholar] [CrossRef]
- Shur, M.; Strelets, M.; Travin, A.; Christophe, J.; Kucukcoskun, K.; Schram, C.; Sack, S.; Abom, M. Experimental/Numerical Study of Ducted-Fan Noise: Effect of Duct Inlet Shape. AIAA J. 2018, 56, 979–996. [Google Scholar] [CrossRef]
- Hrishikeshavan, V.; Black, J.; Chopra, I. Design and Performance of a Quad-Shrouded Rotor Micro Air Vehicle. J. Aircr. 2014, 51, 779–791. [Google Scholar] [CrossRef]
- Rubio, R.; Diaz, P.; Yoon, S. High-Fidelity Computational Analysis of Ducted and Coaxial Rotors for Urban Air Mobility. In Proceedings of the 75th Annual Forum, Philadelphia, PA, USA, 13–16 May 2019. [Google Scholar]
- Akturk, A.; Camci, C. Tip Clearance Investigation of a Ducted Fan Used in VTOL Unmanned Aerial Vehicles—Part I: Baseline Experiments and Computational Validation. J. Turbomach. 2013, 136, 94–113. [Google Scholar] [CrossRef]
- Akturk, A.; Camci, C. Experimental and Computational Assessment of a Ducted-Fan Rotor Flow Model. J. Aircr. 2012, 49, 885–897. [Google Scholar] [CrossRef]
- Deng, S.; Wang, S.; Zhang, Z. Aerodynamic performance assessment of a ducted fan UAV for VTOL applications. Aerosp. Sci. Technol. 2020, 103, 105895. [Google Scholar] [CrossRef]
- Cai, H.; Wu, Z.; Deng, S. Numerical prediction of unsteady aerodynamics for a ducted fan micro air vehicle. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 87–95. [Google Scholar] [CrossRef]
- Li, L.; Huang, G.; Chen, J. Aerodynamic characteristics of a tip-jet fan with a large blade pitch angle. Aerosp. Sci. Technol. 2019, 91, 49–58. [Google Scholar] [CrossRef]
- Chen, J.; Li, L.; Xiang, X. Numerical investigations of ducted fan aerodynamic performance with tip-jet. Aerosp. Sci. Technol. 2018, 78, 510–521. [Google Scholar] [CrossRef]
- Biava, M.; Barakos, G. Optimisation of Ducted Propellers for Hybrid Air Vehicles Using High-Fidelity CFD. Aeronaut. J. 2016, 120, 1632–1657. [Google Scholar] [CrossRef]
- Qing, J.; Yu, H.; Wang, Y. Kriging Assisted Integrated Rotor-Duct Optimization for Ducted Fan in Hover. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Bento, H.; De, V.; Veldhuis, L. Aerodynamic performance and interaction effects of circular and square ducted propeller. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Singh, R.; Jimenez, B.; Avera, M. Investigation of Aerodynamic Interactions in Ducted Rotor Systems. In Proceedings of the AHS 70th Annual Forum, Montréal, QC, Canada, 20–22 May 2014. [Google Scholar]
- Shukla, D.; Komerath, N. Rotor–duct aerodynamic and acoustic interactions at low Reynolds number. Exp. Fluids 2019, 60, 20. [Google Scholar] [CrossRef]
- Colman, M.; Suzuki, S.; Kubo, D. Wind Tunnel Test Results and Performance Prediction for a Ducted Fan with Collective and Cyclic Pitch Actuation for VTOL with Efficient Cruise. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar] [CrossRef]
- Denisenko, P.; Chernyshov, P.; Volkov, K.; Vokin, L.O. Numerical Simulation of the Flow around the Ducted Fan of a Quadcopter and Determination of Its Thrust Characteristics in Various Flight Modes. Russ. Aeronaut. 2021, 64, 224–232. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation k-ω Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar] [CrossRef]
- Catalano, P.; Amato, M. An evaluation of RANS turbulence modeling for aerodynamic applications. Aerosp. Sci. Technol. 2003, 7, 493–509. [Google Scholar] [CrossRef]
- Cai, H.; Zhang, Z.; Deng, S. Numerical Prediction of Unsteady Aerodynamics of a Ducted Fan Unmanned Aerial Vehicle in Hovering. Aerospace 2022, 9, 318. [Google Scholar] [CrossRef]
- Blazek, J. Principles and Applications. Computational Fluid Dynamics. In Computational Fluid Dynamics: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2001; pp. 30–54. [Google Scholar]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Luo, H.; Baum, J.; Lohner, R. An accurate, fast, matrix-free implicit method for computing unsteady flows on unstructured grids. Comput. Fluids 2001, 30, 137–159. [Google Scholar] [CrossRef]
- Mi, B. Numerical investigation on aerodynamic performance of a ducted fan under interferences from the ground, static water and dynamic waves. Aerosp. Sci. Technol. 2020, 100, 105821. [Google Scholar] [CrossRef]
- Ryu, M.; Cho, L.; Cho, J. The Effect of Tip Clearance on Performance of a Counter-Rotating Ducted Fan in a VTOL UAV. Trans. Jpn. Soc. Aeronaut. Space Sci. 2017, 60, 1–9. [Google Scholar] [CrossRef]
- Ohanian, O.; Karni, E.; Londenberg, W.; Gelhausen, P.; Inman, D. Ducted-Fan Force and Moment Control via Steady and Synthetic Jets. J. Aircr. 2011, 48, 514–526. [Google Scholar] [CrossRef]
- Akturk, A.; Camci, C. Double-Ducted Fan as an Effective Lip Separation Control Concept for Vertical-Takeoff-and-Landing Vehicles. J. Aircr. 2022, 59, 233–252. [Google Scholar] [CrossRef]

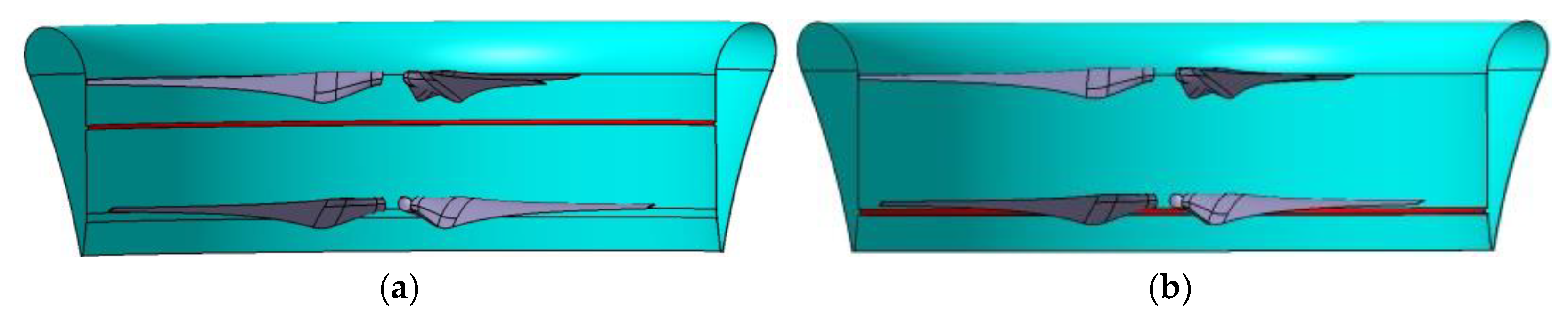
| Parameter | Value |
|---|---|
| Propeller diameter, m | 1.49 |
| Propeller airfoil | CLARK-Y |
| Spacing between propellers, m | 0.32 |
| Chord of duct, m | 0.56 |
| Inner diameter of duct, m | 1.5 |
| Outer diameter of duct, m | 1.78 |
| Tip clearance, m | 0.005 |
| Design, RPM | 3000 |
| VRR Location | Lift of the Upper Propeller (N) | Lift of the Lower Propeller (N) | Lift of Duct (N) | Duct Lift Factor | Power (kw) |
|---|---|---|---|---|---|
| Without VRR | 798.4 | 835.8 | 1168.2 | 0.417 | 81.2 |
| VRR in straight section | 766.8 | 876.7 | 996.4 | 0.377 | 81.3 |
| VRR in diffusion section | 842.3 | 862.5 | 1240.9 | 0.421 | 81.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chen, R.; Lu, J. Experimental and Numerical Studies on the Effect of Airflow Separation Suppression on Aerodynamic Performance of a Ducted Coaxial Propeller in Hovering. Aerospace 2023, 10, 11. https://doi.org/10.3390/aerospace10010011
Wang J, Chen R, Lu J. Experimental and Numerical Studies on the Effect of Airflow Separation Suppression on Aerodynamic Performance of a Ducted Coaxial Propeller in Hovering. Aerospace. 2023; 10(1):11. https://doi.org/10.3390/aerospace10010011
Chicago/Turabian StyleWang, Junjie, Renliang Chen, and Jiaxin Lu. 2023. "Experimental and Numerical Studies on the Effect of Airflow Separation Suppression on Aerodynamic Performance of a Ducted Coaxial Propeller in Hovering" Aerospace 10, no. 1: 11. https://doi.org/10.3390/aerospace10010011
APA StyleWang, J., Chen, R., & Lu, J. (2023). Experimental and Numerical Studies on the Effect of Airflow Separation Suppression on Aerodynamic Performance of a Ducted Coaxial Propeller in Hovering. Aerospace, 10(1), 11. https://doi.org/10.3390/aerospace10010011






