Computational Fluid Dynamics Analyses of a Wing with Distributed Electric Propulsion
Abstract
1. Introduction
1.1. Related Work
1.2. Objective of the Present Work
2. Computational Tools
2.1. Rationale of Selected CFD Solvers
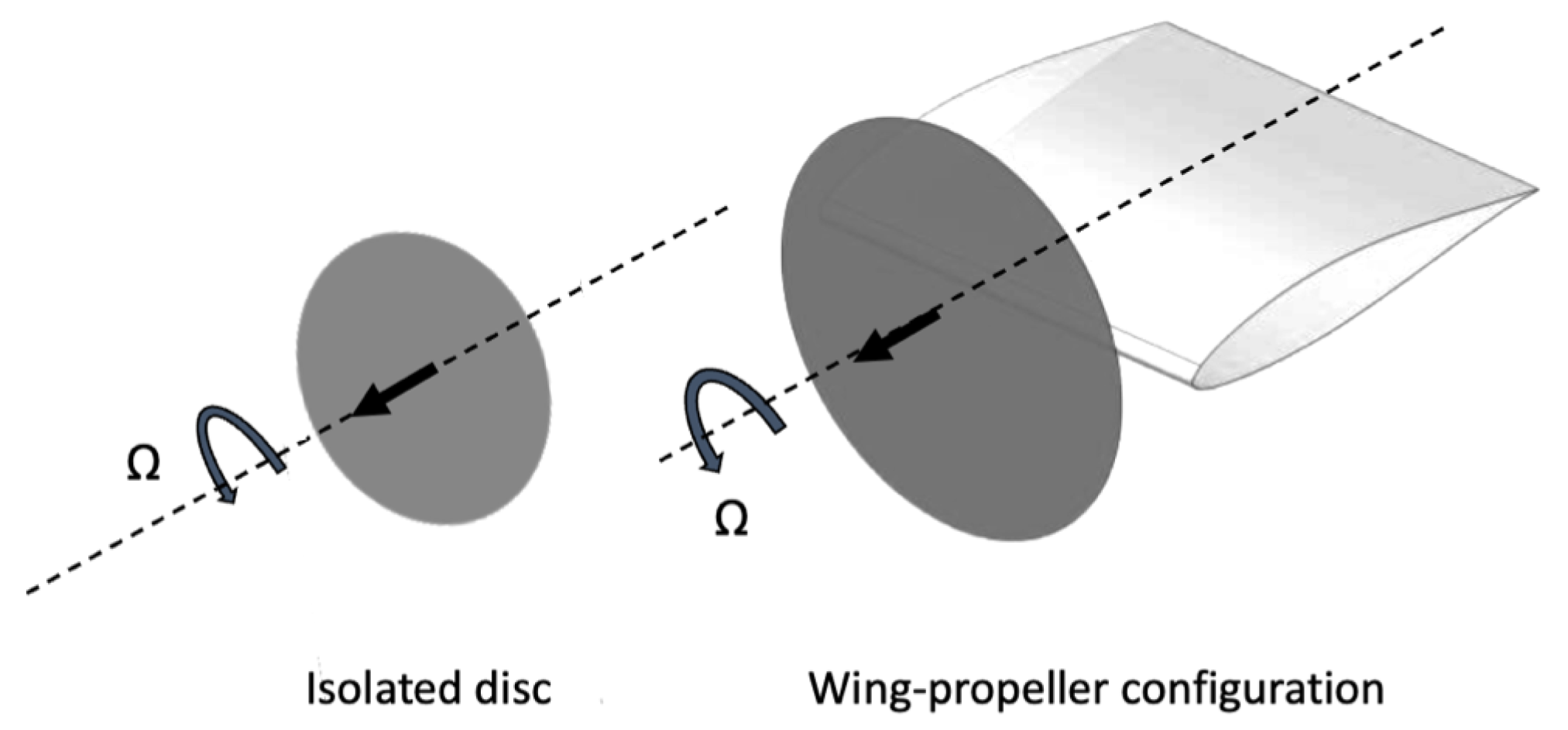
2.2. Propeller Modelling: Actuator Disk Boundary Condition
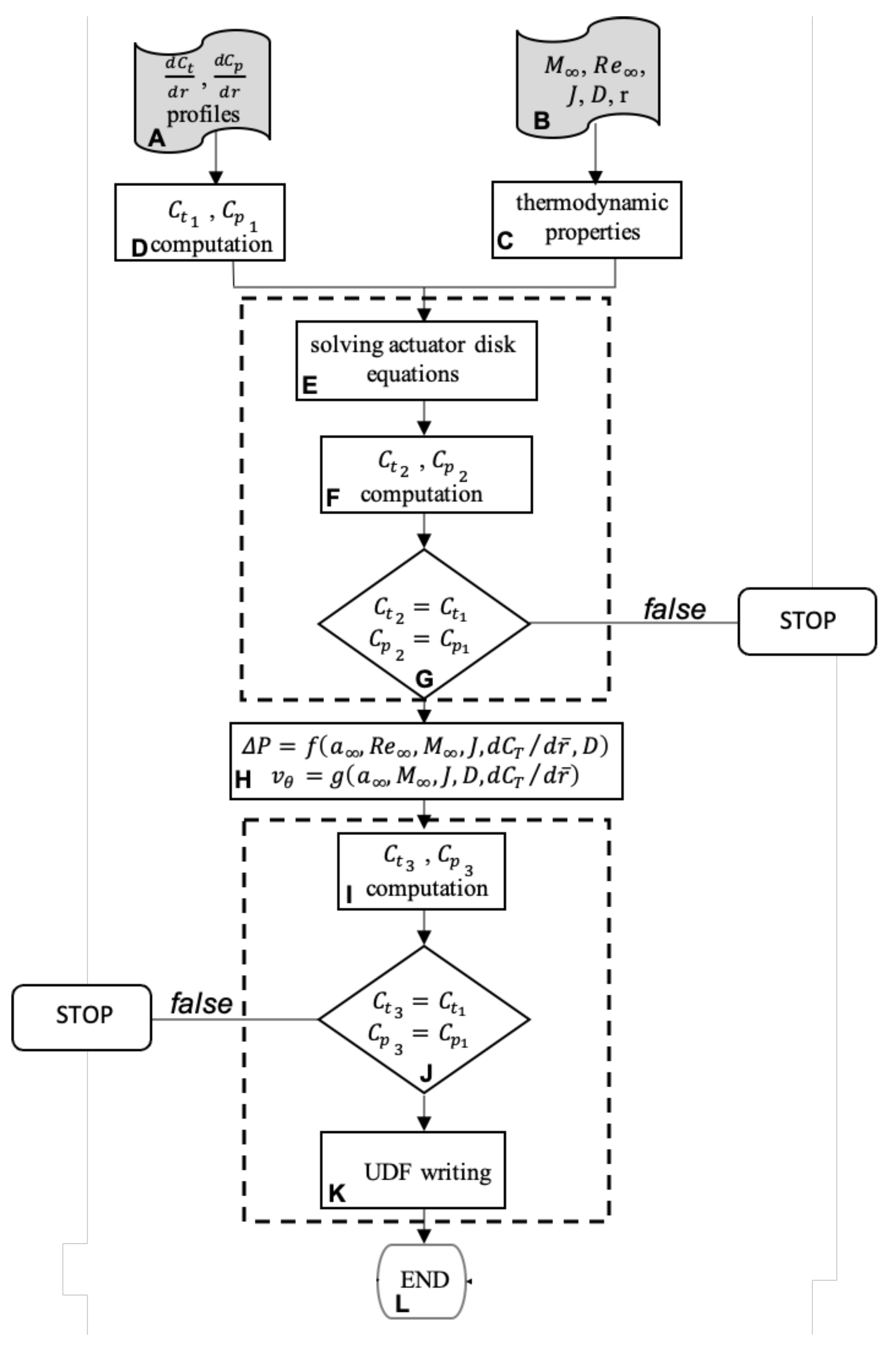
2.3. UDF Flowchart Description
3. Code-to-Code Comparison: Analysed Test Cases
4. Computational Set up of CFD Solvers
4.1. Freestream Conditions and Solution Approach
4.2. Numerical Settings
4.3. Solution Methodology and Turbulence Closure
4.4. Convergence and Stability Criteria
5. Isolated Propeller Test-Case
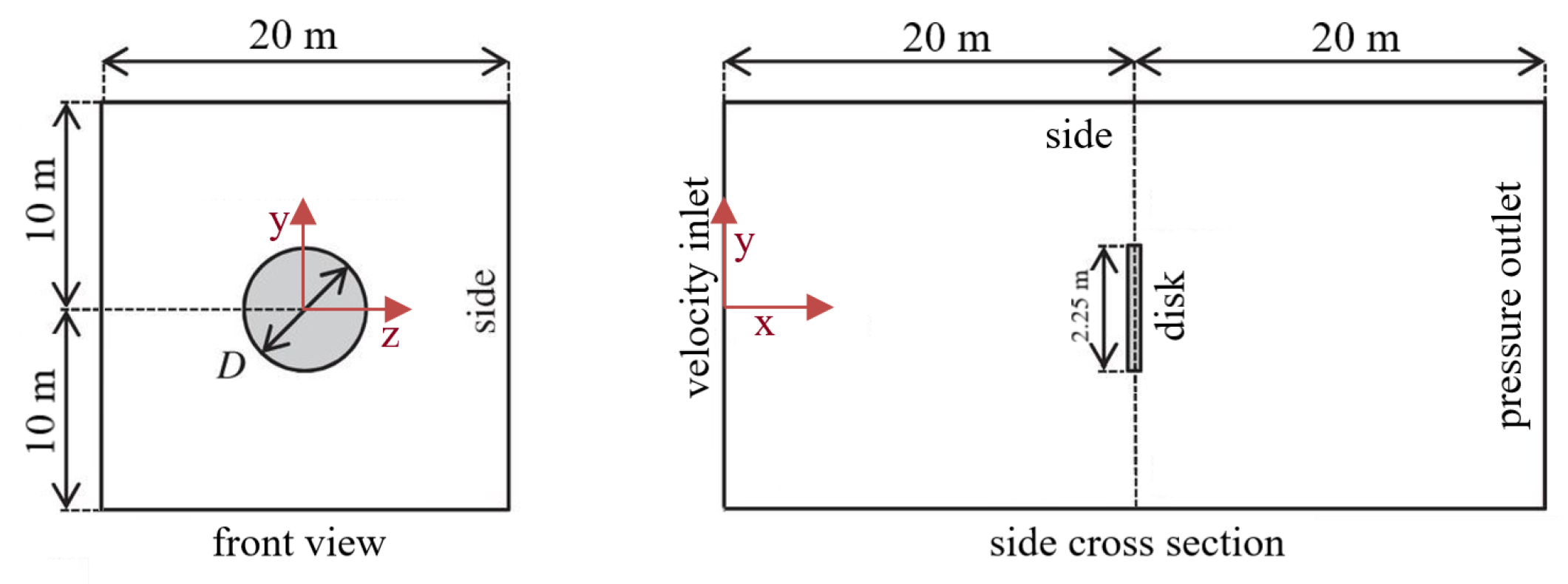
Geometry, Computational Domain and Boundary Conditions
6. Propeller-Wing Interaction Test-Case
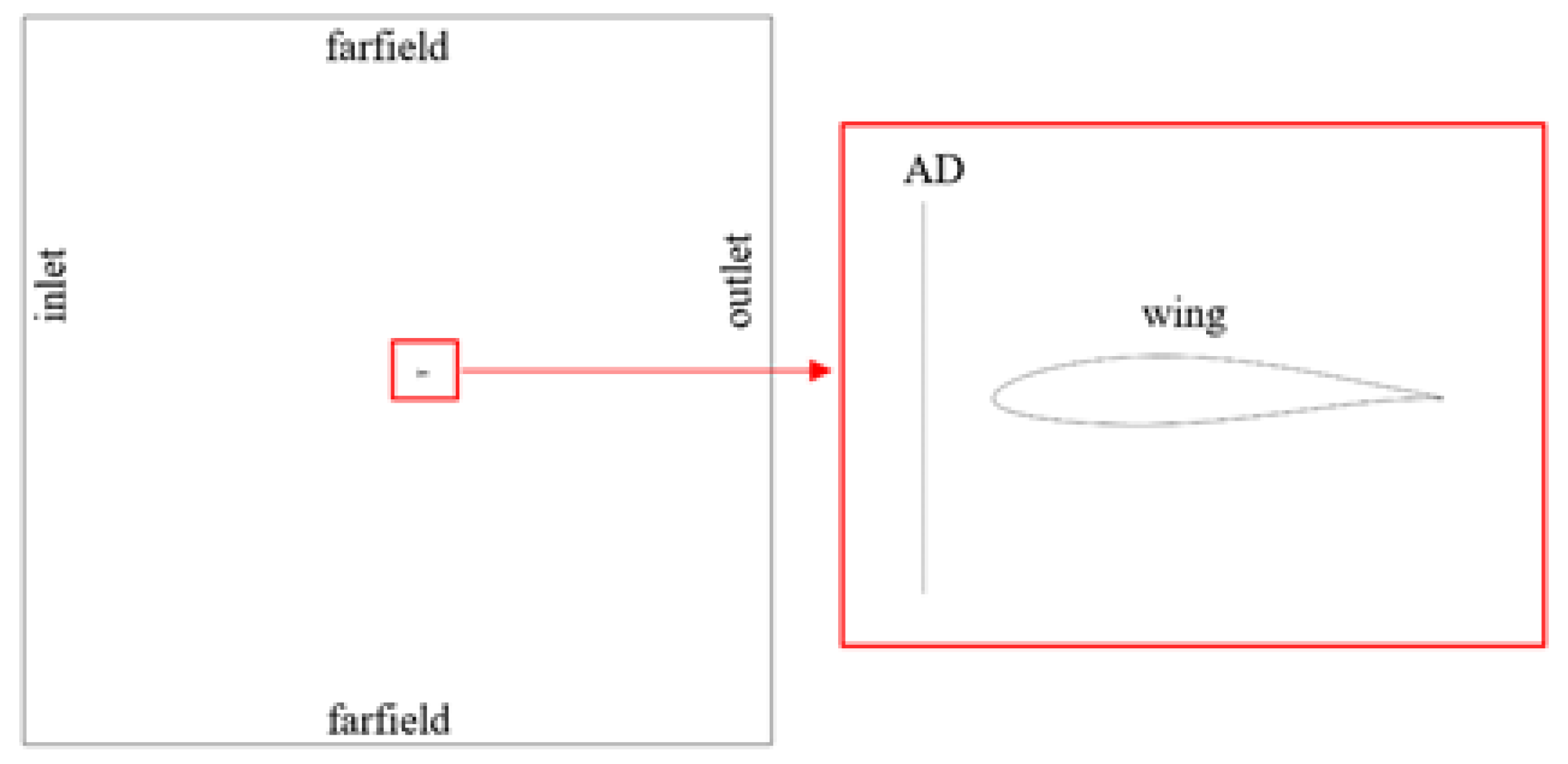
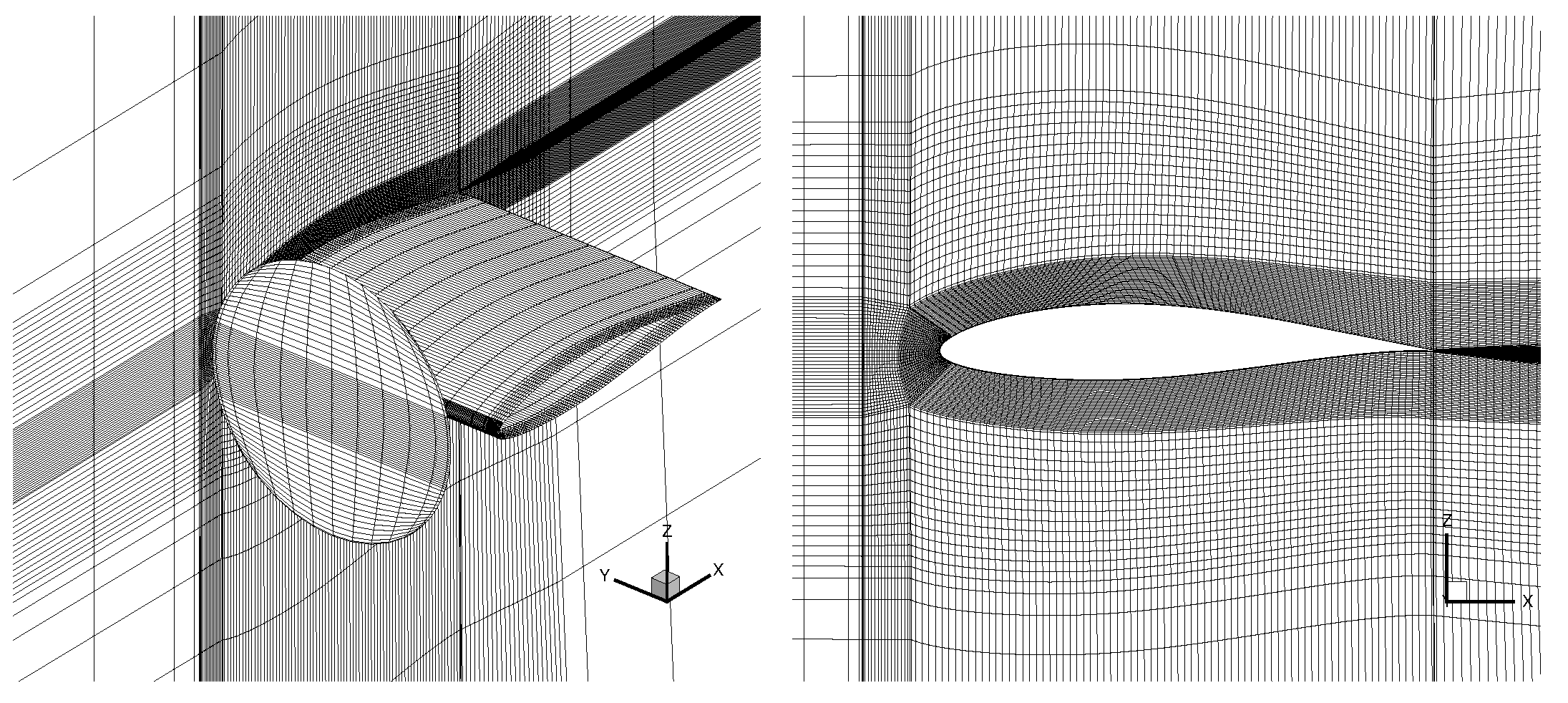
6.1. Geometry, Computational Domain and Boundary Conditions
6.2. Grid Convergence Study
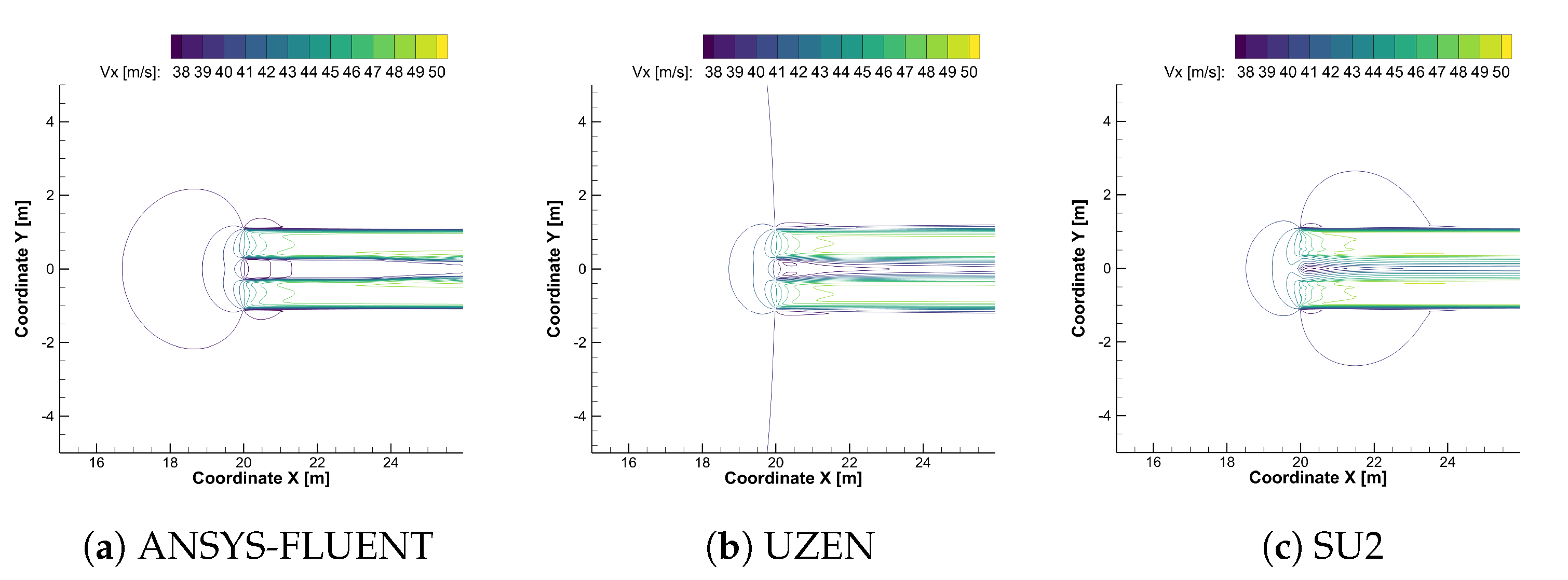
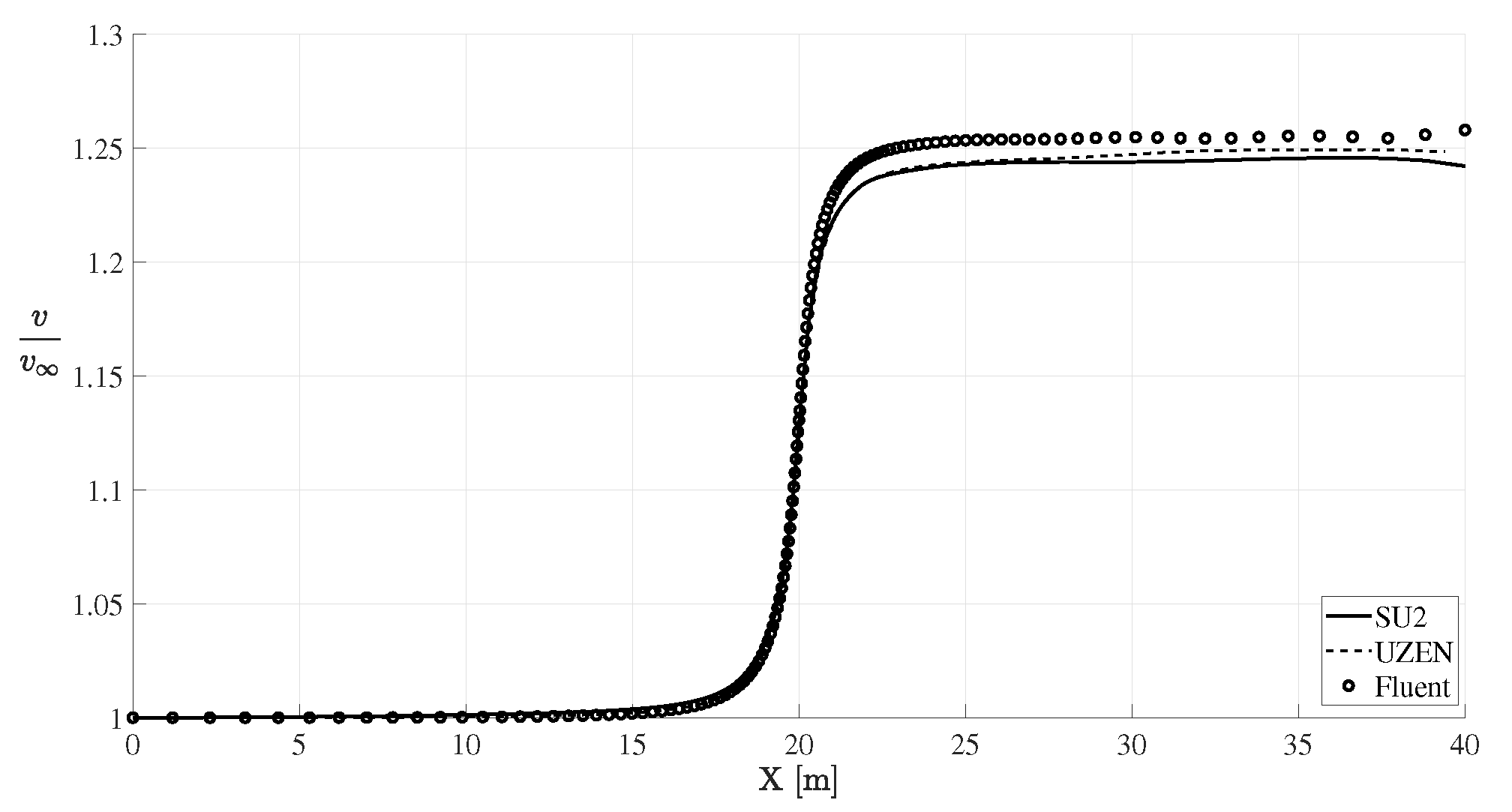
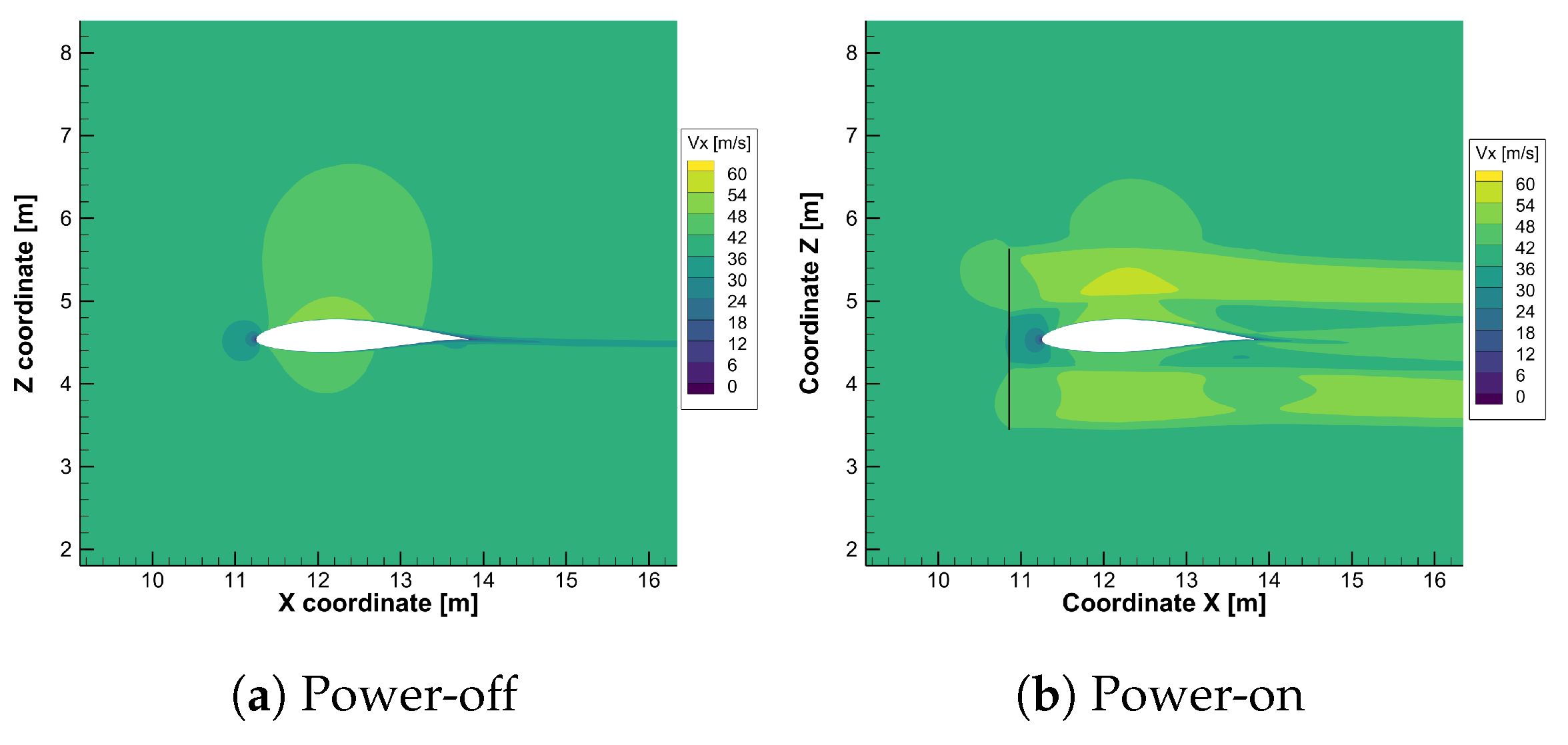
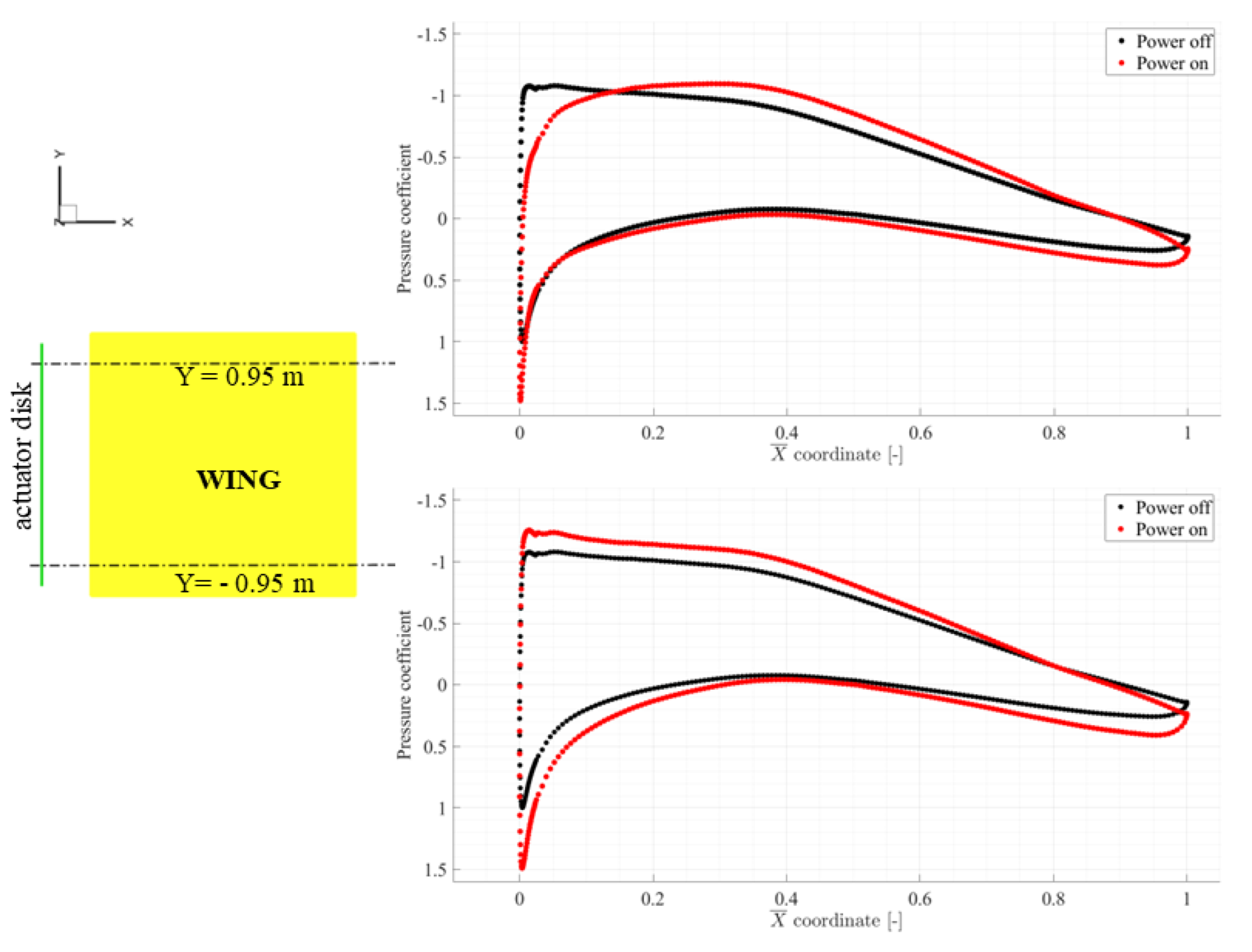
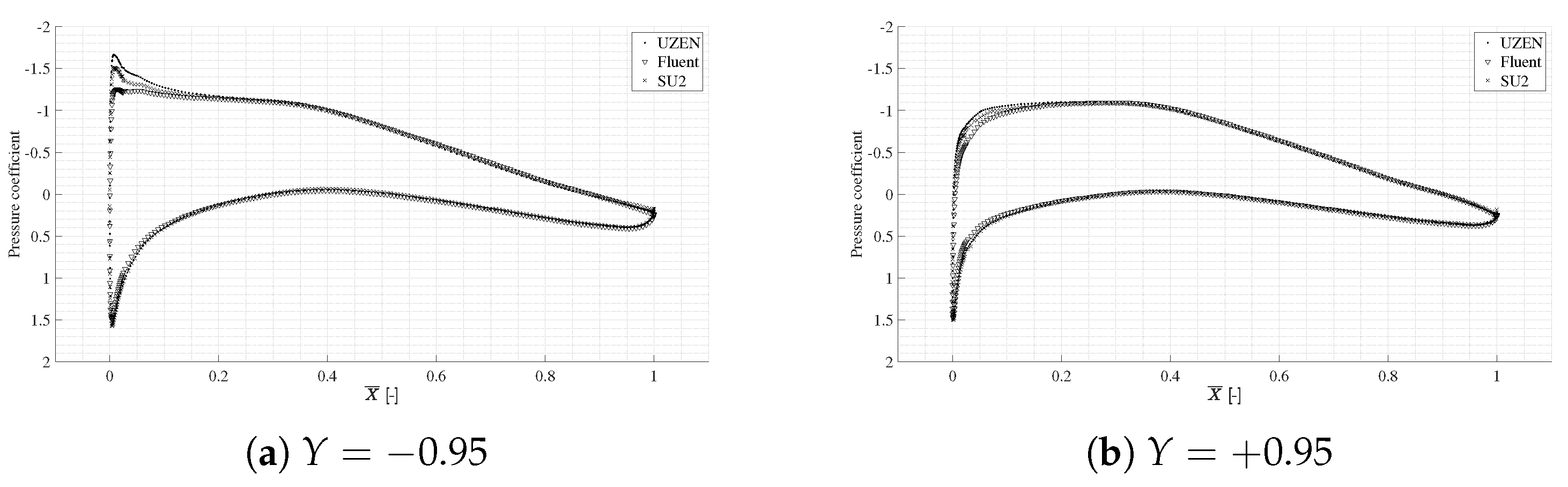
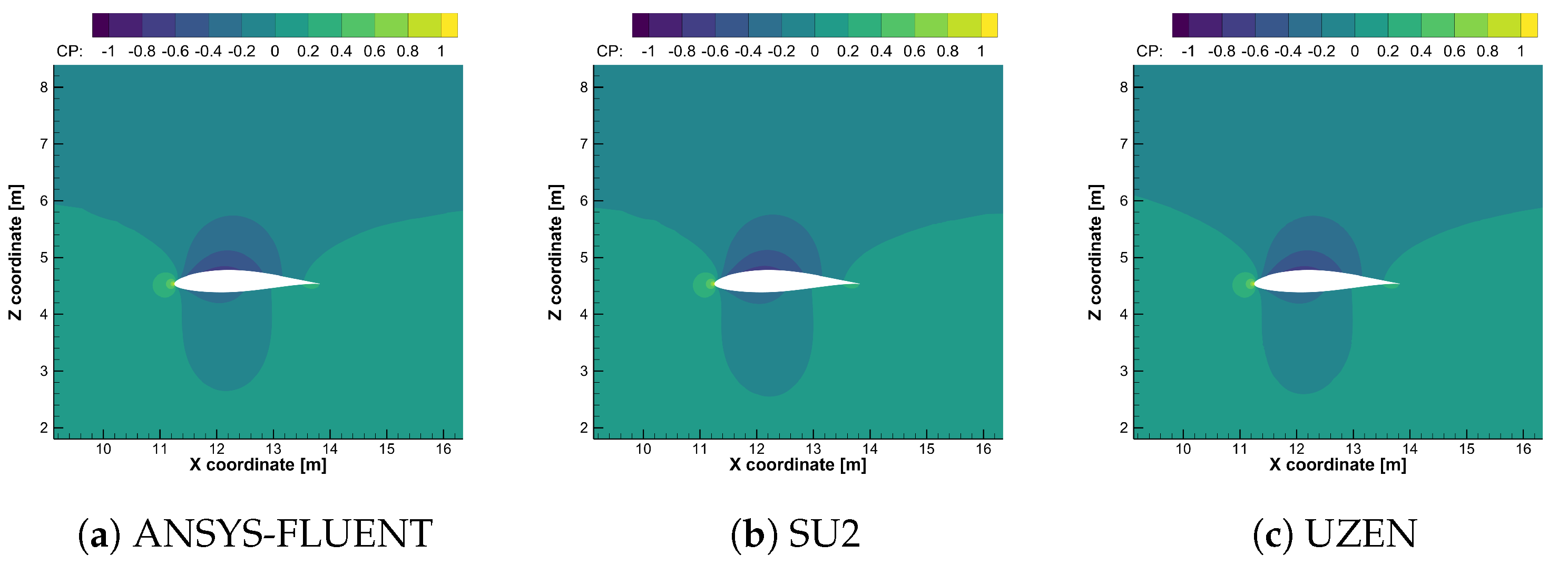
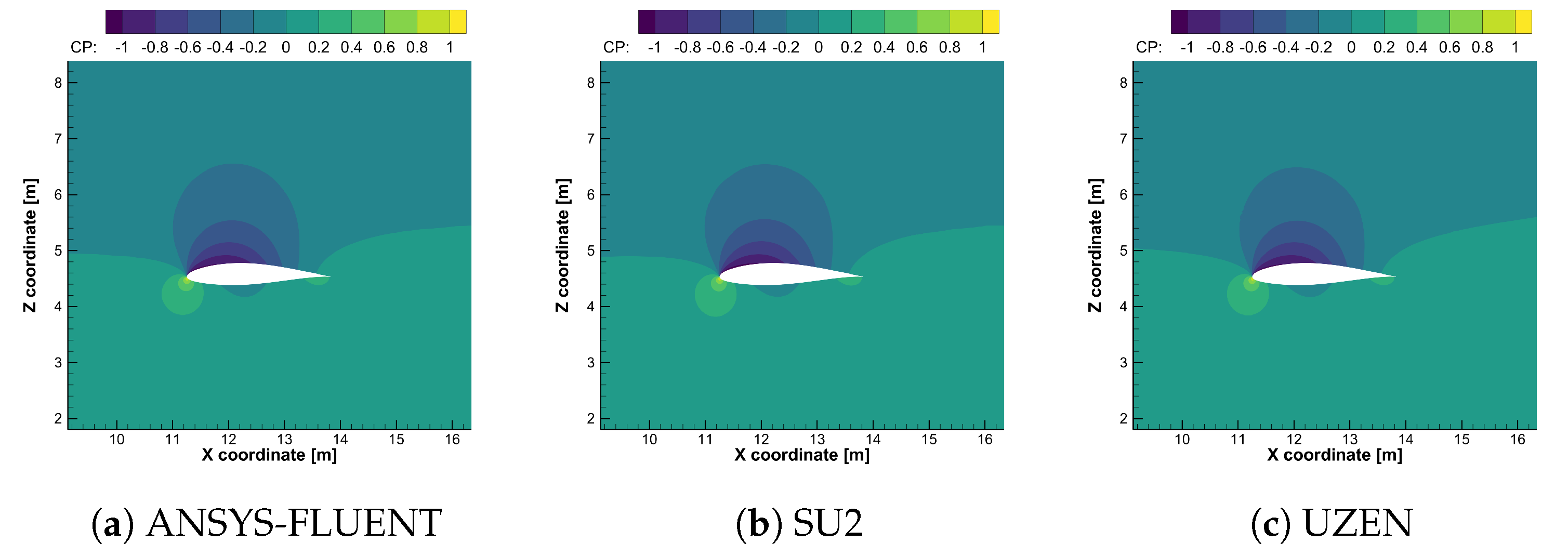
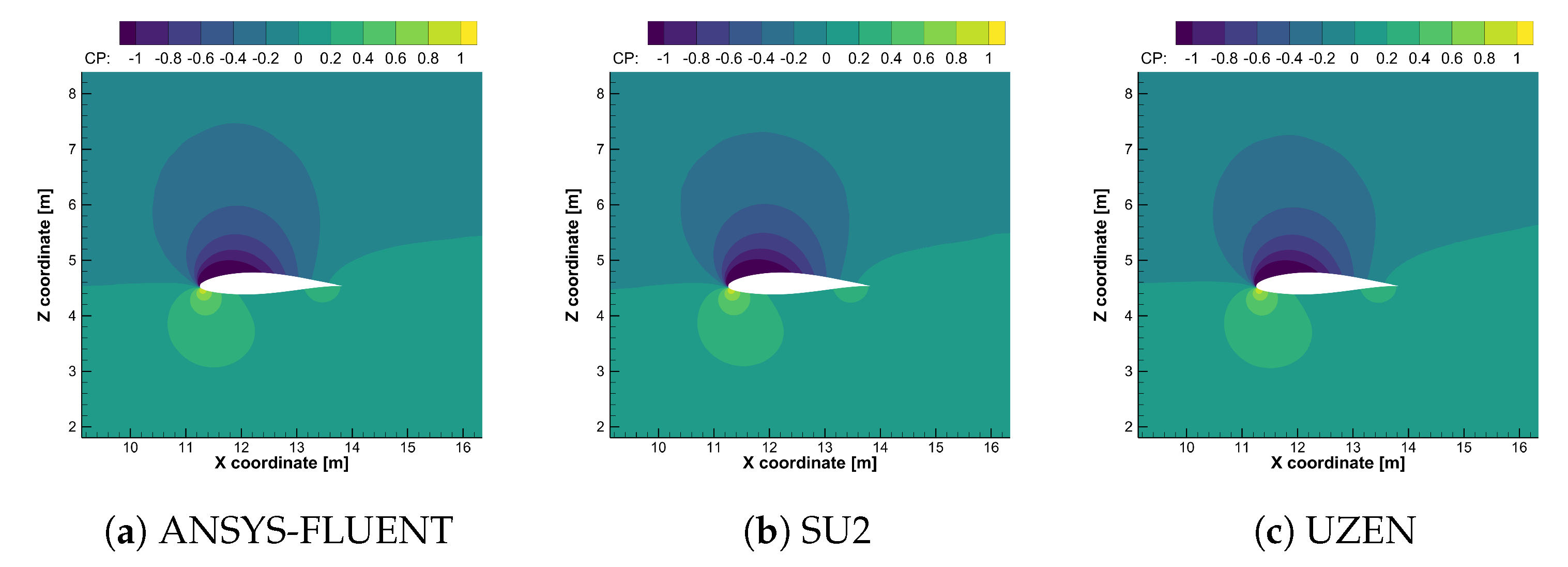
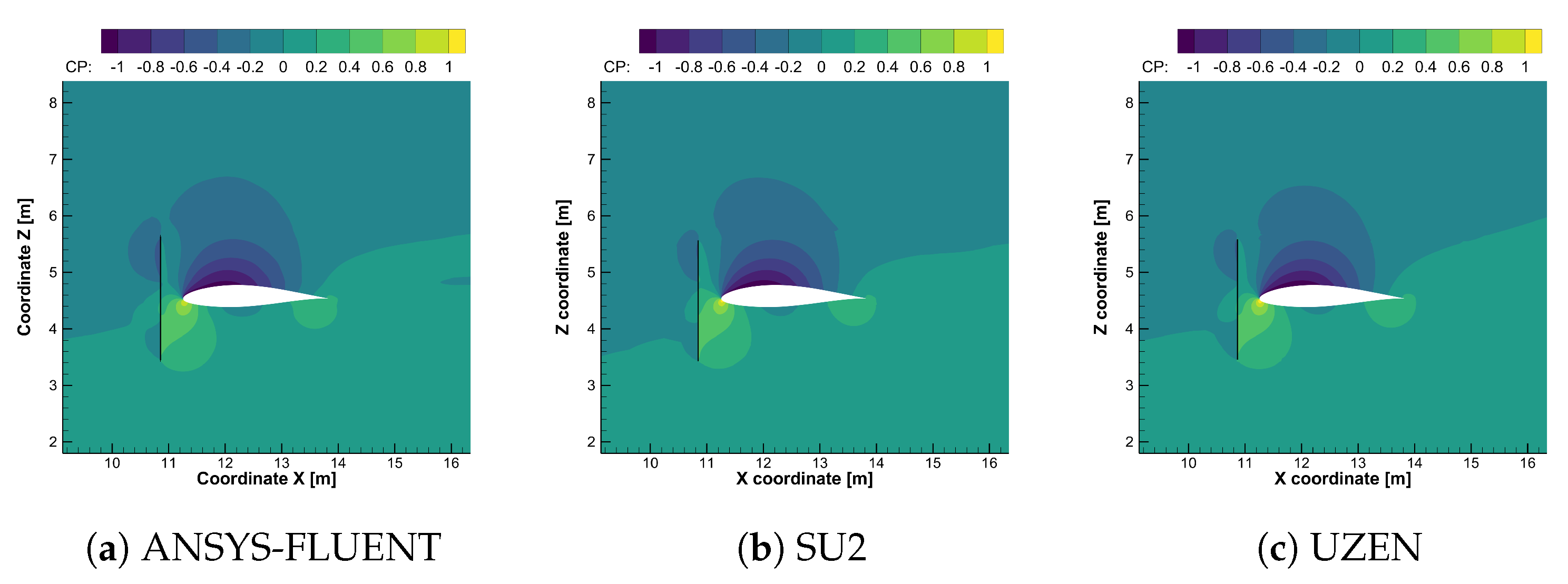
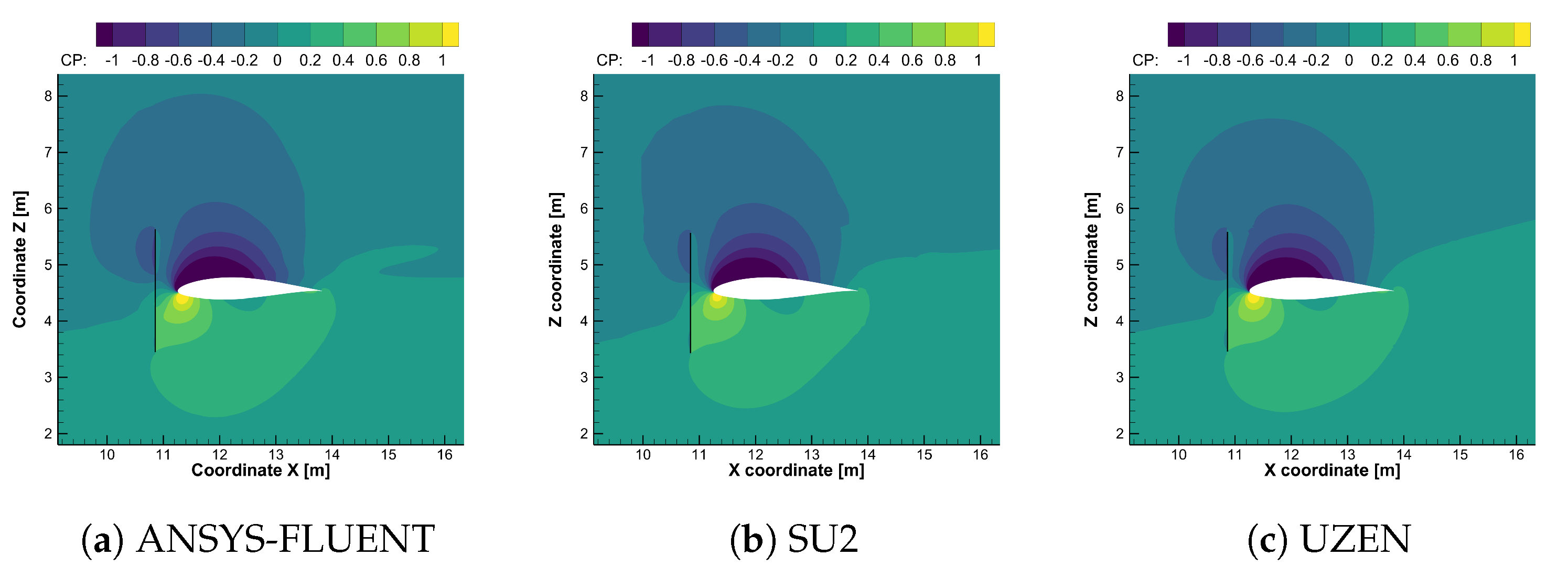
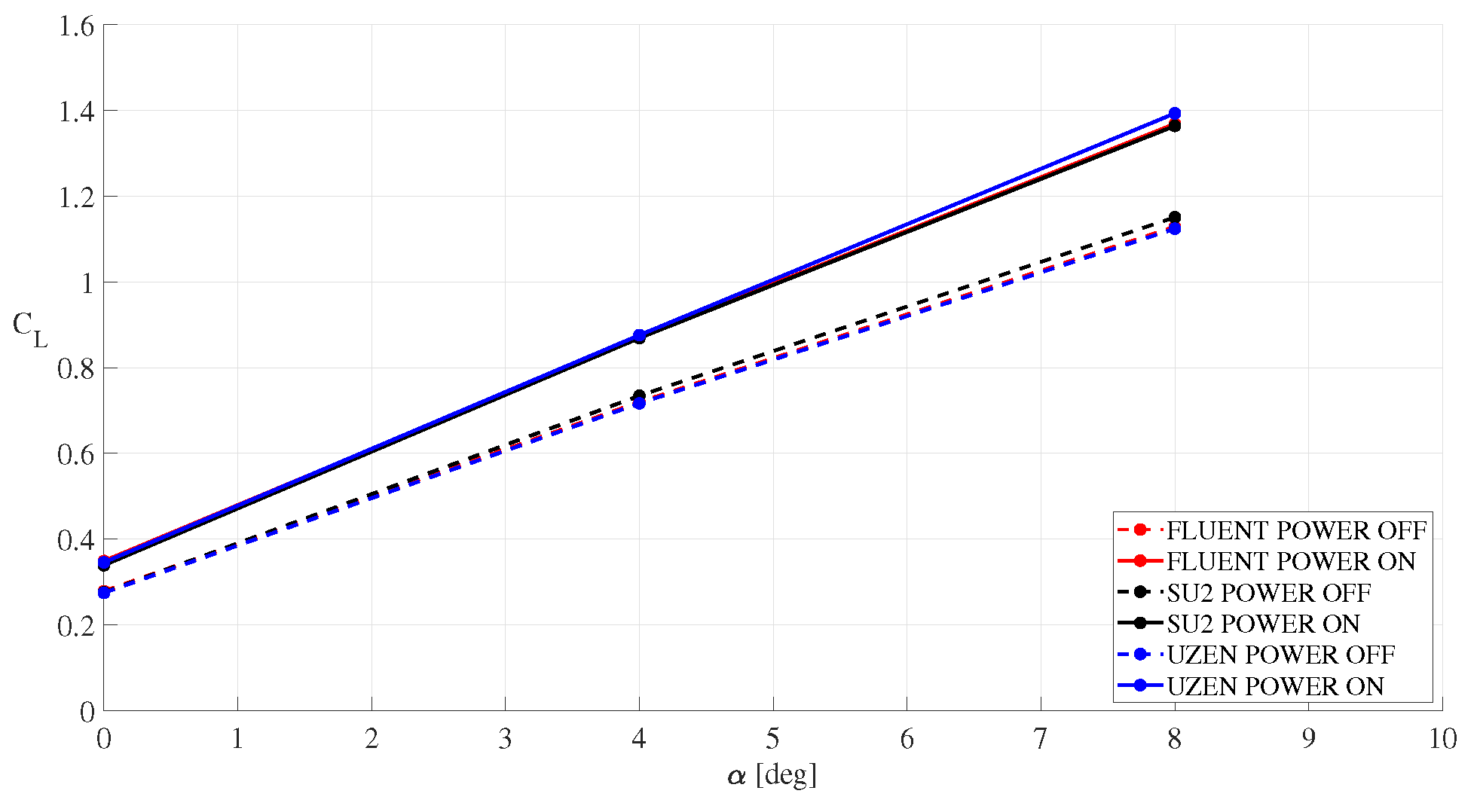
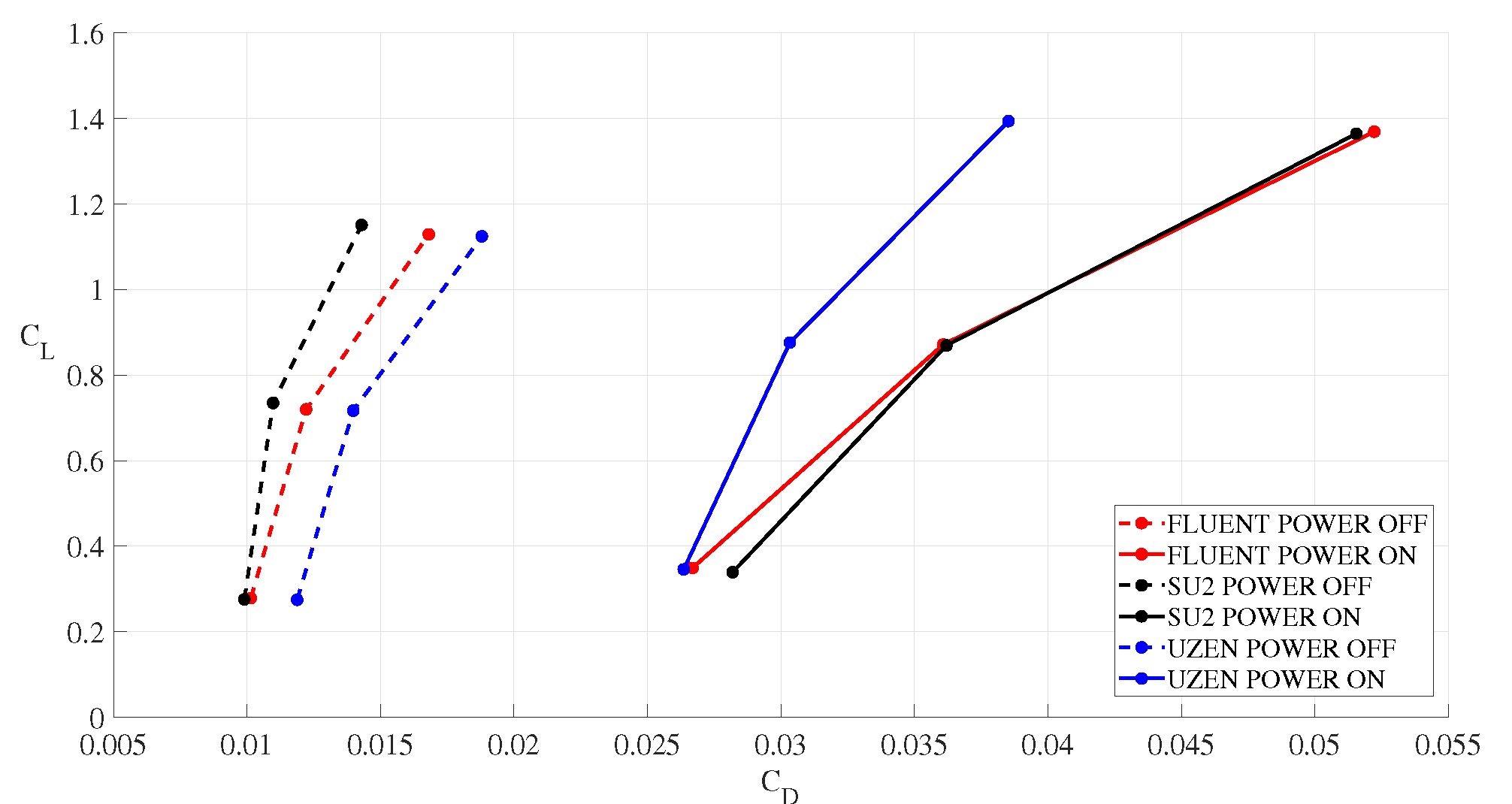
6.3. Computational Results for the Propeller-Wing Interaction
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, D.S.; Fahey, D.W.; Forster, P.M.; Newton, P.J.; Wit, R.C.; Lim, L.L.; Owen, B.; Sausen, R. Aviation and global climate change in the 21st century. Atmos. Environ. 2009, 43, 3520–3537. [Google Scholar] [CrossRef] [PubMed]
- Sehra, A.K.; Whitlow, W. Propulsion and power for 21st century aviation. Prog. Aerosp. Sci. 2004, 40, 199–235. [Google Scholar] [CrossRef]
- Stoll, A.M.; Bevirt, J.; Moore, M.D.; Fredericks, W.J.; Borer, N.K. Drag Reduction Through Distributed Electric Propulsion. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Patterson, M.D.; German, B. Conceptual Design of Electric Aircraft with Distributed Propellers: Multidisciplinary Analysis Needs and Aerodynamic Modeling Development. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- van Arnhem, N.; de Vries, R.; Sinnige, T.; Vos, R.; Eitelberg, G.; Veldhuis, L.L.M. Engineering Method to Estimate the Blade Loading of Propellers in Nonuniform Flow. AIAA J. 2020, 58, 5332–5346. [Google Scholar] [CrossRef]
- Deere, K.A.; Viken, S.A.; Carter, M.B.; Viken, J.K.; Derlaga, J.M.; Stoll, A.M. Comparison of High-Fidelity Computational Tools for Wing Design of a Distributed Electric Propulsion Aircraft. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, AIAA, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Antcliff, K.R.; Capristan, F.M. Conceptual Design of the Parallel Electric- Gas Architecture with Synergistic Utilization Scheme (PEGASUS) Concept. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Snyder, M.H.; Zumwalt, G.W. Effects of wingtip-mounted propellers on wing lift and induced drag. J. Aircr. 1969, 6, 392–397. [Google Scholar] [CrossRef]
- Sinnige, T.; van Arnhem, N.; Stokkermans, T.C.A.; Eitelberg, G.; Veldhuis, L.L.M. Wingtip-Mounted Propellers: Aerodynamic Analysis of Interaction Effects and Comparison with Conventional Layout. J. Aircr. 2019, 56, 295–312. [Google Scholar] [CrossRef]
- Veldhuis, L. Propeller Wing Aerodynamic Interference. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- Gallani, M.A.; Goes, L.C.S.; Nerosky Luiz, A.R. Effects of distributed electric propulsion on the performance of a general aviation aircraft. In Proceedings of the 2020 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), New Orleans, LA, USA, 26–28 August 2020. [Google Scholar]
- Rubin, R.L.; Zhao, D. New Development of Classical Actuator Disk Model for Propellers at Incidence. AIAA J. 2021, 59, 1040–1054. [Google Scholar] [CrossRef]
- Kroo, I. Propeller-wing integration for minimum induced loss. J. Aircr. 1986, 23, 561–565. [Google Scholar] [CrossRef]
- Miranda, L.; Brennan, J. Aerodynamic effects of wingtip-mounted propellers and turbines. In Proceedings of the 4th Applied Aerodynamics Conference, San Diego, CA, USA, 9–11 June 1986. [Google Scholar] [CrossRef]
- Beckers, M.F.; Schollenberger, M.; Lutz, T.; Bongen, D.; Radespiel, R.; Florenciano, J.L.; Funes-Sebastian, D.E. CFD Investigation of High-Lift Propeller Positions for a Distributed Propulsion System. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Patternson, J.J.; Bartlett, G.R. Evaluation of Installed Performance of a Wing-Tip-Mounted Pusher Turboprop on a Semispan Wing; NASA TP-2739; NASA: Washington, DC, USA, 1978. [Google Scholar]
- Kim, H.D.; Perry, A.T.; Ansell, P.J. A Review of Distributed Electric Propulsion Concepts for Air Vehicle Technology. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium, AIAA 2018-4998, Cincinnati, OH, USA, 12–14 July 2018. [Google Scholar] [CrossRef]
- Borer, N.K.; Patterson, M.D.; Viken, J.K.; Moore, M.D.; Bevirt, J.; Stoll, A.M.; Gibson, A.R. Design and Performance of the NASA SCEPTOR Distributed Electric Propulsion Flight Demonstrator. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- NASA. NASA X-57 Maxwell. 2016. Available online: https://www.nasa.gov/press-release/nasa-electric-research-plane-gets-x-number-new-name (accessed on 25 November 2022).
- Patterson, M.D.; Derlaga, J.M.; Borer, N.K. High-Lift Propeller System Configuration Selection for NASA’s SCEPTOR Distributed Electric Propulsion Flight Demonstrator. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- Rankine, W.M.J. On the Mechanical Principles of the Action of Propellers. Trans. Inst. Nav. Archit. 1865, 6, 13–39. [Google Scholar]
- Froude, R. On the Part Played in Propulsion by Differences of Fluid Pressure. Trans. Inst. Nav. Archit. 1865, 30, 390–405. [Google Scholar]
- Dommasch, D. Elements of Propeller and Helicopter Aerodynamics; Pitman Aeronautical Publications; Pitman Publishing Corporation: New York, NY, USA, 1953. [Google Scholar]
- Witkowski, D.P.; Lee, A.K.H.; Sullivan, J.P. Aerodynamic interaction between propellers and wings. J. Aircr. 1989, 26, 829–836. [Google Scholar] [CrossRef]
- Alba, C.; Elham, A.; German, B.J.; Veldhuis, L.L.M. A surrogate- based multi-disciplinary design optimization framework modeling wing-propeller interaction. Aerosp. Sci. Technol. 2018, 78, 721–733. [Google Scholar] [CrossRef]
- Hwang, J.T.; Ning, A. Large-scale multidisciplinary optimization of an electric aircraft for on-demand mobility. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA-2018-1384, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Stokkermans, T.C.; van Arnhem, N.; Sinnige, T.; Veldhuis, L.L.M. Validation and Comparison of RANS Propeller Modeling Methods for Tip-Mounted Applications. AIAA J. 2018, 57, 566–580. [Google Scholar] [CrossRef]
- Moens, F.; Gardarein, P.; Mikkelsen, R. Numerical Simulation of the Propeller/Wing Interactions for Transport Aircraft. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 11–14 June 2001; Volume 57. [Google Scholar] [CrossRef]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2009. [Google Scholar]
- Zhang, T.; Higgins, R.J.; Qiao, G.; Barakos, G.N. Optimization of Distributed Propulsion Using CFD. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Martins, J.R.R.A. RANS-Based Aerodynamic Shape Optimization of a Wing Considering Propeller–Wing Interaction. J. Aircr. 2021, 58, 497–513. [Google Scholar] [CrossRef]
- Palacios, F.; Alonso, J.; Duraisamy, K.; Colonno, M.; Hicken, J.; Aranake, A.; Campos, A.; Copeland, S.; Economon, T.; Lonkar, A.; et al. Stanford University Unstructured (SU⌃2): An open-source integrated computational environment for multi-physics simulation and design. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Marongiu, C.; Catalano, P.; Amato, M.; Iaccarino, G. U-ZEN: A Computational Tool Solving U-Rans Equations for Industrial Unsteady Applications. In Proceedings of the 34th AIAA Fluid Dynamics Conference and Exhibit, Portland, OR, USA, 28 June–1 July 2004; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- ANSYS Academic Research Release 18.1, Help System, Fluent; Ansys, Inc.: Canonsburg, PA, USA, 2018.
- Amato, M.; Paparone, L.; Catalano, P.; Puoti, V. ZEN FLOW SOLVER—Zonal Euler Navier-Stokes Flow Solver USER GUIDE; Technical Report CIRA-UM-AEP-99-054; CIRA—Centro Italiano Ricerche Aerospaziali: Capua, Italy, 1999. [Google Scholar]
- Saetta, E.; Russo, L.; Tognaccini, R. Implementation and validation of a new actuator disk model in SU2. In Proceedings of the SU2 Conference 2020, Virtual Event, 10–12 June 2020. [Google Scholar]
- Available online: https://cordis.europa.eu/project/id/886019 (accessed on 25 July 2021).
- Glauert, H. Airplane Propellers. In Aerodynamic Theory; Durand, W.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1935; Volume IV, pp. 169–360. [Google Scholar]
- Musa, O.; Guoping, H.; Zonghan, Y.; Qian, L. An improved Roe solver for high order reconstruction schemes. Comput. Fluids 2020, 207, 104591. [Google Scholar] [CrossRef]
- Jameson, A. Origins and further development of the Jameson-Smith-Turkel scheme. AIAA J. 2017, 55, 1487–1510. [Google Scholar] [CrossRef]
- Hirsh, C. Numerical Computation of Internal and External Flow; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Swanson, R.C.; Radespiel, R.; Turkel, E. Comparison of Several Dissipation Algorithms for Central Difference Schem; NASA Contract No. NAS1-19480; NASA: Washington, DC, USA, 1997. [Google Scholar]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]


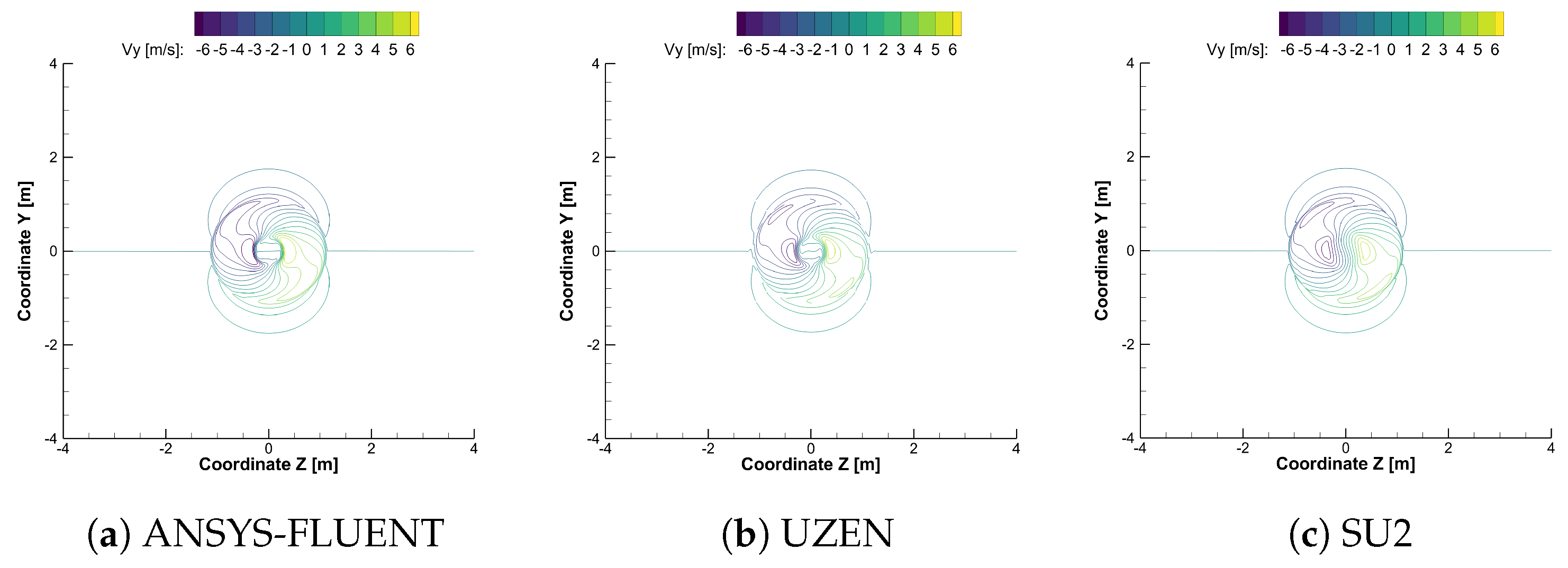
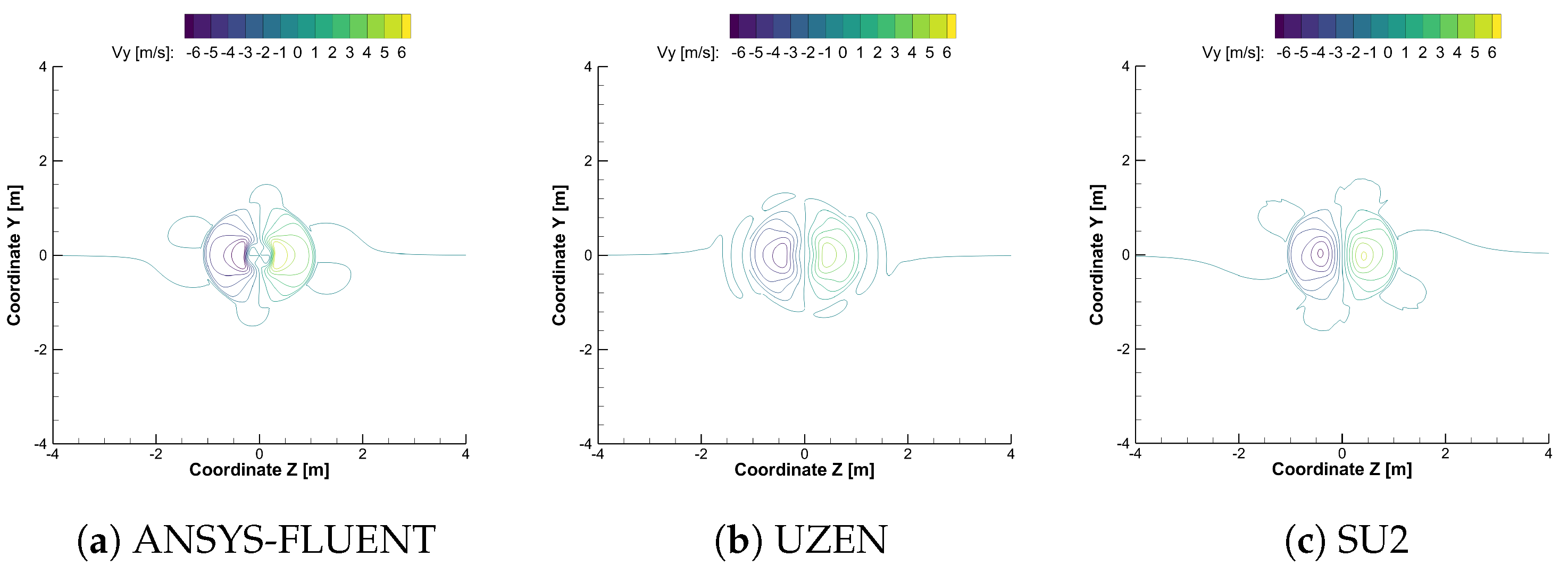
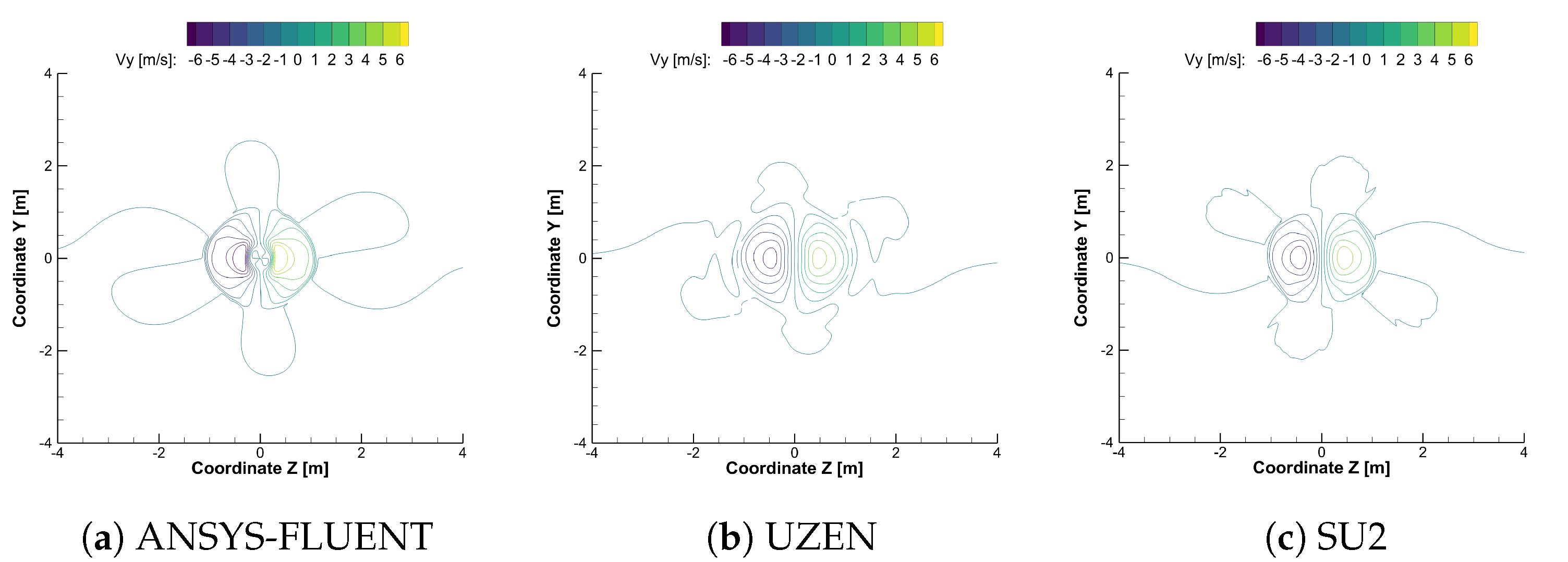
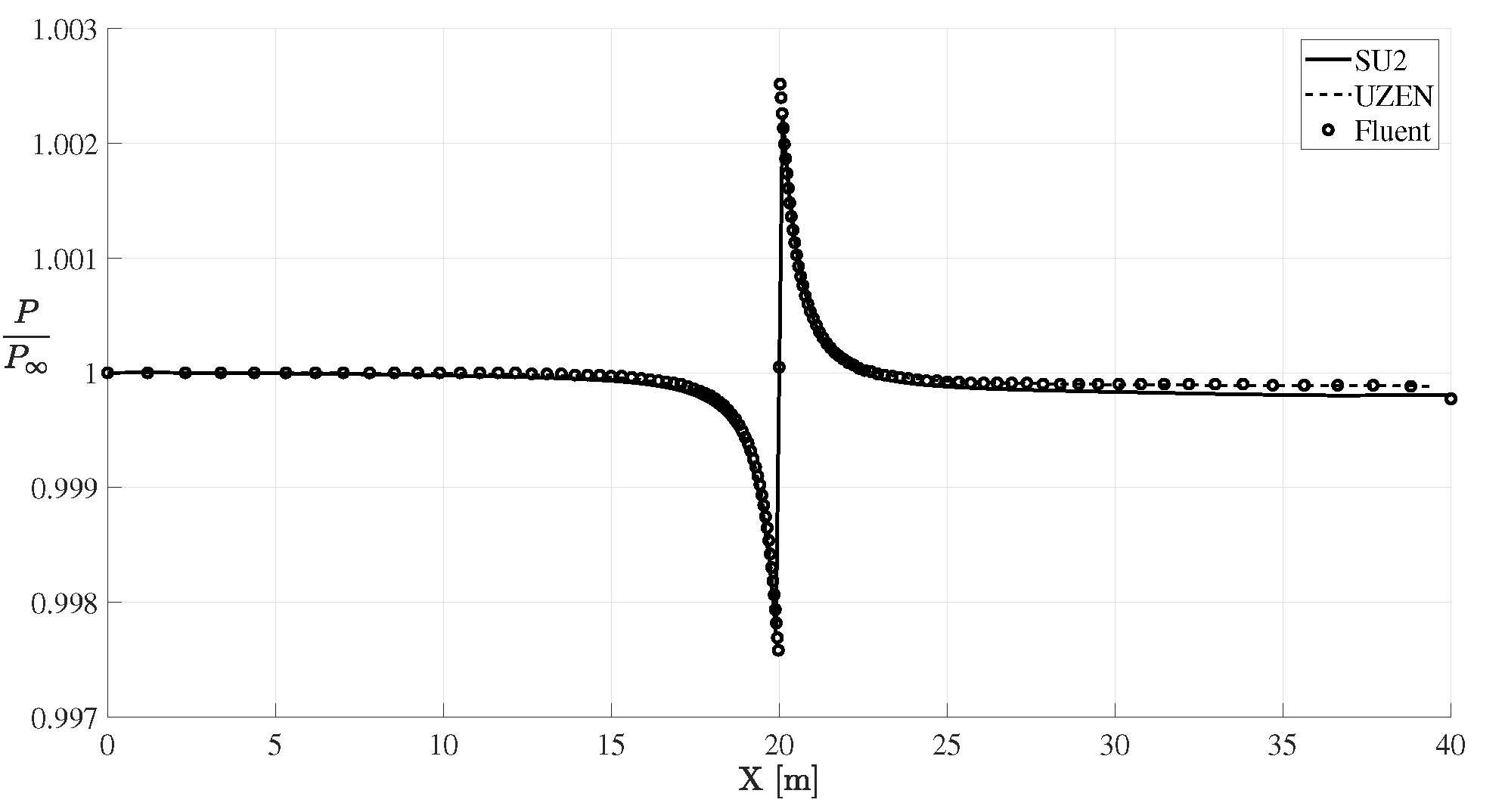
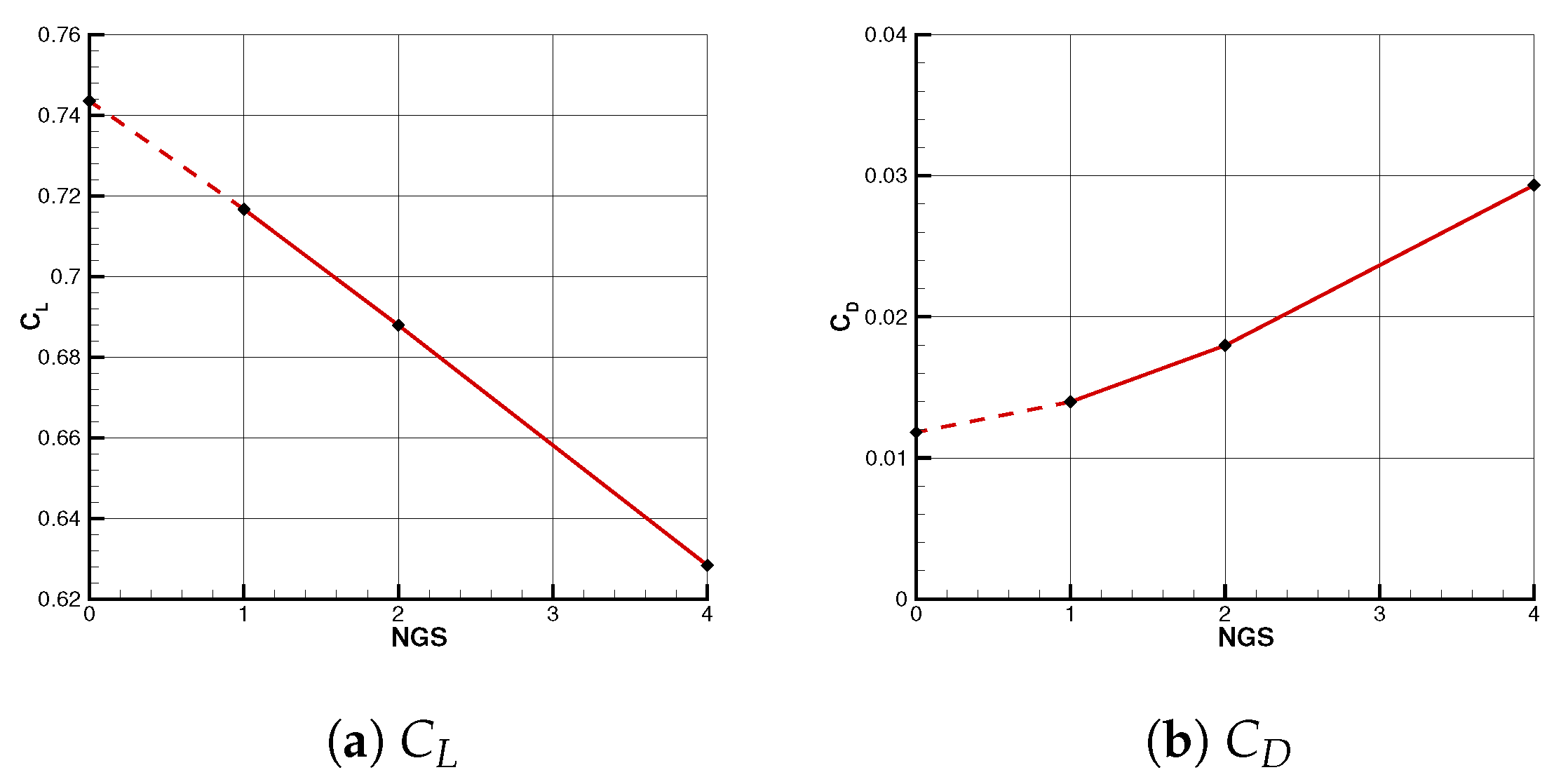

| SOLVER | Isolated Propeller | Convective Scheme |
|---|---|---|
| SU2 (power-off) | ROE (power-off) | ROE (power-off) - JSTMAT (power-on) |
| ANSYS-FLUENT | 2nd Ord. Upwind | 2nd Ord. Upwind |
| U-ZEN | JSTscalar |
| Parameter | Value/Type | SI Unit |
|---|---|---|
| Altitude | 0 | m |
| Free stream Mach number | 0.1175 | - |
| Disk diameter | 2.25 | m |
| Hub | From 0% to 25% of disk radius | - |
| Advance ratio | 0.6316 | - |
| Free stream density, temperature and pressure | ISA at sea level | - |
| Parameter | Value/Type | Measure Unit |
|---|---|---|
| Free stream Reynolds number | - | |
| Reference length | 2.563 | m |
| Free stream Mach number | 0.1175 | - |
| Disk diameter | 2.25 | m |
| Hub | From 0% to 25% of disk radius | - |
| Advance ratio | 0.6316 | - |
| Turbulence intensity | 0.1% | - |
| Turbulence viscosity ratio | 0.1 | - |
| Level | Cells’ Number | Normalized Grid Spacing | ||
|---|---|---|---|---|
| Coarse | 69,504 | 4 | 0.62836 | 0.029346 |
| Medium | 556,032 | 2 | 0.68793 | 0.017974 |
| Fine | 4,448,256 | 1 | 0.7167 | 0.01398 |
| Extrapolated | 0 | 0.74357 | 0.011818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, O.; Aprovitola, A.; de Rosa, D.; Pezzella, G.; Viviani, A. Computational Fluid Dynamics Analyses of a Wing with Distributed Electric Propulsion. Aerospace 2023, 10, 64. https://doi.org/10.3390/aerospace10010064
Russo O, Aprovitola A, de Rosa D, Pezzella G, Viviani A. Computational Fluid Dynamics Analyses of a Wing with Distributed Electric Propulsion. Aerospace. 2023; 10(1):64. https://doi.org/10.3390/aerospace10010064
Chicago/Turabian StyleRusso, Oreste, Andrea Aprovitola, Donato de Rosa, Giuseppe Pezzella, and Antonio Viviani. 2023. "Computational Fluid Dynamics Analyses of a Wing with Distributed Electric Propulsion" Aerospace 10, no. 1: 64. https://doi.org/10.3390/aerospace10010064
APA StyleRusso, O., Aprovitola, A., de Rosa, D., Pezzella, G., & Viviani, A. (2023). Computational Fluid Dynamics Analyses of a Wing with Distributed Electric Propulsion. Aerospace, 10(1), 64. https://doi.org/10.3390/aerospace10010064










