Abstract
Thermal performance has long been recognized as a critical attribute for space systems. Thermal control surface coating is a common method in passive thermal protection. Unfortunately, limited analyzing models and data on the influence of thermal control coatings’ α/ε (absorptivity/emissivity) on the space power system have been published to date. To fill this gap, we proposed a multiphysics model that combined environmental temperature calculating and electrical performance analysis together for the satellite power system. In this paper, different coating materials are applied to the radiator surface and thermal insulation surface, respectively. Additionally, a new concept of energy storage, named energy storage voltage, is introduced. The results are analyzed and parametric fits with different formulas using ordinary least squares are conducted. Finally, the change rules are presented, which will prove particularly useful to the space industry, for example, in thermal designs and on-orbit battery studies.
1. Introduction
As the space environment is complicated, applied thermal control coatings to spacecraft have become a widespread method of passive thermal protection. Thermal control has long been recognized as a critical attribute for space systems and an essential metric in spacecraft design and optimization. For example, rear-surface mirrors were used on satellites’ surfaces to dissipate large amounts of internal heat and provide a low operating temperature [1,2]. Thermal control coatings applied to the space station kept the temperature in acceptable ranges [3]. Changing the emissivity of the solar array surface coating can control the supercooling and overheating of the power generation system [4]. In brief, high flux heat acquisition with tight temperature control is a major requirement in space [5].
To satisfy thermal demands, a lot of new materials were developed as new-type space coatings. Haddad et al. developed a VO2-based tunable-emittance space coating which allowed a positive switching of the emittance with the temperature [6]. Sydney Taylor et al. simulated a VO2-based nanophotonic variable-emittance coating in a cold space environment [7]. Their study results showed that this nanophotonic coating could be used for spacecraft thermal control with excellent temperature stability and resistance to thermal cycling. Another thermoregulating material—Li4Ti5O12 (LTO) was studied by Jyotirmoy Mandal et al. [8]. LTO could transition from a super-broadband optical reflector to a solar absorber and thermal emitter. LTO also attained a large tunable temperature difference (18 ℃) under sunlight, making it a prospective material in space. In addition, Christopher L. Bertagne et al. designed a new radiator concept using shape memory alloy geometry [9]. The thermal-driven deformation effect allowed passive control of the primary surface emissivity.
It is well known that the ratio of absorptivity to emissivity (α/ε) determines a coating’s thermal performance [10]. However, how thermal control coating’s α/ε affects the thermal environment and internal electrical equipment is still unknown. Amir Hossein Fartash in his research studied the barrier coating system under various types of thermal loadings and found that the transient temperature fields strongly depend on the type of thermal load and thermal properties of the coating [11]. Unfortunately, despite the recognition of its importance, only a small amount of research on the electric–thermal behavior of space power systems has been published to date. Most of the analysis models are, however, focused on explaining the temperature variation in thermal design [12,13] and the coating selections based on transient-state temperature [14]. The electric–thermal behavior, changed due to the α/ε, has not been considered yet.
The Li-ion battery in space is instable, and the power system faces many challenges. Large temperature difference brought by light alternation is a unique challenge to satellite power systems [12]. For example, the surfaces of the International Space Station were subjected to temperature cycles between 173 K and 373 K every 45 min [7]. Some active thermal control technologies were added to the space energy system. Shengnan Wang presented a forced gas cooling strategy combined with a liquid cooling plate for Li-ion batteries in space [15]. The temperature uniformity and the temperature control effectiveness could increase by 2.42 times and 2.61 times more than traditional vacuum packages, respectively. Hui-juan Xu used a single-phase fluid loop that employed active control strategies to adjust the cooling ability of the Li-ion battery pack [16]. Additionally, significant reductions in battery capacity happen in cold conditions [17], which is a problem when the satellite moves into the shadow area. Li-ion batteries are very sensitive to temperature. At low operating temperatures, chemical-reaction activity and charge–transfer velocity will be slow, which leads to a decrease in ionic conductivity in the electrolytes and lithium-ion diffusivity within the electrodes [18]. Considering this bad effect, Mingyun Luo reported a full-temperature thermal management with a composite phase change material [19]. This thermal management of Li-ion batteries could provide a comfortable thermal environment of 20–55 °C under extreme conditions of −40~+50 °C. Overcharge is another important reason that may cause the failure of the Li-ion batteries [20]. To avoid overcharge and overdischarge, additional battery control units were added to spacecraft. NASA had re-designed the Li-ion Rechargeable Extravehicular Activity Battery Assembly to reduce the risk of a catastrophic thermal runaway incident [21]. This is an important matter because the performance of batteries directly affects the health of satellites. As a result, the performance analysis model of the power system in the satellite is vital. However, research on how the coating’s α/ε affects the satellite’s inner environment and power system is unclear.
To fill the gap in theoretical studies around α/ε of different coatings, and by the same token observing the electric–thermal behavior of satellite power systems, we conducted a multiphysics model of the satellite power system. The proposed model comprehensively considers the satellite’s environment temperature and the electrical performance of the Li-ion battery. In this study, some coating materials are selected to analyze the impacts of different α/ε on the satellite power system and batteries. Our objective is to find the relationship between surfaces’ α/ε and the electric–thermal behavior of satellite power systems. In addition to finding the change rules, research data parametric fits are conducted with different formulas using ordinary least squares.
The main contributions of this study are as follows:
- (a)
- A multiphysics model is introduced to analyze the electric–thermal behavior of space systems. Dynamic temperature models are developed to simulate the thermal environment of the satellite power system, from which the thermal effects of the surface’s coating can be observed. In temperature-influenced electrical models, the key electrical parameters of the Li-ion battery pack and single cells are expressed.
- (b)
- The change rules of temperatures and electric–thermal behavior with coating’s α/ε is clear. Error analysis and data fitting are conducted to investigate the accuracy of regularities. The results presented in this work should prove useful to the space industry, for example, in thermal designs and on-orbit battery studies.
The remainder of this paper is organized as follows. The architecture of the satellite power system, on behalf of the typical space power system and current issues of interdisciplinary performance, is introduced in Section 2. In Section 3, the comprehensive models of the satellite Li-ion battery power system and the simulation procedure are presented. Based on the model of Section 3, parametric analysis and fitting are displayed in Section 4, and the change rules are qualitatively analyzed. Finally, in Section 5, the study results are evaluated and concluded.
2. Architecture of Space Li-Ion Battery Power System and Current Issues of Interdisciplinary Performance
2.1. Architecture of Space Li-Ion Battery Power System
The space power system is formed by solar arrays, storage batteries, power controller and a power regulator module. Due to its long lifetime and high energy density, the Li-ion battery gradually replaced the traditional energy storage battery and became the main strength of the space energy storage component [22]. The architecture of a satellite and its power system are introduced in Figure 1a. To guarantee the thermal status of the battery pack, thermal bus is added, which could transfer heat to the radiator surface.
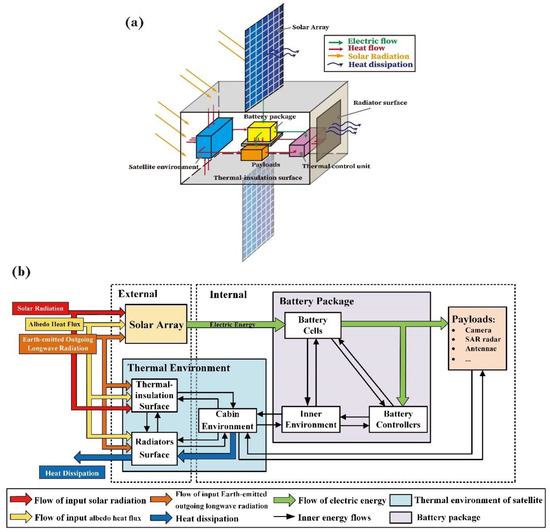
Figure 1.
(a) Structure of the satellite and the energy flow; (b) Energy exchange diagram in the satellite.
The energy flows in the satellite power system are shown in Figure 1b. There are two main energy types in the space Li-ion battery system: electrical energy and thermal energy. Electricity ensures regular work and simultaneously generates thermal energy. As for the thermal energy, in addition to the heat generated by the payloads while operating, solar radiation and earth radiation also have thermal impacts on the space Li-ion power system.
2.2. Problems in Analyzing Interdisciplinary Performance and Electric–Thermal Behavior
As described in the previous section, electrical energy and thermal energy are concomitant in the satellite power system. As the space environment is more particular than the ground, the huge temperature difference and complicated conditions make the interdisciplinary performance of the satellite power system difficult to predict. Li-ion batteries’ designed operating temperature is 25 °C, and the performance of Li-ion batteries is sensitive to temperature changes. Additionally, the heat generated by inner payloads will conversely affect the thermal condition. Keeping the power system in an acceptable condition is significant. However, the electric–thermal behavior of the satellite power system working in space is unclear. Most of the studies are focused on explaining the low-temperature behavior and the degradation mechanism of the PV/battery power system on the ground. Only a small amount of research has been published which noticed the interdisciplinary performance of satellite power systems.
In addition, thermal control coatings which could change the original thermal radiation characteristics of surfaces are widely used in space passive thermal control. The α/ε has a huge impact on the thermal environment of the satellite. Different thermal control coatings have different α/ε. Studies focused on how α/ε affects the electric–thermal behavior of satellites are fewer.
This research aims to form comprehensive models which could describe the thermal state of the satellite and the electric–thermal behavior of the Li-ion battery in the satellite power system. At the same time, trends in the electric–thermal performance of space power systems with changes of coating will be explored.
3. Comprehensive Models of Satellite Li-Ion Battery Power System
In this section, comprehensive models are developed to analyze the performance of the satellite power system. The models are composed of dynamic temperature models and temperature-influenced electrical models. Calculating formulas of some key performance parameters of Li-ion batteries are given in the temperature-influenced electrical models. Dynamic thermal models describe the thermal environments in the satellite and Li-ion battery pack. Then, in Section 3.3, the parameters of different coatings are represented and their α/ε are given. These selected coatings are used in the thermal insulation surface and thermal dissipation surface of the satellite separately. A designed satellite model is given to simulate the on-orbit performance. The parameters of this designed satellite and its orbit are represented in Table 1.

Table 1.
Satellite and orbital parameters.
3.1. Temperature-Influenced Electrical Models
According to the law of conservation of energy, the energy balance equation of a satellite power system is written as Equation (1):
where is the power output by the solar array; is the power output by the Li-ion battery pack; is the power demand by the payloads; and is the unused power. The left side of Equation (1) is the supply side, while the right side is the demand side. As the demands of a satellite are specific, the charging state of the battery pack is determined by the demands and the power generated by the solar array as shown in Equation (2):
where a and b are state coefficients. When a = 1, the battery pack is charging; when b = 1, the battery pack is discharging. The temperature-influenced electric models are obtained below.
- Solar array
The solar array is the only component that produces energy in a PV/battery power system. The energy harvested from the solar array is shown in Equation (3).
where q1 is the input solar radiation and is the photoelectric conversion efficiency. In this study, the voltage of the solar array is considered the optimum output voltage = 30 V. As the temperature also has an impact on the solar array, the revised voltage is obtained as Equation (4) according to the [23]:
where β is the temperature correction coefficient of voltage. From Daniel Tudor Cotfas’s study [24], β was between −0.002 and −0.008 depending on the material of the solar cell. In this research, β is set as −0.006. Additionally, the output current of the solar array is presented in Equation (5):
- Li-ion battery pack
Because of their high energy density and long lifetime, Li-ion batteries are often used as the energy storage battery in satellite power systems. To satisfy the power demands of payloads, many cells are combined in a battery pack. Figure 2 shows the structure of the battery pack. Heat generated in the pack is gathered in the conductive thermal bus, which is associated with the radiator. Beside the pack is the power control unit, which controls the battery’s behaviors in the power system. Auxiliary heating patches are also applied to every single cell.
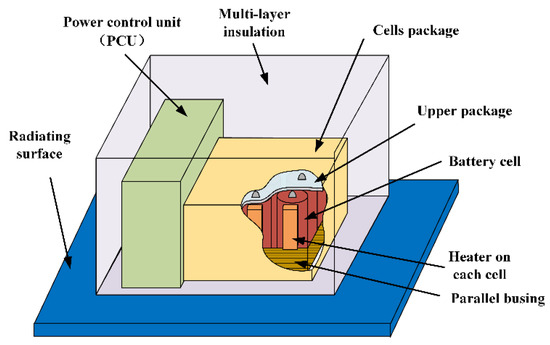
Figure 2.
The structure of the satellite battery pack.
As for the single cell, the inner structure is simplified in Figure 3. is Ohm resistance; is polarization resistance and is self-discharge resistance. To describe the cell’s storage conditions more clearly, energy storage voltage is first introduced in this model. Capacitance is considered as the power storage module in the simplified model and the voltage across the is defined as power-storage voltage . As the and is certain, the state expression of and the energy conservation equation of a cell is shown in Equations (6) and (7). The parameters a and b are on behalf of the states of a single cell. In both dynamic equations, the side with parameter a represents the charging state, while b represents the discharge state.
where iin and iout represent the charging current and discharging current, respectively. Their expressions are written as Equations (8) and (9):
where uin (Equation (10)) and uout (Equation (11)) are controlled by the voltage outputted by solar array Usa and the voltage demanded by payloads UL.
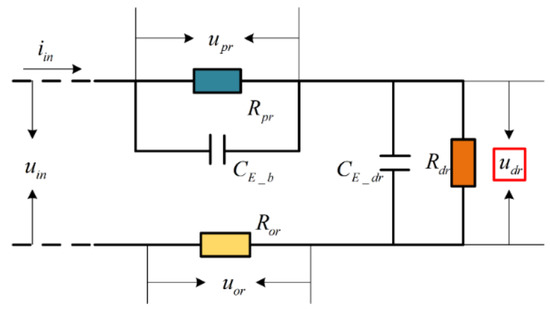
Figure 3.
The simplified inner structure model of a single cell.
The SoC can be described as Equation (12):
where the is the actual capacity. is determined by the cell’s temperature Tb and charge rate It. Because there has no specific expression, can be expressed as Equation (13):
where is nominal capacity and A0, A1, A2 are the fitting parameters. To make the model more comprehensive, the internal resistance , which is influenced by both cell’s temperature Tb and SoC, is shown as Equation (14):
The fitting data and the values of these fitting parameters are shown in Appendix A. The reason to establish Equations (13) and (14) is to roughly express the different influence conditions using one equation. On the one hand, the influence of variables such as temperature, charging rate and SoC on the system capacity and state can be observed. On the other hand, the electrical state of the system will also be fed back into the equations, thus reflecting the electric–thermal coupling effect.
3.2. Dynamic Temperature Models of the Space Power System
- Satellite thermal environment
According to Figure 1b, solar radiation, albedo heat flux and earth-emitted outgoing longwave radiation are the three main radiation sources for a satellite in low Earth orbit [25]. Additionally, in Figure 1b, a satellite’s thermal environment is divided into three parts: thermal-insulation surface, radiator surface and cabin environment. It is considered that temperatures are evenly distributed in these parts. Subscripts c, s, r are defined to represent the cabin environment, thermal-insulation surface with coating and radiator surface separately. Based on the first law of thermodynamics, the average temperature model of three thermal environments is established as Equation (15):
where is the sum of the thermal power produced in the cabin environment; , are the sum of radiation absorbed by the thermal insulation surface and radiator surface, and the equations are shown in Equations (16) and (17). q is the heat flux and the subscript i represents solar radiation, albedo heat flux and earth-emitted outgoing longwave radiation from 1–3, respectively. The input heat fluxes outside the satellite in this study are shown in Figure 4. As the inner heat flux shown in Figure 5 is mainly caused by the payloads, the heat efficiency is set at 60%, according to Shengnan Wang’s research [15].
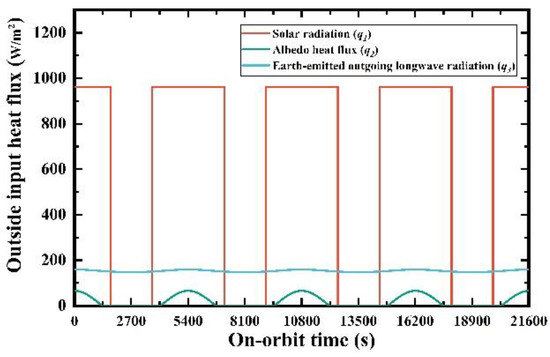
Figure 4.
The input heat fluxes outside the satellite.
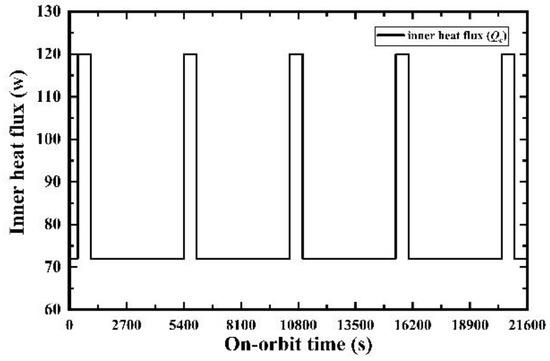
Figure 5.
The inner heat flux input in the satellite power system.
(Equation (18)) is the heat capacity distribution matrix of the thermal environment:
is the heat transfer characteristic matrix within the satellite, as Equation (19):
where k is the overall heat transfer coefficient; subscript cr represents the coefficient between the cabin environment and radiator surface; subscript cs represents the coefficient between the cabin environment and thermal-insulation surface; and subscript sr represents the coefficient between the thermal insulation surface and radiator surface. The specific values are shown in Table 2.

Table 2.
Thermo-physical properties of the satellite and Li-ion battery cell, and other materials.
- Solar array
Because the solar array in the space power system is not the main research object of this research, the temperature of the solar array is simplified as Equation (20):
where is the input solar power (in Equation (21)) and subscript sa represents the solar array. The solar array’s weight , heat capacity , absorbtivity and emissivity are reported in Table 2.
- Li-ion battery pack
According to the pack structure shown in Figure 6, a single battery cell’s temperature is affected by its surroundings’ temperature, the temperature of the enclosure and the temperature of the radiant surface. When the battery pack does not have an upper package, a battery cell’s temperature is established in Equation (22):
where subscript b_ij is the Li-ion cell in i line j row. is the thermal power produced by cell No. ij; is the auxiliary heating power of the No. ij cell and is the efficiency of auxiliary heating. Subscript bc, br, bs mean that the parameter represents the relationship between battery cells and the pack environment, radiator surface, or thermal-insulation surface. is the temperatures in the pack environment and subscript x represents the temperatures in three different zones from 1 to 3.

Figure 6.
Single cells’ distribution in the battery pack and three zones divided by the temperatures. (Representative batteries No. 11, 24, 36 are in deep colors separately.)
In this model, some assumptions are set: (1) any heat exchange form is inexistent between battery cells; (2) cells’ weight mb, heat capacity CH_b, thermal efficiency, heat transfer coefficient kb and heat transfer area Ab are congruous; and (3) the battery pack is divided into three zones according to the temperature distribution shown in Figure 6. The outside cells are defined in the low-temperature zone, as their environment temperature is the lowest, and close to the cabin temperature. The medium-temperature zone comprises cells No. 22, 23, 26, 27, 32, 33, 36, 37. Additionally, cells No. 24, 25, 34, 35 are in the hottest zone in the pack, named the high-temperature zone. The average temperatures of these zones are representative of electric–thermal behavior analysis.
3.3. Selection of Thermal Control Coatings
Though more than one passive thermal control measure must be used in any spacecraft, passive thermal control is the basis of space thermal control. Passive methods rely on the thermal arrangement to adjust the temperature. Thermal control coating is a surface material that can change the surface’s radiation properties to achieve thermal control targets. As is well known, the only way for spacecraft to reject heat obtained from inner equipment and space is thermal radiation; coating selection determines the cooling quality of spacecraft.
The thermal-insulation surfaces absorb a lot of radiation in the sunlight zone which is unexpected to enter the cabin. While in the shadow area, the low-temperature environment leads to heat-preserving demand. Hence, the thermal-insulation surfaces need high α/ε coatings [26]. For satellites, the main purpose of the radiator surface is heat dissipation. The coatings used on the radiator surface should have a relatively low α/ε. Some different coatings are selected in this research, and their absorptivity α, emissivity ε and α/ε are demonstrated in Table 3 and Table 4.

Table 3.
Coating materials for radiator surfaces.

Table 4.
Coating materials for thermal insulation surfaces.
4. Results and Discussions
In this section, thermal and electric analyses are carried out. Three cells (11, 24, 36) belonging to the three zones indicated in Figure 6 are selected to show the research results.
4.1. The Cyclical Effect of on Thermal Performance
- Radiator surfaces
The radiator surface’s thermal performance affects the thermal control directly. After simulation, the average temperature in the battery pack rises from 279 K to 297 K with the increase of αr/ε. In Figure 7a, the best average temperature for the whole pack is between 0.5 to 0.8 in this simulation. When αr/ε < 0.5, there is a dramatic increase in the average temperature. This proved that when in the low αr/ε range, the rise of αr/ε has a greater impact on the average temperature of the Li-ion battery pack.

Figure 7.
The average temperatures of the battery pack and fitting results with different radiator surface’s coatings: (a) The average temperature changing with ; (b) Absolute difference and standard deviation of the single cells’ temperature and the fitting value.
For single cells in Figure 7a, No. 36′s average temperature is closest to the fitting results. Its data points almost fall in the 95% confidence interval of the average temperature fitting line. Some data points of No. 11 and 24 are also in the 95% prediction interval in Figure 7a, and the fitting lines’ parameters are shown in Table 5. The discrete degree of 3 zones’ average temperature climbs with the increasing of αr/ε in Figure 7b should also be noted. When the αr/ε of the radiator surface rises, the temperature difference in the pack would increase, which should be avoided.

Table 5.
The fitting polynomial and parameters of average temperatures changing with .
The single cells’ temperature differences are represented in Figure 8a and the fitting lines’ parameters are shown in Table 6. The temperature difference of the battery decreases with rising. The decline of standard deviation between the fitting result and simulating data in Figure 8b declares that the temperature differences of cells become closer. This phenomenon indicates that the cell’s peak temperature drops and the temperature fluctuation reduces. A moderate temperature is good for Li-ion cells. These observations are not conflicting with the conclusions obtained from Figure 7. Decreases in the temperature difference of cells do not affect the increasing trends of the average temperature in the battery pack. Though higher benefits single cells, the pack’s thermal performance is aforementioned and the of the radiator surface should be relatively lower.
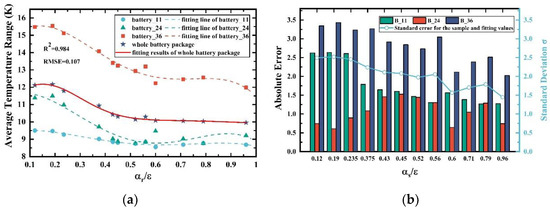
Figure 8.
The average temperature differences of the battery pack and fitting results with different radiator surface’s coatings: (a) The average temperature differences changing with ; (b) Absolute difference and standard deviation of the single cells’ temperature differences and the fitting value.

Table 6.
The fitting polynomial and parameters of average temperature differences changing with .
- Thermal-insulation surfaces
In this part, cells No. 11, 24 and 36 are chosen to represent different temperature zones. The average temperatures changing with are shown in Figure 9a. The pack’s average temperature climbs from 271 K to 283 K. In Figure 9a, the average temperatures of the chosen cells also grow with the increase of . Though the cells’ temperatures in this simulation may be lower, the Li-ion battery pack would have higher performance when .

Figure 9.
The average temperatures of the battery pack and fitting results with different thermal-insulation surface’s coatings: (a) The average temperature changing with in the battery pack; (b) Absolute difference and standard deviation of the single cells’ temperature and the fitting value.
With the statistical analysis of these data, the fitting results are proved in Figure 9a. The least squares method is used in polynomial fittings, and the fitting parameters in different expressions are obtained in Table 7. A 95% confidence interval and a 95% prediction interval of the battery pack’s average temperature are given in Figure 9a. The data points of cell No. 36 are all in the 95% prediction interval, which means that the medium-zone average temperature trend could indicate the pack’s average temperature trend.

Table 7.
The fitting polynomial and parameters of average temperatures changing with .
Figure 9b shows the absolute errors between the cells’ average temperature and the pack’s average temperature. In Figure 9b, the conclusion gained from Figure 9a is proved again: that the average temperature curve of No. 36 can predict the average temperature of the battery pack. Furthermore, the standard deviation has a slump of 6.3 when . The decline of standard deviation means that the gaps among different temperature zones reduce with the growth of .
Figure 10 provides the results and statistical analyses of the temperature differences during the simulation time. The temperature difference is the difference between the maximum temperature and minimum temperature, which reflects the temperature uniformity in the battery pack. The temperature difference decreases with the increase of . Single cells’ temperature differences have similar trends. Therefore, improving the of thermal-insulation surfaces can reduce the temperature difference in the pack. Cells’ fitting parameters are shown in Table 8.

Figure 10.
The average temperatures of the battery pack and fitting results with different thermal-insulation surface coatings: (a) The average temperature differences changing with ; (b) Absolute difference and standard deviation of the single cells’ temperature difference and the fitting value.

Table 8.
The fitting polynomial and parameters of average temperature differences changing with .
For a single cell, the temperature difference in the medium-temperature zone is the highest. The rise of has the greatest impact in the low-temperature zone, as the temperature difference of No. 11 decreased by 35% in Figure 10a. The standard deviation in Figure 10b indicates that the difference between the simulation data point and fitting results is nearly unchanged with .
4.2. The Cyclical Effect of on Electric–Thermal Coupling Behavior
- Radiator surfaces
Figure 11a shows the trend that energy storage voltage changes with , and the fitting results are provided in Appendix B (Table A3, Table A4, Table A5 and Table A6). Different fitting methods are applied to the data and the trends are the same: the energy storage voltage of a single cell increases with the rise of . As the energy storage voltage is used to indicate the electric quantity of battery storage, its change trend is similar to the trend of maximum capacity shown in Figure 11b. With growing, energy storage status improves. The reason for this phenomenon is that the pack’s average temperature rises.
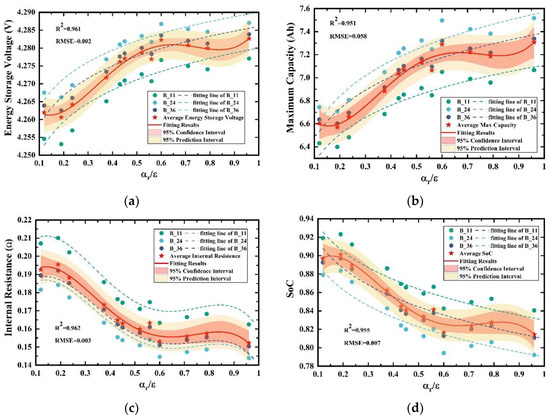
Figure 11.
The electric parameters changing with different radiator surface’s coating: (a) energy storage voltage; (b) maximum capacity; (c) internal resistance; (d) SoC.
The internal resistance drops markedly when is between 0.2 to 0.6. Lower internal resistance means less internal battery pack consumption and higher efficiency. This is also related to the rising temperature. The results are shown in Figure 11a–c. It seems that a higher of radiator surface is better. In contrast, the SoC of the battery pack declines in Figure 11d, which is connected to the increasing maximum capacity. High pack temperature makes the depth of discharge (DOD) grow. When the DoD is above 25%, the aging rate of the battery is accelerated. From this aspect, > 0.6 has disadvantages for electric–thermal behavior.
- Thermal-insulation surfaces
The thermal-insulation surface’s electric–thermal behaviors changing with is shown in Figure 12. Energy storage voltage and maximum capacity increase with rising while internal resistance and SoC fall. Change rules are the same for radiator surface, and the fitting parameters are represented in Appendix B (Table A7, Table A8, Table A9 and Table A10).
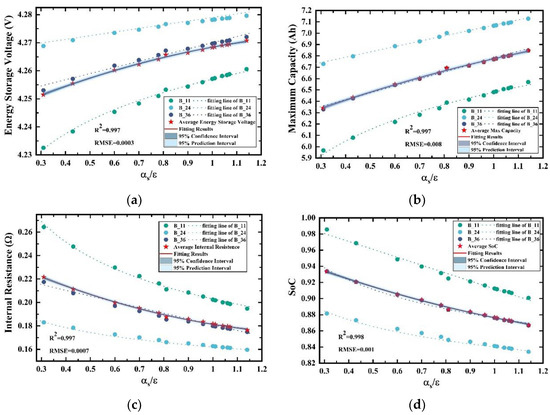
Figure 12.
The electric parameters changing with different thermal-insulation surface’s coating: (a) energy storage voltage; (b) maximum capacity; (c) internal resistance; (d) SoC.
In a word, the electric–thermal behavior changes with the satellite surface’s α/ε, which is independent of the position of surfaces. All the electrical impacts are caused by the temperature. Thus, thermal control is vital for on-orbit satellite power systems.
5. Conclusions
Thermal control is important for on-orbit satellites, and thermal control coatings have long been recognized as an effective method for passive thermal design. Temperatures in satellites are determined by the coatings’ α/ε. However, α/ε’s comprehensive impacts on the satellite environment and the Li-ion battery pack in the power system are not clear. Limited data and statistical analyses of electric–thermal behavior affected by α/ε exist in recent literature. In this work, we fill this gap by conducting multiphysics models of space Li-ion battery power systems and a numerical analysis of electric–thermal behaviors. Additionally, a newly defined characteristic value—energy storage voltage—is introduced to show the energy state of the battery pack. The results from our analysis are:
- The trends in temperature and electric–thermal behavior change with are similar in the radiator surface and thermal insulation surface. Thermal control coatings are selected according to the functions of the surfaces.
- Average temperatures and the temperature differences in the battery pack increase with , while the fluctuation of a single cell’s temperature declines.
- The energy storage state of the battery will be improved and the internal resistance and SoC would drop with the growth of . However, these optimizations come at the cost of higher temperatures.
Our research can provide support for the selection of coating in future space engineering. A limitation of this study is that the selection of coatings does not mention the latest achievements. In forthcoming work, these limitations will be overcome, the electric–thermal behavior regulation will be extended to battery aging studies.
Author Contributions
Each author has made substantial contributions to this work. Their specific contributions are: Methodology, J.X. and Y.S.; Investigation, L.Y.; Writing, J.X.; Project Administration, Y.-Z.L.; Supervision, Y.-Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financially supported by Beijing Institute of Spacecraft System Engineering under grant KH526-065-01.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data and models used in this study are in the published article.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Notation
| Nomenclature | Subscript | ||
| A | Area [m2] | c | Satellite cabin environment |
| S | Solar constant | s | Thermal-insulation-surface |
| P | Power [W] | r | Radiator surface |
| q | Input energy density [W/m2] | sa | Solar array |
| U | Voltage of the battery pack [V] | B | Battery pack |
| I | Current of the battery pack [A] | b | Single battery cell |
| CE | Capacitance [F] | L | Payloads |
| CH | Heat capacity [J/K] | d | Energy storage |
| u | Voltage of a single battery cell [V] | un | Unused |
| i | Current of a single battery cell [A] | max | Maximum |
| R | Resistance [Ω] | in | Input |
| a | Charging coefficient | out | Output |
| b | Discharging coefficient | c | Satellite |
| E | Electric energy [J] | 0 | Initial value |
| SoC | State of capacity | or | Ohm resistance |
| K | Heat transfer coefficient [W/(m2·K)] | pr | Polarization resistance |
| Q | Thermal energy [J] | dr | Self-discharge resistance |
| cs | Cabin environment with thermal-insulation-surface | ||
| Greek symbol | cr | Cabin environment with radiator surface | |
| Absorbtivity | sr | Thermal-insulation-surface with radiator surface | |
| Emissivity | ij | Row and column numbers | |
| Stefan-Boltzmann constant | bc | Battery cell with cabin environment | |
| Efficiency | bs | Battery cell with thermal-insulation-surface | |
| Temperature correction coefficient of PV’s voltage | br | Battery cell with radiator surface | |
| Time [s] | bx | Battery pack’s environment | |
| Capacity [Ah] | T | Values at temperature T K | |
Appendix A
The internal resistance of a battery cell is affected by its temperature and SoC. However, there has no expression to show the relationship between these variables. Data fitting is adopted, and the data from Figure 3.12 in [27] are represented in Table A1. The fitting equation is written as Equation (A1):

Table A1.
Internal resistance vs. temperature at various SoCs.
Table A1.
Internal resistance vs. temperature at various SoCs.
| SoC | SoC | ||||
|---|---|---|---|---|---|
| 258 | 0.05 | 6.1 | 283 | 0.05 | 2.5 |
| 0.3 | 5.8 | 0.3 | 2.1 | ||
| 0.5 | 5.5 | 0.5 | 2 | ||
| 1 | 5.1 | 1 | 2 | ||
| 263 | 0.05 | 5.05 | 288 | 0.05 | 2.1 |
| 0.3 | 4.8 | 0.3 | 1.95 | ||
| 0.5 | 4.6 | 0.5 | 1.8 | ||
| 1 | 4.2 | 1 | 1.8 | ||
| 268 | 0.05 | 4.1 | 293 | 0.05 | 2 |
| 0.3 | 3.9 | 0.3 | 1.85 | ||
| 0.5 | 3.85 | 0.5 | 1.5 | ||
| 1 | 3.5 | 1 | 1.5 | ||
| 273 | 0.05 | 3.55 | 298 | 0.05 | 1.9 |
| 0.3 | 3.1 | 0.3 | 1.8 | ||
| 0.5 | 3 | 0.5 | 1.3 | ||
| 1 | 2.95 | 1 | 1.3 | ||
| 278 | 0.05 | 3 | |||
| 0.3 | 2.65 | ||||
| 0.5 | 2.25 | ||||
| 1 | 2.2 |
Equation (A2) takes the ln of both sides of this equation:
The parameters B0 − B1 were obtained by data fitting: , , (R2 = 0.948).
The expression of capacity, temperature and charging rate is written as Equation (A3):
Fitting data shown in Table A2 are obtained from Figure 2 in [28]. Take the ln of both sides of this equation, and the parameters are calculated: , , (R2 = 0.61).

Table A2.
Capacity vs. temperature at various charging rates.
Table A2.
Capacity vs. temperature at various charging rates.
| 0.25 | 308 | 2.2 | 1 | 308 | 1.98 |
| 298 | 2.05 | 298 | 1.95 | ||
| 278 | 1.81 | 278 | 1.72 | ||
| 268 | 1.65 | 268 | 1.56 | ||
| 258 | 1.49 | 258 | 1.38 | ||
| 0.5 | 308 | 2 | 1.5 | 308 | 1.95 |
| 298 | 1.98 | 298 | 1.91 | ||
| 278 | 1.78 | 278 | 1.72 | ||
| 268 | 1.6 | 268 | 1.58 | ||
| 258 | 1.43 | 258 | 1.39 | ||
| 0.75 | 308 | 1.99 | 2 | 308 | 1.94 |
| 298 | 1.96 | 298 | 1.91 | ||
| 278 | 1.76 | 278 | 1.73 | ||
| 268 | 1.59 | 268 | 1.61 | ||
| 258 | 1.4 | 258 | 1.41 |
Appendix B
The fitting results with radiator surfaces’ are provided in Table A3, Table A4, Table A5 and Table A6 and the fitting results with thermal insulation surfaces’ are provided in Table A7, Table A8, Table A9 and Table A10.

Table A3.
The fitting polynomial and parameters of energy storage voltage changing with .
Table A3.
The fitting polynomial and parameters of energy storage voltage changing with .
| Fitting polynomial 1 | |||||
| Parameters | |||||
| Whole pack | 4.27 | −0.16 | 0.78 | −1.12 | 0.51 |
| Fitting polynomial 2 | |||||
| Parameters | |||||
| B_11 | 4.28 | 0.003 | |||
| B_24 | 4.29 | 0.0027 | |||
| B_36 | 4.286 | 0.0028 | |||
| Error analysis | Whole pack | B_11 | B_24 | B_36 | |
| R-square | 0.961 | 0.895 | 0.89 | 0.894 | |
| RMSE | 0.002 | 0.003 | 0.002 | 0.0025 | |

Table A4.
The fitting polynomial and parameters of maximum capacity changing with .
Table A4.
The fitting polynomial and parameters of maximum capacity changing with .
| Fitting polynomial 1 | |||||
| Parameters | |||||
| Whole pack | 6.97 | −5.83 | 26.71 | −37.49 | 17.05 |
| Fitting polynomial 2 | |||||
| Parameters | |||||
| B_11 | 7.11 | 0.055 | |||
| B_24 | 7.57 | 0.063 | |||
| B_36 | 7.39 | 0.058 | |||
| Error analysis | Whole pack | B_11 | B_24 | B_36 | |
| R-square | 0.951 | 0.9 | 0.89 | 0.895 | |
| RMSE | 0.058 | 0.077 | 0.094 | 0.085 | |

Table A5.
The fitting polynomial and parameters of internal resistance changing with .
Table A5.
The fitting polynomial and parameters of internal resistance changing with .
| Fitting polynomial 1 | |||||
| Parameters | |||||
| Whole pack | 0.18 | 0.31 | −1.51 | 2.17 | −1.00 |
| B_11 | 0.19 | 0.34 | −1.66 | 2.39 | −1.1 |
| B_24 | 0.17 | 0.28 | −1.4 | 2.02 | −0.93 |
| B_36 | 0.17 | 0.3 | −1.46 | 2.1 | −0.97 |
| Error analysis | Whole pack | B_11 | B_24 | B_36 | |
| R-square | 0.962 | 0.962 | 0.962 | 0.962 | |
| RMSE | 0.003 | 0.003 | 0.003 | 0.003 | |

Table A6.
The fitting polynomial and parameters of SoC changing with .
Table A6.
The fitting polynomial and parameters of SoC changing with .
| Fitting polynomial 1 | |||||
| Parameters | |||||
| Whole pack | 0.86 | 0.67 | −3.11 | 4.39 | −2.01 |
| Fitting polynomial 2 | |||||
| Parameters | |||||
| B_11 | −0.46 | 0.11 | 1.29 | ||
| B_24 | −0.49 | 0.12 | 1.28 | ||
| B_36 | −0.47 | 0.11 | 1.28 | ||
| Error analysis | Whole pack | B_11 | B_24 | B_36 | |
| R-square | 0.955 | 0.89 | 0.89 | 0.89 | |
| RMSE | 0.007 | 0.01 | 0.01 | 0.01 | |

Table A7.
The fitting polynomial and parameters of energy storage voltage changing with .
Table A7.
The fitting polynomial and parameters of energy storage voltage changing with .
| Fitting polynomial 1 | ||||
| Parameters | ||||
| Whole pack | 4.24 | 0.04 | −0.01 | |
| Fitting polynomial 2 | ||||
| Parameters | ||||
| B_11 | 4.257 | 0.005 | ||
| Fitting polynomial 3 | ||||
| Parameters | ||||
| B_24 | 0.013 | 4.266 | ||
| B_36 | 0.022 | 4.248 | ||
| Error analysis | Whole pack | B_11 | B_24 | B_36 |
| R-square | 0.997 | 0.995 | 0.987 | 0.979 |
| RMSE | 0.0003 | 0.0006 | 0.0004 | 0.0008 |

Table A8.
The fitting polynomial and parameters of maximum capacity changing with .
Table A8.
The fitting polynomial and parameters of maximum capacity changing with .
| Fitting polynomial 1 | ||||
| Parameters | ||||
| Whole pack | 6.1 | 0.86 | −0.18 | |
| Fitting polynomial 2 | ||||
| Parameters | ||||
| B_11 | 6.48 | 0.075 | ||
| Fitting polynomial 3 | ||||
| Parameters | ||||
| B_24 | 0.47 | 6.6 | ||
| B_36 | 0.61 | 6.17 | ||
| Error analysis | Whole pack | B_11 | B_24 | B_36 |
| R-square | 0.997 | 0.99 | 0.995 | 0.992 |
| RMSE | 0.0008 | 0.018 | 0..009 | 0.014 |

Table A9.
The fitting polynomial and parameters of internal resistance changing with .
Table A9.
The fitting polynomial and parameters of internal resistance changing with .
| Fitting polynomial 1 | ||||
| Parameters | ||||
| Whole pack | 0.25 | −0.1 | 0.03 | |
| Fitting polynomial 2 | ||||
| Parameters | ||||
| B_11 | 0.203 | −0.234 | ||
| B_24 | 0.162 | −0.106 | ||
| Fitting polynomial 3 | ||||
| Parameters | ||||
| B_36 | −0.049 | 0.23 | ||
| Error analysis | Whole pack | B_11 | B_24 | B_36 |
| R-square | 0.997 | 0.995 | 0.99 | 0.975 |
| RMSE | 0.0007 | 0.001 | 0.0007 | 0.002 |

Table A10.
The fitting polynomial and parameters of SoC changing with .
Table A10.
The fitting polynomial and parameters of SoC changing with .
| Fitting polynomial 1 | ||||
| Parameters | ||||
| Whole pack | 0.97 | −0.12 | 0.03 | |
| Fitting polynomial 2 | ||||
| Parameters | ||||
| B_11 | −0.098 | 1.01 | ||
| Fitting polynomial 3 | ||||
| Parameters | ||||
| B_24 | 0.84 | −0.043 | ||
| B_36 | 0.876 | −0.057 | ||
| Error analysis | Whole pack | B_11 | B_24 | B_36 |
| R-square | 0.998 | 0.987 | 0.983 | 0.99 |
| RMSE | 0.001 | 0.003 | 0.002 | 0.002 |
References
- Starner, K.E.; Stark, R.L. Effects of roughness on rear-surface mirror satellite coatings. J. Spacecr. Rocket. 1968, 5, 125–127. [Google Scholar] [CrossRef]
- Putz, B.; Wurster, S.; Edwards, T.; Völker, B.; Milassin, G.; Többens, D.; Semprimoschnig, C.; Cordill, M. Mechanical and optical degradation of flexible optical solar reflectors during simulated low earth orbit thermal cycling. Acta Astronaut. 2020, 175, 277–289. [Google Scholar] [CrossRef]
- Peters, J. System Level Testing of the Passive Thermal Control System for Space Station Freedom. In Proceedings of the 23rd International Conference on Environmental Systems, Colorado Springs, Colorado, 12–15 July 1993. [Google Scholar] [CrossRef]
- Foster, J.A.; Aglietti, G.S. Strategies for Thermal Control of a Multifunctional Power Structure Solar Array. J. Aerosp. Eng. 2012, 25, 454–462. [Google Scholar] [CrossRef][Green Version]
- Swanson, T.D.; Birur, G.C. NASA thermal control technologies for robotic spacecraft. Appl. Therm. Eng. 2003, 23, 1055–1065. [Google Scholar] [CrossRef]
- Haddad, E.; Kruzelecky, R.V.; Hendaoui, A.; Chaker, M.; Jamroz, W. Large Tuneability IR Emittance Thermal Control Coating for Space Applications. In Proceedings of the 43rd International Conference on Environmental Systems, Vail, CO, USA, 14–18 July 2013. [Google Scholar] [CrossRef]
- Taylor, S.; Boman, N.; Chao, J.; Wang, L. Cryothermal vacuum measurement of thermochromic variable-emittance coatings with heating/cooling hysteresis for spacecraft thermal management. Appl. Therm. Eng. 2021, 199, 117561. [Google Scholar] [CrossRef]
- Mandal, J.; Du, S.; Dontigny, M.; Zaghib, K.; Yu, N.; Yang, Y. Li4Ti5O12: A Visible-to-Infrared Broadband Electrochromic Material for Optical and Thermal Management. Appl. Phys. Lett. 2019, 115, 073902. [Google Scholar] [CrossRef]
- Bertagne, C.L.; Cognata, T.J.; Sheth, R.B.; Dinsmore, C.E.; Hartl, D.J. Testing and analysis of a morphing radiator concept for thermal control of crewed space vehicles. Appl. Therm. Eng. 2017, 124, 986–1002. [Google Scholar] [CrossRef]
- Johnson, J.; Cerbus, C.; Haines, A.; Kenny, M. Review of Improved Thermal Control Coating Development for NASA’s SEE Program. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 10–13 January 2013. [Google Scholar] [CrossRef]
- Fartash, A.H.; Poursaeidi, E. Thermal analysis of thermal barrier coating systems under transient and time harmonic thermal loads. Appl. Therm. Eng. 2022, 208, 118225. [Google Scholar] [CrossRef]
- Athirah, N.; Afendi, M.; Hafizan, K.; Amin, N.; Majid, M.A. Stress and Thermal Analysis of CubeSat Structure. Appl. Mech. Mater. 2014, 554, 426–430. [Google Scholar] [CrossRef]
- Corpino, S.; Caldera, M.; Nichele, F.; Masoero, M.; Viola, N. Thermal design and analysis of a nanosatellite in low earth orbit. Acta Astronaut. 2015, 115, 247–261. [Google Scholar] [CrossRef]
- Reyes, L.A.; Cabriales-Gómez, R.; Chávez, C.E.; Bermúdez-Reyes, B. Thermal modeling of CIIIASat nanosatellite: A tool for thermal barrier coating selection. Appl. Therm. Eng. 2020, 166, 114651. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Li, Y. A forced gas cooling circle packaging with liquid cooling plate for the thermal management of li-ion batteries under space environment. Appl. Therm. Eng. 2017, 123, 929–939. [Google Scholar] [CrossRef]
- Xu, H.-J.; Wang, J.-X.; Li, Y.-Z.; Bi, Y.-J.; Gao, L.-J. A Thermoelectric-Heat-Pump Employed Active Control Strategy for the Dynamic Cooling Ability Distribution of Liquid Cooling System for the Space Station’s Main Power-Cell-Arrays. Entropy 2019, 21, 578. [Google Scholar] [CrossRef] [PubMed]
- Bonkile, M.P.; Ramadesigan, V. Physics-based models in PV-battery hybrid power systems: Thermal management and degradation analysis. J. Energy Storage 2020, 31, 101458. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Luo, M.; Song, J.; Ling, Z.; Zhang, Z.; Fang, X. Phase change material coat for battery thermal management with integrated rapid heating and cooling functions from −40 °C to 50 °C. Mater. Today Energy 2021, 20, 100652. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Fang, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Mater. Today Energy 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Thomas, P.B.; Margot, L.W. Spacecraft Li-Ion Battery Power System State-of-Practice: A Critical Review. In Proceedings of the 2018 International Energy Conversion Engineering Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Schoen, A.; Powers, A.R.; Arastu, A.; Canter, S.; Hall, J. High Performance Lithium Ion Battery Systems Development for Long Life Geostationary Satellites. In Proceedings of the 3rd International Energy Conversion Engineering Conference, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Bazarbayev, R.; Yakubov, K.; Kurbanov, D.; Allaniyazov, A.; Balakumar, S.; Kamalov, A.; Janabergenova, G.; Wei, Q.; Qian, H.; Polvonnazirov, I.; et al. Performance of crystalline Si solar cells and module on temperature and illumination intensity. Mater. Today: Proc. 2022, 64, 1661–1665. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Cotfas, P.A.; Machidon, O.M. Study of Temperature Coefficients for Parameters of Photovoltaic Cells. Int. J. Photoenergy 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Bonnici, M.; Mollicone, P.; Fenech, M.; Azzopardi, M.A. Analytical and numerical models for thermal related design of a new pico-satellite. Appl. Therm. Eng. 2019, 159, 113908. [Google Scholar] [CrossRef]
- Shrestha, S.; Del Pino, C.B.; Malayoglu, U. Inorganic White Thermal-Control Coatings for Extreme Space Environments. J. Spacecr. Rocket. 2016, 53, 1061–1067. [Google Scholar] [CrossRef]
- Gong, X. Modeling of Lithium-ion Battery Considering Temperature and Aging Uncertainties. Ph.D. Thesis, University of Michigan Dearborn, Dearborn, MI, USA, 2016; p. 53. [Google Scholar]
- Li, L.; Xie, Y.; Cao, L.; Huang, K. Analysis of different cathode materials of lithium-ion battery capacity characteristics. Chin. J. Power Sources 2017, 41, 1677–1680. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).