Ensembles for Viticulture Climate Classifications of the Willamette Valley Wine Region
Abstract
:1. Introduction
2. Materials and Methods
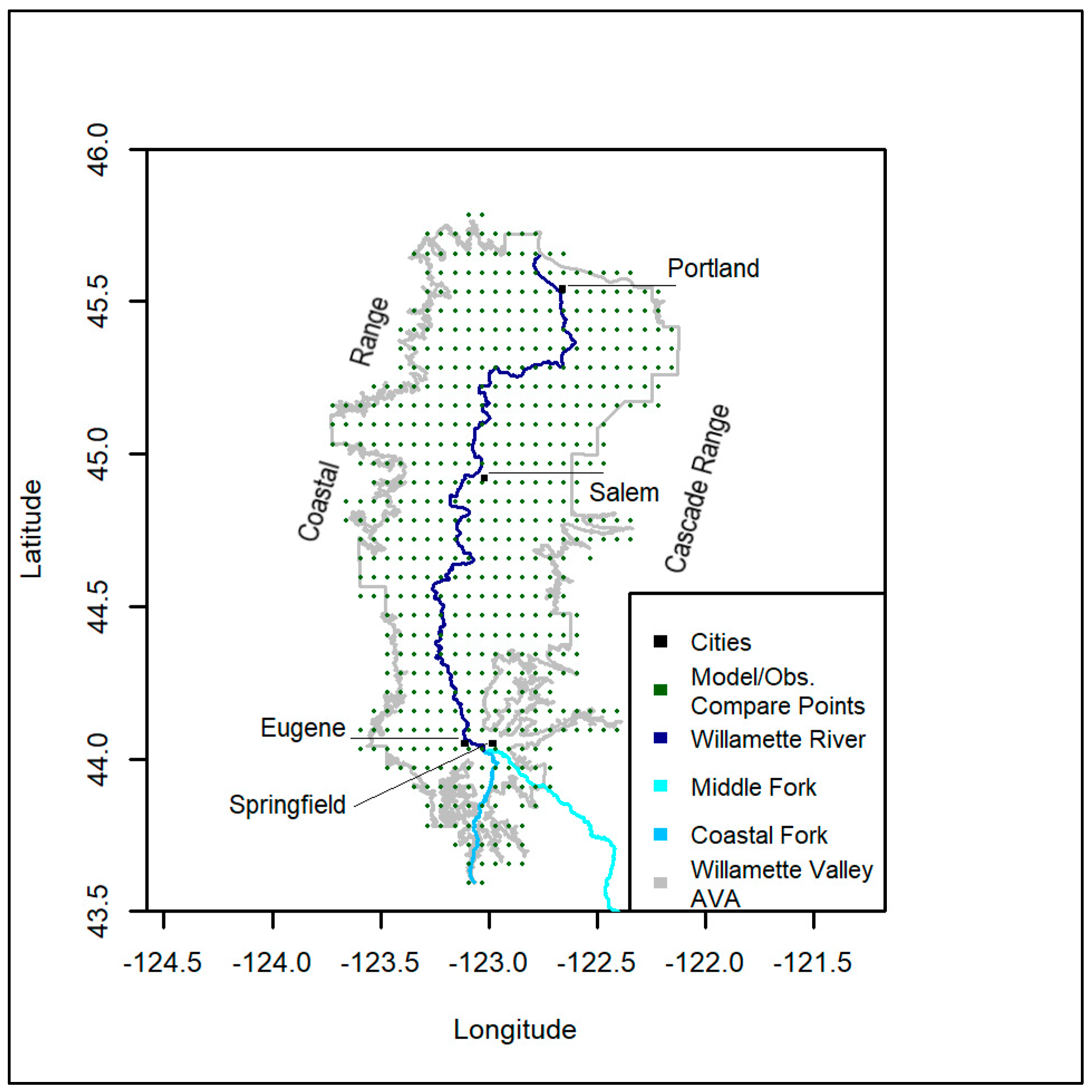
2.1. Study Region
2.2. Time Series Data
2.3. Viticulture Climate Indices and Processed Datasets for Prediction Specific Modeling Analyses
2.4. Modeling Averaging Methods
2.4.1. Model
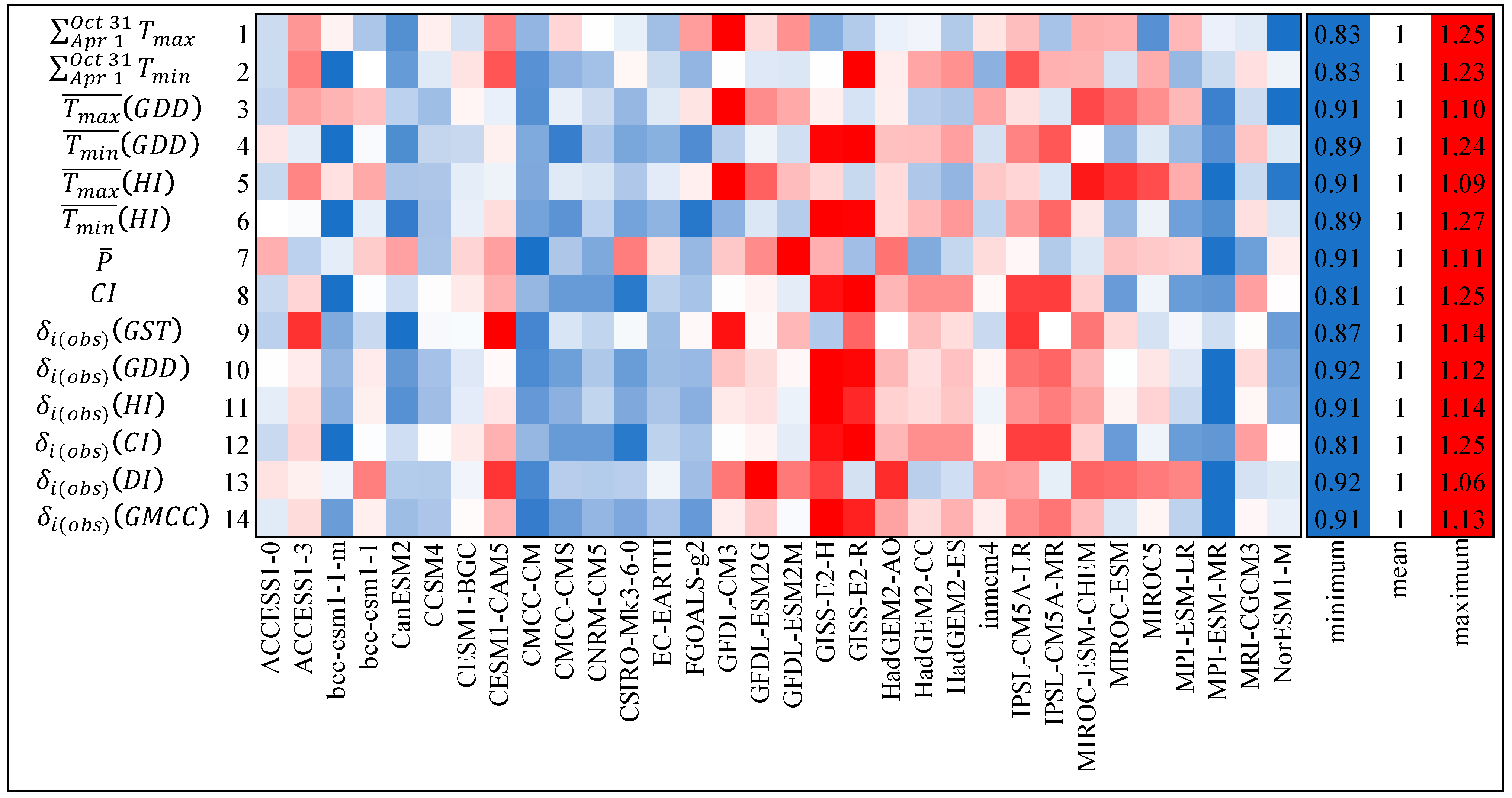
2.4.2. Skill Weighting
2.4.3. Skill and Model Interdependence Weighting
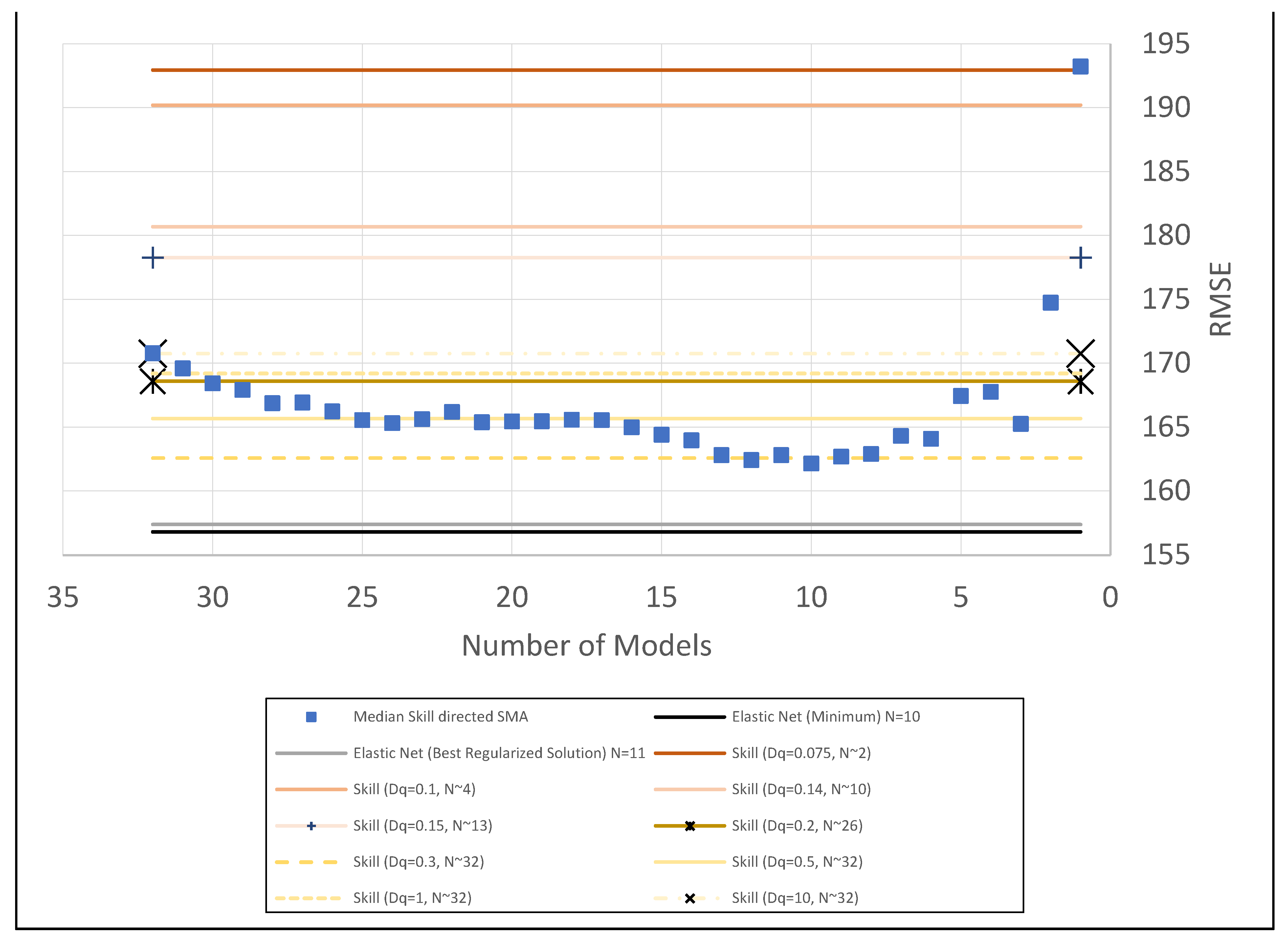
2.4.4. Model Median Skill Directed Simple Model Averaging
2.4.5. Elastic-Net Regularization
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Winkler, J.; Cook, J.; Kliewer, W.M.; Lider, L.A. General Viticulture, 4th ed.; University of California: Berkeley, CA, USA, 1974. [Google Scholar]
- Carbonneau, A. Ecophysiologie de la vigne et terroir. In Terroir, Zonazione Viticoltura; Fregoni, M., Schuster, D., Paoletti, A., Eds.; Phytoline: Piacenza, Italy, 2003; pp. 61–102. [Google Scholar]
- Jones, G.V.; Duff, A.; Hall, A.; Myers, J. Spatial Analysis of Climate in Winegrape Growing Regions in the Western United States. Am. J. Enol. Vitic. 2010, 61, 313–326. [Google Scholar]
- Shaw, T.B. Climate change and the evolution of the Ontario cool climate wine regions in Canada. J. Wine Res. 2016, 28, 13–45. [Google Scholar] [CrossRef]
- Coombe, B. Influence of temperature on composition and quality of grapes. Acta Hortic. 1987, 206, 23–36. [Google Scholar] [CrossRef]
- Hunter, J.J.; Bonnardot, V. Climatic requirements for optimal physiological processes: A factor in viticultural zoning. In Proceedings of the 4th International Symposium on Viticultural Zoning, Avignon, France, 17–20 June 2002; pp. 553–565. [Google Scholar]
- Hunter, J.J.; Deloire, A. Terroir and vine water relation effects on grape ripening and wine quality of Syrah/R99. In Proceedings of the VIth International Terroir Congress, Bordeaux and Montpellier, France, 3–7 July 2006. [Google Scholar]
- Deloire, A.; Vaudour, E.; Carey, V.A.; Bonnardot, V.; van Leeuwen, C. Grapevine responses to terroir: A global approach. OENO One 2005, 39, 149–162. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, C.; Garnier, C.; Agut, C.; Baculat, B.; Barbeau, G.; Besnard, E.; Bois, B.; Boursiquot, J.-M.; Chuine, I.; Dessup, T.; et al. Heat requirements for grapevine varieties is essential infor-mation to adapt plant material in a changing climate. In Proceedings of the 7th International Terroir Congress, Nyon, Switzerland, 19–23 May 2008. [Google Scholar]
- Badr, G.; Hoogenboom, G.; Abouali, M.; Moyer, M.; Keller, M. Analysis of several bioclimatic indices for viticultural zoning in the Pacific Northwest. Clim. Res. 2018, 76, 203–223. [Google Scholar] [CrossRef]
- Quenol, H.; Atauri, I.G.D.C.; Bois, B.; Sturman, A.; Bonnardot, V.; Le Roux, R. Which climatic modeling to assess climate change impacts on vineyards? OENO One 2017, 51, 91–97. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Knutti, R.; Sedláček, J.; Sanderson, B.M.; Lorenz, R.; Fischer, E.M.; Eyring, V. A climate model projection weighting scheme accounting for performance and interdependence. Geophys. Res. Lett. 2017, 44, 1909–1918. [Google Scholar] [CrossRef] [Green Version]
- Massoud, E.; Espinoza, V.; Guan, B.; Waliser, D. Global Climate Model Ensemble Approaches for Future Projections of Atmospheric Rivers. Earth’s Future 2019, 7, 1136–1151. [Google Scholar] [CrossRef] [Green Version]
- Massoud, E.C.; Lee, H.; Gibson, P.B.; Loikith, P.; Waliser, D.E. Bayesian Model Averaging of Climate Model Projections Constrained by Precipitation Observations over the Contiguous United States. J. Hydrometeorol. 2020, 21, 2401–2418. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Wehner, M.; Knutti, R. Skill and independence weighting for multi-model assessments. Geosci. Model Dev. 2017, 10, 2379–2395. [Google Scholar] [CrossRef] [Green Version]
- Wootten, A.; Massoud, E.; Sengupta, A.; Waliser, D.; Lee, H. The Effect of Statistical Downscaling on the Weighting of Multi-Model Ensembles of Precipitation. Climate 2020, 8, 138. [Google Scholar] [CrossRef]
- Knutti, R.; Masson, D.; Gettelman, A. Climate model genealogy: Generation CMIP5 and how we got there. Geophys. Res. Lett. 2013, 40, 1194–1199. [Google Scholar] [CrossRef]
- Masson, D.; Knutti, R. Climate model genealogy. Geophys. Res. Lett. 2011, 38, 08703. [Google Scholar] [CrossRef]
- Annan, J.D.; Hargreaves, J. Understanding the CMIP3 Multimodel Ensemble. J. Clim. 2011, 24, 4529–4538. [Google Scholar] [CrossRef]
- Sanderson, B.; Knutti, R. On the interpretation of constrained climate model ensembles. Geophys. Res. Lett. 2012, 39, 16708. [Google Scholar] [CrossRef] [Green Version]
- Sanderson, B.; Knutti, R.; Caldwell, P. A Representative Democracy to Reduce Interdependency in a Multimodel Ensemble. J. Clim. 2015, 28, 5171–5194. [Google Scholar] [CrossRef] [Green Version]
- Herger, N.; Abramowitz, G.; Knutti, R.; Angélil, O.; Lehmann, K.; Sanderson, B.M. Selecting a climate model subset to optimise key ensemble properties. Earth Syst. Dyn. 2018, 9, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Yu, X.; Wang, Y.; He, X.; Pan, M.; Zhang, M.; Liu, Y.; Ren, L.; Sheffield, J. The Optimal Multimodel Ensemble of Bias-Corrected CMIP5 Climate Models over China. J. Hydrometeorol. 2020, 21, 845–863. [Google Scholar] [CrossRef]
- Lorenz, R.; Herger, N.; Sedláček, J.; Eyring, V.; Fischer, E.M.; Knutti, R. Prospects and Caveats of Weighting Climate Models for Summer Maximum Temperature Projections Over North America. J. Geophys. Res. Atmos. 2018, 123, 4509–4526. [Google Scholar] [CrossRef]
- Doherty, J. Calibration and Uncertainty Analysis for Complex Environmental Models; Watermark Numerical Computing: Brisbane, Australia, 2015; ISBN 978-0-9943786-0-6. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Simon, N.; Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent. J. Stat. Softw. 2011, 39, 1–13. [Google Scholar] [CrossRef]
- Tibshirani, R.; Bien, J.; Friedman, J.H.; Hastie, T.; Simon, N.; Taylor, J.; Tibshirani, R.J. Strong rules for discarding predictors in lasso-type problems. J. R. Stat. Soc. Ser. B Stat. Methodol. 2012, 74, 245–266. [Google Scholar] [CrossRef]
- Gareth, J.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Jones, G.V. Climate and terroir: Impacts of climate variability and change on wine. In Fine Wine and Terroir: The Geoscience Perspective; Macqueen, R.W., Meinert, L.D., Eds.; Geoscience Canada Reprint Series No.; Geo-logical Association of Canada: St. John’s, NL, Canada, 2006; p. 203. [Google Scholar]
- Huglin, M. Nouveau Mode d’Évaluation des Possibilités Héliothermiques d’un Milieu Viticole. C.R. Acad. Agr. Fr. 1978, 64, 1117–1126. [Google Scholar]
- Tonietto, J. Les macroclimats viticoles mondiaux et l’influence du mésoclimat sur la typicité de la Syrah et du Muscat de Hambourg dans le sud de la France: Méthodologie de caráctérisation. Ph.D. Thesis, Ecole Nationale Supérieure Agronomique, Montpellier, France, 1999; p. 233. [Google Scholar]
- Riou, C.; Becker, N.; Sotes Ruiz, V.; Gomez-Miguel, V.; Carbonneau, A.; Panagiotou, M.; Calo, A.; Costacurta, A.; de Castro, R.; Pinto, A.; et al. Le Déterminisme Climatique de la Maturation du Raisin: Applica-tion au Zonage de la Teneur em Sucre Dans la Communauté Européenne; Office des Publications Officielles des Communau-tés Européennes: Luxembourg, 1994; p. 322. [Google Scholar]
- Tonietto, J.; Carbonneau, A. A multicriteria climatic classification system for grape-growing regions worldwide. Agric. For. Meteorol. 2004, 124, 81–97. [Google Scholar] [CrossRef] [Green Version]
- Huglin, P.; Schneider, C. Biologie et Écologie de la Vigne; Lavoisier: Paris, France, 1998. [Google Scholar]
- Pierce, D.W.; Cayan, D.R.; Thrasher, B. Statistical Downscaling Using Localized Constructed Analogs (LOCA)*. J. Hydrometeorol. 2014, 15, 2558–2585. [Google Scholar] [CrossRef]
- Pierce, D.W.; Cayan, D.R.; Maurer, E.P.; Abatzoglou, J.; Hegewisch, K.C. Improved Bias Correction Techniques for Hydrological Simulations of Climate Change*. J. Hydrometeorol. 2015, 16, 2421–2442. [Google Scholar] [CrossRef]
- Livneh, B.; Rosenberg, E.A.; Lin, C.; Nijssen, B.; Mishra, V.; Andreadis, K.M.; Maurer, E.; Lettenmaier, D.P. A Long-Term Hydrologically Based Dataset of Land Surface Fluxes and States for the Conterminous United States: Update and Extensions. J. Clim. 2013, 26, 9384–9392. [Google Scholar] [CrossRef]
- Wine Spectator. Vintage Charts. Oregon: Pinot Noir. Available online: https://www.winespectator.com/vintage-charts/region/oregon (accessed on 1 December 2020).
- Schultze, S.R.; Sabbatini, P. Implications of a Climate-Changed Atmosphere on Cool-Climate Viticulture. J. Appl. Meteorol. Clim. 2019, 58, 1141–1153. [Google Scholar] [CrossRef]
- Blanco-Ward, D.; Ribeiro, A.; Barreales, D.; Castro, J.; Verdial, J.; Feliciano, M.; Viceto, C.; Rocha, A.; Carlos, C.; Silveira, C.; et al. Climate change potential effects on grapevine bioclimatic indices: A case study for the Portuguese demarcated Douro Region (Portugal). BIO Web Conf. 2019, 12, 01013. [Google Scholar] [CrossRef]
- Cabré, F.; Nuñez, M. Impacts of climate change on viticulture in Argentina. Reg. Environ. Chang. 2020, 20, 1–12. [Google Scholar] [CrossRef]
- Cardell, M.F.; Amengual, A.; Romero, R. Future effects of climate change on the suitability of wine grape production across Europe. Reg. Environ. Chang. 2019, 19, 2299–2310. [Google Scholar] [CrossRef]
- Mihai, I.L.; Valeriu, P.C.; Renan, L.; Herve, Q.; Cyril, T.; Lucian, S. Projections of Climate Suitability for Wine Production for the Cotnari Wine Region (Romania). Present. Environ. Sustain. Dev. 2019, 13, 5–18. [Google Scholar] [CrossRef]
- Mavromatis, T.; Koufos, G.C.; Koundouras, S.; Jones, G.V. Adaptive capacity of winegrape varieties cultivated in Greece to climate change: Current trends and future projections. OENO One 2020, 54, 1201–1219. [Google Scholar] [CrossRef]
- Santos, M.; Fonseca, A.; Fraga, H.; Jones, G.V.; Santos, J.A. Bioclimatic conditions of the Portuguese wine denominations of origin under changing climates. Int. J. Clim. 2020, 40, 927–941. [Google Scholar] [CrossRef]
- Sirnik, I. Spatial-temporal analysis of climate change impact on viticultural regions Valencia DO and Goriška Brda. Ph.D. Thesis, Universitat Politècnica València, Valencia, Spain, 2019. [Google Scholar]
- Teslić, N.; Vujadinović, M.; Ruml, M.; Ricci, A.; Vuković, A.; Parpinello, G.P.; Versari, A. Future climatic suitability of the Emilia-Romagna (Italy) region for grape production. Reg. Environ. Chang. 2019, 19, 599–614. [Google Scholar] [CrossRef]
- Trbic, G.; Djurdjevic, V.I.; Mandic, M.V.; Ivanisevic, M.; Cupac, R.; Bajic, D.; Zahirovic, E.; Filipovic, D.; Dekic, R.; Popov, T.; et al. The impact of climate change on grapevines in Bosnia and Herzegovina. Euro-Mediterr. J. Environ. Integr. 2021, 6, 1–9. [Google Scholar] [CrossRef]
- Oregon Wine Board. 2019 Oregon Vineyard and Winery Report. Available online: https://industry.oregonwine.org/resources/reports-studies/2019-oregon-vineyard-and-winery-report/ (accessed on 2 September 2020).
- Vano, J.; Hamman, J.; Gutmann, E.; Wood, A.; Mizukami, N.; Clark, M.; Pierce, D.W.; Cayan, D.R.; Wobus, C.; Nowak, K.; et al. Comparing Downscaled LOCA and BCSD CMIP5 Climate and Hydrology Projections-Release of Downscaled LOCA CMIP5 Hydrology. Available online: https://gdo-dcp.ucllnl.org/downscaled_cmip_projections/techmemo/LOCA_BCSD_hydrology_tech_memo.pdf (accessed on 2 December 2020).
- Shin, Y.; Lee, Y.; Park, J.-S. A Weighting Scheme in A Multi-Model Ensemble for Bias-Corrected Climate Simulation. Atmosphere 2020, 11, 775. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the stability of inverse problems. Dokl. Akad. Nauk. SSSR 1943, 39, 195–198. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Prediction, Inference and Data Mining, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather. Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Qian, J. An Introduction to Glmnet. Available online: https://glmnet.stanford.edu/articles/glmnet.html (accessed on 23 January 2021).
- Doherty, J.; Welter, D. A short exploration of structural noise. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Parker, A.K.; de Cortázar-Atauri, I.G.; Gény, L.; Spring, J.-L.; Destrac, A.; Schultz, H.; Molitor, D.; Lacombe, T.; Graça, A.; Monamy, C.; et al. Temperature-based grapevine sugar ripeness modelling for a wide range of Vitis vinifera L. cultivars. Agric. For. Meteorol. 2020, 285–286, 107902. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of Average, Uncertainty Range, and Reliability of Regional Climate Changes from AOGCM Simulations via the “Reliability Ensemble Averaging” (REA) Method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]

| Authors | Wine Region/Study Area | Bioclimatic Indices 1 |
|---|---|---|
| Blanco-Ward et al. [45] | The Portuguese Douro Demarcated Region | WI, HI, CI, DI |
| Cabré and Nuñez [46] | Argentinean provinces of Mendoza, San Juan, La Rioja, Salta and Catamarca | GST, CI, GSP, DSTmin |
| Cardell et al. [47] | Europe | Tmax, AP, GST, WI, HI, RET, WB |
| Irimia et al. [48] | Cotnari (Romania) | GST, HI |
| Koufos et al. [49] | Aigialia, Chalkidiki, Crete, Drama, Kavala, Limnos, Marania, Naousa, Nemea, Pyrgos, Rodos, Samos, Santorini, Tripoli (Greece) | GDD |
| Santos et al. [50] | 50 protected denominations of origin and sub-regions throughout mainland Portugal | HI, DI |
| Sirnik [51] | Valencia (Spain) and Goriška Brda (Slovenia) | WI, HI, DI |
| Teslic et al. [52] | Emilia-Romagna | Tmean, HI, CI, GSl, GSed, GSst, Ptot, DI, DSI, FFP, FF, LF |
| Trbic et al. [53] | 3 locations in Bosnia and Herzegovina | HI, CI, DI, GMCC |
| Prediction | Dataset Description | Model/Observation Dataset Sizes |
|---|---|---|
| GST | 553562 = 61,936 | |
| GDD a | 5535672 = 433,552 | |
| HI b | 5535662 = 371,616 | |
| CI | 553561 = 30,968 | |
| DI b | 5535663 = 557,424 | |
| GMCC b | 55356(63 + 1) = 588,392 |
| CI | HI | |||||||
|---|---|---|---|---|---|---|---|---|
| DI | ||||||||
| GST | GDD | GMCC | ||||||
| Model | ||||||||
| ACCESS1-0 | 244.771 | 175.139 | 2.475 | 1.570 | 1.520 | 2.517 | 1.509 | 1.677 |
| ACCESS1-3 | 282.841 | 204.605 | 2.631 | 1.505 | 1.672 | 2.689 | 1.504 | 1.574 |
| bcc-csm1-1-m | 259.278 | 151.427 | 2.614 | 1.354 | 1.294 | 2.606 | 1.341 | 1.601 |
| bcc-csm1-1 | 238.086 | 183.287 | 2.602 | 1.523 | 1.600 | 2.657 | 1.489 | 1.656 |
| CanESM2 | 221.319 | 160.250 | 2.469 | 1.386 | 1.531 | 2.487 | 1.354 | 1.686 |
| CCSM4 | 260.058 | 178.384 | 2.439 | 1.478 | 1.601 | 2.489 | 1.437 | 1.562 |
| CESM1-BGC | 246.888 | 188.197 | 2.550 | 1.481 | 1.640 | 2.549 | 1.490 | 1.650 |
| CESM1-CAM5 | 288.032 | 211.412 | 2.517 | 1.551 | 1.730 | 2.561 | 1.566 | 1.687 |
| CMCC-CM | 233.042 | 158.486 | 2.368 | 1.421 | 1.445 | 2.440 | 1.396 | 1.479 |
| CMCC-CMS | 266.691 | 166.287 | 2.516 | 1.369 | 1.381 | 2.545 | 1.380 | 1.563 |
| CNRM-CM5 | 255.646 | 169.015 | 2.485 | 1.461 | 1.380 | 2.535 | 1.454 | 1.532 |
| CSIRO-Mk3-6-0 | 250.895 | 184.803 | 2.429 | 1.418 | 1.310 | 2.491 | 1.396 | 1.710 |
| EC-EARTH | 236.074 | 175.140 | 2.505 | 1.430 | 1.503 | 2.547 | 1.418 | 1.644 |
| FGOALS-g2 | 281.068 | 166.505 | 2.567 | 1.385 | 1.471 | 2.595 | 1.348 | 1.549 |
| GFDL-CM3 | 320.326 | 183.522 | 2.786 | 1.469 | 1.602 | 2.805 | 1.416 | 1.659 |
| GFDL-ESM2G | 265.095 | 177.986 | 2.652 | 1.514 | 1.623 | 2.720 | 1.479 | 1.701 |
| GFDL-ESM2M | 284.170 | 177.658 | 2.625 | 1.489 | 1.561 | 2.640 | 1.448 | 1.796 |
| GISS-E2-H | 230.396 | 183.046 | 2.556 | 1.888 | 1.971 | 2.616 | 1.916 | 1.677 |
| GISS-E2-R | 239.828 | 225.547 | 2.497 | 1.903 | 2.006 | 2.518 | 1.902 | 1.556 |
| HadGEM2-AO | 251.507 | 186.377 | 2.558 | 1.623 | 1.721 | 2.612 | 1.568 | 1.717 |
| HadGEM2-CC | 252.912 | 198.520 | 2.462 | 1.625 | 1.786 | 2.491 | 1.623 | 1.533 |
| HadGEM2-ES | 239.594 | 201.824 | 2.454 | 1.672 | 1.785 | 2.461 | 1.675 | 1.579 |
| inmcm4 | 263.054 | 165.371 | 2.629 | 1.491 | 1.615 | 2.629 | 1.458 | 1.645 |
| IPSL-CM5A-LR | 272.671 | 211.333 | 2.572 | 1.715 | 1.905 | 2.617 | 1.672 | 1.626 |
| IPSL-CM5A-MR | 237.304 | 196.434 | 2.502 | 1.776 | 1.908 | 2.538 | 1.752 | 1.567 |
| MIROC-ESM-CHEM | 277.020 | 195.943 | 2.715 | 1.532 | 1.678 | 2.779 | 1.551 | 1.595 |
| MIROC-ESM | 276.154 | 176.654 | 2.686 | 1.439 | 1.383 | 2.757 | 1.424 | 1.663 |
| MIROC5 | 222.107 | 197.340 | 2.651 | 1.500 | 1.580 | 2.736 | 1.493 | 1.658 |
| MPI-ESM-LR | 274.320 | 167.181 | 2.610 | 1.443 | 1.386 | 2.655 | 1.394 | 1.654 |
| MPI-ESM-MR | 251.487 | 175.201 | 2.346 | 1.392 | 1.375 | 2.355 | 1.375 | 1.480 |
| MRI-CGCM3 | 249.066 | 188.684 | 2.486 | 1.616 | 1.757 | 2.519 | 1.560 | 1.523 |
| NorESM1-M | 212.750 | 180.521 | 2.324 | 1.501 | 1.608 | 2.365 | 1.480 | 1.634 |
| GST | GDD | HI | CI | DI | GMCC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Skill Weighting | |||||||||||
| N | RMSE | N | RMSE | N | RMSE | N | RMSE | N | RMSE | N | RMSE |
| 2 | 192.95 | 2 | 1.93 | 2 | 1.93 | 1 | 1.29 | 2 | 1.79 | 2 | 1.77 |
| 4 | 190.19 | 5 | 1.92 | 4 | 1.92 | 4 | 1.24 | 4 | 1.70 | 10 | 1.60 |
| 10 | 180.68 | 10 | 1.85 | 9 | 1.89 | 9 | 1.20 | 9 | 1.67 | 11 | 1.57 |
| 13 | 178.27 | 22 | 1.61 | 20 | 1.66 | 14 | 1.16 | 20 | 1.59 | 21 | 1.50 |
| 26 | 168.59 | 28 | 1.55 | 27 | 1.58 | 21 | 1.14 | 27 | 1.56 | 23 | 1.48 |
| 32 | 162.58 | 30 | 1.52 | 30 | 1.55 | 24 | 1.14 | 30 | 1.53 | 29 | 1.43 |
| 32 | 165.67 | 32 | 1.50 | 32 | 1.52 | 32 | 1.15 | 32 | 1.46 | 32 | 1.40 |
| 32 | 169.20 | 32 | 1.51 | 32 | 1.53 | 32 | 1.18 | 32 | 1.42 | 32 | 1.41 |
| 32 | 170.76 | 32 | 1.52 | 32 | 1.54 | 32 | 1.20 | 32 | 1.43 | 32 | 1.42 |
| Skill and Model Interdependence Weighting | |||||||||||
| N | RMSE | N | RMSE | N | RMSE | N | RMSE | N | RMSE | N | RMSE |
| 2 | 193.03 | 2 | 1.93 | 2 | 1.93 | 1 | 1.29 | 1 | 1.79 | 2 | 1.77 |
| 3 | 191.09 | 4 | 1.92 | 3 | 1.92 | 3 | 1.25 | 6 | 1.73 | 10 | 1.64 |
| 6 | 183.59 | 9 | 1.87 | 8 | 1.91 | 8 | 1.20 | 12 | 1.71 | 11 | 1.62 |
| 10 | 181.50 | 18 | 1.65 | 18 | 1.75 | 13 | 1.19 | 19 | 1.65 | 23 | 1.55 |
| 24 | 172.79 | 28 | 1.59 | 27 | 1.67 | 20 | 1.15 | 21 | 1.62 | 25 | 1.53 |
| 32 | 164.74 | 30 | 1.55 | 30 | 1.61 | 23 | 1.14 | 28 | 1.60 | 30 | 1.46 |
| 32 | 167.06 | 32 | 1.50 | 32 | 1.53 | 32 | 1.14 | 32 | 1.53 | 32 | 1.41 |
| 32 | 174.76 | 32 | 1.51 | 32 | 1.53 | 32 | 1.18 | 32 | 1.42 | 32 | 1.41 |
| 32 | 178.34 | 32 | 1.53 | 32 | 1.56 | 32 | 1.21 | 32 | 1.43 | 32 | 1.42 |
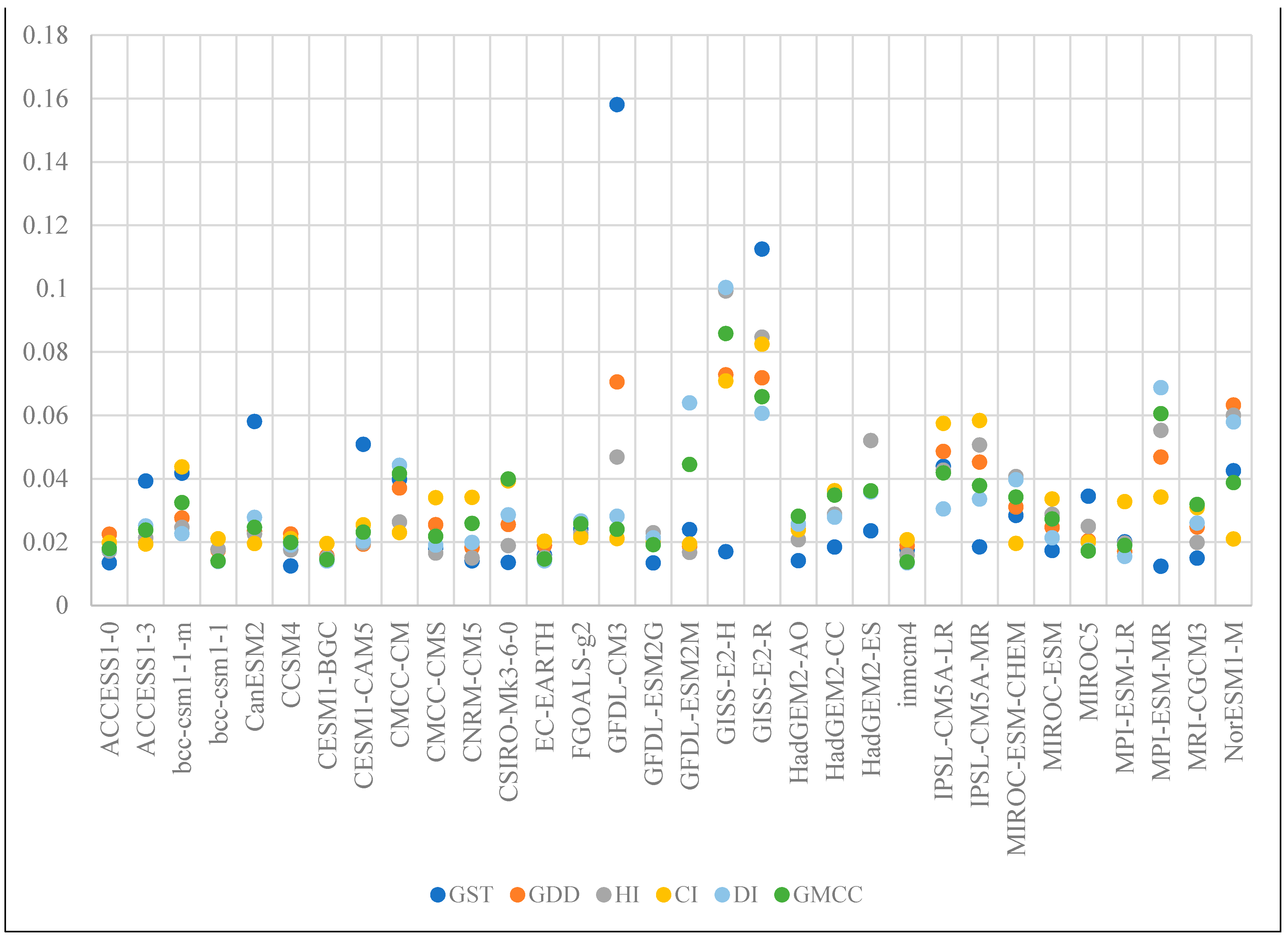
| Viticulture Climate Classification Index | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | GST | GDD | HI | CI | DI | GMCC | DI * | GMCC * |
| ACCESS1-0 | 0 | 0.020 | 0.014 | 0.147 | 0.030 | 0.030 | 0.039 | 0.047 |
| ACCESS1-3 | 0 | 0.015 | 0.011 | 0 | 0.023 | 0.018 | 0.053 | 0.047 |
| bcc-csm1-1-m | 0 | 0 | 0.013 | 0.264 | 0.023 | 0.030 | 0.028 | 0.044 |
| bcc-csm1-1 | 0.084 | 0 | 0 | 0 | 0 | 0 | 7.59 10−3 | 0.003 |
| CanESM2 | 0.173 | 0.090 | 0.095 | 0.090 | 0.080 | 0.084 | 0.040 | 0.044 |
| CCSM4 | 0 | 0.034 | 0.013 | 0 | 0.026 | 0.037 | 0.065 | 0.064 |
| CESM1-BGC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CESM1-CAM5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CMCC-CM | 0.144 | 0.100 | 0.082 | 0.136 | 0.085 | 0.098 | 0.096 | 0.101 |
| CMCC-CMS | 0 | 0.038 | 0.047 | 0.025 | 0.051 | 0.054 | 0.049 | 0.051 |
| CNRM-CM5 | 0.056 | 0.056 | 0.054 | 0.042 | 0.068 | 0.075 | 0.083 | 0.091 |
| CSIRO-Mk3-6-0 | 0 | 0.078 | 0.068 | 0 | 0.059 | 0.060 | 0.037 | 0.037 |
| EC-EARTH | 0 | 0.005 | 0.016 | 0 | 5.39 × 10−7 | 3.35 × 10−6 | 0 | 0 |
| FGOALS-g2 | 0 | 0.068 | 0.068 | 0.030 | 0.070 | 0.074 | 0.038 | 0.046 |
| GFDL-CM3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.010 | 0.004 |
| GFDL-ESM2G | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GFDL-ESM2M | 0 | 0.019 | 0.022 | 0 | 0.015 | 0.015 | 0 | 0 |
| GISS-E2-H | 0.172 | 0.015 | 0 | 0 | 0 | 0 | 0 | 0 |
| GISS-E2-R | 0 | 0 | 0 | 0 | 0 | 0 | 0.011 | 0.001 |
| HadGEM2-AO | 0 | 0.011 | 0.011 | 0.031 | 0.009 | 0.006 | 0 | 0 |
| HadGEM2-CC | 0 | 0.030 | 0.023 | 0 | 0.055 | 0.050 | 0.129 | 0.115 |
| HadGEM2-ES | 0.089 | 0.055 | 0.067 | 0.021 | 0.071 | 0.070 | 0.072 | 0.068 |
| inmcm4 | 0.037 | 0.055 | 0.067 | 0 | 0.043 | 0.041 | 0 | 0 |
| IPSL-CM5A-LR | 0 | 0 | 0 | 0 | 0.002 | 0 | 0.052 | 0.036 |
| IPSL-CM5A-MR | 0 | 0.038 | 0.034 | 0.075 | 0.036 | 0.035 | 0.041 | 0.043 |
| MIROC-ESM-CHEM | 0 | 0 | 0 | 0 | 0 | 0 | 0.014 | 0.009 |
| MIROC-ESM | 0.091 | 0.053 | 0.062 | 0.001 | 0.045 | 0.040 | 0 | 0.002 |
| MIROC5 | 0.008 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MPI-ESM-LR | 0 | 0 | 0 | 0 | 0 | 0 | 0.012 | 0.011 |
| MPI-ESM-MR | 0 | 0.086 | 0.099 | 0.060 | 0.092 | 0.082 | 0.065 | 0.072 |
| MRI-CGCM3 | 0 | 0.040 | 0.049 | 0.072 | 0.043 | 0.036 | 0.009 | 0.019 |
| NorESM1-M | 0.146 | 0.092 | 0.085 | 0 | 0.073 | 0.064 | 0.037 | 0.034 |
| Non-Zero Count | 10 | 21 | 21 | 13 | 22 | 21 | 22 | 23 |
| GST | GDD | HI | CI | DI | GMCC | |
|---|---|---|---|---|---|---|
| GST | 1 | 0.518 | 0.456 | 0.083 | 0.394 | 0.408 |
| GDD | 1 | 0.966 | 0.192 | 0.946 | 0.936 | |
| HI | 1 | 0.219 | 0.944 | 0.919 | ||
| CI | 1 | 0.311 | 0.361 | |||
| DI | 0.121 | 0.501 | 0.415 | 0.234 | 1 | 0.987 |
| GMCC | 0.134 | 0.565 | 0.490 | 0.373 | 0.980 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skahill, B.; Berenguer, B.; Stoll, M. Ensembles for Viticulture Climate Classifications of the Willamette Valley Wine Region. Climate 2021, 9, 140. https://doi.org/10.3390/cli9090140
Skahill B, Berenguer B, Stoll M. Ensembles for Viticulture Climate Classifications of the Willamette Valley Wine Region. Climate. 2021; 9(9):140. https://doi.org/10.3390/cli9090140
Chicago/Turabian StyleSkahill, Brian, Bryan Berenguer, and Manfred Stoll. 2021. "Ensembles for Viticulture Climate Classifications of the Willamette Valley Wine Region" Climate 9, no. 9: 140. https://doi.org/10.3390/cli9090140
APA StyleSkahill, B., Berenguer, B., & Stoll, M. (2021). Ensembles for Viticulture Climate Classifications of the Willamette Valley Wine Region. Climate, 9(9), 140. https://doi.org/10.3390/cli9090140





