Validation of the High-Altitude Wind and Rain Airborne Profiler during the Tampa Bay Rain Experiment
Abstract
1. Introduction
2. HIWRAP Measurements, Calibration and Geophysical Retrieval Algorithms
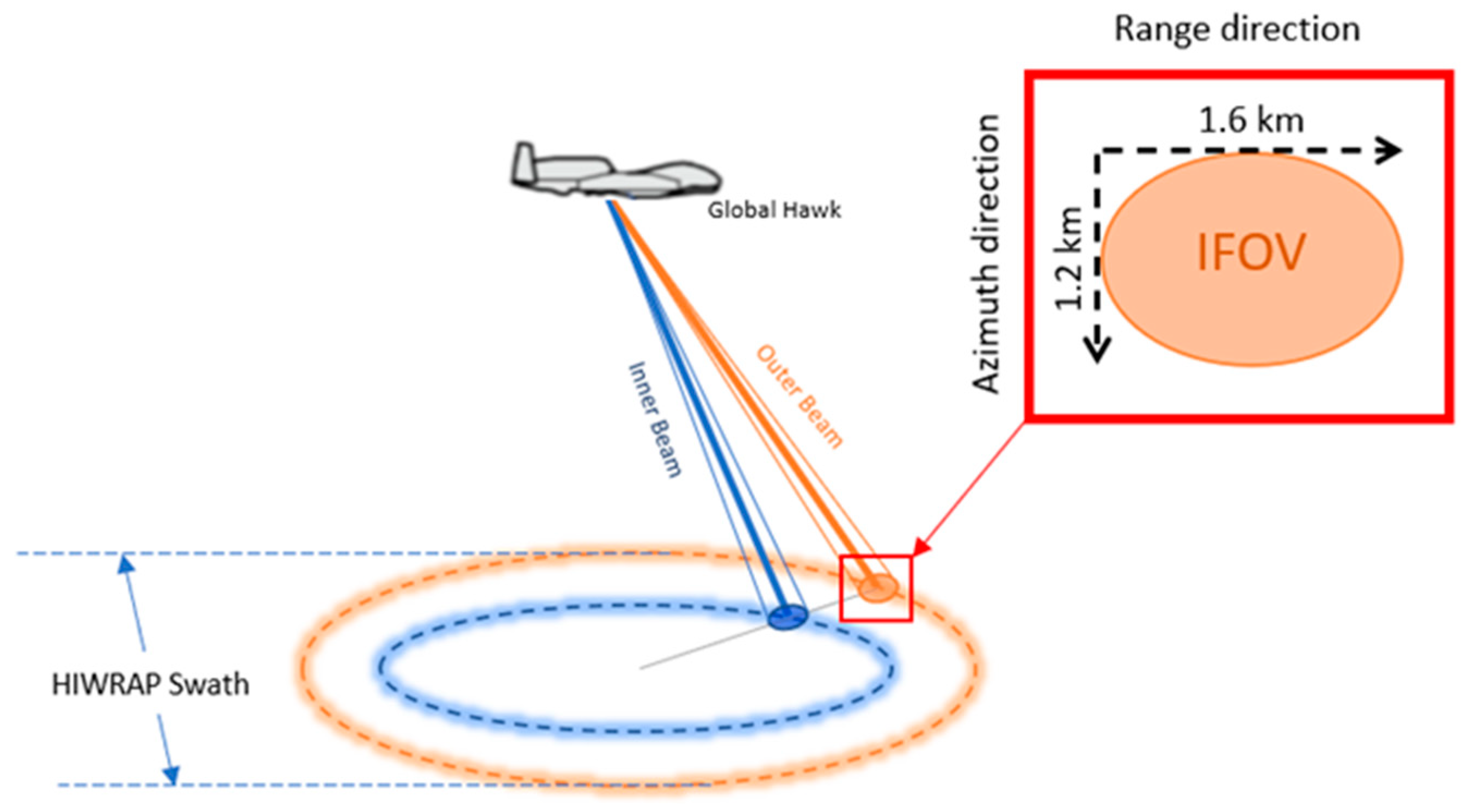
2.1. HIWRAP Instrument
2.2. Data Processing
2.2.1. Radar Calibration
2.2.2. Rain Rate Retrieval
2.2.3. HIWRAP OVW Retrievals
3. HIWRAP Geophysical Retrieval Validation
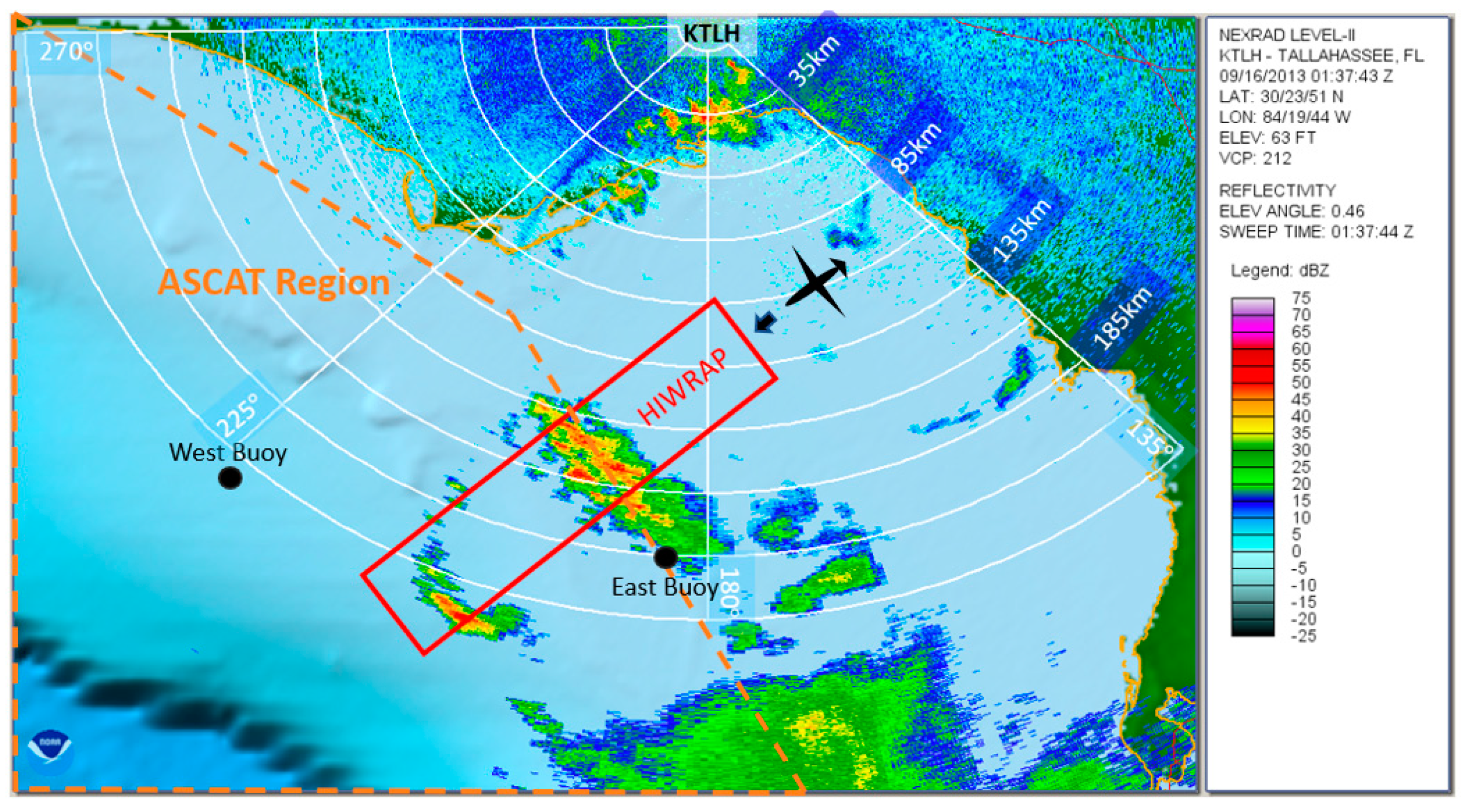
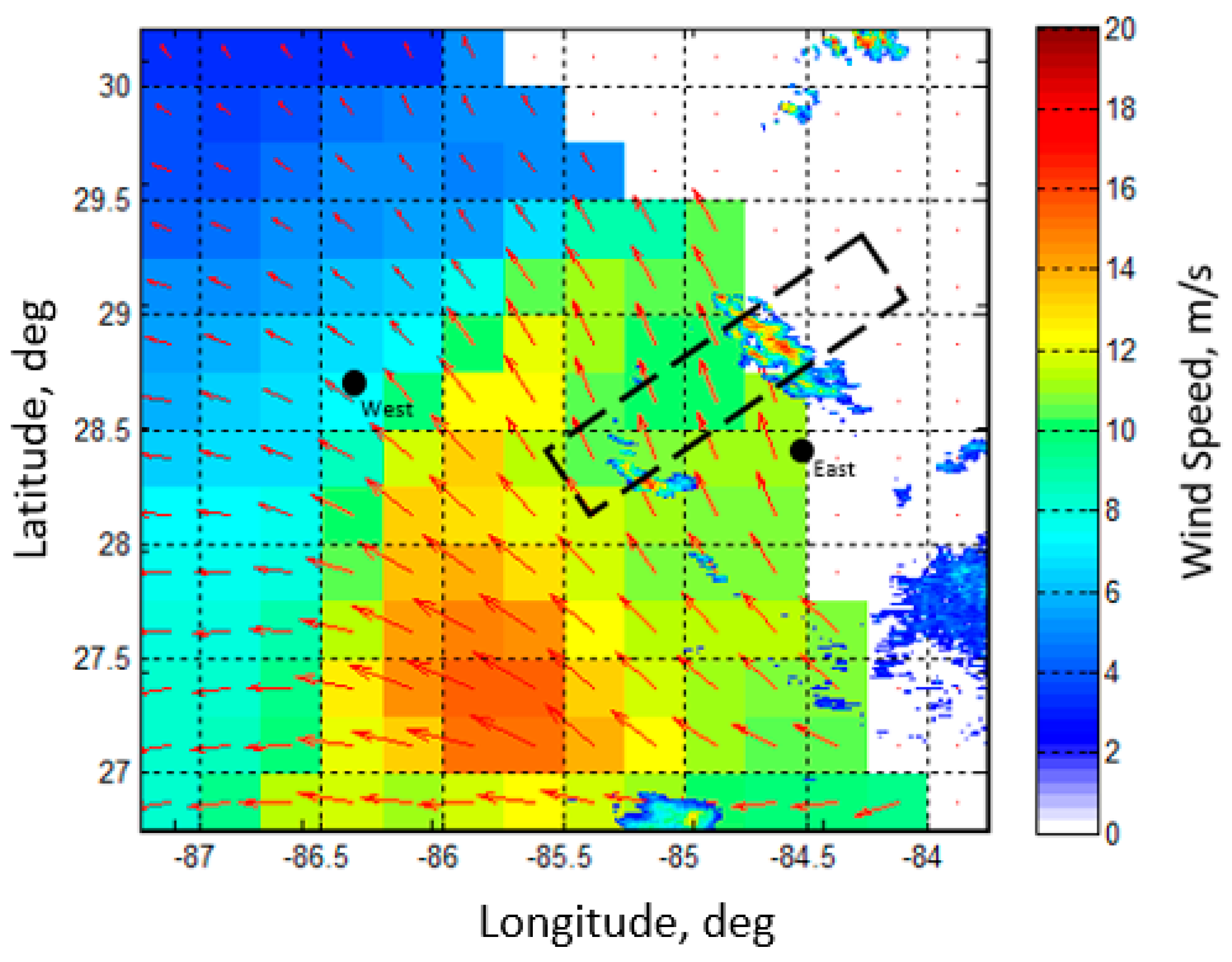
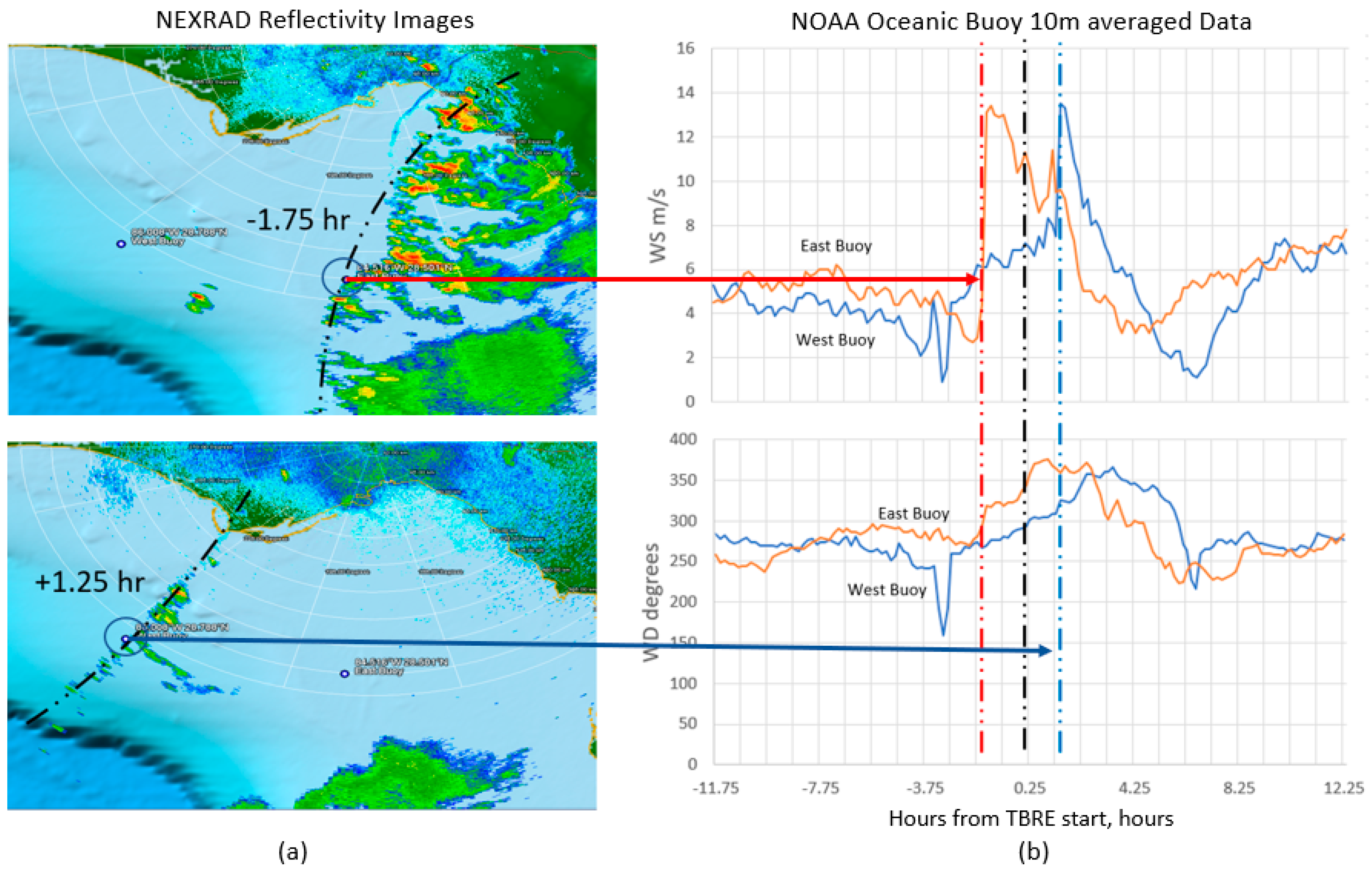
3.1. Collocated Measurements
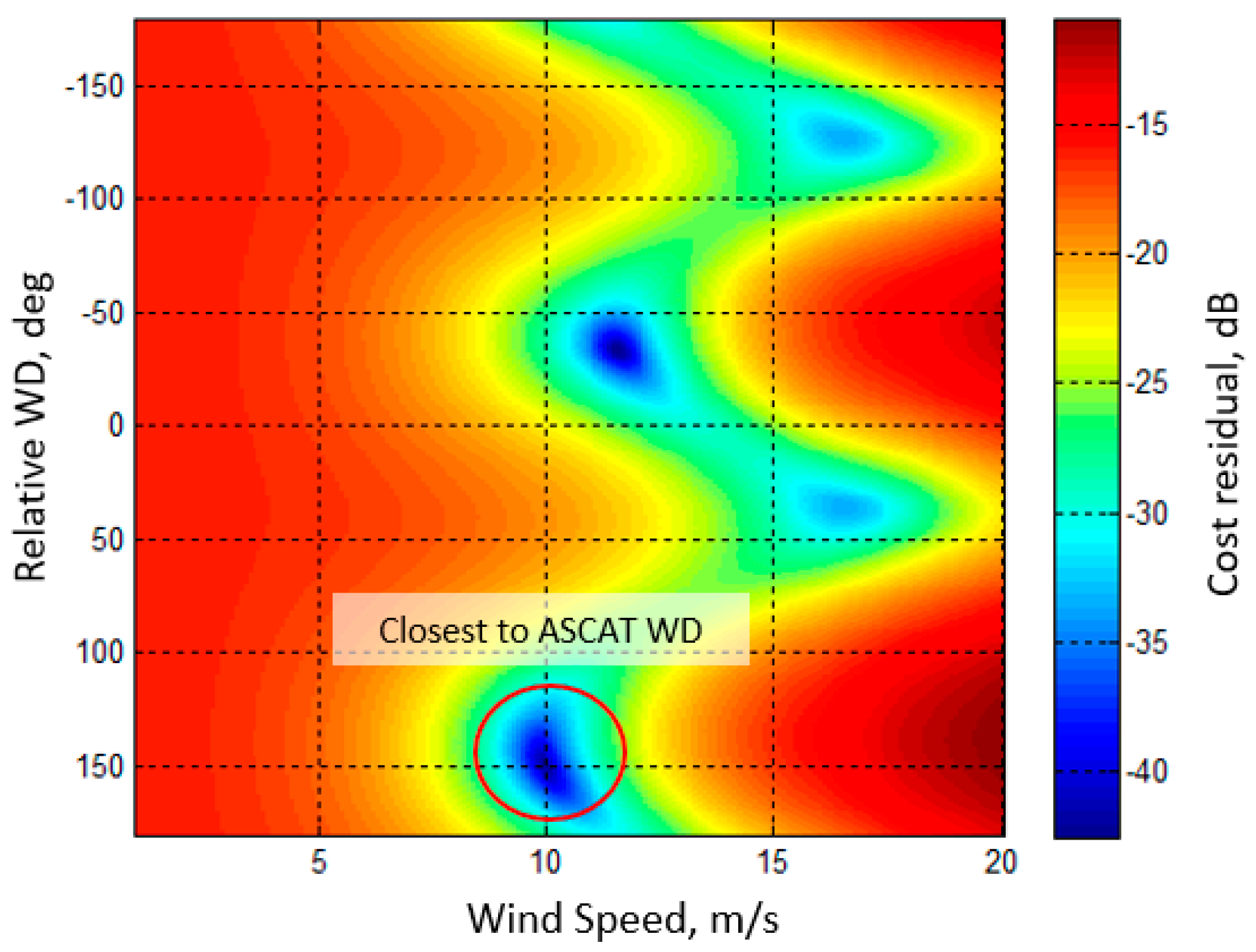
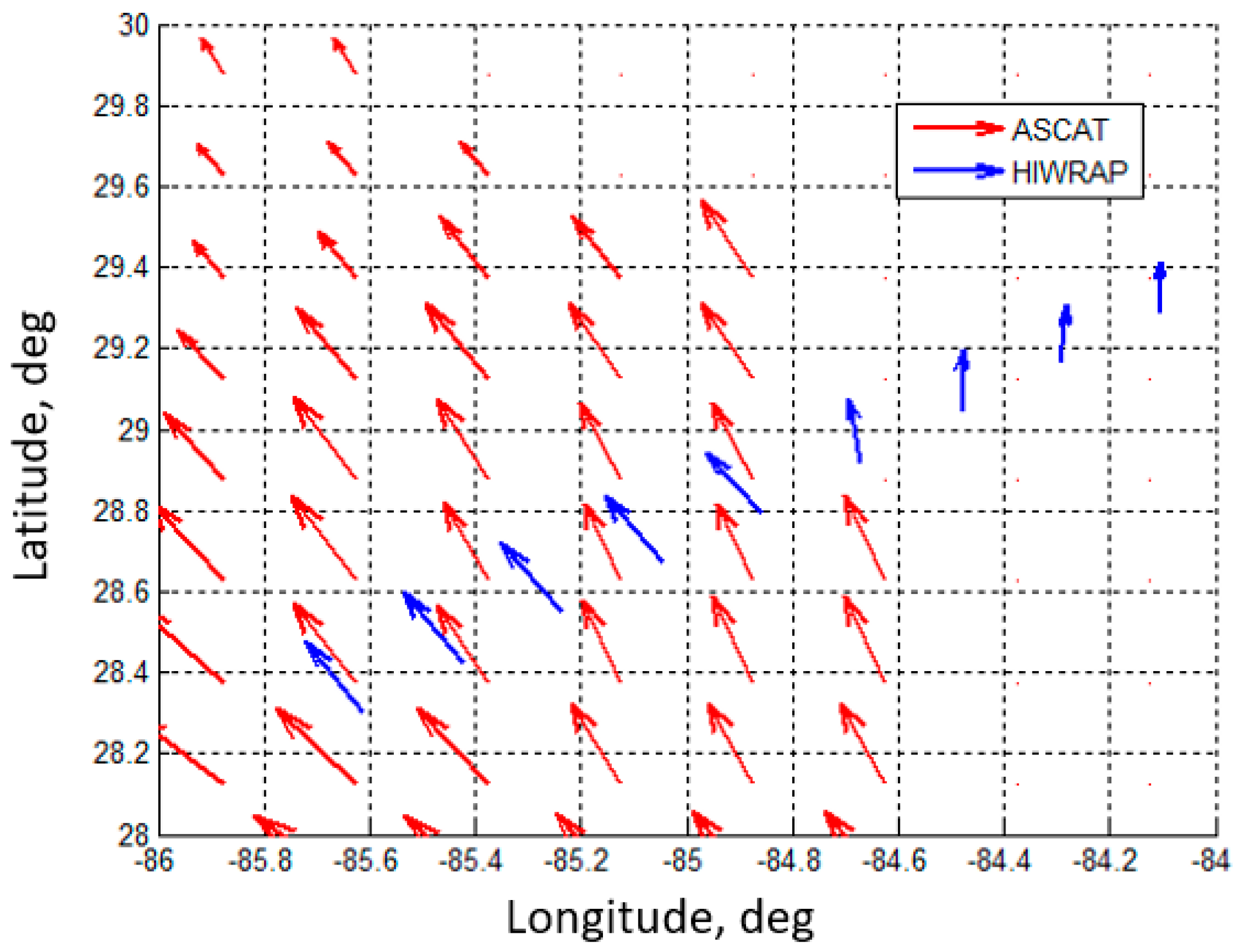
3.2. HIWRAP Ocean Wind Vector Validation
3.3. HIWRAP Rain Rate Validation
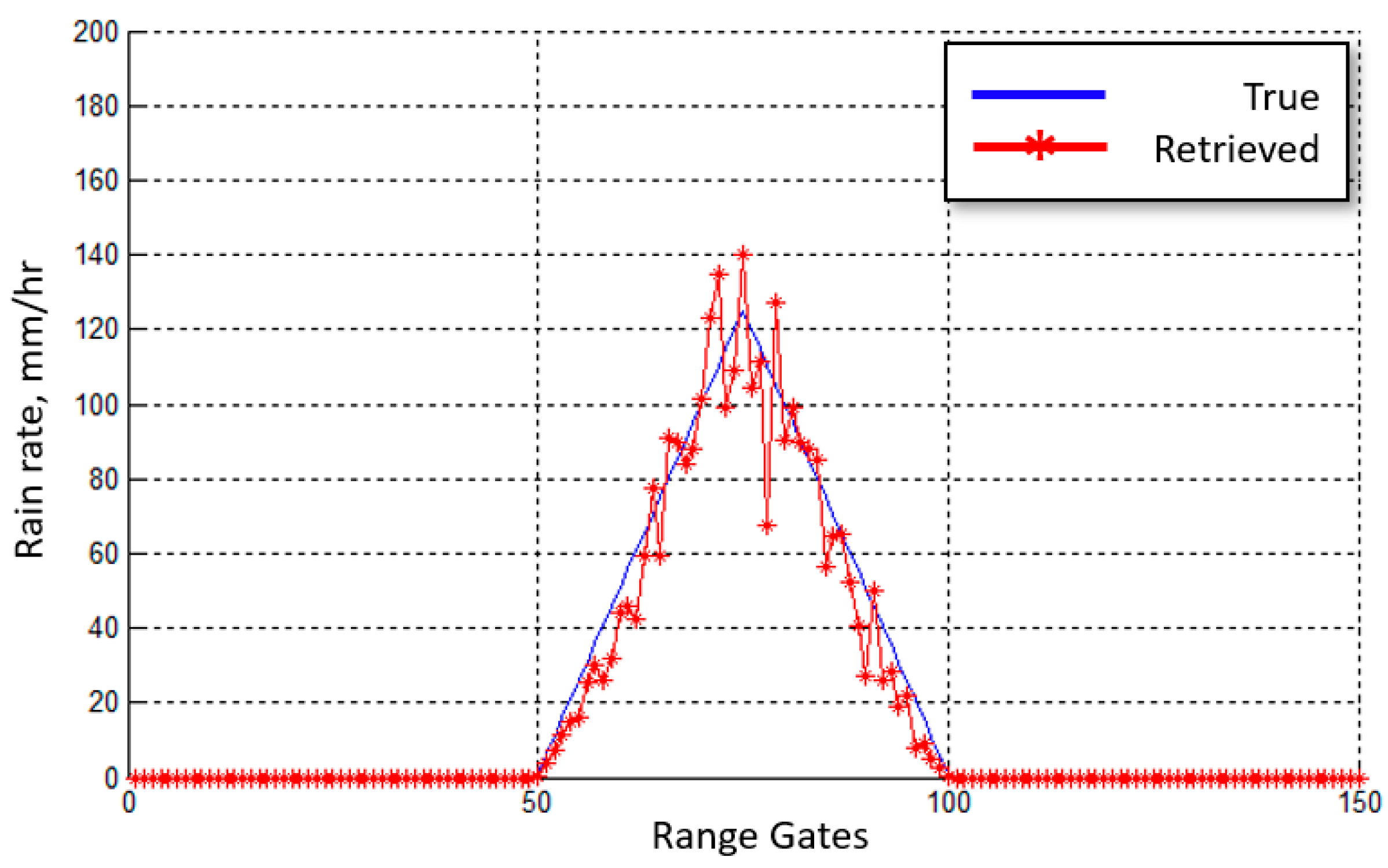
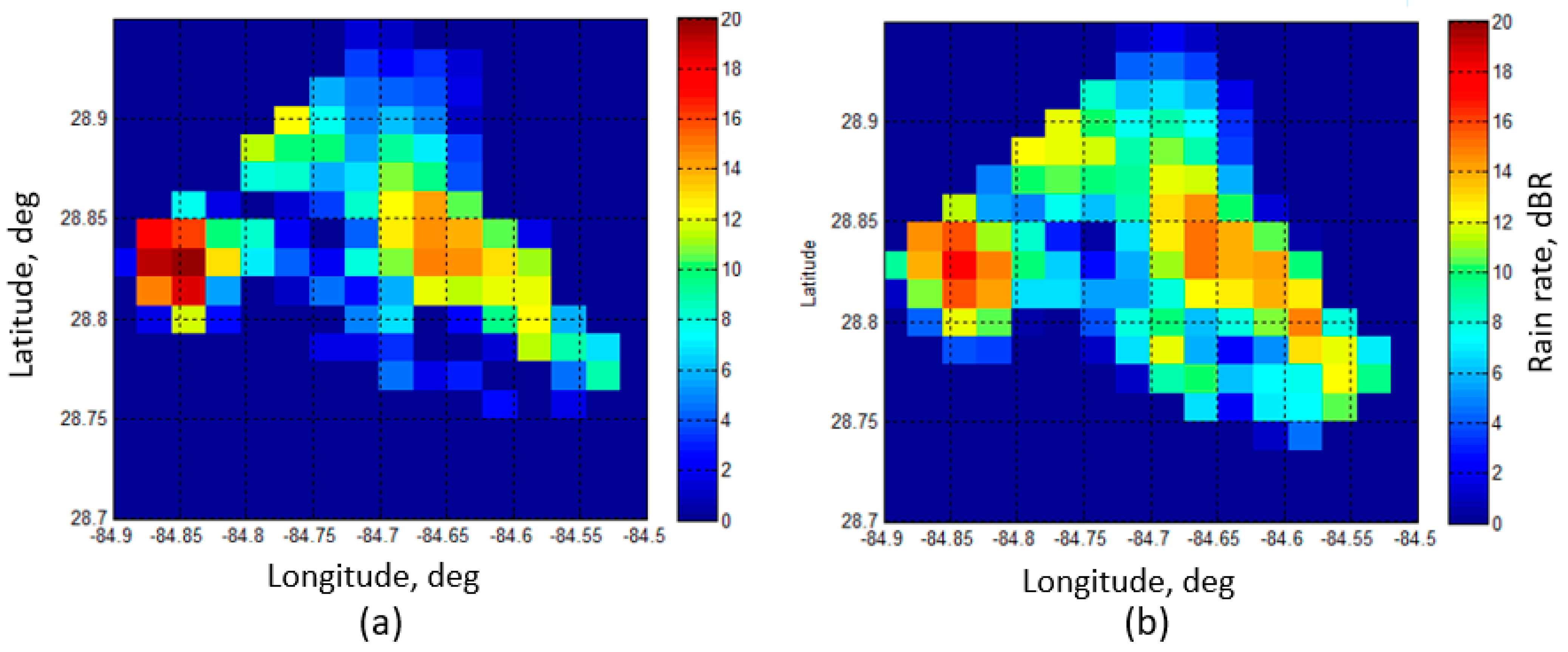
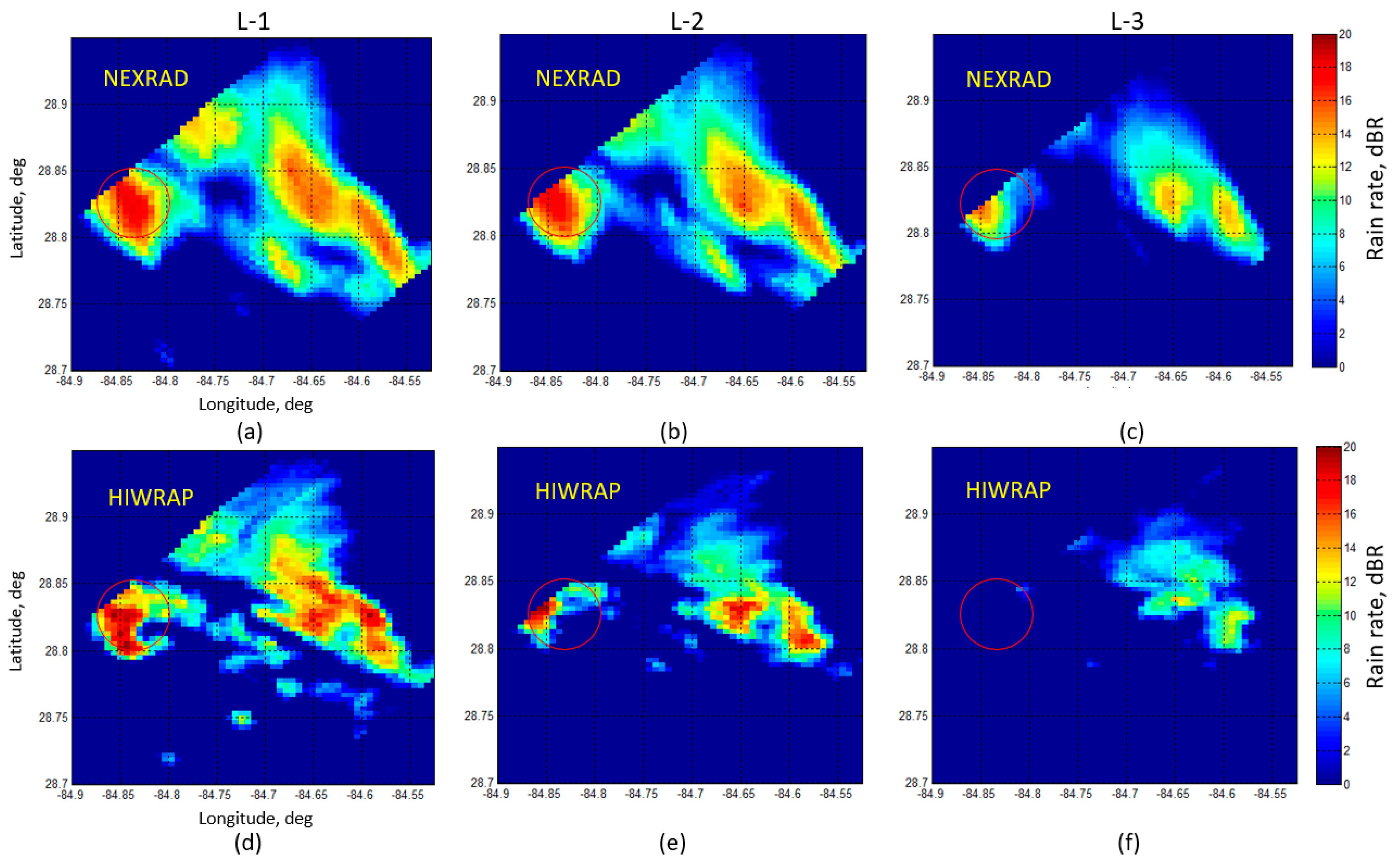
3.3.1. HIWRAP and NEXRAD Rain Rate Comparisons at Low Resolution
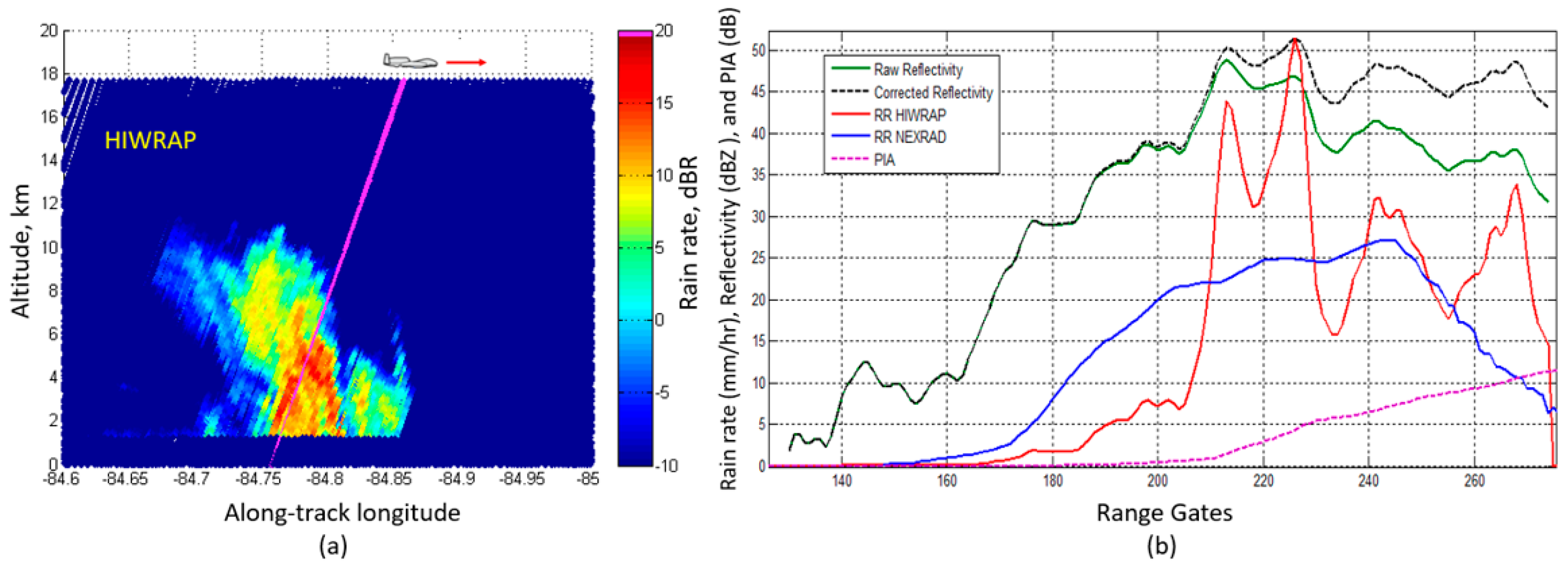
3.3.2. HIWRAP and NEXRAD Rain Rate Comparisons at High Resolution
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. HIWRAP Calibration and Rain Retrieval Algorithms
Appendix A.1. Airborne Calibration Using the Ocean Normalized Radar Cross-Section
Appendix A.1.1. Measured Normalized Radar Cross-Section ()
Appendix A.1.2. Calibration
Appendix A.2. Single-Frequency Rain Rate Retrieval (SFR3)
Divergence Mitigation through Z–R Correction
Appendix B. NEXRAD Spatial Interpolator
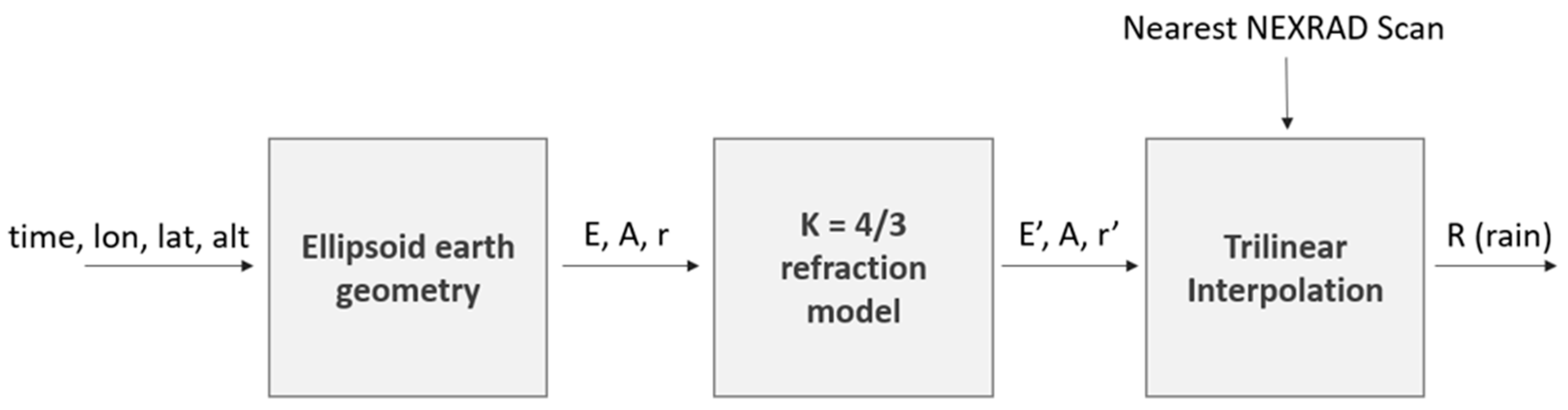
Appendix B.1. Temporal Alignment
Appendix B.2. Ellipsoid Earth Geometry
Appendix B.3. Refraction Model
Appendix B.4. Trilinear Interpolation of Rain
References
- Braun, S.A.; Newman, P.A.; Heymsfield, G.M. NASA’s Hurricane and Severe Storm Sentinel (HS3) Investigation. Bull. Am. Meteorol. Soc. 2016, 97, 2085–2102. [Google Scholar] [CrossRef]
- HS3 Hurricane Mission—NASA. Available online: https://www.nasa.gov/mission_pages/hurricanes/missions/hs3/index.html (accessed on 20 May 2021).
- Alasgah, A.; Jacob, M.; Jones, L.; Schneider, L. Validation of the Hurricane Imaging Radiometer Forward Radiative Transfer Model for a Convective Rain Event. Remote Sens. 2019, 11, 2650. [Google Scholar] [CrossRef]
- Heymsfield, G.M.; Tian, T. Hurricane and Severe Storm Sentinel (HS3) High-Altitude Imaging Wind and Rain Airborne Profiler (Hiwrap). Dataset Available online from the NASA Global Hydrology Resource Center DAAC, Huntsville, Alabama, USA. 2015. Available online: http://dx.doi.org/10.5067/HS3/HIWRAP/DATA101 (accessed on 17 March 2021).
- Office of the Federal Coordinator for Meteorological Services and Sup-Porting Research. Federal Meteorological Handbook No. 11: Doppler Radar Meteorological Observations, Part B: Doppler Radar Theory and Meteorology; Report FCM-H11B-1990; Interim Version One: Rockville, MD, USA, 1990. Available online: https://www.icams-portal.gov/publications/fmh/FMH11/fmh-11B-2005.pdf (accessed on 20 May 2021).
- Portabella, M.; Stoffelen, A.; Belmonte Rivas, M.; Verhoef, A.; Verspeek, J.; Vogelzang, J. ASCAT Scatterometer wind data processing. Instrumentation ViewPoint. ESA Bull. 2000, 102, 19–27. [Google Scholar]
- Li, L.; Heymsfield, G.; Carswell, J.; Schaubert, D.; McLinden, M.; Creticos, J.; Perrine, M.; Coon, M.; Cervantes, J.; Vega, M.; et al. The NASA High-Altitude Imaging Wind and Rain Airborne Profiler (HIWRAP). IEEE Trans. Geosci. Remote Sens. 2015, 54, 298–310. [Google Scholar] [CrossRef]
- Alasgah, A. Hurricane Imaging Radiometer (HIRAD) Tropical Rainfall Retrievals. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2019. [Google Scholar]
- Benker, S.C.; Langford, R.P.; Pavlis, T.L. Positional accuracy of the Google Earth terrain model derived from stratigraphic unconformities in the Big Bend region, Texas, USA. Geocarto Int. 2011, 26, 291–303. [Google Scholar] [CrossRef]
- Probert-Jones, J.R. The radar equation in meteorology. Q. J. R. Meteorol. Soc. 1962, 88, 485–495. [Google Scholar] [CrossRef]
- Rao, U.N.; Sarkar, A.; Mohan, M. Theoretical Z-R relationship for precipitating systems using Mie scattering approach. Indian J. Radio Space Phys. 2005, 34, 191–196. [Google Scholar]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; The University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Chi, C.-Y.; Li, F. A comparative study of several wind estimation algorithms for spaceborne scatterometers. IEEE Trans. Geosci. Remote Sens. 1988, 26, 115–121. [Google Scholar] [CrossRef]
- Wentz, F.J.; Smith, D.K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations. J. Geophys. Res. Space Phys. 1999, 104, 11499–11514. [Google Scholar] [CrossRef]
- Shaffer, S.; Dunbar, R.; Hsiao, S.; Long, D. A median-filter-based ambiguity removal algorithm for NSCAT. IEEE Trans. Geosci. Remote. Sens. 1991, 29, 167–174. [Google Scholar] [CrossRef]
- Weissman, D.E.; Stiles, B.W.; Hristova-Veleva, S.M.; Long, D.G.; Smith, D.K.; Hilburn, K.A.; Jones, W.L. Challenges to Satellite Sensors of Ocean Winds: Addressing Precipitation Effects. J. Atmos. Ocean. Technol. 2012, 29, 356–374. [Google Scholar] [CrossRef]
- Schneider, L.; Jones, W.L. Analysis of spatially and temporally disjoint precipitation datasets to estimate the 3D distri-bution of rain. In Proceedings of the IEEE IGARSS 2017, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Meneghini, R.; Liao, L. Modified Hitschfeld–Bordan Equations for Attenuation-Corrected Radar Rain Reflectivity: Application to Nonuniform Beamfilling at Off-Nadir Incidence. J. Atmos. Ocean. Technol. 2013, 30, 1149–1160. [Google Scholar] [CrossRef]
- Iguchi, T.; Meneghini, R. Intercomparison of Single-Frequency Methods for Retrieving a Vertical Rain Profile from Airborne or Spaceborne Radar Data. J. Atmos. Ocean. Technol. 1994, 11, 1507–1516. [Google Scholar] [CrossRef]
- Maki, M.; Keenan, T.D.; Sasaki, Y.; Nakamura, K. Characteristics of the Raindrop Size Distribution in Tropical Continental Squall Lines Observed in Darwin, Australia. J. Appl. 2001, 40, 1393–1412. [Google Scholar] [CrossRef]
- Ellipsoidal and Cartesian Coordinates Conversion—Navipedia. Available online: https://gssc.esa.int/navipedia/index.php/Ellipsoidal_and_Cartesian_Coordinates_Conversion (accessed on 17 March 2021).
- Transformations between ECEF and ENU Coordinates—Navipedia. Available online: https://gssc.esa.int/navipedia/index.php/Transformations_between_ECEF_and_ENU_coordinates (accessed on 17 March 2021).
- Doerry, A.W. Earth Curvature and Atmospheric Refraction Effects on Radar Signal Propagation; Sandia Report; Sandia National Laboratories: Albuquerque, NM, USA, 2013.



| Rain Rate (mm h−1) | Mean | std | Points |
|---|---|---|---|
| Inner Beam Forward Looking | |||
| HIWRAP | 9.39 | 9.93 | 75 |
| NEXRAD | 9.60 | 9.35 | 87 |
| HIWRAP/NEXRAD | 0.85 | 0.37 | 61 |
| Inner Aft Looking | |||
| HIWRAP | 9.92 | 11.53 | 75 |
| NEXRAD | 9.03 | 9.34 | 87 |
| HIWRAP/NEXRAD | 0.82 | 0.26 | 45 |
| Outer Beam Forward Looking | |||
| HIWRAP | 7.88 | 9.06 | 87 |
| NEXRAD | 10.15 | 9.71 | 115 |
| HIWRAP/NEXRAD | 0.62 | 0.23 | 78 |
| Outer Beam Aft Looking | |||
| HIWRAP | 7.57 | 10.10 | 92 |
| NEXRAD | 9029 | 9.62 | 116 |
| HIWRAP/NEXRAD | 0.63 | 0.22 | 81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coto, J.; Jones, W.L.; Heymsfield, G.M. Validation of the High-Altitude Wind and Rain Airborne Profiler during the Tampa Bay Rain Experiment. Climate 2021, 9, 89. https://doi.org/10.3390/cli9060089
Coto J, Jones WL, Heymsfield GM. Validation of the High-Altitude Wind and Rain Airborne Profiler during the Tampa Bay Rain Experiment. Climate. 2021; 9(6):89. https://doi.org/10.3390/cli9060089
Chicago/Turabian StyleCoto, Jonathan, W. Linwood Jones, and Gerald M. Heymsfield. 2021. "Validation of the High-Altitude Wind and Rain Airborne Profiler during the Tampa Bay Rain Experiment" Climate 9, no. 6: 89. https://doi.org/10.3390/cli9060089
APA StyleCoto, J., Jones, W. L., & Heymsfield, G. M. (2021). Validation of the High-Altitude Wind and Rain Airborne Profiler during the Tampa Bay Rain Experiment. Climate, 9(6), 89. https://doi.org/10.3390/cli9060089





