2.1. Dynamic Optimization Model
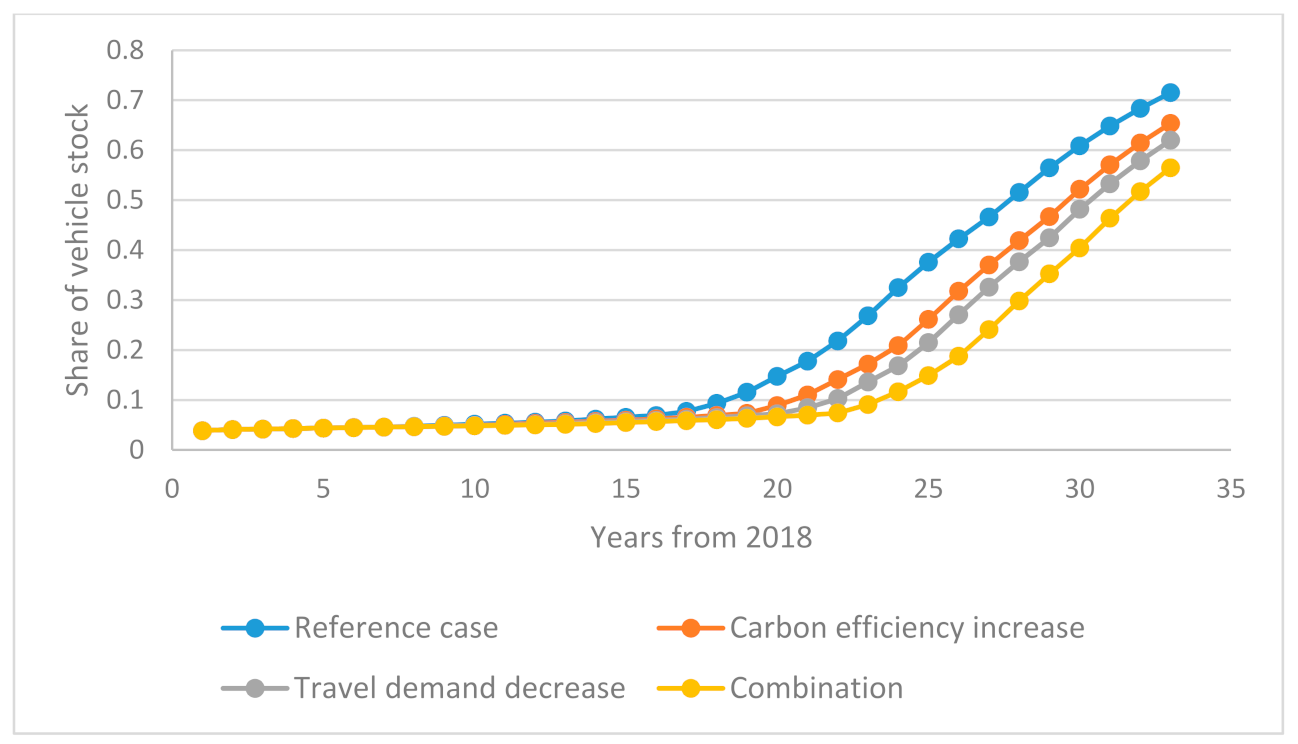
The minimum cost of CO2 reduction in emissions from light-duty vehicles by changing the allocation of carbon intensive vehicles is calculated within a discrete time non-linear dynamic programming model. The change is made from fossil fuel vehicles, F, that run on either gasoline or diesel to hybrid, H, and electric, E, vehicles. There are a variety of hybrid vehicles that utilize more than one form of energy. The most widely used are hybrid gasoline and hybrid diesel that run on a combination of fossil fuel and electricity. They mostly derive electricity either through an internal generation system, such as regenerative braking, or through a plug-in charging system. Other types that could be considered hybrid include semi-biofuel-driven vehicles. A simplification in this study is that all these varieties of hybrid cars, defined as vehicles that run on a mix of fossil fuel and more than 5% biofuel, semi-electric and semi-biofuel or semi-fossil fuel are classified as hybrid vehicles. Electric vehicles are defined as battery-powered fully electric-driven vehicles. Vehicles that run solely on electricity have zero exhaust emissions, but emission is dependent on the source of electricity.
The stock of vehicles
in each country
, in the EU and UK for vehicle type
, at time
is determined by a constant depreciation rate
, which differs among the countries and vehicle types, and the purchase of new vehicles
, which is written as:
where
for
.
The demand for travel
, is exogenous to the model and measured in the number of kilometers traveled. The demand is expected to increase over time at different rates in the EU countries and UK (EC, 2016), which is written as a country specific constant annual rate of increase,
. It is assumed that the travel intensity measured as kilometers travelled per vehicle,
fi, differs among countries but is the same for vehicle types, i.e.,
. The restriction on the travel demand for each country and time period is then written as:
Emissions of CO
2 from travel in each country and period of time
is measured as the product of consumption of fuel type
per kilometer
, kilometers travelled per vehicle
, and the number of vehicles per engine energy type,
. A technological improvement in fuel efficiency in each country, i.e., in
, is assumed where the emission per kilometer is decreasing at an annual rate of
, where
. This assumption is in line with the observed fuel efficiency increase of passenger cars in the EU in the last few decades [
19]. A simplification is made by assuming exogenous increases in fuel efficiency. This is in contrast to the relatively large body of literature on endogenous development of the transport vehicles technology development occurs as a response to, among other things, investment, demand generated by income growth and environmental regulatory pressures (e.g., [
20,
21]), learning by research (e.g., [
8]) and learning by doing (e.g., [
22]). The justification for this simplification is the calculation of costs only for car owners in different EU countries to reach the CO
2 emission targets, which are assumed to perceive technological development as given. Total emission at time
t,
, is then the sum of emission from the stock of vehicle type in EU-27 member states (MS) and UK:
where
shows the emission per km in period
t at the annual rate of carbon efficiency
αj by vehicle type
j from period 0.
Within the EU, there are no targets for reductions in emissions specifically from light-duty vehicles but only from the transport sector by 2050. Therefore, successive changes in emission targets,
, where
T is the target year 2050, are made in order to derive an EU-UK cost function for 2050. The emission constraint is written as:
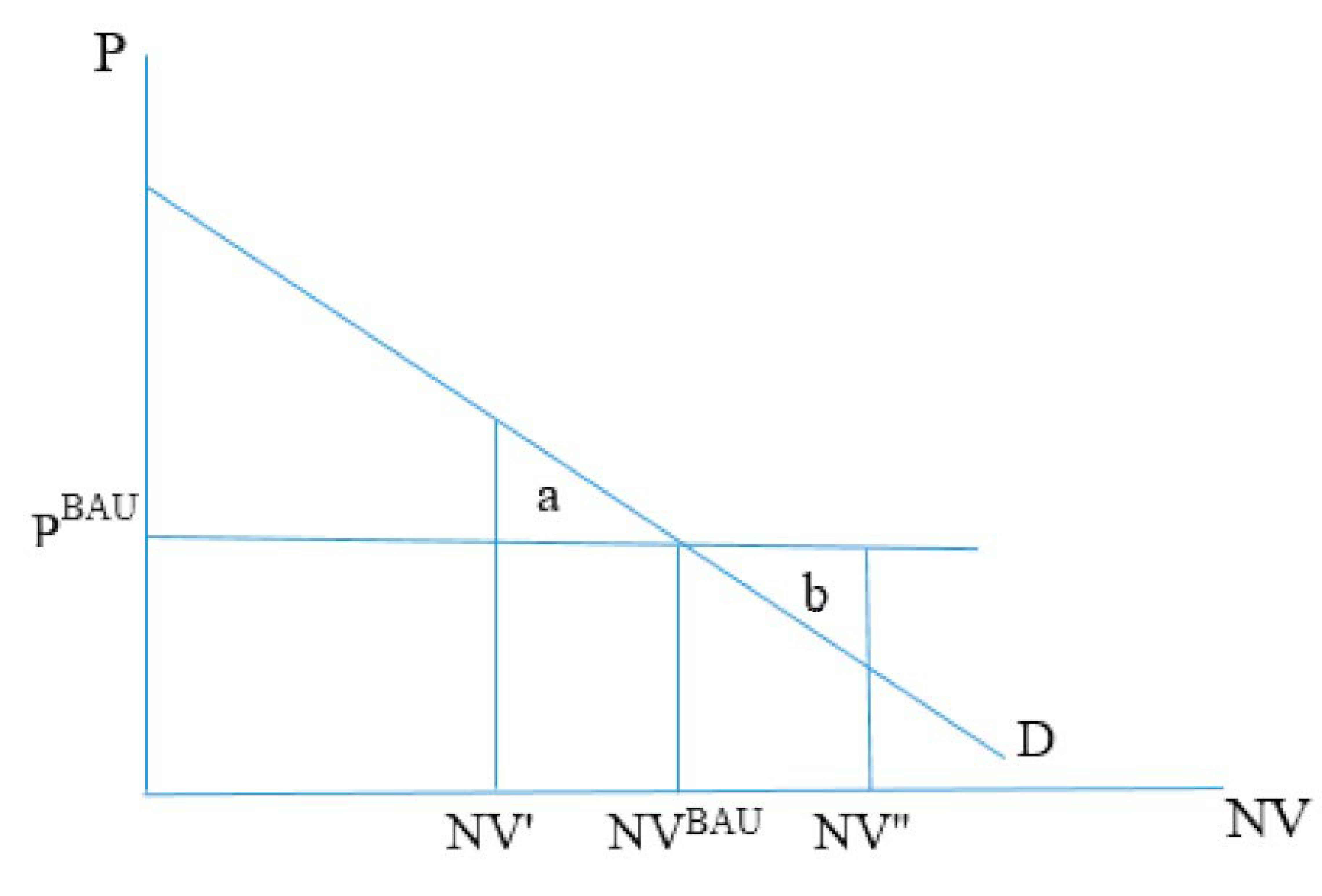
The cost of reducing emission from fossil fuel vehicles through changes in the allocation of vehicles is denoted , which is calculated as decreases in consumer surplus from the demand of in the business-as-usual case. By assumption, the prices in the BAU show consumers willingness to pay for each car type, which includes perceived costs of driving the car, depreciation, etc. The cost from deviation from these prices and quantities then reflects consumer losses from paying a higher price than willingness to pay for hybrid and electric cars and from lost values in excess of the price for fossil fuel cars. Changes in consumer surplus are estimated by assumption of linear demand functions, which are derived from data on price elasticities, price and demand for in the reference year . It is then assumed that the prices are given and that the demand function in each country and for each vehicle type shifts according to changes in travel demand in the business as usual.
The costs of new cars may change over time because of, among other things, the fall in the price of electric cars due to improved batteries. Similar to technological change in fuel efficiency, we assign an exogenous and monotonic change in costs, which is written as:
where
is the annual rate of change in the costs of passenger car. The cost function is assumed to be continuous, decreasing and convex in its arguments. This is to ensure that the second-order conditions of minimization are satisfied.
The decision problem is formulated as minimizing total cost in present terms,
TC, under restriction on travel demand and maximum emission, Equations (3) and (4) respectively, which is written as:
Subject to Equations (1)–(5), where
is the discount factor with the social discount rate
, which is assumed to be the same for all countries. The properties of the cost-effective solution are derived from the first-order condition:
where
. The parameter
denotes the marginal cost of achieving the emission target in year 2050, and
is the marginal cost of travel demand in each country and time period. According to Equation (7), a cost-effective solution requires that marginal cost of an emission reduction in the target year is equal for all countries and vehicles and amounts to
θ. This implies that,
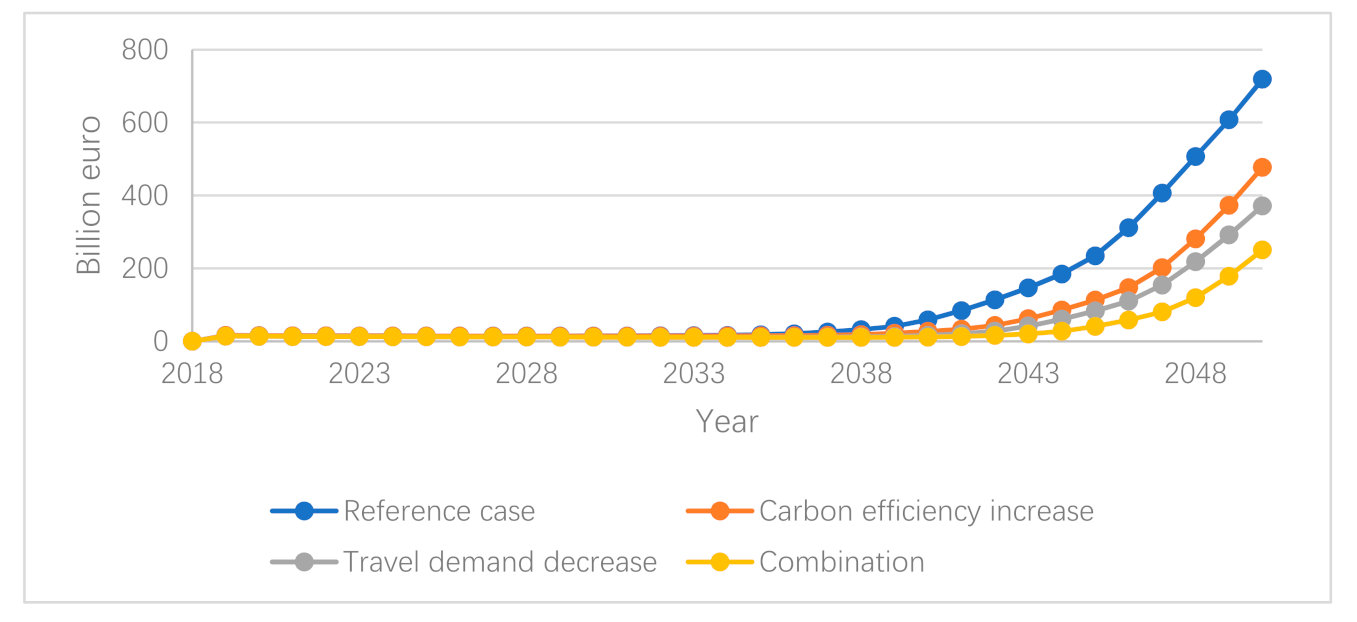
ceteris paribus, car switches are targeted towards reductions in vehicles with relatively large impacts on emission reductions, i.e., large carbon emission per kilometer, as shown by the denominator at the left hand side of Equation (7). When considering optimal timing of vehicle changes there are two counter acting forces. The discount factor and the exogenous changes in carbon efficiency and prices of non-fossil fuel cars favor delays of cars shifts since the cost of and emissions from new cars decrease over time. On the other hand, the increasing travel demand over time requires sufficiently early switches in order to obtain the emission constraint, shown by the second term within brackets on the left hand side of Equation (7).
2.2. Distributional Effects
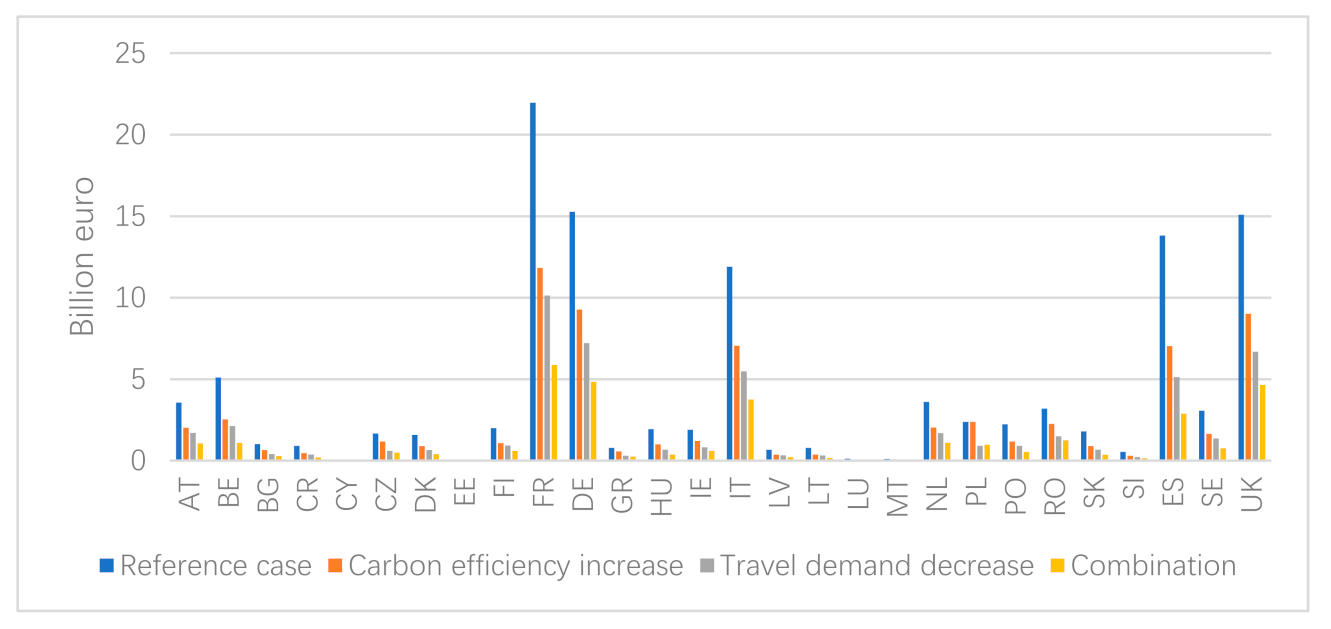
The cost-effective solutions will give rise to allocation of costs among countries, the effects of which can be of concern for policy makers. For example, the allocation of emission reductions in the effort sharing scheme for meeting the 2030 EU climate target accounts for fairness [
23]. The targets to be achieved are then divided among the countries according to their GDP/capita where the emission target is relatively low for low income countries, and vice versa. Several studies have shown that environmental taxation of cars and/or fuel is in general progressive although some studies show regressive effects (see review in [
11]). It is common to measure existence and magnitude of regressivity/progressivity by the Suits index, which relates the proportion of accumulated costs to proportions of accumulated income for different groups [
24]. The index is zero when costs are proportional to income, it is negative when low income groups face proportionally large share of total cost, and positive when the proportion of costs is relatively large for high income countries.
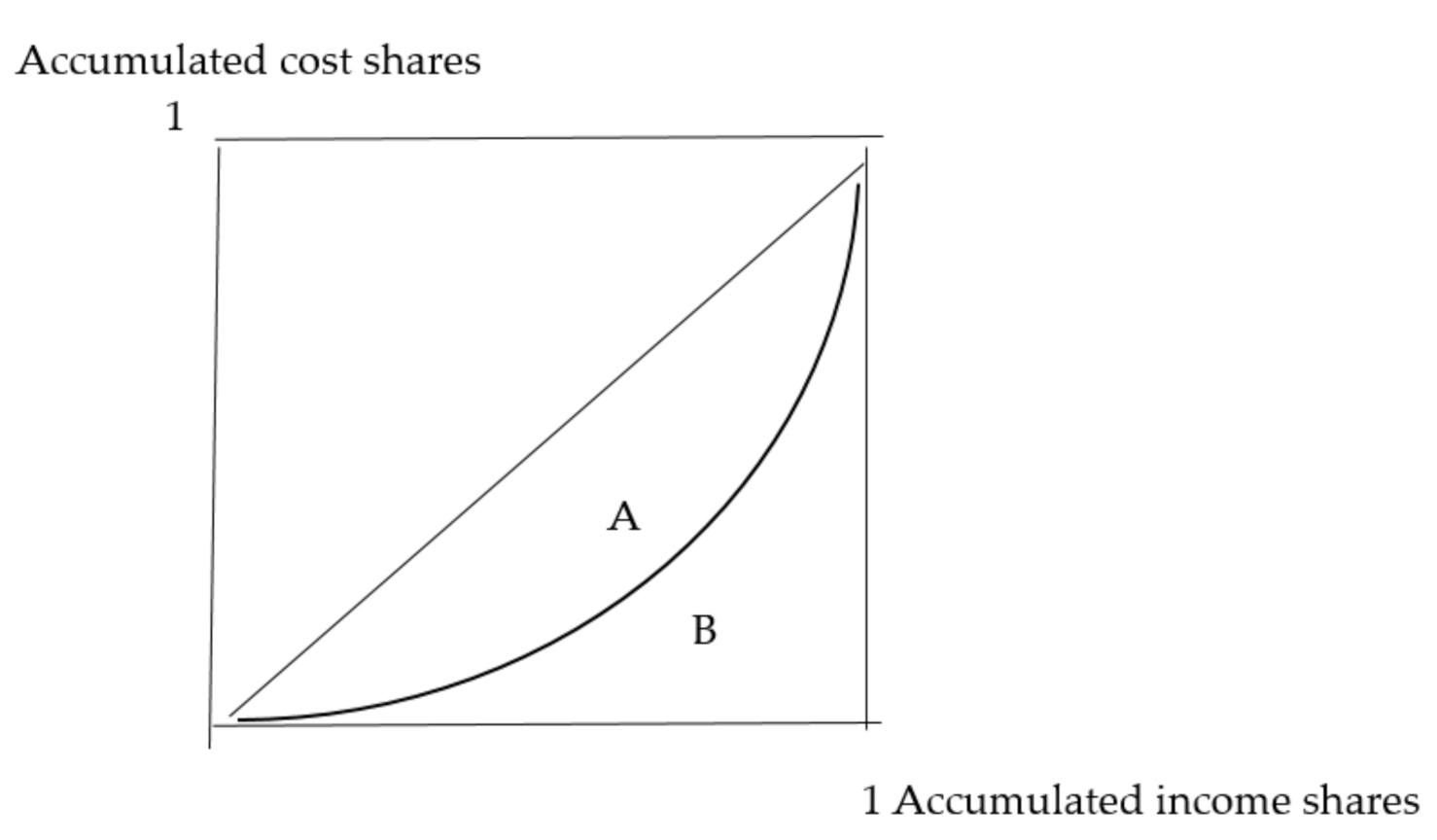
The calculation of the Suits index is based on the construction of Lorenz curves, which relate the accumulated emission reduction cost shares to income shares for the counties. Two different curves are illustrated in
Figure 1 where the
Y-axis shows accumulated increasing cost shares and the
X-axis is the accumulated increasing income shares. The linear Lorenz curve shows a neutral allocation of costs when the Suits index is zero since the share of the cost burden is the same as the share of total income at all levels. The nonlinear curve illustrates a progressive allocation where low income groups pay a relatively low share of the total cost.
The Suits index was calculated as the ratio between the area
A in relation to the area with a neutral allocation of costs, i.e., the area under the line that corresponds to 0.5 (i.e.,
area A + area B). We then had that the Suits index corresponded to
Area A/0.5, which gives
1 − AreaB/0.5 since
Area A = 0.5 − Area B (see e.g., [
11]). In this study
Area B was calculated as the sum of trapezoid areas of accumulated shares of income and costs for each country.
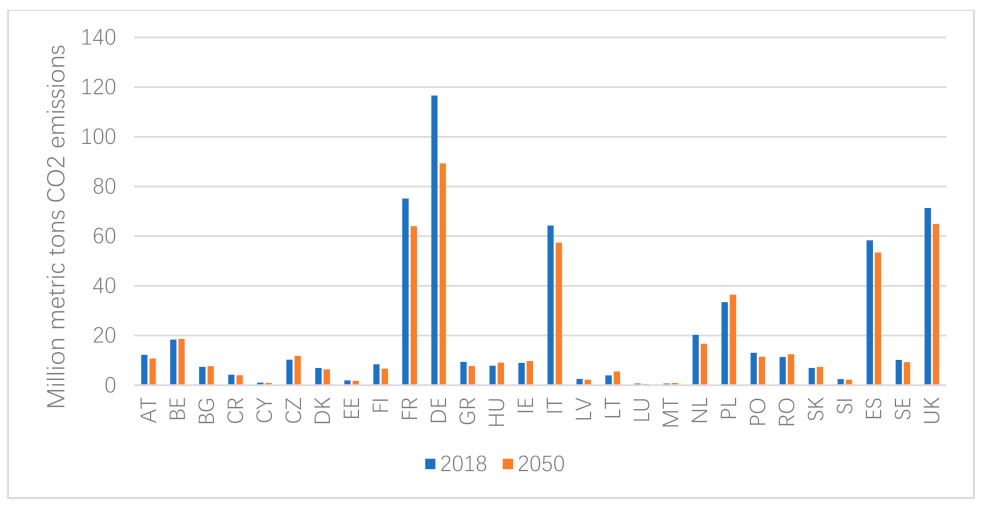
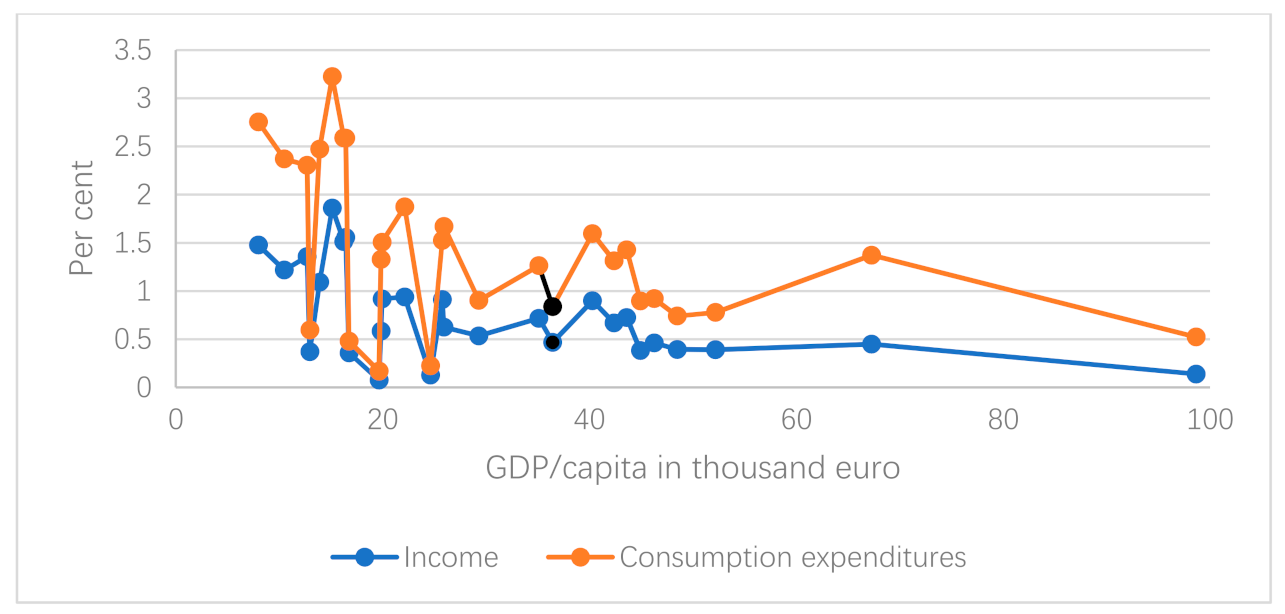
The Suits index may hide costs that are high in relation to income for some groups (e.g., [
14]). In order to examine this, we also calculated cost in relation to prosperity, measured as income per capita, for the EU MS and UK.