Influence of Climate Conditions on the Temporal Development of Wheat Yields in a Long-Term Experiment in an Area with Pleistocene Loess
Abstract
1. Introduction
1.1. Background
1.2. Objectives of this Study
| Author | Location | Crop | Described Factors of Influence |
|---|---|---|---|
| [26] | Germany | Wheat, barley, | Yield fluctuations of wheat and barley are mainly caused by precipitation and temperature in June in selected federal states of Germany |
| [27] | Germany | Wheat, barley, | The influence of precipitation and temperature on the yield development of wheat, barley and maize in selected districts in Bavaria with special consideration of development stages |
| [13] | Germany | Wheat | Development of heat and drought events and the change in wheat yield |
| [9] | Germany | Wheat | Influence of temporary waterlogging on growth, nutrient concentration, and yield of wheat |
| [7] | Denmark | Wheat | Effect of average temperature, global radiation, and daily precipitation on wheat yields in Denmark (over 17 years) |
| [6] | Europe | Wheat | Effect of mean monthly temperature, global radiation, and cumulative rainfall on the yields of winter wheat (over 34 years) |
| [5] | Europe | Wheat, barley | Temperature explains most of the yield fluctuations in Europe |
| [4] | Canada | - | Effects of climate change and CO2 increase on potential agricultural production in Southern Québec, Canada |
| [28] | Mexico | Wheat | Mexico: 25% increase in wheat yield in the last two decades due to higher night temperatures |
| [29] | USA | Spring wheat | Impacts of day versus night temperatures on spring wheat yields: A comparison of empirical and CERES wheat 2.0 model predictions in three locations |
| [30] | USA | Wheat | Simulating the influence of vernalization, photoperiod, and optimum temperature on wheat developmental rates |
| [31] | USA | Wheat, maize | Sensitivity of seeds to brief episodes of hot temperatures (e.g., flowering) |
| [32] | Europe | Wheat | Sensitivity of wheat varieties grown in Europe to heat, drought, frost, and precipitation |
| [33] | India | Wheat | Effect of lack of water on the yield of winter wheat |
| [15] | Australia | Wheat | Influence of temperature increases on the yield |
| [34] | Australia | Wheat | The effect of duration of heat stress during grain filling on two wheat varieties differing in heat tolerance: grain growth and fractional protein accumulation |
| [11] | China | Wheat | Influence of frost on yield in the jointing stage |
| [35] | China | Wheat | Influence of heat on the grain filling phase in wheat |
| [14] | - | Cereal | Influence of heat on different stages of development of the reproductive phase in different cereal varieties |
| [12] | - | Wheat | Summary of frost and heat damage models that can estimate the impact on the yield |
| [36] | - | Wheat | Summary of optimal and lethal temperatures of wheat during different stages of development |
| [37] | - | Wheat | Influence of waterlogging in different growth phases on the yield |
2. Materials and Methods
2.1. General Description, Soil, and Physiography of the Dürnast Long-Term Study Area
2.2. General Description Experimental Design, Wheat Varieties, and Amount of Fertilizer
2.3. Independent Parameters for the Derivation of Yield
2.4. Statistical Analyses
2.4.1. Calculation of Dataset 1
2.4.2. Calculation of Dataset 2
2.5. Statistical Procedures
- Autocorrelation of regression residuals: Durbin–Watson test;If residuals are not independent, there is autocorrelation. This means that a variable correlates with itself at a different time. We use SPSS to test first-order autocorrelation and thus whether a residual correlates with its direct neighbor. However, in this study, it would make little sense to check autocorrelation because it is very unlikely that the measurements or residuals with a distance of three years are dependent. In such cases, testing the independence of the residuals can be omitted.
- Homoscedasticity (no autocorrelation in regression residuals, homogeneity of variance): plot of residuals against predicted values;
- Normally distributed residuals; and
- Multicollinearity (two independent variables are highly correlated): tolerance and variance inflation factor (VIF).
3. Results
3.1. Temporal Course of the Yields
3.2. Derivation of Yields with Monthly Predictors
3.3. Derivation of Yields with Annual Predictors
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hatfield, J.L.; Boote, K.J.; Fay, P.; Hahn, L.; Izaurralde, R.C.; Kimball, B.A.; Mader, T.; Morgan, J.; Ort, D.; Polley, W.; et al. Agriculture. In The Effects of Climate Change on Agriculture, Land Resources, water Resources, and Biodiversity in the United States; Backlund, P., Janetos, A., Schimel, D., Eds.; U.S. Climate Change Science Program and the Subcommittee on Global Change Research: Washington, DC, USA, 2008; p. 362. Available online: https://www.fs.fed.us/rm/pubs_other/rmrs_2008_backlund_p003.pdf (accessed on 1 November 2019).
- Hatfield, J.L.; Prueger, J.H. Agroecology: Implications for plant response to climate change. In Crop Adaptation to Climate Change; Yadav, S.S., Redden, R.J., Hatfield, J.L., Lotze-Campen, H., Hall, A.E., Eds.; Wiley-Blackwell: West Sussex, UK, 2001; pp. 27–43. [Google Scholar]
- Wittwer, S. Food, Climate, and Carbon Dioxide: The Global Environment and World Food Production; CRC Press: Boca Raton, FL, USA, 1995; 236p, ISBN 0-87371-796-1. [Google Scholar]
- Brassard, J.P.; Singh, B. Effects of climate change and CO2 increase on potential agricultural production in Southern Québec, Canada. Clim. Res. 2007, 34, 105–117. [Google Scholar] [CrossRef]
- Trinka, M.; Olesen, J.E.; Kersebaum, K.C.; Rötter, R.P.; Brázdil, R.; Eitzinger, J. Changing regional weather-crop yield relationships across Europe between 1901 and 2012. Clim. Res. 2016, 70, 195–214. [Google Scholar] [CrossRef]
- Peltonen-Sainio, P.; Jauhiainen, L.; Trnka, M.; Olesen, J.E.; Calanca, P.; Eckersten, H.; Eitzinger, J.; Gobin, A.; Kersebaum, K.C.; Kozyrai, J.; et al. Coincidence of variation in yield and climate in Europe. Agric. Ecosyst. Environ. 2010, 139, 483–489. [Google Scholar] [CrossRef]
- Kristensen, K.; Schelde, K.; Olesen, J.E. Winter wheat yield response to cli-mate variability in Denmark. J. Agric. Sci. 2011, 149, 33–47. [Google Scholar] [CrossRef]
- Deutschländer, T.; Dalelane, C. Auswertung Regionaler Klimaprojektionen für Deutschland Hinsichtliche der Änderung des Extremverhaltens von Temperatur, Niederschlag und Windgeschwindigkeit; Abschlussbericht, Offenbach am Main, DWD: Offenbach, Hesse, Germany, 2012. [Google Scholar]
- Wollmer, A.-C.; Pitmann, K.; Mühling, K.-H. Einfluss von temporärer Überstauung auf Wachstum, Nährstoffkonzentration und Ertrag von Weizen. In Thomas Ebertseder (Hg.): Kongressband 2016 Rostock. Vorträge zum Generalthema: Anforderungen an die Verwertung von Reststoffen in der Landwirtschaft. Darmstadt; VDLUFA-Verlag VDLUFA-Schriftenreihe: Darmstadt, Germany, 2016; Volume 73, pp. 138–142. [Google Scholar]
- Oberforster, M. Resistenz Gegen Biotischen Stress in der Pflanzenzüchtung. Resistenz Gegen Abiotischen Stress in der Pflanzenzüchtung; 63. Tagung, 19–21 November 2012; Lehr- und Forschungsanstalt für Landwirtschaft Raumberg-Gumpenstein: Raumberg-Gumpenstein, Irdning, Austria, 2012. [Google Scholar]
- Wu, Y.F.; Zhong, X.L.; Hu, X.; Ren, D.C.; Lv, G.H.; Wei, C.Y.; Song, J.Q. Frost affects grain yield components in winter wheat. N. Z. J. Crop. Hortic. Sci. 2014, 42, 194–204. [Google Scholar] [CrossRef]
- Barlow, K.M.; Christy, B.P.; O’leary, G.J.; Riffkin, P.A.; Nuttall, J.G. Simulating the impact of extreme heat and frost events on wheat crop production: A review. Field Crop. Res. 2015, 171, 109–119. [Google Scholar] [CrossRef]
- Lüttger, A.B.; Feike, T. Development of heat and drought related extreme weather events and their effect on winter wheat yields in Germany. Theor. Appl. Clim. 2018, 132, 15–29. [Google Scholar] [CrossRef]
- Barnabás, B.; Jäger, K.; Fehér, A. The effect of drought and heat stress on re-productive processes in cereals. Plant Cell Environ. 2008, 31, 11–38. [Google Scholar] [CrossRef]
- Asseng, S.; Forster, I.; Turner, N.C. The impact of temperature variability on wheat yields. Glob. Chang. Biol. 2011, 17, 997–1012. [Google Scholar] [CrossRef]
- Bayerische Landesanstalt für Landwirtschaft Freising (LfL). Weizenkrankheiten—LfL-Merblatt; Bayerische Landesanstalt für Landwirtschaft: Freising, Germany, 2018. [Google Scholar]
- Hooker, R.H. The weather and the crops in eastern England, 1885–1921. Q. J. R. Meteorol. Soc. 1922, 48, 115–138. [Google Scholar] [CrossRef]
- Baumann, H.; Weber, E. Attempt of a statistical analysis of the relation between weather and yield by multiple regression. Notes Ger. Natl. Meteorol. Serv. 1966, 37–41. [Google Scholar]
- Swanson, E.R.; Nyankori, J. Influence of weather and technology on corn and soy bean yield trends. Agric. Meteorol. 1979, 20, 327–342. [Google Scholar] [CrossRef]
- Chmielewski, F.-M.; Potts, J.M. The relationship between crop yields from an experiment in southern England and long-term climate variations. Agric. For. Meteorol. 1995, 73, 43–66. [Google Scholar] [CrossRef]
- Alexandrov, V.A.; Hoogenboom, G. Climate variation and crop production in Georgia, USA, during the twentieth century. Clim. Res. 2001, 17, 33–43. [Google Scholar] [CrossRef]
- Soja, A.-M.; Soja, G. Dokumentation von Auswirkungen extremer Wetterereignisse auf die Landwirtschaftliche Produktion. In Startprojekt Klimaschutz: StartClim.3b—Erste Analysen Extremer Wetterereignisse und ihrer Auswirkungen in Österreich; ARC Seibersdorf Reserach: Seibersdorf, Austria; 106p, Available online: http://141.244.189.116/fileadmin/user_upload/StartClim2003_reports/StCl03b.pdf (accessed on 8 December 2019).
- Bernhofer, C.; Hänsl, S.; Schaller, A.; Pluntke, T. Charakterisierung von Meteorologischer Trockenheit; Landesamt, F.U., Landwirtschaft, U.G., Eds.; Sächsisches Landesamt für Umwelt, Landwirtschaft und Geologie Dresden, Schriftenreihe: Schriftenreihe, Germany, 2015. [Google Scholar]
- Beitz, R. Witterung und Klima. Available online: http://www.forstliche-umweltkontrolle-bb.de/r3_klima.php (accessed on 1 January 2020).
- Riek, W.; Kallweit, R.; Russ, A. Analyse der Hauptkomponenten des Wärmehaushalts brandenburgischer Wälder auf der Grundlage regionaler Klimaszenarien—Abgrenzung von Risikogebieten und Schlussfolgerung für ein Klima-Monitoring. Wald. Landsch. Nat. 2012, 13, 17–32. [Google Scholar]
- Dendl, M. Ertragsschwankungen von Weizen und Gerste und deren Ursachen in Ausgewählten Bundesländern Deutschlands. Diploma Thesis, Technische Universität München, Lehrstuhl für Pflanzenernährung, Freising, Germany, 2008; p. 50, submitted. [Google Scholar]
- Olszynski, A. Der Einfluss von Niederschlag und Temperatur auf die Ertragsentwicklung von Weizen, Gerste und Mais in ausgewählten Landkreisen Bayerns unter besonderer Berücksichtigung der Entwicklungsstadien. Bachelor’s Thesis, Technische Universität München Lehrstuhl für Pflanzenernährung, Freising, Germay, 2013; 85p. submitted. [Google Scholar]
- Lobell, D.; Field, C. Global scale climate-crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2007, 2. [Google Scholar] [CrossRef]
- Lobell, D.B.; Ortiz-Monasterio, J.I.; Anser, P.; Matson, P.A.; Naylor, R.L.; Falcon, W.P. Analysis of wheat yield and climatic trends in Mexico. Field Crop. Res. 2005, 94, 250–256. [Google Scholar]
- McMaster, G.S.; White, J.W.; Hunt, L.A.; Jamieson, P.D.; Dhillon, S.S.; Ortiz-Monasteriop, J.I. Simulating the Influence of Vernalization, Photoperiod and Optimum Temperature on Wheat Developmental Rates. Ann. Bot. 2008, 102, 561–569. [Google Scholar] [CrossRef]
- Wheeler, T.R.; Craufurd, P.Q.; Ellis, R.H.; Porter, J.R.; Vara Prasad, P.V. Temperature variability and the yield of annual crops. Agric. Ecosyst. Environ. 2000, 82, 159–167. [Google Scholar]
- Mäkinen, H.; Kaseva, J.; Trnka, M.; Balek, J.; Kersebaum, K.C.; Nendel, C. Sensitivity of European wheat to extreme weather. Field Crop. Res. 2018, 222, 209–217. [Google Scholar] [CrossRef]
- Gupta, N.K.; Gupta, S.; Kumar, A. Effect of Water Stress on Physiological Attributes and their Relationship with Growth and Yield of Wheat Cultivars at Different Stages. J. Agron. Crop. Sci. 2001, 186, 55–62. [Google Scholar] [CrossRef]
- Stone, P.J.; Nicolas, M.E. Wheat cultivars vary widely in their responses of grain yield and quality to short periods of post-anthesis heat stress. Aust. J. Plant Physiol. 1994, 21, 887–900. [Google Scholar] [CrossRef]
- Wang, X.; Hou, L.; Lu, Y.; Wu, B.; Gong, X.; Liu, M. Metabolic adaptation of wheat grain contributes to a stable filling rate under heat stress. J. Exp. Bot. 2018, 69, 5531–5545. [Google Scholar] [CrossRef] [PubMed]
- Porter, J.R.; Gawith, M. Temperatures and the growth and development of wheat: A review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar] [CrossRef]
- Ghobadi, M.E.; Ghobadi, M.; Zebarjadi, A. Effect of waterlogging at different growth stages on some morphological traits of wheat varieties. Int. J. Biometeorol. 2017, 61, 635–645. [Google Scholar] [CrossRef]
- Arbeitsgruppe, B. Bodenkundliche Kartieranleitung. 5. Verbesserte und erweiterte Auflage (Herausgegeben von der Bundesanstalt für Geowissenschaften und Rohstoffe in Zusammenarbeit mit den Staatlichen Geologischen Diensten der Bundesrepublik Deutschland; Schweizerbart’sche Verlagsbuchhandlung: Hannover, Germany, 2005. [Google Scholar]
- Heil, K.; Schmidhalter, U. Improved evaluation of field experiments by ac-counting for inherent soil variability. Eur. J. Agron. 2017, 89, 1–15. [Google Scholar] [CrossRef]
- Bundesministeriums der Justiz und für Verbraucherschutz. Gesetz zur Schätzung des landwirtschaftlichen Kulturbodens (Bodenschätzungsgesetz—BodSchätzG). Available online: https://www.gesetze-im-internet.de/bodsch_tzg_2008/BodSch%C3%A4tzG.pdf (accessed on 10 October 2019).
- Bundessortenamt. Beschreibende Sortenliste Getreide, Mais, Ölfrüchte, Leguminosen (großkörnig), Hackfrüchte (außer Kartoffeln). In Bundessortenamt (Beschreibende Sortenliste Getreide, Mais, Ölfrüchte, Leguminosen (großkörnig), Hackfrüchte (außer Kartoffeln)); Bundessortenamt: Hannover, Germany, 2017; ISBN 2190-6130. [Google Scholar]
- IBM. IBM SPSS Forecasting 20; IBM Corporation: Hannover, Germany, 2011. [Google Scholar]
- Sterzel, T. Correlation Analysis of Climate Variables and Wheat Yield Data on Various Aggregation Levels in Germany and the EU-15 Using GIS and Statistical Methods, with a Focus on Wave Years; PIK Report PIK-108; Potsdam-Institut fuer Klimafolgenforschung e.V.: Potsdam, Germany, 2007; 122p. [Google Scholar]
- Gröbmaier, J. Ökonomische Auswirkungen des Klimawandels auf den Marktfruchtbau und Bewertung von Anpassungsoptionen am Beispiel von Ernteversicherung. Ph.D. Thesis, Fakultät Wissenschaftszentrum Freising, Freising, Germany, 2012. [Google Scholar]
- Lütke Entrup, N.; Schäfer, B.C. Lehrbuch des Pflanzenbaues, 3rd ed.; Agroconcept: Bonn, Germany, 2011. [Google Scholar]
- Jahn, M.; Wagner, C.; Sellmann, J. Ertragsverluste durch wichtige Pilzkrankheiten in Winterweizen im Zeitraum 2003 bis 2008. Versuchsergebnisse aus 12 deutschen Bundesländern. J. Für Kult. 2012, 64, 273–285. [Google Scholar]
- Börner, H.; Aumann, J.; Schlüter, K. Pflanzenkrankheiten und Pflanzenschutz, 8th ed.; Springer-Lehrbuch: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Dietz, T.; Weigelt, H. Böden unter landwirtschaftlicher Nutzung: 48 Bodenprofile in Farbe; BLV-Verl.-Ges: München, Germany, 1991; 108p. [Google Scholar]
- Hoogenboom, G. Contribution of agrometeorology to the simulation of crop production and its applications. Agric. For. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- White, J.W.; Hoogenboom, G.; Kimball, B.A.; Wall, G.W. Methodologies for simulating impacts of climate change on crop production. Field Crop. Res. 2011, 124, 357–368. [Google Scholar] [CrossRef]

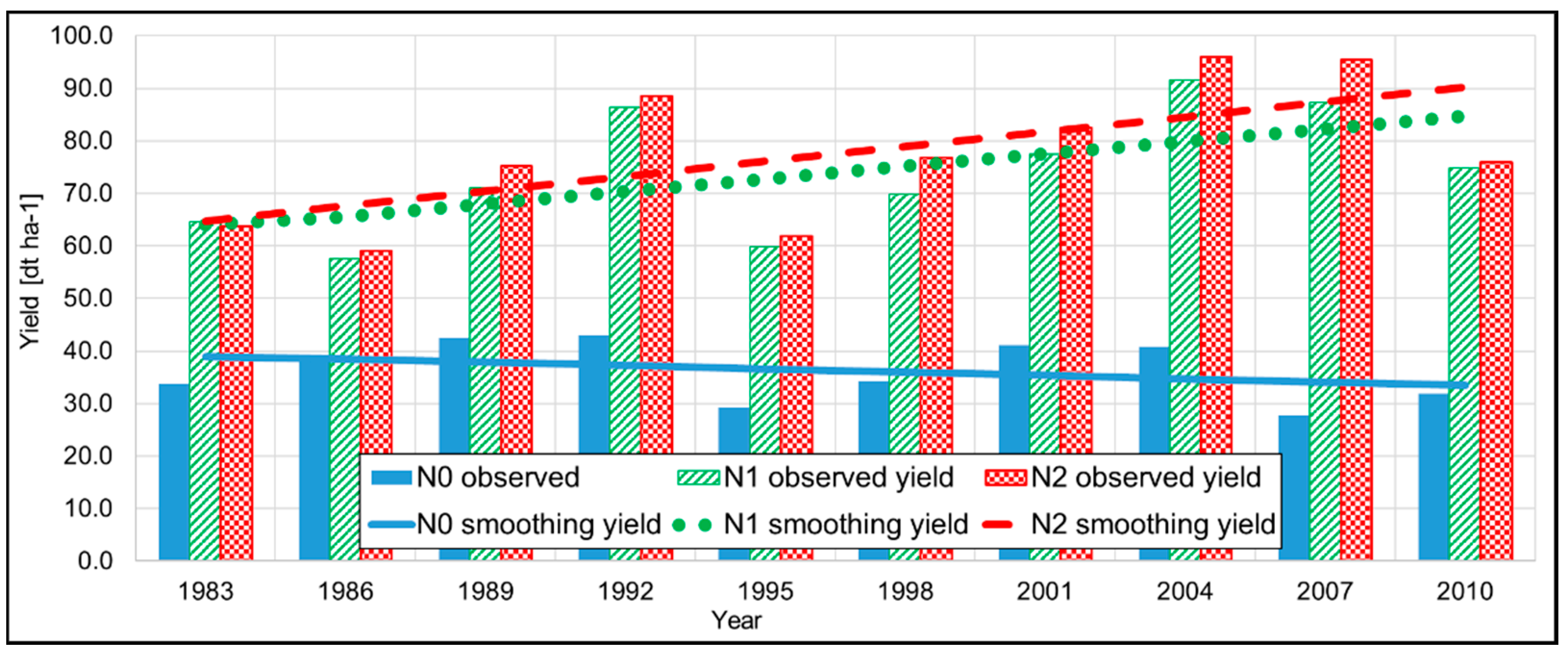
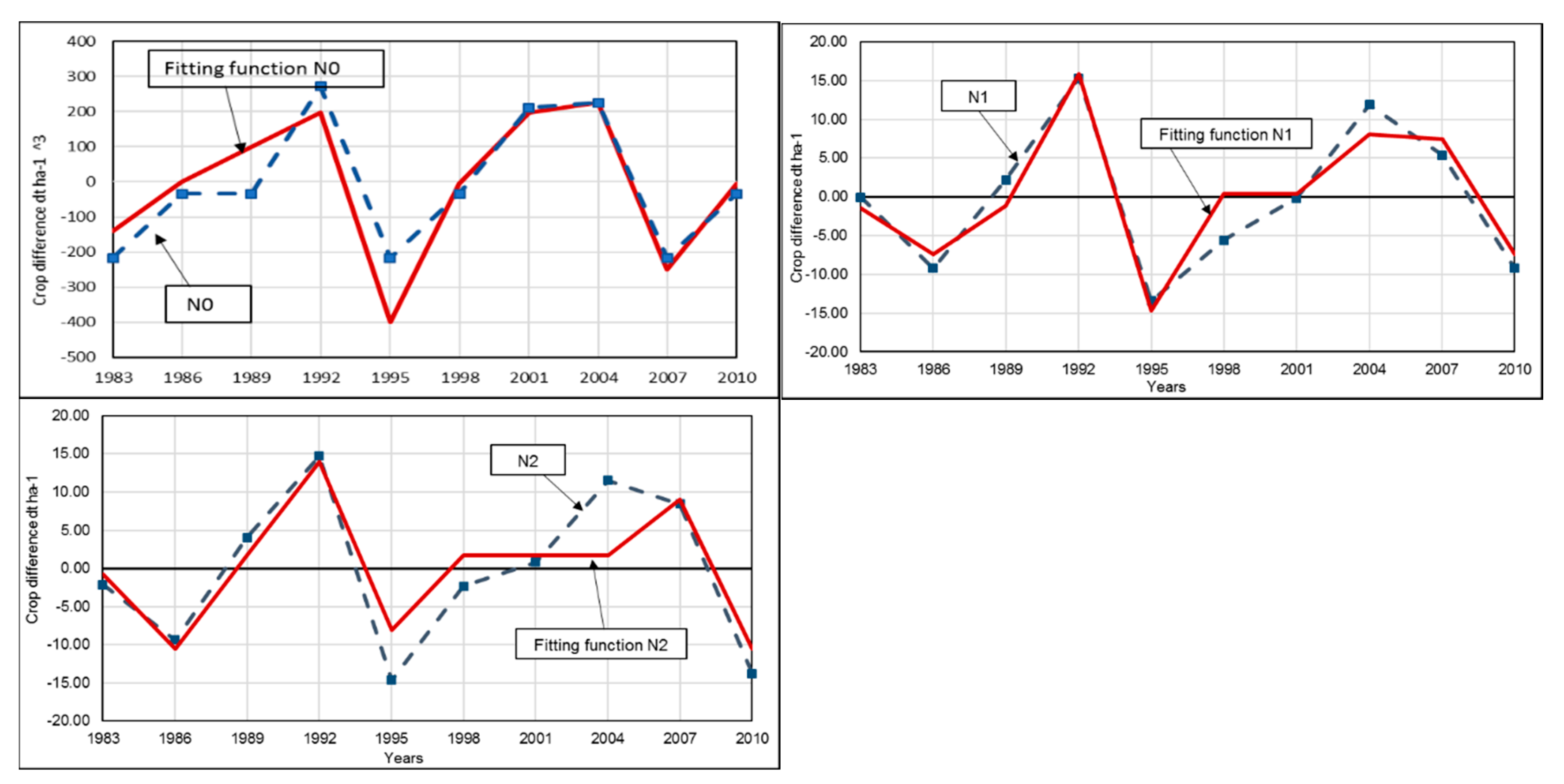
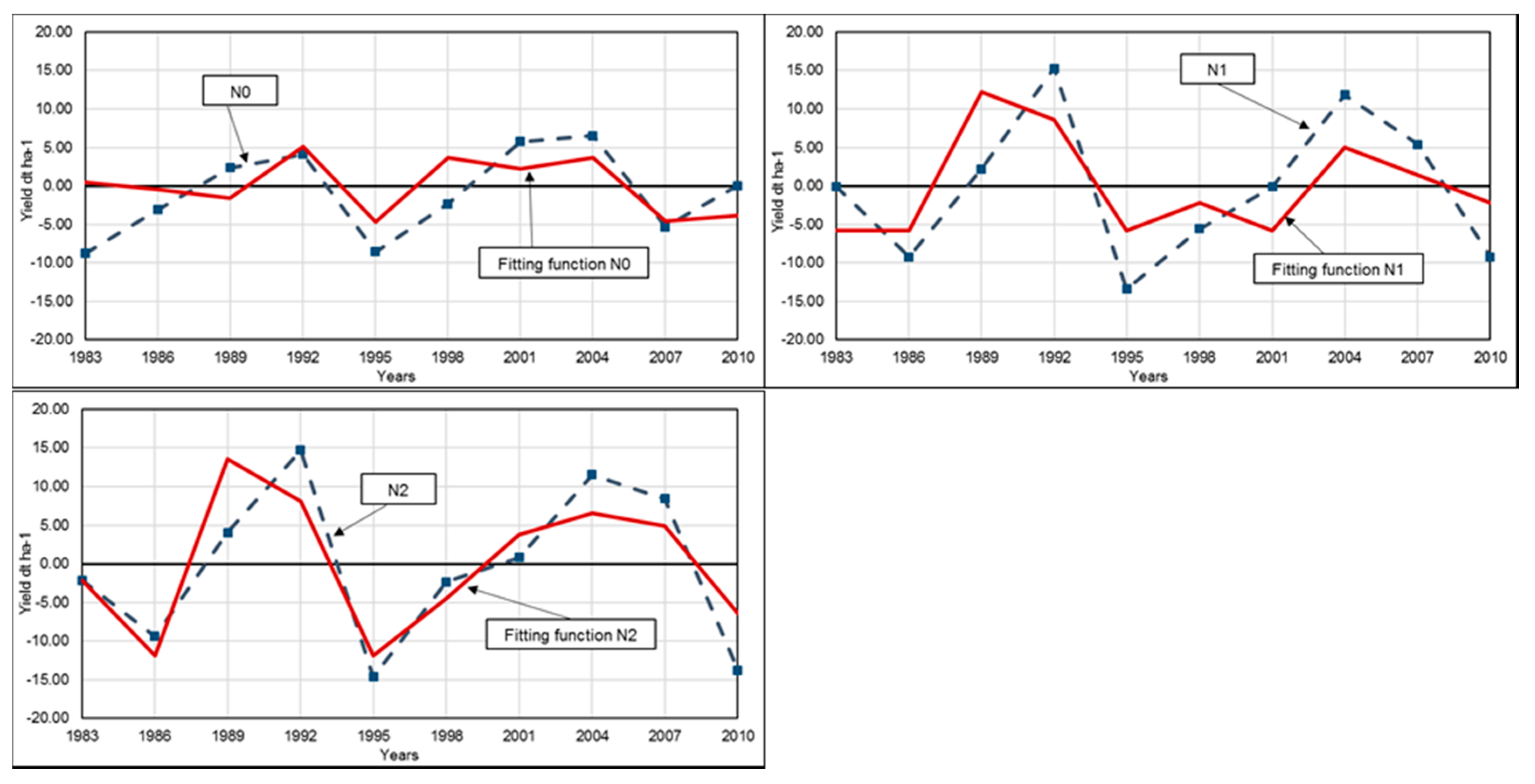
| Parameter | Value (Range) | |||
|---|---|---|---|---|
| Elevation (m) | 470 (469–472) | |||
| Slope (rad) | 0.05 (0.05–0.09) | |||
| Aspect (rad) | 2.64 (1.97–3.46) | |||
| Soil vertical layer | 0–25 cm | 25–50 cm | 50–75 cm | |
| Soil texture (kg kg−1) | Clay | 20.8 (15.7–27.3) | 23.3 (15.2–34.9) | 26.2 (13.6–34.8) |
| Silt | 61.5 (54.4–67.5) | 61.7 (35.7–72.9) | 60.7 (32.8–76.8) | |
| Sand | 16.6 (11.9–21.3) | 14.4 (8.5–40.5) | 12.4 (5.3–46.8) | |
| Skeleton | 1.2 (0.0–3.0) | 0.6 (0.0–7.0) | 0.4 (0.0–3.0) | |
| pH | 6.44 (5.94–6.84) | 6.36 (5.96–7.12) | 6.31 (5.98–7.18) | |
| C content (%) | 1.18 (0.94–1.38) | 0.56 (0.35–1.14) | 0.4 (0.22–1.11) | |
| N content (%) | 0.1 (0.08–0.12) | 0.06 (0.03–0.12) | 0.04 (0.02–0.12) | |
| Year | Wheat Cultivar | N Fertilizer (kg ha−1) | |
|---|---|---|---|
| Low | High | ||
| 1980 | Winter Caribo | 100 | 150 |
| 1983 | Winter Caribo | 100 | 150 |
| 1986 | Winter Kronjuwel | 100 | 150 |
| 1989 | Winter Obelisk | 100 | 150 |
| 1992 | Winter Orestis | 100 | 150 |
| 1995 | Winter Astron | 100 | 150 |
| 1998 | Winter Astron | 100 | 150 |
| 1992 | Winter Obelisk | 100 | 150 |
| 1995 | Winter Astron | 100 | 150 |
| 1998 | Winter Astron | 100 | 150 |
| 2001 | Winter Ludwig | 100 | 150 |
| 2004 | Winter Tommi | 140 | 180 |
| 2007 | Winter Tommi | 140 | 180 |
| 2010 | Winter Tommi | 140 | 180 |
| 2012 | Spring Kadrilj | 120 | 180 |
| 2015 | Spring Lennox | 120 | 180 |
| Variable | Definition/Time Range | Formula for the Derivation of the Indices |
| Precipitation intensity (PI) | Sum of days on which a certain amount of precipitation occurs | |
| PI1: >0–1 mm per day | ||
| PI2: >1–10 mm per day | ||
| PI3: >10 mm per day | ||
| Monthly values from October to August | where P is precipitation (mm) and n denotes number of days | |
| Rain-free days (P0) | Sum of days without precipitation (P0); monthly values from October to August | where N is height of precipitation |
| Temperature threshold (TT) | Sum of the days on which the threshold values of 5 or 10 °C are exceeded; monthly values from October to August | where Tmax is the daily maximum temperature (°C) |
| Summer days (SD) | Sum of the days on which the air temperature exceeds 25 °C; monthly values from October to August | |
| Heat days (HD) | Sum of the days on which the air temperature exceeds 30 °C; monthly values from October to August | |
| Frost days (FT) | Sum of the days on which the air temperature falls below the value 0 °C; monthly values from October to August | where Tmin is the daily minimum temperature (°C) |
| Average temperature (Ty) per year | where Tempd is the diurnal mean air temperature of the day, n is the number of days per year | |
| Average temperature (Tv) main vegetation period | where n is the number of days per main vegetation period | |
| Precipitation sum (Py) | Sum of precipitation per year, (calculated for every year) | where Pd is precipitation per day |
| Rain factor (RF) | Relationship of precipitation/temperature per year, (calculated for every year) | where Py is the annual precipitation and Ty is the average annual temperature |
| Dryness index de Martonne-Reichel (DI) | Evaluates the effect of precipitation on plant physiology and precipitation distribution during the main vegetation period | where 10 indicates that negative values in the denominator should be avoided, K is the number of days with precipitation ≥ 1.0 mm, and 120 is the multiannual average number of days with precipitation in Germany (main vegetation period) |
| Air humidity (AH) | Evaluates the effect of precipitation on plant physiology; annual values | |
| Aridity index (AI) | Evaluates the effect of precipitation on plant physiology; main vegetation period | |
| Summer index (SIy) | Sum of days with daily maximum of air temperature above 5 °C; yearly | |
| Summer index (SIv) | Sum of days with daily maximum of air temperature above 5 °C; main vegetation period | |
| Winter index (WI) | Sum of days with daily maximum of air temperature above 5 °C from November to April | |
| Frost alternating days (FAD) | Sum of days (October to April) with a change of temperatures above and below 0 °C within a day, between consecutive days | |
| Early frost index (EFI) | Sum of the days on which the minimum air temperature falls below 0 °C from July to October | |
| Late frost index (LFI) | Sum of the days on which the minimum air temperature falls below 0 °C from April to July | |
| Variable | Definition/Time Range | |
| Frost severity (FS) | Annual minimum of temperature | |
| Begin/end of the main vegetation period | First week of the year on which the threshold value of 5 °C is permanently exceeded (at least 5 days)/mid-August | |
| Frost index per Liu (FI_Liu) | Sum of the days on which the minimum air temperature is below −3 °C and the temperature difference is at least 8 °C from the mean value of the last 20 days; from September to May | |
| Frost shock (FS) | Sum of the days on which the air temperature drops by 15 °C within 24 h and the minimum air temperature falls below −3 °C; annual values | |
| Summer cold per Liu (SC_Liu) | Sum of the difference between the minimum temperature and the mean minimum temperature of the last 20 days exceeding 8 °C | |
| Climatic main vegetation time duration 1 (CL1) | Number of days with the longest period in which the air temperature exceeds 10 °C; values per year | |
| Climatic main vegetation time duration 2 (CL2) | Number of 5-day periods with a maximum diurnal air temperature above 10 °C; values per year | |
| Global radiation (GR) | Sum of global radiation; annual values | |
| Influence | Effects Eliminated by Residuals | Effects Remain in Residuals |
|---|---|---|
| Biological and chemical | New varieties Herbicides Insecticides Fertilizer, fertilization level | Diseases Pest infestation |
| Mechanical management | Technical Equipment Processing | |
| Management advancement | Crop rotation | |
| Atmospheric | Climate change | Weather deviations, Extreme weather events |
| Regression Coefficient | Unit Predictor | Sig. | β Coefficient Standardized | RMSE (dt ha−1) | R2 Adj. | |
|---|---|---|---|---|---|---|
| Residuals unfertilized control^3 | 271.42 | ** | 4.27 | 0.775 | ||
| −61.007 × temperature threshold 2 (TT2) April | number of days | ** | −0.822 | |||
| 319.656 × TT2 February | number of days | * | 0.492 | |||
| Residuals low fertilization level | −22,035 | * | 2.90 | 0.862 | ||
| 1.859 × N0 June | number of days | ** | 0.651 | |||
| −1.532 × temperature threshold 1 (TT1) December | number of days | ** | −0.446 | |||
| Residuals high fertilization level | −46.209 | *** | 4.04 | 0.804 | ||
| 2.835 × rain-free days (P0) June | number of days | *** | 0.909 | |||
| Yield unfertilized control | 43.902 | ** | 3.60 | 0.487 | ||
| −1.499 × temperature threshold 2 (TT2) April | number of days | * | −0.738 | |||
| Yield low fertilization level | 90.973 | ** | 7.63 | 0.471 | ||
| −3.142 × temperature threshold 1 (TT1) December | number of days | * | −0.728 | |||
| Yield high fertilization level | 29.120 | n.s. | 8.65 | 0.472 | ||
| 2.968 × rain-free days (P0) June | number of days | * | 0.729 |
| Regression Coefficient | Unit Predictor | Sig. | β Coefficient, Standardized | RMSE (dt ha−1) | R2 Adj. | |
|---|---|---|---|---|---|---|
| Residuals unfertilized control | 19.697 | ** | 4.41 | 0.403 | ||
| −1.056 × aridity index (AI) | number of days | ** | −6.85 | |||
| Residuals low fertilization | −5.752 | n.s. | 6.35 | 0.439 | ||
| 3.595 × early frost index (EFI) | number of days | * | 0.708 | |||
| Residuals high fertilization | −11.914 | * | 5.03 | 0.648 | ||
| 3.526 × early frost index (EFI) | number of days | * | 0.636 | |||
| 1.960 × winter index (WI) | number of days | * | 0.486 | |||
| Crop unfertilized control | 58.083 | ** | 3.73 | 0.45 | ||
| −1.171 × aridity index (AI) | number of days | * | −0.715 | |||
| Crop low fertilization | 72.608 | ** | 5.07 | 0.733 | ||
| −1.830 × summer cold per Liu (SC_Liu) | number of days | ** | −0.686 | |||
| 3.990 × early frost index (EFI) | number of days | ** | 0.625 | |||
| Crop high fertilization | −173.24 | * | 5.90 | 0.719 | ||
| −0.00021 × global radiation (GR) | watt-hour m2 | ** | 0.692 | |||
| 4.194 × early frost index (EFI) | number of days | * | 0.579 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heil, K.; Lehner, A.; Schmidhalter, U. Influence of Climate Conditions on the Temporal Development of Wheat Yields in a Long-Term Experiment in an Area with Pleistocene Loess. Climate 2020, 8, 100. https://doi.org/10.3390/cli8090100
Heil K, Lehner A, Schmidhalter U. Influence of Climate Conditions on the Temporal Development of Wheat Yields in a Long-Term Experiment in an Area with Pleistocene Loess. Climate. 2020; 8(9):100. https://doi.org/10.3390/cli8090100
Chicago/Turabian StyleHeil, Kurt, Anna Lehner, and Urs Schmidhalter. 2020. "Influence of Climate Conditions on the Temporal Development of Wheat Yields in a Long-Term Experiment in an Area with Pleistocene Loess" Climate 8, no. 9: 100. https://doi.org/10.3390/cli8090100
APA StyleHeil, K., Lehner, A., & Schmidhalter, U. (2020). Influence of Climate Conditions on the Temporal Development of Wheat Yields in a Long-Term Experiment in an Area with Pleistocene Loess. Climate, 8(9), 100. https://doi.org/10.3390/cli8090100





