Independence of Future Changes of River Runoff in Europe from the Pathway to Global Warming
Abstract
1. Introduction
2. Materials and Methods
- (a)
- The daily time series of Q were smoothed with a monthly running mean before fitting an extreme value distribution, guaranteeing that medium-term lows were considered in the fit;
- (b)
- The generalized extreme value (GEV) distribution was used instead of the GPD, due to the excessive proximity of the GPD threshold to 0 in many pixels;
- (c)
- The pixels with a fitted GEV shape parameter < −0.5 were excluded from the analysis;
- (d)
- The time-varying 15 year low return level QL15 was preferred to the 100 year one, due to the excessive proximity of the latter to 0 in many points.
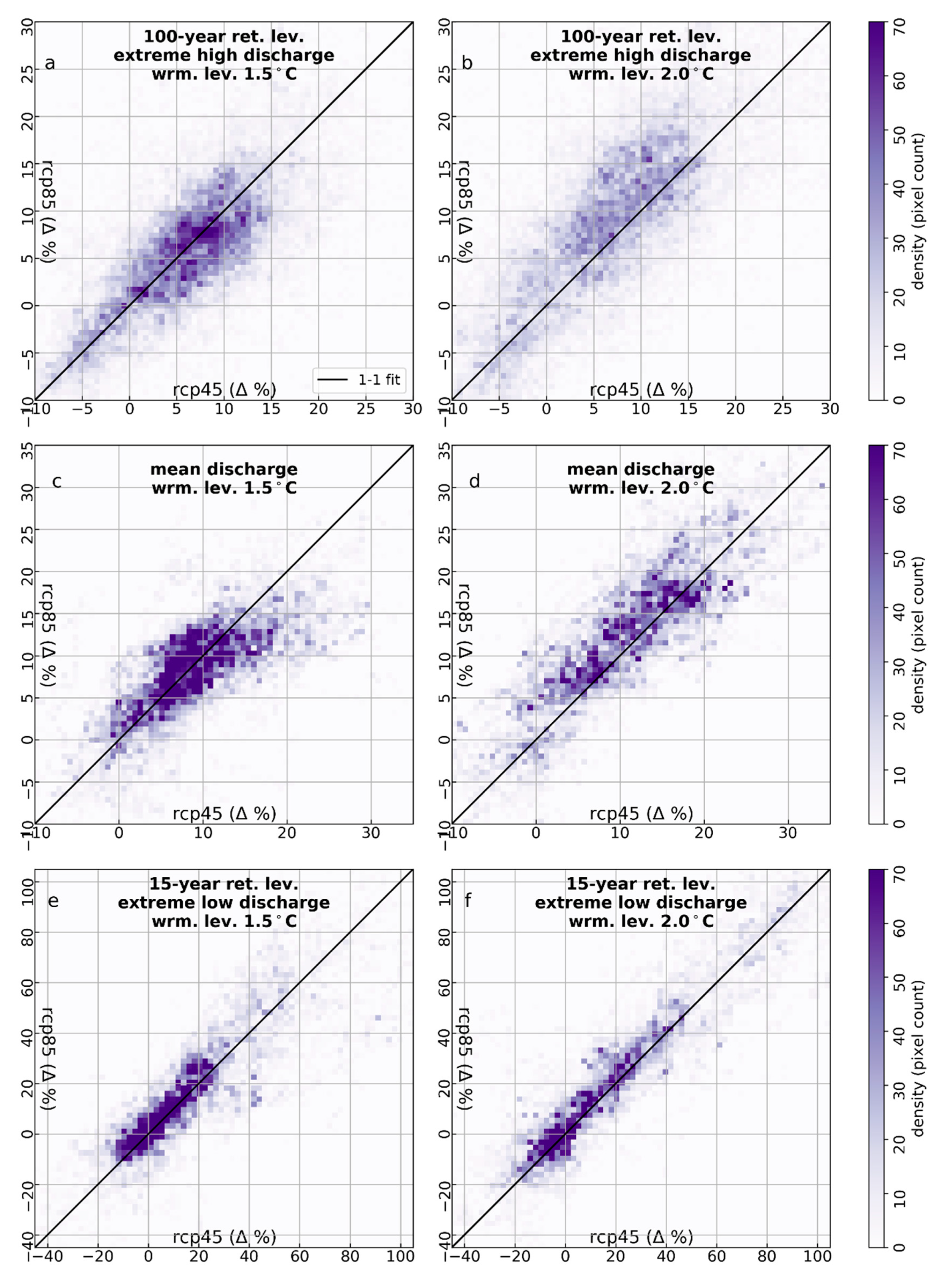
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Paprotny, D.; Sebastian, A.; Morales-Nápoles, O.; Jonkman, S.N. Trends in flood losses in Europe over the past 150 years. Nat. Commun. 2018, 9, 1985. [Google Scholar] [CrossRef] [PubMed]
- Feyen, L.; Dankers, R. Impact of global warming on streamflow drought in Europe. J. Geophys. Res. 2009, 114, D17116. [Google Scholar] [CrossRef]
- Calzadilla, A.; Rehdanz, K.; Betts, R.; Falloon, P.; Wiltshire, A.; Tol, R.S.J. Climate change impacts on global agriculture. Clim. Chang. 2013, 120, 357–374. [Google Scholar] [CrossRef]
- Jorda-Capdevila, D.; Gampe, D.; Huber García, V.; Ludwig, R.; Sabater, S.; Vergoñós, L.; Acuña, V. Impact and mitigation of global change on freshwater-related ecosystem services in Southern Europe. Sci. Total Environ. 2019, 651, 895–908. [Google Scholar] [CrossRef] [PubMed]
- Betts, A.K. Land-Surface-Atmosphere Coupling in Observations and Models. J. Adv. Model. Earth Syst. 2009, 1, 18. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. Understanding catchment behavior through stepwise model concept improvement. Water Resour. Res. 2008, 44, 13. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations - the CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Grizzetti, B.; Pistocchi, A.; Liquete, C.; Udias, A.; Bouraoui, F.; Van De Bund, W. Human pressures and ecological status of European rivers. Sci. Rep. 2017, 7, 205. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science (80) 2017, 357, 588–590. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: new high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Beven, K. I believe in climate change but how precautionary do we need to be in planning for the future? Hydrol. Process. 2011, 25, 1517–1520. [Google Scholar] [CrossRef]
- van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Bianchi, A.; Dosio, A. Assessment of future flood hazard in Europe using a large ensemble of bias-corrected regional climate simulations. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar]
- Alfieri, L.; Burek, P.; Feyen, L.; Forzieri, G. Global warming increases the frequency of river floods in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2247–2260. [Google Scholar] [CrossRef]
- Forzieri, G.; Feyen, L.; Rojas, R.; Flörke, M.; Wimmer, F.; Bianchi, A. Ensemble projections of future streamflow droughts in Europe. Hydrol. Earth Syst. Sci. 2014, 18, 85–108. [Google Scholar] [CrossRef]
- Wanders, N.; Wada, Y.; Van Lanen, H.A.J. Global hydrological droughts in the 21st century under a changing hydrological regime. Earth Syst. Dyn. 2015, 6, 1–15. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef]
- Arnell, N.W.; Lloyd-Hughes, B. The global-scale impacts of climate change on water resources and flooding under new climate and socio-economic scenarios. Clim. Chang. 2014, 122, 127–140. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Pfahl, S.; O’Gorman, P.A.; Fischer, E.M. Understanding the regional pattern of projected future changes in extreme precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Lugeri, N.; Dankers, R.; Hirabayashi, Y.; Döll, P.; Pińskwar, I.; Dysarz, T.; Hochrainer, S.; Matczak, P. Assessing river flood risk and adaptation in Europe-review of projections for the future. Mitig. Adapt. Strateg. Glob. Chang. 2010, 15, 641–656. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef]
- United Nations Convention on Climate Change. Paris Agreement; United Nations Convention on Climate Chang: New York, NY, USA, 2015. [Google Scholar]
- Mitchell, D.; James, R.; Forster, P.M.; Betts, R.A.; Shiogama, H.; Allen, M. Realizing the impacts of a 1.5 °C warmer world. Nat. Clim. Chang. 2016, 6, 735–737. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Salamon, P.; Beck, H.E.; Lorini, V.; Alfieri, L.; Zsoter, E.; Dadson, S.J. Calibration of the Global Flood Awareness System (GloFAS) using daily streamflow data. J. Hydrol. 2018, 566, 595–606. [Google Scholar] [CrossRef]
- Donnelly, C.; Greuell, W.; Andersson, J.; Gerten, D.; Pisacane, G.; Roudier, P.; Ludwig, F. Impacts of climate change on European hydrology at 1.5, 2 and 3 degrees mean global warming above preindustrial level. Clim. Chang. 2017, 143, 13–26. [Google Scholar] [CrossRef]
- Dottori, F.; Szewczyk, W.; Ciscar, J.-C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Chang. 2018, 8, 781–786. [Google Scholar] [CrossRef]
- Thober, S.; Kumar, R.; Wanders, N.; Marx, A.; Pan, M.; Rakovec, O.; Samaniego, L.; Sheffield, J.; Wood, E.F.; Zink, M. Multi-model ensemble projections of European river floods and high flows at 1.5, 2, and 3 degrees global warming. Environ. Res. Lett. 2018, 13, 014003. [Google Scholar] [CrossRef]
- Roudier, P.; Andersson, J.C.M.; Donnelly, C.; Feyen, L.; Greuell, W.; Ludwig, F. Projections of future floods and hydrological droughts in Europe under a +2 °C global warming. Clim. Chang. 2016, 135, 341–355. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.A.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global Changes in Drought Conditions Under Different Levels of Warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Bisselink, B.; de Roo, A.; Bernhard, J.; Gelati, E. Future Projections of Water Scarcity in the Danube River Basin Due to Land Use, Water Demand and Climate Change. J. Environ. Geogr. 2018, 11, 25–36. [Google Scholar] [CrossRef]
- Zickfeld, K.; Arora, V.K.; Gillett, N.P. Is the climate response to CO2 emissions path dependent? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Schaeffer, M.; Hare, W.; Rahmstorf, S.; Vermeer, M. Long-term sea-level rise implied by 1.5 °C and 2 °C warming levels. Nat. Clim. Chang. 2012, 2, 867–870. [Google Scholar] [CrossRef]
- Bärring, L.; Strandberg, G. Does the projected pathway to global warming targets matter? Environ. Res. Lett. 2018, 13, 024029. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419. [Google Scholar] [CrossRef]
- Maule, C.F.; Mendlik, T.; Christensen, O.B. The effect of the pathway to a two degrees warmer world on the regional temperature change of Europe. Clim. Serv. 2017, 7, 3–11. [Google Scholar] [CrossRef]
- Pfeifer, S.; Rechid, D.; Reuter, M.; Viktor, E.; Jacob, D. 1.5°, 2°, and 3° global warming: visualizing European regions affected by multiple changes. Reg. Environ. Chang. 2019, 19, 1777–1786. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Lehner, F.; Sanderson, B.M.; Xu, Y. Does extreme precipitation intensity depend on the emissions scenario? Geophys. Res. Lett. 2015, 42, 8767–8774. [Google Scholar] [CrossRef]
- Good, P.; Booth, B.B.B.; Chadwick, R.; Hawkins, E.; Jonko, A.; Lowe, J.A. Large differences in regional precipitation change between a first and second 2 K of global warming. Nat. Commun. 2016, 7, 13667. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Lin, L.; Zhang, X.; Zhang, H.; Liu, L.; Xu, Y. Scenario dependence of future changes in climate extremes under 1.5 °C and 2 °C global warming. Sci. Rep. 2017, 7, 46432. [Google Scholar] [CrossRef] [PubMed]
- Beven, K.J.; Aspinall, W.P.; Bates, P.D.; Borgomeo, E.; Goda, K.; Hall, J.W.; Page, T.; Phillips, J.C.; Simpson, M.; Smith, P.J.; et al. Epistemic uncertainties and natural hazard risk assessment – Part 2: What should constitute good practice? Nat. Hazards Earth Syst. Sci. 2018, 18, 2769–2783. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Krysanova, V.; Benestad, R.E.; Hov, Ø.; Piniewski, M.; Otto, I.M. Uncertainty in climate change impacts on water resources. Environ. Sci. Policy 2018, 79, 1–8. [Google Scholar] [CrossRef]
- Van der Knijff, J.M.; De Roo, A.P.J. LISFLOOD Distributed Water Balance and Flood Simulation Model; European Commission: Ispra, Italy, 2008. [Google Scholar]
- Burek, P.; de Roo, A.; van der Knijff, J.M. LISFLOOD—Distributed Water Balance and Flood Simulation Model—Revised User Manual; OPOCE: Luxembourg, 2013. [Google Scholar]
- Samaniego, L.; Thober, S.; Kumar, R.; Wanders, N.; Rakovec, O.; Pan, M.; Zink, M.; Sheffield, J.; Wood, E.F.; Marx, A. Anthropogenic warming exacerbates European soil moisture droughts. Nat. Clim. Chang. 2018, 8, 421–426. [Google Scholar] [CrossRef]
- Hutton, C.; Wagener, T.; Freer, J.; Han, D.; Duffy, C.; Arheimer, B. Most computational hydrology is not reproducible, so is it really science? Water Resour. Res. 2016, 52, 7548–7555. [Google Scholar] [CrossRef]
- Añel, J.A. Comment on “Most computational hydrology is not reproducible, so is it really science?” by Christopher Hutton et al. Water Resour. Res. 2017, 53, 2572–2574. [Google Scholar] [CrossRef]
- LISFLOOD Dvlp. Grp. The Distributed Water Balance and Flood Simulation Model (LISFLOOD), Github Repository. 2018. Available online: https://github.com/ec-jrc/lisflood-code (accessed on 13 January 2020).
- Ntegeka, V.; Salamon, P.; Gomes, G.; Sint, H.; Lorini, V.; Thielen, J.; Zambrano, H. EFAS-Meteo: A European daily high-resolution gridded meteorological data set for 1990–2011; Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Dosio, A. Projections of climate change indices of temperature and precipitation from an ensemble of bias-adjusted high-resolution EURO-CORDEX regional climate models. J. Geophys. Res. 2016, 121, 5488–5511. [Google Scholar] [CrossRef]
- Casanueva, A.; Kotlarski, S.; Herrera, S.; Fernández, J.; Gutiérrez, J.M.; Boberg, F.; Colette, A.; Christensen, O.B.; Goergen, K.; Jacob, D.; et al. Daily precipitation statistics in a EURO-CORDEX RCM ensemble: added value of raw and bias-corrected high-resolution simulations. Clim. Dyn. 2016, 47, 719–737. [Google Scholar] [CrossRef]
- Burek, P.; van der Knijff, J.M.; Ntegeka, V. LISVAP Evaporation Pre-Processor for the LISFLOOD Water Balance and Flood Simulation Model; Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]
- LISFLOOD Dvlp. Grp. The Evaporation Pre-Processor for LISFLOOD (LISVAP) Model, Github Repository. 2018. Available online: https://github.com/ec-jrc/lisflood-lisvap (accessed on 13 January 2020).
- Batista e Silva, F.; Gallego, J.; Lavalle, C. A high-resolution population grid map for Europe. J. Maps 2013, 9, 16–28. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.; Voukouvalas, E.; Sartini, L.; Feyen, L.; Besio, G.; Alfieri, L. The transformed-stationary approach: A generic and simplified methodology for non-stationary extreme value analysis. Hydrol. Earth Syst. Sci. 2016, 20, 3527–3547. [Google Scholar] [CrossRef]
- Girden, E.R. ANOVA: Repeated Measures; Sage Publications: Thousand Oaks, CA, USA, 1992; ISBN 0-8039-4257-5. (Paperback). [Google Scholar]
- Blanca, M.J.; Alarcón, R.; Bendayan, R.; Arnau, J.; Bono, R. Non-normal data: Is ANOVA still a valid option? Psicothema 2017, 29, 552–557. [Google Scholar]
- Welch, B.L. THE GENERALIZATION OF ‘STUDENT’S’ PROBLEM WHEN SEVERAL DIFFERENT POPULATION VARLANCES ARE INVOLVED. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef]
- SciPy Developers Scientific Computing Tools for Python—SciPy.org. Available online: https://www.scipy.org/about.html (accessed on 13 January 2020).
- Beven, K. Facets of uncertainty: epistemic uncertainty, non-stationarity, likelihood, hypothesis testing, and communication. Hydrol. Sci. J. 2016, 61, 1652–1665. [Google Scholar] [CrossRef]
- Beven, K.; Westerberg, I. On red herrings and real herrings: disinformation and information in hydrological inference. Hydrol. Process. 2011, 25, 1676–1680. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Hartmann, D.L. The atmospheric energy constraint on global-mean precipitation change. J. Clim. 2014, 27, 757–768. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Z.; Xu, Y.; Fu, Q. Sensitivity of precipitation extremes to radiative forcing of greenhouse gases and aerosols. Geophys. Res. Lett. 2016, 43, 9860–9868. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Z.; Xu, Y.; Fu, Q.; Dong, W. Larger Sensitivity of Precipitation Extremes to Aerosol Than Greenhouse Gas Forcing in CMIP5 Models. J. Geophys. Res. Atmos. 2018, 123, 8062–8073. [Google Scholar] [CrossRef]
- Lamarque, J.F.; Kyle, P.P.; Meinshausen, M.; Riahi, K.; Smith, S.J.; van Vuuren, D.P.; Conley, A.J.; Vitt, F. Global and regional evolution of short-lived radiatively-active gases and aerosols in the Representative Concentration Pathways. Clim. Chang. 2011, 109, 191–212. [Google Scholar] [CrossRef]
- Tabari, H.; Hosseinzadehtalaei, P.; AghaKouchak, A.; Willems, P. Latitudinal heterogeneity and hotspots of uncertainty in projected extreme precipitation. Environ. Res. Lett. 2019, 14, 124032. [Google Scholar] [CrossRef]
- Schneider, C.; Laizé, C.L.R.; Acreman, M.C.; Flörke, M. How will climate change modify river flow regimes in Europe? Hydrol. Earth Syst. Sci. 2013, 17, 325–339. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; López-Moreno, I.I.; Vicente-Serrano, S.M.; Lasanta-Martínez, T.; Beguería, S. Mediterranean water resources in a global change scenario. Earth-Science Rev. 2011, 105, 121–139. [Google Scholar] [CrossRef]
- Arnell, N.W. The effect of climate change on hydrological regimes in Europe: A continental perspective. Glob. Environ. Chang. 1999, 9, 5–23. [Google Scholar] [CrossRef]
- Gampe, D.; Nikulin, G.; Ludwig, R. Using an ensemble of regional climate models to assess climate change impacts on water scarcity in European river basins. Sci. Total Environ. 2016, 573, 1503–1518. [Google Scholar] [CrossRef]
- Dankers, R.; Feyen, L. Climate change impact on flood hazard in Europe: An assessment based on high-resolution climate simulations. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Formetta, G.; Feyen, L. Empirical evidence of declining global vulnerability to climate-related hazards. Glob. Environ. Chang. 2019, 57, 101920. [Google Scholar] [CrossRef]
| RCP8.5, Year of Warming Level | RCP4.5, Year of Warming Level | |||
|---|---|---|---|---|
| CORDEX Model Name | 1.5 °C | 2 °C | 1.5 °C | 2 °C |
| CLMcom-CCLM4-8-17_CNRM-CERFACS-CNRM-CM5 | 2029 | 2044 | 2035 | 2057 |
| CLMcom-CCLM4-8-17_ICHEC-EC-EARTH | 2026 | 2041 | 2033 | 2056 |
| CLMcom-CCLM4-8-17_MPI-M-MPI-ESM-LR | 2028 | 2044 | 2034 | 2064 |
| DMI-HIRHAM5-ICHEC-EC-EARTH | 2028 | 2043 | 2032 | 2054 |
| IPSL-INERIS-WRF331F | 2021 | 2035 | 2023 | 2042 |
| KNMI-RACMO22E-ICHEC-EC-EARTH | 2026 | 2042 | 2032 | 2056 |
| SMHI-RCA4_CNRM-CERFACS-CNRM-CM5 | 2029 | 2044 | 2035 | 2057 |
| SMHI-RCA4_ICHEC-EC-EARTH | 2026 | 2041 | 2033 | 2056 |
| SMHI-RCA4_IPSL-IPSL-CM5A-MR | 2021 | 2035 | 2023 | 2042 |
| SMHI-RCA4_MOHC-HadGEM2-ES | 2018 | 2030 | 2021 | 2037 |
| SMHI-RCA4_MPI-M-MPI-ESM-LR | 2028 | 2044 | 2034 | 2064 |
| % Explained Variance | % Points Where p-Value ≤ 0.05 | |||
|---|---|---|---|---|
| Variable | Warming Level | σ2within | σ2between | |
| QH100 | 1.5 °C | 98.6% | 1.4% | 0.1% |
| 2.0 °C | 97.0% | 3.0% | 2.0% | |
| QM | 1.5 °C | 98.2% | 1.8% | 0.2% |
| 2.0 °C | 96.0% | 4.0% | 4.4% | |
| QL15 | 1.5 °C | 97.2% | 2.8% | 0.7% |
| 2.0 °C | 97.1% | 2.9% | 1.2% | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mentaschi, L.; Alfieri, L.; Dottori, F.; Cammalleri, C.; Bisselink, B.; Roo, A.D.; Feyen, L. Independence of Future Changes of River Runoff in Europe from the Pathway to Global Warming. Climate 2020, 8, 22. https://doi.org/10.3390/cli8020022
Mentaschi L, Alfieri L, Dottori F, Cammalleri C, Bisselink B, Roo AD, Feyen L. Independence of Future Changes of River Runoff in Europe from the Pathway to Global Warming. Climate. 2020; 8(2):22. https://doi.org/10.3390/cli8020022
Chicago/Turabian StyleMentaschi, Lorenzo, Lorenzo Alfieri, Francesco Dottori, Carmelo Cammalleri, Berny Bisselink, Ad De Roo, and Luc Feyen. 2020. "Independence of Future Changes of River Runoff in Europe from the Pathway to Global Warming" Climate 8, no. 2: 22. https://doi.org/10.3390/cli8020022
APA StyleMentaschi, L., Alfieri, L., Dottori, F., Cammalleri, C., Bisselink, B., Roo, A. D., & Feyen, L. (2020). Independence of Future Changes of River Runoff in Europe from the Pathway to Global Warming. Climate, 8(2), 22. https://doi.org/10.3390/cli8020022





