Long-Term Rainfall Trends and Their Variability in Mainland Portugal in the Last 106 Years
Abstract
1. Introduction
2. Materials and Methods
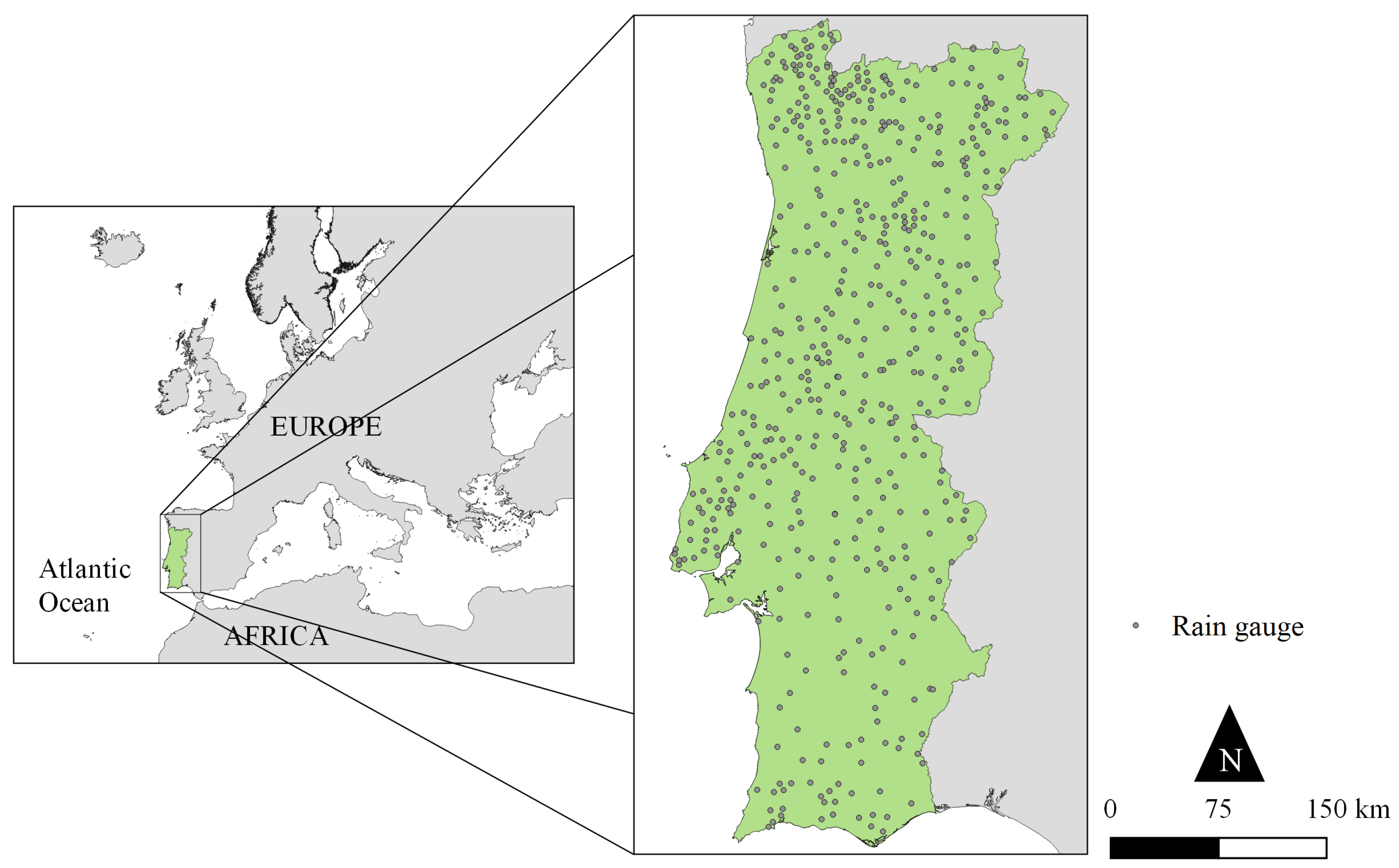
2.1. Study Area
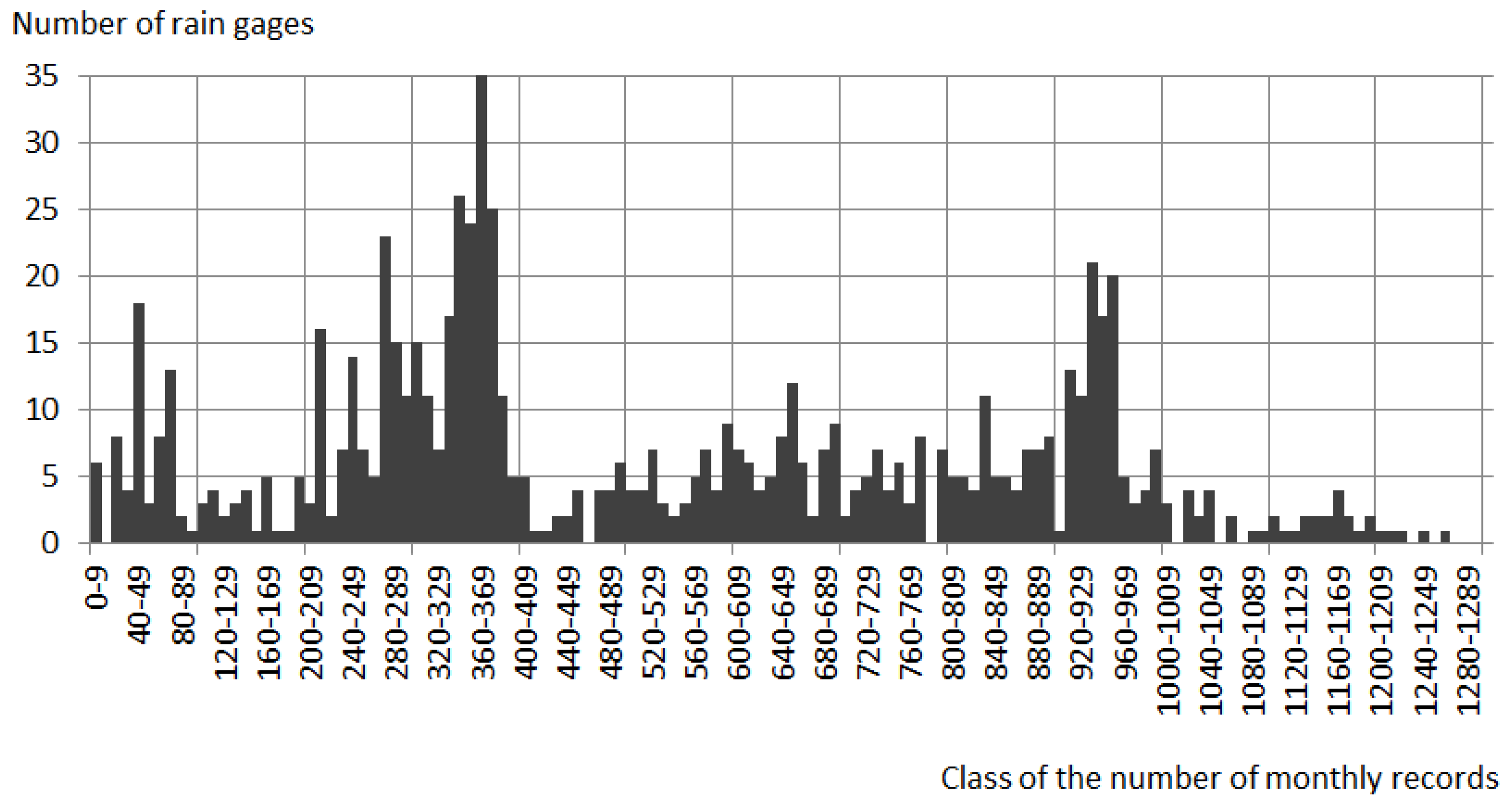
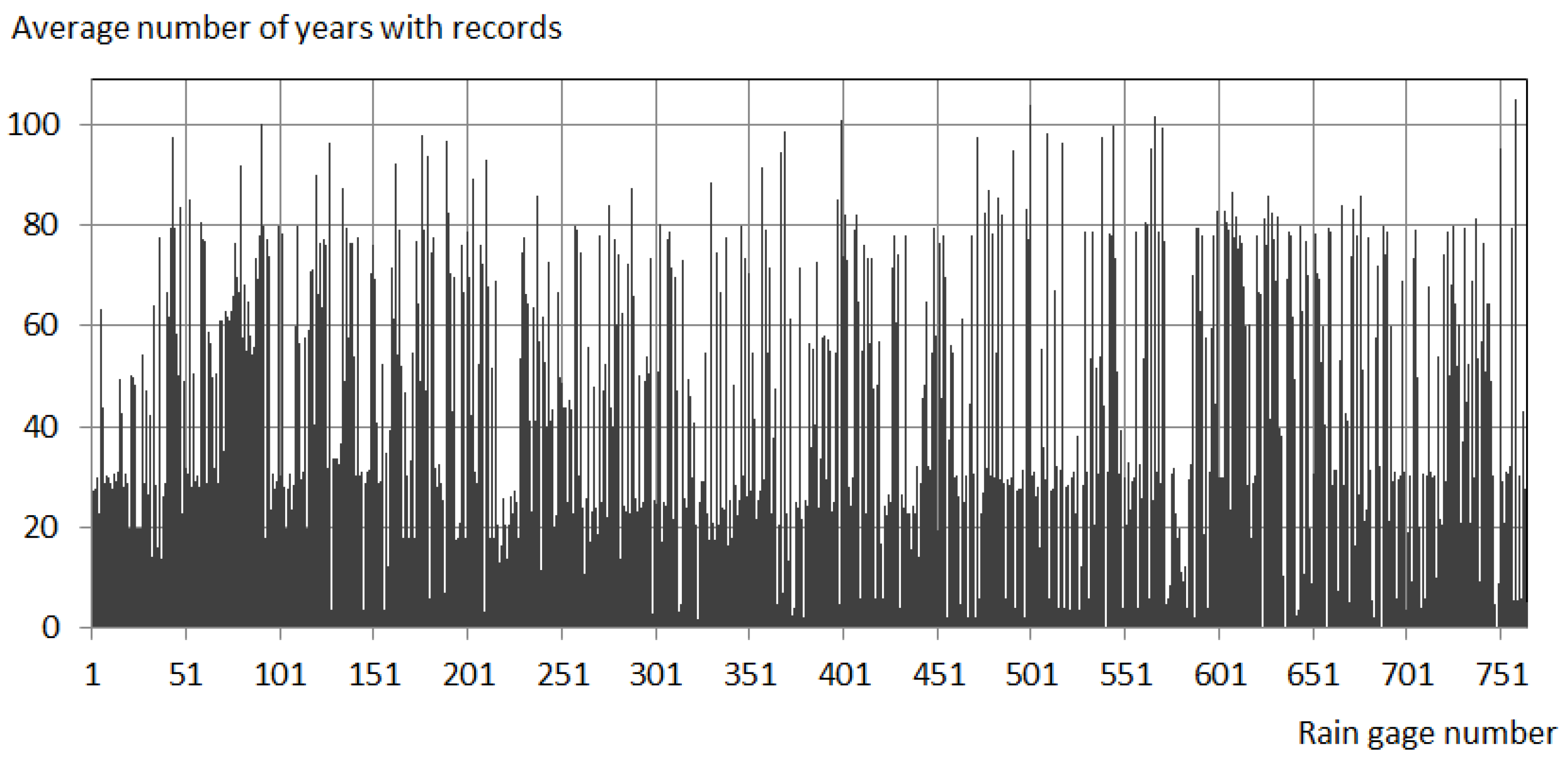
2.2. Rainfall Dataset
2.3. Long-Term Trend Analysis Models
3. Results
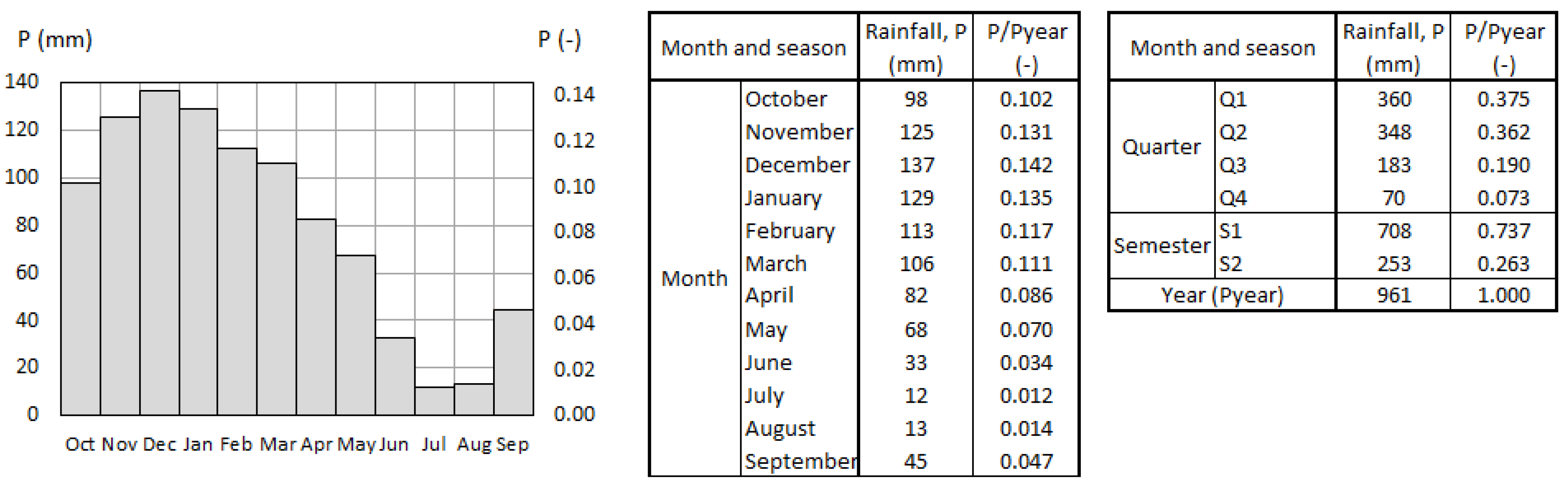
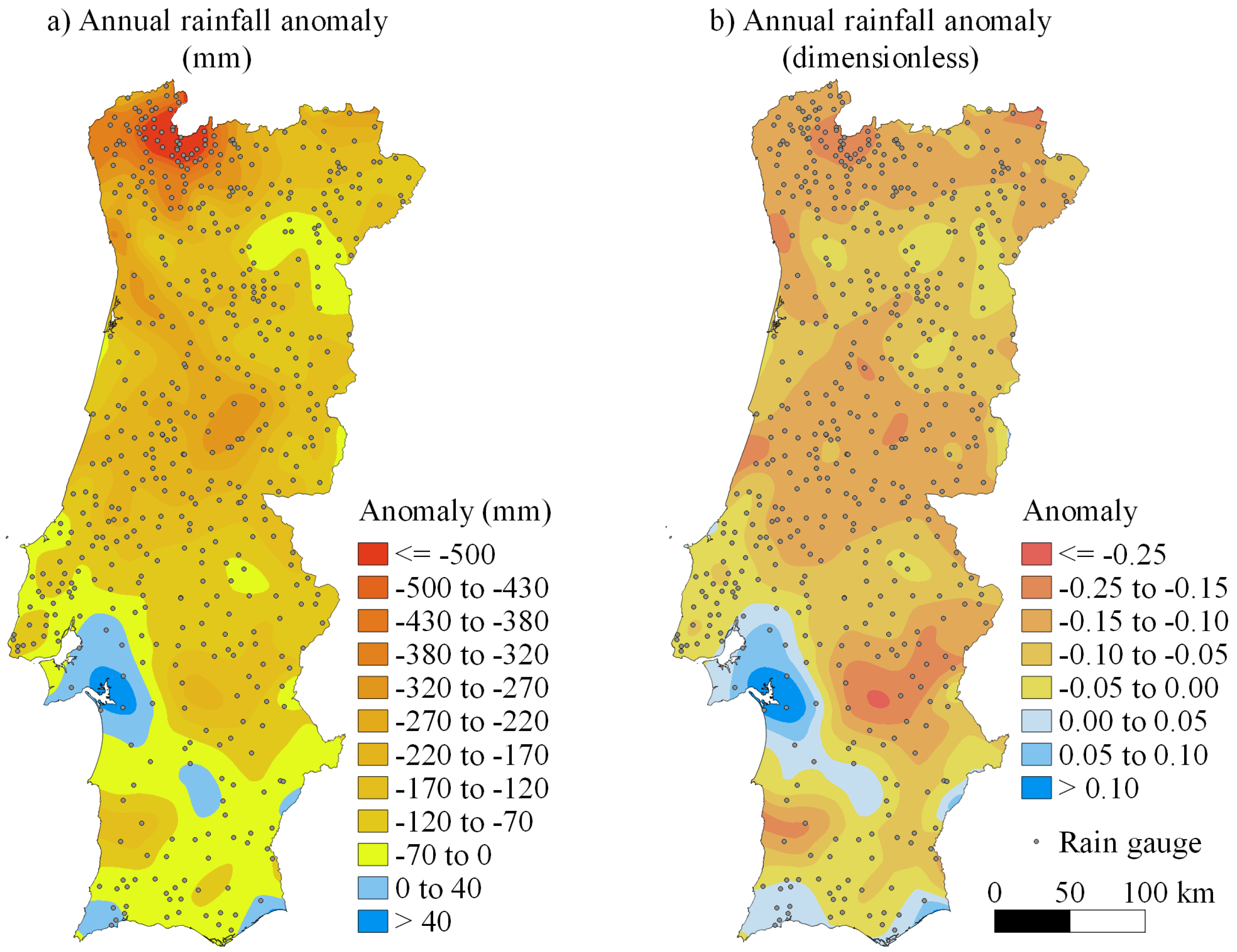
3.1. Rainfall Characterization
3.2. Mann-Kendall Test and Sen’s Slope Estimates
3.3. Sequential Variability of the Rainfall
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Briffa, K.; Van Der Schrier, G.; Jones, P. Wet and dry summers in Europe since 1750: Evidence of increasing drought. Int. J. Climatol. J. R. Meteorol. Soc. 2009, 29, 1894–1905. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Pfahl, S.; O’Gorman, P.A.; Fischer, E.M. Understanding the regional pattern of projected future changes in extreme precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- McCarthy, J.J.; Canziani, O.F.; Leary, N.A.; Dokken, D.J.; White, K.S. Climate Change 2001: Impacts, Adaptation, and Vulnerability: Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001; Volume 2. [Google Scholar]
- Parry, M.; Parry, M.L.; Canziani, O.; Palutikof, J.; Van der Linden, P.; Hanson, C. Climate Change 2007: Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; Volume 4. [Google Scholar]
- Barros, V.; Field, C.; Dokke, D.; Mastrandrea, M.; Mach, K.; Bilir, T.E.; Chatterjee, M.; Ebi, K.; Estrada, Y.; Genova, R.; et al. Climate Change 2014: Impacts, Adaptation, and Vulnerability-Part B: Regional Aspects-Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Bates, B.; Kundzewicz, Z.; Wu, S. Climate Change and Water; Intergovernmental Panel on Climate Change IPCC Secretariat: Geneva, Switzerland, 2008. [Google Scholar]
- Khan, M.Z.K.; Sharma, A.; Mehrotra, R. Global seasonal precipitation forecasts using improved sea surface temperature predictions. J. Geophys. Res. Atmos. 2017, 122, 4773–4785. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Vicente-Serrano, S.M.; Gimeno, L.; Nieto, R. Stability of the seasonal distribution of precipitation in the Mediterranean region: Observations since 1950 and projections for the 21st century. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Muñoz, J.M.H. Assessing the Impact of Climate Variability on Seasonal Streamflow Forecasting in the Iberian Peninsula. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2015. [Google Scholar]
- Ojeda, M.M.d.V.G.V. Climate-Change Projections in the Iberian Peninsula: A Study of the Hydrological Impacts. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2018. [Google Scholar]
- Soares, P.M.; Cardoso, R.M.; Ferreira, J.J.; Miranda, P.M. Climate change and the Portuguese precipitation: ENSEMBLES regional climate models results. Clim. Dyn. 2015, 45, 1771–1787. [Google Scholar] [CrossRef]
- Miranda, P.; Coelho, F.; Tomé, A.R.; Valente, M.A.; Carvalho, A.; Pires, C.; Pires, H.O.; Pires, V.C.; Ramalho, C. 20th century Portuguese climate and climate scenarios. Climate Change in Portugal. Scenarios, Impacts and Adaptation Measures—SIAM Project; Santos, F.D., Forbes, K., Moita, R., Eds.; Gradiva Publishers: Lisbon, Portugal, 2002; pp. 23–83. [Google Scholar]
- Santos, F.D.; Forbes, K.; Moita, R. Climate change in Portugal: Scenarios, Impacts and Adaptation Measures: SIAM Project. In Gradiva; S. Fischer Verlag: Frankfurt, Germany, 2002. [Google Scholar]
- Santos, F.D.; Miranda, P. Alterações Climáticas em Portugal. Cenários, Impactos e Medidas de Adaptação: Projecto SIAM II-1ª Edição; Unidade de Silvicultura e Produtos Florestais: Lisboa, Portugal, 2006; Volume 14, p. 281. [Google Scholar]
- Santo, F.E.; Ramos, A.M.; de Lima, M.I.P.; Trigo, R.M. Seasonal changes in daily precipitation extremes in mainland Portugal from 1941 to 2007. Reg. Environ. Chang. 2014, 14, 1765–1788. [Google Scholar] [CrossRef]
- Gibelin, A.L.; Déqué, M. Anthropogenic climate change over the Mediterranean region simulated by a global variable resolution model. Clim. Dyn. 2003, 20, 327–339. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Norrant, C.; Douguédroit, A. Monthly and daily precipitation trends in the Mediterranean (1950–2000). Theor. Appl. Climatol. 2006, 83, 89–106. [Google Scholar] [CrossRef]
- De Luis, M.; Gonzalez-Hidalgo, J.C.; Longares, L.A.; Stepanek, P. Seasonal precipitation trends in the Mediterranean Iberian Peninsula in second half of 20th century. Int. J. Climatol. 2009, 29, 1312–1323. [Google Scholar] [CrossRef]
- Philandras, C.; Nastos, P.; Kapsomenakis, J.; Douvis, K.; Tselioudis, G.; Zerefos, C. Long term precipitation trends and variability within the Mediterranean region. Nat. Hazards Earth Syst. Sci. 2011, 11, 3235. [Google Scholar] [CrossRef]
- Fernández-Montes, S.; Rodrigo, F.S.; Seubert, S.; Sousa, P.M. Spring and summer extreme temperatures in Iberia during last century in relation to circulation types. Atmos. Res. 2013, 127, 154–177. [Google Scholar] [CrossRef]
- Lionello, P.; Abrantes, F.; Gacic, M.; Planton, S.; Trigo, R.M.; Ulbrich, U. The climate of the Mediterranean region: Research progress and climate change impacts. Reg. Environ. Chang. 2014, 14, 1679–1684. [Google Scholar] [CrossRef]
- Andrade, C.; Belo-Pereira, M. Assessment of droughts in the Iberian Peninsula using the WASP-Index. Atmos. Sci. Lett. 2015, 16, 208–218. [Google Scholar] [CrossRef]
- Páscoa, P.; Gouveia, C.; Russo, A.; Trigo, R.M. Drought trends in the Iberian Peninsula over the last 112 years. Adv. Meteorol. 2017, 2017. [Google Scholar] [CrossRef]
- Portela, M.M.; Espinosa, L.A.; Studart, T.; Zelenakova, M. Rainfall Trends in Southern Portugal at Different Time Scales. In International Congress on Engineering and Sustainability in the XXI Century; Springer: Cham, Switzerland, 2019; pp. 3–19. [Google Scholar]
- Santos, J.; Corte-Real, J.; Leite, S. Weather regimes and their connection to the winter rainfall in Portugal. Int. J. Climatol. J. R. Meteorol. Soc. 2005, 25, 33–50. [Google Scholar] [CrossRef]
- Cubasch, U.; Wuebbles, D.; Chen, D.; Facchini, M.C.; Frame, D.; Mahowald, N.; Winther, J.G. Introduction. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Girons Lopez, M.; Wennerström, H.; Nordén, L.Å.; Seibert, J. Location and density of rain gauges for the estimation of spatial varying precipitation. Geogr. Ann. Ser. Phys. Geogr. 2015, 97, 167–179. [Google Scholar] [CrossRef]
- Portela, M.M.; Carvalho Quintela, A.D. Indícios de mudança climática em séries de precipitação em Portugal Continental. Recur. Hídricos 1998, 19, 41–74. [Google Scholar]
- Portela, M.M.; Carvalho Quintela, A.d. A diminuiçào da precipitaçào em épocas do año como indício de mudança climática: Casos estudiados em Portugal continental. Ing. Agua 2001, 8, 79–92. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Marques, A.C.; de Lima, J.; Coelho, M. Precipitation trends in mainland Portugal in the period 1941–2000. IAHS Publ. 2007, 310, 94. [Google Scholar]
- Rodrigo, F.; Trigo, R.M. Trends in daily rainfall in the Iberian Peninsula from 1951 to 2002. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 513–529. [Google Scholar] [CrossRef]
- Santos, J.F.; Portela, M.M. Quantificação de tendências em séries de precipitação mensal e anual em Portugal Continental. In Seminário Ibero-Americano Sobre Sistemas de Abastecimento Urbano (SEREA); SEREA: Lisboa, Portugal, 2008; Volume 8. [Google Scholar]
- De Lima, M.; Carvalho, S.; de Lima, J. Investigating annual and monthly trends in precipitation structure: An overview across Portugal. Nat. Hazards Earth Syst. Sci. 2010, 10, 2429. [Google Scholar] [CrossRef]
- De Lima, M.; Carvalho, S.; de Lima, J.; Coelho, M. Trends in precipitation: Analysis of long annual and monthly time series from mainland Portugal. Adv. Geosci. 2010, 25. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Santo, F.E.; Ramos, A.M.; Trigo, R.M. Trends and correlations in annual extreme precipitation indices for mainland Portugal, 1941–2007. Theor. Appl. Climatol. 2015, 119, 55–75. [Google Scholar] [CrossRef]
- Portela, M.M.; Santos, J.F.; Silva, A. Trends in rainfall and streamflow series: Portuguese case studies. Int. J. Saf. Secur. Eng. 2014, 4, 221–248. [Google Scholar] [CrossRef]
- Nunes, A.; Lourenço, L. Precipitation variability in Portugal from 1960 to 2011. J. Geogr. Sci. 2015, 25, 784–800. [Google Scholar] [CrossRef]
- Pereira, L.S.; Louro, V.; Do Rosário, L.; Almeida, A. Desertification, territory and people, a holistic approach in the Portuguese context. In Desertification in the Mediterranean Region. A Security Issue; Springer Science & Business Media: Berlin, Germany, 2006; pp. 269–289. [Google Scholar]
- Trigo, R.M.; DaCamara, C.C. Circulation weather types and their influence on the precipitation regime in Portugal. Int. J. Climatol. J. R. Meteorol. Soc. 2000, 20, 1559–1581. [Google Scholar] [CrossRef]
- Belo-Pereira, M.; Dutra, E.; Viterbo, P. Evaluation of global precipitation data sets over the Iberian Peninsula. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and temporal variability of droughts in Portugal. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- SNIRH. Sistema Nacional de Informação de Recursos Hídricos (2020): APA—Agência Portuguesa do Ambiente; SNIRH: Lisboa, Portugal, 2020. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econ. J. Econ. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin Press: Oxford, UK, 1948. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- McKinley, S.; Levine, M. Cubic spline interpolation. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Earls, J.; Dixon, B. Spatial interpolation of rainfall data using ArcGIS: A comparative study. In Proceedings of the 27th Annual ESRI International User Conference, San Diego, CA, USA, 18–22 June 2007; Volume 31. [Google Scholar]
- PNA. Relatório n.º 1. Caracterização geral dos recursos hídricos e suas atualizações, enquadramento legal dos Planos e balanço hídricos do 1º ciclo. In Plano Nacional da Água; APA—Agência Portuguesa do Ambiente; SNIRH: Lisboa, Portugal, 2015. [Google Scholar]
- Clark, I. Practical Geostatistics; Applied Science Publishers: London, UK, 1979; Volume 3. [Google Scholar]
- Sneyers, R. Technical Note No 143 on the Statistical Analysis of Series of Observations; World Meteorological Organization: Geneva, Switzerland, 1990. [Google Scholar]
- Baines, P.G.; Folland, C.K. Evidence for a rapid global climate shift across the late 1960s. J. Clim. 2007, 20, 2721–2744. [Google Scholar] [CrossRef]
- Young, T.; Mohlenkamp, M. Introduction to Numerical Methods and Matlab Programming; Lecture Notes; Ohio University: Athens, OH, USA, 2008. [Google Scholar]
- Pimenta, M.T.; Santos, M.J.; Rodrigues, R. A proposal of indices to identify desertification prone areas. Jornadas de Reflexión Sobre el Anexo IV de Aplicatión para el Mediterrâneo Norte–Convenio de Lucha Contra la Desertificación, Murcia (Spain); LUCDEME Project: Almeria, Spain, 1997. [Google Scholar]
- Costa, M.A.M.; Moors, E.J.; Fraser, E.D. Socioeconomics, policy, or climate change: What is driving vulnerability in southern Portugal? Ecol. Soc. 2011, 16. [Google Scholar]
- Santos, M.; Fragoso, M. Precipitation variability in Northern Portugal: Data homogeneity assessment and trends in extreme precipitation indices. Atmos. Res. 2013, 131, 34–45. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1089. [Google Scholar] [CrossRef]
- Sen, Z. Spatial Modeling Principles in Earth Sciences; Springer: New York, NY, USA, 2016. [Google Scholar]
- Kenney, J. Moving averages. Math. Stat. 1962, 1, 221–223. [Google Scholar]
- WMO. International Meteorological Vocabulary. World Meteorological Organization-No. 182; Technical Report 182; WMO/OMM/IMGW: Geneva, Switzerland, 1992; ISBN 978-92-63-02182-3. [Google Scholar]
- WMO. WMO Guidelines on the Calculation of Climate Normals; Technical Report WMO-No. 1203; WMO/OMM/IMGW: Geneva, Switzerland, 2017; ISBN 978-92-63-11203-3. [Google Scholar]
- Greve, P.; Orlowsky, B.; Mueller, B.; Sheffield, J.; Reichstein, M.; Seneviratne, S.I. Global assessment of trends in wetting and drying over land. Nat. Geosci. 2014, 7, 716–721. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.; Zhang, T.; Pegion, P. On the increased frequency of Mediterranean drought. J. Clim. 2012, 25, 2146–2161. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Gonzalez Miralles, D.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25 global gridded precipitation (1979-2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Parker, W.S. Reanalyses and observations: What’s the difference? Bull. Am. Meteorol. Soc. 2016, 97, 1565–1572. [Google Scholar] [CrossRef]
- Rodríguez-Puebla, C.; Nieto, S. Trends of precipitation over the Iberian Peninsula and the North Atlantic Oscillation under climate change conditions. Int. J. Climatol. 2010, 30, 1807–1815. [Google Scholar] [CrossRef]
- De Castro, M.; Martín-Vide, J.; Alonso, S. The climate of Spain: Past, present and scenarios for the 21st century. A Preliminary Assessment of the Impacts in Spain Due to the Effects of Climate Change; ECCE Project-Final Report; Ministerio de Medio Ambiente: Madrid, Spain, 2005. [Google Scholar]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term climate change: Projections, commitments and irreversibility. In Climate Change 2013-The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1029–1136. [Google Scholar]
- Carvalho, A.; Schmidt, L.; Santos, F.D.; Delicado, A. Climate change research and policy in Portugal. Wiley Interdiscip. Rev. Clim. Chang. 2014, 5, 199–217. [Google Scholar] [CrossRef]
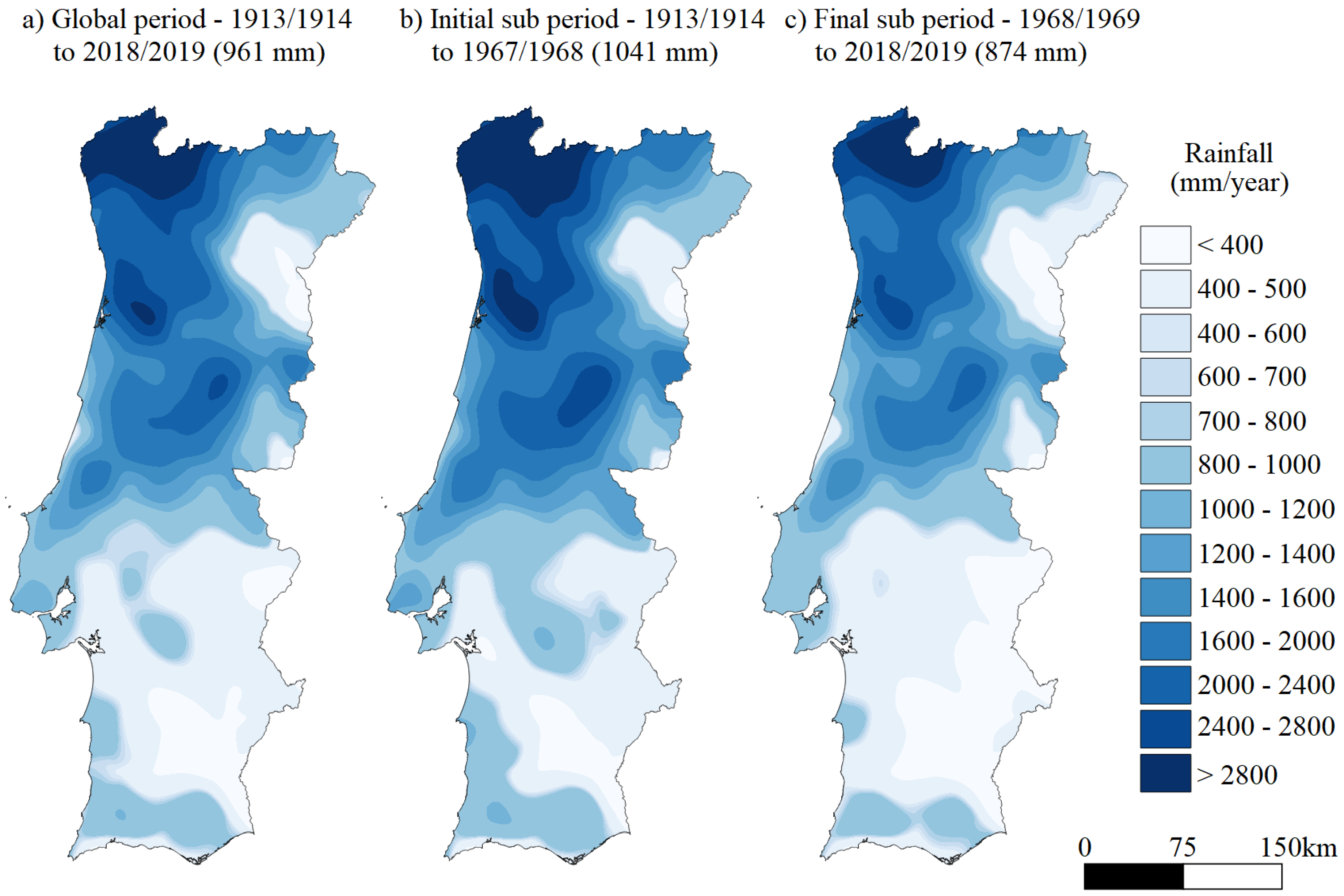
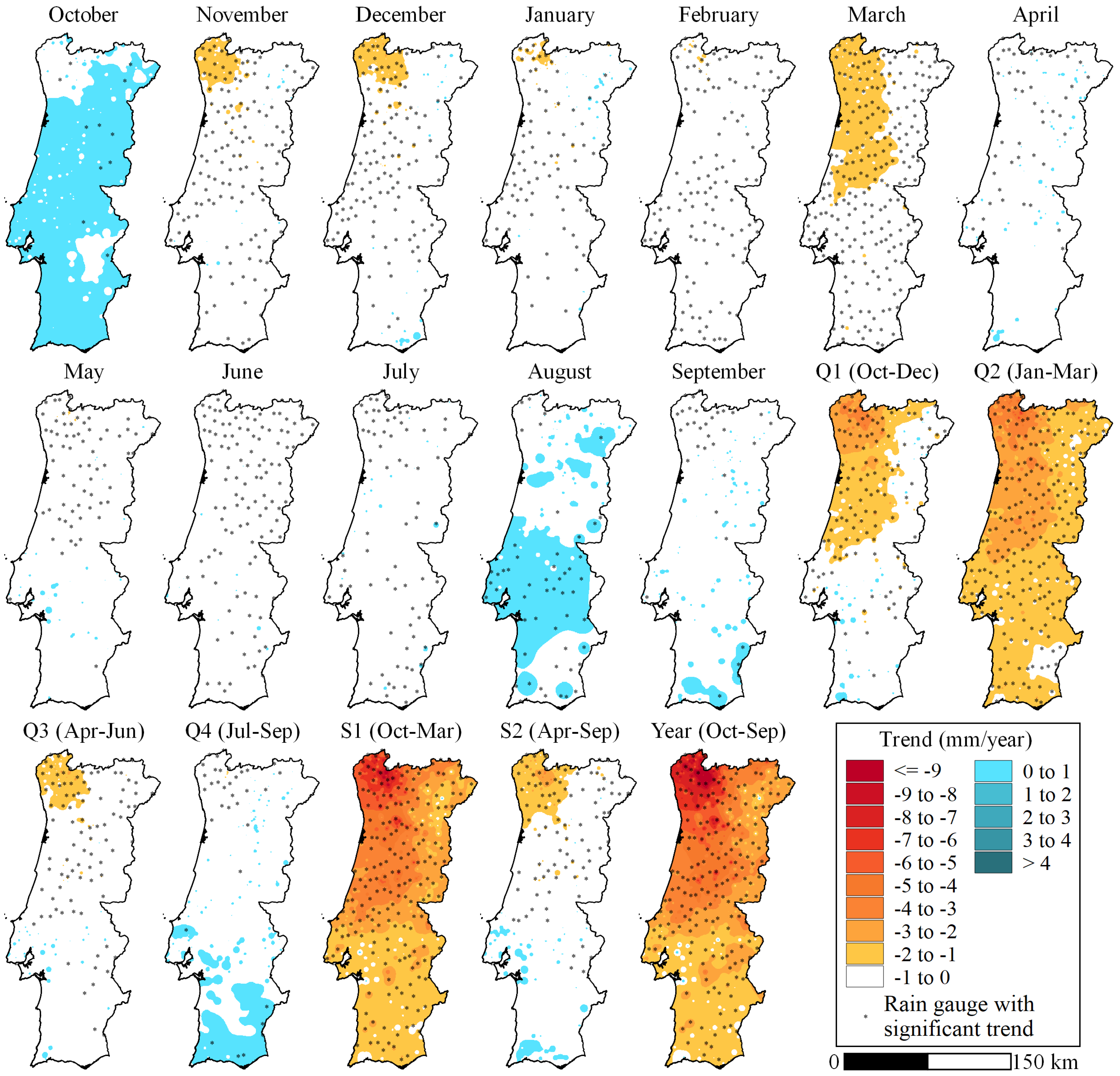
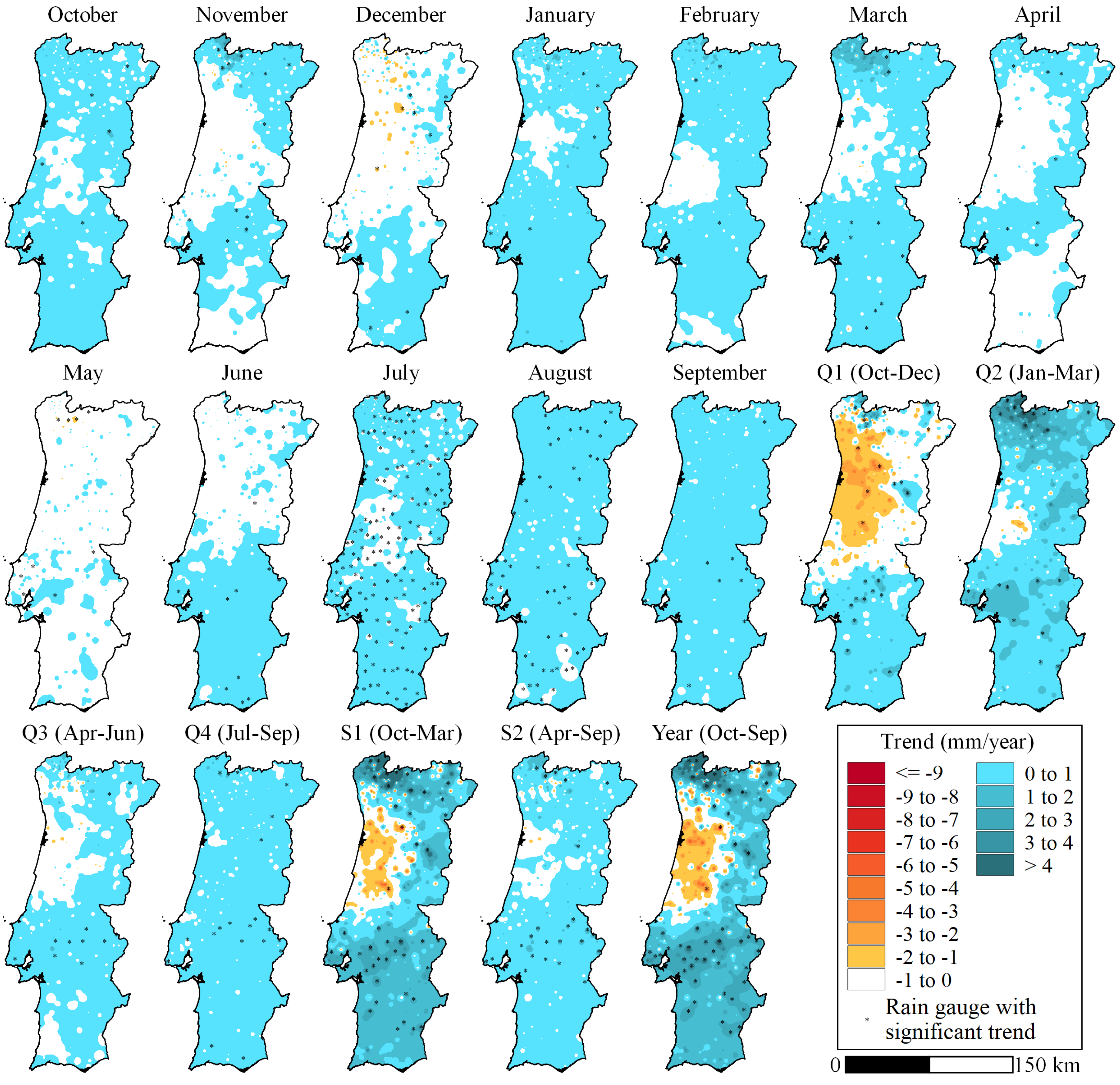
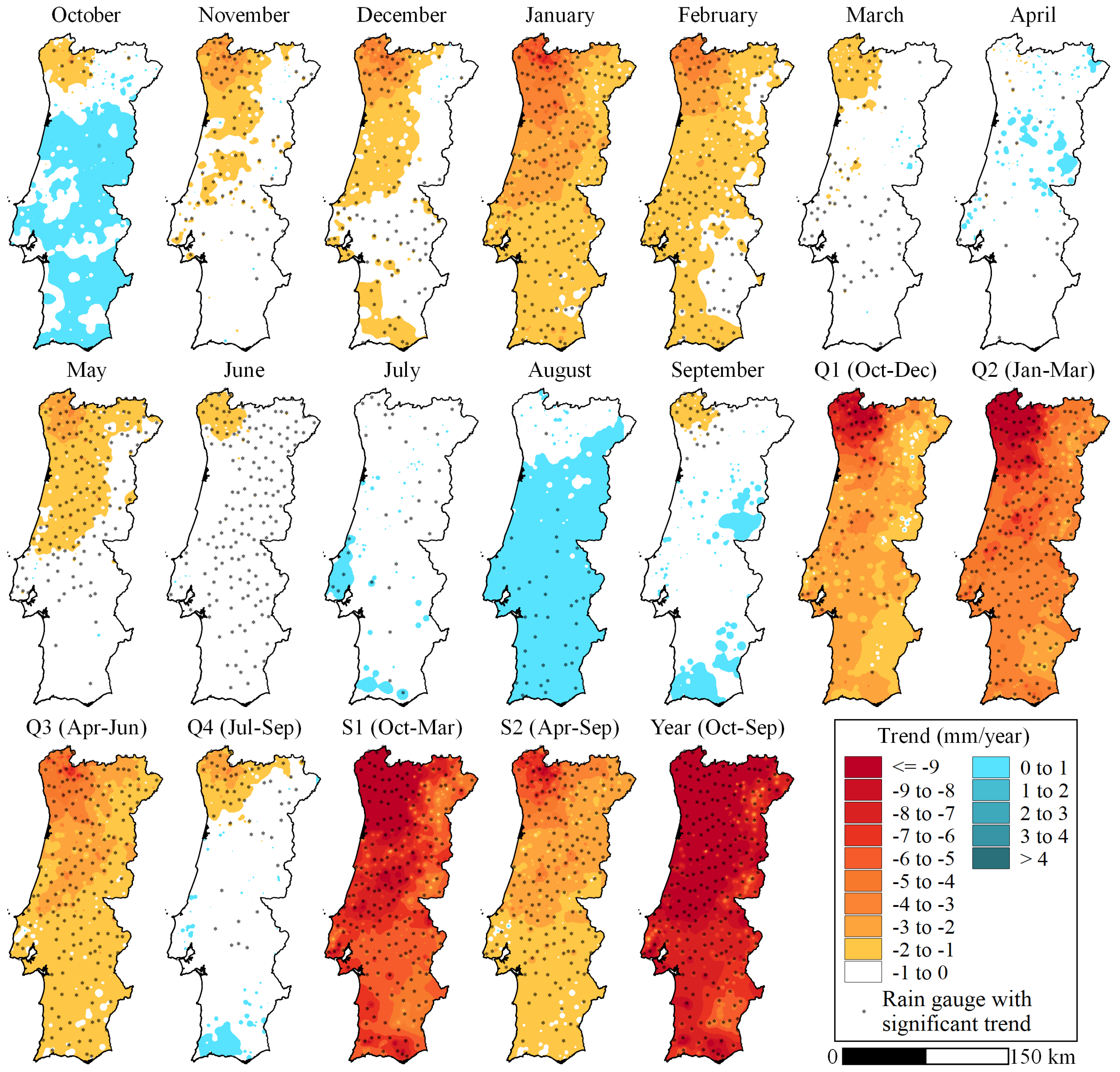


| Period of the Year | 106-Year Global Period (1913/1914 to 2018/2019) | 55-Year Initial Sub-Period (1913/1914 to 1967/1968) | 51-Year Final Sub-Period (1968/1969 to 2018/2019) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Positive Trends | Negative Trends | Positive Trends | Negative Trends | Positive Trends | Negative Trends | ||||||||||
| Number of Rain Gauges | Maximum Value (mm/year) | Number of Rain Gauges | Maximum Value (mm/year) | Mean Value (mm/year) | Number of Rain Gauges | Maximum Value (mm/year) | Number of Rain Gauges | Maximum Value (mm/year) | Mean Value (mm/year) | Number of Rain Gauges | Maximum Value (mm/year) | Number of Rain Gauges | Maximum Value (mm/year) | Mean Value (mm/year) | |
| October | 9 | 0.67 | 2 | −0.71 | 0.24 | 8 | 2.75 | 0 | – | 1.31 | 0 | – | 17 | −3.19 | −2.17 |
| November | 0 | – | 263 | −2.89 | −0.85 | 24 | 4.45 | 0 | – | 2.12 | 0 | – | 134 | −5.51 | −2.25 |
| December | 1 | 0.15 | 231 | −2.94 | −0.95 | 6 | 1.99 | 3 | −2.95 | 0.20 | 0 | – | 179 | −6.29 | −2.40 |
| January | 1 | 0.26 | 124 | −2.74 | −0.86 | 6 | 1.90 | 1 | −0.55 | 0.83 | 0 | – | 479 | −9.45 | −2.72 |
| February | 0 | – | 189 | −2.57 | −0.58 | 3 | 2.92 | 0 | – | 2.10 | 0 | – | 353 | −5.92 | −2.09 |
| March | 0 | – | 517 | −2.92 | −0.92 | 13 | 3.36 | 0 | – | 1.49 | 0 | – | 89 | −3.13 | −1.31 |
| April | 0 | – | 65 | −0.94 | −0.48 | 10 | 1.77 | 0 | – | 1.06 | 0 | – | 25 | −1.93 | −0.97 |
| May | 0 | – | 145 | −1.50 | −0.56 | 2 | 0.49 | 10 | −1.92 | −0.76 | 0 | – | 312 | −4.87 | −1.59 |
| June | 0 | – | 230 | −0.99 | −0.34 | 11 | 0.89 | 2 | −0.85 | 0.22 | 0 | – | 338 | −2.9 | −0.72 |
| July | 23 | 0.40 | 113 | −0.98 | −0.30 | 42 | 0.50 | 220 | −0.98 | −0.38 | 10 | 0.92 | 30 | −0.97 | −0.18 |
| August | 58 | 0.90 | 14 | −0.96 | 0.16 | 64 | 0.90 | 12 | −0.80 | 0.20 | 42 | 0.90 | 3 | −0.46 | 0.29 |
| September | 4 | 0.84 | 72 | −0.79 | −0.36 | 12 | 1.19 | 0 | – | 0.45 | 0 | 79 | −2.67 | −1.26 | |
| Q1 | 1 | 1.00 | 221 | −5.58 | −2.15 | 23 | 9.93 | 8 | −6.88 | 0.07 | 0 | – | 175 | −14.68 | −6.00 |
| Q2 | 0 | – | 492 | −7.28 | −2.15 | 25 | 13.54 | 0 | – | 0.28 | 0 | – | 492 | −19.97 | −5.26 |
| Q3 | 0 | – | 193 | −3.77 | −1.08 | 12 | 1.90 | 0 | – | 0.03 | 0 | – | 372 | −9.46 | −2.83 |
| Q4 | 7 | 0.68 | 73 | −1.38 | −0.59 | 21 | 2.30 | 1 | −0.28 | 0.03 | 0 | – | 127 | −4.84 | −1.89 |
| S1 | 0 | – | 446 | −12.19 | −3.61 | 63 | 21.14 | 3 | −10.39 | 0.69 | 0 | – | 461 | −36.84 | −8.74 |
| S2 | 0 | – | 189 | −4.16 | −1.40 | 31 | 5.24 | 0 | – | 0.11 | 0 | – | 399 | −12.71 | −3.44 |
| Year | 0 | – | 428 | −15.36 | −4.27 | 74 | 26.58 | 3 | −11.60 | 0.89 | 0 | – | 505 | −49.98 | −11.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portela, M.M.; Espinosa, L.A.; Zelenakova, M. Long-Term Rainfall Trends and Their Variability in Mainland Portugal in the Last 106 Years. Climate 2020, 8, 146. https://doi.org/10.3390/cli8120146
Portela MM, Espinosa LA, Zelenakova M. Long-Term Rainfall Trends and Their Variability in Mainland Portugal in the Last 106 Years. Climate. 2020; 8(12):146. https://doi.org/10.3390/cli8120146
Chicago/Turabian StylePortela, Maria Manuela, Luis Angel Espinosa, and Martina Zelenakova. 2020. "Long-Term Rainfall Trends and Their Variability in Mainland Portugal in the Last 106 Years" Climate 8, no. 12: 146. https://doi.org/10.3390/cli8120146
APA StylePortela, M. M., Espinosa, L. A., & Zelenakova, M. (2020). Long-Term Rainfall Trends and Their Variability in Mainland Portugal in the Last 106 Years. Climate, 8(12), 146. https://doi.org/10.3390/cli8120146







