GPS Precipitable Water Vapor Estimations over Costa Rica: A Comparison against Atmospheric Sounding and Moderate Resolution Imaging Spectrometer (MODIS)
Abstract
1. Introduction
2. Materials and Methods
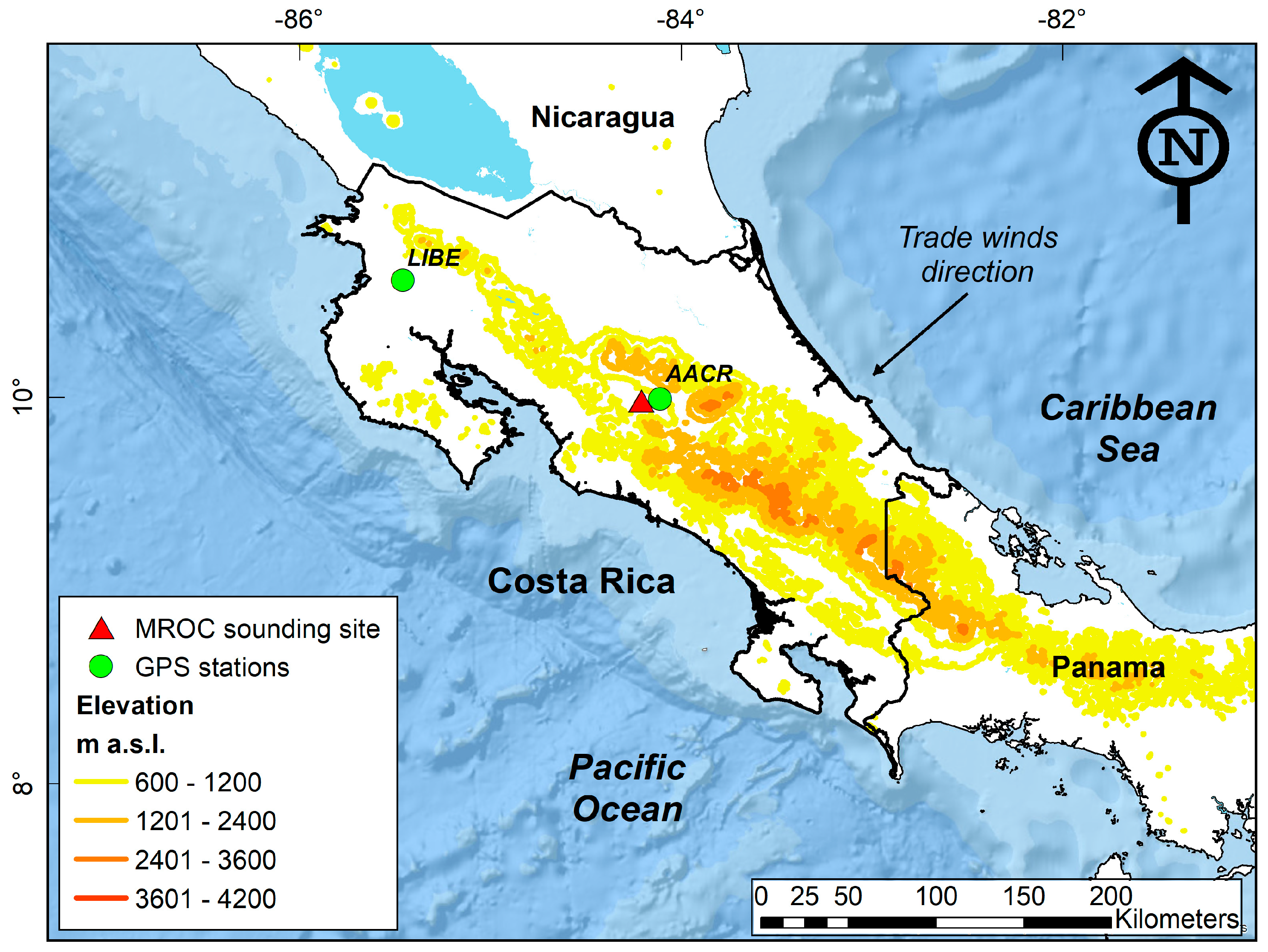
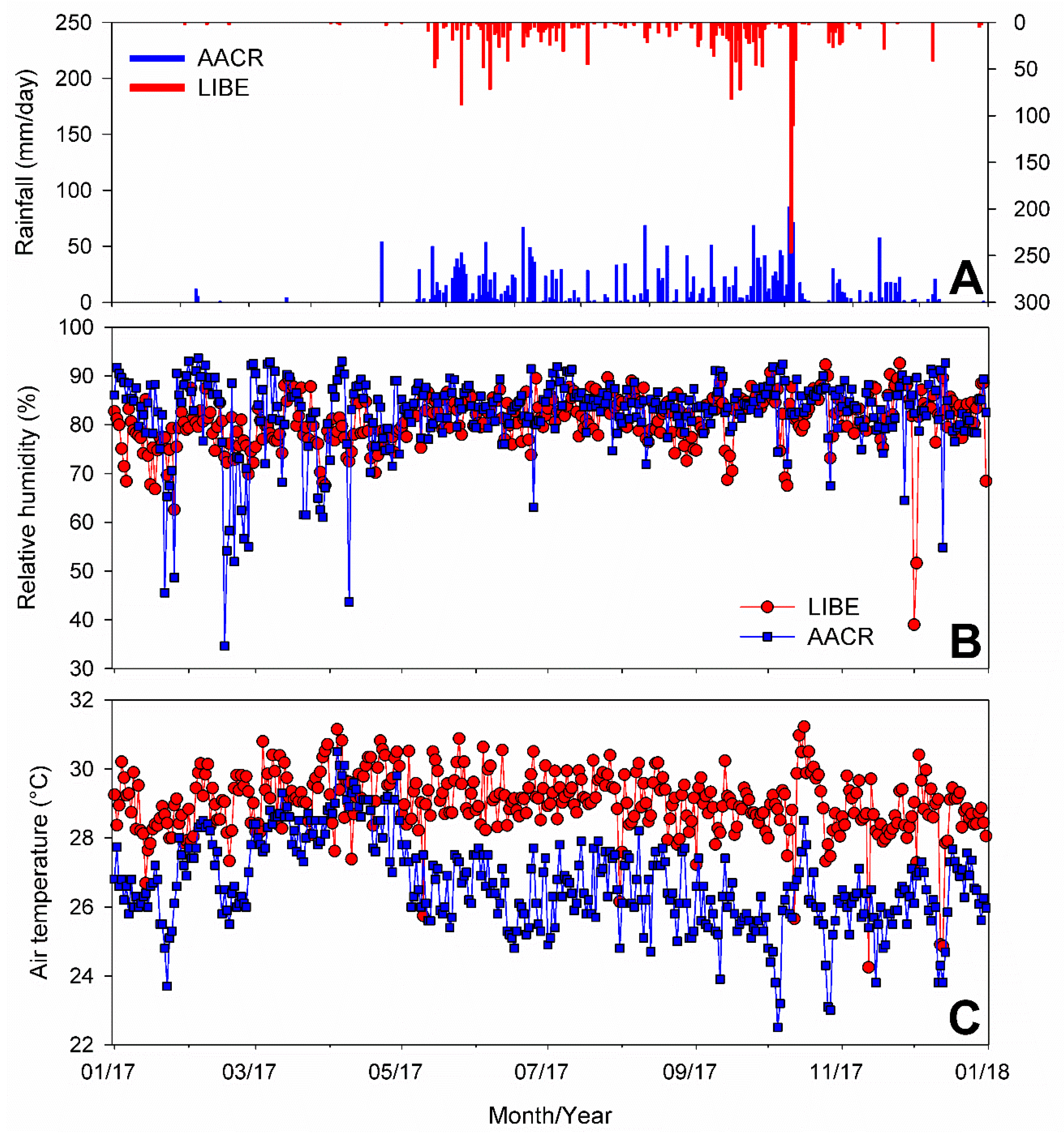
2.1. Climatic Characteristics of Costa Rica
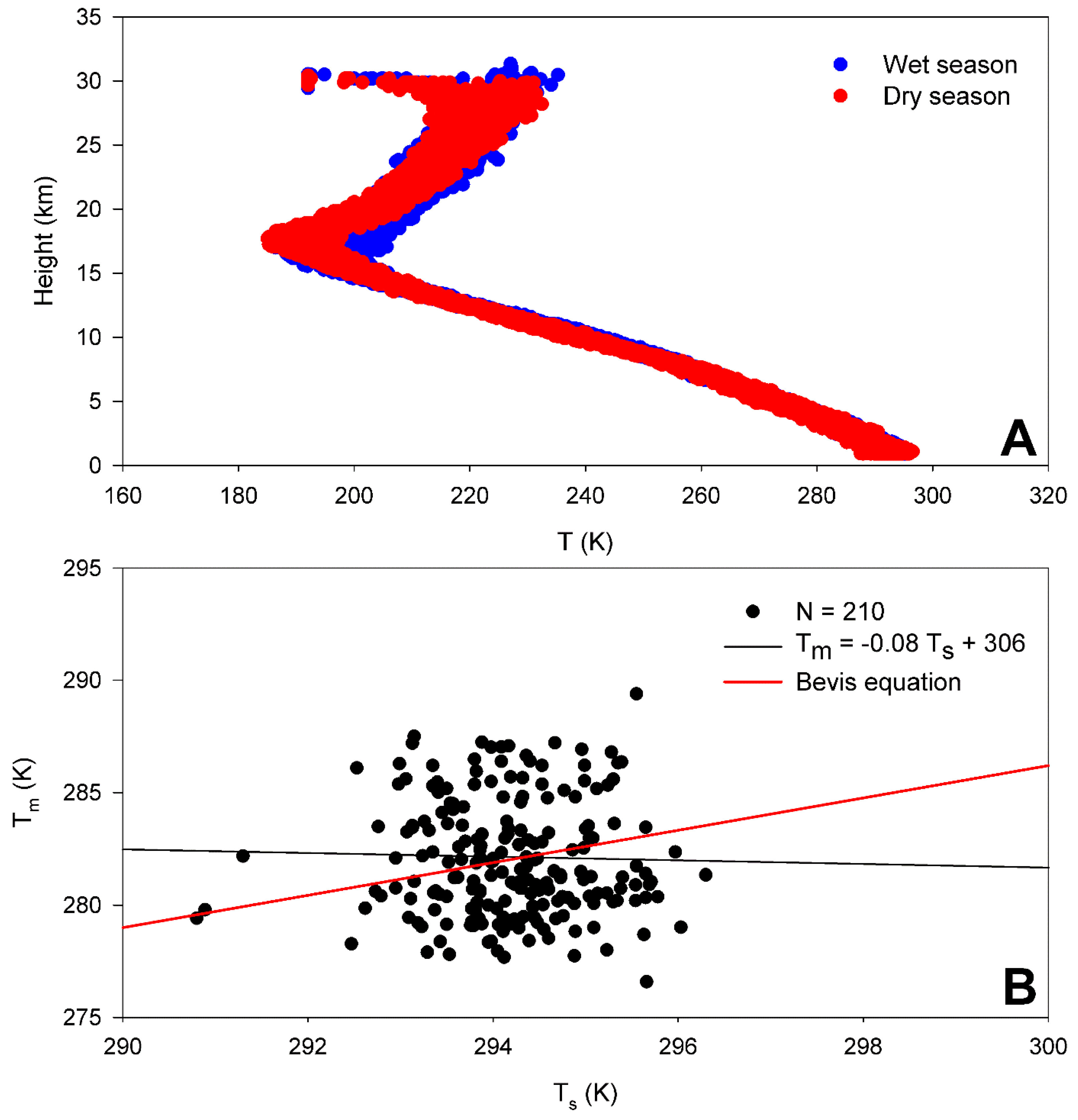
2.2. GPS and Atmospheric Sounding Data
2.3. GPS Data Processing
2.4. MODIS Data
2.5. HYSPLIT Air Mass back Trajectory Analysis
2.6. Statistical Analysis
3. Results
3.1. Seasonal Variations of GPS PWV in AACR and LIBE
3.2. GPS PWV Comparison to Other Estimations Methods and MRL Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trenberth, K.E.; Fasullo, J.; Smith, L. Trends and variability in column-integrated atmospheric water vapor. Clim. Dyn. 2005, 24, 741–758. [Google Scholar] [CrossRef]
- Kumar, S.; Allan, R.P.; Zwiers, F.; Lawrence, D.M.; Dirmeyer, P.A. Revisiting trends in wetness and dryness in the presence of internal climate variability and water limitations over land. Geophys. Res. Lett. 2015, 42, 10867–10875. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Robertson, F.R.; Takacs, L.; Molod, A.; Mocko, D. Atmospheric Water Balance and Variability in the MERRA-2 Reanalysis. J. Clim. 2017, 30, 1177–1196. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric Water Vapor, Convection, and Climate. Rev. Geophys. 2010, 48, RG2001. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Lu, N.; Qin, J.; Yang, K.; Gao, Y.; Xu, X.; Koike, T. On the use of GPS measurements for moderate resolution imaging spectrometer precipitable water vapor evaluation over southern Tibet. J. Geophys. Res. 2011, 116, 1–7. [Google Scholar] [CrossRef]
- Jakobson, E.; Ohvril, H.; Elgered, G. Diurnal variability of precipitable water in the Baltic Region, impact on transmittance of the direct solar radiation. Boreal Environ. Res. 2008, 14, 45–55. [Google Scholar]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.; Ware, R. GPS Meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.; Cachorro, V.; Costa, M.; Román, R.; Bennouna, Y. Validation of MODIS integrated water vapor product against reference GPS data at the Iberian Peninsula. Int. J. Appl. Earth Obs. 2017, 63, 214–221. [Google Scholar] [CrossRef][Green Version]
- Koulali, A.; Ouazar, D.; Bock, O.; Fadil, A. Study of seasonal-scale atmospheric water cycle with ground-based GPS receivers, radiosondes and NWP models over Morocco. Atmos. Res. 2012, 104–105, 273–291. [Google Scholar] [CrossRef]
- MODIS Atmosphere. Available online: https://modis-atmosphere.gsfc.nasa.gov/products/daily (accessed on 15 January 2019).
- Gui, K.; Che, H.; Chen, Q.; Zeng, Z.; Liu, H.; Wang, Y.; Zheng, Y.; Sun, T.; Liao, T.; Wang, H.; et al. Evaluation of radiosonde, MODIS-NIR-Clear, and AERONET precipitable water vapor using IGS ground-based GPS measurements over China. Atmos. Res. 2017, 197, 461–473. [Google Scholar] [CrossRef]
- Gao, B.C.; Kaufman, Y.J. Water vapor retrievals using moderate resolution imaging spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. Atmos. 2003, 108, 1007–1021. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Cachorro, V.E.; Álvarez-Zapatero, P.; Román, R.; Loyola, D.; Costa, M.J.; Wang, H.; González Abad, G.; et al. Inter-comparison of integrated water vapor from satellite instruments using reference GPS data at the Iberian Peninsula. Remote Sens. Environ. 2018, 204, 729–740. [Google Scholar] [CrossRef]
- Diedrich, H.; Wittchen, F.; Preusker, R.; Fischer, J. Representativeness of total column water vapour retrievals from instruments on polar orbiting satellites. Atmos. Chem. Phys. 2016, 16, 8331–8339. [Google Scholar] [CrossRef]
- Nilsson, T.; Böhm, J.; Wijaya, D.D.; Tresch, A.; Nafisi, V.; Schuh, H. Path Delays in the Neutral Atmosphere. In Atmospheric Effects in Space; Böhm, J., Schuh, H., Eds.; Springer: Berlin, Germany, 2013; pp. 73–129. [Google Scholar]
- Waylen, M.E. Interannual variability of monthly precipitation in Costa Rica. J. Clim. 1996, 9, 2607–2613. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Amador, J.A.; Alfaro, E.J.; Quesada, B. Hydrological climate change projections for Central America. J. Hydrol. 2013, 495, 94–112. [Google Scholar] [CrossRef]
- Saénz, F.; Durán-Quesada, A.M.A. Climatology of low level wind regimes over Central America using a weather type classification approach. Front. Earth Sci. 2015, 3, 1–18. [Google Scholar] [CrossRef]
- Powell, G.V.N.; Barborak, J.; Rodriguez, S.M. Assessing representativeness of protected natural areas in Costa Rica for conserving biodiversity: A preliminary gap analysis. Biol. Conser. 2000, 93, 35–41. [Google Scholar] [CrossRef]
- Esquivel-Hernández, G.; Sánchez-Murillo, R.; Birkel, C.; Good, S.P.; Boll, J. Hydroclimatic and ecohydrological resistance/resilience conditions across tropical biomes of Costa Rica. Ecohydrology 2017. [CrossRef]
- Alfaro, E.J. Some Characteristics of the Annual Precipitation Cycle in Central America and their Relationships with its Surrounding Tropical Oceans. Top. Meteor. Ocean. 2002, 9, 103. [Google Scholar]
- Jet Propulsion Laboratory; California Institute of Technology. The Automatic Precise Positioning Service of the Global Differential GPS (GDGPS) System. Available online: http://apps.gdgps.net (accessed on 25 February 2018).
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Atmospheric soundings. Available online: http://weather.uwyo.edu/upperair/sounding.html (accessed on 29 February 2018).
- Benevides, P.; Catalao, J.; Miranda, P.M.A. On the inclusion of GPS precipitable water vapor in the nowcasting of rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Namaoui, H.; Kahlouche, S.; Belbachir, A.; Malderen, R.; Brenot, H.; Pottiaux, E. Water vapor and its comparison with radiosonde and ERA—Interim Data in Algeria. Adv. Atmos. Sci. 2017, 34, 623–634. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites. In The Use of Artificial Satellites for Geodesy; Henriksen, S.W., Mancini, A., Chovitz, B.H., Eds.; The American Geophysical Union: Washington, DC, USA, 1972; Volume 15, pp. 247–251. [Google Scholar]
- Wang, H.; Wei, M.; Li, G.; Zhou, S.; Zeng, Q. Analysis of precipitable water vapor from GPS measurements in Chengdu region: Distribution and evolution characteristics in autumn. Adv. Space Res. 2013, 52, 656–667. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rockend, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteor. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Ross, R.J.; Rosenfeld, S. Estimating mean weighted temperature of the atmosphere for Global Positioning System applications. J. Geophys. Res. 1997, 102, 21719–21730. [Google Scholar] [CrossRef]
- Atmosphere Discipline Team Imager Products. Water Vapor Algorithm Overview. Available online: https://modis-atmos.gsfc.nasa.gov/products/water-vapor/algorithm-overview (accessed on 3 April 2019).
- Mooney, P.A.; Mulligan, F.J.; Fealy, R. Comparison of ERA—40, ERA—Interim and NCEP/NCAR reanalysis data with observed surface air temperatures over Ireland. J. Clim. 2011, 31, 545–557. [Google Scholar] [CrossRef]
- Giovanni. The Bridge between Data and Science (v 4.28). Available online: https://giovanni.gsfc.nasa.gov/giovanni (accessed on 22 February 2018).
- Stein, A.F.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.B.; Cohen, M.D. NOAA’s HYSPLIT Atmospheric Transport and Dispersion Modeling System. Bull. Am. Meteor. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
- Su, L.; Yuan, Z.; Fung, J.C.H.; Lau, A.K.H. A comparison of HYSPLIT backward trajectories generated from two GDAS datasets. Sci. Total Environ. 2015, 506–507, 527–537. [Google Scholar] [CrossRef]
- van der Ent, R.J.; Tuinenburg, O.A. The residence time of water in the atmosphere revisited. Hydrol. Earth Syst. Sci. 2017, 21, 779–790. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple comparisons among means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
- Fernández, L.I.; Salio, P.; Natali, M.P.; Meza, A.M. Estimation of precipitable water vapour from GPS measurements in Argentina: Validation and qualitative analysis of results. Adv. Space Res. 2010, 46, 879–894. [Google Scholar] [CrossRef]
- Shi, F.; Xin, J.; Yang, L.; Cong, Z.; Liu, R.; Ma, Y.; Wang, Y.; Lu, X.; Zhao, L. The first validation of the precipitable water vapor of multisensor satellites over the typical regions in China. Remote Sens Environ. 2018, 206, 107–122. [Google Scholar] [CrossRef]
- Vernimmen RR, E.; Hooijer, A.; Mamenun, A.E.; van Dijk AI, J.M. Evaluation and bias correction of satellite rainfall data for drought monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef]
- Román, R.; Antón, M.; Cachorro, V.E.; Loyola, D.; Ortiz de Galisteo, J.P.; de Frutos, A.; Romero Campos, P.M. Comparison of total water vapor column from GOME-2 on MetOp-A against ground-based GPS measurements at the Iberian Peninsula. Sci. Total Environ. 2015, 533, 317–328. [Google Scholar] [CrossRef]
- Durán-Quesada, A.M.; Gimeno, L.; Amador, J.A.; Nieto, R. Moisture sources for Central America: Identification of moisture sources using a Lagrangian analysis technique. J. Geophys. Res. 2010, 115, D05103. [Google Scholar]
- Magaña, V.; Amador, J.A.; Medina, S. The midsummer drought over Mexico and Central America. J. Clim. 2010, 12, 1577–1588. [Google Scholar] [CrossRef]
- Schoeberl, M.R.; Selkirk, H.B.; Vömel, H.; Douglass, A.R. Sources of seasonal variability in tropical upper troposphere and lower stratosphere water vapor and ozone: Inferences from the Ticosonde data set at Costa Rica. J. Geophys. Res. Atmos. 2015, 120, 9684–9701. [Google Scholar] [CrossRef]
- Selkirk, H.B.; Vömel, H.; Valverde, J.M.; Pfister, L.; Diaz, J.A.; Fernández, W.; Amador, J.; Stolz, W.; Peng, G.S. Detailed structure of the tropical upper troposphere and lower stratosphere as revealed by balloon sonde observations of water vapor, ozone, temperature, and winds during the NASA TCSP and TC4 campaigns. J. Geophys. Res. 2010, 115, D00J19. [Google Scholar] [CrossRef]
- Fujiwara, M.; Vömel, H.; Hasebe, F.; Shiotani, M.; Ogino, S.-Y.; Iwasaki, S.; Nishi, N.; Shibata, T.; Shimizu, K.; Nishimoto, E.; et al. Seasonal to decadal variations of water vapor in the tropical lower stratosphere observed with balloon-borne cryogenic frost point hygrometers. J. Geophys. Res. 2010, 115, D18304. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
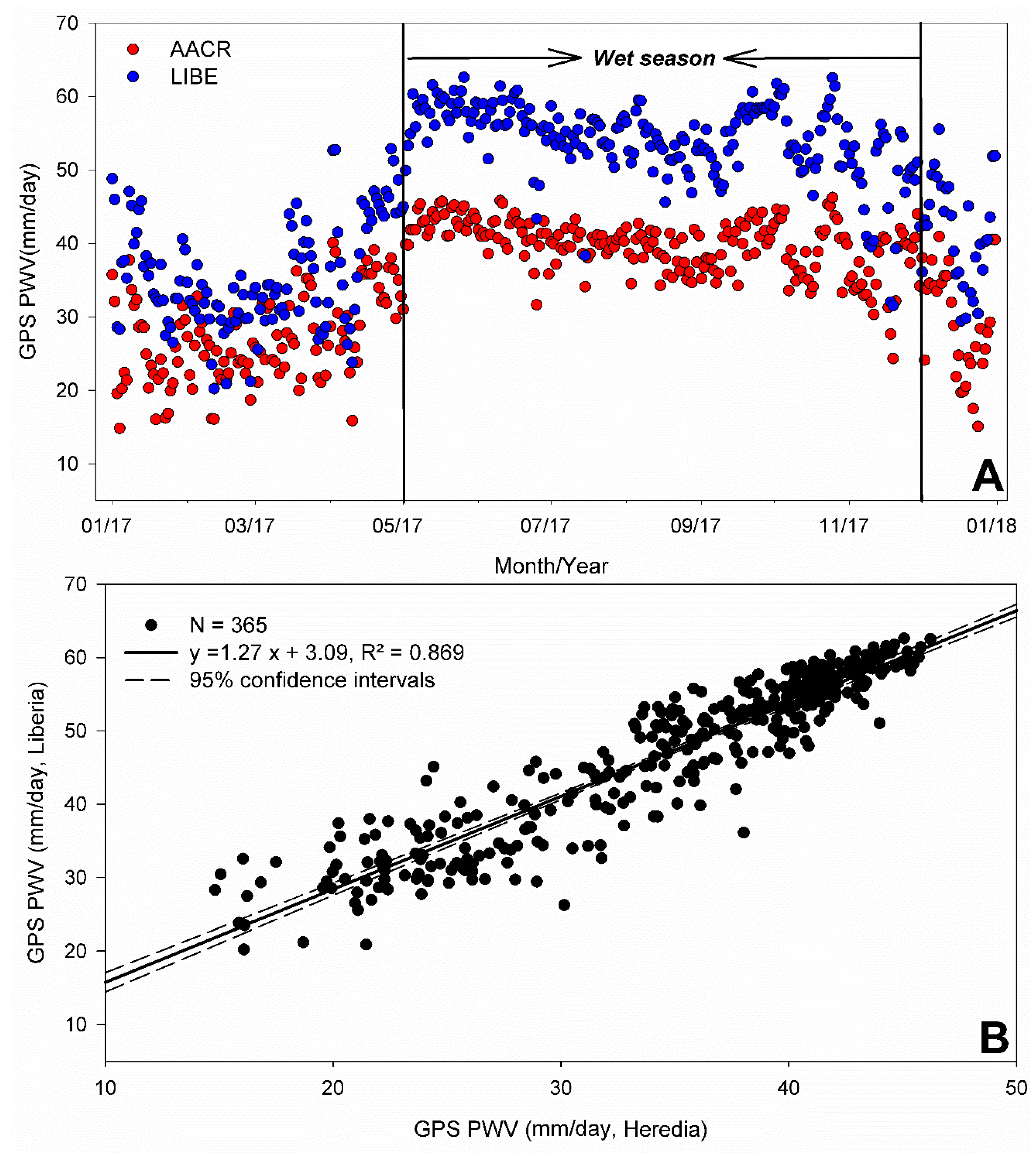
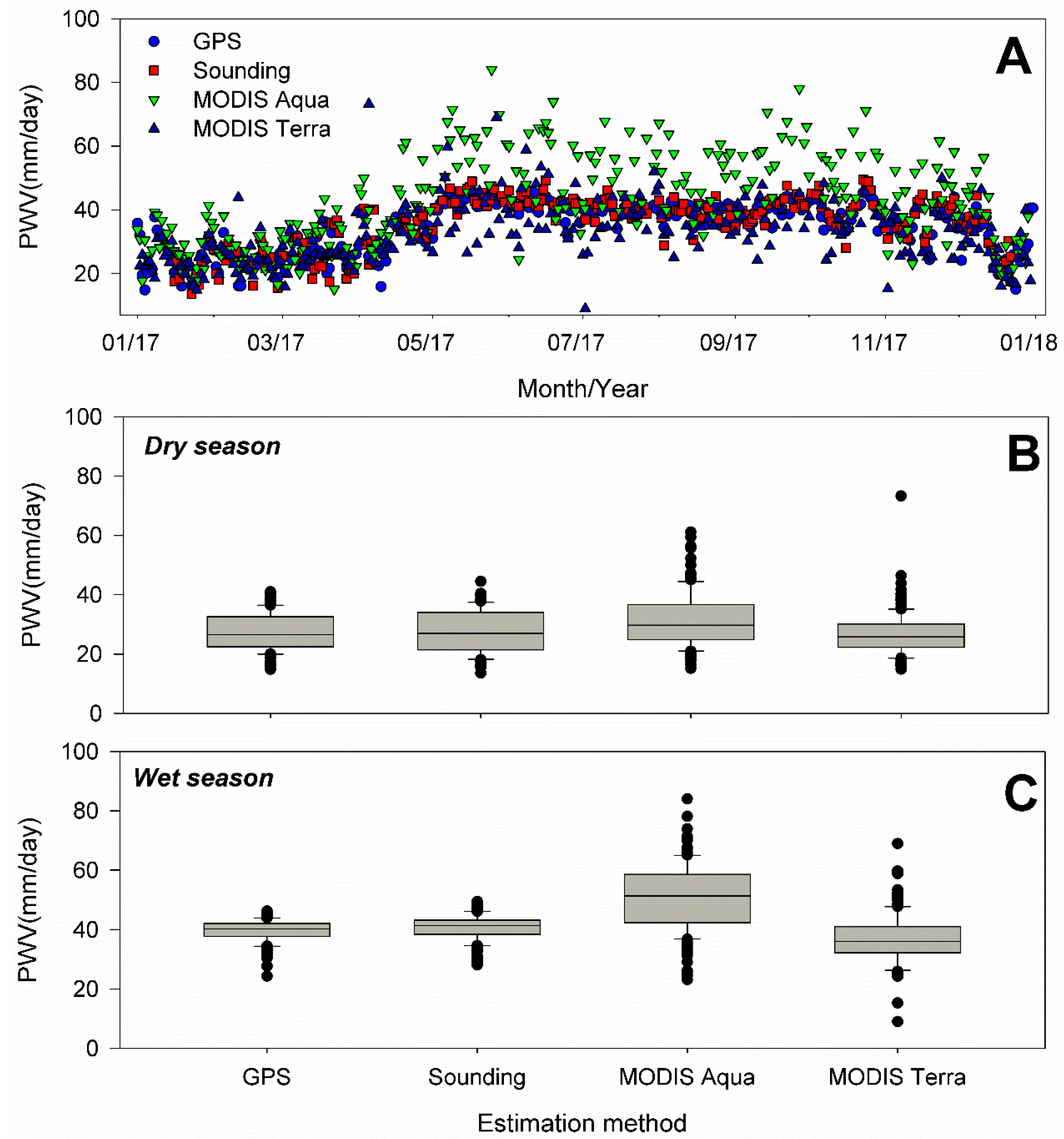
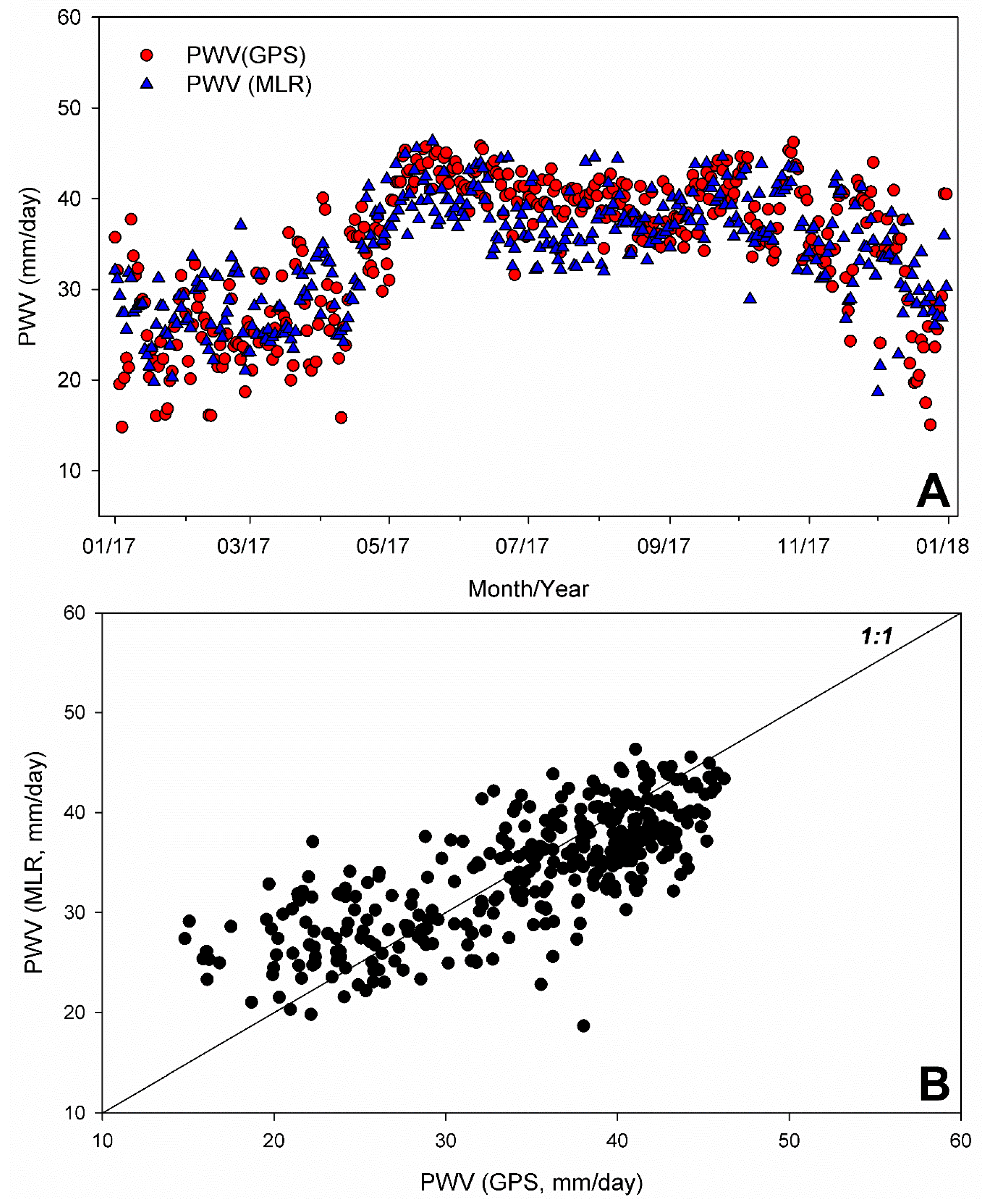
| Station | AACR | LIBE | MROC |
|---|---|---|---|
| Latitude (decimal degrees) | 9.9386 | 10.6305 | 9.9944 |
| Longitude (decimal degrees) | −84.1179 | −85.4380 | −84.2079 |
| Elevation (m a.s.l.) | 1159 | 132 | 912 |
| Δ distance (km) 1 | 11.5 | 152 | -- |
| Δ elevation (m a.s.l.) 1 | +247 | −780 | -- |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos-Arias, P.; Esquivel-Hernández, G.; Valverde-Calderón, J.F.; Rodríguez-Rosales, S.; Moya-Zamora, J.; Sánchez-Murillo, R.; Boll, J. GPS Precipitable Water Vapor Estimations over Costa Rica: A Comparison against Atmospheric Sounding and Moderate Resolution Imaging Spectrometer (MODIS). Climate 2019, 7, 63. https://doi.org/10.3390/cli7050063
Campos-Arias P, Esquivel-Hernández G, Valverde-Calderón JF, Rodríguez-Rosales S, Moya-Zamora J, Sánchez-Murillo R, Boll J. GPS Precipitable Water Vapor Estimations over Costa Rica: A Comparison against Atmospheric Sounding and Moderate Resolution Imaging Spectrometer (MODIS). Climate. 2019; 7(5):63. https://doi.org/10.3390/cli7050063
Chicago/Turabian StyleCampos-Arias, Polleth, Germain Esquivel-Hernández, José Francisco Valverde-Calderón, Stephanie Rodríguez-Rosales, Jorge Moya-Zamora, Ricardo Sánchez-Murillo, and Jan Boll. 2019. "GPS Precipitable Water Vapor Estimations over Costa Rica: A Comparison against Atmospheric Sounding and Moderate Resolution Imaging Spectrometer (MODIS)" Climate 7, no. 5: 63. https://doi.org/10.3390/cli7050063
APA StyleCampos-Arias, P., Esquivel-Hernández, G., Valverde-Calderón, J. F., Rodríguez-Rosales, S., Moya-Zamora, J., Sánchez-Murillo, R., & Boll, J. (2019). GPS Precipitable Water Vapor Estimations over Costa Rica: A Comparison against Atmospheric Sounding and Moderate Resolution Imaging Spectrometer (MODIS). Climate, 7(5), 63. https://doi.org/10.3390/cli7050063





