Evaluation of Gridded Multi-Satellite Precipitation Estimation (TRMM-3B42-V7) Performance in the Upper Indus Basin (UIB)
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
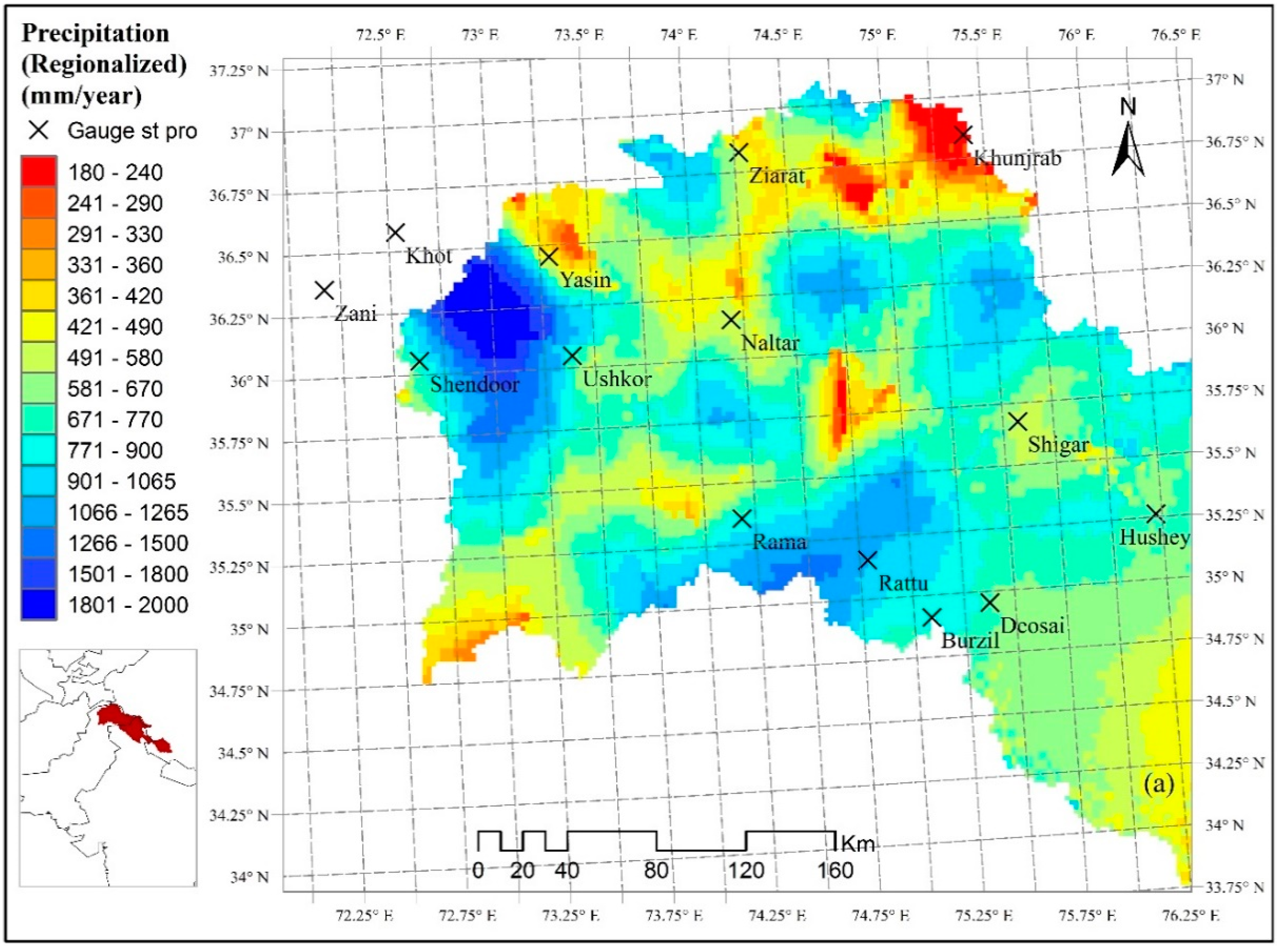
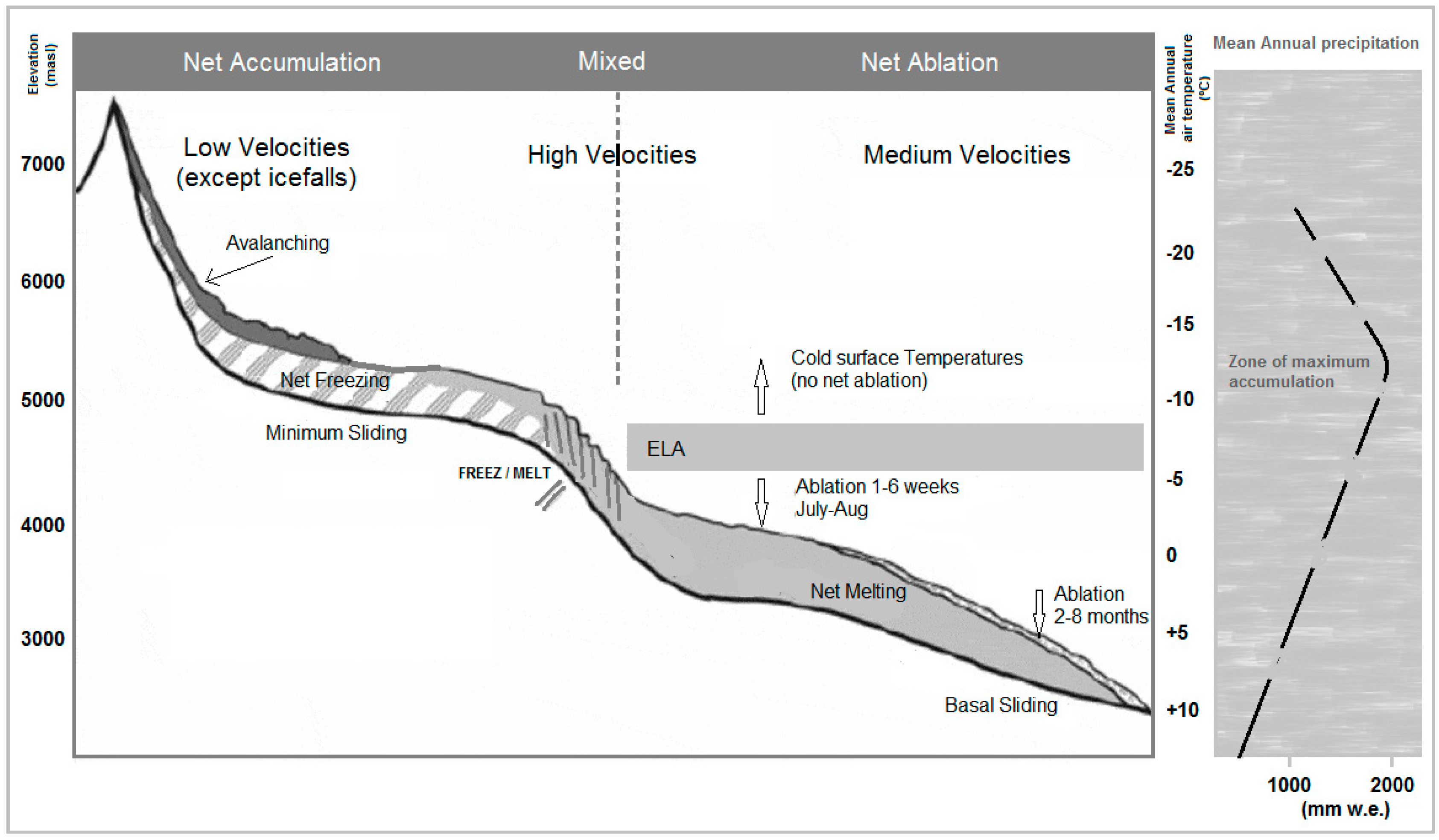
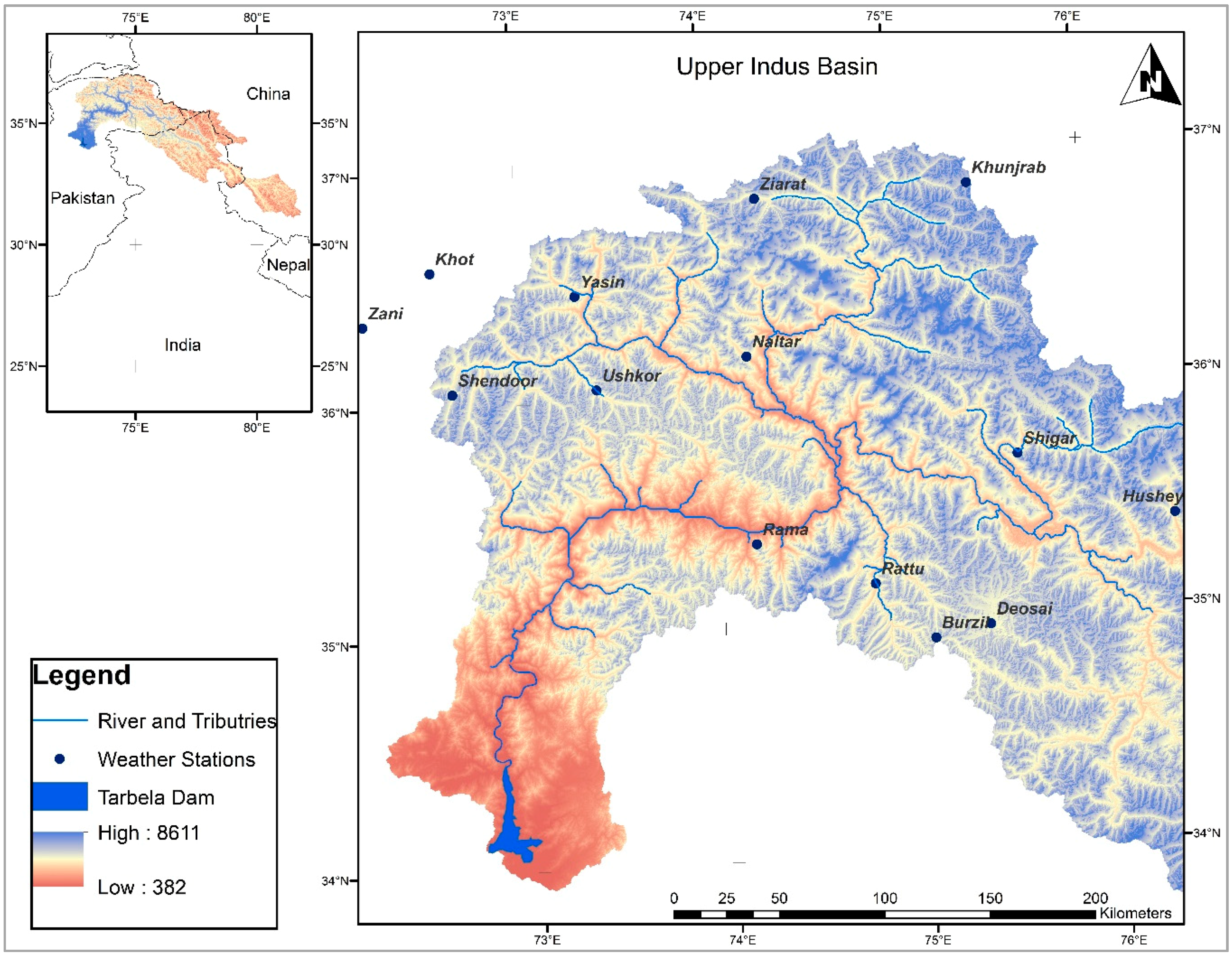
2.1.1. Study Area: The Upper Indus River Basin (UIB)
2.1.2. Data
TMPA Data (TRMM-3B42-V7)
Observed Ground-Based Data
2.2. Methods
3. Results and Discussion
3.1. Statistical Analysis for Daily, Monthly, Annual, and Seasonal Agreggates
3.1.1. Skill Statistics for TRMM Precipitation Estimates (Daily Aggregates)
3.1.2. Skill Statistics for TRMM Precipitation Estimates (Monthly and Annual Aggregates)
3.1.3. Skill Statistics for TRMM Precipitation Estimates (Seasonal Aggregates)
3.2. Categorical Statistics
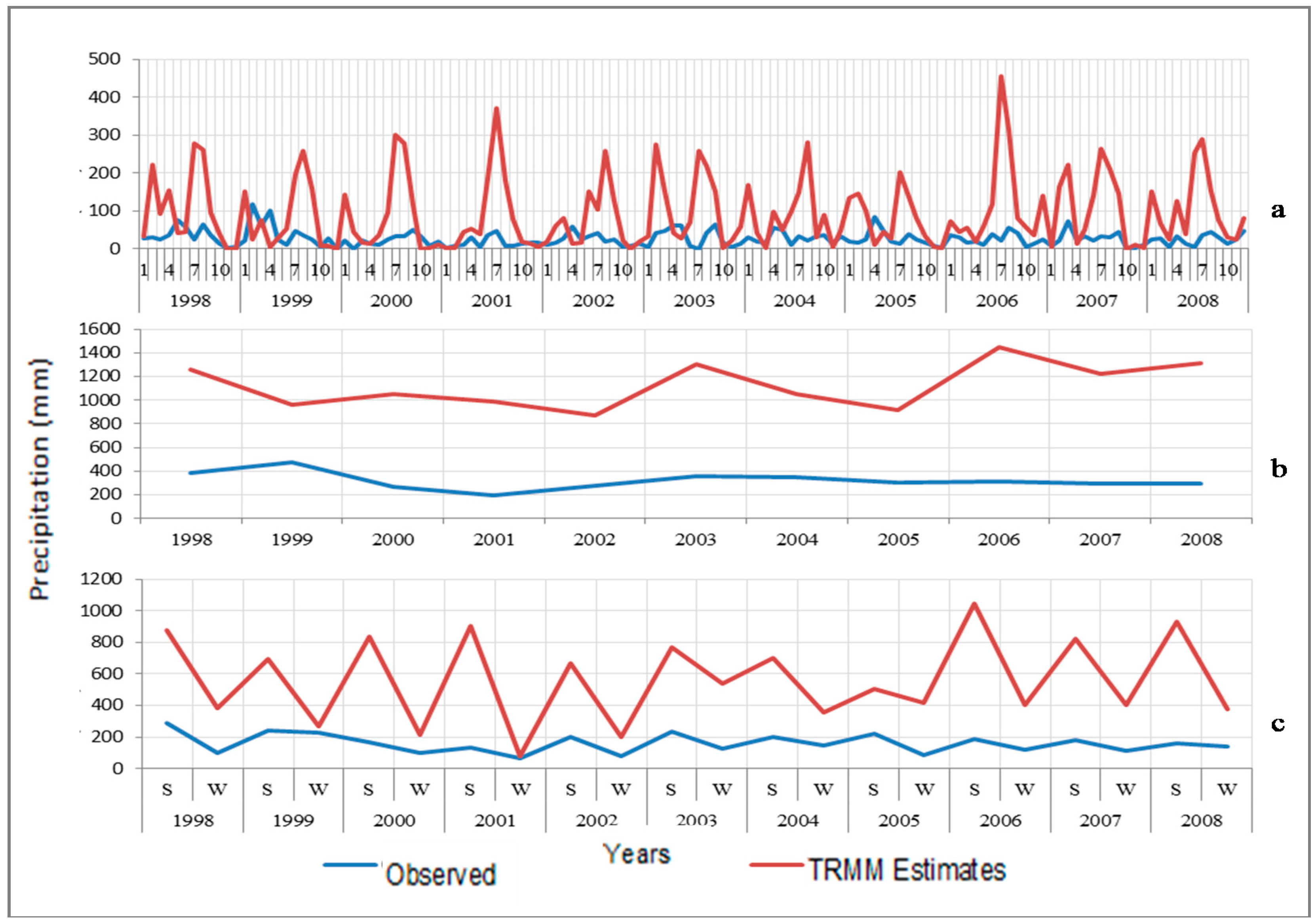
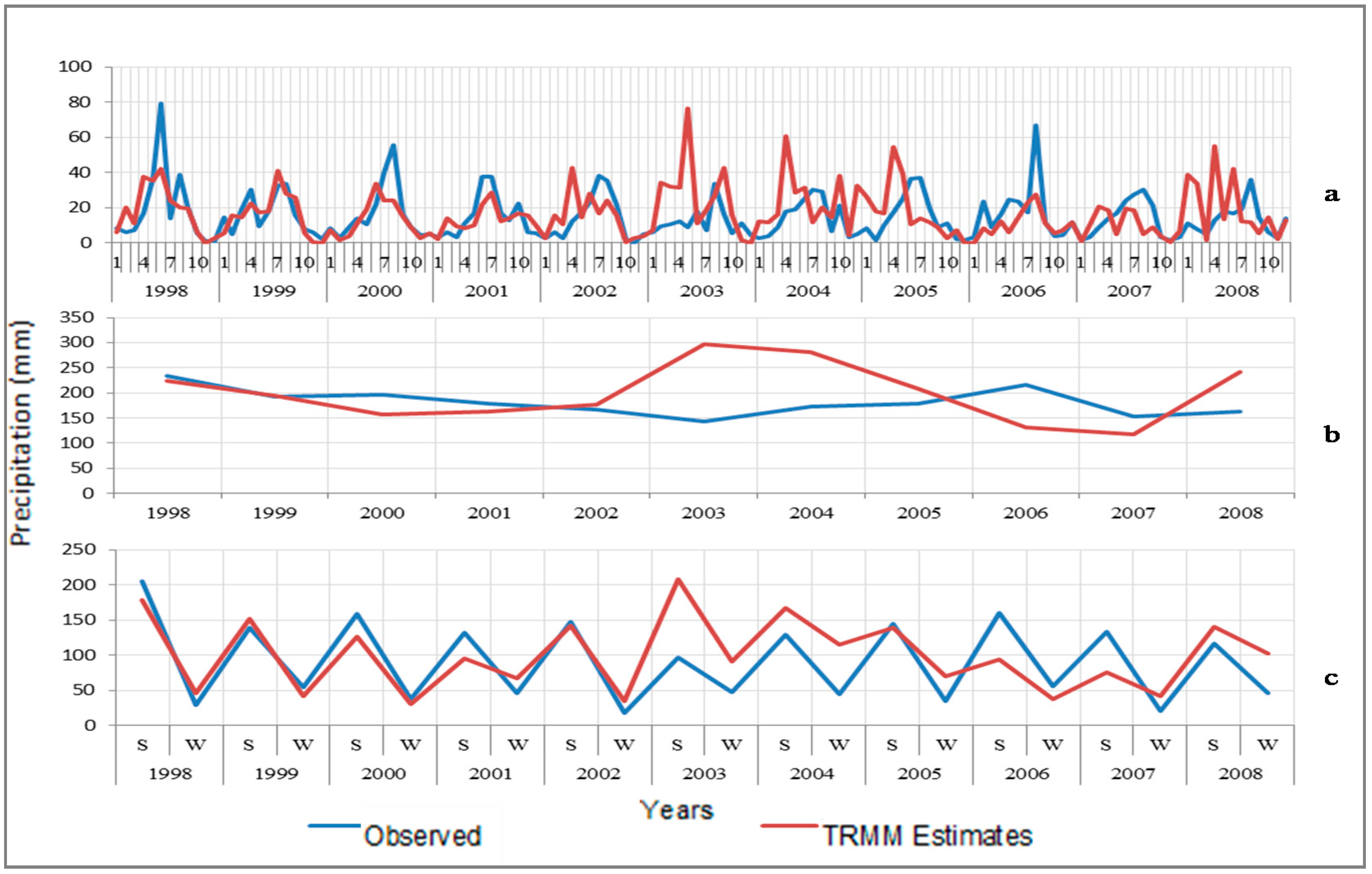
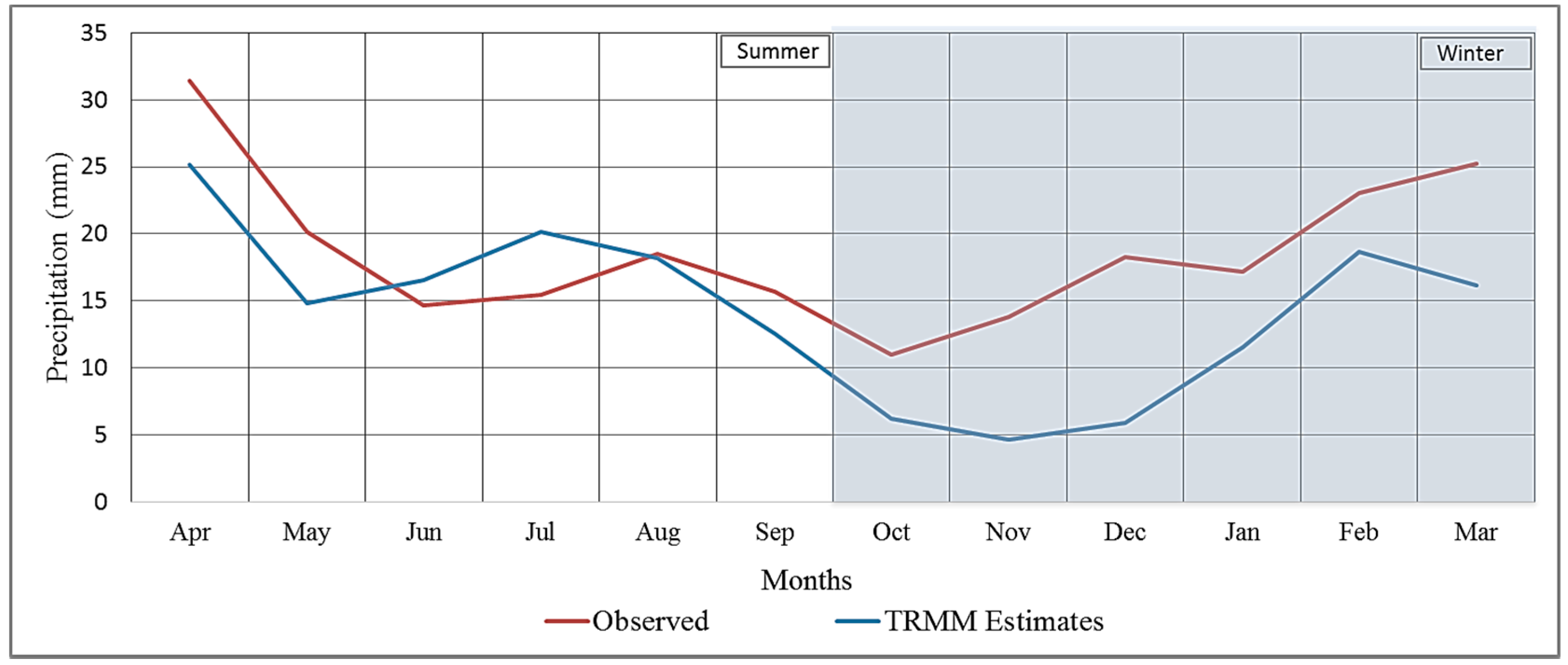
3.3. Visual Comparison
4. Discussion and Conclusions
- (1)
- The TRMM-3B42-V7 product has an overall poor agreement with the observed rainfall gauge data in the study area, and this holds for all temporal scales considered.
- (2)
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Santos Villar, D.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef]
- Hasanpour Kashani, M.; Dinpashoh, Y. Evaluation of efficiency of different estimation methods for missing climatological data. Stoch. Environ. Res. Risk Assess. 2012, 26, 59–71. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Pegram, G.; Deyzel, I.; Sinclair, S.; Visser, P.; Terblanche, D.; Green, G. Daily mapping of 24 h rainfall at pixel scale over South Africa using satellite, radar and raingauge data. In Proceedings of the 2nd International Precipitation Working Group (IPWG) Workshop, Monterey, CA, USA, 25–28 October 2004. [Google Scholar]
- Ghile, Y.; Schulze, R.; Brown, C. Evaluating the performance of ground-based and remotely sensed near real-time rainfall fields from a hydrological perspective. Hydrol. Sci. J. 2010, 55, 497–511. [Google Scholar] [CrossRef]
- Oke, A.M.C.; Frost, A.J.; Beesley, C.A. The use of TRMM satellite data as a predictor in the spatial interpolation of daily precipitation over Australia. In Proceedings of the 18th World IMACS/MODSIM Congress, Cairns, Australia, 13–17 July 2009. [Google Scholar]
- Chiew, F.H.; Vaze, J.; Viney, N.R.; Jordan, P.W.; Perraud, J.M.; Zhang, L.; Teng, J.; Young, W.J.; Peña Arancibia, J.; Morden, R.A.; et al. Rainfall-Runoff Modelling across the Murray-Darling Basin; A Report to the Australian Government from the CSIRO Murray-Darling Basin Sustainable Yields Project; CSIRO: Canberra, Australia, 2008. [Google Scholar]
- Hughes, D.A. Comparison of satellite rainfall data with observations from gauging station networks. J. Hydrol. 2006, 327, 399–410. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorl. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.I.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A Kalman Filter Approach to the Global Satellite Mapping of Precipitation (GSMaP) from Combined Passive Microwave and Infrared Radiometric Data. JMSJ 2009, 87A, 137–151. [Google Scholar] [CrossRef]
- Aonashi, K.; Awaka, J.; Hirose, M.; Kozu, T.; Kubota, T.; Liu, G.; Shige, S.; Kida, S.; Seto, S.; Takahashi, N.; et al. GSMaP Passive Microwave Precipitation Retrieval Algorithm: Algorithm Description and Validation. JMSJ 2009, 87A, 119–136. [Google Scholar] [CrossRef]
- Turk, F.J.; Rohaly, G.D.; Hawkins, J.; Smith, E.A.; Marzano, F.S.; Mugnai, A.; Levizzani, V. Meteorological applications of precipitation estimation from combined SSM/I, TRMM and infrared geostationary satellite data. In Microwave Radiometry and Remote Sensing of the Earth’s Surface and Atmosphere; VSP Intl. Sci. Publ.: Zeist, The Netherlands, 2000; pp. 353–363. [Google Scholar]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorl. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Andermann, C.; Bonnet, S.; Gloaguen, R. Evaluation of precipitation data sets along the Himalayan front. Geochem. Geophys. Geosyst. 2011, 12. [Google Scholar] [CrossRef]
- Amir Khan, A.; Pant, N.C.; Ravindra, R.; Alok, A.; Gupta, M.; Gupta, S. A precipitation perspective of the Hydrosphere-cryosphere interaction in the Himalaya. Geol. Soc. Lond. Spec. Publ. 2018, 462, 73–87. [Google Scholar] [CrossRef]
- Hussain, S.; Song, X.; Ren, G.; Hussain, I.; Han, D.; Zaman, M.H. Evaluation of gridded precipitation data in the Hindu Kush–Karakoram–Himalaya mountainous area. Hydrol. Sci. J. 2017, 62, 2393–2405. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a Long-Term Daily Gridded Precipitation Dataset for Asia Based on a Dense Network of Rain Gauges. Bull. Am. Meteorl. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Palazzi, E.; Filippi, L.; von Hardenberg, J. Insights into elevation-dependent warming in the Tibetan Plateau-Himalayas from CMIP5 model simulations. Clim. Dyn. 2017, 48, 3991–4008. [Google Scholar] [CrossRef]
- Wijngaard, R.R.; Lutz, A.F.; Nepal, S.; Khanal, S.; Pradhananga, S.; Shrestha, A.B.; Immerzeel, W.W. Future changes in hydro-climatic extremes in the Upper Indus, Ganges, and Brahmaputra River basins. PLoS ONE 2017, 12, e0190224. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.J.; Koch, M. Correction and informed regionalization of precipitation data in a high mountainous region (Upper Indus Basin) and its effect on SWAT-modelled discharge. Unpublished work. 2018. [Google Scholar]
- Wilheit, T.T. Some Comments on Passive Microwave Measurement of Rain. Bull. Am. Meteorl. Soc. 1986, 67, 1226–1232. [Google Scholar] [CrossRef]
- Janowiak, J.E.; Joyce, R.J.; Yarosh, Y. A Real-Time Global Half-Hourly Pixel-Resolution Infrared Dataset and Its Applications. Bull. Am. Meteorl. Soc. 2001, 82, 205–217. [Google Scholar] [CrossRef]
- Ali, K.F.; de Boer, D.H. Spatial patterns and variation of suspended sediment yield in the upper Indus River basin, northern Pakistan. J. Hydrol. 2007, 334, 368–387. [Google Scholar] [CrossRef]
- Hewitt, K. Hazards of melting as an option: Upper Indus Glaciers, I&II. DAWN, 20 May 2001. [Google Scholar]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza River basin, Karakoram Range, Northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Wake, C.P. Glaciochemical Investigations as a Tool for Determining the Spatial and Seasonal Variation of Snow Accumulation in the Central Karakoram, Northern Pakistan. Ann. Glaciol. 1989, 13, 279–284. [Google Scholar] [CrossRef]
- Hewitt, K. Glacier Change, Concentration, and Elevation Effects in the Karakoram Himalaya, Upper Indus Basin. Mt. Res. Dev. 2011, 31, 188–200. [Google Scholar] [CrossRef]
- Ali, S.; Li, D.; Congbin, F.; Khan, F. Twenty first century climatic and hydrological changes over Upper Indus Basin of Himalayan region of Pakistan. Environ. Res. Lett. 2015, 10, 14007. [Google Scholar] [CrossRef]
- Hasson, S. Future Water Availability from Hindukush-Karakoram-Himalaya upper Indus Basin under Conflicting Climate Change Scenarios. Climate 2016, 4, 40. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N. Effect of orography on precipitation in the western Himalayan region. J. Hydrol. 1997, 199, 183–206. [Google Scholar] [CrossRef]
- Dhar, O.N.; Rakhecha, P.R. The effect of elevation on monsoon rainfall distribution in the central Himalayas. In Monsoon Dynamics; Lighthill, M.J., Pearce, R.P., Eds.; Cambridge University Press: New York, NY, USA, 1981; pp. 253–260. [Google Scholar]
- Dahri, Z.H.; Ludwig, F.; Moors, E.; Ahmad, B.; Khan, A.; Kabat, P. An appraisal of precipitation distribution in the high-altitude catchments of the Indus basin. Sci. Total Environ. 2016, 548–549, 289–306. [Google Scholar] [CrossRef] [PubMed]
- Pang, H.; Hou, S.; Kaspari, S.; Mayewski, P.A. Influence of regional precipitation patterns on stable isotopes in ice cores from the central Himalayas. Cryosphere 2014, 8, 289–301. [Google Scholar] [CrossRef]
- Archer, D. Contrasting hydrological regimes in the upper Indus Basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
- Mayor, Y.G.; Tereshchenko, I.; Fonseca-Hernández, M.; Pantoja, D.A.; Montes, J.M. Evaluation of Error in IMERG Precipitation Estimates under Different Topographic Conditions and Temporal Scales over Mexico. Remote Sens. 2017, 9, 503. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences. An Introduction; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Palazzi, E.; von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Khan, A.J. Estimating the Effects of Climate Change on the Water Resources in the Upper Indus Basin (UIB). Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2018. [Google Scholar]

| Description | No. | Station | Latitude (◦) | Longitude (◦) | Altitude (m) |
|---|---|---|---|---|---|
| High Altitude (2367–4440 m.a.s.l.) stations operated by Water and Power Development Authority (WAPDA), Pakistan | 1 | Burzil | 34.91 | 75.90 | 4030 |
| 2 | Deosai | 35.09 | 75.54 | 4149 | |
| 3 | Hushey | 35.42 | 76.37 | 3075 | |
| 4 | Khot | 36.52 | 72.58 | 3505 | |
| 5 | Khunjrab | 36.84 | 75.42 | 4440 | |
| 6 | Naltar | 36.17 | 74.18 | 2898 | |
| 7 | Rama | 35.36 | 74.81 | 3179 | |
| 8 | Rattu | 35.15 | 74.8 | 2718 | |
| 9 | Shendoor | 36.09 | 72.55 | 3712 | |
| 10 | Shigar | 35.63 | 75.53 | 2367 | |
| 11 | Ushkor | 36.05 | 73.39 | 3051 | |
| 12 | Yasin | 36.45 | 73.3 | 3350 | |
| 13 | Zani | 36.33 | 72.17 | 3895 | |
| 14 | Ziarat | 36.77 | 74.46 | 3020 |
| Observed Values (Gauge Data) | Total | |||
|---|---|---|---|---|
| YES | NO | |||
| Estimated Values (TRMM estimates) | YES | -a -Hits | -b -False Alarms | Total—Yes Estimated |
| NO | -c -Misses | -d -Correct Negative | Total—No Estimated | |
| Total | Total—Yes Observed | Total—No Observed | Totala + b + c + d | |
| Sub-Basin | Station | Daily | ||||
|---|---|---|---|---|---|---|
| r | rBIAS | MBE (mm) | MAE (mm) | RMSE (mm) | ||
| Southern UIB | Burzil | 0.22 | −0.42 | −11.77 | 16.20 | 20.76 |
| Deosai | 0.10 | 0.99 | 4.41 | 14.53 | 26.33 | |
| Rama | 0.23 | −0.22 | −16.20 | 18.31 | 27.44 | |
| Rattu | 0.14 | 0.69 | −7.90 | 18.12 | 29.24 | |
| Eastern UIB | Shigar | 0.08 | 1.31 | −3.99 | 10.24 | 17.81 |
| Hushey | 0.14 | −0.07 | −5.73 | 10.79 | 14.73 | |
| Northwestern UIB | Khot | 0.19 | 0.70 | 0.49 | 4.93 | 8.08 |
| Naltar | 0.25 | 0.24 | −11.94 | 15.39 | 21.10 | |
| Shendoor | 0.16 | 1.48 | 1.22 | 9.46 | 15.67 | |
| Ushkor | 0.21 | 0.70 | −0.51 | 8.16 | 12.74 | |
| Yasin | 0.10 | 5.27 | 24.24 | 28.68 | 46.57 | |
| Zani | 0.13 | −0.14 | −15.23 | 19.16 | 26.96 | |
| Northern UIB | Khunjrab | 0.15 | −0.27 | −5.50 | 10.52 | 15.40 |
| Ziarat | 0.14 | 0.71 | −0.94 | 6.05 | 9.48 | |
| Basin average | 0.16 | 0.78 | −3.53 | 13.61 | 20.88 | |
| Maximum | 0.25 | 5.27 | 24.24 | 28.68 | 46.57 | |
| Minimum | 0.08 | −0.42 | −16.20 | 4.93 | 8.08 | |
| Sub-Basin | Station | Monthly | Annual | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r | rBIAS | MBE (mm) | MAE (mm) | RMSE (mm) | r | rBIAS | MBE (mm) | MAE (mm) | RMSE (mm) | ||
| Southern UIB | Burzil | 0.55 | −0.28 | −56.80 | 58.73 | 112.8 | 0.43 | −1.05 | −391.5 | 391.5 | 407.7 |
| Deosai | 0.22 | 0.17 | 21.65 | 43.62 | 78.95 | −0.37 | 0.24 | 146.6 | 201.4 | 234.6 | |
| Rama | 0.54 | −0.36 | −78.26 | 79.54 | 165.9 | 0.78 | −2.05 | −538.5 | 538.5 | 574.8 | |
| Rattu | 0.20 | −0.20 | −39.31 | 61.32 | 119.10 | 0.30 | −0.58 | −264.9 | 274.1 | 353.8 | |
| Eastern UIB | Shigar | 0.02 | −0.21 | −19.42 | 36.56 | 78.26 | −0.11 | −0.62 | −133.2 | 179.7 | 249.8 |
| Hushey | 0.09 | −0.24 | −29.19 | 39.72 | 101.9 | −0.15 | −0.79 | −193.2 | 230.3 | 339.6 | |
| Northwestern UIB | Khot | 0.51 | −0.21 | −26.52 | 39.47 | 74.14 | 0.29 | −0.65 | −182.0 | 242.7 | 250.9 |
| Naltar | 0.60 | −0.31 | −58.62 | 60.17 | 120.6 | 0.12 | −1.32 | −395.1 | 395.1 | 416.3 | |
| Shendoor | 0.42 | 0.08 | 6.53 | 22.08 | 37.34 | 0.54 | 0.13 | 40.4 | 66.4 | 99.1 | |
| Ushkor | 0.52 | −0.03 | −1.82 | 19.19 | 39.41 | 0.62 | −0.05 | −14.7 | 79.1 | 110.5 | |
| Yasin | 0.21 | 1.36 | 118.3 | 126.7 | 241.2 | 0.10 | 0.72 | 806.0 | 806.0 | 827.5 | |
| Zani | 0.49 | −0.34 | −75.05 | 77.98 | 154.91 | 0.52 | −1.69 | −508.3 | 508.3 | 532.6 | |
| Northern UIB | Khunjrab | 0.39 | 0.05 | 2.26 | 13.13 | 23.40 | −0.28 | 0.09 | 18.3 | 52.0 | 70.0 |
| Ziarat | 0.38 | −0.07 | −5.39 | 15.23 | 32.62 | 0.55 | −0.15 | −30.6 | 73.4 | 104.7 | |
| Basin average | 0.61 | −0.23 | −9.09 | 14.15 | 20.98 | 0.57 | −0.24 | −117.3 | 117.3 | 134.1 | |
| Maximum | 0.60 | 1.36 | 118.3 | 126.7 | 241.2 | 0.78 | 0.72 | 806.0 | 806.0 | 827.5 | |
| Minimum | 0.02 | −0.36 | −78.26 | 13.13 | 23.40 | −0.37 | −2.05 | −538.50 | 51.96 | 69.96 | |
| Sub-Basin | Station | Summer Season | Winter Season | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r | rBIAS | MBE (mm) | MAE (mm) | RMSE (mm) | r | rBIAS | MBE (mm) | MAE (mm) | RMSE (mm) | ||
| Southern UIB | Burzil | 0.35 | −0.48 | −190.8 | 190.8 | 201.5 | 0.05 | −0.50 | −200.7 | 200.7 | 226.0 |
| Deosai | −0.42 | 0.27 | 68.1 | 101.0 | 123.5 | −0.14 | 0.31 | 78.6 | 116.9 | 139.6 | |
| Ramma | 0.68 | −0.54 | −198.7 | 198.7 | 213.9 | 0.60 | −0.92 | −339.9 | 339.9 | 371.4 | |
| Rattu | 0.49 | 0.09 | 25.8 | 101.0 | 127.9 | −0.01 | −1.00 | −290.8 | 290.8 | 357.1 | |
| Eastern UIB | Shigar | −0.09 | −0.22 | −36.9 | 106.0 | 156.6 | −0.10 | −0.57 | −96.3 | 105.4 | 127.9 |
| Hushey | 0.22 | −0.35 | −83.2 | 103.7 | 156.3 | −0.55 | −0.46 | −109.9 | 132.2 | 189.3 | |
| Northwestern UIB | Khot | −0.11 | −0.03 | −4.1 | 38.1 | 48.3 | 0.33 | 0.16 | 22.2 | 29.2 | 34.8 |
| Naltar | 0.48 | −0.50 | −203.8 | 203.8 | 220.6 | 0.17 | −0.47 | −191.6 | 191.6 | 205.9 | |
| Shendoor | 0.57 | 0.42 | 56.1 | 56.7 | 79.6 | −0.02 | −0.12 | −15.9 | 61.1 | 65.6 | |
| Ushkor | 0.49 | 0.17 | 31.0 | 71.9 | 84.1 | 0.65 | −0.25 | −45.9 | 55.3 | 85.7 | |
| Yasin | −0.35 | 2.94 | 593.6 | 593.6 | 615.2 | 0.22 | 1.05 | 212.5 | 212.5 | 244.1 | |
| Zani | 0.52 | −0.66 | −268.8 | 268.8 | 301.3 | 0.57 | −0.59 | −239.8 | 239.8 | 256.1 | |
| Northern UIB | Khunjrab | 0.09 | −0.21 | −41.3 | 91.8 | 109.2 | 0.56 | −0.72 | −141.1 | 157.5 | 166.9 |
| Ziarat | 0.56 | −0.02 | −2.5 | 36.2 | 47.4 | 0.54 | −0.20 | −28.4 | 44.8 | 65.3 | |
| Basin average | 0.60 | 0.00 | −5.18 | 30.1 | 38.7 | 0.36 | −0.4 | −96.51 | 96.5 | 109.1 | |
| Maximum | 0.68 | 2.94 | 593.6 | 593.6 | 615.2 | 0.65 | 1.05 | 212.5 | 339.9 | 371.4 | |
| Minimum | −0.42 | −0.66 | −268.8 | 36.2 | 47.4 | −0.55 | −1.00 | −339.9 | 29.2 | 34.8 | |
| Sub-Basin | Station | Ac | FBI | POD | FAR | CSI | TSS |
|---|---|---|---|---|---|---|---|
| Southern UIB | Burzil | 0.57 | 0.75 | 0.42 | 0.45 | 0.31 | 0.12 |
| Deosai | 0.57 | 1.01 | 0.61 | 0.39 | 0.44 | 0.14 | |
| Ramma | 0.55 | 1.27 | 0.50 | 0.61 | 0.28 | 0.08 | |
| Rattu | 0.51 | 1.48 | 0.56 | 0.62 | 0.29 | 0.04 | |
| Eastern UIB | Shigar | 0.60 | 1.30 | 0.41 | 0.68 | 0.22 | 0.08 |
| Hushey | 0.57 | 0.83 | 0.40 | 0.52 | 0.28 | 0.10 | |
| Northwestern UIB | Khot | 0.65 | 1.34 | 0.57 | 0.58 | 0.32 | 0.25 |
| Naltar | 0.62 | 0.86 | 0.40 | 0.53 | 0.28 | 0.14 | |
| Shendoor | 0.56 | 1.16 | 0.40 | 0.65 | 0.23 | 0.04 | |
| Ushkor | 0.61 | 1.07 | 0.42 | 0.60 | 0.26 | 0.12 | |
| Yasin | 0.67 | 1.03 | 0.44 | 0.58 | 0.27 | 0.20 | |
| Zani | 0.55 | 0.86 | 0.35 | 0.59 | 0.24 | 0.03 | |
| Northern UIB | Khunjrab | 0.55 | 1.04 | 0.43 | 0.58 | 0.27 | 0.06 |
| Ziarat | 0.60 | 0.73 | 0.35 | 0.52 | 0.25 | 0.10 | |
| Basin average | 0.58 | 1.05 | 0.45 | 0.56 | 0.28 | 0.11 | |
| Maximum | 0.67 | 1.48 | 0.61 | 0.68 | 0.44 | 0.25 | |
| Minimum | 0.51 | 0.73 | 0.35 | 0.39 | 0.22 | 0.03 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.J.; Koch, M.; Chinchilla, K.M. Evaluation of Gridded Multi-Satellite Precipitation Estimation (TRMM-3B42-V7) Performance in the Upper Indus Basin (UIB). Climate 2018, 6, 76. https://doi.org/10.3390/cli6030076
Khan AJ, Koch M, Chinchilla KM. Evaluation of Gridded Multi-Satellite Precipitation Estimation (TRMM-3B42-V7) Performance in the Upper Indus Basin (UIB). Climate. 2018; 6(3):76. https://doi.org/10.3390/cli6030076
Chicago/Turabian StyleKhan, Asim Jahangir, Manfred Koch, and Karen Milena Chinchilla. 2018. "Evaluation of Gridded Multi-Satellite Precipitation Estimation (TRMM-3B42-V7) Performance in the Upper Indus Basin (UIB)" Climate 6, no. 3: 76. https://doi.org/10.3390/cli6030076
APA StyleKhan, A. J., Koch, M., & Chinchilla, K. M. (2018). Evaluation of Gridded Multi-Satellite Precipitation Estimation (TRMM-3B42-V7) Performance in the Upper Indus Basin (UIB). Climate, 6(3), 76. https://doi.org/10.3390/cli6030076





