Mapping Precipitation, Temperature, and Evapotranspiration in the Mkomazi River Basin, Tanzania
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source and Data Cleaning
2.3. Spatial Interpolation of Rainfall
2.4. Spatial Interpolation of Temperature and Evapotranspiration
3. Results
3.1. Dataset
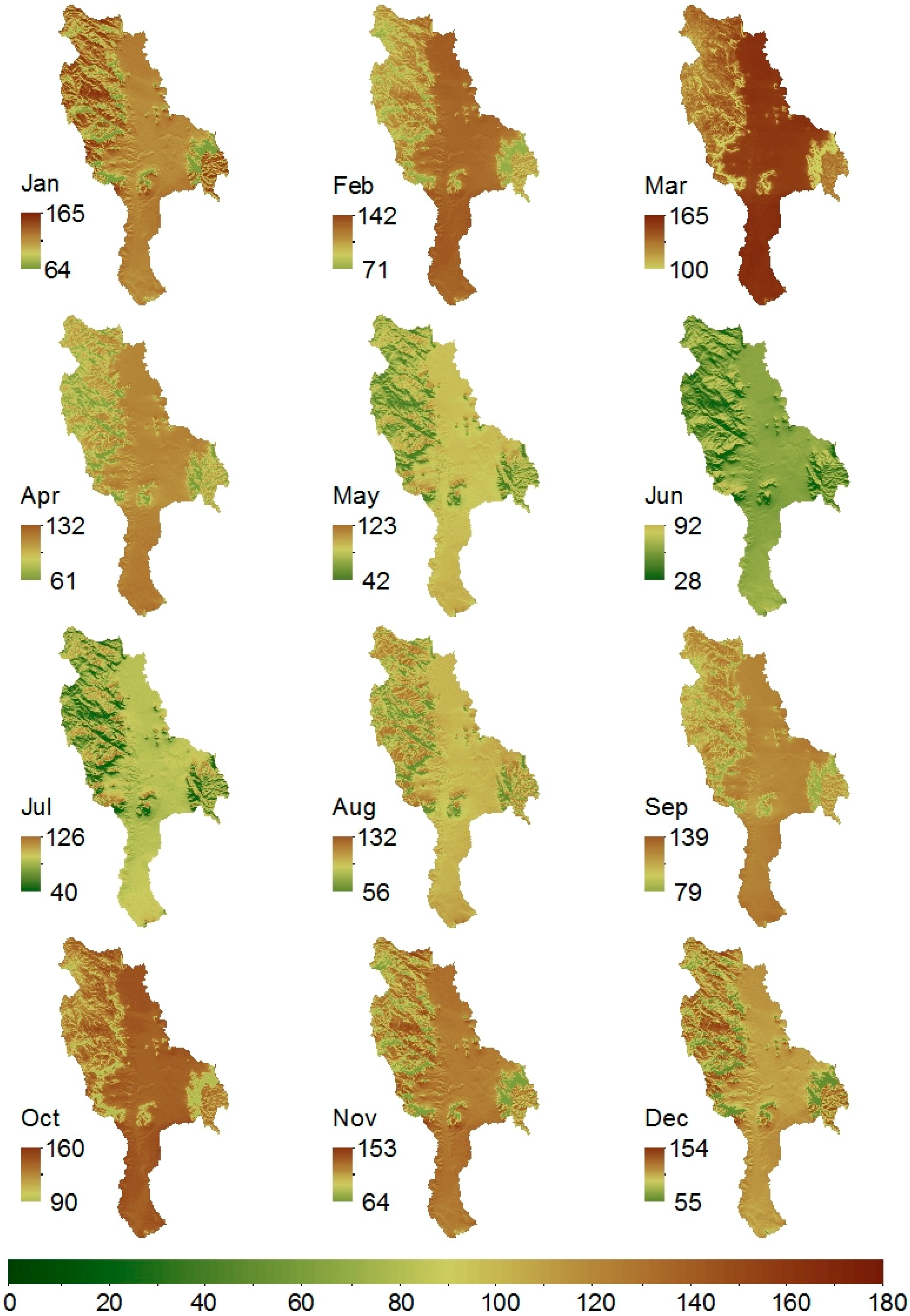
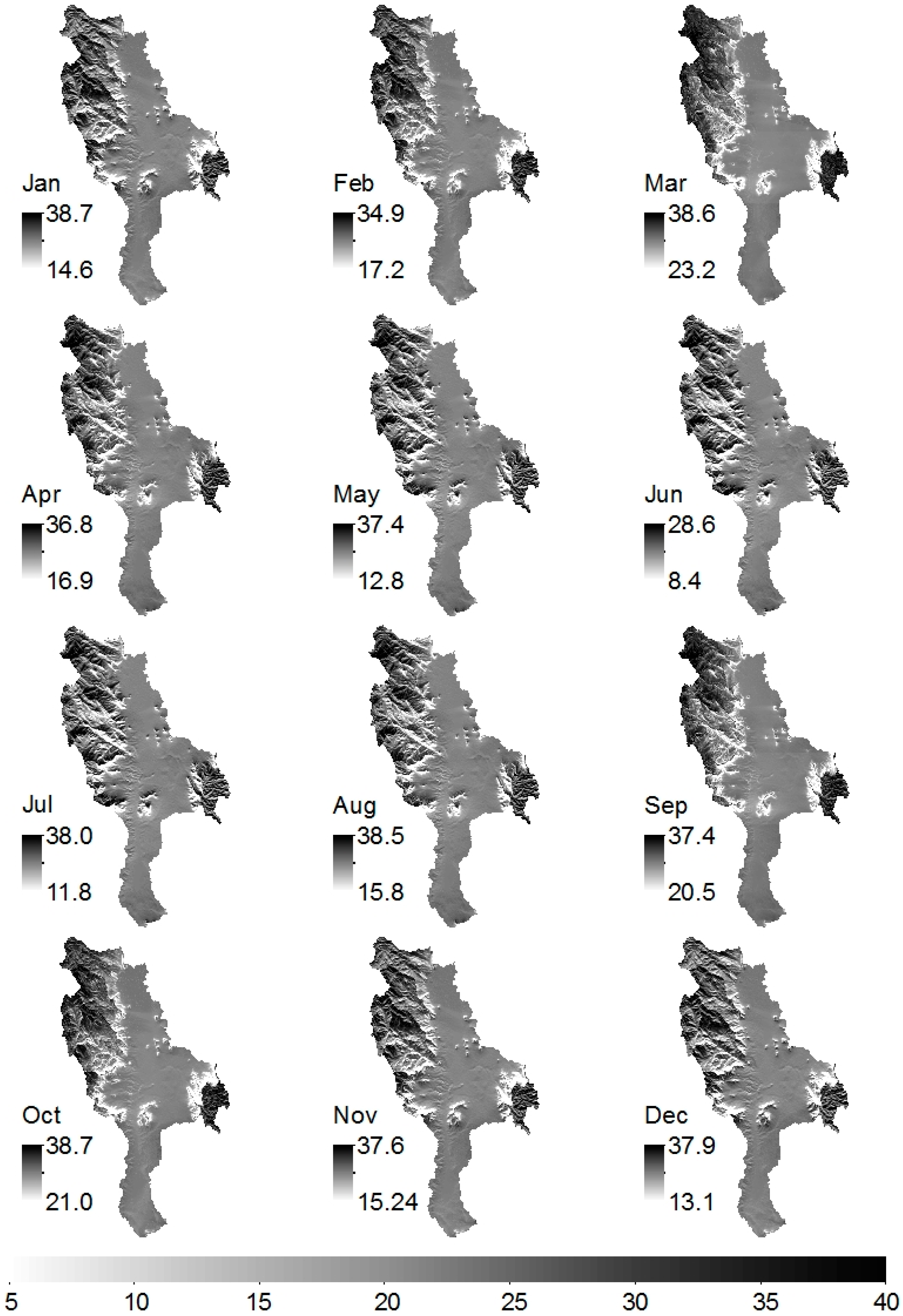
3.2. Spatial Modelling and Mapping of Rainfall, ETo, and Temperature
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trenberth, K.E.; Smith, L.; Qian, T.T.; Dai, A.; Fasullo, J. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. J. Hydrometeorol. 2007, 8, 758–769. [Google Scholar] [CrossRef]
- Ward, A.D.; Trimble, S.W. Environmental Hydrology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 1–118. ISBN 1566706165. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper 56; Food and Agriculture Organization: Rome, Italy, 1998; pp. 26–40. [Google Scholar]
- Barry, R.G. Mountain Weather & Climate, 2nd ed.; Routledge: New York, NY, USA, 1992; pp. 1–180. ISBN 0415071127. [Google Scholar]
- Diaz, H.F. Climate Variability and Change in High Elevation Regions: Past, Present & Future, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 1–4. ISBN 1402013868. [Google Scholar]
- Whiteman, C.D. Mountain Meteorology: Fundamentals and Applications, 1st ed.; Oxford University Press: New York, NY, USA, 2000; pp. 3–204. ISBN 0195132718. [Google Scholar]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists, 1st ed.; Geoscience Australia: Canberra, Australia, 2008; pp. 4–95. ISBN 1921498307. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation, 1st ed.; Oxford University Press: New York, NY, USA, 1997; pp. 125–436. ISBN 0195115384. [Google Scholar]
- Mair, A.; Fares, A. Comparison of Rainfall Interpolation Methods in a Mountainous Region of a Tropical Island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Martínez-Cob, A. Multivariate geostatistical analysis of evapotranspiration and precipitation in mountainous terrain. J. Hydrol. 1996, 174, 19–35. [Google Scholar] [CrossRef]
- Chapman, L.; Thornes, J.E. The Use of Geographic Information Systems in Climatology and Meteorology. Prog. Phys. Geogr. 2003, 27, 313–330. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Phillips, D.L. A Statistical-Topographic Model for Mapping Climatological Precipitation over Mountainous Terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Gómez, J.; Etchevers, J.; Monterroso, A.; Gay, C.; Campo, J.; Martínez, M. Spatial estimation of mean temperature and precipitation in areas of scarce meteorological information. Atmosfera 2008, 21, 35–56. [Google Scholar]
- Vicente-Serrano, S.M.; Lanjeri, S.; Lopez-Moreno, J. Comparison of different procedures to map reference evapotranspiration using geographical information systems and regression-based techniques. Int. J. Climatol. 2007, 27, 1103–1118. [Google Scholar] [CrossRef]
- Basist, A.; Bell, G.D.; Meentemeyer, V. Statistical Relationships between Topography and Precipitation Patterns. J. Clim. 1994, 7, 1305–1315. [Google Scholar] [CrossRef]
- Camberlin, P.; Philippon, N. The East African March-May Rainy Season: Associated Atmospheric Dynamics and Predictability over the 1968–97 Period. J. Clim. 2002, 15, 1002–1019. [Google Scholar] [CrossRef]
- Mutai, C.C.; Ward, M.N. East African Rainfall and the Tropical Circulation/Convection on Intraseasonal to Interannual Timescales. J. Clim. 2000, 13, 3915–3939. [Google Scholar] [CrossRef]
- Slingo, J.; Spencer, H.; Hoskins, B.; Berrisford, P.; Black, E. The meteorology of the Western Indian Ocean, and the influence of the East African Highlands. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2005, 363, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Kijazi, A.L.; Reason, C.J.C. Relationships between intraseasonal rainfall variability of coastal Tanzania and ENSO. Theor. Appl. Climatol. 2005, 82, 153–176. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.S.; Terray, P.; Guilyardi, E.; Gualdi, S.; Delecluse, P. Two Independent Triggers for the Indian Ocean Dipole/Zonal Mode in a Coupled GCM. J. Clim. 2005, 18, 3428–3449. [Google Scholar] [CrossRef]
- Latif, M.; Dommenget, D.; Dima, M.; Grotzner, A. The Role of Indian Ocean Sea Surface Temperature in Forcing East African Rainfall Anomalies during December–January 1997/98. J. Clim. 1999, 12, 3497–3504. [Google Scholar] [CrossRef]
- Hastenrath, S.; Polzin, D.; Mutai, C. Diagnosing the 2005 Drought in Equatorial East Africa. J. Clim. 2007, 20, 4628–4637. [Google Scholar] [CrossRef]
- Bjørndalen, J.E. Tanzania’s vanishing rain forests—Assessment of nature conservation values, biodiversity and importance for water catchment. Agric. Ecosyst. Environ. 1992, 40, 313–334. [Google Scholar] [CrossRef]
- PBWO; IUCN. Pangani River System; State of the Basin Report; PWBO: Moshi, Tanzania; IUCN Eastern Africa Regional Program: Nairobi, Kenya, 2007. [Google Scholar]
- Xu, C.Y.; Tunemar, L.; Chen, Y.Q.D.; Singh, V.P. Evaluation of seasonal and spatial variations of lumped water balance model sensitivity to precipitation data errors. J. Hydrol. 2006, 324, 80–93. [Google Scholar] [CrossRef]
- Dingman, S.L.; Seelyreynolds, D.M.; Reynolds, R.C. Application of Kriging to Estimating Mean Annual Precipitation in a Region of Orographic Influence. Water Resour. Bull. 1988, 24, 329–339. [Google Scholar] [CrossRef]
- Reek, T.; Doty, S.R.; Owen, T.W. A Deterministic Approach to the Validation of Historical Daily Temperature and Precipitation Data from the Cooperative Network. Am. Meteorol. Soc. 1992, 73, 753–762. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q.; Qian, W. Quality Control of Daily Meteorological Data in China, 1951–2000: A New Dataset. Int. J. Climatol. 2004, 24, 853–870. [Google Scholar] [CrossRef]
- Begert, M.; Schlegel, T.; Kirchhofer, W. Homogeneous Temperature and Precipitation Series of Switzerland from 1864 to 2000. Int. J. Climatol. 2005, 25, 65–80. [Google Scholar] [CrossRef]
- Keiser, D.T.; Griffiths, J.F. Problems Associated with Homogeneity Testing in Climate Variation Studies: A Case Study of Temperature in the Northern Great Plains, USA. Int. J. Climatol. 1997, 17, 497–510. [Google Scholar] [CrossRef]
- Mitchell, T.D.; Jones, P.D. An Improved Method of Constructing a Database of Monthly Climate Observations and Associated High-Resolution Grids. Int. J. Climatol. 2005, 25, 693–712. [Google Scholar] [CrossRef]
- Lanzante, J.R. Resistant, Robust and Non-Parametric Techniques for the Analysis of Climate Data: Theory and Examples, Including Applications to Historical Radiosonde Station Data. Int. J. Climatol. 1996, 16, 1197–1226. [Google Scholar] [CrossRef]
- Shiffler, R.E. Maximum Z-Scores and Outliers. Am. Stat. 1988, 42, 79–80. [Google Scholar]
- Smith, R.B. The Influence of Mountains on the Atmosphere. Adv. Geophys. 1979, 21, 87–230. [Google Scholar]
- Jiang, Q.F. Moist dynamics and orographic precipitation. Tellus 2003, 55, 301–316. [Google Scholar] [CrossRef]
- Ninyerola, M.; Pons, X.; Roure, J.M. Monthly precipitation mapping of the Iberian Peninsula using spatial interpolation tools implemented in a Geographic Information System. Theor. Appl. Climatol. 2007, 89, 195–209. [Google Scholar] [CrossRef]
- Marquinez, J.; Lastra, J.; Garcia, P. Estimation models for precipitation in mountainous regions: The use of GIS and multivariate analysis. J. Hydrol. 2003, 270, 1–11. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Fu, P.D.; Rich, P.M. A geometric solar radiation model with applications in agriculture and forestry. Comput. Electron. Agric. 2002, 37, 25–35. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley & Sons: New York, USA, 1998; Volume 1, pp. 15–460. ISBN 0471170828. [Google Scholar]
- Kotz, S.; Balakrishnan, N.; Johnson, N.L. Continuous Multivariate Distributions: Models and Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2004; Volume 1, ISBN 0471654035. [Google Scholar]
- Häntzschel, J.; Goldberg, V.; Bernhofer, C. GIS-based regionalisation of radiation, temperature and coupling measures in complex terrain for low mountain ranges. Meteorol. Appl. 2005, 12, 33–42. [Google Scholar] [CrossRef]
- Smith, R.B.; Barstad, I. A Linear Theory of Orographic Precipitation. J. Atmos. Sci. 2004, 61, 1377–1391. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng.-ASCE 2003, 129, 53–63. [Google Scholar] [CrossRef]
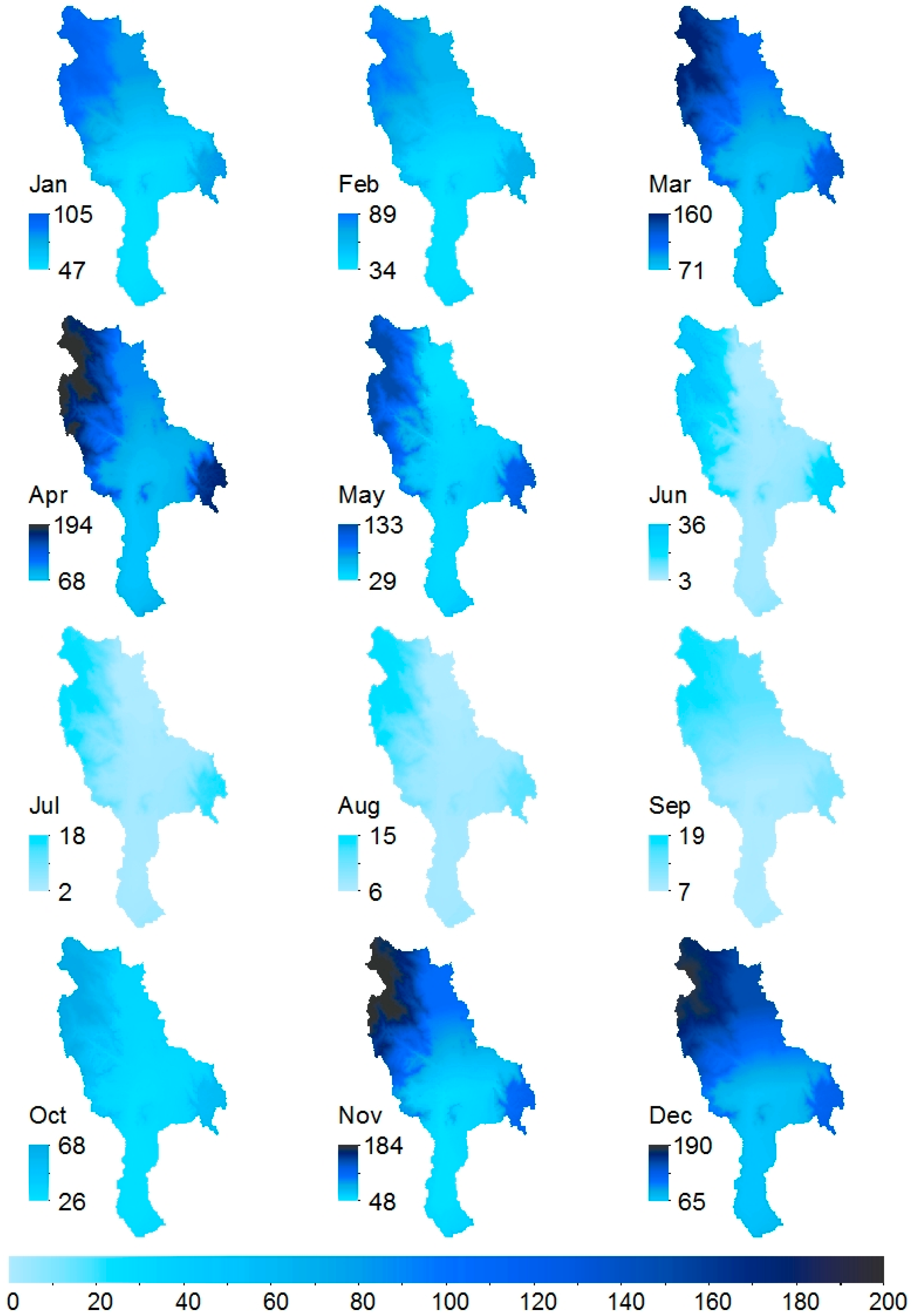

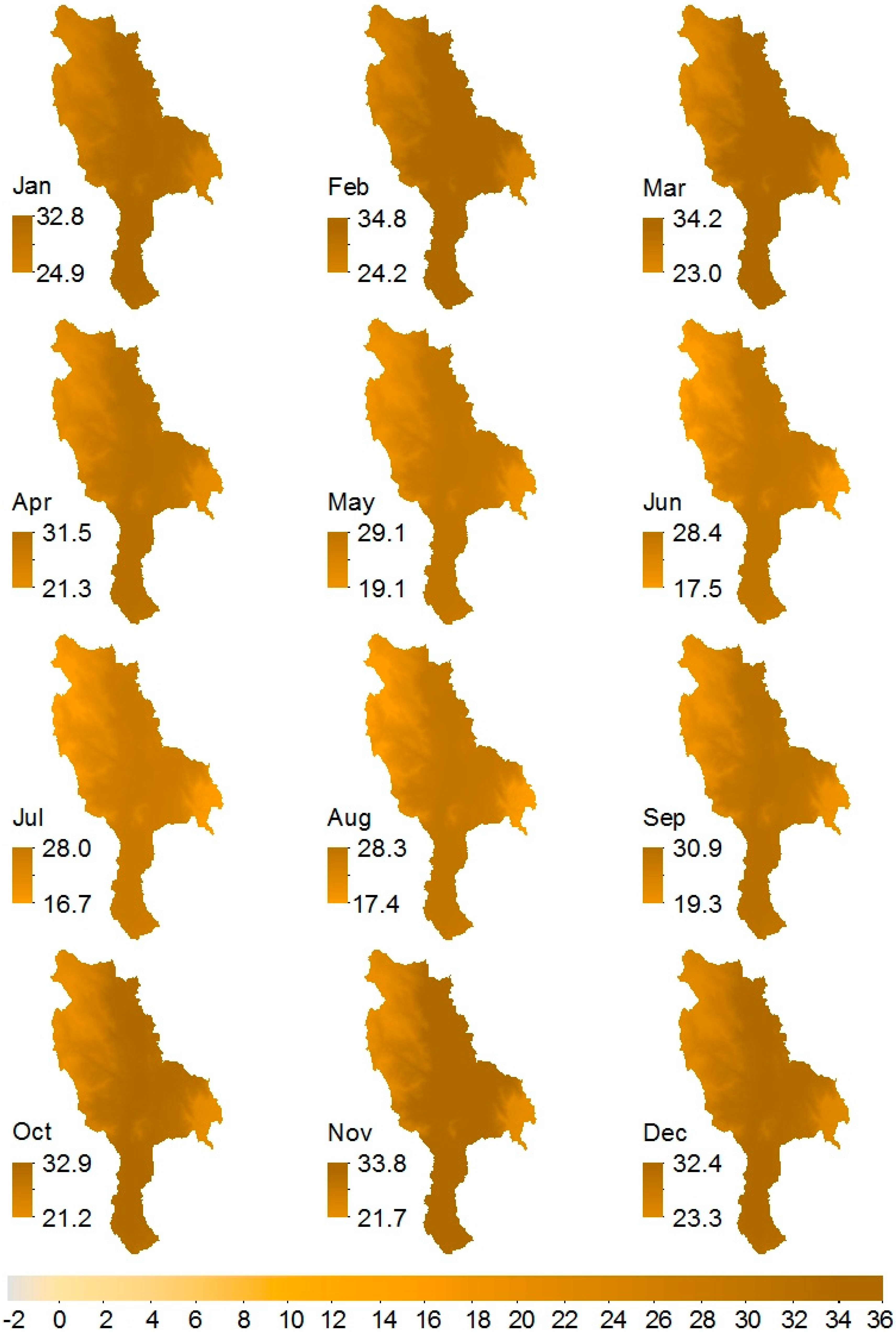
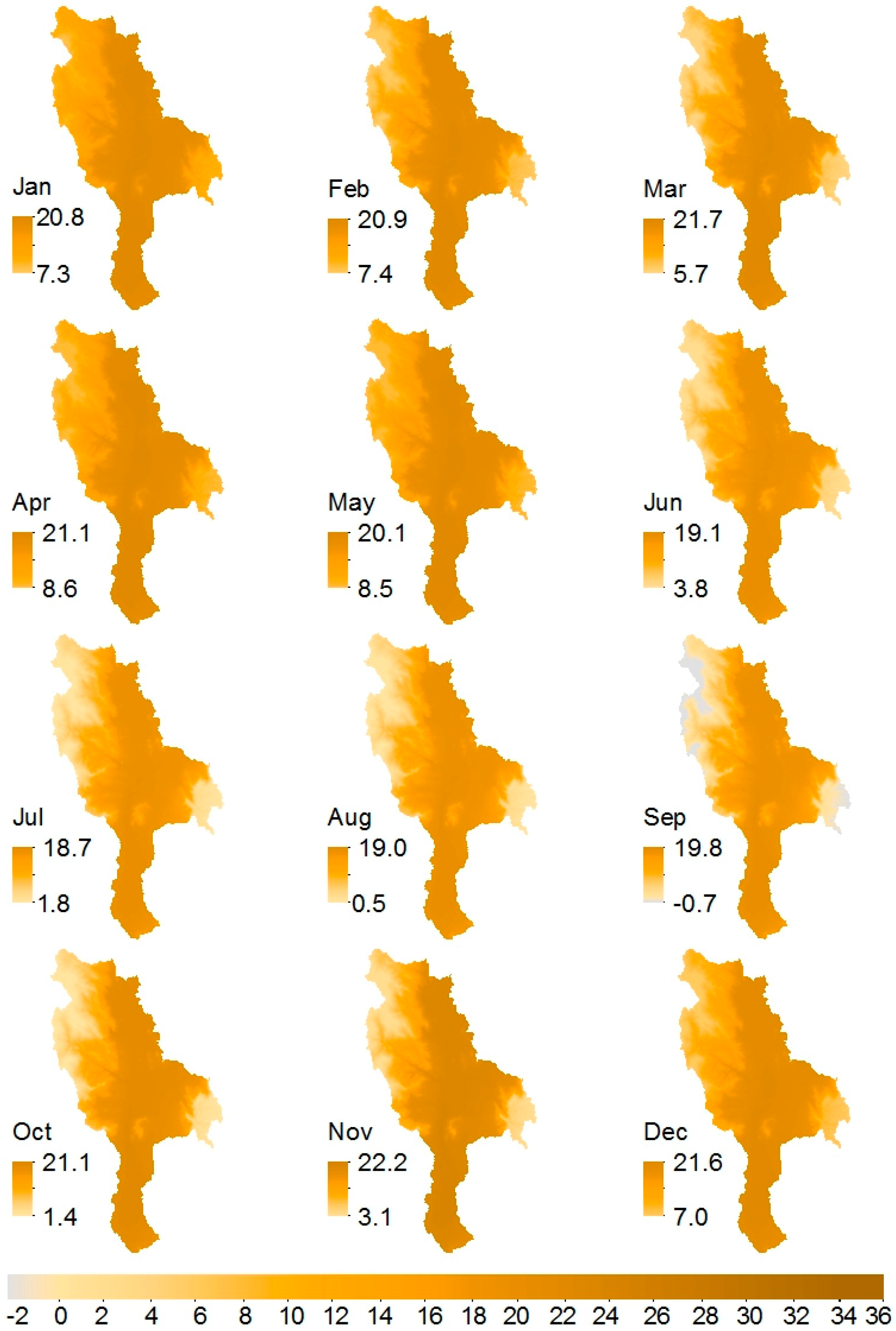
| Station Number | Gauge Name | Gauge ID | Elevation (m a.s.l.) | Latitude | Longitude | Record Length | Missing (%) |
|---|---|---|---|---|---|---|---|
| 1 | Suji Mission l | 9437004 | 1371 | −4.317 | 37.850 | 1923−2008 | 18 (32) |
| 2 | Mazinde Factory l | 9438019 | 1996 | −4.700 | 38.217 | 1929−2010 | 6 (7) |
| 3 | Hassan Sisal Estate l | 9437001 | 914 | −4.333 | 37.850 | 1933−2007 | 21 (29) |
| 4 | Same Met l | 9437003 | 860 | −4.083 | 37.733 | 1934−2011 | 1 (0) |
| 5 | Buiko Hydromet l | 9438009 | 534 | −4.650 | 38.050 | 1962−2005 | 1 (11) |
| 6 | Shume Forest l | 9438012 | 1889 | −4.700 | 38.200 | 1937−1997 | 5 (6) |
| 7 | Gologolo Forest House l | 9438047 | 1920 | −4.700 | 38.233 | 1964−2009 | 41 (41) |
| 8 | Gologolo l | 9438037 | 1882 | −4.700 | 38.233 | 1955−1986 | 7 (56) |
| 9 | Mlomboza r | 9438046 | 2286 | −4.700 | 38.250 | 1964−1997 | 1 (29) |
| 10 | Mtae Pr Court l | 9438066 | 1559 | −4.483 | 38.233 | 1971−2010 | 22 (22) |
| 11 | Shagavu Forest Nursery l | 9438049 | 1981 | −4.533 | 38.233 | 1964−2011 | 6 (6) |
| 12 | Shagavu l | 9438034 | 1828 | −4.533 | 38.217 | 1955−2011 | 5 (3) |
| 13 | Gonja Estate w | 9438011 | 584 | −4.300 | 38.033 | 1937−1988 | 10 (50) |
| 14 | Kalimawe w | 9438040 | 488 | −4.417 | 38.083 | 1963−2010 | 40 (41) |
| 15 | Ndungu Sisal Estate w | 9438051 | 533 | −4.367 | 38.050 | 1966−2002 | 16 (34) |
| 16 | Tia Dam w | 9437010 | 1676 | −4.233 | 37.950 | 1962−2010 | 32 (31) |
| 101 | * Lushoto Hydromet | 9438076 | 1631 | −4.783 | 38.267 | 1989−1994 | 1 (1) |
| 102 | * Moshi Airport | 9337004 | 854 | −3.350 | 37.333 | 1958−1993 | 2 (18) |
| 103 | * Same Met | 9437003 | 860 | −4.083 | 37.733 | 1958−2010 | 8 (2) |
| January | February | March | April | May | June | July | August | September | October | November | December | Annual Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | MV ± SD | |
| Station Number | Rainfall (mm) | ||||||||||||
| 1 | 92 ± 71 | 72 ± 53 | 142 ± 97 | 120 ± 61 | 52 ± 35 | 12 ± 14 | 5 ± 7 | 8 ± 11 | 10 ± 15 | 31 ± 40 | 129 ± 105 | 165 ± 89 | 838 ± 50 |
| 2 | 55 ± 58 | 57 ± 46 | 82 ± 62 | 142 ± 69 | 131 ± 77 | 31 ± 31 | 16 ± 21 | 15 ± 19 | 13 ± 29 | 41 ± 57 | 66 ± 46 | 75 ± 50 | 724 ± 47 |
| 3 | 60 ± 50 | 43 ± 35 | 87 ± 79 | 71 ± 45 | 40 ± 28 | 7 ± 17 | 5 ± 10 | 5 ± 15 | 8 ± 15 | 23 ± 29 | 63 ± 62 | 81 ± 59 | 493 ± 37 |
| 4 | 54 ± 53 | 43 ± 41 | 91 ± 89 | 107 ± 62 | 64 ± 52 | 12 ± 17 | 4 ± 7 | 10 ± 15 | 13 ± 22 | 39 ± 43 | 62 ± 62 | 63 ± 51 | 562 ± 43 |
| 5 | 42 ± 46 | 34 ± 32 | 59 ± 55 | 71 ± 46 | 46 ± 38 | 10 ± 13 | 7 ± 14 | 6 ± 10 | 4 ± 10 | 27 ± 34 | 32 ± 41 | 45 ± 56 | 383 ± 33 |
| 6 | 74 ± 60 | 56 ± 37 | 129 ± 83 | 149 ± 71 | 72 ± 40 | 14 ± 16 | 8 ± 17 | 5 ± 7 | 10 ± 18 | 37 ± 36 | 91 ± 59 | 95 ± 57 | 740 ± 42 |
| 7 | 64 ± 47 | 53 ± 39 | 101 ± 67 | 115 ± 59 | 67 ± 37 | 17 ± 16 | 12 ± 25 | 8 ± 19 | 13 ± 29 | 38 ± 34 | 85 ± 58 | 76 ± 56 | 649 ± 41 |
| 8 | 89 ± 80 | 75 ± 62 | 134 ± 91 | 170 ± 91 | 90 ± 59 | 22 ± 26 | 13 ± 26 | 11 ± 19 | 15 ± 33 | 50 ± 31 | 116 ± 53 | 102 ± 54 | 887 ± 52 |
| 9 | 86 ± 71 | 83 ± 51 | 141 ± 92 | 172 ± 70 | 142 ± 113 | 41 ± 41 | 20 ± 30 | 14 ± 23 | 15 ± 23 | 54 ± 58 | 113 ± 102 | 129 ± 90 | 1010 ± 64 |
| 10 | 47 ± 41 | 43 ± 36 | 75 ± 67 | 144 ± 61 | 92 ± 58 | 13 ± 13 | 9 ± 10 | 12 ± 14 | 15 ± 24 | 51 ± 46 | 100 ± 57 | 147 ± 101 | 748 ± 44 |
| 11 | 83 ± 58 | 61 ± 45 | 120 ± 72 | 140 ± 56 | 55 ± 36 | 7 ± 9 | 4 ± 5 | 5 ± 7 | 9 ± 13 | 52 ± 51 | 127 ± 71 | 167 ± 93 | 830 ± 43 |
| 12 | 102 ± 81 | 75 ± 55 | 132 ± 68 | 150 ± 51 | 61 ± 39 | 7 ± 10 | 4 ± 6 | 7 ± 9 | 9 ± 14 | 53 ± 51 | 140 ± 71 | 186 ± 108 | 926 ± 47 |
| 13 | 107 ± 67 | 84 ± 77 | 141 ± 124 | 118 ± 95 | 44 ± 36 | 8 ± 13 | 4 ± 8 | 9 ± 12 | 18 ± 24 | 39 ± 36 | 148 ± 82 | 229 ± 128 | 949 ± 59 |
| 14 | 47 ± 51 | 40 ± 36 | 63 ± 56 | 70 ± 51 | 25 ± 21 | 4 ± 5 | 2 ± 3 | 5 ± 6 | 13 ± 36 | 21 ± 15 | 38 ± 36 | 61 ± 45 | 389 ± 30 |
| 15 | 74 ± 84 | 62 ± 57 | 93 ± 98 | 86 ± 67 | 32 ± 31 | 3 ± 8 | 1 ± 4 | 3 ± 6 | 11 ± 20 | 28 ± 31 | 85 ± 77 | 127 ± 93 | 605 ± 48 |
| 16 | 117 ± 127 | 81 ± 75 | 153 ± 96 | 172 ± 70 | 62 ± 50 | 11 ± 16 | 5 ± 6 | 13 ± 16 | 22 ± 29 | 69 ± 59 | 244 ± 172 | 251 ± 162 | 1200 ± 73 |
| Maximum Temperature (°C) | |||||||||||||
| 101 | 28.1 ± 1.0 | 28.5 ± 0.8 | 27.6 ± 0.9 | 25.4 ± 0.4 | 23.2 ± 0.7 | 21.9 ± 0.6 | 21.4 ± 0.4 | 21.9 ± 0.4 | 23.9 ± 0.3 | 26.0 ± 0.6 | 26.6 ± 0.4 | 27.0 ± 0.4 | |
| 102 | 31.3 ± 1.4 | 32.8 ± 1.2 | 32.2 ± 1.8 | 29.7 ± 1.3 | 27.3 ± 1.1 | 26.0 ± 0.4 | 25.5 ± 0.3 | 26.0 ± 0.5 | 28.5 ± 0.4 | 30.8 ± 0.5 | 31.9 ± 0.7 | 31.1 ± 0.8 | |
| 103 | 30.9 ± 1.6 | 32.4 ± 1.2 | 31.7 ± 1.5 | 29.1 ± 1.0 | 26.7 ± 1.0 | 26.2 ± 0.5 | 25.8 ± 0.3 | 26.1 ± 0.6 | 28.2 ± 0.4 | 30.2 ± 0.5 | 30.7 ± 0.8 | 29.9 ± 1.1 | |
| Minimum Temperature (°C) | |||||||||||||
| 101 | 12.9 ± 1.0 | 12.9 ± 0.3 | 12.2 ± 0.5 | 13.7 ± 0.7 | 13.2 ± 0.4 | 10.1 ± 1.1 | 8.7 ± 0.9 | 8.0 ± 0.5 | 7.6 ± 0.3 | 9.5 ± 1.4 | 10.8 ± 0.6 | 12.8 ± 0.9 | |
| 102 | 17.7 ± 0.5 | 17.8 ± 0.9 | 18.5 ± 0.4 | 19.1 ± 0.2 | 18.5 ± 0.2 | 16.8 ± 0.4 | 16.0 ± 0.5 | 15.6 ± 0.5 | 16.0 ± 0.7 | 17.3 ± 0.4 | 18.3 ± 0.4 | 18.4 ± 0.7 | |
| 103 | 18.4 ± 1.0 | 18.4 ± 0.9 | 18.3 ± 1.0 | 17.9 ± 0.8 | 16.9 ± 0.9 | 15.2 ± 0.9 | 14.4 ± 0.9 | 14.6 ± 1.0 | 15.1 ± 0.8 | 16.8 ± 1.0 | 18.1 ± 0.7 | 18.6 ± 0.8 | |
| Rainfall (mm) | Temperature (°C) | |||||||
|---|---|---|---|---|---|---|---|---|
| Leeward | Windward | Maximum | Minimum | |||||
| R2 | F | R2 | F | R2 | F | R2 | F | |
| January | 0.32 (0.28) | 81.0 | 0.17 (0.47) | 17.8 | 0.99 | 28.6 | 0.98 | 33.1 |
| February | 0.53 (0.43) | 128.9 | 0.36 (0.28) | 29.8 | 0.99 | 38.6 | 0.98 | 39.3 |
| March | 0.38 (0.30) | 145.9 | 0.43 (0.48) | 76.3 | 0.99 | 38.5 | 0.99 | 27.1 |
| April | 0.76 (0.72) | 543.7 | 0.83 (0.85) | 333.9 | 0.98 | 27.9 | 0.96 | 20.1 |
| May | 0.42 (0.31) | 187.7 | 0.86 (0.89) | 373.2 | 0.98 | 25.9 | 0.93 | 13.1 |
| June | 0.31 (0.18) | 41.1 | 0.79 (0.75) | 94.0 | 0.99 | 68.6 | 0.95 | 20.9 |
| July | 0.35 (0.22) | 24.2 | 0.77 (0.56) | 42.6 | 0.99 | 51.0 | 0.96 | 25.7 |
| August | 0.12 (0.04) | 4.5 | 0.75 (0.65) | 24.0 | 0.99 | 66.6 | 0.98 | 48.4 |
| September | 0.32 (0.25) | 14.2 | 0.15 (0.66) | 2.6 | 0.99 | 92.4 | 0.99 | 65.9 |
| October | 0.52 (0.43) | 84.0 | 0.66 (0.93) | 76.5 | 0.98 | 33.3 | 0.99 | 40.4 |
| November | 0.43 (0.39) | 199.4 | 0.21 (0.80) | 66.1 | 0.95 | 17.2 | 0.99 | 45.4 |
| December | 0.22 (0.22) | 123.0 | 0.05 (0.47) | 14.8 | 0.91 | 9.6 | 0.99 | 44.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mmbando, G.A.; Kleyer, M. Mapping Precipitation, Temperature, and Evapotranspiration in the Mkomazi River Basin, Tanzania. Climate 2018, 6, 63. https://doi.org/10.3390/cli6030063
Mmbando GA, Kleyer M. Mapping Precipitation, Temperature, and Evapotranspiration in the Mkomazi River Basin, Tanzania. Climate. 2018; 6(3):63. https://doi.org/10.3390/cli6030063
Chicago/Turabian StyleMmbando, Godfrey A., and Michael Kleyer. 2018. "Mapping Precipitation, Temperature, and Evapotranspiration in the Mkomazi River Basin, Tanzania" Climate 6, no. 3: 63. https://doi.org/10.3390/cli6030063
APA StyleMmbando, G. A., & Kleyer, M. (2018). Mapping Precipitation, Temperature, and Evapotranspiration in the Mkomazi River Basin, Tanzania. Climate, 6(3), 63. https://doi.org/10.3390/cli6030063




