Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective
Abstract
1. Introduction
2. Data and Methods
3. Results
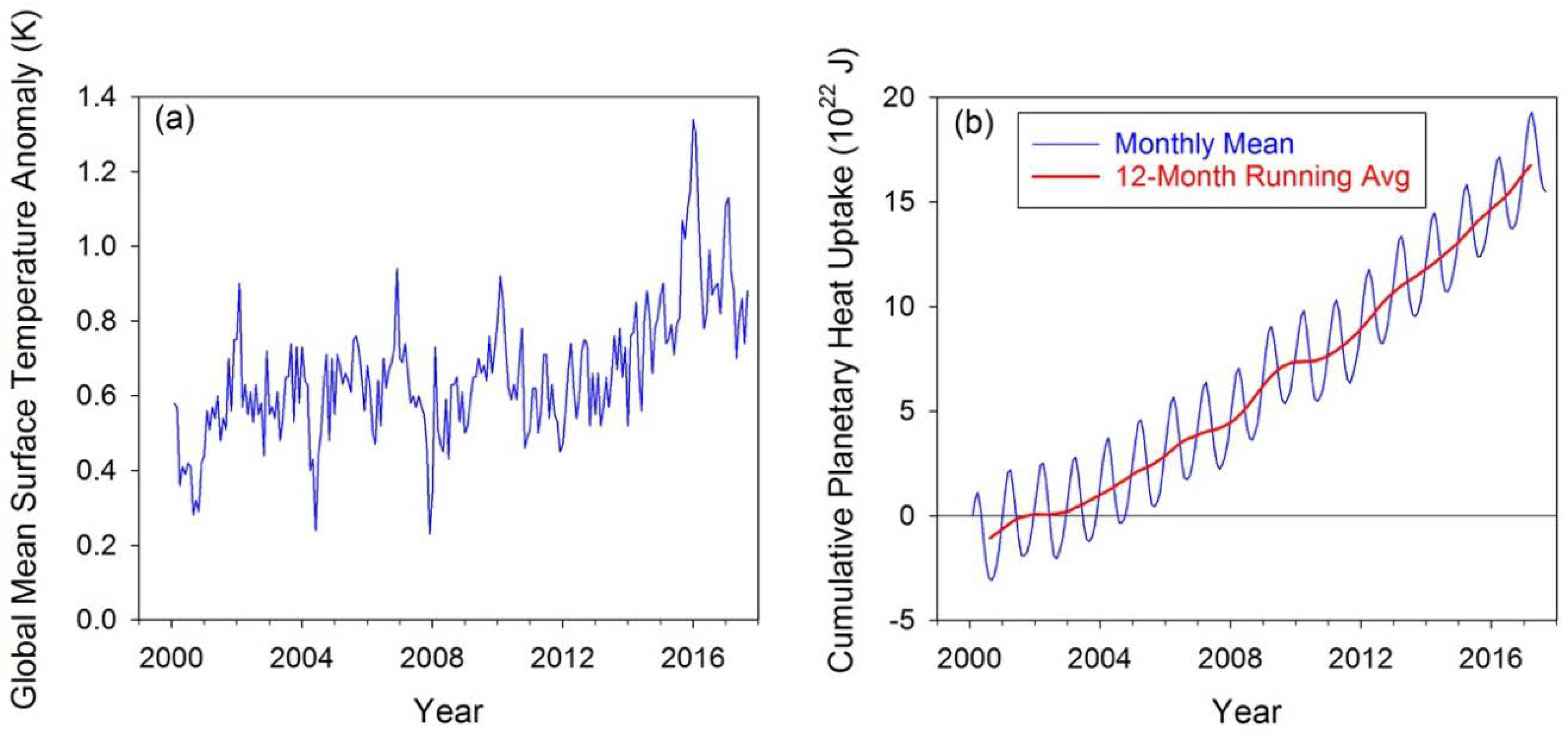
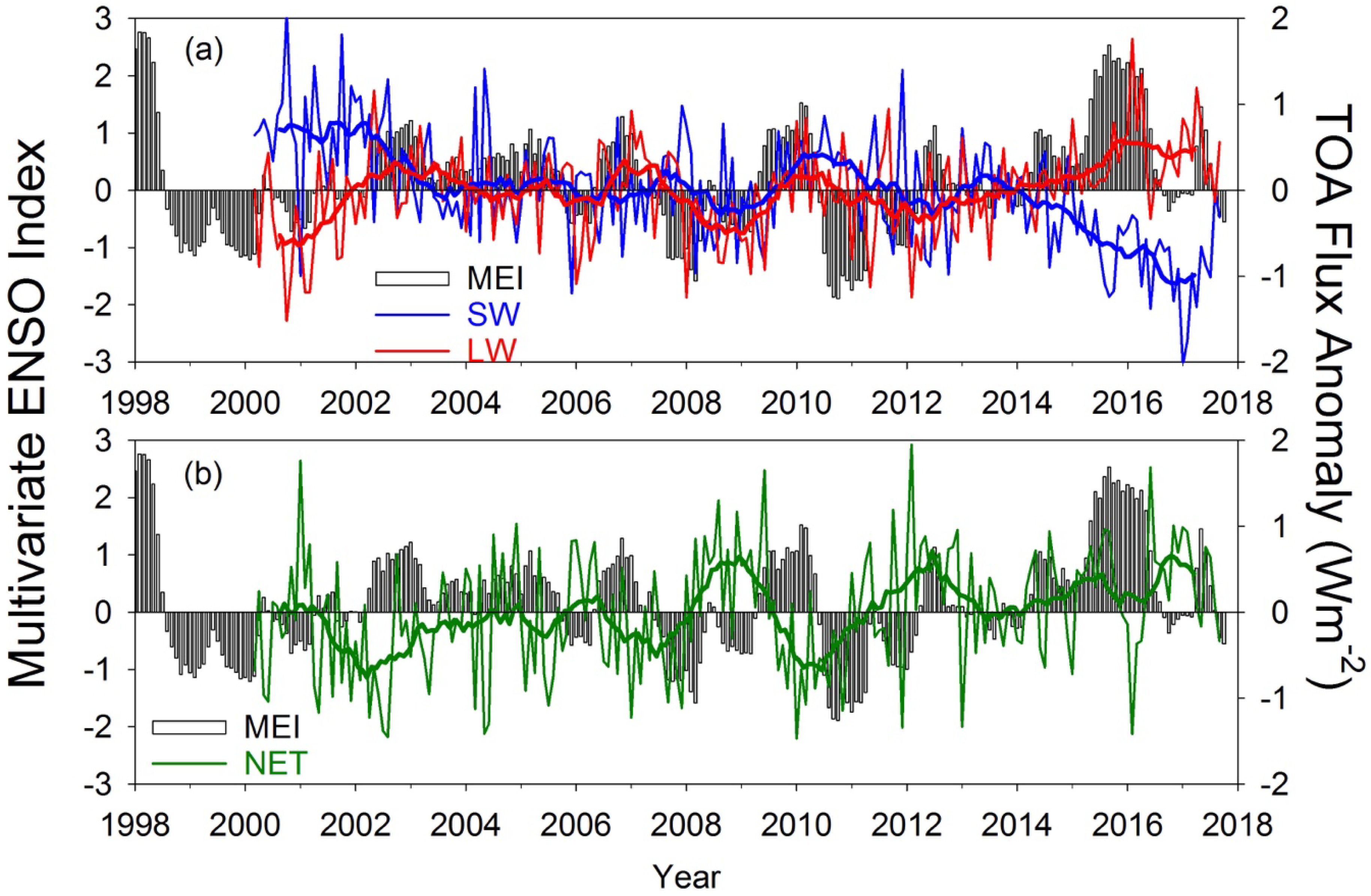
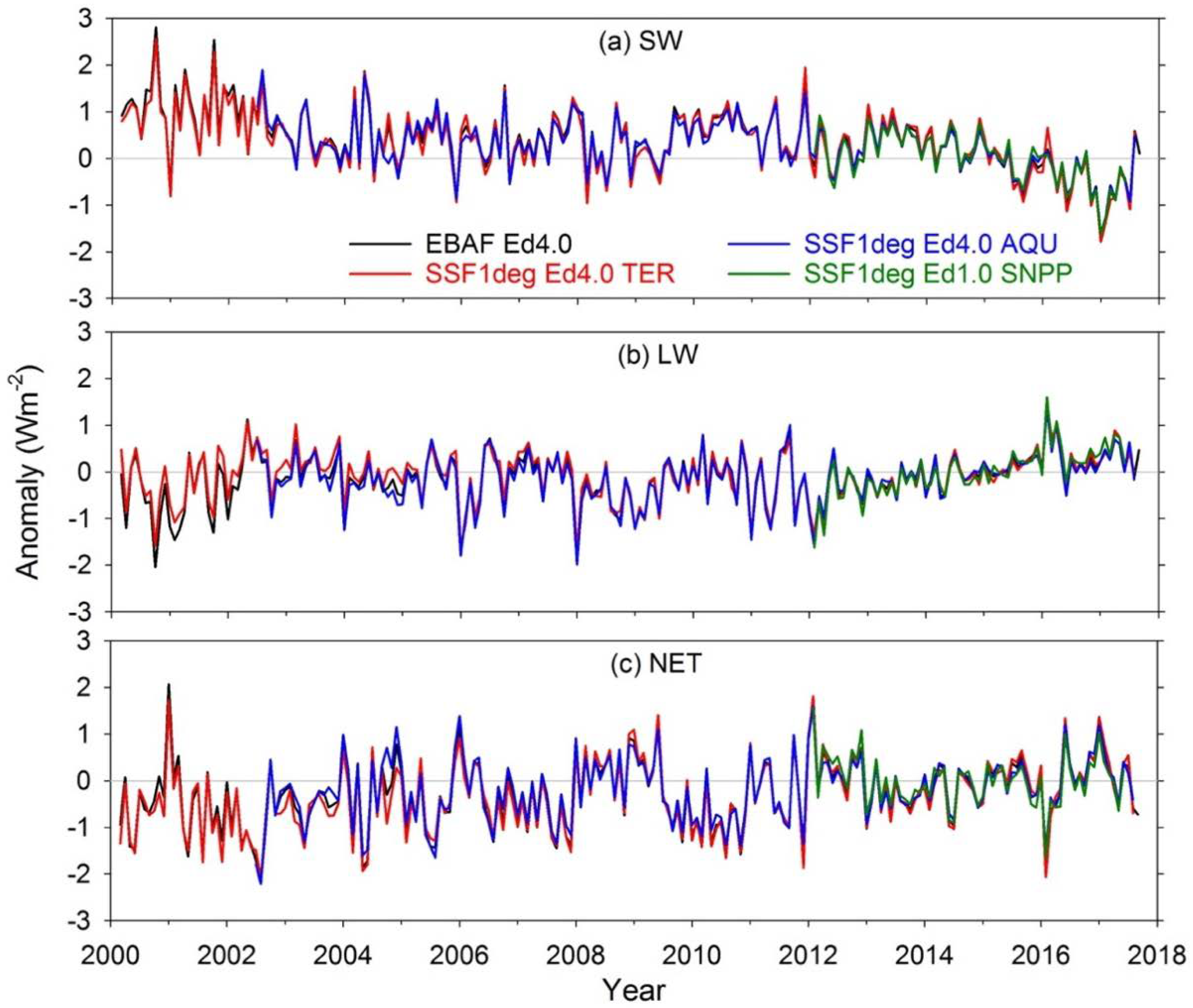
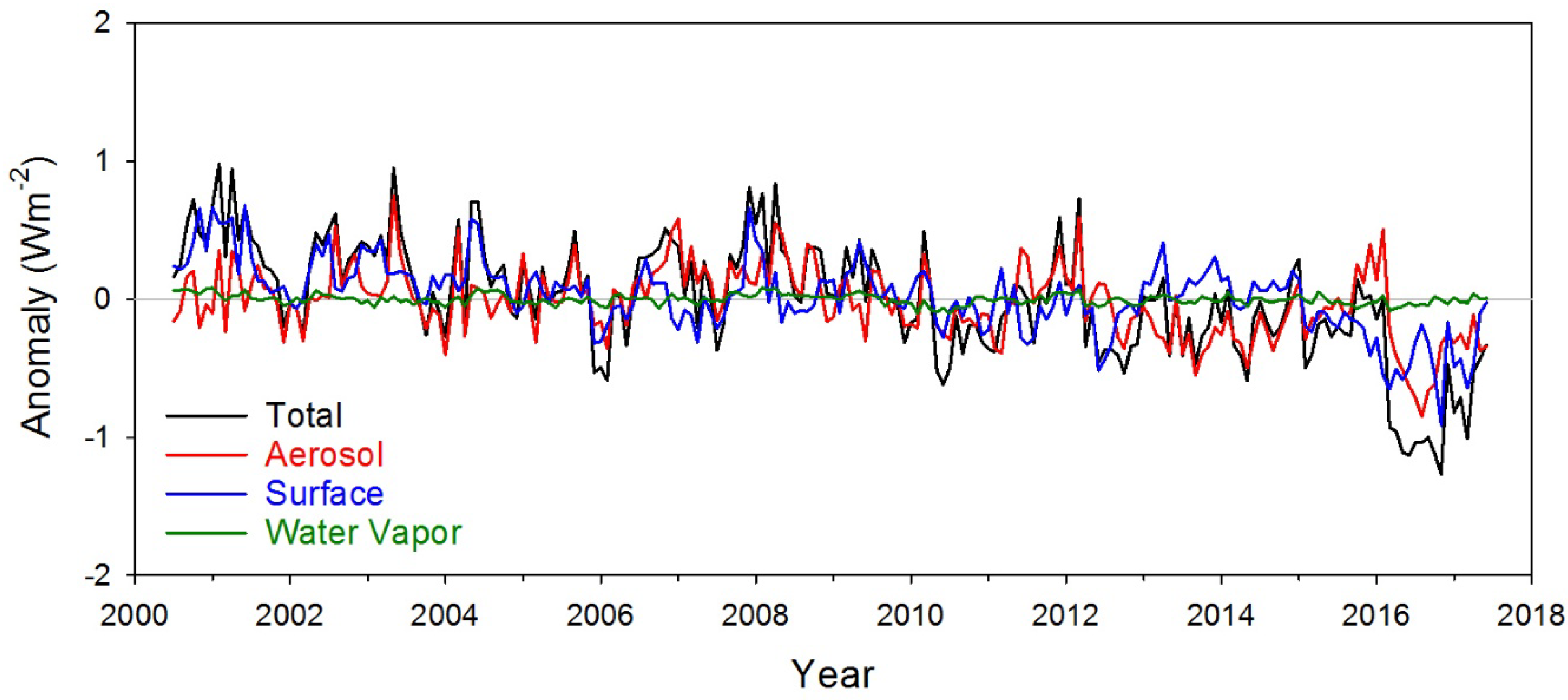
3.1. Global TOA Radiation Variation
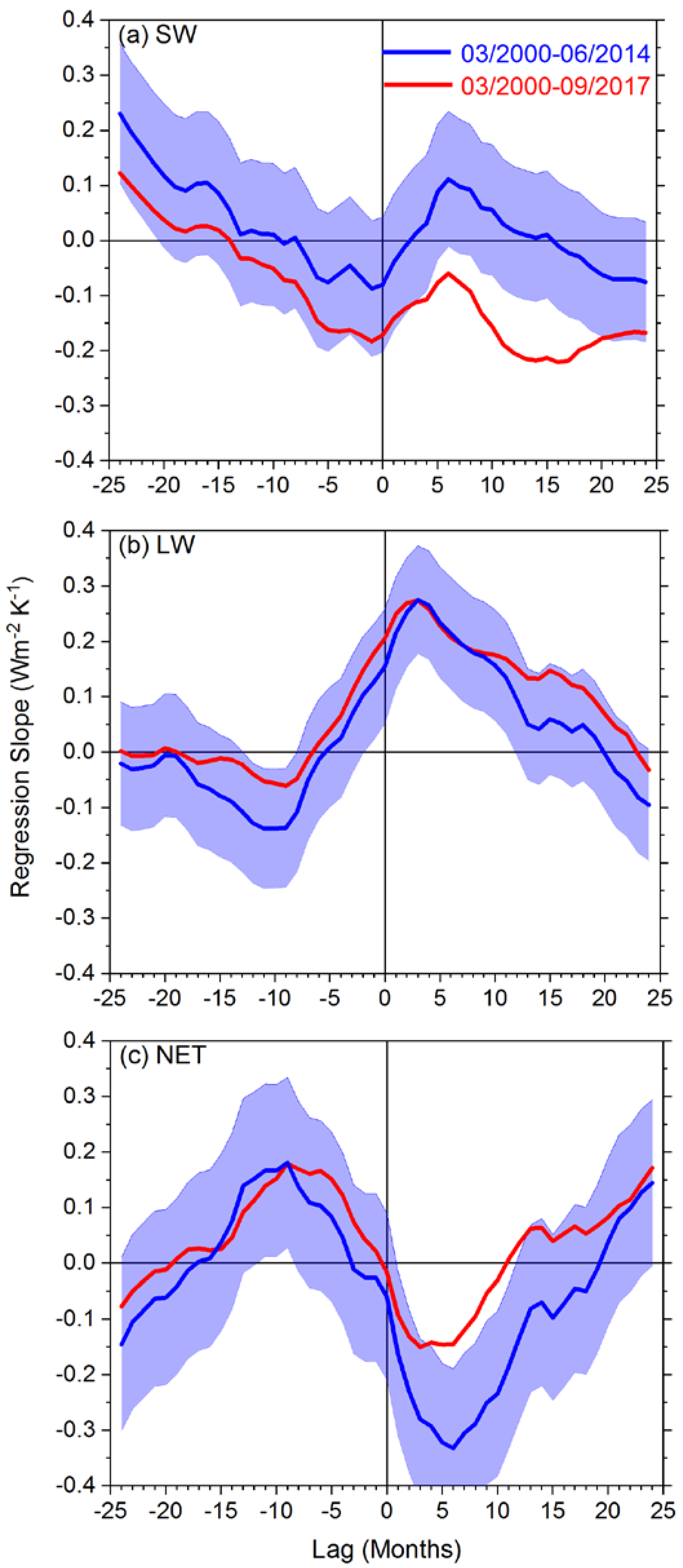
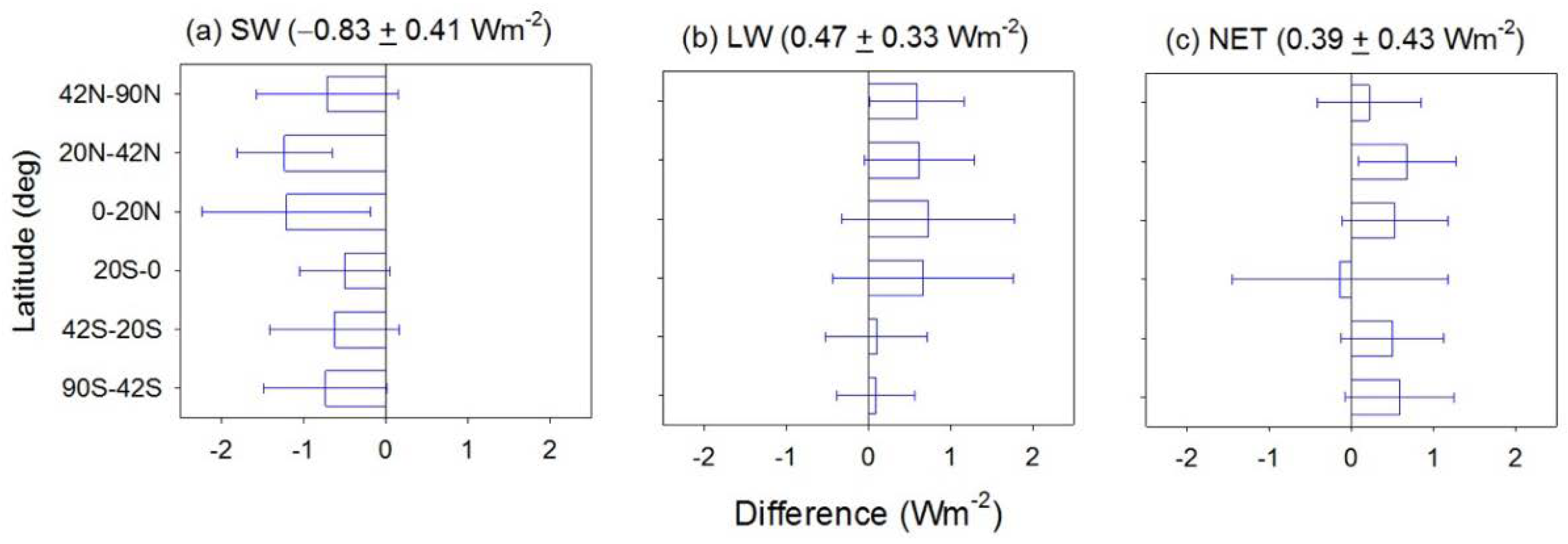
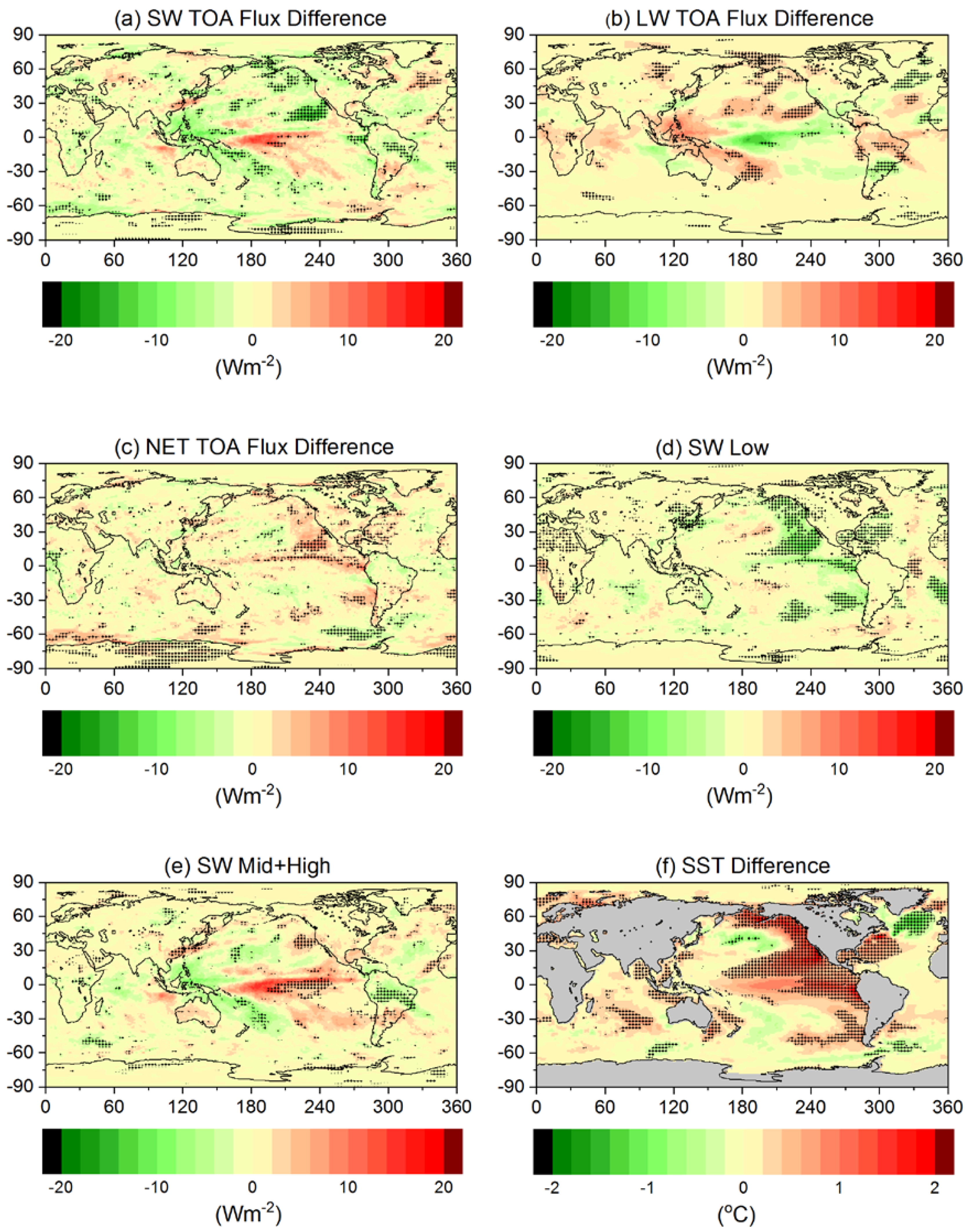
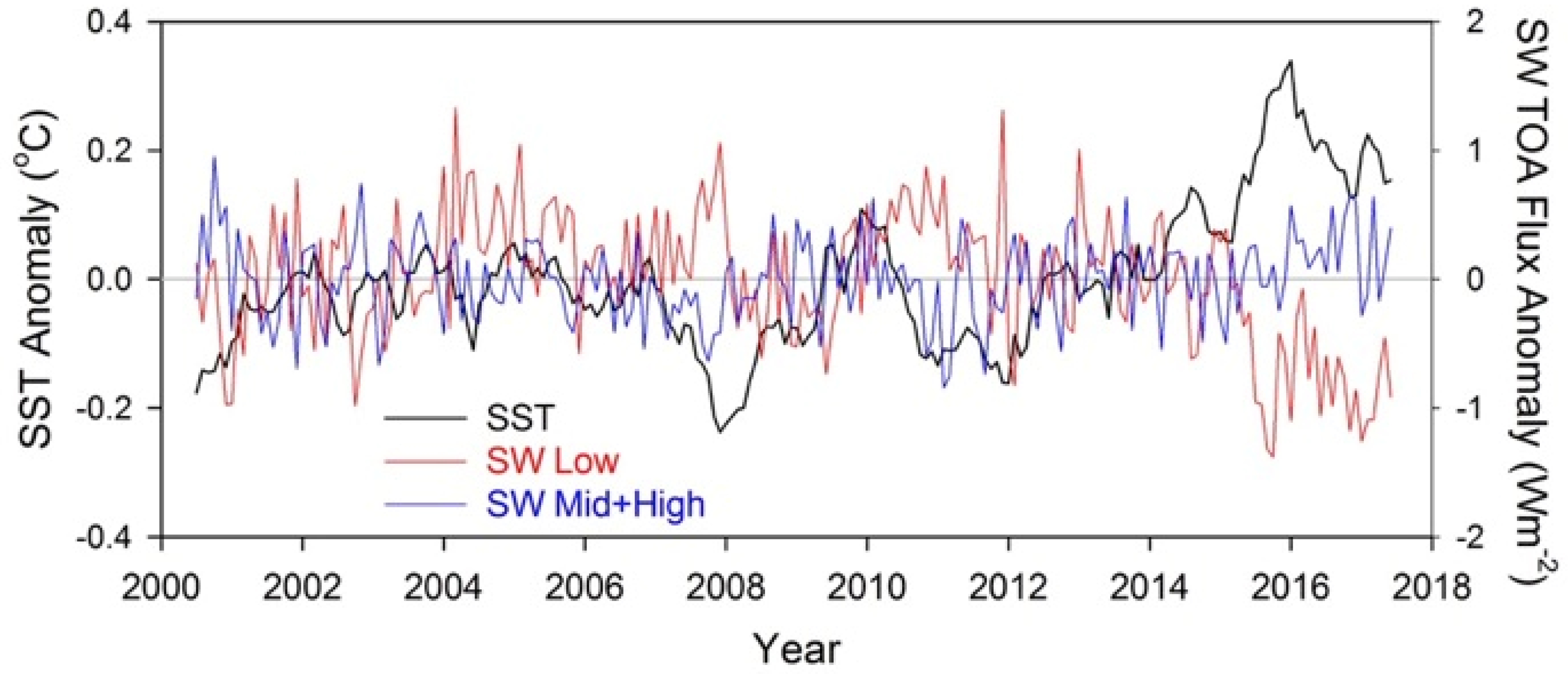
3.2. All-Sky TOA Flux Differences between Post-Hiatus and Hiatus Periods
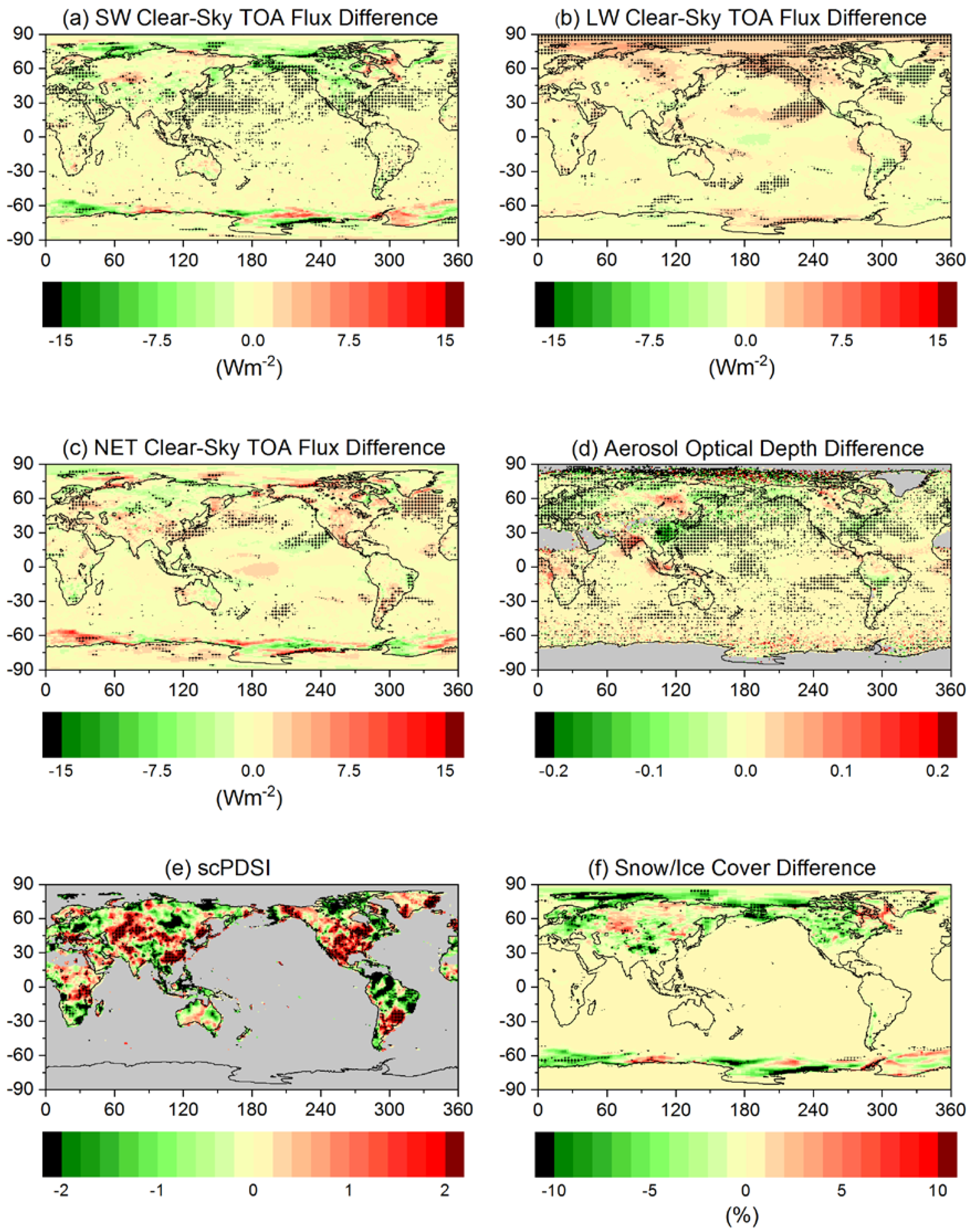
3.3. Clear-Sky TOA Flux Differences between Post-Hiatus and Hiatus Periods
4. Temperature Tendency Difference between Post-Hiatus and Hiatus Periods
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rhein, M.A.; Rintoul, S.R.; Aoki, S.; Campos, E.; Chambers, D.; Feely, R.A.; Gulev, S.; Johnson, G.C.; Josey, S.A.; Kostianoy, A.; et al. Observations: Ocean. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., et al., Eds.; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 255–315. [Google Scholar]
- Hansen, J.; Sato, M.; Kharecha, P.; von Schuckmann, K. Earth’s energy imbalance and implications. Atmos. Chem. Phys. 2011, 11, 13421–13449. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Palmer, M.D.; Trenberth, K.E.; Cazenave, A.; Chambers, D.; Champollion, N.; Hansen, J.; Josey, S.A.; Loeb, N.; Mathieu, P.-P.; et al. An imperative to monitor Earth’s energy imbalance. Nat. Clim. Chang. 2016, 6, 138–144. [Google Scholar] [CrossRef]
- Xie, S.-P.; Kosaka, Y.; Okumura, Y.M. Distinct energy budgets for anthropogenic and natural changes during global warming hiatus. Nat. Geosci. 2016, 9, 29–33. [Google Scholar] [CrossRef]
- Hansen, J. Earth’s Energy Imbalance: Confirmation and Implications. Science 2005, 308, 1431–1435. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term Climate Change: Projections, Commitments and Irreversibility. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., et al., Eds.; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 1029–1136. [Google Scholar]
- Palmer, M.D.; McNeall, D.J.; Dunstone, N.J. Importance of the deep ocean for estimating decadal changes in Earth’s radiation balance: Importance of Deep Ocean. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Yan, X.-H.; Boyer, T.; Trenberth, K.; Karl, T.R.; Xie, S.-P.; Nieves, V.; Tung, K.-K.; Roemmich, D. The global warming hiatus: Slowdown or redistribution?: The Global Warming Hiatus. Earths Future 2016, 4, 472–482. [Google Scholar] [CrossRef]
- Trenberth, K.E. Has there been a hiatus? Science 2015, 349, 691–692. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, D.L.; Tank, A.M.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.A.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., et al., Eds.; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 159–254. [Google Scholar]
- Balmaseda, M.A.; Trenberth, K.E.; Källén, E. Distinctive climate signals in reanalysis of global ocean heat content: Signals in Ocean Heat Content. Geophys. Res. Lett. 2013, 40, 1754–1759. [Google Scholar] [CrossRef]
- Meehl, G.A.; Hu, A.; Arblaster, J.M.; Fasullo, J.; Trenberth, K.E. Externally Forced and Internally Generated Decadal Climate Variability Associated with the Interdecadal Pacific Oscillation. J. Clim. 2013, 26, 7298–7310. [Google Scholar] [CrossRef]
- England, M.H.; McGregor, S.; Spence, P.; Meehl, G.A.; Timmermann, A.; Cai, W.; Gupta, A.S.; McPhaden, M.J.; Purich, A.; Santoso, A. Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat. Clim. Chang. 2014, 4, 222–227. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Balmaseda, M.A. Earth’s Energy Imbalance. J. Clim. 2014, 27, 3129–3144. [Google Scholar] [CrossRef]
- Santer, B.D.; Bonfils, C.; Painter, J.F.; Zelinka, M.D.; Mears, C.; Solomon, S.; Schmidt, G.A.; Fyfe, J.C.; Cole, J.N.S.; Nazarenko, L.; et al. Volcanic contribution to decadal changes in tropospheric temperature. Nat. Geosci. 2014, 7, 185–189. [Google Scholar] [CrossRef]
- Solomon, S.; Daniel, J.S.; Neely, R.R.; Vernier, J.-P.; Dutton, E.G.; Thomason, L.W. The Persistently Variable “Background” Stratospheric Aerosol Layer and Global Climate Change. Science 2011, 333, 866–870. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Zelinka, M.D.; Klein, S.A. Impact of decadal cloud variations on the Earth’s energy budget. Nat. Geosci. 2016, 9, 871–874. [Google Scholar] [CrossRef]
- Bond, N.A.; Cronin, M.F.; Freeland, H.; Mantua, N. Causes and impacts of the 2014 warm anomaly in the NE Pacific: 2014 Warm Anomaly in the NE Pacific. Geophys. Res. Lett. 2015, 42, 3414–3420. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Tseng, Y.-H.; Ding, R.; Huang, X. The warm Blob in the northeast Pacific—The bridge leading to the 2015/16 El Niño. Environ. Res. Lett. 2017, 12, 054019. [Google Scholar] [CrossRef]
- Allan, R.P.; Liu, C.; Loeb, N.G.; Palmer, M.D.; Roberts, M.; Smith, D.; Vidale, P.-L. Changes in global net radiative imbalance 1985–2012. Geophys. Res. Lett. 2014, 41, 5588–5597. [Google Scholar] [CrossRef] [PubMed]
- Loeb, N.G.; Lyman, J.M.; Johnson, G.C.; Allan, R.P.; Doelling, D.R.; Wong, T.; Soden, B.J.; Stephens, G.L. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat. Geosci. 2012, 5, 110–113. [Google Scholar] [CrossRef]
- Johnson, G.C.; Lyman, J.M.; Loeb, N.G. Improving estimates of Earth’s energy imbalance. Nat. Clim. Chang. 2016, 6, 639–640. [Google Scholar] [CrossRef]
- Wong, T.; Wielicki, B.A.; Lee, R.B.; Smith, G.L.; Bush, K.A.; Willis, J.K. Reexamination of the Observed Decadal Variability of the Earth Radiation Budget Using Altitude-Corrected ERBE/ERBS Nonscanner WFOV Data. J. Clim. 2006, 19, 4028–4040. [Google Scholar] [CrossRef]
- Lyman, J.M.; Good, S.A.; Gouretski, V.V.; Ishii, M.; Johnson, G.C.; Palmer, M.D.; Smith, D.M.; Willis, J.K. Robust warming of the global upper ocean. Nature 2010, 465, 334–337. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Conroy, J.L.; Domingues, C.M.; Fasullo, J.T.; Gilson, J.; et al. A review of global ocean temperature observations: Implications for ocean heat content estimates and climate change: Review of Ocean Observations. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Smith, D.M.; Allan, R.P.; Coward, A.C.; Eade, R.; Hyder, P.; Liu, C.; Loeb, N.G.; Palmer, M.D.; Roberts, C.D.; Scaife, A.A. Earth’s energy imbalance since 1960 in observations and CMIP5 models: Earth’s energy imbalance since 1960. Geophys. Res. Lett. 2015, 42, 1205–1213. [Google Scholar] [CrossRef] [PubMed]
- Roemmich, D.; Church, J.; Gilson, J.; Monselesan, D.; Sutton, P.; Wijffels, S. Unabated planetary warming and its ocean structure since 2006. Nat. Clim. Chang. 2015, 5, 240–245. [Google Scholar] [CrossRef]
- Lewandowsky, S.; Risbey, J.S.; Oreskes, N. On the definition and identifiability of the alleged “hiatus” in global warming. Sci. Rep. 2015, 5, 16784. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like interdecadal variability: 1900–93. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-Atmosphere (TOA) Edition-4.0 Data Product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef]
- Wetherald, R.T.; Manabe, S. Cloud Feedback Processes in a General Circulation Model. J. Atmos. Sci. 1988, 45, 1397–1415. [Google Scholar] [CrossRef]
- Thorsen, T.J.; Kato, S.; Loeb, N.G.; Rose, F.G. Observation-based decomposition of radiative perturbations and radiative kernels. J. Clim. 2018, in press. [Google Scholar]
- Rose, F.G.; Rutan, D.A.; Charlock, T.; Smith, G.L.; Kato, S. An Algorithm for the Constraining of Radiative Transfer Calculations to CERES-Observed Broadband Top-of-Atmosphere Irradiance. J. Atmos. Ocean. Technol. 2013, 30, 1091–1106. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Collins, W.D.; Rasch, P.J.; Eaton, B.E.; Khattatov, B.V.; Lamarque, J.-F.; Zender, C.S. Simulating aerosols using a chemical transport model with assimilation of satellite aerosol retrievals: Methodology for INDOEX. J. Geophys. Res. Atmos. 2001, 106, 7313–7336. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary Enhanced Temporal Interpolation for CERES Flux Products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. Measuring the strength of ENSO events: How does 1997/1998 rank? Weather 1998, 53, 315–324. [Google Scholar] [CrossRef]
- Brodzik, M.J.; Stewart, J.S. Near-Real-Time SSM/I-SSMIS EASE-Grid Daily Global Ice Concentration and Snow Extent; Version 5; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [Google Scholar]
- Van der Schrier, G.; Barichivich, J.; Briffa, K.R.; Jones, P.D. A scPDSI-based global data set of dry and wet spells for 1901–2009: Variations in the Self-Calibrating PDSI. J. Geophys. Res. Atmos. 2013, 118, 4025–4048. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Trenberth, K.E. The Annual Cycle of the Energy Budget. Part I: Global Mean and Land–Ocean Exchanges. J. Clim. 2008, 21, 2297–2312. [Google Scholar] [CrossRef]
- Victor, D.G.; Kennel, C.F. Ditch the 2 °C warming goal. Nature 2014, 514, 30–31. [Google Scholar] [CrossRef] [PubMed]
- Brown, P.T.; Li, W.; Jiang, J.H.; Su, H. Unforced Surface Air Temperature Variability and Its Contrasting Relationship with the Anomalous TOA Energy Flux at Local and Global Spatial Scales. J. Clim. 2016, 29, 925–940. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Caron, J.M.; Stepaniak, D.P.; Worley, S. Evolution of El Niño–Southern Oscillation and global atmospheric surface temperatures. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Forster, P.M. Inference of Climate Sensitivity from Analysis of Earth’s Energy Budget. Annu. Rev. Earth Planet. Sci. 2016, 44, 85–106. [Google Scholar] [CrossRef]
- Loeb, N.G.; Su, W.; Kato, S. Understanding Climate Feedbacks and Sensitivity Using Observations of Earth’s Energy Budget. Curr. Clim. Chang. Rep. 2016, 2, 170–178. [Google Scholar] [CrossRef]
- Chung, E.-S.; Soden, B.J.; Clement, A.C. Diagnosing Climate Feedbacks in Coupled Ocean–Atmosphere Models. Surv. Geophys. 2012, 33, 733–744. [Google Scholar] [CrossRef]
- Klein, S.A.; Hartmann, D.L.; Norris, J.R. On the relationship among low-cloud structure, sea surface temperature, and atmospheric circulation in the summertime Northeast Pacific. J. Clim. 1995, 8, 1140–1155. [Google Scholar] [CrossRef]
- Wood, R. Stratocumulus Clouds. Mon. Weather Rev. 2012, 140, 2373–2423. [Google Scholar] [CrossRef]
- Myers, T.A.; Mechoso, C.R.; Cesana, G.V.; DeFlorio, M.J.; Waliser, D.E. Cloud Feedback Key to Marine Heatwave off Baja California. Geophys. Res. Lett. 2018, 45, 4345–4352. [Google Scholar] [CrossRef]
- Mayer, M.; Alonso Balmaseda, M.; Haimberger, L. Unprecedented 2015/2016 Indo-Pacific Heat Transfer Speeds Up Tropical Pacific Heat Recharge. Geophys. Res. Lett. 2018, 45, 3274–3284. [Google Scholar] [CrossRef] [PubMed]
- Josey, S.A.; Hirschi, J.J.-M.; Sinha, B.; Duchez, A.; Grist, J.P.; Marsh, R. The recent atlantic cold anomaly: Causes, consequences, and related phenomena. Annu. Rev. Mar. Sci. 2017, 10, 475–501. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Jiang, J.H.; Gu, Y.; Diner, D.; Worden, J.; Liou, K.-N.; Su, H.; Xing, J.; Garay, M.; Huang, L. Decadal-scale trends in regional aerosol particle properties and their linkage to emission changes. Environ. Res. Lett. 2017, 12, 054021. [Google Scholar] [CrossRef]
- Paulot, F.; Paynter, D.; Ginoux, P.; Naik, V.; Horowitz, L. Changes in the aerosol direct radiative forcing from 2001 to 2015: Observational constraints and regional mechanisms. Atmos. Chem. Phys. 2018. [Google Scholar] [CrossRef]
- Jin, Y.; Andersson, H.; Zhang, S. Air Pollution Control Policies in China: A Retrospective and Prospects. Int. J. Environ. Res. Public Health 2016, 13, 1219. [Google Scholar] [CrossRef] [PubMed]
- Xing, J.; Pleim, J.; Mathur, R.; Pouliot, G.; Hogrefe, C.; Gan, C.-M.; Wei, C. Historical gaseous and primary aerosol emissions in the United States from 1990 to 2010. Atmos. Chem. Phys. 2013, 13, 7531–7549. [Google Scholar] [CrossRef]
- Weiss, J.L.; Castro, C.L.; Overpeck, J.T. Distinguishing Pronounced Droughts in the Southwestern United States: Seasonality and Effects of Warmer Temperatures. J. Clim. 2009, 22, 5918–5932. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Kimball, B.A.; Nakayama, F.S. The Dependence of Bare Soil Albedo on Soil Water Content. J. Appl. Meteorol. Climatol. 1975, 14, 109–113. [Google Scholar] [CrossRef]
- Brown, P.T.; Li, W.; Li, L.; Ming, Y. Top-of-atmosphere radiative contribution to unforced decadal global temperature variability in climate models. Geophys. Res. Lett. 2014, 41, 5175–5183. [Google Scholar] [CrossRef]
| Parameter | Data Product | Temporal Range | Reference |
|---|---|---|---|
| TOA Flux | CERES EBAF Ed4.0 CERES SSF1deg | March 2000–September 2017 | [31] |
| Cloud Properties and Surface Albedo | CERES SYN1deg Ed4.0 | March 2000–September 2017 | [38] |
| Surface Temperature | GISTEMP | February 2000–September 2017 | [39] |
| SST and Niño 3.4 Index | Extended Reconstructed Sea Surface Temperature (ERSST) v5 averages | July 2000–June 2017 | [19] |
| MEI | ESRL MEI | January 1998–September 2017 | [40] |
| 0.55 μm AOD | MYD04 Collection 6 | July 2002–June 2017 | [32] |
| Snow & Ice Cover | Near-Real-Time SSM/I-SSMIS EASE-Grid Daily Global Ice Concentration and Snow Extent | July 2000–June 2017 | [41] |
| Drought Index | Self-calibrating Palmer Drought Severity Index (scPDSI) | July 2000–June 2014 | [42] |
| TER | AQU | SNPP | ||
|---|---|---|---|---|
| SW | EBAF | 0.12 | 0.11 | 0.12 |
| TER | - | 0.19 | 0.19 | |
| AQU | - | 0.083 | ||
| LW | EBAF | 0.16 | 0.092 | 0.13 |
| TER | - | 0.19 | 0.13 | |
| AQU | - | 0.16 | ||
| NET | EBAF | 0.15 | 0.15 | 0.17 |
| TER | - | 0.26 | 0.22 | |
| AQU | - | 0.18 |
| scPDSI | Class |
|---|---|
| >4.0 | extremely wet |
| 3.0:4.0 | severely wet |
| 2.0:3.0 | moderately wet |
| 1.0:2.0 | slightly wet |
| 0.5:1.0 | incipient wet spell |
| −0.5:0.5 | near normal |
| −0.5:−1.0 | incipient dry spell |
| −1.0:−2.0 | slightly dry |
| −2.0:−3.0 | moderately dry |
| −3.0:−4.0 | severely dry |
| <−4.0 | extremely dry |
| ASR | −OLR | |||||
|---|---|---|---|---|---|---|
| Hiatus | 0.0084 | 0.060 | 0.612 | 0.552 | 0.527 | 0.085 |
| Post-Hiatus | 0.0732 | 0.525 | 1.007 | 0.482 | 1.391 | −0.384 |
| Difference | 0.065 | 0.464 | 0.395 | −0.070 | 0.864 | −0.469 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loeb, N.G.; Thorsen, T.J.; Norris, J.R.; Wang, H.; Su, W. Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective. Climate 2018, 6, 62. https://doi.org/10.3390/cli6030062
Loeb NG, Thorsen TJ, Norris JR, Wang H, Su W. Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective. Climate. 2018; 6(3):62. https://doi.org/10.3390/cli6030062
Chicago/Turabian StyleLoeb, Norman G., Tyler J. Thorsen, Joel R. Norris, Hailan Wang, and Wenying Su. 2018. "Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective" Climate 6, no. 3: 62. https://doi.org/10.3390/cli6030062
APA StyleLoeb, N. G., Thorsen, T. J., Norris, J. R., Wang, H., & Su, W. (2018). Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective. Climate, 6(3), 62. https://doi.org/10.3390/cli6030062





