Evaluation and Modeling of Urban Heat Island Intensity in Basel, Switzerland
Abstract
1. Introduction
2. Materials and Methods
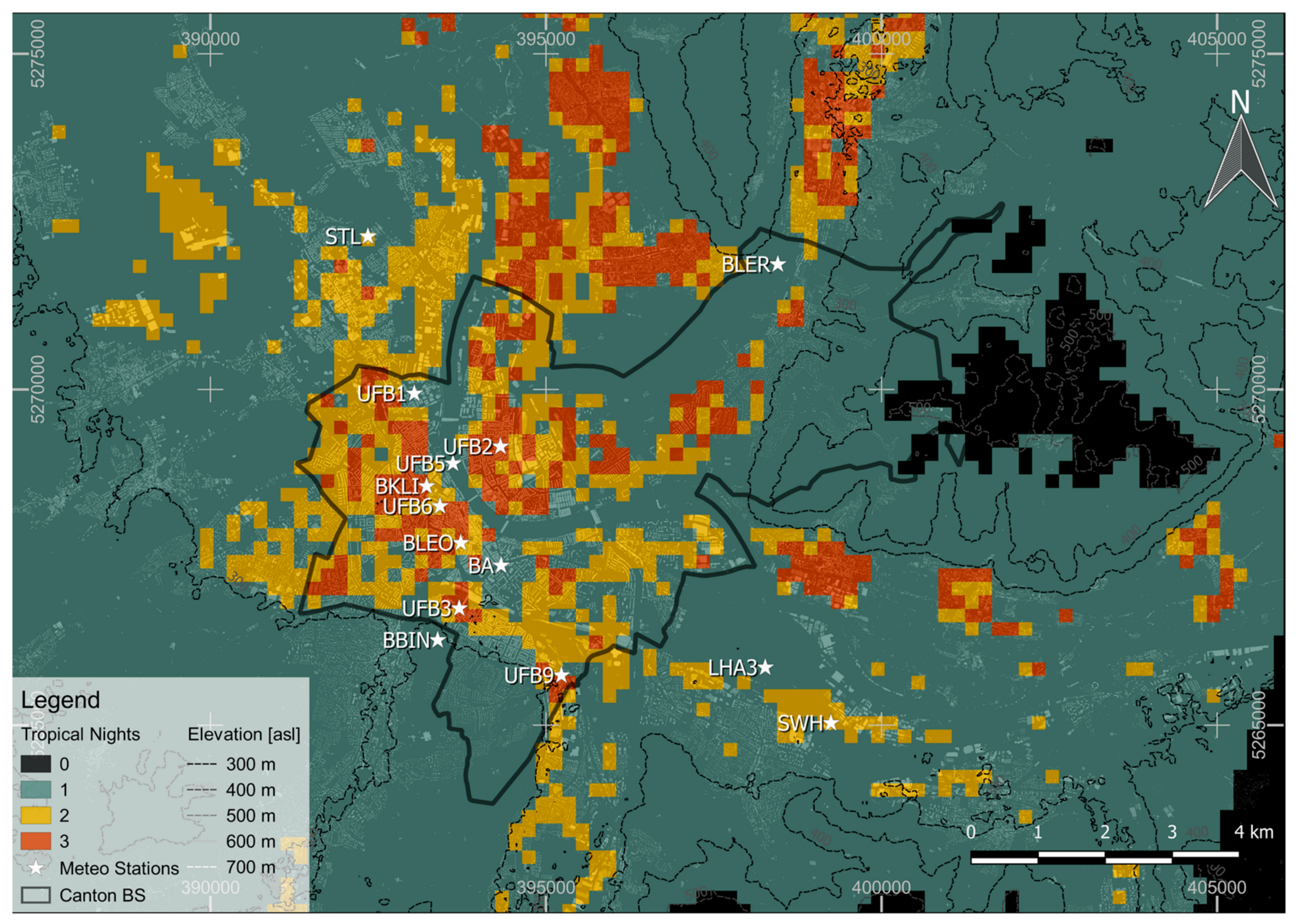
2.1. Site Description
2.2. Air Temperature Measurements
2.3. Urban Surface Properties
2.3.1. Landsat Data
2.3.2. Urban Morphology
2.3.3. Land Cover
2.4. Method
2.4.1. State of the Art
2.4.2. Method Description
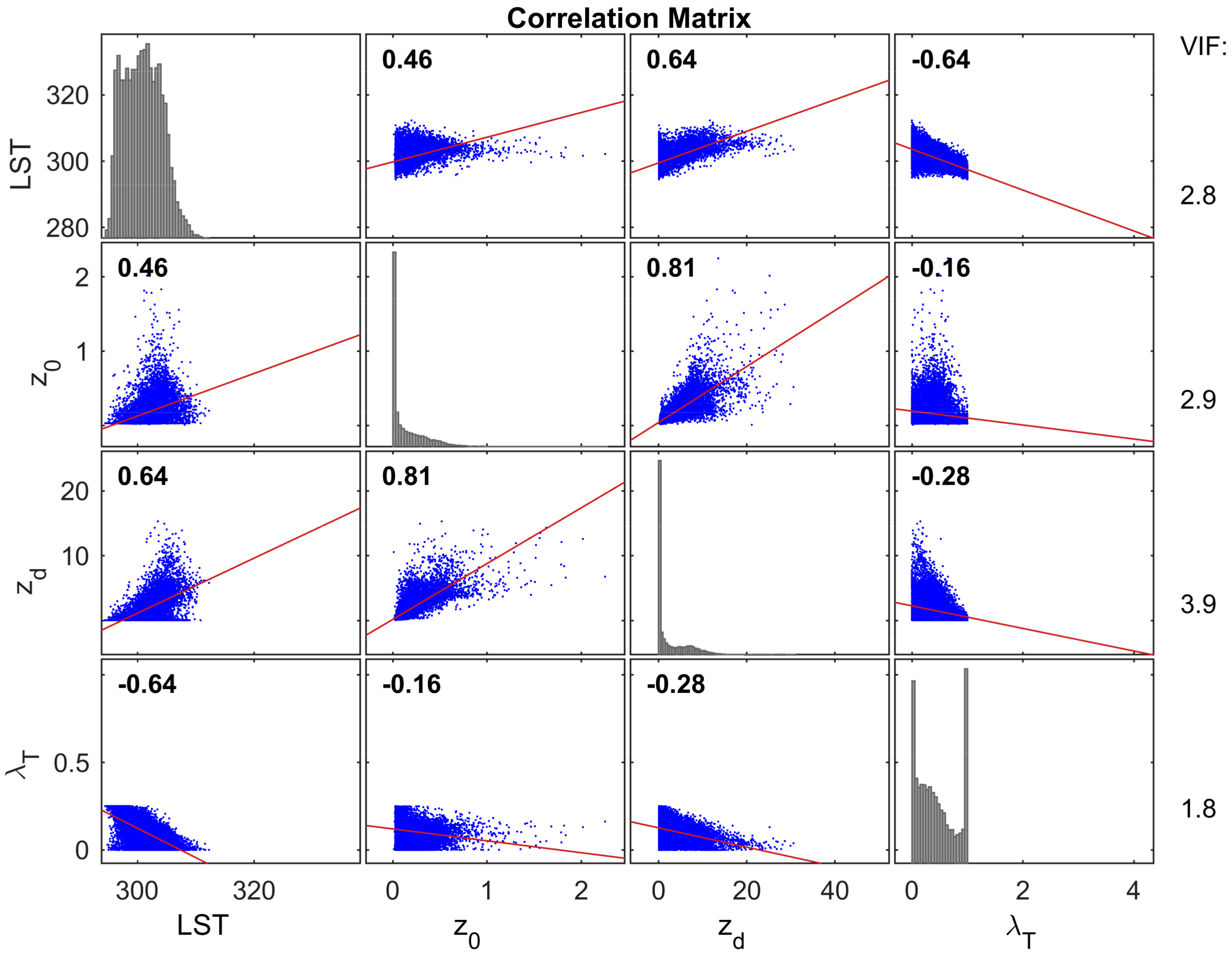
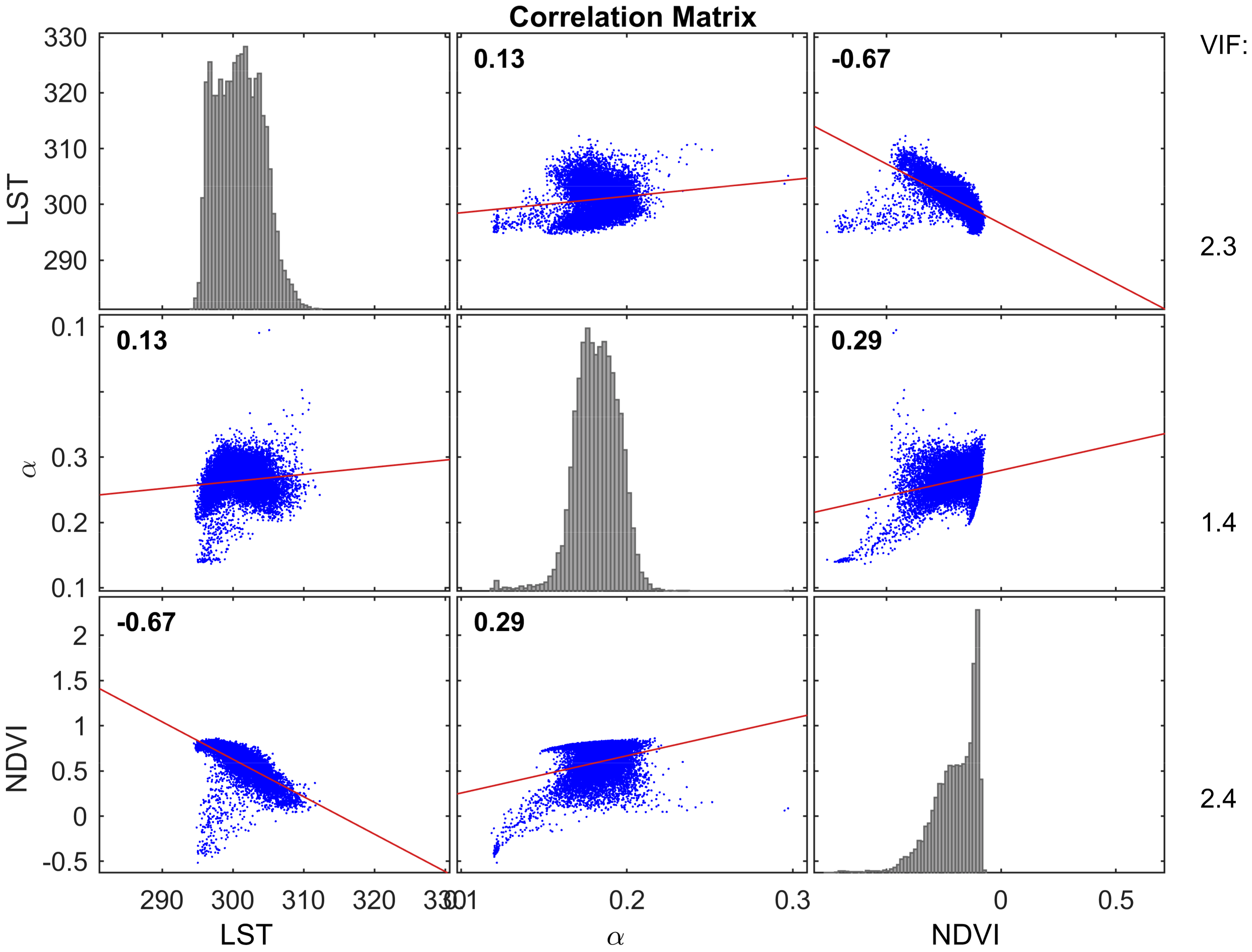
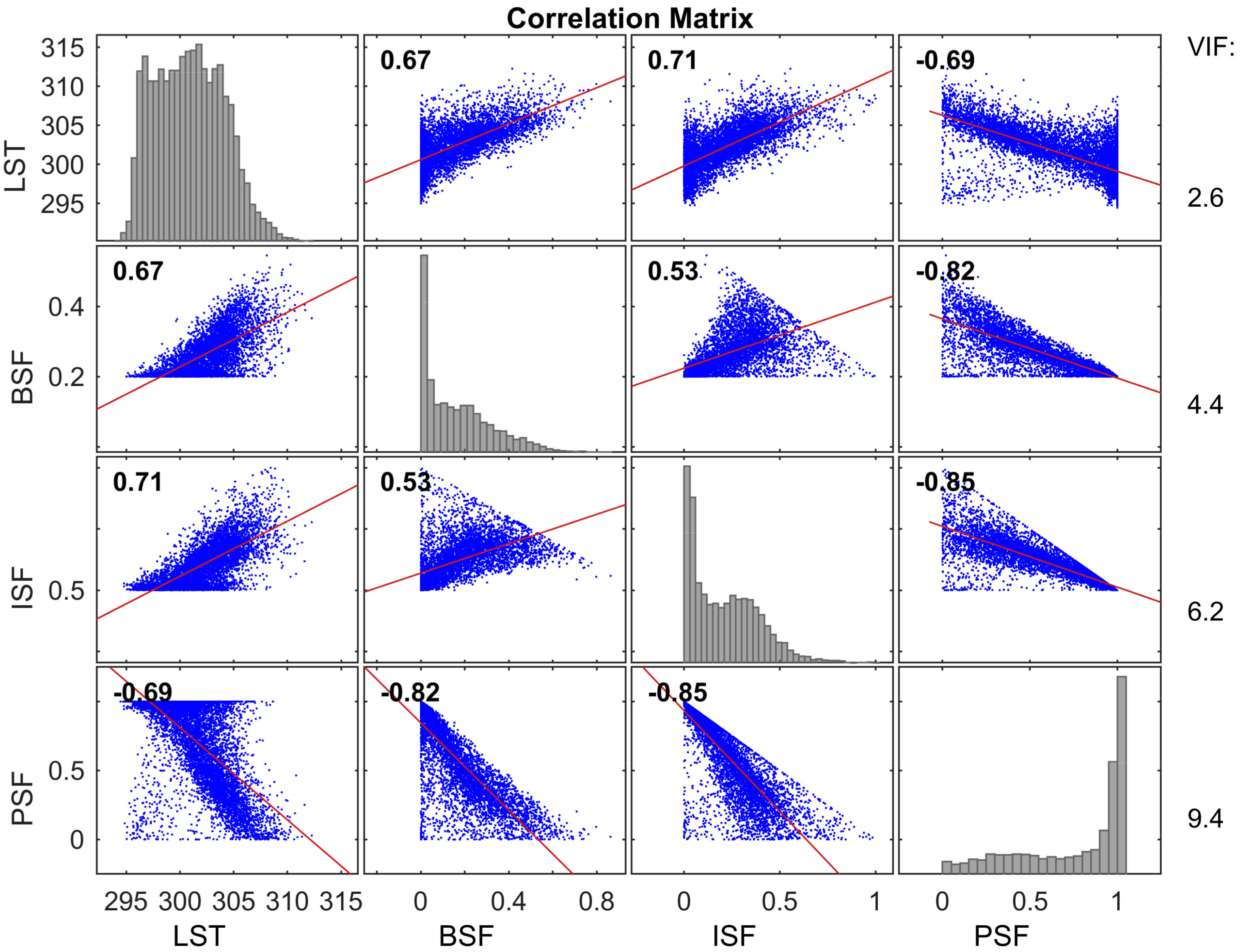
2.4.3. Suitability Tests and Predictor Selection
2.4.4. Multiple Linear Regression
2.4.5. Validation
3. Results
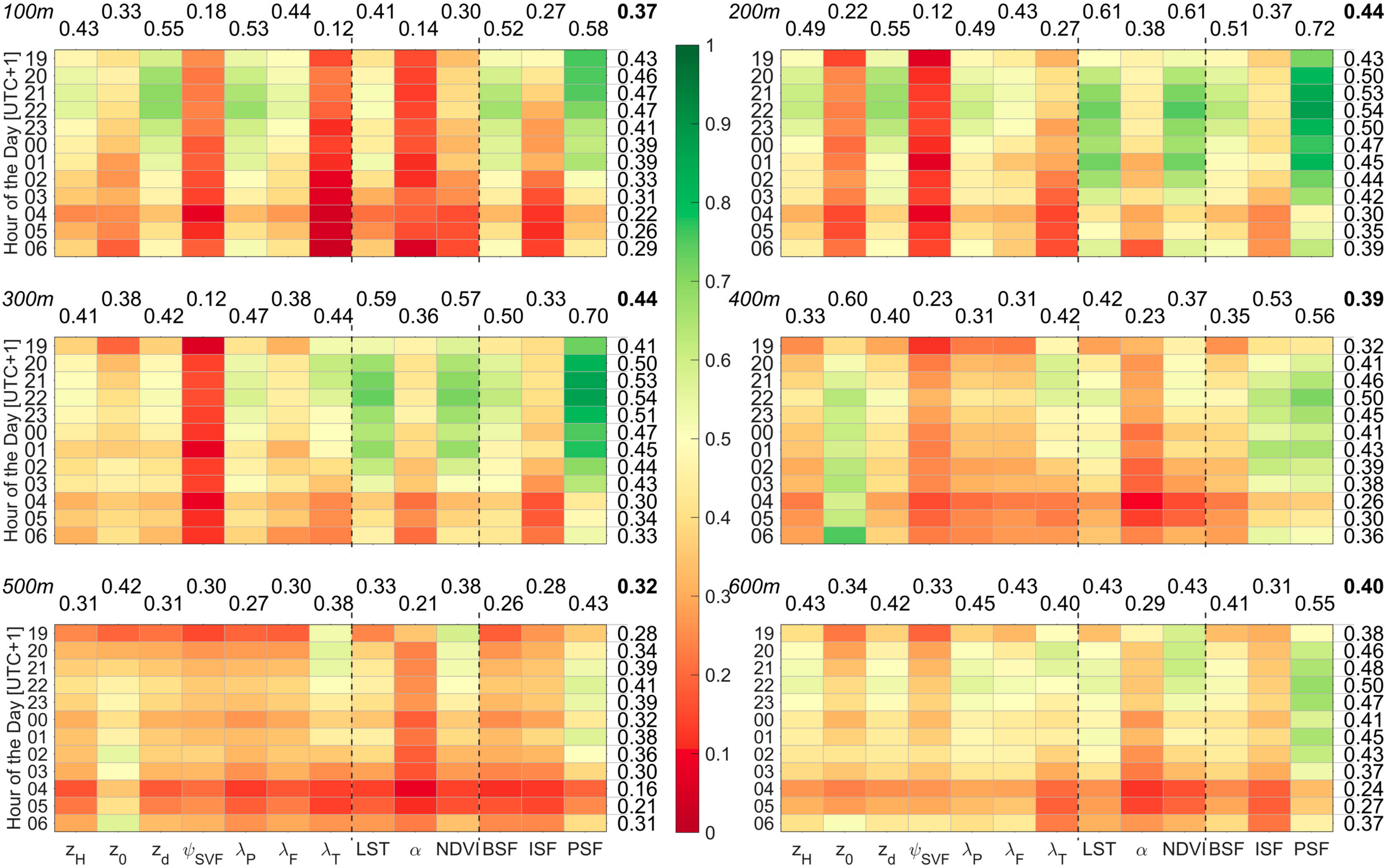
3.1. Suitability Test and Predictor Selection
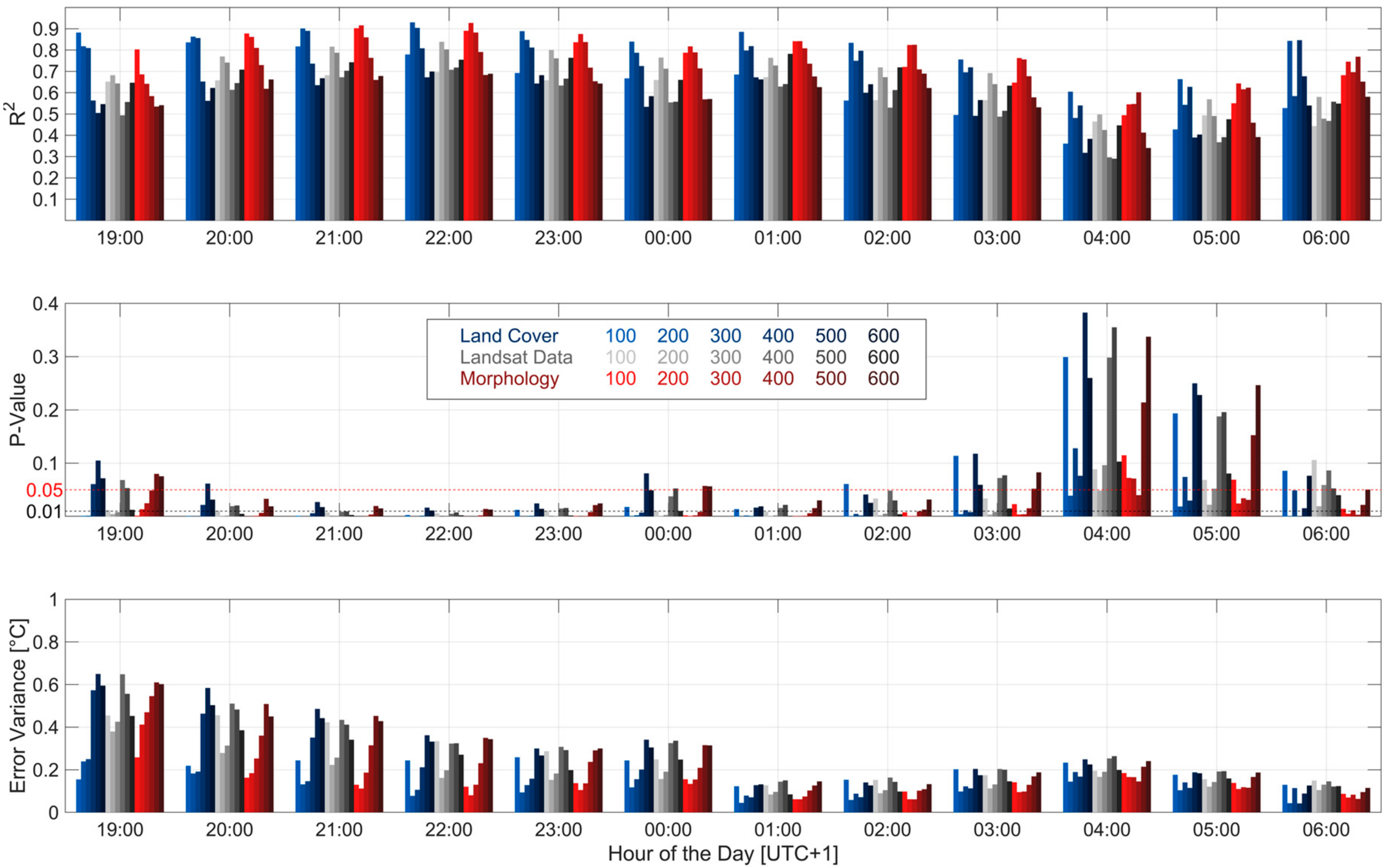
3.2. Multiple Linear Regression
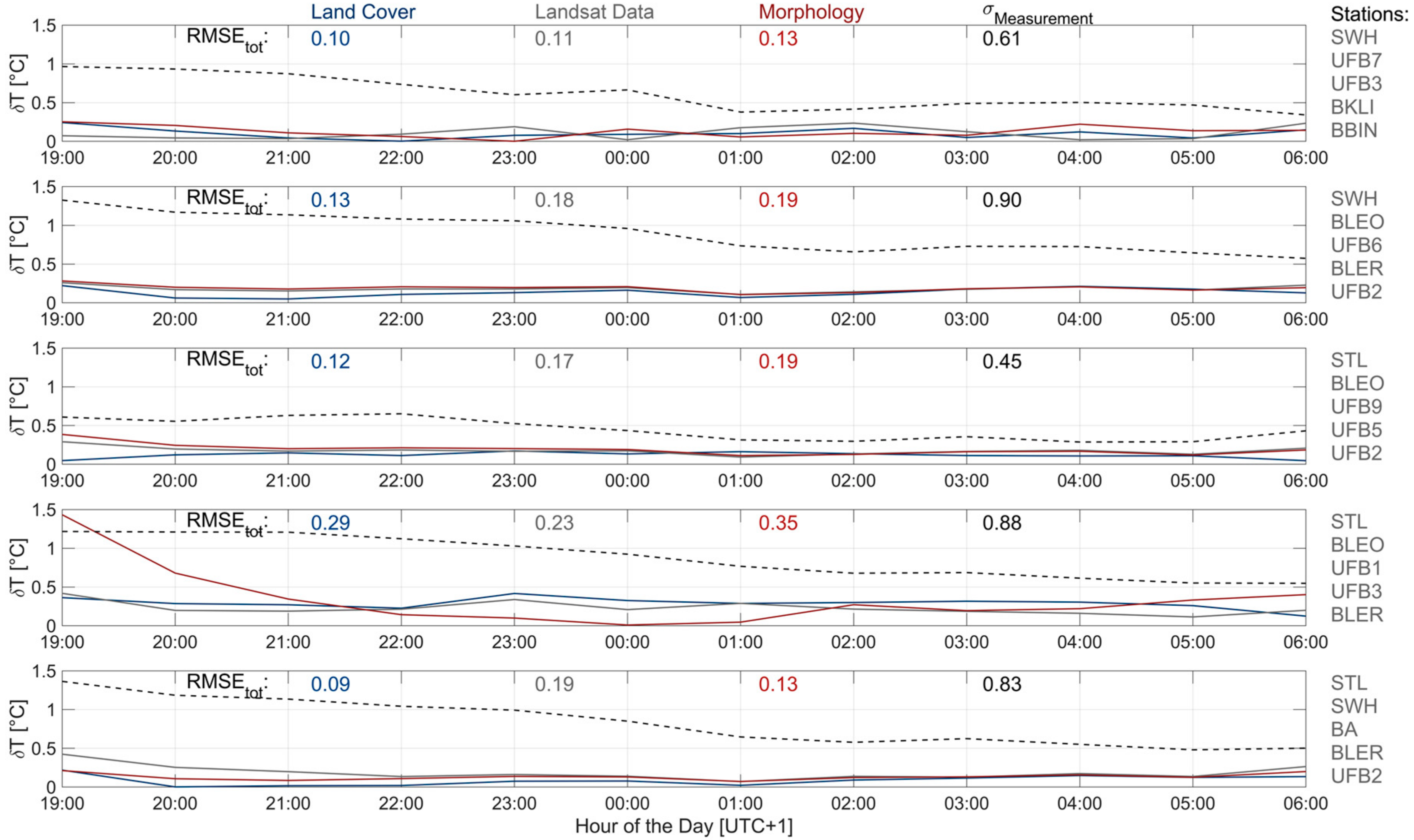
3.3. Validation
4. Discussion
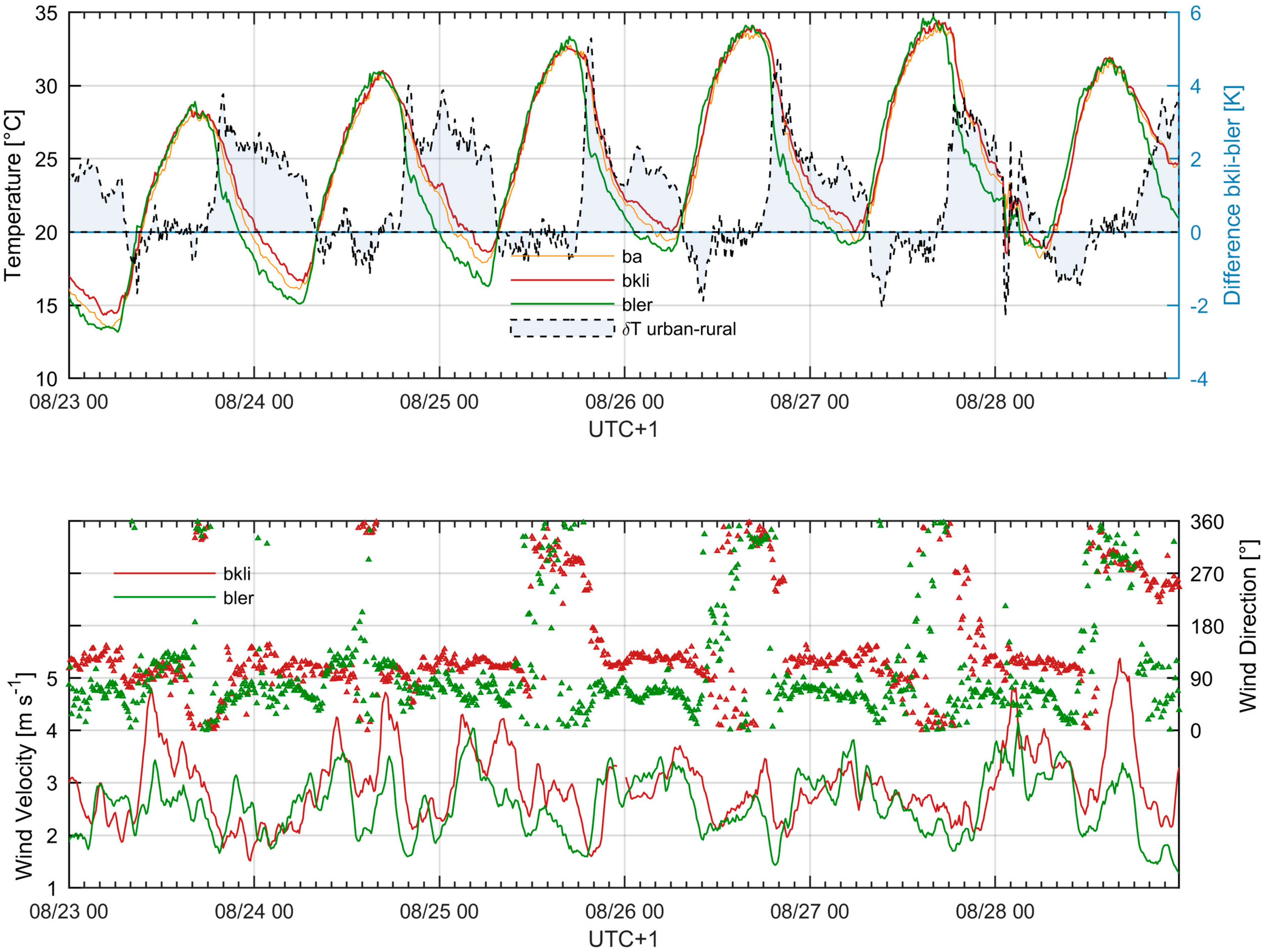
4.1. Synoptic Conditions and Meteorological Measurements
4.2. Model Output
4.3. Statistical Measures
4.4. Potentials
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- WHO. Global Health Observatory Data Repository. Available online: http://apps.who.int/gho/data/node.main.nURBPOP?lang=en (accessed on 13 December 2016).
- López-Moreno, E.; Oyeyinka, O.; Mboup, G. State of the World’s Cities 2010/2011. Bridging the Urban Divide; Earthscan: London, UK, 2008; p. 220. ISBN 978-1-84971-176-0. [Google Scholar]
- Oke, T.R.; Fuggle, R.F. Comparison of urban/rural counter and net radiation at night. Bound.-Layer Meteorol. 1972, 2, 290–308. [Google Scholar] [CrossRef]
- Oke, T.R. The distinction between canopy and boundary-layer urban heat islands. Atmosphere 1976, 14, 268–277. [Google Scholar] [CrossRef]
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Oke, T.R.; Johnson, G.T.; Steyn, D.G.; Watson, I.D. Simulation of surface urban heat islands under ‘ideal’ conditions at night Part 2: Diagnosis of causation. Bound.-Layer Meteorol. 1991, 56, 339–358. [Google Scholar] [CrossRef]
- Roth, M.; Oke, T.R.; Emery, W.J. Satellite-derived urban heat islands from three coastal cities and the utilization of such data in urban climatology. Int. J. Remote Sens. 1989, 10, 1699–1720. [Google Scholar] [CrossRef]
- Karl, T.R.; Diaz, H.F.; Kukla, G. Urbanization: Its detection and effect in the united states climate record. J. Clim. 1988, 1, 1099–1123. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Ren, C.; Ng, E.; Katzschner, L. Urban climatic map studies: A review. Int. J. Climatol. 2011, 31, 2213–2233. [Google Scholar] [CrossRef]
- Parlow, E.; Vogt, R.; Feigenwinter, C. The urban heat island of Basel—Seen from different perspectives. DIE ERDE J. Geogr. Soc. Berl. 2014, 145, 96–110. [Google Scholar] [CrossRef]
- Mayer, H.; Holst, J.; Dostal, P.; Imbery, F.; Schindler, D. Human thermal comfort in summer within an urban street canyon in Central Europe. Meteorol. Z. 2008, 17, 241–250. [Google Scholar] [CrossRef]
- Clarke, J.F.; Bach, W. Comparison of the comfort conditions in different urban and suburban microenvironments. Int. J. Biometeorol. 1971, 15, 41–54. [Google Scholar] [CrossRef] [PubMed]
- Scherer, D.; Fehrenbach, U.; Lakes, T.; Lauf, S.; Meier, F.; Schuster, C. Quantification of heat-stress related mortality hazard, vulnerability and risk in Berlin, Germany. DIE ERDE J. Geogr. Soc. Berl. 2014, 144, 238–259. [Google Scholar] [CrossRef]
- Ragettli, M.S.; Vicedo-Cabrera, A.M.; Schindler, C.; Roosli, M. Exploring the association between heat and mortality in Switzerland between 1995 and 2013. Environ. Res. 2017, 158, 703–709. [Google Scholar] [CrossRef] [PubMed]
- Schär, C.; Jendritzky, G. Climate change: Hot news from summer 2003. Nature 2004, 432, 559–560. [Google Scholar] [CrossRef] [PubMed]
- Robine, J.-M.; Cheung, S.L.; Roy, S.L.; Oyen, H.V.; Griffiths, C.; Michel, J.-P.; Herrmann, F.R. Death toll exceeded 70,000 in Europe during the summer of 2003. C. R. Biol. 2008, 331, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Vicedo-Cabrera, A.M.; Ragettli, M.S.; Schindler, C.; Roosli, M. Excess mortality during the warm summer of 2015 in Switzerland. Swiss Med. Wkly 2016, 146, 12. [Google Scholar] [CrossRef] [PubMed]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Gerstengarbe, F.-W.; Werner, P.C. Katalog der Großwetterlagen Europas nach Paul Hess und Helmuth Brezowsky (1881–2004); Potsdam Institude for Climate Impact Research (PIK): Potsdam, Germany, 2005. [Google Scholar]
- Karl, T.R.; Trenberth, K.E. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. The urban energy balance. Prog. Phys. Geogr. 1988, 12, 471–508. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Best, M.; Barlow, J.; Arnfield, A.J.; Baik, J.-J.; Baklanov, A.; Belcher, S.; Bruse, M.; Calmet, I.; Chen, F.; et al. Urban surface energy balance models: Model characteristics and methodology for a comparison study. In Meteorological and Air Quality Models for Urban Areas; Baklanov, A., Grimmond, C.S.B., Mahura, A., Athanassiadou, M., Eds.; Springer: Berlin, Germany, 2009; pp. 97–124. [Google Scholar]
- Christen, A.; Vogt, R. Energy and radiation balance of a central European city. Int. J. Climatol. 2004, 24, 1395–1421. [Google Scholar] [CrossRef]
- Nunez, M.; Oke, T.R. The energy balance of an urban canyon. J. Appl. Meteorol. 1977, 16, 11–19. [Google Scholar] [CrossRef]
- Parlow, E. Correction of terrain controlled illumination effects in satellite data. In Progress in Environmental Remote Sensing Research and Applications; Parlow, E., Ed.; Balkema: Rotterdam, The Netherlands, 1996; pp. 139–145. [Google Scholar]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. Error sources on the land surface temperature retrieved from thermal infrared single channel remote sensing data. Int. J. Remote Sens. 2006, 27, 999–1014. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Chrysoulakis, N. Estimation of the all-wave urban surface radiation balance by use of ASTER multispectral imagery and in situ spatial data. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Marconcini, M.; Gastellu-Etchegorry, J.-P.; Grimmong, C.S.B.; Feigenwinter, C.; Lindberg, F.; Del Frate, F.; Klostermann, J.; Mi, Z.; Esch, T.; et al. Anthropogenic heat flux estimation from space. In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, UAE, 6–8 March 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Heat storage in urban areas: Local-scale observations and evaluation of a simple model. J. Appl. Meteorol. 1999, 38, 922–940. [Google Scholar] [CrossRef]
- Christen, A.; Vogt, R.; Rotach, M.; Parlow, E. First results from BUBBLE II: Partioning of turbulent heat fluxes over urban surfaces. In Proceedings of the Fourth Symposium on the Urban Environment, Norfolk, VA, USA, 19 May 2002; American Meteorological Society: Norfolk, VA, USA, 2002; pp. 137–138. [Google Scholar]
- Parlow, E. Net radiation in the REKLIP-area—A spatial approach using satellite data. In Progress in Environmental Remote Sensing Research and Applications; Parlow, E., Ed.; Balkema: Rotterdam, The Netherlands, 1996. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- MeteoSwiss. Climate Normals Basel/Binningen. Reference Period 1981–2010; Federal Office of Meteorology and Climatology MeteoSwiss: Zurich, Switzerland, 2016. [Google Scholar]
- Scherer, D.; Fehrenbach, U.; Beha, H.D.; Parlow, E. Improved concepts and methods in analysis and evaluation of the urban climate for optimizing urban planning processes. Atmos. Environ. 1999, 33, 4185–4193. [Google Scholar] [CrossRef]
- Rotach, M.W.; Vogt, R.; Bernhofer, C.; Batchvarova, E.; Christen, A.; Clappier, A.; Feddersen, B.; Gryning, S.E.; Martucci, G.; Mayer, H.; et al. BUBBLE—An urban boundary layer meteorology project. Theor. Appl. Climatol. 2005, 81, 231–261. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Feigenwinter, C.; Triantakonstantis, D.; Penyevskiy, I.; Tal, A.; Parlow, E.; Fleishman, G.; Düzgün, S.; Esch, T.; Marconcini, M. A conceptual list of indicators for urban planning and management based on Earth observation. ISPRS Int. J. Geo-Inf. 2014, 3, 980–1002. [Google Scholar] [CrossRef]
- Basel-Stadt. Basel-Stadt in Zahlen 2015; Statistisches Amt des Kantons Basel-Stadt: Basel, Switzerland, 2015. [Google Scholar]
- Oke, T.R.; Cleugh, H.A.; Grimmond, S.; Schmid, H.P.; Roth, M. Evaluation of spatially-averaged fluxes of heat, mass and momentum in the urban boundary layer. Weather Clim. 1989, 9, 14–21. [Google Scholar]
- Stewart, I.; Oke, T. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Wicki, A.; Parlow, E. Attribution of local climate zones using a multitemporal land use/land cover classification scheme. J. Appl. Remote Sens. 2017, 11, 026001. [Google Scholar] [CrossRef]
- Barsi, J.; Barker, J.; Schott, J. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. In Proceedings of the Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; IEEE: Toulouse, France, 2003; Volume 5, pp. 3014–3016. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martìnez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Wicki, A.; Parlow, E. Multiple regression analysis for unmixing of surface temperature data in an urban environment. Remote Sens. 2017, 9, 684. [Google Scholar] [CrossRef]
- Wang, C.; Myint, S.; Wang, Z.; Song, J. Spatio-Temporal Modeling of the Urban Heat Island in the Phoenix Metropolitan Area: Land Use Change Implications. Remote Sens. 2016, 8, 185. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL). J. Hydrol. 1998, 212, 213–229. [Google Scholar] [CrossRef]
- Lindberg, F.; Grimmond, C.S.B.; Gabey, A.; Huang, B.; Kent, C.W.; Sun, T.; Theeuwes, N.E.; Järvi, L.; Ward, H.C.; Capel-Timms, I.; et al. Urban Multi-scale Environmental Predictor (UMEP): An integrated tool for city-based climate services. Environ. Model. Softw. 2018, 99, 70–87. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound.-Layer Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Kanda, M.; Inagaki, A.; Miyamoto, T.; Gryschka, M.; Raasch, S. A New Aerodynamic Parametrization for Real Urban Surfaces. Bound.-Layer Meteorol. 2013, 148, 357–377. [Google Scholar] [CrossRef]
- Basel-Stadt. Geoportal Kanton Basel-Stadt; Grundbuch- und Vermessungsamt des Kantons Basel-Stadt: Basel, Switzerland, 2016. [Google Scholar]
- Marconcini, M.; Heldens, W.; Del Frate, F.; Latini, D.; Mitraka, Z.; Lindberg, F. EO-based products in support of urban heat fluxes estimation. In Proceedings of the Joint Urban Remote Sensing Event (JURSE), Dubai, UAE, 6–8 March 2017; IEEE: Dubai, UAE, 2017; pp. 1–4. [Google Scholar]
- Caselles, V.; Lopez Garcia, M.J.; Melia, J.; Perez Cueva, A.J. Analysis of the heat-island effect of the city of Valencia, Spain, through air temperature transects and NOAA satellite data. Theor. Appl. Climatol. 1991, 43, 195–203. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Saaroni, H. Airborne video thermal radiometry as a tool for monitoring microscale structures of the urban heat island. Int. J. Remote Sens. 1997, 18, 3039–3053. [Google Scholar] [CrossRef]
- Nichol, J.E.; Fung, W.Y.; Lam, K.-S.; Wong, M.S. Urban heat island diagnosis using ASTER satellite images and ‘in situ’ air temperature. Atmos. Res. 2009, 94, 276–284. [Google Scholar] [CrossRef]
- Seidel, J.; Ketzler, G.; Bechtel, B.; Thies, B.; Philipp, A.; Böhner, J.; Egli, S.; Eisele, M.; Herma, F.; Langkamp, T.; et al. Mobile measurement techniques for local and micro-scale studies in urban and topo-climatology. DIE ERDE J. Geogr. Soc. Berl. 2016, 147, 15–39. [Google Scholar] [CrossRef]
- Maras, I.; Buttstädt, M.; Hahmann, J.; Hofmeister, H.; Schneider, C. Investigating public places and impacts of heat stress in the city of Aachen, Germany. DIE ERDE J. Geogr. Soc. Berl. 2013, 144, 290–303. [Google Scholar] [CrossRef]
- Gallo, K.P.; Tarpley, J.D.; McNab, A.L.; Karl, T.R. Assessment of urban heat islands: A satellite perspective. Atmos. Res. 1995, 37, 37–43. [Google Scholar] [CrossRef]
- Gallo, K.P.; McNab, A.L.; Karl, T.R.; Brown, J.F.; Hood, J.J.; Tarpley, J.D. The use of a vegetation index for assessment of the urban heat island effect. Int. J. Remote Sens. 1993, 14, 2223–2230. [Google Scholar] [CrossRef]
- Gallo, K.P.; Owen, T.W. Satellite-based adjustments for the urban heat island temperature bias. J. Appl. Meteorol. 1999, 38, 806–813. [Google Scholar] [CrossRef]
- Epperson, D.L.; Davis, J.M.; Bloomfield, P.; Karl, T.R.; McNab, A.L.; Gallo, K.P. Estimating the urban bias of surface shelter temperatures using upper-air and satellite data. Part II: Estimation of the urban bias. J. Appl. Meteorol. 1995, 34, 340–357. [Google Scholar] [CrossRef]
- Dousset, B. AVHRR-derived cloudiness and surface temperature patterns over the Los Angeles area and their relationships to land use. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; Volume 4, pp. 2132–2137. [Google Scholar] [CrossRef]
- Stoll, M.J.; Brazel, A.J. Surface-air temperature relationships in the urban environment of Phoenix, Arizona. Phys. Geogr. 1992, 13, 160–179. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Nichol, J. Remote sensing of urban heat islands by day and night. Photogramm. Eng. Remote Sens. 2005, 71, 613–621. [Google Scholar] [CrossRef]
- Fu, G.; Shen, Z.; Zhang, X.; Shi, P.; Zhang, Y.; Wu, J. Estimating air temperature of an alpine meadow on the Northern Tibetan Plateau using MODIS land surface temperature. Acta Ecol. Sin. 2011, 31, 8–13. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, L.; Zhang, H.; Zhang, Y.; Dai, X. Air temperature field distribution estimations over a Chinese mega-city using MODIS land surface temperature data: The case of Shanghai. Front. Earth Sci. 2015, 10, 38–48. [Google Scholar] [CrossRef]
- Mao, K.B.; Tang, H.J.; Wang, X.F.; Zhou, Q.B.; Wang, D.L. Near-surface air temperature estimation from ASTER data based on neural network algorithm. Int. J. Remote Sens. 2008, 29, 6021–6028. [Google Scholar] [CrossRef]
- Myint, S.W.; Wentz, E.A.; Brazel, A.J.; Quattrochi, D.A. The impact of distinct anthropogenic and vegetation features on urban warming. Landsc. Ecol. 2013, 28, 959–978. [Google Scholar] [CrossRef]
- Cresswell, M.P.; Morse, A.P.; Thomson, M.C.; Connor, S.J. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model. Int. J. Remote Sens. 1999, 20, 1125–1132. [Google Scholar] [CrossRef]
- Cristóbal, J.; Ninyerola, M.; Pons, X. Modeling air temperature through a combination of remote sensing and GIS data. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Bechtel, B.; Zakšek, K.; Oßenbrügge, J.; Kaveckis, G.; Böhner, J. Towards a satellite based monitoring of urban air temperatures. Sustain. Cities Soc. 2017, 34, 22–31. [Google Scholar] [CrossRef]
- Vogt, J.V.; Viau, A.A.; Paquet, F. Mapping regional air temperature fields using satellite-derived surface skin temperatures. Int. J. Climatol. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
- Ninyerola, M.; Pons, X.; Roure, J.M. A methodological approach of climatological modelling of air temperature and precipitation through gis techniques. Int. J. Climatol. 2000, 20, 1823–1841. [Google Scholar] [CrossRef]
- Wang, C.; Middel, A.; Myint, S.W.; Kaplan, S.; Brazel, A.J.; Lukasczyk, J. Assessing local climate zones in arid cities: The case of Phoenix, Arizona and Las Vegas, Nevada. ISPRS J. Photogramm. Remote Sens. 2018, 141, 59–71. [Google Scholar] [CrossRef]
- O’brien, R.M. A caution regarding rules of thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Craney, T.A.; Surles, J.G. Model-dependent Variance Inflation Factor cutoff values. Qual. Eng. 2002, 14, 391–403. [Google Scholar] [CrossRef]
- Spronken-Smith, R.A.; Oke, T.R. The thermal regime of urban parks in two cities with different summer climates. Int. J. Remote Sens. 1998, 19, 2085–2104. [Google Scholar] [CrossRef]
- Kuttler, W. Climate change on the urban scale—Effects and counter-measures in Central Europe. In Human and Social Dimensions of Climate Change; InTech: Garching bei München, Germany, 2012. [Google Scholar] [CrossRef]
- Pichierri, M.; Bonafoni, S.; Biondi, R. Satellite air temperature estimation for monitoring the canopy layer heat island of Milan. Remote Sens. Environ. 2012, 127, 130–138. [Google Scholar] [CrossRef]
- Eliasson, I.; Upmanis, H. Nocturnal airflow from urban parks-implications for city ventilation. Theor. Appl. Climatol. 2000, 66, 95–107. [Google Scholar] [CrossRef]
- Blennow, K. Modelling minimum air temperature in partially and clear felled forests. Agric. For. Meteorol. 1998, 91, 223–235. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B. MODIS-based estimation of air temperature of the Tibetan Plateau. J. Geogr. Sci. 2013, 23, 627–640. [Google Scholar] [CrossRef]
- Mostovoy, G.V.; Filippova, M.G.; Kakani, V.G.; Reddy, K.R.; King, R.L. Statistical estimation of daily maximum and minimum air temperatures from MODIS LST data over the State of Mississippi. GIScience Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef]
- Emamifar, S.; Rahimikhoob, A.; Noroozi, A.A. Daily mean air temperature estimation from MODIS land surface temperature products based on M5 model tree. Int. J. Climatol. 2013, 33, 3174–3181. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Bechtel, B.; Wiesner, S.; Zaksek, K. Estimation of dense time series of urban air temperatures from multitemporal geostationary satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4129–4137. [Google Scholar] [CrossRef]
- Feigenwinter, C.; Parlow, E.; Vogt, R.; Schmutz, M.; Chrysoulakis, N.; Lindberg, F.; Marconcini, M.; del Frate, F. Spatial distribution of sensible and latent heat flux in the URBANFLUXES case study city Basel (Switzerland). In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, UAE, 6–8 March 2017; pp. 1–4. [Google Scholar] [CrossRef]
| Station | Code | Height [a.s.l.] | Height [a.g.l.] | Sensor | LCZ |
|---|---|---|---|---|---|
| Basel-Binningen | BBIN | 316 | 2 | ASPTC | D9 |
| Feldbergstrasse | UFB2 | 256 | 15 | Decagon VP3 | 2 |
| A2 Hard | LHA3 | 275 | 6 | Thygan | AE |
| Klingelbergstrasse | BKLI | 286 | 28 | ASPTC | 2 |
| Lange Erlen | BLER | 273 | 10 | HMP45C | D |
| Johanniter-Brücke | UFB5 | 256 | 19(4) * | WXT520 | GA |
| Meret-Oppenheim | UFB3 | 280 | 20 | WXT520 | 210 |
| Hirzbodenweg | UFB7 | 270 | 25 | WXT520 | 6 |
| Novartis | UFB1 | 256 | 75 | WXT520 | 102 |
| Dreispitz | UFB9 | 284 | 18 | Decagon VP3 | 102 |
| Petersplatz | UFB6 | 268 | 24 | Decagon VP3 | 2A |
| Aeschenplatz | BA | 270 | 40 | HMP45C | 2 |
| Leonhard | BLEO | 273 | 41 | HMP45C | 23 |
| Schweizerhalle | SWH | 280 | 25 | HMP45C | E10 |
| St. Louis | STL | 247 | 4 | HMP45C | 6 |
| Statistics | Method | 100 m | 200 m | 300 m | 400 m | 500 m | 600 m |
|---|---|---|---|---|---|---|---|
| Mean R2 | Land Cover | 0.64 | 0.82 | 0.75 | 0.72 | 0.56 | 0.58 |
| Landsat Data | 0.60 | 0.71 | 0.66 | 0.54 | 0.57 | 0.66 | |
| Morphology | 0.75 | 0.79 | 0.76 | 0.70 | 0.60 | 0.57 | |
| 0.05-level significance fulfilled [%] | Land Cover | 58 | 100 | 83 | 83 | 50 | 58 |
| Landsat Data | 75 | 100 | 75 | 58 | 50 | 83 | |
| Morphology | 83 | 92 | 92 | 100 | 58 | 50 | |
| 0.01-level significance fulfilled [%] | Land Cover | 33 | 83 | 67 | 67 | 0 | 0 |
| Landsat Data | 25 | 75 | 75 | 17 | 17 | 50 | |
| Morphology | 67 | 75 | 67 | 67 | 0 | 0 | |
| Mean Error Variance [°C] | Land Cover | 0.20 | 0.11 | 0.14 | 0.21 | 0.31 | 0.28 |
| Landsat Data | 0.26 | 0.17 | 0.20 | 0.30 | 0.29 | 0.23 | |
| Morphology | 0.14 | 0.13 | 0.16 | 0.21 | 0.28 | 0.29 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wicki, A.; Parlow, E.; Feigenwinter, C. Evaluation and Modeling of Urban Heat Island Intensity in Basel, Switzerland. Climate 2018, 6, 55. https://doi.org/10.3390/cli6030055
Wicki A, Parlow E, Feigenwinter C. Evaluation and Modeling of Urban Heat Island Intensity in Basel, Switzerland. Climate. 2018; 6(3):55. https://doi.org/10.3390/cli6030055
Chicago/Turabian StyleWicki, Andreas, Eberhard Parlow, and Christian Feigenwinter. 2018. "Evaluation and Modeling of Urban Heat Island Intensity in Basel, Switzerland" Climate 6, no. 3: 55. https://doi.org/10.3390/cli6030055
APA StyleWicki, A., Parlow, E., & Feigenwinter, C. (2018). Evaluation and Modeling of Urban Heat Island Intensity in Basel, Switzerland. Climate, 6(3), 55. https://doi.org/10.3390/cli6030055






