Rainfall Variability in January in the Federal District of Brazil from 1981 to 2010
Abstract
:1. Introduction
2. Materials and Methods
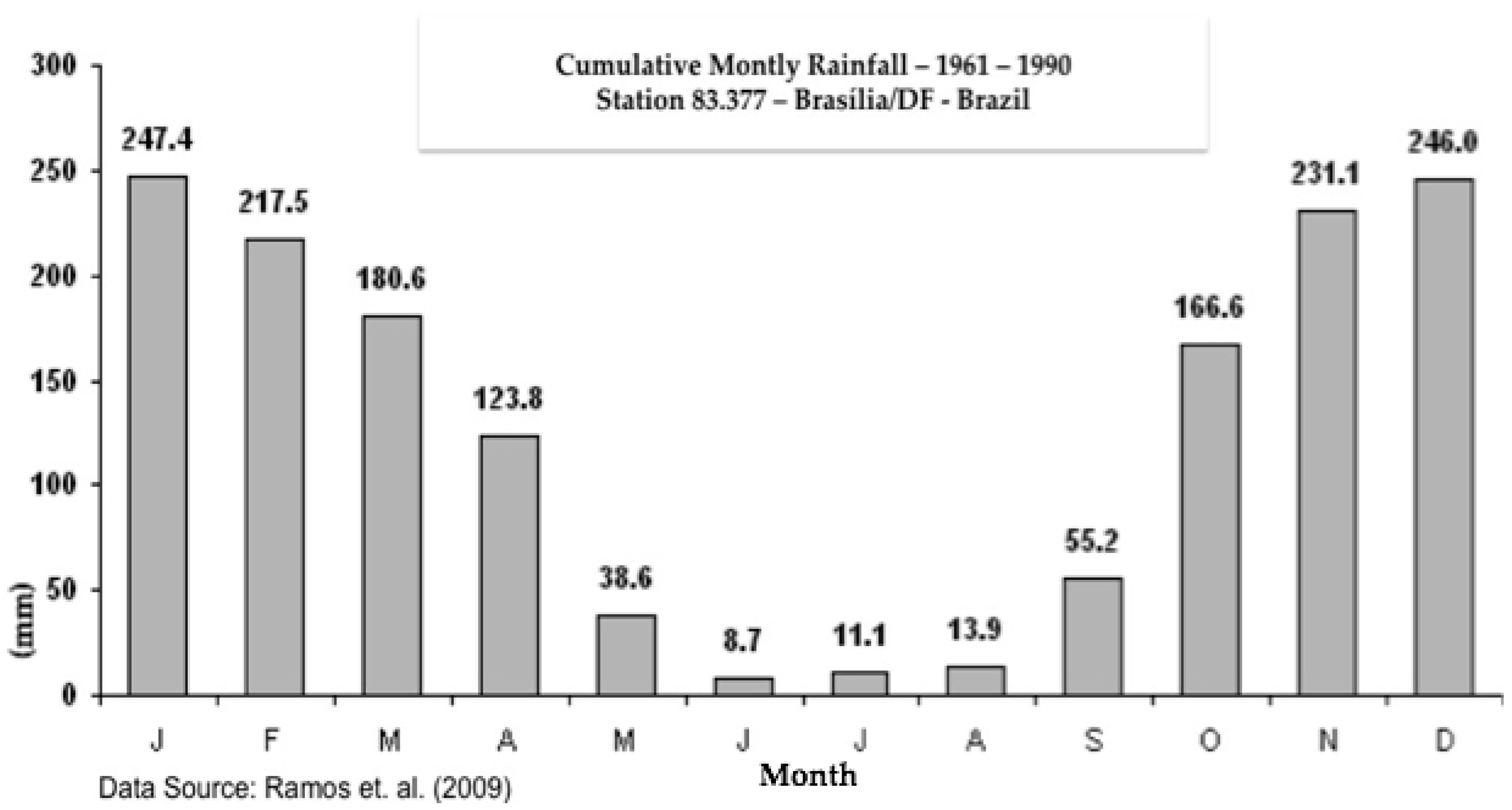
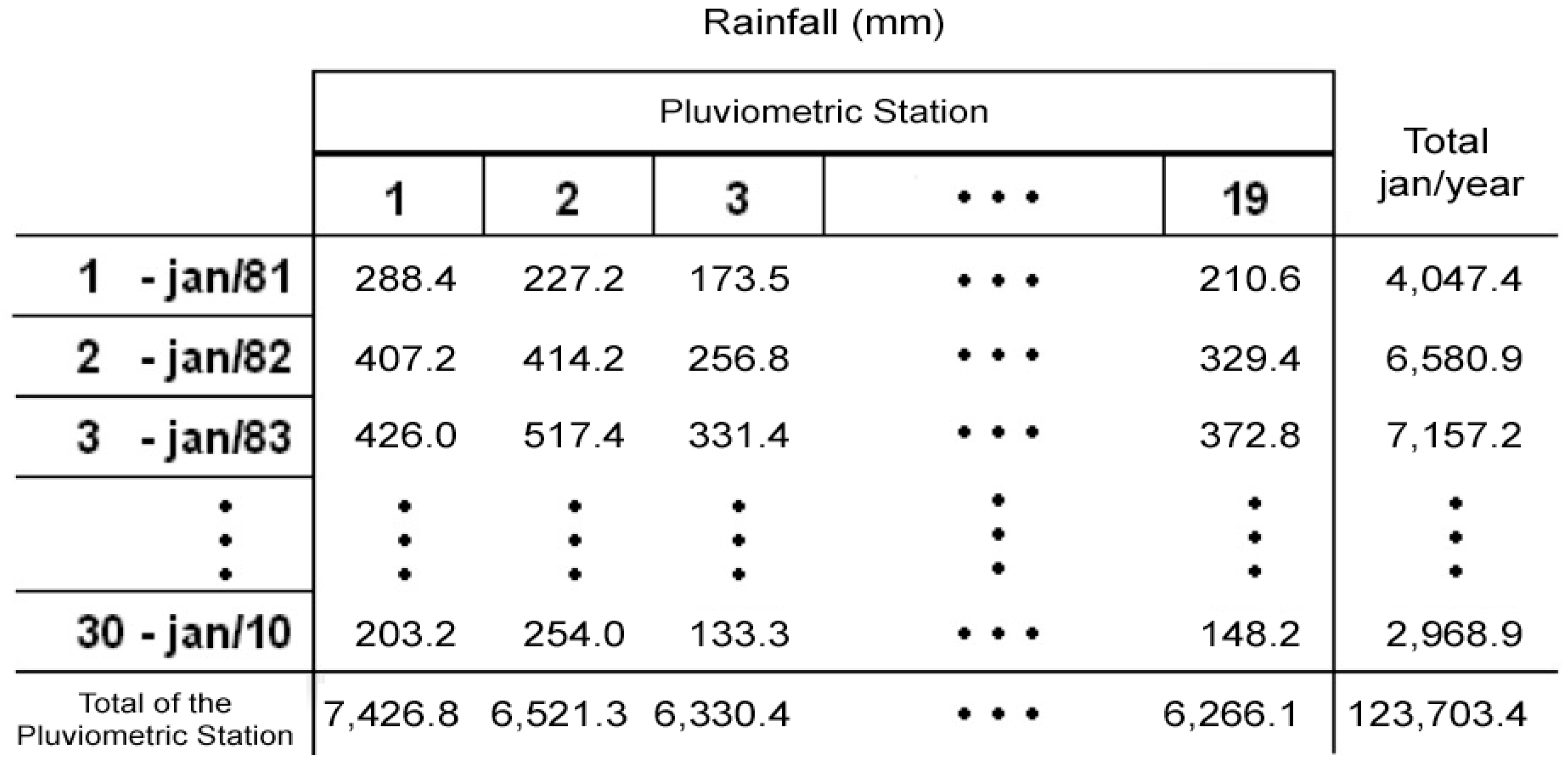
2.1. Rainfall Data
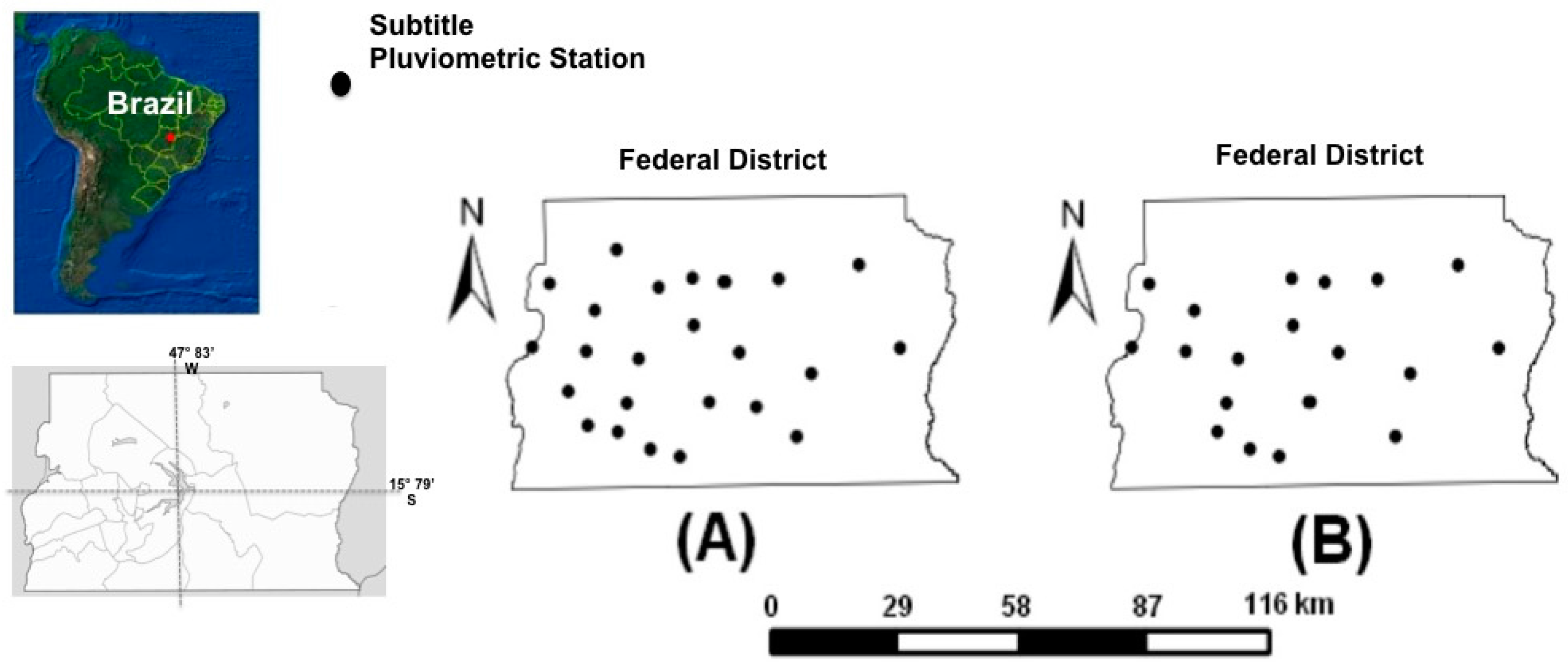
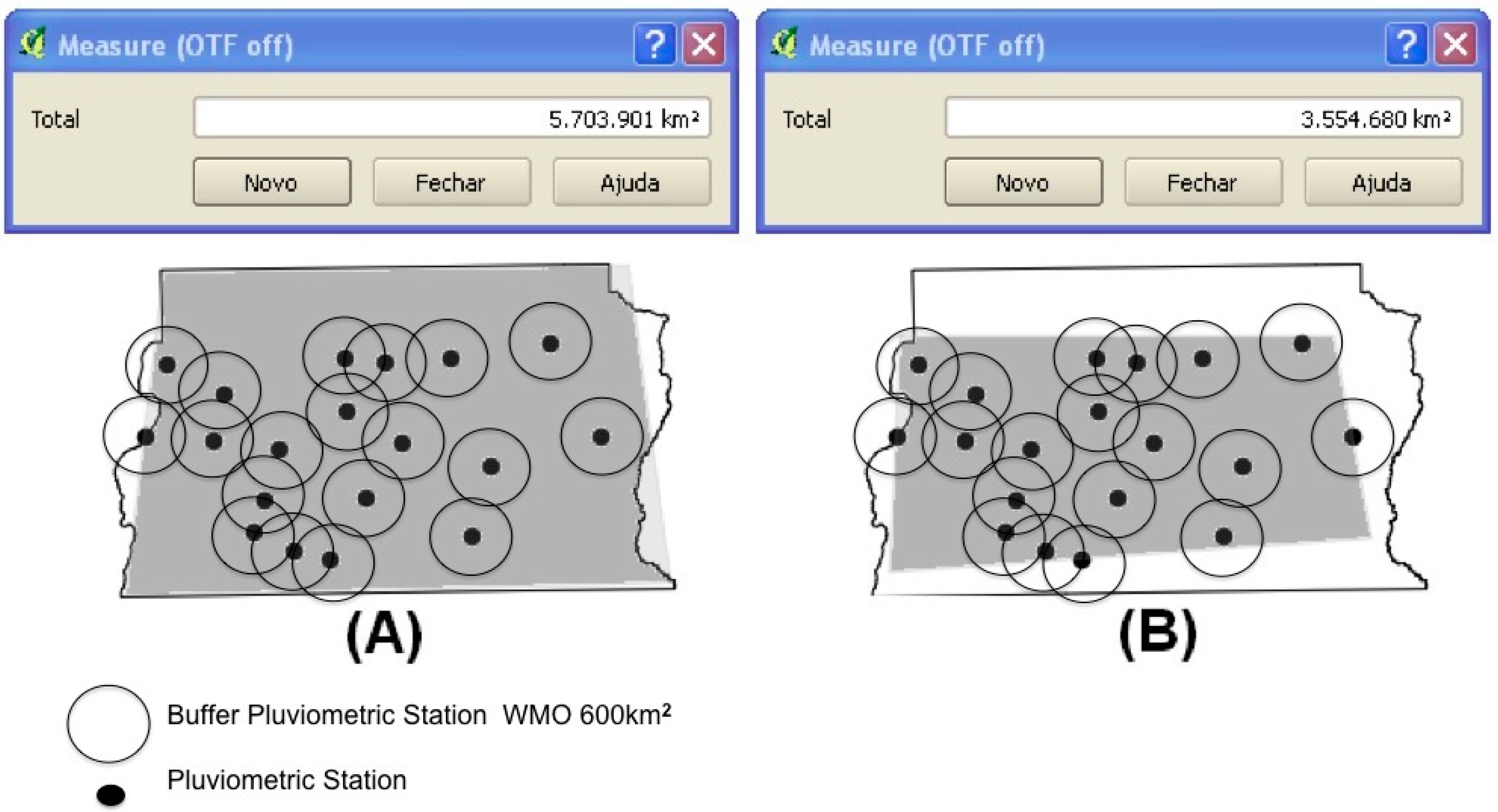
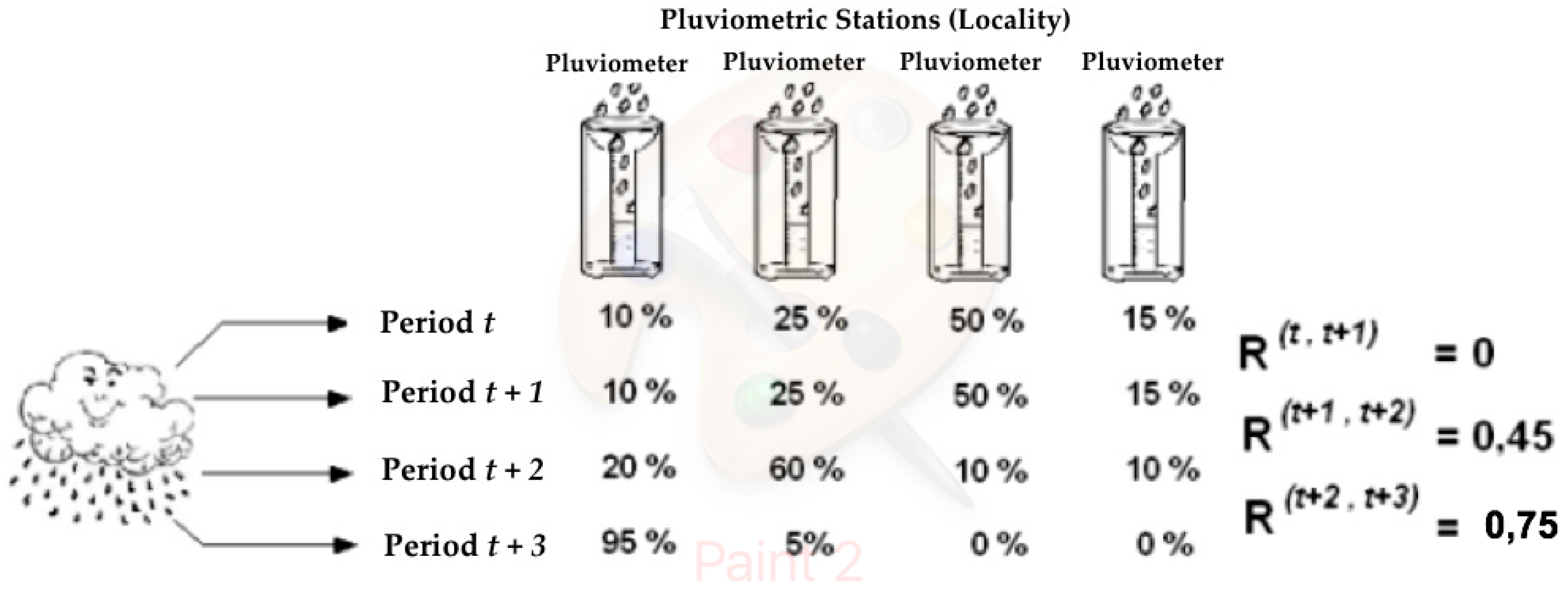
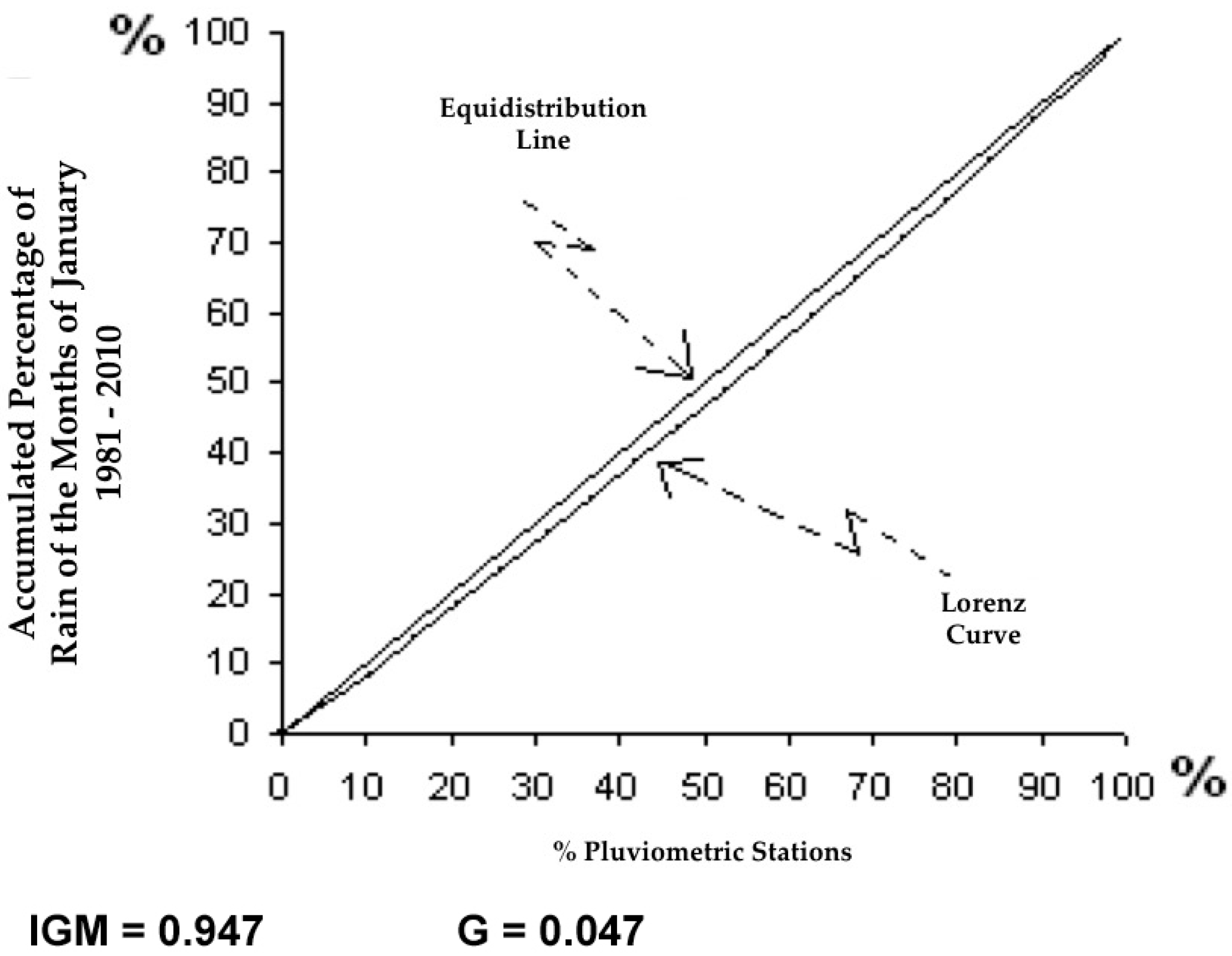
2.2. Spatial Representativeness of the 19 Rain Gauges
3. Results
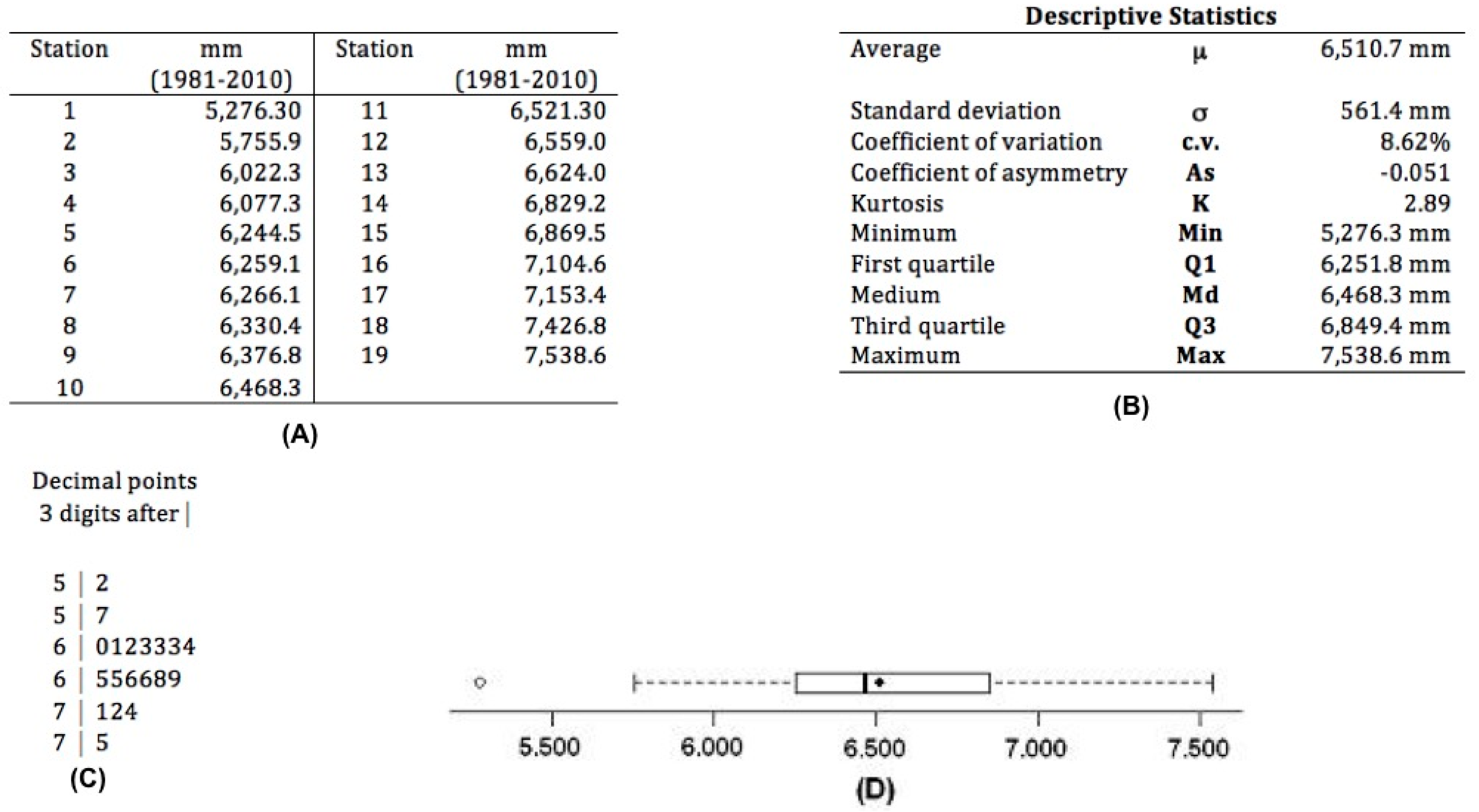
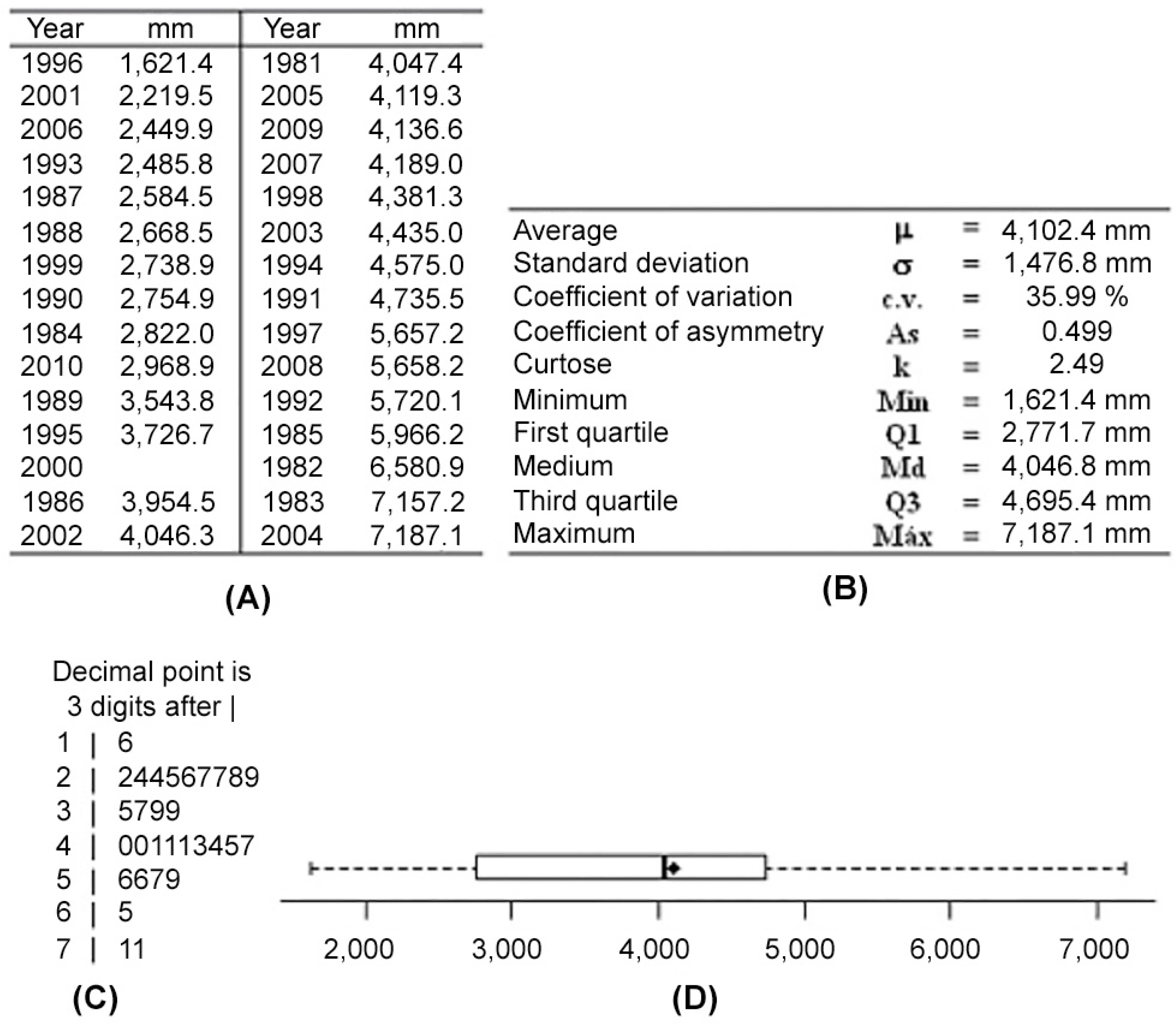
3.1. Descriptive Statistics of Rainfall Distribution at the 19 Rain Gauges
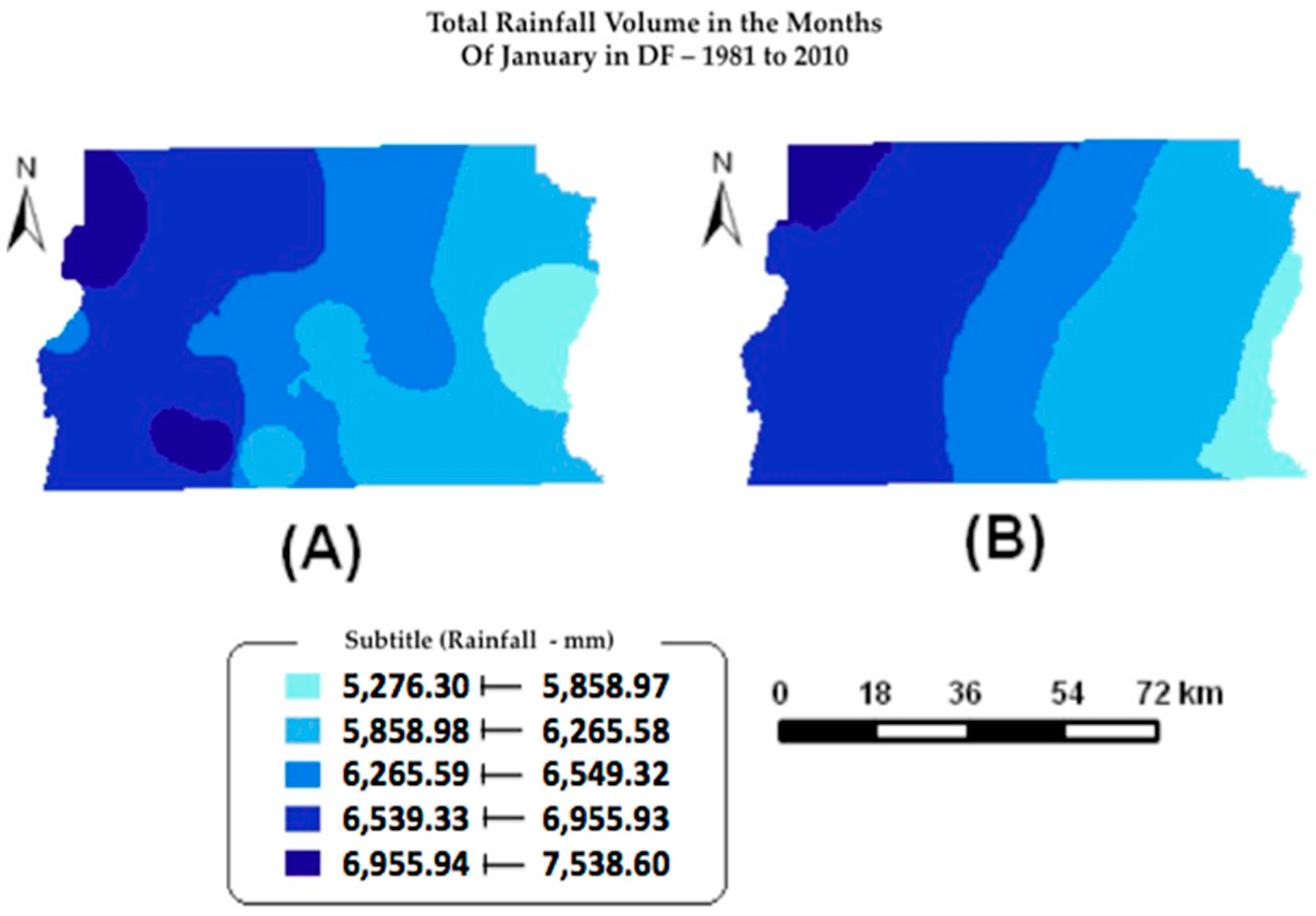
3.2. Map of Total Volume of Rainfall in the Federal District in the Months of January from 1981 to 2010
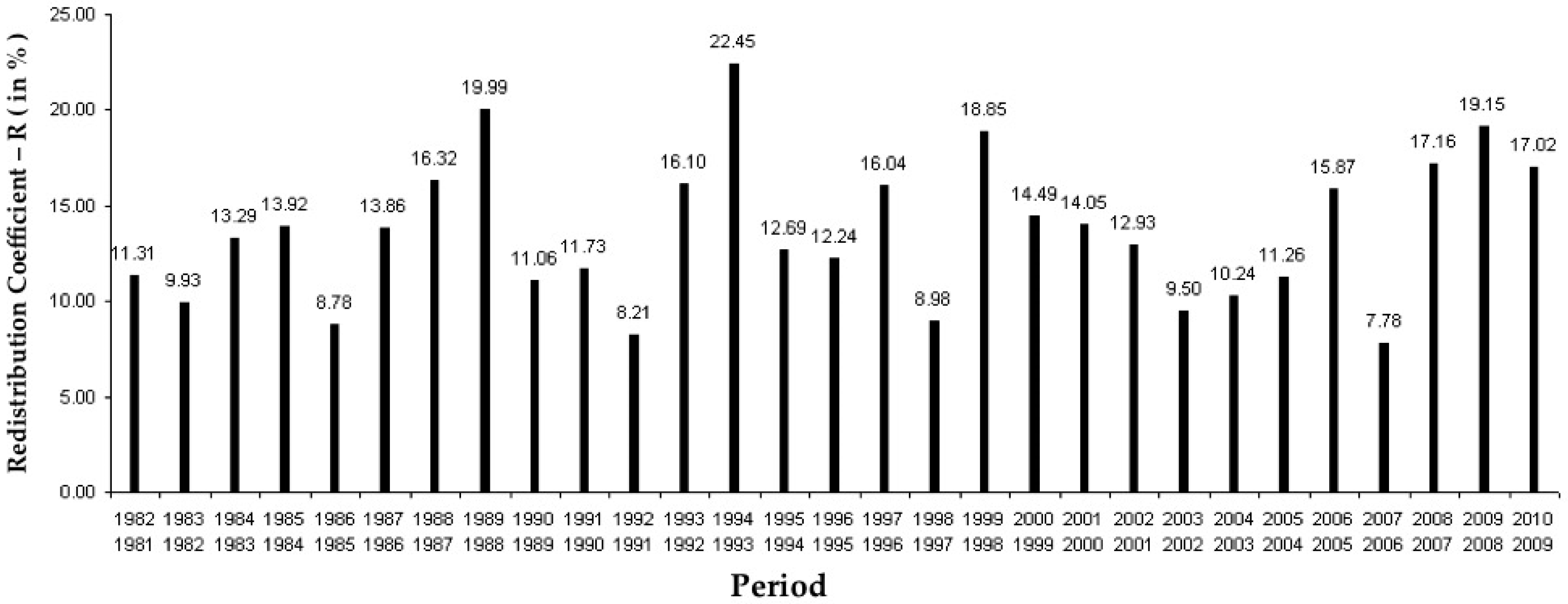
3.3. Dynamic of Rainfall Distribution at the 19 Rain Gauges
3.4. Descriptive Statistics for Rainfall Distribution in the Months of January from 1981 to 2010
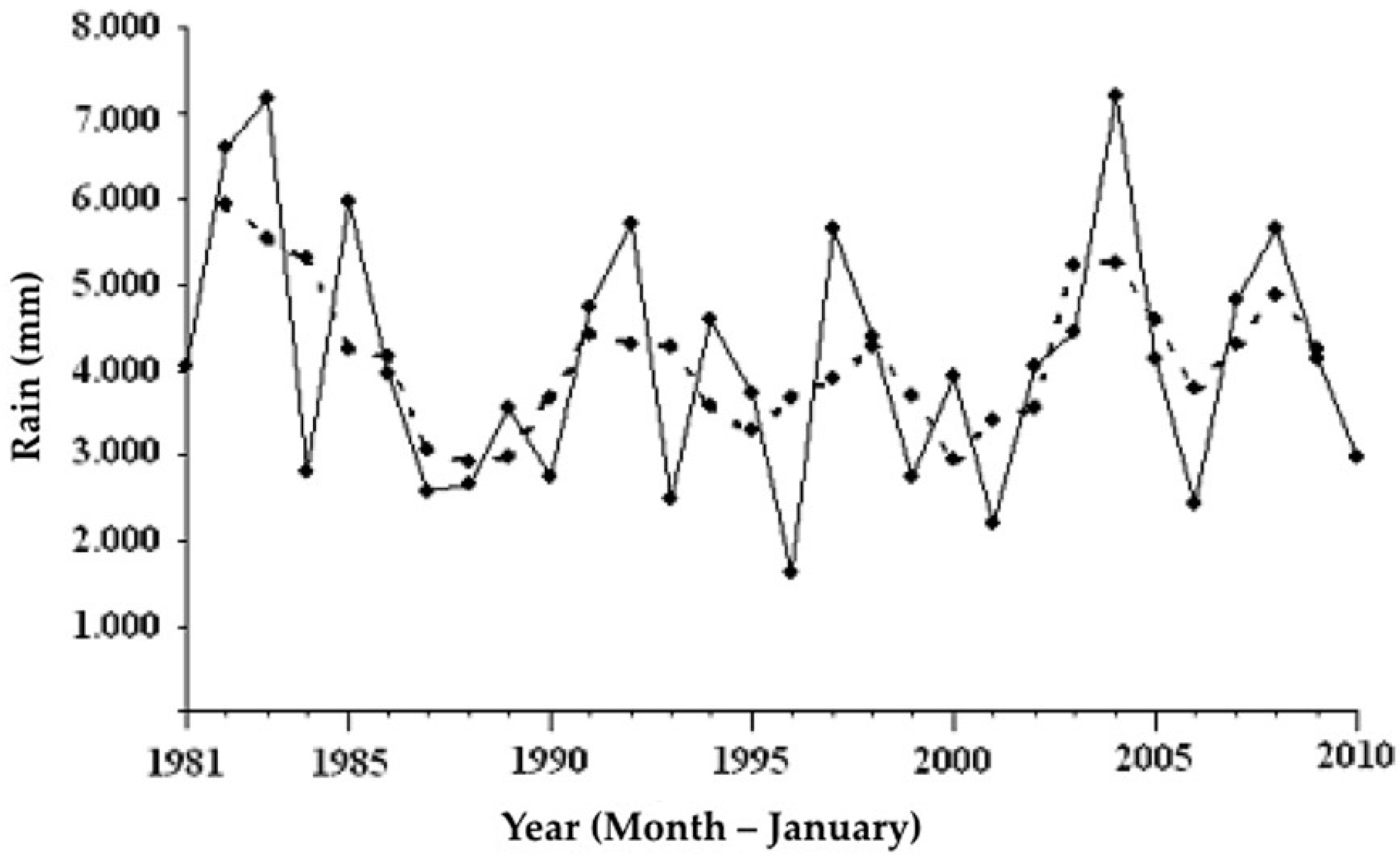
3.5. Time Series of Rainfall at the 19 Rain Gauges in the Months of January from 1981 to 2010
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Andrade, N.L.R.; Xavier, F.V.; Alves, E.C.F.R.; Silveira, A.; Oliveira, C.U.R. Caracterização Morfométrica e Pluviométrica da Bacia do Rio Manso—MT, Geociências; Rio Claro: Antioquia, Colombia, 2008; pp. 237–248. [Google Scholar]
- Setti, A.A.; Lima, J.E.F.W.; Chaves, A.G.M.; Pereira, I.C. Introdução ao Gerenciamento de Recursos Hídricos, 2nd ed.; Agência Nacional de Energia Elétrica, Superintendência de Estudos e Informações Hidrológicas: Brasília, Brazil, 2000. [Google Scholar]
- Lima, J.E.F.W. Determinação e Simulação da Evapotranspiração de Uma Bacia Hidrográfica do Cerrado; Universidade de Brasília: Brasília, Brazil, 2000. [Google Scholar]
- Campos, J.E.G. Hidrogeologia do Distrito Federal: Bases Para a Gestão dos Recursos Hídricos Subterrâneos; Revista Brasileira de Geociências: São Paulo, Brazil, 2004. [Google Scholar]
- Ramos, A.M.; dos Santos, L.A.R.; Fortes, L.T.G. Normais Climatológicas do Brasil: 1961–1990; INMET: Brasília, Brazil, 2009. [Google Scholar]
- Da Anunciação, Y.M.T. Regimes de Tempo e Precipitação Extrema de Verão Observados e Simulados na Região Central do Brasil. 101 f. (PHD in Geoscienses) Tese, Instituto de Geociências, Universidade de Brasília, Brasília, Brazil, 2013. [Google Scholar]
- Steinke, V.A.; Steinke, E.T.; Saito, C.H. Estimativa Da Temperatura De Superfície Em Áreas Urbanas Em Processo De Consolidação: Reflexões E Experimento Em Planaltina-DF. Rev. Bras. Climatol. 2010, 6, 37–56. [Google Scholar]
- Reinke, C.P.; da Silveira, R.B.; Reinke, R.L. Estudo Preliminar do Início e Término da Estação Chuvosa em Brasília. Available online: http://www.cbmet2010.com/anais/ (accessed on 22 November 2012).
- Oliveira, L.F.C.; Fioreze, A.P.; Medeiros, M.M.; Silva, M.A.S. Comparação de Metodologias de Preenchimento de Falhas de Séries Históricas de Precipitação Pluvial Annual; Revista Brasileira de Engenharia Agrícola e Ambiental: Campina Grande, Brazil, 2010. [Google Scholar]
- Gerardi, L.H.O.; Silva, B.C.N. Quantificação em Geografia; Difel: São Paulo, Brazil, 1981. [Google Scholar]
- IEMA/SEMATEC/UnB. Inventário Hidrogeológico e dos Recursos Hídricos Superficiais do Distrito Federal; IEMA/SEMATEC/UnB: Brasília, Brazil, 1998. [Google Scholar]
- Steinke, V.A.; e Steinke, E.T. Variação espaço-temporal da pluviosidade no Distrito Federal e seus condicionantes. In Simpósio Brasileiro De Climatologia Geográfica; 1 CD ROM; UFRJ: Rio de Janeiro, Brazil, 2001; pp. 21–31. [Google Scholar]
- Barros, J.R. A Chuva no Distrito Federal: O Regime e as Excepcionalidades do Ritmo. Rio Claro. 221 f. (Mestrado) Dissertação, Instituto de Geociências e Ciências Exatas, Departamento de Geografia, Universidade Estadual Paulista, Brasília, Brazil, 2003. [Google Scholar]
- Diniz, F.A. O clima de Brasília. In Disquete, Power Point, Palestra Proferida na Semana Meteorológica; INMET: Brasília, Brazil, 2004. [Google Scholar]
- Castro Filho, H.C.; Steinke, E.T.; Steinke, V.A. Análise espacial da precipitação pluviométrica na bacia do lago paranoá comparação de métodos de interpolação. Rev. Geon. 2012, 1, 336–345. [Google Scholar]
- Souza, J. Estatística Econômica e Social; Campus: Rio de Janeiro, Brazil, 1977. [Google Scholar]
- Morettin, P.A.; Toloi, C.M. Séries Temporais; Atual: São Paulo, Brazil, 1986. [Google Scholar]
- Steinke, V.A.; Sano, E.E. Semi-automatic identification, gis-based morphometry of geomorphic features of federal district of Brazil. Rev. Brasil. Geomorfol. 2011, 12, 3–9. [Google Scholar] [CrossRef]
- Steinke, V.A.; Pinto, M.L.C.; Araújo Neto, M.D.; Steinke, E.T. Proposed Relief Map of the Suitability of the Maranhão River Basin, Brazil, for Anthropogenic Use. J. Geogr. Inf. Syst. 2016, 8, 351–360. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinke, V.A.; Palhares de Melo, L.A.M.; Torres Steinke, E. Rainfall Variability in January in the Federal District of Brazil from 1981 to 2010. Climate 2017, 5, 68. https://doi.org/10.3390/cli5030068
Steinke VA, Palhares de Melo LAM, Torres Steinke E. Rainfall Variability in January in the Federal District of Brazil from 1981 to 2010. Climate. 2017; 5(3):68. https://doi.org/10.3390/cli5030068
Chicago/Turabian StyleSteinke, Valdir Adilson, Luis Alberto Martins Palhares de Melo, and Ercília Torres Steinke. 2017. "Rainfall Variability in January in the Federal District of Brazil from 1981 to 2010" Climate 5, no. 3: 68. https://doi.org/10.3390/cli5030068
APA StyleSteinke, V. A., Palhares de Melo, L. A. M., & Torres Steinke, E. (2017). Rainfall Variability in January in the Federal District of Brazil from 1981 to 2010. Climate, 5(3), 68. https://doi.org/10.3390/cli5030068





