Influence of Parameter Sensitivity and Uncertainty on Projected Runoff in the Upper Niger Basin under a Changing Climate
Abstract
1. Introduction
2. Materials and Methods
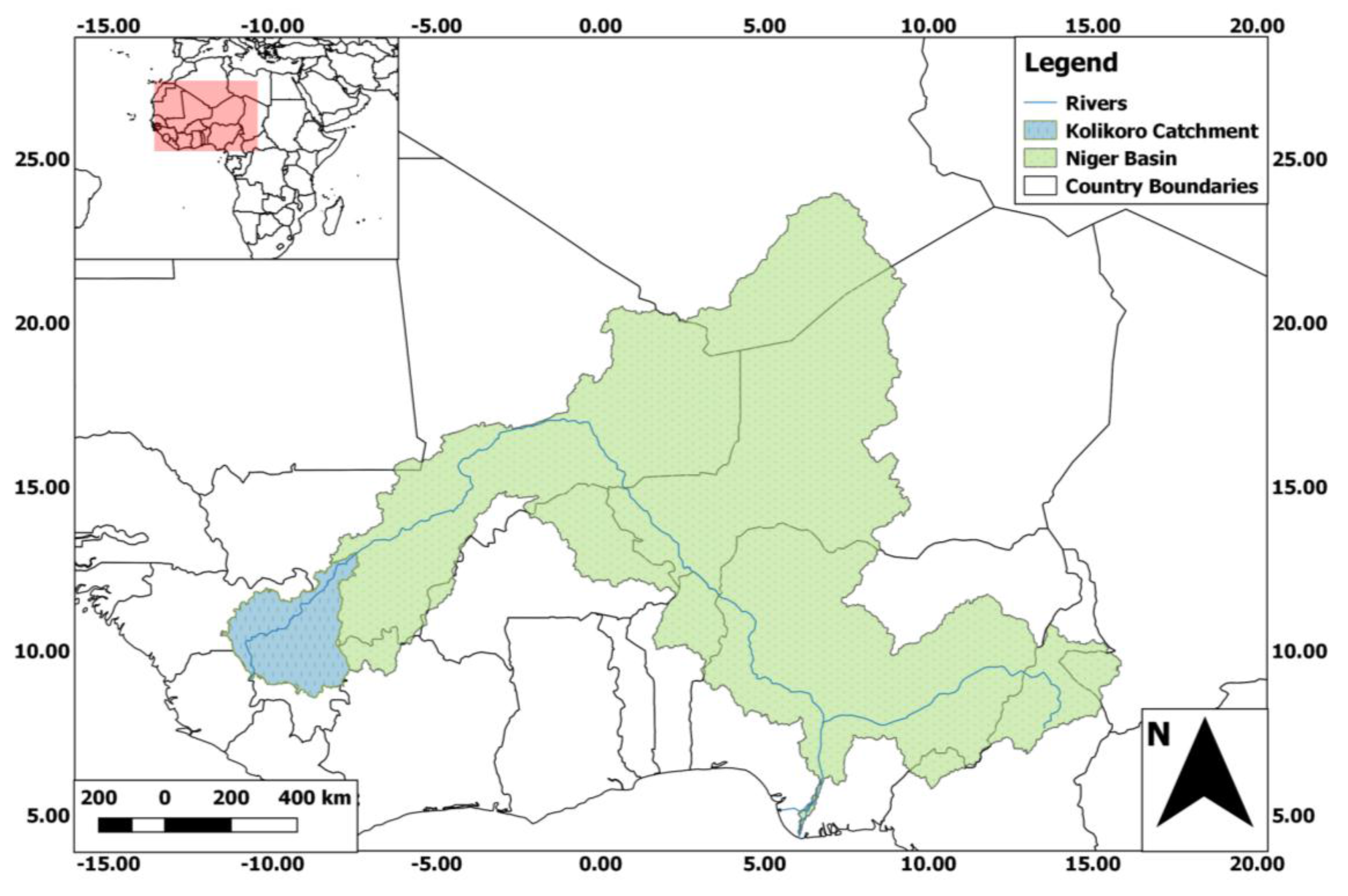
2.1. Study Area
2.2. Modelling Framework
2.2.1. Hydrological Models
2.2.2. Uncertainty and Sensitivity Analysis
2.3. Data
2.3.1. Observations
2.3.2. Future Projections
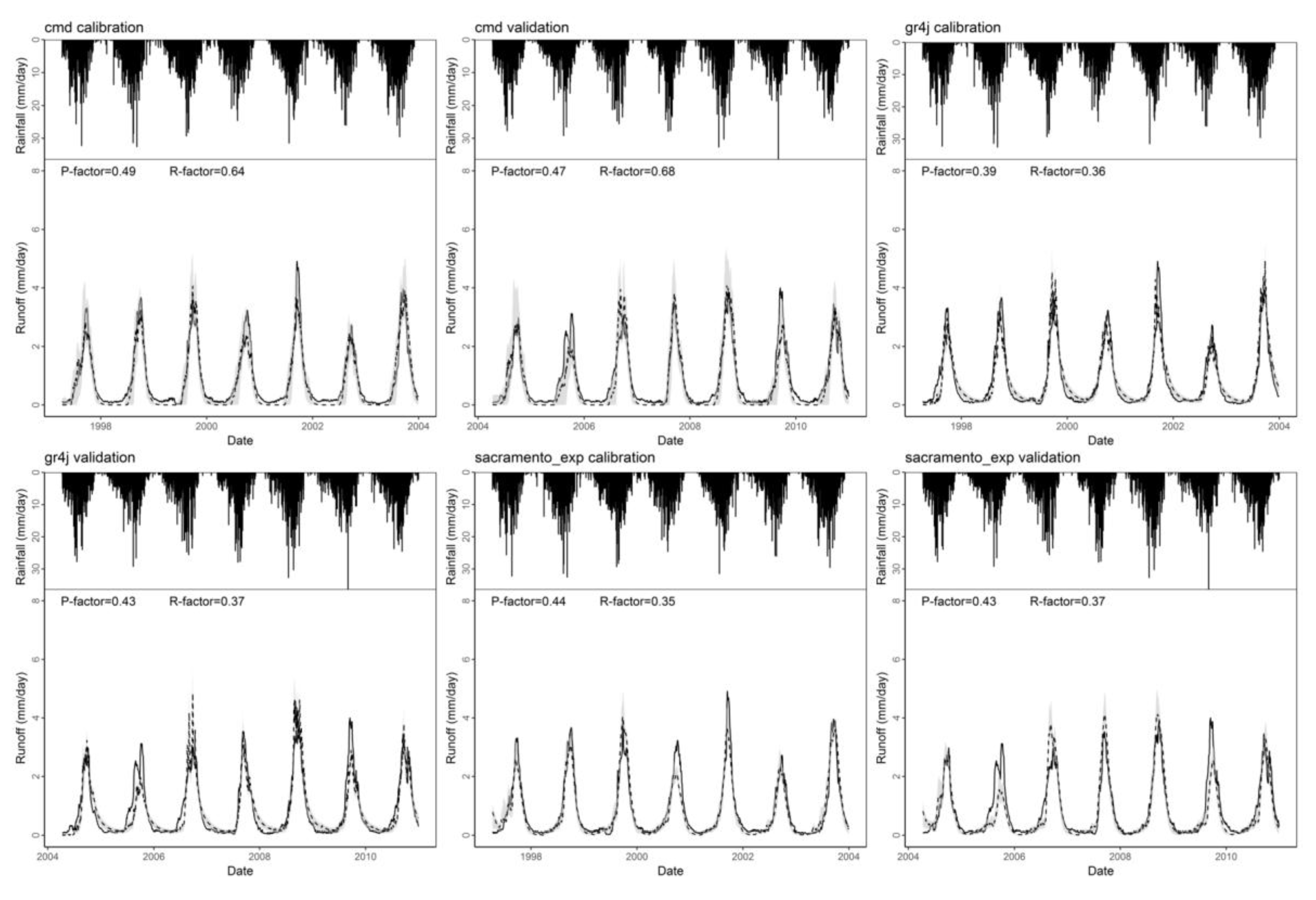
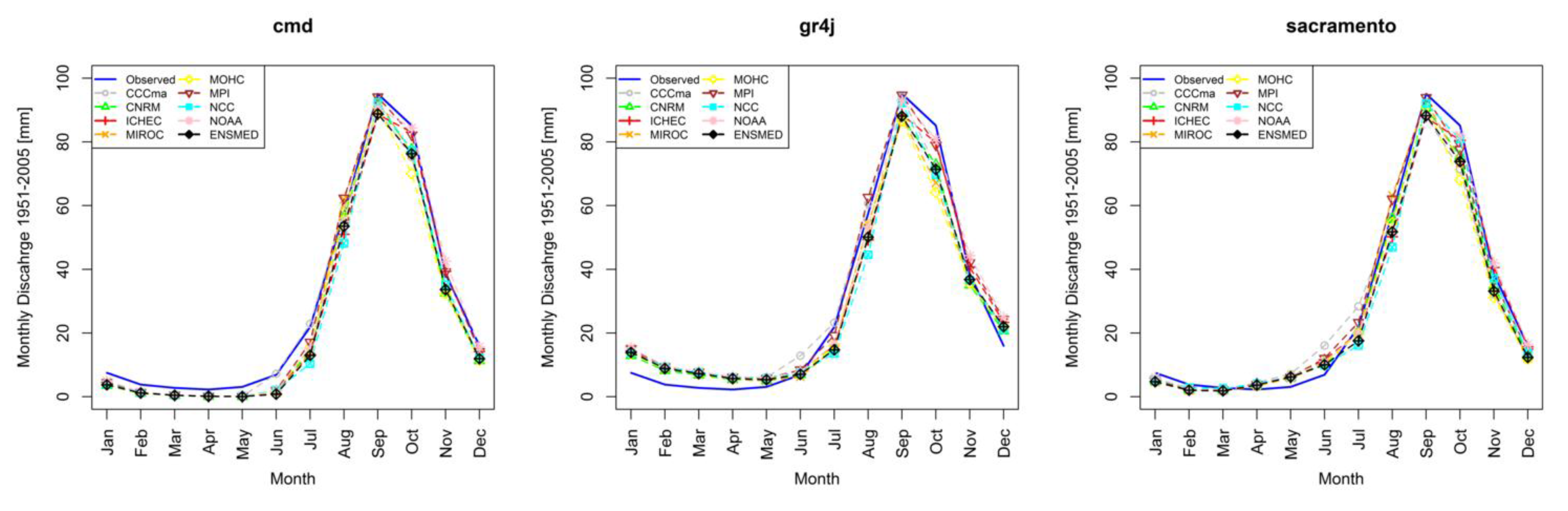
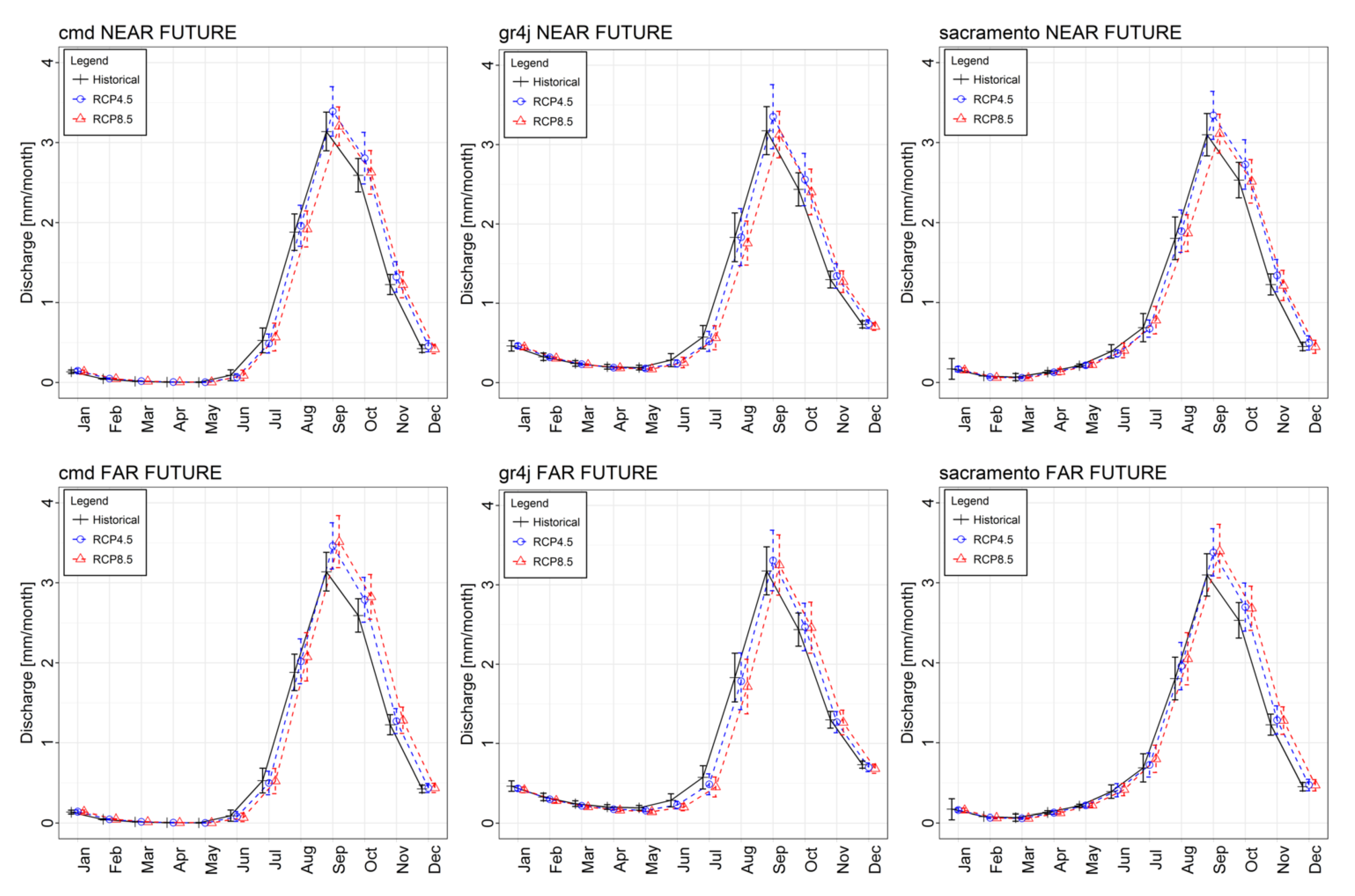
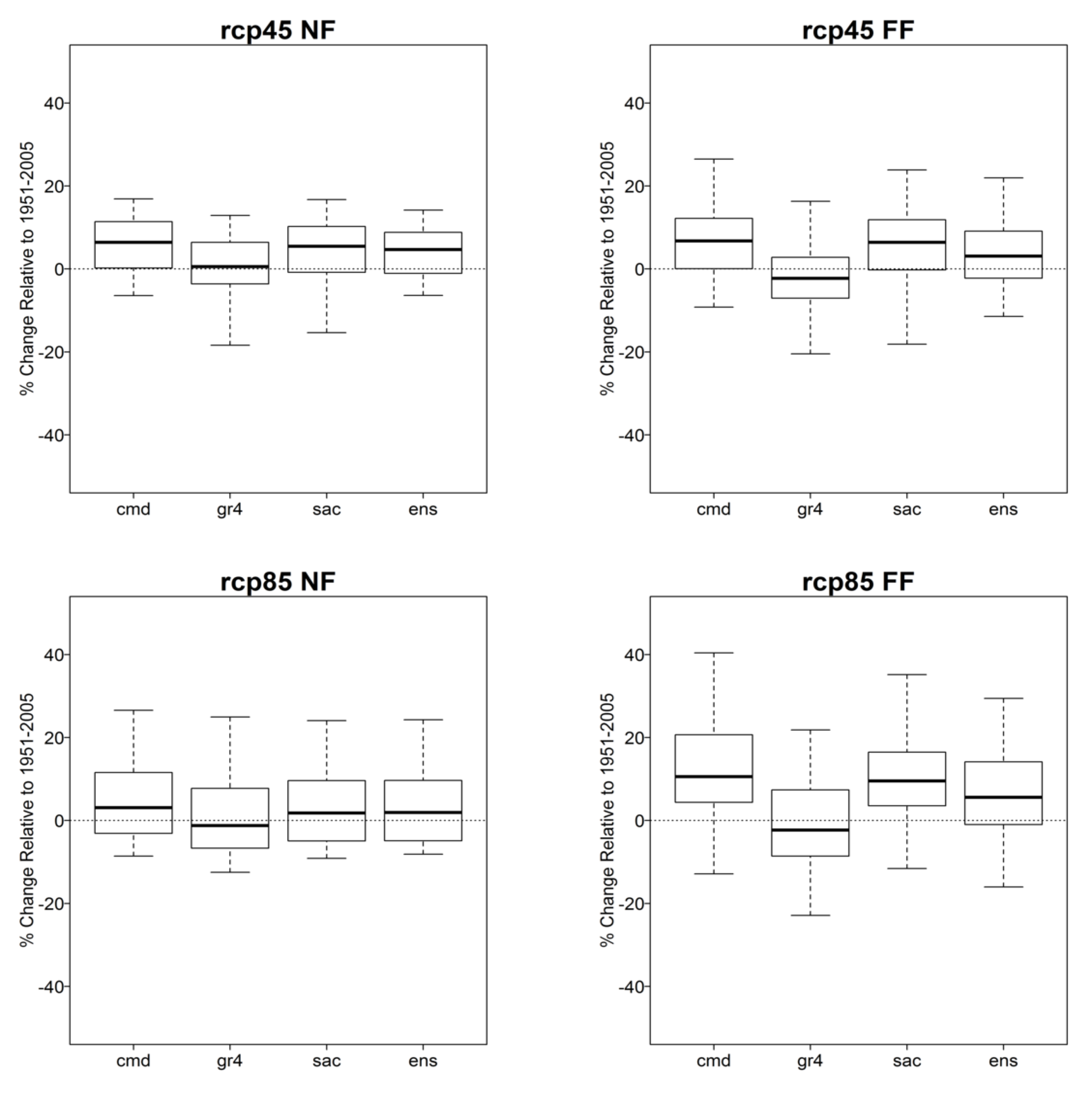
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Druyan, L.M. Studies of 21st-century precipitation trends over West Africa. Int. J. Climatol. 2011, 31, 1415–1424. [Google Scholar] [CrossRef]
- Sylla, M.B.; Giorgi, F.; Coppola, E.; Mariotti, L. Uncertainties in daily rainfall over Africa: Assessment of gridded observation products and evaluation of a regional climate model simulation. Int. J. Climatol. 2013, 33, 1805–1817. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian standardized rainfall index revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- Oyerinde, G.T.; Hountondji, F.C.C.; Wisser, D.; Diekkrüger, B.; Lawin, A.E.; Odofin, A.J.; Afouda, A. Hydro-climatic changes in the Niger basin and consistency of local perceptions. Reg. Environ. Chang. 2015, 15, 1627–1637. [Google Scholar] [CrossRef]
- KfW Adaptation to climate change in the upper and middle Niger River Basin. Available online: http://ccsl.iccip.net/niger_river_basin.pdf (accessed on 12 February 2017).
- Mahe, G.; Paturel, J.-E.; Servat, E.; Conway, D.; Dezetter, A. The impact of land use change on soil water holding capacity and river flow modelling in the Nakambe River, Burkina-Faso. J. Hydrol. 2005, 300, 33–43. [Google Scholar] [CrossRef]
- Descroix, L.; Mahé, G.; Lebel, T.; Favreau, G.; Galle, S.; Gautier, E.; Olivry, J.-C.; Albergel, J.; Amogu, O.; Cappelaere, B. Spatio-temporal variability of hydrological regimes around the boundaries between Sahelian and Sudanian areas of West Africa: A synthesis. J. Hydrol. 2009, 375, 90–102. [Google Scholar] [CrossRef]
- Uhlenbrook, S.; Seibert, J.; Leibundgut, C.; Rodhe, A. Prediction uncertainty of conceptual rainfall-runoff models caused by problems in identifying model parameters and structure. Hydrol. Sci. J. 1999, 44, 779–797. [Google Scholar] [CrossRef]
- Oyerinde, G.T.; Wisser, D.; Hountondji, F.C.C.; Odofin, A.J.; Lawin, A.E.; Afouda, A.; Diekkrüger, B. Quantifying Uncertainties in Modeling Climate Change Impacts on Hydropower Production. Climate 2016, 4, 1–15. [Google Scholar] [CrossRef]
- Kay, A.L.; Davies, H.N.; Bell, V.A.; Jones, R.G. Comparison of uncertainty sources for climate change impacts: Flood frequency in England. Clim. Chang. 2009, 92, 41–63. [Google Scholar] [CrossRef]
- Vetter, T.; Huang, S.; Aich, V.; Yang, T.; Wang, X.; Krysanova, V.; Hattermann, F. Multi-model climate impact assessment and intercomparison for three large-scale river. Earth Syst. Dyn. 2015, 6, 17–43. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, 1–22. [Google Scholar] [CrossRef]
- Knutti, R.; Sedláč, J. Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Chang. 2013, 3, 369–373. [Google Scholar] [CrossRef]
- Giorgi, F.; Francisco, R. Evaluating uncertainties in the prediction of regional climate change. Geophys. Res. Lett. 2000, 27, 1295–1298. [Google Scholar] [CrossRef]
- Cornelissen, T.; Diekkrüger, B.; Giertz, S. A comparison of hydrological models for assessing the impact of land use and climate change on discharge in a tropical catchment. J. Hydrol. 2013, 498, 221–236. [Google Scholar] [CrossRef]
- Yira, Y.; Diekkrüger, B.; Steup, G.; Bossa, A.Y. Impact of climate change on hydrological conditions in a tropical West African catchment using an ensemble of climate simulations. Hydrol. Earth Syst. Sci. 2017, 21, 2143–2161. [Google Scholar] [CrossRef]
- Ogilvie, A.; Mahéé, G.; Ward, J.; Serpantiéé, G.; Lemoalle, J.; Morand, P.; Barbier, B.; Kaczan, D.; Lukasiewicz, A.; Paturel, J.; et al. Water, agriculture and poverty in the Niger River basin. Water Int. 2010, 35, 594–622. [Google Scholar] [CrossRef]
- Andrews, F.T.; Croke, B.F.W.; Jakeman, A.J. An open software environment for hydrological model assessment and development. Environ. Model. Softw. 2011, 26, 1171–1185. [Google Scholar] [CrossRef]
- Croke, B.F.W.; Jakeman, A.J. A catchment moisture deficit module for the IHACRES rainfall-runoff model. Environ. Model. Softw. 2004, 19, 1–5. [Google Scholar] [CrossRef]
- Burnash, R.J. The NWS River Forecast System—Catchment Modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resource Publications: Littleton, CO, USA, 2012; p. 1144. [Google Scholar]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Oyerinde, G.T.; Fademi, I.O.; Denton, O.A. Modeling runoff with satellite-based rainfall estimates in the Niger basin. Cogent Food Agric. 2017, 3, 1–23. [Google Scholar] [CrossRef]
- Oyerinde, G.; Hountondji, F.C.C.; Lawin, A.E.; Odofin, A.J.; Afouda, A.; Diekkrüger, B. Improving Hydro-Climatic Projections with Bias-Correction in Sahelian Niger Basin, West Africa. Climate 2017, 5, 1–18. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J. Evaluation of several rainfall products used for hydrological applications over West Africa using two high-resolution gauge networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M. Graphical Goodness of Fit Description. Available online: https://www.rforge.net/doc/packages/hydroGOF/ggof.html (accessed on 17 May 2017).
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Criss, R.E.; Winston, W.E. Do Nash values have value? Discussion and alternate proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Chaibou Begou, J.; Jomaa, S.; Benabdallah, S.; Bazie, P.; Afouda, A.; Rode, M. Multi-Site Validation of the SWAT Model on the Bani Catchment: Model Performance and Predictive Uncertainty. Water 2016, 8, 178. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vad. Zone J. 2004, 3, 1340. [Google Scholar] [CrossRef]
- Soetaert, K.; Petzoldt, T. Inverse Modelling, Sensitivity and Monte Carlo Analysis in R Using Package FME. J. Stat. Softw. 2010, 33, 1–28. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; Mcnab, A.; Rudolf, B.; Schneider, U. The Global Precipitation Climatology Project ( GPCP ) Combined Precipitation Dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model? J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. EOS Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Metz, M. A new GRASS GIS toolkit for Hortonian analysis of drainage networks. Comput. Geosci. 2011, 37, 1162–1173. [Google Scholar] [CrossRef]
- Lucio, P.; Molion, L.; Valadão, C.; Conde, F.; Ramos, A.; MLD, M. Dynamical outlines of the rainfall variability and the ITCZ role over the West Sahel. Atmos. Clim. Sci. 2012, 2, 337–350. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Mounkaila, M.S.; Abiodun, B.J.; Bayo Omotosho, J. Assessing the capability of CORDEX models in simulating onset of rainfall in West Africa. Theor. Appl. Climatol. 2014. [Google Scholar] [CrossRef]
- Tall, M.; Sylla, M.B.; Diallo, I.; Pal, J.S.; Faye, A.; Mbaye, M.L.; Gaye, A.T. Projected impact of climate change in the hydroclimatology of Senegal with a focus over the Lake of Guiers for the twenty-first century. Theor. Appl. Climatol. 2016, 1–11. [Google Scholar] [CrossRef]
- Ravazzani, G.; Dalla Valle, F.; Gaudard, L.; Mendlik, T.; Gobiet, A.; Mancini, M. Assessing Climate Impacts on Hydropower Production: The Case of the Toce River Basin. Climate 2016, 4, 16. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Su, F.; Duan, X.; Chen, D.; Hao, Z.; Cuo, L. Evaluation of the Global Climate Models in the CMIP5 over the Tibetan Plateau. J. Clim. 2013, 26, 3187–3208. [Google Scholar] [CrossRef]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. Effect of different uncertainty sources on the skill of 10 day ensemble low flow forecasts for two hydrological models. Water Resour. Res. 2013, 49, 4035–4053. [Google Scholar] [CrossRef]
- Nicolle, P.; Pushpalatha, R.; Perrin, C.; François, D.; Thiéry, D.; Mathevet, T.; Le Lay, M.; Besson, F.; Soubeyroux, J.M.; Viel, C.; et al. Benchmarking hydrological models for low-flow simulation and forecasting on French catchments. Hydrol. Earth Syst. Sci. 2014, 18, 2829–2857. [Google Scholar] [CrossRef]
- Thapa, B.R.; Ishidaira, H.; Pandey, V.P.; Shakya, N.M. A multi-model approach for analyzing water balance dynamics in Kathmandu Valley, Nepal. J. Hydrol. Reg. Stud. 2017, 9, 149–162. [Google Scholar] [CrossRef]
- Lambert, S.J.; Boer, G.J. CMIP1 evaluation and intercomparison of coupled climate models. Clim. Dyn. 2001, 17, 83–106. [Google Scholar] [CrossRef]
- Diallo, I.; Sylla, M.B.; Giorgi, F.; Gaye, A.T.; Camara, M. Multimodel GCM-RCM Ensemble-Based Projections of Temperature and Precipitation over West Africa for the Early 21st Century. Int. J. Geophys. 2012, 2012, 1–19. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F.; Perrin, C. Multimodel evaluation of twenty lumped hydrological models under contrasted climate conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1171–1189. [Google Scholar] [CrossRef]

| Parameter | Description | Range | Calibrated Value | r Values between Mean Simulated Runoff and Parameters | |
|---|---|---|---|---|---|
| IHACRES-CMD | |||||
| f | Plant stress threshold as a proportion of d. | 0.01–3 | 0.723 | −0.791 | |
| e | Temperature to PET conversion factor. | 0.01–1.5 | 0.795 | −0.587 | |
| d | Threshold for producing flow. | 50–550 | 402.798 | −0.171 | |
| GR4J | |||||
| x1 | maximum capacity of the production store (mm). | 100–1200 | 891.941 | −0.950 | |
| x2 | groundwater exchange coefficient (mm). | −5–+3 | −0.564 | 0.129 | |
| x3 | one day ahead maximum capacity of the routing store (mm). | 20–300 | 214.509 | −0.209 | |
| x4 | time base of unit hydrograph (time steps). | 1.1–2.9 | 2.807 | −0.007 | |
| Sacramento | |||||
| uztwm | Upper zone tension water maximum capacity (mm). | 1–150 | 75.367 | −0.173 | |
| uzfwm | Upper zone free water maximum capacity (mm). | 1–150 | 82.171 | 0.015 | |
| uzk | Lateral drainage rate of upper zone free water expressed as a fraction of contents per day. | 0.5–1 | 0.207 | 0.019 | |
| pctim | The fraction of the catchment which produces impervious runoff during low flow conditions. | 0.1–1 | 0.073 | 0.918 | |
| adimp | The additional fraction of the catchment which exhibits impervious characteristics when the catchment’s tension water requirements are met. | 0–0.4 | 0.002 | −0.031 | |
| zperc | Maximum percolation (from upper zone free water into the lower zone) rate coefficient. | 1–250 | 70.797 | 0.003 | |
| rexp | An exponent determining the rate of change of the percolation rate with changing lower zone water contents. | 0–5 | 4.700 | 0.005 | |
| lztwm | Lower zone tension water maximum capacity (mm). | 1–500 | 10.424 | −0.336 | |
| lzfsm | Lower zone supplemental free water maximum capacity (mm). | 1–1000 | 251.439 | 0.103 | |
| lzfpm | Lower zone primary free water maximum capacity (mm). | 1–1000 | 576.492 | 0.091 | |
| lzsk | Lateral drainage rate of lower zone supplemental free water expressed as a fraction of contents per day. | 0.02–0.25 | 0.155 | 0.007 | |
| lzpk | Lateral drainage rate of lower zone primary free water expressed as a fraction of contents per day. | 0.0004–0.25 | 0.038 | 0.005 | |
| pfree | Direct percolation fraction from upper to lower zone free water. | 0–0.6 | 0.017 | 0.025 | |
| Modelling Center (or Group) | Institute ID | Model Name |
|---|---|---|
| Canadian Centre for Climate Modelling and Analysis | CCCMA | CanESM2 |
| Centre National de Recherches Météorologiques/Centre Européen de Recherche et Formation Avancée en Calcul Scientifique | CNRM-CERFACS | CNRM-CM5 |
| NOAA Geophysical Fluid Dynamics Laboratory | NOAA GFDL | GFDL-ESM2M |
| Met Office Hadley Centre (additional HadGEM2-ES realizations contributed by Instituto Nacional de Pesquisas Espaciais) | MOHC | HadGEM2-ES |
| Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology | MIROC | MIROC5 |
| Max-Planck-Institut für Meteorologie (Max Planck Institute for Meteorology) | MPI-M | MPI-ESM-LR |
| Norwegian Climate Centre | NCC | NorESM1-M |
| EC-EARTH consortium | ICHEC | EC-EARTH |
| Models | ME | RMSE | RSD | NSE | KGE | VE |
|---|---|---|---|---|---|---|
| Calibration (1997–2003) | ||||||
| Sacramento | −0.07 | 0.31 | 0.93 | 0.91 | 0.89 | 0.77 |
| GR4J | 0.01 | 0.36 | 0.92 | 0.88 | 0.90 | 0.72 |
| IHACRES-CMD | −0.10 | 0.30 | 0.99 | 0.92 | 0.88 | 0.75 |
| Validation (2004–2010) | ||||||
| Sacramento | −0.06 | 0.43 | 1.02 | 0.81 | 0.88 | 0.7 |
| GR4J | −0.02 | 0.39 | 0.95 | 0.84 | 0.9 | 0.69 |
| IHACRES-CMD | −0.12 | 0.37 | 1.05 | 0.86 | 0.84 | 0.71 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyerinde, G.T.; Diekkrüger, B. Influence of Parameter Sensitivity and Uncertainty on Projected Runoff in the Upper Niger Basin under a Changing Climate. Climate 2017, 5, 67. https://doi.org/10.3390/cli5030067
Oyerinde GT, Diekkrüger B. Influence of Parameter Sensitivity and Uncertainty on Projected Runoff in the Upper Niger Basin under a Changing Climate. Climate. 2017; 5(3):67. https://doi.org/10.3390/cli5030067
Chicago/Turabian StyleOyerinde, Ganiyu Titilope, and Bernd Diekkrüger. 2017. "Influence of Parameter Sensitivity and Uncertainty on Projected Runoff in the Upper Niger Basin under a Changing Climate" Climate 5, no. 3: 67. https://doi.org/10.3390/cli5030067
APA StyleOyerinde, G. T., & Diekkrüger, B. (2017). Influence of Parameter Sensitivity and Uncertainty on Projected Runoff in the Upper Niger Basin under a Changing Climate. Climate, 5(3), 67. https://doi.org/10.3390/cli5030067






