Detailed Urban Heat Island Projections for Cities Worldwide: Dynamical Downscaling CMIP5 Global Climate Models

Abstract

A new dynamical downscaling methodology to analyze the impact of global climate change on the local climate of cities worldwide is presented. The urban boundary layer climate model UrbClim is coupled to 11 global climate models contained in the Coupled Model Intercomparison Project 5 archive, conducting 20-year simulations for present (1986–2005) and future (2081–2100) climate conditions, considering the Representative Concentration Pathway 8.5 climate scenario. The evolution of the urban heat island of eight different cities, located on three continents, is quantified and assessed, with an unprecedented horizontal resolution of a few hundred meters. For all cities, urban and rural air temperatures are found to increase strongly, up to 7 °C. However, the urban heat island intensity in most cases increases only slightly, often even below the range of uncertainty. A potential explanation, focusing on the role of increased incoming longwave radiation, is put forth. Finally, an alternative method for generating urban climate projections is proposed, combining the ensemble temperature change statistics and the results of the present-day urban climate.

1. Introduction

There is increasing concern regarding the impact of global climate change on cities. Together with drought and flooding, extreme heat stress is perceived as a problem that may increase considerably if no action is taken. Indeed, global climate models (GCMs) predict an overall increase in air temperature and, consistently, also a rise of the number, frequency and intensity of heat waves [1,2]. Schär et al. [3] estimate that, in the future, extremely hot conditions, as occurred in Europe during the summer of 2003, could become more common.

Additionally, cities tend to be warmer than their rural surroundings, a phenomenon called the urban heat island (UHI), exposing urban residents to much higher levels of heat stress than people living in the nearby rural areas. In particular, cities experience higher air temperatures than their rural surroundings, with night-time temperature differences up to 10 °C under favorable conditions [4]. Considering that cities are home to the majority of humans and given also that cities are particularly vulnerable because of the concentration of infrastructure and economic activity, this is all the more relevant.

Yet, little or no information is available regarding future urban climate. Especially, climate projections at the scale of urban agglomerations are lacking, which is in part related to the computational constraints fine-scale climate models are facing. There have been efforts to study the response of urban and rural areas to climate change separately by coupling urban surface schemes in global climate models [5,6]. However, because of their coarse resolution, they may not capture mesoscale or local features and feedbacks, which are important for UHI development [7].

Furthermore, regional climate models with increasingly high resolutions are used to downscale global climate scenarios. McCarthy et al. [8] applied a 25-km resolution to study the UHIs of several cities in the U.K. under an A1B scenario. Kusuka et al. [9] used an even higher resolution of 3 km, but limited their simulations to one month in a study over the largest urban areas in Japan. In another study on both urban expansion and climate change with a 2-km resolution mesoscale model, Argüeso et al. [10] found a strong effect on nocturnal temperatures due to urbanization, which enhanced the climate change signal at local scales in Sydney (Australia). Since mesoscale models become exceedingly slow because of numerical stability constraints when going towards kilometer-scale resolutions, long model integrations are difficult to achieve. Some authors propose alternative methods to project the global climate at the regional scale with dynamical and statistical techniques and then simulating the local scale with an offline urban model or boundary layer scheme with a resolution of 1 km [7,11].

Despite their considerable efforts, these studies fail to either reach a horizontal resolution high enough to resolve all urban-scale features or simulation lengths long enough to deduce sound statistics. Moreover, all of these studies are based on the outputs of only one or two driving GCMs, whereas forcing by an ensemble of GCM outputs is required in order to properly represent the uncertainty associated with the global climate projections, as recommended by the Intergovernmental Panel on Climate Change (IPCC) [12].

In order to remedy this, a new urban climate model, UrbClim, was developed [13], which takes into account advection and feedback processes between the urban surface and the atmosphere, which cannot be included in studies with offline surface schemes. The model operates at a horizontal model resolution of a few hundred meters, which is unprecedented for this kind of study, while achieving an accuracy comparable to that of existing traditional models, but at a speed that is more than a hundred times higher. As a result, UrbClim is capable of covering periods long enough (tens of years) to deduce relevant climate statistics.

The goal of this study is to couple UrbClim to as large as possible an ensemble of GCMs contained in the Coupled Model Intercomparison Project 5 (CMIP5) archive of the IPCC and conducting simulations for present (1986–2005) and future (2081–2100) climate conditions, considering the Representative Concentration Pathway (RCP) 8.5 scenario, to assess the evolution of the UHI for a number of cities all over the world.

The remainder of this paper is organized as follows. In Section 2, the urban boundary layer climate model is described and evaluated for a focal city. This section further provides the presentation of a general applicable UHI indicator, as well as a description of how the input data for the model are adapted for operation at a global scale. In Section 3, the procedure to couple the model to the GCMs is explained, including all details on the preparation of the required input data. Section 4 presents the main results and discussions of this research, while conclusions are drawn in Section 5.

2. Numerical Model, Experiment Setup and Model Evaluation

2.1. The UrbClim Model

UrbClim is an urban climate model designed to simulate and study the UHI effect and other urban climate variables (wind speed, humidity, etc.) at a spatial resolution of a few hundred meters [13]. The model scales large-scale weather conditions down to the agglomeration scale and computes the impact of urban development on the most important weather parameters. UrbClim consists of a land surface scheme containing simplified urban physics, coupled to a 3D atmospheric boundary layer module. The latter is tied to synoptic-scale meteorological fields through the lateral and top boundary conditions, to ensure that the synoptic forcing is properly taken into account. The land surface scheme is based on the soil-vegetation-atmosphere transfer scheme of De Ridder and Schayes [14], but is extended to account for urban surface physics. This urbanization is accomplished in a rather simple way, by representing the urban surface as a rough impermeable slab, with appropriate values for the albedo, emissivity, thermal conductivity and volumetric heat capacity. The main feature of the extension of the scheme is the inclusion of a parameterization of the inverse Stanton number, which is known to be much higher in urban areas [15,16]. All of the details can be found in De Ridder et al. [13].

While most other recent urban surface exchange models (e.g., [17,18,19]) provide some canopy level detail, by decomposing the urban fabric into roof, wall and road facets, we have chosen to establish UrbClim on the simpler inverse Stanton number (bulk) approach, for several reasons. For one, urban canopy models need to specify transfer coefficients between the building facets and the canopy air. Many models, also recent ones, rely on fairly ancient parameterizations, e.g., by Jürges [20] (used in, e.g., [17]) or Rowley et al. [21] (used in, e.g., [18,19]). Whereas these wall transfer coefficients were established by means of scale experiments, the Stanton-based heat transfer coefficients in UrbClim are obtained from a series of real-world experiments that we conducted on actual cities, using remotely-sensed surface thermal infrared temperature [16,22,23]. While doing so entails disregarding certain physical processes occurring within the urban canopy, our approach is based on observations from actual urban areas, rather than it having to rely on scale model experiments. Moreover, it has been shown that the use of the inverse Stanton number framework is consistent with Monin-Obukhov similarity theory [15]. Finally, we want to simulate a considerable number of cities all over the world, and a detailed urban canopy model would require high detail regarding canopy characteristics (geometrical, material constants, etc.), for which the available datasets for most cities are at best scanty.

The land surface scheme in UrbClim takes part of its input variables (wind speed, temperature and specific humidity close to the surface) from values simulated in the atmospheric boundary layer model, a basic 3D model of the lower atmosphere, extending to a height of a few kilometers. This model is represented by conservation equations for horizontal momentum (considering zonal and meridional wind speed components u and v, respectively), potential temperature, specific humidity and mass (involving the vertical wind speed component w). Pressure fields are not calculated internally, but prescribed from a large-scale host model from which UrbClim receives its boundary conditions; hence, only the synoptic-scale pressure gradient is accounted for. By doing so, we avoid the complexities associated with a full mesoscale meteorological model. More importantly, it allows the use of much longer time increments in the numerical solver and a lower model top (since no absorbing layer is required to damp gravity waves), which makes the model much faster.

The first model level is situated at 10 m above the displacement height. The 2-m temperature, which this study focusses on, is estimated diagnostically by extrapolation, using profile functions specified in De Ridder et al. [13]. For urban surfaces, the vertical extrapolation is performed down to the roof level, assuming that the resulting temperature is representative for the urban canyon as a whole, which is assumed homogeneously mixed. This homogeneous mixing assumption in the urban canopy layer is supported by several studies (e.g., [24,25]).

Terrain elevation data are taken from the GMTED2010 Dataset [26], which has a global coverage and is freely available. The spatial distribution of land cover types, needed for the specification of required land surface parameters, is taken from the CORINE land cover data for Europe [27]. The percentage urban land cover is specified using the urban soil sealing raster data files distributed by the European Environment Agency. Maps of the vegetation cover fraction are obtained from the Normalized Difference Vegetation Index (NDVI) acquired by the MODIS instrument on-board the TERRA satellite platform. Vegetation cover fraction is specified as a function of the NDVI using a linear relationship proposed by Gutman and Ignatov [28] and then interpolated to the model grid. Model grid cells featuring exclusively non-urban land use types are divided into vegetation and bare soil (the complementary fraction). In the case of grid cells containing urban land use, the urban fraction as derived from the soil sealing data takes precedence over the NDVI-based fractional vegetation cover data in case both sum to over 100%. In case they sum to less than that, the remaining fraction is assigned to bare soil. Note that even though the parameter space is fixed for each land cover type in the model, spatial heterogeneity is assured by the spatial variability of the soil sealing and vegetation cover fractions of a grid cell, which define the effective roughness length of a grid cell through the inverse Stanton number framework.

Each of the surface types within a grid cell has its own energy balance and corresponding temperature, although the model employs aggregated values for both the aerodynamic and the thermal roughness length parameters. The reason for doing so is that we consider model applications with spatial resolutions of the order of a few hundred meters, and it is fair to assume that at this scale, turbulent intensities, as represented by the aerodynamic resistances, are fairly homogenous. The urban surface cover has an associated very low thermal roughness length, which strongly inhibits the turbulent transfer of heat from the urban substrate to the atmosphere, so that a relatively large share of the available radiant surface energy flux is converted to storage heat, rather than to turbulent sensible heating of the atmosphere. This, together with the typically high values of thermal inertia of urban materials, leads to the large storage heat flux values typically observed (or estimated as a residual of the surface energy balance) over urban areas [29].

The urban substrate is represented as a massive slab, which is discretized into six vertical layers, and its specific volumetric heat capacity (2 × 10⁶ J·m⁻³·K⁻¹) and thermal conductivity (2 W·m⁻¹·K⁻¹) values are in line with the values found in the literature for urban areas (see, e.g., [30,31]). Evaporation from the urban surface is included by implementing a fractional surface wetness parameter, which accounts for the amount of water stored on the urban substrate, calculated as the difference between precipitation on the urban fraction and evaporation of the stored water. The maximal fraction of wet surface is set as 0.14, with a maximum storage capacity of 1.17 kg·m⁻². Both parameters have been estimated recently by Wouters et al. [32]. The evolution of the temperature profile in the soil is calculated using the same heat diffusion equations as those used for the urban slab. The main difference is that, for soil, the volumetric heat capacity and thermal conductivity are functions of soil moisture content, as in De Ridder and Schayes [14]. Water transport in the soil is described by means of Richards’ equation [33], accounting for infiltration of rain water in the soil and the uptake of soil water by plant roots. Here, also, the reader is referred to De Ridder and Schayes [14] for more details.

In this study, the UrbClim model is applied to simulate a 20-year reference period (1986–2005) and a future period (2081–2100), directly driven by either meteorological data from the ERA-Interim reanalysis of the European Centre for Medium-range Weather Forecasting (ECMWF) or GCM output fields from the CMIP5 archive of the IPCC (see Section 3.1). The study focusses on the summer months (e.g., June, July and August in the Northern Hemisphere), since this is the period when the highest temperature events and strongest UHIs occur. Each year, the UrbClim simulations are initialized on 1 May at 0000 LT, resulting in a one-month spin-up before the start of the analysis on 1 June each summer, in order to ensure model equilibrium between external forcing and internal dynamics, especially in terms of soil variables. Initial soil temperature and soil moisture data are taken from the driving ERA-Interim reanalysis or GCM, respectively.

2.2. Model Evaluation

The UrbClim model has already been subjected to exhaustive validation regarding its energy fluxes, wind variables, 2-m air temperatures and urban-rural temperature differences for the cities of Ghent (Belgium), Bilbao (Spain) and Toulouse (France) in De Ridder et al. [13]. Error statistics from the UrbClim model were compared to these from a large number of urban surface schemes, evaluated in an international intercomparison study [34]. When evaluating the performance of UrbClim regarding energy fluxes for the city of Toulouse over a full summer season, the root mean square error on the sensible heat flux (49 W·m⁻²) was smaller than any of the December–January values presented in Best and Grimmond [34], which are in the range of 5–6134 W·m⁻². Furthermore, the error statistics of 2-m air temperatures at different sites pointed to an overall good performance of the model, with a bias of a few tenths of a degree, a root mean square error around 1.4 °C and a correlation coefficient with a value of 0.95. This puts our simple model in the same performance category as that of more detailed and complete mesoscale models (see, e.g., [35,36,37,38]).

Lauwaet et al. [39] evaluated the simulated UHI effect for the city of Brussels (Belgium) during the summer of 2008 and found that the model was able to reproduce the observed differences in time series of 2-m air temperatures from 3 different stations, with very small positive biases, root mean square errors around 1 °C and correlation coefficients up to 0.7. Furthermore, the land surface temperatures from the UrbClim land surface scheme have already been validated in the past with satellite data for the city of Paris and the German Ruhr area, yielding good comparisons between simulated and observed land surface temperatures from thermal infrared satellite imagery [16,22,23].

For the city of Antwerp (Belgium), which is the focal city of this study, we performed 2-m air temperature measurements on a location inside the densely built-up city center (Oosterwijk, 51.2085 N, 4.4101 E) and a rural location southeast of the city center (Vremde, 51.1660 N, 4.5487 E) for the month of August 2012. In Figure 1, the model’s ability to reproduce the observed urban-rural temperature differences is assessed. This quantity is quite hard to correctly reproduce, as it arises as a rather small difference of two values exhibiting a comparatively large diurnal amplitude. Nevertheless, the time series and error statistics show a fair agreement between the simulated and observed temperature differences, with almost no bias, a root mean square error in the order of 1 °C and a correlation coefficient over 0.7.

From all of the studies and results listed above, we can conclude that the UrbClim model performs satisfactorily and seems well suited to address the research questions in this study.

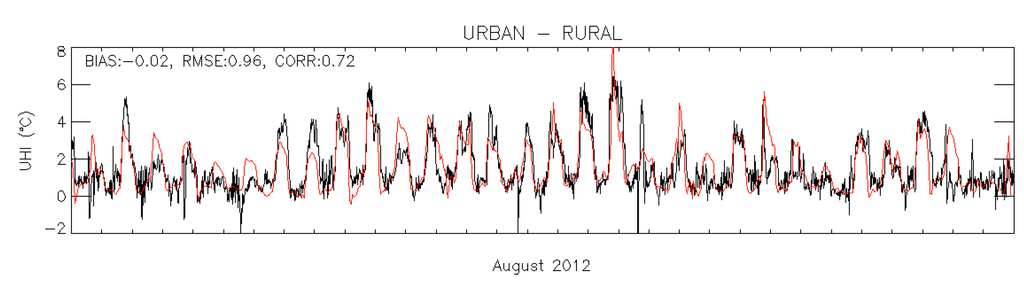
Figure 1. Urban-rural 2-m air temperature difference between the city center and the rural station for the measurements (black) and the UrbClim model (red), for August 2012. Error statistics (model bias, root mean square error and correlation coefficient) are given in the top left of the figure. UHI, urban heat island. The location of both stations is denoted in Figure 2.

Figure 1. Urban-rural 2-m air temperature difference between the city center and the rural station for the measurements (black) and the UrbClim model (red), for August 2012. Error statistics (model bias, root mean square error and correlation coefficient) are given in the top left of the figure. UHI, urban heat island. The location of both stations is denoted in Figure 2.

2.3. UHI Indicator Definition

Since the goal of this study is to quantify and assess the evolution of the UHI of several cities worldwide, it is important to define a clear and general applicable indicator for the UHI. The indicator needs to quantify the difference in 2-m air temperature between the urban and the rural part of the city domains. Because the air temperature UHI effect reaches a maximum in the late evening and early night, we take care to include the (nocturnal) minimum temperatures in the indicator.

The resulting temperature indicator quantifies the heat stress in the simulated domain using the temperature during warm summer nights. More specifically, we consider the temporal 95th percentile of the minimum temperatures for the summer period, i.e., the minimum temperature that is exceeded on average 5 times each summer (considering that summer extends over the period June–August). For cities in a hilly environment, the UHI effect is often blurred by topographical effects. Therefore, all air temperatures are henceforth corrected for terrain height by rescaling them to the average city height, applying a lapse rate of 6.5 K·km⁻¹. As an example, Figure 2 shows the resulting indicator for the city of Antwerp, based on an UrbClim simulation for the period 1986–2005.

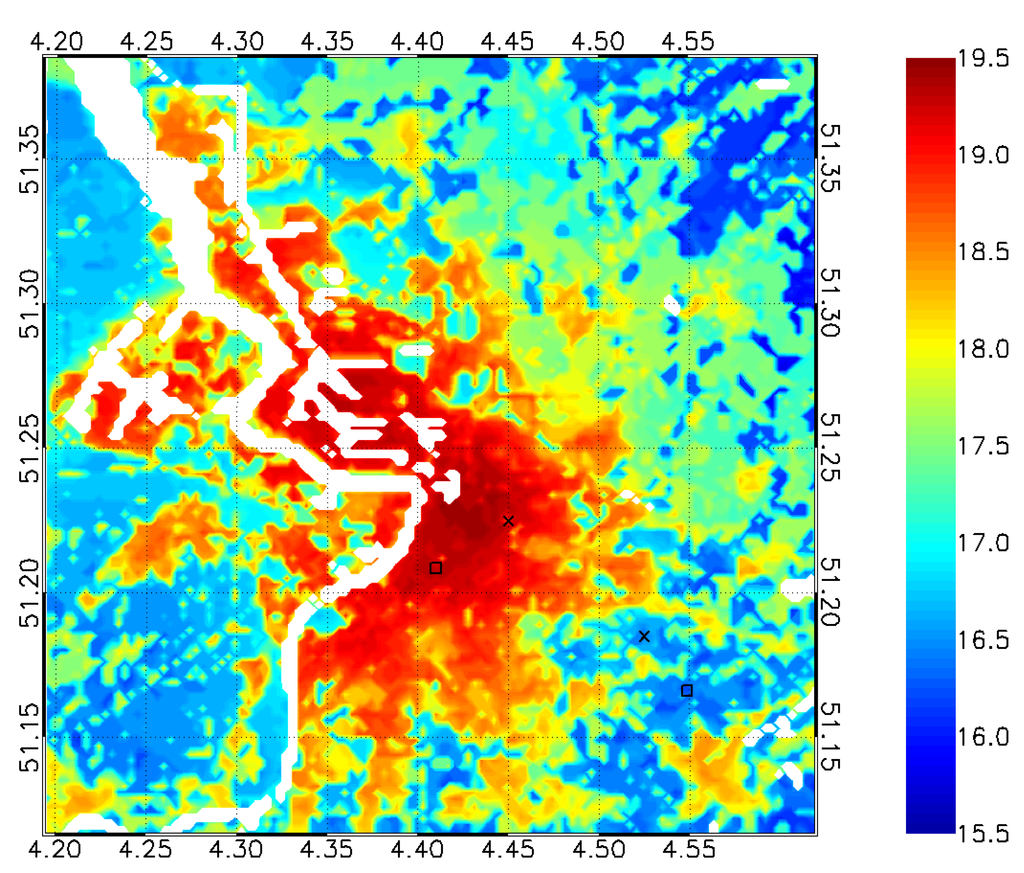
Figure 2. Temperature indicator for Antwerp for the period 1986–2005, based on ERA-Interim-driven UrbClim simulations. The urban and rural measurement locations from Figure 1 are denoted with a black square. The spatial P90 and P10 locations are denoted with a black cross. Grid cells over water are omitted from the analysis.

Figure 2. Temperature indicator for Antwerp for the period 1986–2005, based on ERA-Interim-driven UrbClim simulations. The urban and rural measurement locations from Figure 1 are denoted with a black square. The spatial P90 and P10 locations are denoted with a black cross. Grid cells over water are omitted from the analysis.

The UHI effect is quantified as the difference between the urban and the rural value of the temperature indicator. Here, we define the rural value as the spatial 10th percentile in the domain under investigation. Analogously, the urban value is defined using the spatial 90th percentile. In order to only consider parameter values above land, we neglect the grid cells above water in calculating the percentiles. For the city of Antwerp, this results in an UHI effect of 2.3 °C, just slightly lower than the UHI effect from the measurements (2.5 °C).

As mentioned before, the UHI indicator depends only on the 2-m air temperature; effects of wind speed and (relative) humidity are not taken into account. Although physiological studies indicate that both of these parameters are also important for the impact of heat stress on humans, the IPCC 5th Assessment Report (AR5) [12] questions their treatment in GCMs, especially when looking at local scales.

2.4. Towards the Global Applicability of the UrbClim Model

In this study, the focus is on eight different cities, as shown in Table 1. These correspond to the target cities of the EU-FP7 projects RAMSES [40] and NACLIM [41]. Table 1 shows for each city its location, the applied UrbClim domain size and model resolution and the summer months for which the simulations are performed. Two of the target cities are outside Europe (Rio de Janeiro and New York). The main difficulty in setting up UrbClim simulations for non-European cities is related to the availability of suitable terrain data. For European cities, we rely on the CORINE land cover data and the European Environment Agency soil sealing data, which are available for Europe only.

Table 1. Specifications of the cities, domains and periods considered here.

City	Country	Latitude (°)	Longitude (°)	Domain Size (km2)	Model Resolution	Summer Period
Almada	Portugal	38.68	9.16	30 × 30	250 m	June–August
Antwerp	Belgium	51.25	4.41	30 × 30	250 m	June–August
Berlin	Germany	52.52	13.38	50 × 50	250 m	June–August
Bilbao	Spain	43.26	−2.92	30 × 30	250 m	June–August
London	U.K.	51.51	−0.13	90 × 90	500 m	June–August
New York	USA	40.71	−74.01	120 × 120	1 km	June–August
Rio de Janeiro	Brazil	−22.84	−43.32	70 × 70	500 m	January–March
Skopje	Macedonia	42.00	21.43	30 × 30	250 m	June–August

Table 1. Specifications of the cities, domains and periods considered here.

City	Country	Latitude (°)	Longitude (°)	Domain Size (km2)	Model Resolution	Summer Period
Almada	Portugal	38.68	9.16	30 × 30	250 m	June–August
Antwerp	Belgium	51.25	4.41	30 × 30	250 m	June–August
Berlin	Germany	52.52	13.38	50 × 50	250 m	June–August
Bilbao	Spain	43.26	−2.92	30 × 30	250 m	June–August
London	U.K.	51.51	−0.13	90 × 90	500 m	June–August
New York	USA	40.71	−74.01	120 × 120	1 km	June–August
Rio de Janeiro	Brazil	−22.84	−43.32	70 × 70	500 m	January–March
Skopje	Macedonia	42.00	21.43	30 × 30	250 m	June–August

There are some alternatives for the CORINE land cover data, but none of them achieves the 100-m resolution of the CORINE dataset. The highest resolution alternative is the GlobCover dataset, which provides land cover data at 300-m resolution. As a second alternative, MODIS provides land use data at 500-m resolution. There are differences in classifications between GlobCover or MODIS land use, on the one hand, and the CORINE land cover dataset, on the other hand. Most of these, for instance the different treatment of harbors, which in MODIS and GlobCover are often classified as “bare soil”, while CORINE classifies them as “industrial areas”, are quite easily resolved by comparing the composed land cover with satellite data and modifying some class definitions by hand. A more subtle difference comprises the categorization of urban areas. Whereas CORINE makes a distinction between urban and suburban areas, GlobCover and MODIS contain only one class with artificial structures. It turns out that GlobCover mainly underestimates the size of cities, whereas MODIS appears to have a tendency to overestimate the size of urban areas [42]. Since the modelling of urban heat islands crucially relies on correct city delimitations, corrective measures are taken based on a visual comparison with satellite data. For Rio de Janeiro and New York, we have made an overlay between the GlobCover and the MODIS land use data, where the city limits of the former are used as the boundary of the inner “urban areas”, and the city limits of the latter are used as the boundary of the outer “suburban area”.

Regarding the soil sealing information, the EEA soil sealing data provide the covering of the ground by an impermeable material on a 100-m scale for Europe, and similar datasets are not available at the global level. Although the Visible Infrared Imaging Radiometer Suite (VIIRS) impervious surfaces dataset does provide similar data, the resolution of this dataset is far from sufficient. Hence, we chose to apply a different strategy, establishing a relation between the land use data, the NDVI and the soil sealing. In detail, the soil sealing in an urban grid cell is determined as a function of the GlobCover and MODIS land use and the NDVI in the cell and the neighboring cells, where the neighboring cells under consideration form a 2 × 2 km² square around the cell. Since the soil sealing in non-urban cells is typically much lower than the soil sealing in urban cells, the soil sealing of non-urban cells is set to zero. The regression has been constructed and validated for European cities via a leave-one-out principle, i.e., the regression parameters were derived using the data for Almada, Berlin, Bilbao, London and Skopje and validated using the data for Antwerp. The regression acquires an explained variance of R² = 0.67. Following this evaluation based on independent data, the regression can be applied to non-European cities, and now, for any city, the terrain input for UrbClim can be constructed.

The procedures to reconstruct land cover and soil sealing described above were validated using UrbClim simulation results for Antwerp. Since the soil sealing regression described above was established without using any data for Antwerp, this method provides an independent validation of the complete procedure outlined in the previous paragraphs. UrbClim runs with GlobCover/MODIS land cover and reconstructed soil sealing were performed for the period 1986–2005, and the results of these runs were compared with output data for the same period, but obtained with CORINE land use and EEA soil sealing data. Figure 3 compares the difference between the rural and the urban temperature for the month of August 2003. As described above, the rural and urban temperature are defined as the 10th, respectively the 90th, spatial percentile occurring in the domain. The time series of the simulations exhibit a good degree of similarity; the differences between both simulations are smaller than the uncertainty of the UrbClim output. The largest difference found for the period 1986–2005 amounts to 0.47 °C, the root mean square error being 0.10 °C. The correlation between both time series amounts to 0.997. We can conclude that the scheme to specify terrain parameters based on GlobCover and MODIS data has been successfully validated.

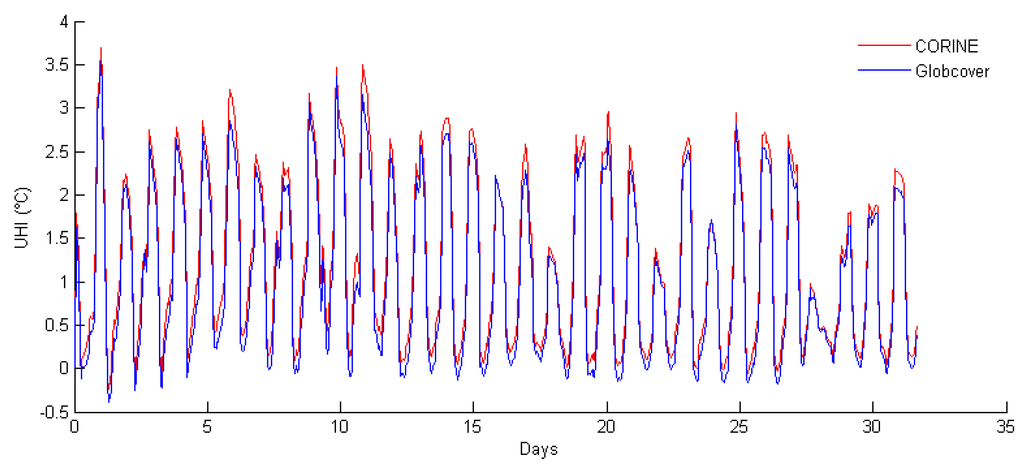
Figure 3. UHI intensity in Antwerp during August 2003 for the CORINE (red) and GlobCover/MODIS (blue) test simulations.

Figure 3. UHI intensity in Antwerp during August 2003 for the CORINE (red) and GlobCover/MODIS (blue) test simulations.

3. Coupling to GCM Output Fields

In order to make urban climate projections for the distant future (2081–2100), we need to rely on GCM output fields instead of the ERA-Interim forcing, which is used as a forcing for the UrbClim model for the reference (1986–2005) period. It is not ideal to force UrbClim using just one GCM. Rather, the model requires forcing by an ensemble of GCM outputs, in order to properly represent the uncertainty associated with the global climate projections. This will make it possible to obtain mean values and mean tendencies, together with an uncertainty range around them. The latest version of the IPCC report [12] also substantiates this as good practice, highlighting that the agreement between ensemble means and climate data exceeds the agreement with any single climate model by a large amount.

The IPCC report [12] identifies four climate scenarios, ranging from very strong mitigation scenarios (RCP2.6) to a business-as-usual scenario (RCP8.5). Due to CPU-limitations, we have only considered climate projections using the RCP8.5 scenario. Based on what is shown in AR5, it is reasonable to assume that, to first order, results for other RCP scenarios can be estimated simply by scaling between the reference (current) state and the RCP8.5 scenario. In any case, the reference case and the RCP8.5 scenario defines a range for presenting climate projection results. Note that, for the urban climate projections, the ERA-Interim runs are considered as the benchmark for the future climate projections. In Section 3.4, it is explained how the ERA-Interim reference period is made to match with the GCM-based reference period.

3.1. Input from the GCMs for Climate Projections

One of the main difficulties when switching from using ECMWF reanalysis data to CMIP5 GCM output fields is that of data availability. Indeed, while the ECMWF data are quite comprehensive, e.g., providing vertical profiles with a great level of detail (fine layers, many variables) every three hours, data available in the CMIP5 archive are much more limited. The minimal input requirements of the UrbClim model set a constraint on the GCMs of which outputs can be used to make urban climate projections. Table 2 provides a list with the necessary meteorological input parameters and the minimal time increment required for these variables when using them as forcing input for UrbClim.

Table 2. List of required meteorological input data to drive the UrbClim model.

Category	Variable	Required Time Increment
Surface	Downwelling short-wave radiation	3 h
	Downwelling long-wave radiation	3 h
	Surface air pressure	3 h
	Air temperature at surface	3 h
	U component of wind velocity at surface	3 h
	V component of wind velocity at surface	3 h
	Specific humidity at surface	3 h
Sea	Sea surface temperature	monthly
Precipitation	Total precipitation	3 h
	Convective precipitation	3 h
Vertical profiles	U component of wind velocity	6 h
	V component of wind velocity	6 h
	Temperature profile	6 h
	Specific humidity profile	6 h
Soil	Soil temperature	monthly
	Soil moisture content	monthly

Table 2. List of required meteorological input data to drive the UrbClim model.

Category	Variable	Required Time Increment
Surface	Downwelling short-wave radiation	3 h
	Downwelling long-wave radiation	3 h
	Surface air pressure	3 h
	Air temperature at surface	3 h
	U component of wind velocity at surface	3 h
	V component of wind velocity at surface	3 h
	Specific humidity at surface	3 h
Sea	Sea surface temperature	monthly
Precipitation	Total precipitation	3 h
	Convective precipitation	3 h
Vertical profiles	U component of wind velocity	6 h
	V component of wind velocity	6 h
	Temperature profile	6 h
	Specific humidity profile	6 h
Soil	Soil temperature	monthly
	Soil moisture content	monthly

Following a detailed scrutiny of the CMIP5 archives, it was found that 11 climate institutes provide model output in which all required parameters are available at a suitable time increment. In order to reduce the computational complexity, for each participating institute, a single model is selected according to the data availability and the model performance derived from the IPCC AR5. The list of GCMs used and their latitude and longitude grid size is shown in Table 3.

Table 3. List of global climate models (GCMs) used to drive the UrbClim model.

Model	Institute	ΔLon (°)	ΔLat (°)
ACCESS1.0	CSIRO/BOM	1.875	1.25
BNU_ESM	BNU	2.8125	2.79
CCSM4	NCAR	1.25	0.94
CNRM_CM5	CNRM	1.40625	1.4
FGOALS-G2	CAS	2.8125	2.79
GFDL-ESM2M	GFDL	2.5	2.02
GISS-E2-R	NASA	2.5	2
HadGem2-ES	MOHC	1.875	1.25
IPSL-CM5A-MR	IPSL	2.5	1.2676
MIROC-ESM-CHEM	Univ. Tokyo	2.8125	2.79
MRI-CGCM3	MRI	1.125	1.1121

Table 3. List of global climate models (GCMs) used to drive the UrbClim model.

Model	Institute	ΔLon (°)	ΔLat (°)
ACCESS1.0	CSIRO/BOM	1.875	1.25
BNU_ESM	BNU	2.8125	2.79
CCSM4	NCAR	1.25	0.94
CNRM_CM5	CNRM	1.40625	1.4
FGOALS-G2	CAS	2.8125	2.79
GFDL-ESM2M	GFDL	2.5	2.02
GISS-E2-R	NASA	2.5	2
HadGem2-ES	MOHC	1.875	1.25
IPSL-CM5A-MR	IPSL	2.5	1.2676
MIROC-ESM-CHEM	Univ. Tokyo	2.8125	2.79
MRI-CGCM3	MRI	1.125	1.1121

3.2. Construction of Vertical Profiles

Although the CMIP5 archives provide six-hourly vertical profiles, it should be noted that we cannot simply and solely use the six-hourly profiles as external driving fields for the UrbClim model. Indeed, the six-hourly frequency is far from sufficient, as UrbClim requires a forcing with a well-resolved diurnal cycle. This is particularly important in the context of urban climate modelling, which attaches much importance to the daily minimum and maximum temperatures, which clearly cannot be properly contained in data available at six-hourly intervals only. Even the three-hourly interval we aim for is perhaps a bit limited, but no finer temporal resolution is available within CMIP5 (at least not for a sizeable ensemble of GCM results). From our experience with the ECMWF’s three-hourly forcing frequency, we know at least that UrbClim results obtained with this forcing frequency compare favorably with observations. One of the challenges is therefore to reconstruct the vertical profiles of the required quantities on a three-hourly time frequency, based on the six-hourly information available in the CMIP5 archives.

The first step is to make the six-hourly profiles uniform, since there are two different types of vertical level definitions in the output data of the GCMs. For some models, the data are provided on hybrid sigma pressure level systems. In these systems, the output data are provided on scaled pressure levels, whereas the (geopotential) height of the pressure levels is not part of the output of the GCMs. It must therefore be calculated using the hypsometric equation,

$$h=\frac{R}{g}\overline{T}\ln \left(\frac{p_s}{p}\right)$$

(1)

where h indicates the height above the surface, p the pressure at height h, p_s is the surface pressure, $\overline{T}$ the layer mean virtual temperature and R and g denote the gas constant for air and the gravitational acceleration, respectively. Other models make use of a hybrid height level systems. Similarly to the definition of the pressure in hybrid pressure systems, the level height is now defined as a function of the terrain height and some constants, such that the lowest levels closely follow the terrain height, while the higher levels are more or less constant with respect to the mean sea surface height. In these hybrid sigma height level systems, the pressure of the model levels is not provided, and hence, the hypsometric equation is once more used to provide a link between the level pressure and the level height.

In summary, using the hypsometric equation, the formats of all of the vertical profiles can be equalized. These rescaled six-hourly vertical profiles for temperature, humidity and wind velocity can then serve as input for a statistical tool to compose three-hourly profiles. This statistical approach however not only uses the six-hourly profile, but also three-hourly surface quantities (in particular, the turbulent energy and momentum fluxes) are used. Indeed, while for the selected GCMs, the vertical profile data are available at a six-hourly time step, surface quantities (including the turbulent surface fluxes) are available at three-hourly time step. It is precisely this extra information that provides an aid in reconstructing the vertical profiles at the three-hourly time steps in between a pair of six-hourly data.

Using these input data, three-hourly forcing profiles are obtained by means of a regression based on a neural network approach. The neural networks are trained with ERA-Interim data from the period 1986–2005, and the method is thereafter validated with independent data, using ERA-Interim data for the period 2006–2013. In the neural networks, we use six-hourly profiles of temperature, wind speed and humidity and three-hourly surface data of the same parameters as explanatory variables to interpolate the six-hourly profile data. For each variable, a separate neural network is established. We opt for a two-layer feed-forward network with sigmoid hidden neurons and linear output neurons (Figure 4). To keep computer memory burden within bounds, the networks are trained using a conjugate-gradient method.

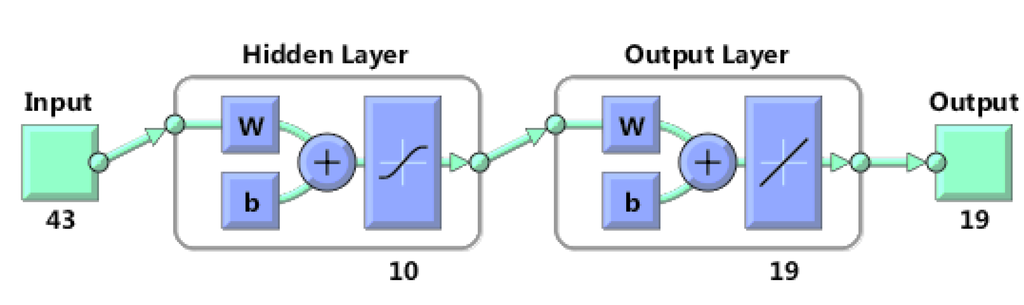
Figure 4. Setup of the neural networks.

Figure 4. Setup of the neural networks.

Figure 5 gives an example of the performance of the neural network-based interpolation method. This is of course just a demonstration for a temperature profile at one particular moment in time, but the error statistics based on a large number of profiles confirm the good performance of this method.

Figure 5. Vertical temperature profile from ERA-Interim (blue), together with the reconstructed (interpolated) profile (red).

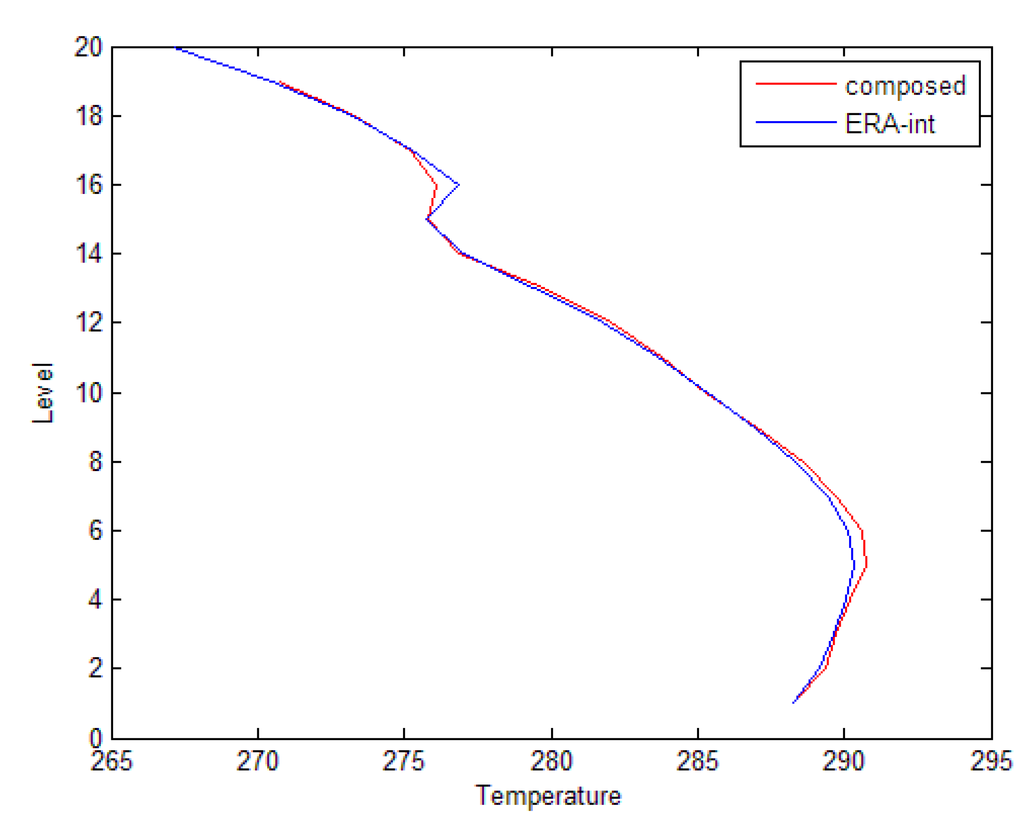
Figure 5. Vertical temperature profile from ERA-Interim (blue), together with the reconstructed (interpolated) profile (red).

3.3. Precipitation Downscaling

Thunderstorms producing convective precipitation in summer have typical length scales of a few kilometers. This resolution cannot be resolved by the GCMs (>1–2° grid cells) or ERA-Interim (0.75° grid cells). Therefore, all of the models apply precipitation parameterization schemes. These schemes produce correct total rainfall amounts for the grid cell area, but they do not capture the local peaks in rainfall, which are important when modelling the local climate. Furthermore, the larger the grid cells, the more drizzle is produced by the model, since there will always be a small part of the grid cell where it is raining. Therefore, it is necessary to downscale the rainfall from the GCMs to a suitable resolution. Since UrbClim is focusing on temperatures and not on runoff or flooding, the peak rainfall amounts are perhaps less important, as long as the total rainfall amount is correctly reproduced for the model domain. UrbClim has delivered good validation results while being fed with raw ERA-Interim rainfall data, so it was decided to take the spatial resolution of ERA-Interim as a reference and to downscale the GCM rainfall data to this resolution. Doing so also enhances the comparability of the results.

First, a number of ERA-Interim grid cells is selected surrounding the UrbClim domain, corresponding to the resolution of the GCM to be downscaled (e.g., a 3 × 3° GCM grid cell corresponds to a 4 × 4 grid cell domain in ERA-Interim). Then, all of the ERA-Interim reference rainfall data (June–August of the period 1986–2005) are used to derive a linear relation between the rainfall amount in the 4 × 4 subdomain and the center grid cell covering the UrbClim domain. This is done separately for convective and large-scale precipitation (see Figure 6). Later on, the slope factors of these relations will be used.

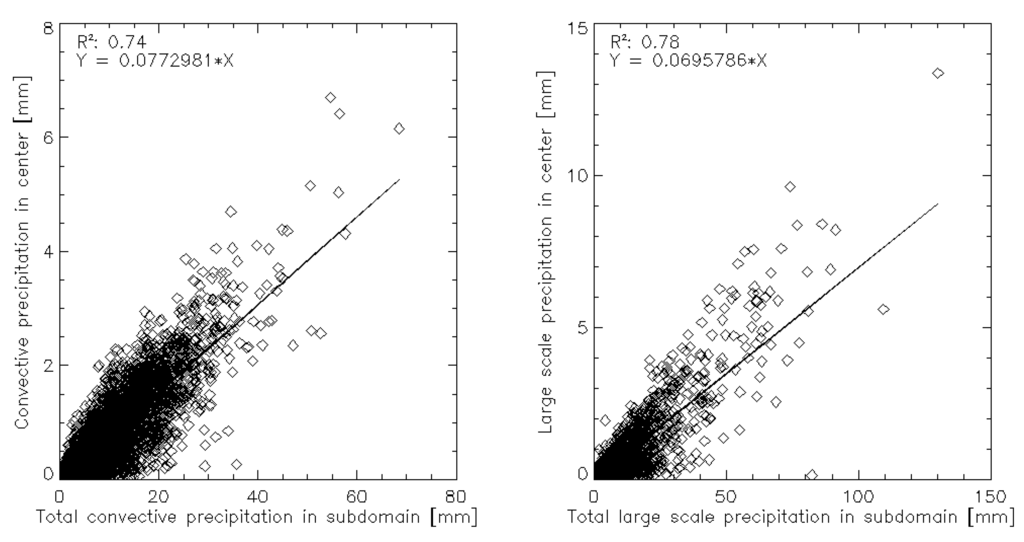
Figure 6. Statistical relations established between GCM and ERA-Interim precipitation, for convective-only precipitation (left) and large-scale precipitation (right).

Figure 6. Statistical relations established between GCM and ERA-Interim precipitation, for convective-only precipitation (left) and large-scale precipitation (right).

Subsequently, a histogram is created for precipitation values, using a value resolution of 1 mm, reflecting the number of times the total precipitation in the subdomain had the considered value while no precipitation occurred in the center grid cell. As can be imagined, the lower the total precipitation, the more ‘0’-values are present in the center cell. For every class in the histogram, the probability of a ‘0’-value in the grid center is calculated.

Finally, the GCM rainfall data for the grid cell covering the UrbClim domain are selected. For every time step when rainfall is present, a random number between zero and one is created. If this random number is below the probability of the corresponding histogram class, the rainfall is set to zero. If the random number is above the probability threshold, then the rainfall is multiplied with the slope factor derived previously.

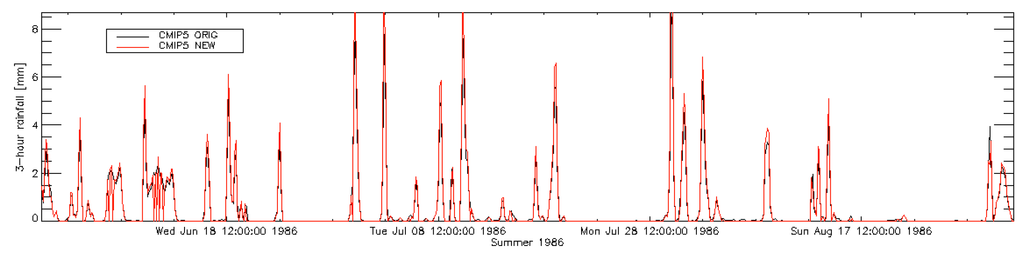
Figure 7. Precipitation time series from the MIROC-ESM-CHEM GCM after the processing step described in the main text. The black line denotes the original rainfall amounts, and the red line is the downscaled version.

Figure 7. Precipitation time series from the MIROC-ESM-CHEM GCM after the processing step described in the main text. The black line denotes the original rainfall amounts, and the red line is the downscaled version.

In this way, we are able to significantly reduce the amount of unrealistic rainfall drizzle, while increasing the peak rainfall to ERA-Interim standards, at the same time preserving the timing and amounts of rainfall from the GCM. In Figure 7, we show results from the MIROC-ESM-CHEM model for the Antwerp domain during the summer of 1986. The peak rainfall is increased, and the number of very small rainfall events is reduced significantly, which make the precipitation values more realistic and suitable to force UrbClim simulations.

3.4. Bias Correction

The first test for the UrbClim simulations forced with input from the CMIP5 GCM fields consists of a comparison with ERA-interim forced simulation results, for the reference period (1986–2005). Of course, a day-by-day comparison is nonsensical, but in principle, the 20-year statistics should agree. However, large discrepancies show up, even when considering averages over the full period of 20 years. There are many reasons why the UrbClim simulations with the model output of the GCMs do not match the simulations with ERA-Interim as the meteorological driver. Although the GCMs are improving constantly, they are still far from perfect, especially if one concentrates on a single location in the world. Moreover, the grids of the GCMs are very coarse compared to the ERA-Interim grid, which of course may cause major differences. For instance, the height of the grid cell in which the city is located compared to the ERA-Interim grid cell is often very different, especially in mountainous areas. Yet, it is reasonable to enforce that the ERA-interim runs should be considered as the benchmark. Therefore, we introduce a bias correction that reduces the differences between (1) the urban climate simulated with ERA-Interim meteorological input and (2) the urban climate simulated with the GCM as a driver, for the reference period.

The bias correction rescales, for each grid point of the UrbClim domain separately, the mean and the variance of the hourly temperatures of the CMIP5 reference run to those of the ERA-Interim runs for the reference period. A different scaling is applied for each summer month. Hence, we rescale T(i,j,t), the temperature in grid cell (i,j) at time t corresponding to month M and hour h, by:

$$T\left(i,j,t\right)\to \left(T\left(i,j,t\right)-{\langle \langle T_{i,j}^{M,h}\rangle \rangle }_{GC{M}_{ref}}\right).\frac{{\sigma }_{i,j}^{M,h}{|}_{ERA-int}}{{\sigma }_{i,j}^{M,h}{|}_{GC{M}_{ref}}}+{\langle \langle T_{i,j}^{M,h}\rangle \rangle }_{GC{M}_{ref}}$$

(2)

where $\langle \langle T_{i,j}^{M,h}\rangle {\rangle }_{GCM}$ is the mean temperature at hour h during month M according to the UrbClim simulations using the GCM, $\langle \langle T_{i,j}^{M,h}\rangle {\rangle }_{ERA-int}$ is the same quantity for the ERA-interim simulation and ${\sigma }_{i,j}^{M,h}{|}_{GCM}$ and ${\sigma }_{i,j}^{M,h}{|}_{ERA-int}$ are the corresponding standard deviations. Using (2), bias-corrected temperature data are calculated for the reference period for all considered CMIP5 models. Table 4 provides an overview of the mean bias correction for all cities and GCMs. Clearly, the numbers and trends differ largely, both in between cities and models.

Furthermore, the output temperatures for the scenario runs (i.e., climate projections, for which no reference benchmark is available) are rescaled according to the bias correction for the reference period. In detail, the output temperatures of the scenario runs are rescaled such that the increase in mean temperature and standard deviation in the original (non-bias corrected) output is mimicked in the bias-corrected versions. Mathematically, this implies:

$$T\left(i,j,t\right)\to \left(T\left(i,j,t\right)-\langle \langle T_{i,j}^{M,h}\rangle {\rangle }_{GC{M}_{scen}}\right).\frac{{\sigma }_{i,j}^{M,h}{|}_{ERA-int}}{{\sigma }_{i,j}^{M,h}{|}_{GC{M}_{ref}}}+\langle \langle T_{i,j}^{M,h}\rangle {\rangle }_{ERA-int}+\langle \langle T_{i,j}^{M,h}\rangle {\rangle }_{GC{M}_{scen}}-\langle \langle T_{i,j}^{M,h}\rangle {\rangle }_{GC{M}_{ref}}$$

(3)

Table 4. Overview of the magnitude of the applied bias correction (in °C) on the domain-wide mean temperatures for the reference period (1986–2005) for all models and cities.

	Almada	Antwerp	Berlin	Bilbao	London	New York	Rio	Skopje
ACCESS1.0	−1.1	−1.9	−2.0	+2.8	−2.2	−0.1	+1.3	−1.5
BNU_ESM	−6.4	−2.2	−1.7	−2.4	−4.1	−3.1	+1.5	−3.5
CCSM4	−2.4	−0.5	−1.2	+1.3	−0.9	−1.0	+0.5	−0.9
CNRM_CM5	−0.9	−2.2	−3.9	+1.1	−3.5	−1.3	−0.7	+0.1
FGOALS-G2	+0.8	+1.2	−0.6	+4.0	+0.1	+2.4	+3.0	+0.2
GFDL-ESM2M	−4.2	+1.2	+0.5	+1.0	+1.2	+0.8	−0.8	−0.3
GISS-E2-R	−2.1	+0.7	+0.6	+1.8	−0.1	+1.9	−0.9	+3.6
HadGem2-ES	−0.1	−2.8	−4.2	+3.4	−2.9	−1.3	−0.1	−1.4
IPSL-CM5A-MR	+1.2	−1.5	−0.9	−0.8	−2.4	−0.5	+0.3	+1.5
MIROC-ESM-CHEM	−3.1	−1.3	−1.9	+1.4	−1.3	−3.4	+2.1	+0.4
MRI-CGCM3	−0.5	+0.9	+1.1	+2.8	+1.0	+2.3	+1.0	+3.3

Table 4. Overview of the magnitude of the applied bias correction (in °C) on the domain-wide mean temperatures for the reference period (1986–2005) for all models and cities.

	Almada	Antwerp	Berlin	Bilbao	London	New York	Rio	Skopje
ACCESS1.0	−1.1	−1.9	−2.0	+2.8	−2.2	−0.1	+1.3	−1.5
BNU_ESM	−6.4	−2.2	−1.7	−2.4	−4.1	−3.1	+1.5	−3.5
CCSM4	−2.4	−0.5	−1.2	+1.3	−0.9	−1.0	+0.5	−0.9
CNRM_CM5	−0.9	−2.2	−3.9	+1.1	−3.5	−1.3	−0.7	+0.1
FGOALS-G2	+0.8	+1.2	−0.6	+4.0	+0.1	+2.4	+3.0	+0.2
GFDL-ESM2M	−4.2	+1.2	+0.5	+1.0	+1.2	+0.8	−0.8	−0.3
GISS-E2-R	−2.1	+0.7	+0.6	+1.8	−0.1	+1.9	−0.9	+3.6
HadGem2-ES	−0.1	−2.8	−4.2	+3.4	−2.9	−1.3	−0.1	−1.4
IPSL-CM5A-MR	+1.2	−1.5	−0.9	−0.8	−2.4	−0.5	+0.3	+1.5
MIROC-ESM-CHEM	−3.1	−1.3	−1.9	+1.4	−1.3	−3.4	+2.1	+0.4
MRI-CGCM3	−0.5	+0.9	+1.1	+2.8	+1.0	+2.3	+1.0	+3.3

In the remainder of this study, the urban climate projection results presented are always based on a comparison between bias-corrected data for the reference period and bias-corrected data for the scenario runs.

4. Results and Discussion

4.1. UHI Projection Results

In the previous section, the methodology for generating the urban climate projections was introduced. Here, we present the main results and discuss the future urban climate more in detail. The focus is on the UHI-indicator introduced before, which yields the minimal temperature during the five percent warmest summer nights. By way of demonstration, we first present results for Antwerp. Subsequently, we focus on the comparison between the eight cities under investigation.

Figure 8 shows the influence of climate change on the temperature indicator for Antwerp. As mentioned before, in this study, UrbClim is driven by meteorological input of 11 GCMs; hence, the final result consists of an ensemble mean, together with an uncertainty range. Uncertainties are indicated using the “likely range” defined in the IPCC report. This likely range constitutes a 5%–95% range (±1.64 standard deviations) across the ensemble distribution. Both the ensemble mean rural and urban 95th percentile of the minimal temperatures increase by approximately 4.5 °C. Due to the large spread in the GCM results, also the uncertainty on the urban and rural temperatures is rather large, which implies that the lower error margin for the urban temperature is lower than the mean for the rural temperature and that the upper error margin for the rural temperature is higher than the mean for the urban temperature.

In Figure 9, the resulting map of the temperature indicator for the period 2081–2100 for the whole model domain of Antwerp is presented. When comparing Figure 9 and Figure 2, it is clear that, while the temperatures increase considerably between the current-day situation and the end-of-the-century scenario, there is no appreciable difference in the spatial patterns between the map of the temperature indicator for the reference period and the temperature indicator for the future period. The mean increase in the UHI-indicator is 0.07, with an uncertainty of ±0.07 °C. This uncertainty on the change in the UHI-indicator is calculated using the standard deviation of the UHI-indicator for both the reference period and the end-of-the-century and the standard rules for the propagation of uncertainty. The overall temperature increase is thus much larger than the increase in the UHI effect. Hence, we can conclude that the temperature increase of the background dominates the urban and rural temperature changes.

Subsequently, we focus on the comparison between the eight cities under investigation. Table 5 summarizes the changes in the 95th percentile of the minimum rural and urban temperatures and the changes in the UHI-indicator between the reference period (1986–2005) and the end of the century (2081–2100), based on the 11 GCMs considered here. Note that the results of this table are in accord with the results of the most recent IPCC report (AR5). Whereas the warming in Rio appears to be less than the expected average (regional-scale) warming, Skopje experiences, as most of the Mediterranean region, a very considerable temperature increase. For all cities, except Rio de Janeiro, the UHI-indicator increases slightly, although the increase often is below the error margin. For Rio de Janeiro, the UHI-indicator decreases, but the magnitude of the decrease is again negligible in comparison with the increase of the urban and rural temperatures. As was the case for Antwerp, the change in the UHI indicator is much smaller than the change in the urban and rural temperatures themselves.

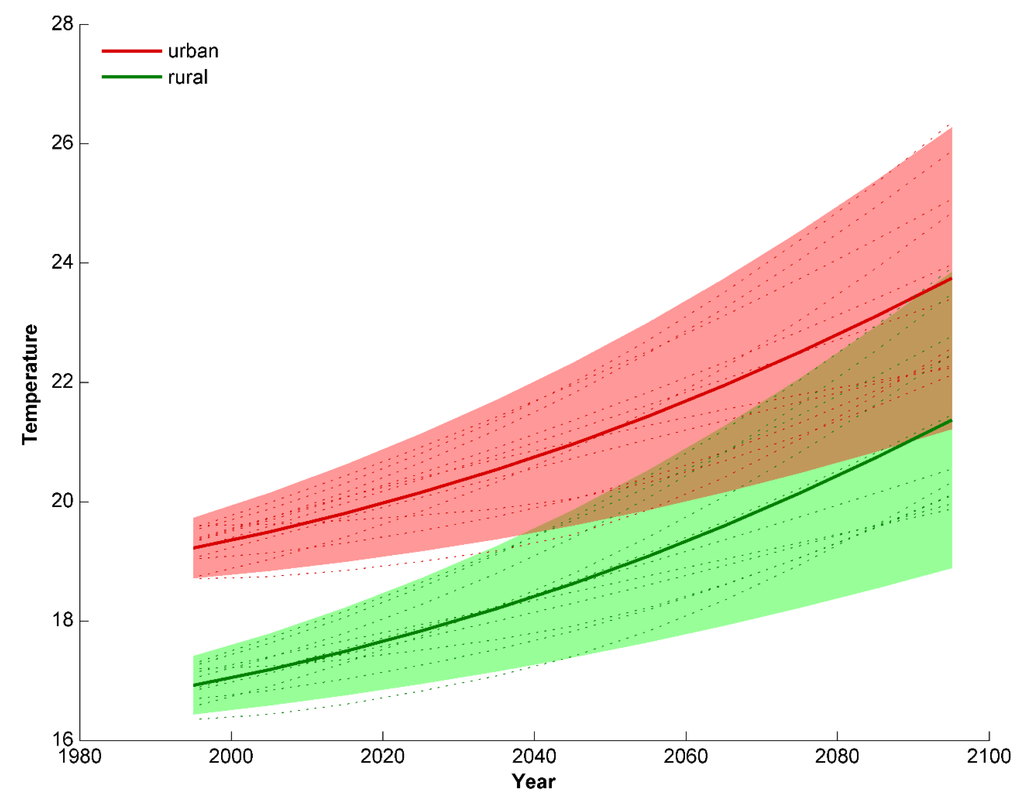
Figure 8. Evolution of the rural (green) and urban (red) 95th percentile of the minimum temperature in Antwerp. The thick lines show the ensemble mean, while the shaded areas indicate the 5%–95% range based on assuming a normal distribution for the ensemble. Dotted lines indicate the results obtained with the individual GCM forcings. Note that in order to construct this figure, also model results for the period 2026–2045 were used, and an interpolation was made to span the periods not covered by the simulations.

Figure 8. Evolution of the rural (green) and urban (red) 95th percentile of the minimum temperature in Antwerp. The thick lines show the ensemble mean, while the shaded areas indicate the 5%–95% range based on assuming a normal distribution for the ensemble. Dotted lines indicate the results obtained with the individual GCM forcings. Note that in order to construct this figure, also model results for the period 2026–2045 were used, and an interpolation was made to span the periods not covered by the simulations.

Figure 9. Temperature indicator for Antwerp for the period 2081–2100, based on the 11 GCM-driven simulations.

Figure 9. Temperature indicator for Antwerp for the period 2081–2100, based on the 11 GCM-driven simulations.

Table 5. Change in the UHI indicator between the reference period (1986–2005) and the end of the century future (2081–2100) under Representative Concentration Pathway (RCP) 8.5 conditions. The rightmost column gives the estimated uncertainty on the change in the UHI indicator.

City	Ref. UHI (°C)	ΔRural (°C)	ΔUrban (°C)	ΔUHI (°C)	Uncertainty (°C)
Almada	2.47	4.51	4.58	0.07	0.07
Antwerp	2.30	4.12	4.20	0.08	0.07
Berlin	2.70	4.53	4.64	0.11	0.09
Bilbao	2.12	4.56	4.63	0.08	0.06
London	2.98	4.31	4.32	0.01	0.08
New York	3.57	4.87	5.08	0.21	0.12
Rio	2.95	3.30	3.18	-0.12	0.10
Skopje	2.25	6.74	6.85	0.10	0.09

Table 5. Change in the UHI indicator between the reference period (1986–2005) and the end of the century future (2081–2100) under Representative Concentration Pathway (RCP) 8.5 conditions. The rightmost column gives the estimated uncertainty on the change in the UHI indicator.

City	Ref. UHI (°C)	ΔRural (°C)	ΔUrban (°C)	ΔUHI (°C)	Uncertainty (°C)
Almada	2.47	4.51	4.58	0.07	0.07
Antwerp	2.30	4.12	4.20	0.08	0.07
Berlin	2.70	4.53	4.64	0.11	0.09
Bilbao	2.12	4.56	4.63	0.08	0.06
London	2.98	4.31	4.32	0.01	0.08
New York	3.57	4.87	5.08	0.21	0.12
Rio	2.95	3.30	3.18	-0.12	0.10
Skopje	2.25	6.74	6.85	0.10	0.09

4.2. Discussion Regarding the UHI Intensity Changes

A striking aspect of the results presented above is that, while overall temperatures increase quite greatly in the RCP8.5 scenario, the UHI intensity does not appear to change significantly with climate change, as observed rather consistently among all cities considered. This is a bit puzzling, given (1) that GCMs predict an increase in the intensity, duration and frequency of heat waves and (2) that UHI intensity normally increases during heat waves [43]. It would appear straightforward to assume an increase also in the average UHI intensity. Yet, this increase of the UHI strength does not take place.

A possible explanation for this finding involves downwelling longwave radiation. Indeed, with an increasing amount of greenhouse gases in the atmosphere, the downwelling longwave radiation is also projected to increase. It has been reported before by Oleson et al. [44] that increased longwave radiation warms rural areas more than urban areas at night. In a sensitivity study done for the Brussels area, Lauwaet et al. [39] demonstrated that the increase of air temperature near the ground following enhanced radiation is much more effective over rural areas than over urban areas. In other words, the extra downwelling longwave radiation that results from the enhanced amount of greenhouse gases typically yields a higher temperature increase over rural areas than over a city.

The reason for this behavior is that, at night-time, vertical temperature profiles in rural areas are generally characterized by a more or less strong inversion, the stability of which inhibits much vertical mixing. The extra heat at the surface, caused by the enhanced longwave radiation absorption, is therefore distributed over a relatively small vertical extent, thus resulting in a rather strong increase in temperature. Over urban areas, which have a rather neutral or even slightly positive buoyant temperature profile, the extra heat is distributed over a much larger vertical domain, i.e., the heating is much “diluted”, so to say, yielding a much lower temperature increase. This mechanism can explain why we find little changes in the overall UHI intensities, whereas meteorological variables from the GCMs support stronger UHIs.

Previous reported research on this topic came to similar conclusions. Fischer et al. [5] and Oleson [6] studied the effect of several greenhouse gas scenarios on UHI intensities by the end of the century on a global scale and also found little changes in the UHI values, as the urban and rural areas showed a similar warming trend. McCarthy et al. [8] also obtained rather constant, although not static, UHI values for the cities in the United Kingdom under climate change conditions in their regional climate model simulations. Lemonsu et al. [11] and Hamdi et al. [7] reported a relatively strong decrease in the night-time UHI intensities of Paris (−1 °C) and Brussels (−0.36 °C), respectively. They could attribute these changes to a large reduction of the summer rainfall amounts by the end of the century in their simulations, strongly diminishing the evaporation from vegetation and soils in the rural areas, which gives rise to higher rural temperatures and, hence, a smaller UHI. However, only one driving GCM was used in their studies, so they could not estimate the resulting dispersion with respect to alternative global climate models.

It should be noted that our (and the studies discussed above) simulations did not account for potential future urban growth, an effect that typically increases the urban-rural contrasts.

4.3. Applying a Statistical Method

Performing the urban climate projections using UrbClim is a time- and computation-demanding task. To simulate the future urban climate for a medium-sized city (like Antwerp or Skopje) on a resolution of 250 m, considering 20-year periods and 11 driving GCMs, takes approximately three CPU years. Moreover, also processing three-hourly CMIP5-data for all parameters that are required by UrbClim is an immense task. Due to the huge amount of GCM-data, the processing is very slow and labor intensive. Taking both problems into consideration, we worked out an alternative method for the UrbClim simulations, in which the future urban climate is obtained by statistically rescaling the current urban climate.

The statistical urban climate projections proceed in two steps. In the first step, UrbClim analyzes the current urban climate in the same way as described above. The model downscales the ERA-Interim reanalysis data for the reference period 1986–2005 and computes the impact of urban development on the most important weather parameters. Subsequently, the effects of climate change are added in a statistical way: daily minimal temperatures are rescaled according to the temperature changes observed in an ensemble of GCMs. In order to obtain an as simple as possible procedure, only temperature changes are taken into account, and we simply neglect the alteration of other meteorological parameters, such as humidity, precipitation and wind.

More in detail, we first determine, for each of the considered GCMs, the change of the daily minimum temperature as a function of the percentile of the temperature. For instance, we determine the difference between the 75th percentile of the daily minimal temperature in the future period (2081–2100) and the reference period (1986–2005). Subsequently, an ensemble average is performed. Since the different GCMs use different grids, this procedure includes an interpolation of the data to a regular longitude-latitude grid.

In order to obtain daily temperature time series for the future, the ensemble temperature change statistics and the results of the current urban climate analysis are combined. For each day, the daily minimal temperatures of all of the grid cells are rescaled according to the rescaling of the associated temperature percentile of the rural temperature. For instance, if the rural value of the minimal temperature of a day accords with the 75th percentile of all minimal temperatures for the reference period, we add the increase of the 75th percentile (according to the ensemble statistics) to the minimal temperature of that day, for all of the grid cells. Note that we make use of the rural value of the temperature to determine the rescaling, since we assume that the output of the GCMs corresponds with this value (i.e., with the temperature without the added effect of the urban development).

This procedure results in a rescaled temperature time series for 20 years, which is used as the temperature series for the future climate. Therefore, finally, the temperature indicator and the UHI effect can be calculated in the same way as before, but with the rescaled temperature series as input. Figure 10 presents the resulting map for the city of Antwerp, as well as the spatial differences with Figure 9, based on the GCM-driven ensemble. There is very good agreement between the previous results of the urban climate projections and the new statistical methodology. The differences between both maps are rather small, with an absolute difference always under 0.5 °C, which is smaller than the uncertainty in the mean value from the 11 GCM-ensemble, 0.63 °C. The uncertainty in the mean value is calculated by dividing the variance of the ensemble by the square root of the number of ensemble members. The difference map shows a remarkable SW-NE pattern, which can be explained by the dominant wind patterns in the simulation results. Whereas the dominant wind direction in the ERA-Interim simulations is S, SW and W, leading to advection of heat from the city to the downwind part of the model domain, the dominant wind direction in the future changes in most of the GCMs to N and NE. Since these changes are not taken into account in the statistical method, they become visible on the difference map.

Figure 10. Temperature indicator for Antwerp for the period 2081–2100, based on the statistical method (left) and the differences with the map in Figure 9, based on the 11 GCM-driven simulations (right).

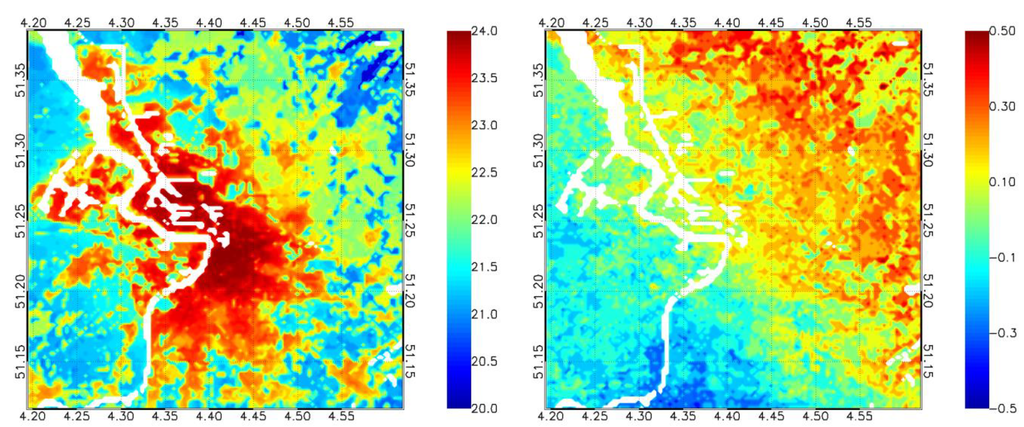
Figure 10. Temperature indicator for Antwerp for the period 2081–2100, based on the statistical method (left) and the differences with the map in Figure 9, based on the 11 GCM-driven simulations (right).

The method described above provides a rather crude methodology to obtain a temperature series that can be used as an example time series for the future climate. The new time series only takes into account the (ensemble mean) temperature change. However, since the end result is statistically similar to the regular urban climate projections, at least for the city of Antwerp, a broad range of advantages appears. Firstly, this new methodology is much, much faster than running the complete UrbClim climate projections. For a small city as Antwerp, a procedure that requires approximately three CPU-years can be performed in a CPU-week. Secondly, since only daily minimal temperatures are used, the amount of required GCM data is reduced significantly, which makes the method easily applicable to a global scale. Therefore, we conclude that this method is suitable to quickly produce a first approximation for the future urban temperatures and the future UHI effect.

5. Conclusions

In this paper, an original methodology in order to analyze the impact of global climate change on the local climate of cities worldwide is proposed. More particularly, the urban boundary layer climate model UrbClim is coupled to the GCMs contained in the IPCC CMIP5 archive and used to conduct long simulations for present (1986–2005) and future (2081–2100) climate conditions (and considering the RCP8.5 climate scenario). This dynamical downscaling method allows quantifying and assessing the evolution of the UHI of several cities worldwide, with an unprecedented horizontal resolution of a few hundred meters. In this study, the focus is on eight different cities, located on three continents. For the non-European cities, a methodology is worked out to replace the default CORINE land use and EEA soil sealing data by GlobCover and MODIS land use data. An independent validation of the procedure revealed that differences between simulated time series with either one of the input datasets were always smaller than the model uncertainty, and the correlation between the time series amounted to 0.997.

The UrbClim model has been extensively validated in the past regarding its ability to reproduce the temperature contrast between urban and rural areas. Here, a validation has been performed for the city of Antwerp, and the model was able to reproduce the observed differences in time series of air temperatures from different stations, with almost no bias, root mean square errors below 1 °C and correlation coefficients above 0.7. Afterwards, a globally-applicable indicator for the UHI is defined that quantifies the difference in 2-m air temperature between the urban and the rural part of the city domains. This indicator is based on the temporal 95th percentile of the height-corrected minimum temperatures for the summer period, i.e., the minimum temperature that is exceeded on average five times each summer. The UHI effect is then quantified as the difference between the urban and the rural value of this map, i.e., the spatial 90th and 10th percentile in the domain under investigation.

In order to properly represent the uncertainty associated with the global climate projections, UrbClim is forced by an ensemble of GCM outputs. When investigating the CMIP5 archives, it was found that 11 climate institutes provide model output in which all required parameters are available at a suitable time increment. However, there were three main issues connected to the use of the GCM output as driving meteorological input for UrbClim. Firstly, vertical profile data were available only at a six-hourly time step, which is insufficient to properly resolve the diurnal cycle. To remedy this, a neural network routine was set up, using as input ERA-Interim data, to bridge the gap between the required time frequency of the vertical profiles in UrbClim (three-hourly) and the best resolution present in the CMIP5 archives (six-hourly). Secondly, UrbClim requires precipitation data at a fine scale level (i.e., the city and its direct surroundings), while the GCM output is provided at a much coarser resolution, thus neglecting local thunderstorms, among other things. Hence, a downscaling routine based on ERA-Interim data was established. Finally, a bias correction was needed to bridge the gap between urban climate results simulated with ERA-Interim meteorological input, considered as the benchmark, and simulation results with the GCM as a driver.

The simulation results for all eight cities were analyzed to examine how rural and urban areas might respond differently to changes in climate. The results showed that for all cities, urban and rural air temperatures both increased rather evenly, with a maximal increase of almost 7 °C for Skopje, located in the Mediterranean region. However, the UHI indicator in most cases increased only slightly, often even below the range of uncertainty. A discussion on this outcome focused on the role of increased incoming longwave radiation in the future, which is known to have a diversifying effect on nocturnal rural and urban temperature profiles, hence limiting an increase in the UHI [39]. Note that our simulations did not account for potential future urban growth, an effect that typically increases the urban-rural contrasts.

Finally, an alternative method for the urban climate projections is presented, in which the future urban climate is obtained by statistically rescaling the current urban climate, in order to avoid the very expensive and CPU-demanding GCM-forced ensemble simulations. Herein, the ensemble temperature change statistics and the results of the current urban climate analysis were combined. The result of this method was compared to the GCM-driven ensemble model output for the city of Antwerp, focusing solely on the UHI indicator. Differences between both maps were found to be small, with an absolute difference always under 0.5 °C, which is smaller than the uncertainty in the mean value from the 11 GCM-ensemble. Hence, this statistical method provides a valuable alternative to produce a quick estimate of future urban temperatures and the UHI effect.