Land Use/Cover Response to Rainfall Variability: A Comparing Analysis between NDVI and EVI in the Southwest of Burkina Faso
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
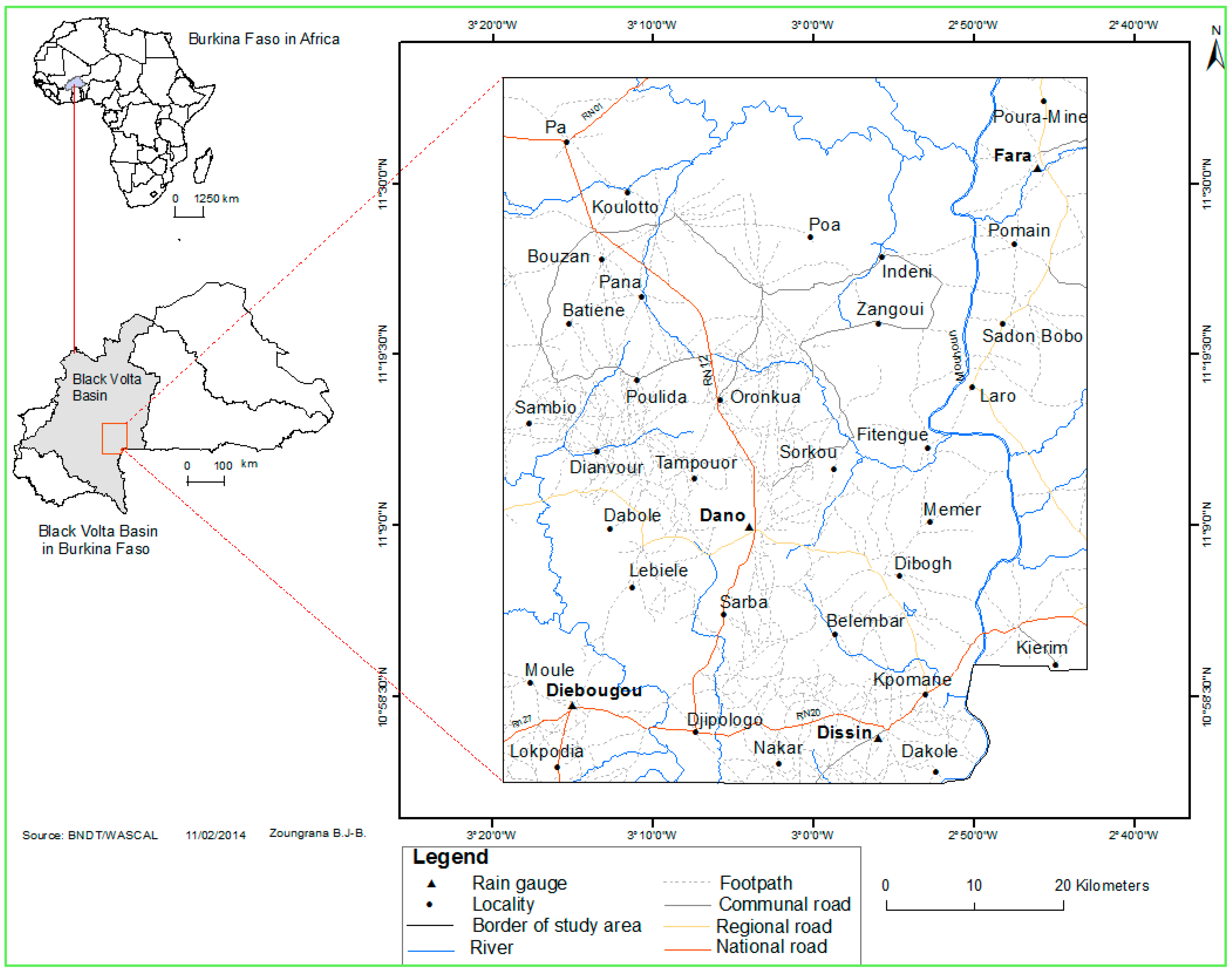
2.2. Data Acquisition and Processing
2.2.1. Land Use/Covers and Persistent Areas Mapping
2.2.2. Rainfall Data
| Indicators | Description |
|---|---|
| Amount of pcp (lag 1 month) | 1 month lag precipitation |
| Cumulated 2 months pcp | Sum of precipitation of current and previous 1 month |
| Cumulated 3 months pcp | Sum of precipitation of current and previous 2 months |
| Cumulated 4 months pcp | Sum of precipitation of current and previous 3 months |
2.2.3. Vegetation Indices
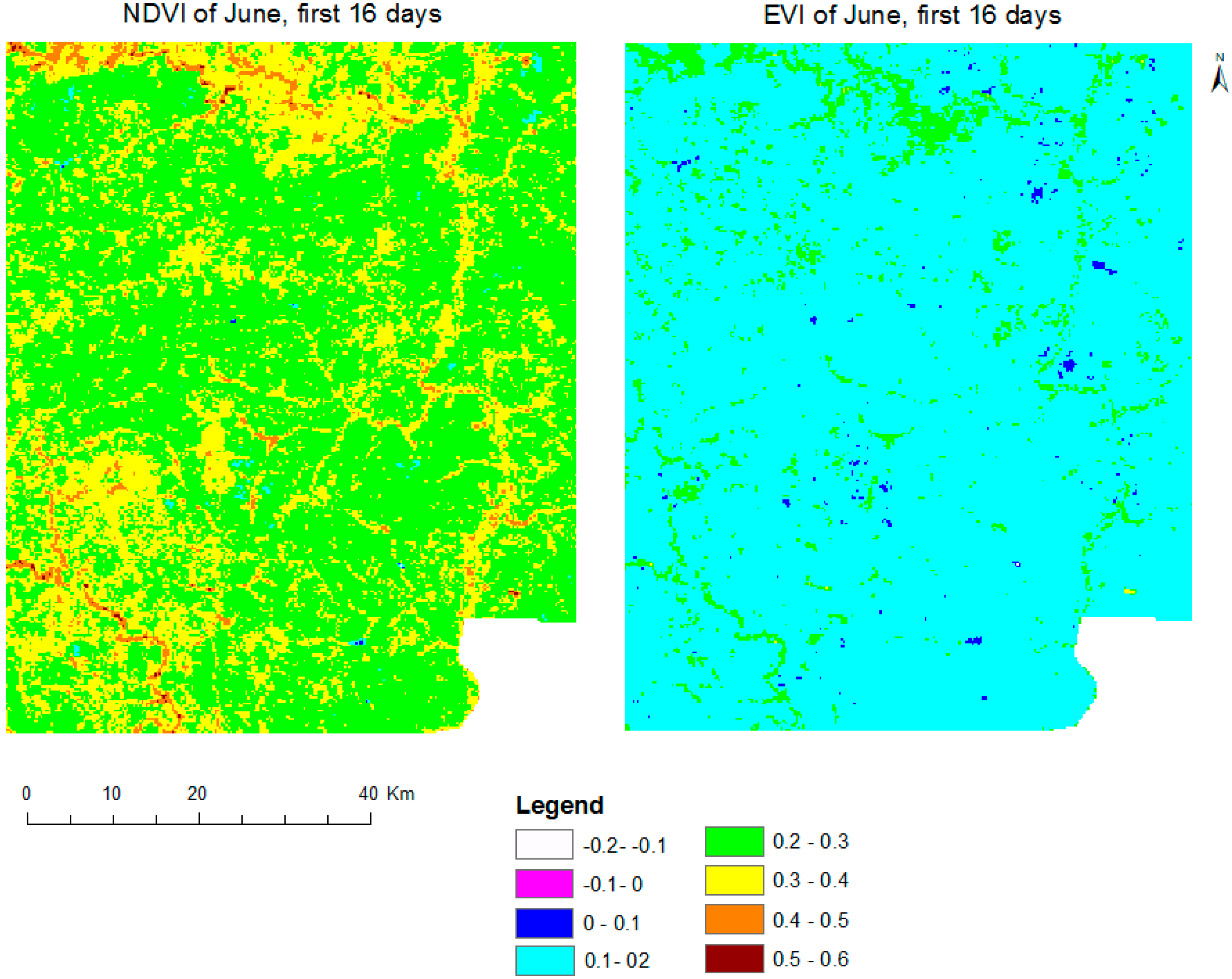
3. Results and Discussion
3.1. Persistent Land Use/Cover Map
3.2. Rainfall Variability between Stations
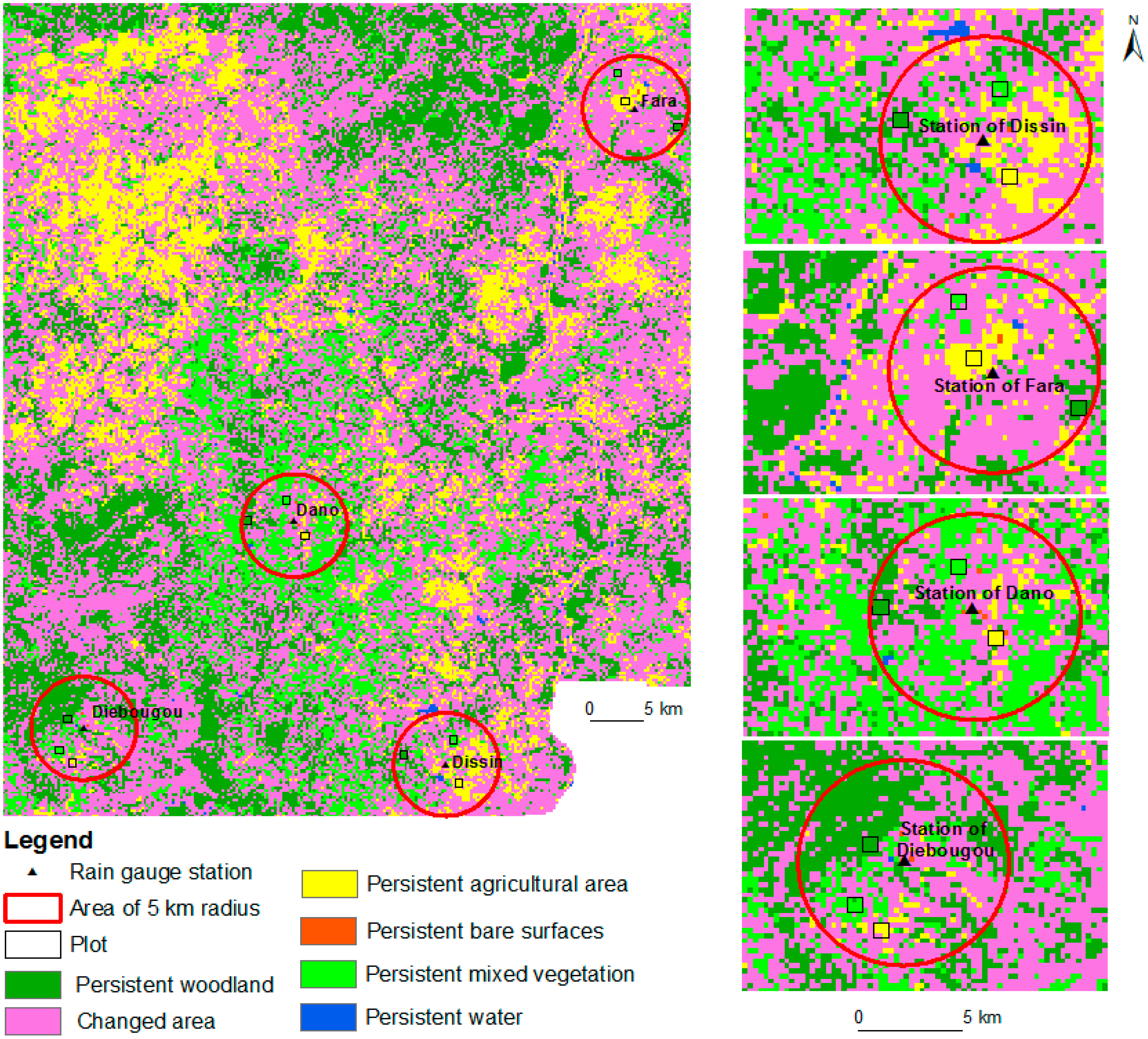
| LULC | Percentage |
|---|---|
| Persistent woodland | 21.77 |
| Persistent mixed vegetation | 10.59 |
| Persistent agricultural area | 12.95 |
| Persistent water | 0.15 |
| Persistent bare surfaces | 0.04 |
| Changed area | 54.50 |
| Station | Dano | Fara | Diebougou | Dissin | Mean Total Annual Rainfall |
|---|---|---|---|---|---|
| Dano | 1 | 0.885 | 0.850 | 0.917 | 897.20 |
| Fara | 0.885 | 1 | 0.874 | 0.899 | 880.81 |
| Diebougou | 0.850 | 0.874 | 1 | 0.848 | 723.48 |
| Dissin | 0.917 | 0.899 | 0.848 | 1 | 949.97 |
3.3. Correlation Analysis between Land Use/Covers and the Indicators of Rainfall
3.3.1. NDVI as LULC Indicator
| Station | LULC | 1 month Lag pcp | Cum. 2 Months pcp | Cum. 3 Months pcp | Cum. 4 Months pcp |
|---|---|---|---|---|---|
| Dano | Agricultural area | 0.861 | 0.848 | 0.934 | 0.943 |
| Mixed vegetation | 0.849 | 0.937 | 0.917 | 0.825 | |
| Woodland | 0.864 | 0.893 | 0.945 | 0.917 | |
| Fara | Agricultural area | 0.896 | 0.921 | 0.944 | 0.880 |
| Mixed vegetation | 0.860 | 0.911 | 0.918 | 0.846 | |
| Woodland | 0.849 | 0.903 | 0.919 | 0.850 | |
| Diebougou | Agricultural area | 0.843 | 0.873 | 0.929 | 0.899 |
| Mixed vegetation | 0.829 | 0.909 | 0.898 | 0.798 | |
| Woodland | 0.824 | 0.869 | 0.913 | 0.871 | |
| Dissin | Agricultural area | 0.855 | 0.873 | 0.911 | 0.878 |
| Mixed vegetation | 0.859 | 0.896 | 0.912 | 0.858 | |
| Woodland | 0.875 | 0.891 | 0.924 | 0.877 |
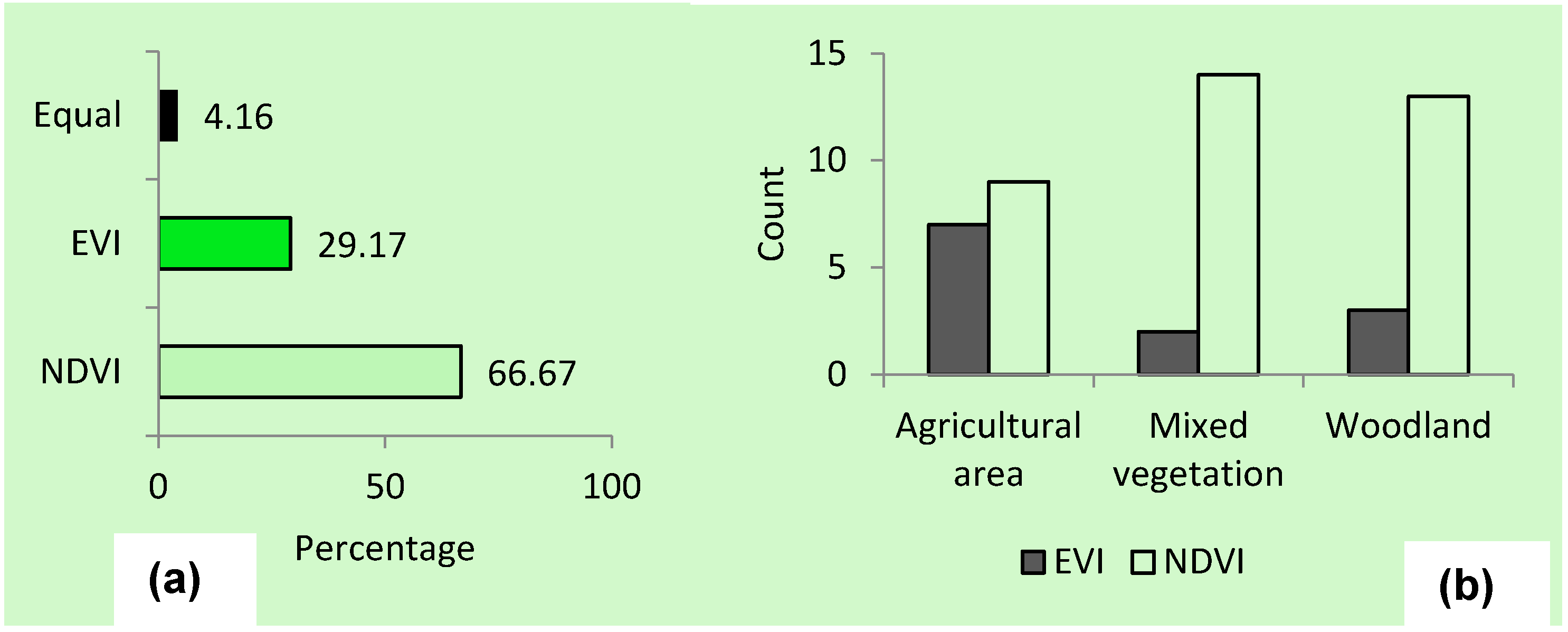
3.3.2. EVI as LULC indicator and comparative analysis with NDVI
| Station | LULC | 1 Month Lag pcp | Cum. 2 Months pcp | Cum. 3 Months pcp | Cum. 4 Months pcp |
|---|---|---|---|---|---|
| figureDano | Agricultural area | 0.872 | 0.887 | 0.946 | 0.922 |
| Mixed vegetation | 0.830 | 0.939 | 0.893 | 0.783 | |
| Woodland | 0.859 | 0.904 | 0.942 | 0.890 | |
| Fara | Agricultural area | 0.856 | 0.907 | 0.907 | 0.832 |
| Mixed vegetation | 0.836 | 0.910 | 0.897 | 0.812 | |
| Woodland | 0.796 | 0.904 | 0.876 | 0.778 | |
| Diebougou | Agricultural area | 0.859 | 0.897 | 0.932 | 0.877 |
| Mixed vegetation | 0.828 | 0.927 | 0.889 | 0.768 | |
| Woodland | 0.844 | 0.903 | 0.925 | 0.857 | |
| Dissin | Agricultural area | 0.844 | 0.881 | 0.901 | 0.844 |
| Mixed vegetation | 0.831 | 0.896 | 0.890 | 0.811 | |
| Woodland | 0.860 | 0.908 | 0.916 | 0.840 |
| Station | LULC | 1 Month Lag pcp | Cum. 2 Months pcp | Cum. 3 Months pcp | Cum. 4 Months pcp |
|---|---|---|---|---|---|
| Dano | Agricultural area | EVI | EVI | EVI | NDVI |
| Mixed vegetation | NDVI | EVI | NDVI | NDVI | |
| Woodland | NDVI | EVI | NDVI | NDVI | |
| Fara | Agricultural area | NDVI | NDVI | NDVI | NDVI |
| Mixed vegetation | NDVI | NDVI | NDVI | NDVI | |
| Woodland | NDVI | Equal | NDVI | NDVI | |
| Diebougou | Agricultural area | EVI | EVI | EVI | NDVI |
| Mixed vegetation | NDVI | EVI | NDVI | NDVI | |
| Woodland | EVI | EVI | EVI | NDVI | |
| Dissin | Agricultural area | NDVI | EVI | NDVI | NDVI |
| Mixed vegetation | NDVI | Equal | NDVI | NDVI | |
| Woodland | NDVI | EVI | NDVI | NDVI |
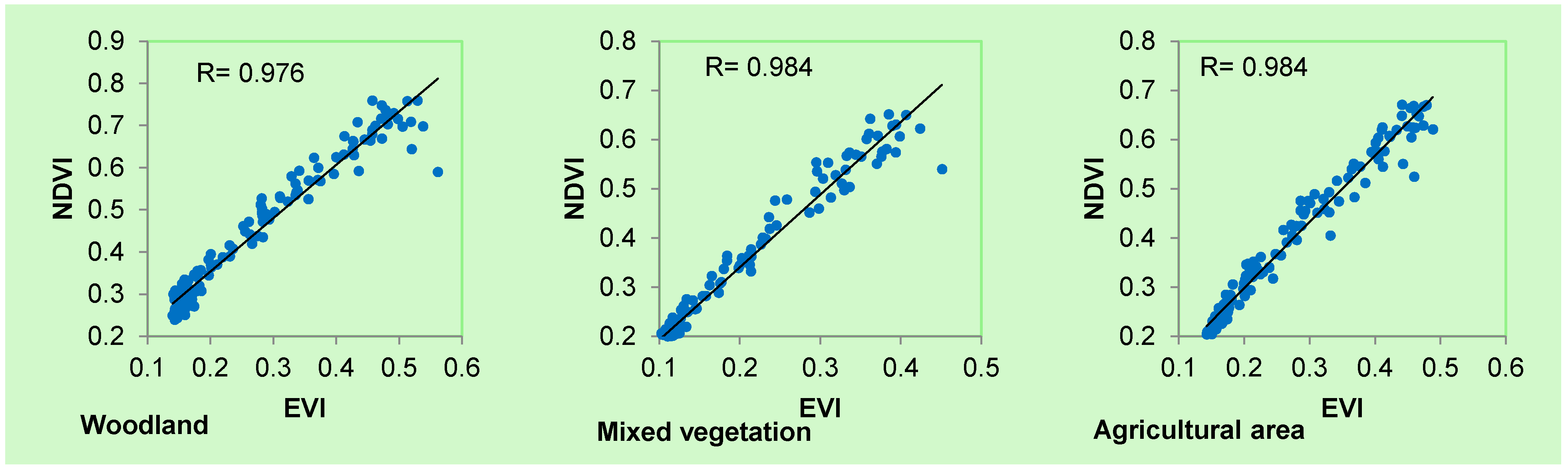
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IPCC. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007; p. 104. [Google Scholar]
- Lambin, E.F. Modeling and monitoring land-cover change processes in tropical regions. Prog. Phys. Geogr. 1997, 21, 375–393. [Google Scholar] [CrossRef]
- Nightingale, J.M.; Phinn, S.R. Assessment of relationships between precipitation and satellite derived vegetation condition within South Australia. Aust. Geogr. Stud. 2003, 41, 180–195. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Davenport, M.L.; Maloa, A.R. A comparison of the vegetation response to rainfall in the sahel and east africa, using normalized difference vegetation index from NOAA AVHRR. Clim. Chang. 1990, 17, 209–241. [Google Scholar] [CrossRef]
- Gessner, U.; Naeimi, V.; Klein, I.; Kuenzer, C.; Klein, D.; Dech, S. The relationship between precipitation anomalies and satellite-derived vegetation activity in Central Asia. Glob. Planet. Chang. 2013, 110, 74–87. [Google Scholar] [CrossRef]
- Eklundh, L. Estimating relations between AVHRR NDVI and rainfall in East Africa at 10-day and monthly time scales. Int. J. Remote Sens. 1998, 19, 563–568. [Google Scholar] [CrossRef]
- Richard, Y.; Poccard, I. A statistical study of NDVI sensitivity to seasonal and interannual rainfall variations in Southern Africa. Int. J. Remote Sens. 1998, 19, 2907–2920. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Stevens, F.R.; Gibbes, C.; Southworth, J.; Binford, M.W. Linking vegetation response to seasonal precipitation in the Okavango-Kwando-Zambezi catchment of southern Africa. Int. J. Remote Sens. 2012, 33, 6783–6804. [Google Scholar] [CrossRef]
- Chaoka, R.T.; Alemaw, B.F.; Tsige, D.M. Modeling and understanding the relationship between vegetation and rainfall of a tropical watershed using remote sensing data and GIS. JOSH 2007, 7, 47–61. [Google Scholar]
- Hashemi, S.A. Investigation of relationship between rainfall and vegetation index by using NOAA/AVHRR satellite images. World Appl. Sci. J. 2011, 14, 1678–1682. [Google Scholar]
- Boken, V.K.; Chandra, S. Estimating leaf area index for an arid region using spectral data. Afr. Crop. Sci. J. 2012, 20, 215–223. [Google Scholar]
- Fontes de Sousa, L.; Braga, C.C.; Braga, R.C.; Dantas, M.P. Interrelationship between rainfall and vegetation index by remote sensing. JHRS 2014, 4, 87–99. [Google Scholar]
- Bobée, C.; Ottlé, C.; Maignan, F.; de Noblet-Ducoudré, N.; Maugis, P.; Lézine, A.-M.; Ndiaye, M. Analysis of vegetation seasonality in Sahelian environments using MODIS LAI, in association with land cover and rainfall. J. Arid Environ. 2012, 84, 38–50. [Google Scholar] [CrossRef]
- Farrar, T.J.; Nicholson, S.E.; Lare, A.R. The influence of soil type on the relationships between NDVI, rainfall, and soil moisture in semiarid Botswana. II. NDVI response to soil moisture. Remote Sens. Environ. 1994, 50, 121–133. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A.R. A feedback based modification of the NDV I to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Huete, A.R.; van Leeuwen, W.J.D.; Hua, G.; Qi, J.; Chehbouni, A. Normalization of multidirectionalred and NIR reflectances with the SAVI. Remote Sens. Environ. 1992, 41, 143–154. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Weia, D.; Xub, X.; Wanga, H. An assessment of correlation on MODIS-NDVI and EVI with natural vegetation coverage in Northern Hebei Province, China. Proc. Environ. Sci. 2010, 2, 964–969. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L. A comparison of MODIS 250-m EVI and NDVI data for crop mapping: A case study for southwest Kansas. Int. J. Remote Sens. 2010, 31, 805–830. [Google Scholar] [CrossRef]
- Cord, A.; Conrad, C.; Schmidt, M.; Dech, S. Standardized FAO-LCCS land cover mapping in heterogeneous tree savannas of West Africa. J. Arid Environ. 2010, 74, 1083–1091. [Google Scholar] [CrossRef]
- Duadze, S.E.K. Land Use and Land Cover Study of the Savannah Ecosystem in the Upper West Region (Ghana) Using Remote Sensing; Cuvillier Verlag: Göttingen, Germany.
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Forkuor, G.; Conrad, C.; Thiel, M.; Ullmann, T.; Zoungrana, E. Integration of optical and Synthetic Aperture Radar imagery for improving crop mapping in Northwestern Benin, West Africa. Remote Sens. 2014, 6, 6472–6499. [Google Scholar] [CrossRef]
- USGS Global Visualization Viewer. Available online: http://glovis.usgs.gov/ (accessed on 03 October 2012).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Akar, O.; Güngör, O. Classification of multispectral images using Random Forest algorithm. J. Geod. Geoinf. 2013, 2, 105–112. [Google Scholar]
- Waske, B.; Braun, M. Classifier ensembles for land cover mapping using multi temporal SAR imagery. ISPRS J. Photogr. Remote Sens. 2009, 64, 450–457. [Google Scholar]
- MODIS Reprojection Tool Web Interface (MRTWeb). Available online: https://mrtweb.cr.usgs.gov/ (accessed on 06 June 2014).
- Colditz, R.R.; Conrad, C.; Wehrmann, T.; Schmidt, M.; Dech, S. TiSeG: A flexible software tool for time-series generation of MODIS data utilizing the quality assessment science data set. IEEE Trans. Geosci. Remote 2008, 46, 3296–3308. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical-biophysical relationships of vegetation spectra without background contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data. Principles and Practices; CRC Press Inc.: London, UK, 2009. [Google Scholar]
- Davenport, M.L.; Nicholson, S.E. On the relation between rainfall and the Normalized Difference Vegetation Index for diverse vegetation types in East Africa. Int. J. Remote Sens. 1993, 14, 2369–2389. [Google Scholar] [CrossRef]
- Méndez-Barroso, L.A.; Vivoni, E.R.; Watts, C.J.; Rodríguez, J.C. Seasonal and interannual relations between precipitation, surface soil moisture and vegetation dynamics in the North American monsoon region. J. Hydrol. 2009, 377, 59–70. [Google Scholar] [CrossRef]
- Jamali, S.; Seaquist, J.; Ardö, J.; Eklundh, L. Investigating temporal relationships between rainfall, soil moisture and MODIS-derived NDVI and EVI for six sites in Africa. Savanna 2011, 21, 547–550. [Google Scholar]
- Zhao, B.; Yan, Y.N.; Guo, H.Q.; He, M.M.; Gu, Y.J.; Li, B. Monitoring rapid vegetation succession in estuarine wetland using time series MODIS-based indicators: An application in the Yangtze River Delta area. Ecol. Indic. 2009, 9, 346–356. [Google Scholar] [CrossRef]
- Sims, D.A.; Luo, H.; Hastings, S.; Oechel, W.C.; Rahman, A.F.; Gamon, J.A. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a Southern California chaparral ecosystem. Remote Sens. Environ. 2006, 103, 289–303. [Google Scholar] [CrossRef]
- Lu, H.; Raupach, M.R.; Mc Vicar, T.R.; Barrett, D.J. Decomposition of vegetation cover into woody and herbaceous components using AVHRR NDVI time series. Remote Sens. Environ. 2003, 86, 1–18. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zoungrana, B.J.-B.; Conrad, C.; Amekudzi, L.K.; Thiel, M.; Da, E.D. Land Use/Cover Response to Rainfall Variability: A Comparing Analysis between NDVI and EVI in the Southwest of Burkina Faso. Climate 2015, 3, 63-77. https://doi.org/10.3390/cli3010063
Zoungrana BJ-B, Conrad C, Amekudzi LK, Thiel M, Da ED. Land Use/Cover Response to Rainfall Variability: A Comparing Analysis between NDVI and EVI in the Southwest of Burkina Faso. Climate. 2015; 3(1):63-77. https://doi.org/10.3390/cli3010063
Chicago/Turabian StyleZoungrana, Benewinde J.-B., Christopher Conrad, Leonard K. Amekudzi, Michael Thiel, and Evariste Dapola Da. 2015. "Land Use/Cover Response to Rainfall Variability: A Comparing Analysis between NDVI and EVI in the Southwest of Burkina Faso" Climate 3, no. 1: 63-77. https://doi.org/10.3390/cli3010063
APA StyleZoungrana, B. J.-B., Conrad, C., Amekudzi, L. K., Thiel, M., & Da, E. D. (2015). Land Use/Cover Response to Rainfall Variability: A Comparing Analysis between NDVI and EVI in the Southwest of Burkina Faso. Climate, 3(1), 63-77. https://doi.org/10.3390/cli3010063






