Trends and Spatial Patterns of Drought Affected Area in Southern South America
Abstract
:1. Introduction
2. Data and Methodology
2.1. Precipitation Data
2.2. Standardized Precipitation Index

| Category | SPI | Probability |
|---|---|---|
| Wet (W) | ≥1.00 | 15.9% |
| Normal (N) | −0.99 to 0.99 | 68.2% |
| Moderate drought (MD) | −1.49 to −1.00 | 9.2% |
| Severe drought (SD) | −1.99 to −1.50 | 4.4% |
| Extreme drought (ED) | ≤−2.00 | 2.3% |
2.3. Trends Estimation
- Initialize: i = 1, and define r0 = x(t).
- Identify the extremes (maximum and minimum) of r0, and generate the upper and lower envelopes connecting all the local extrema through a cubic spline interpolation.
- Calculate the mean envelope m(j = 1).
- Subtract the mean envelope to the time series in order to obtain the first sub time series h(j = 1) (h(j = 1) = r0 − m(j = 1)).
- Treat h(j = 1) as r0 and repeat steps 2 to 4 with j = j + 1 as many times as needed, until the envelopes being symmetric to zero mean under certain criteria. The final h(j) is designated as Ci.
- Define again r0 = x(t) − Ci and i = i + 1, and then repeat steps 2 to 5. When i = N and the residual becomes a monotonic function or a function only containing one internal extremum from which no more IFM can be extracted, a complete sifting process of series x(t) by EMD stops. The decomposition results can be expressed as:
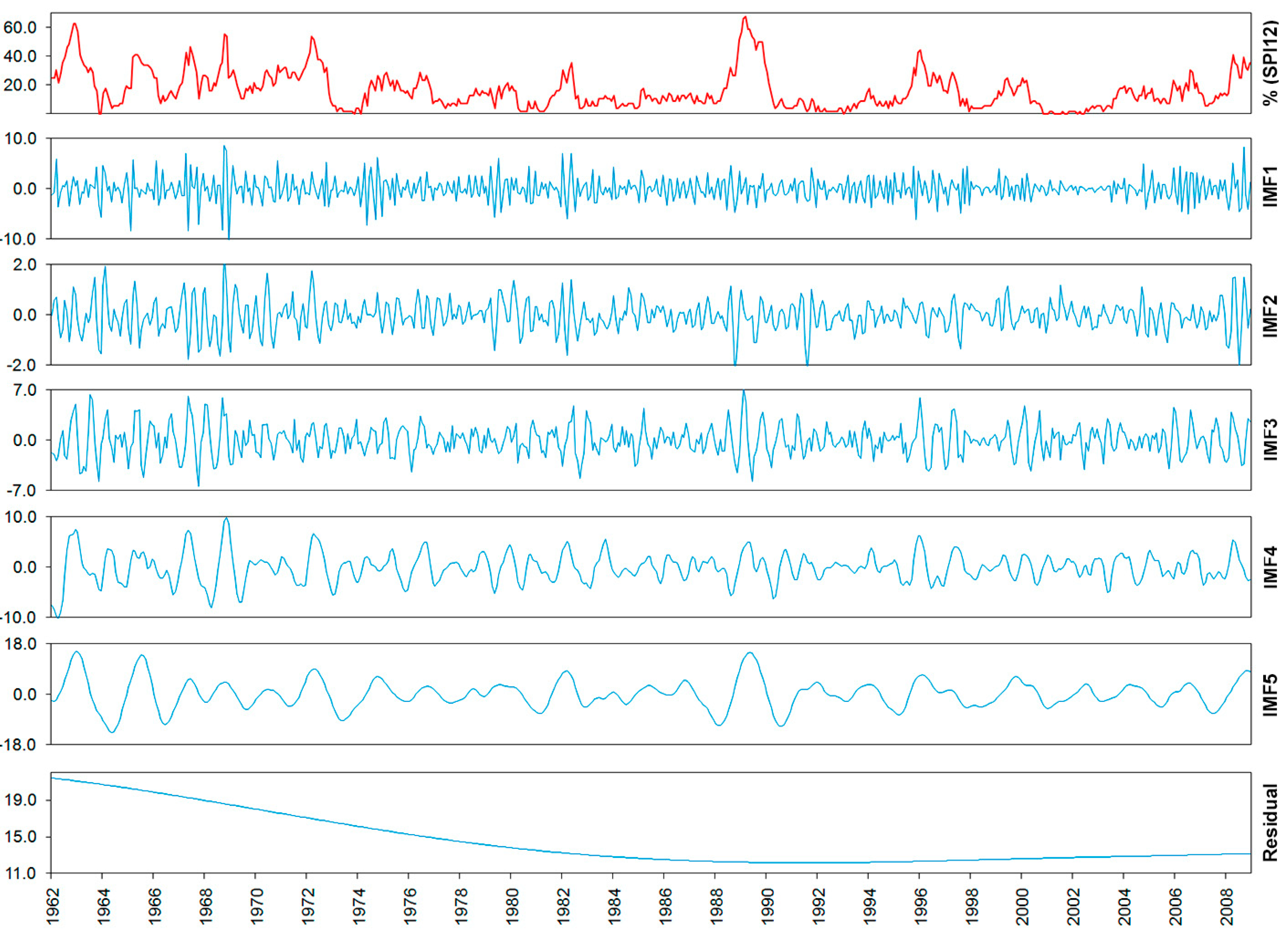
3. Results and Discussion
3.1. Temporal Evolution of the Number of Meteorological Stations with Drought Conditions
3.2. Trends in the Number of Meteorological Stations with Moderate Drought Conditions
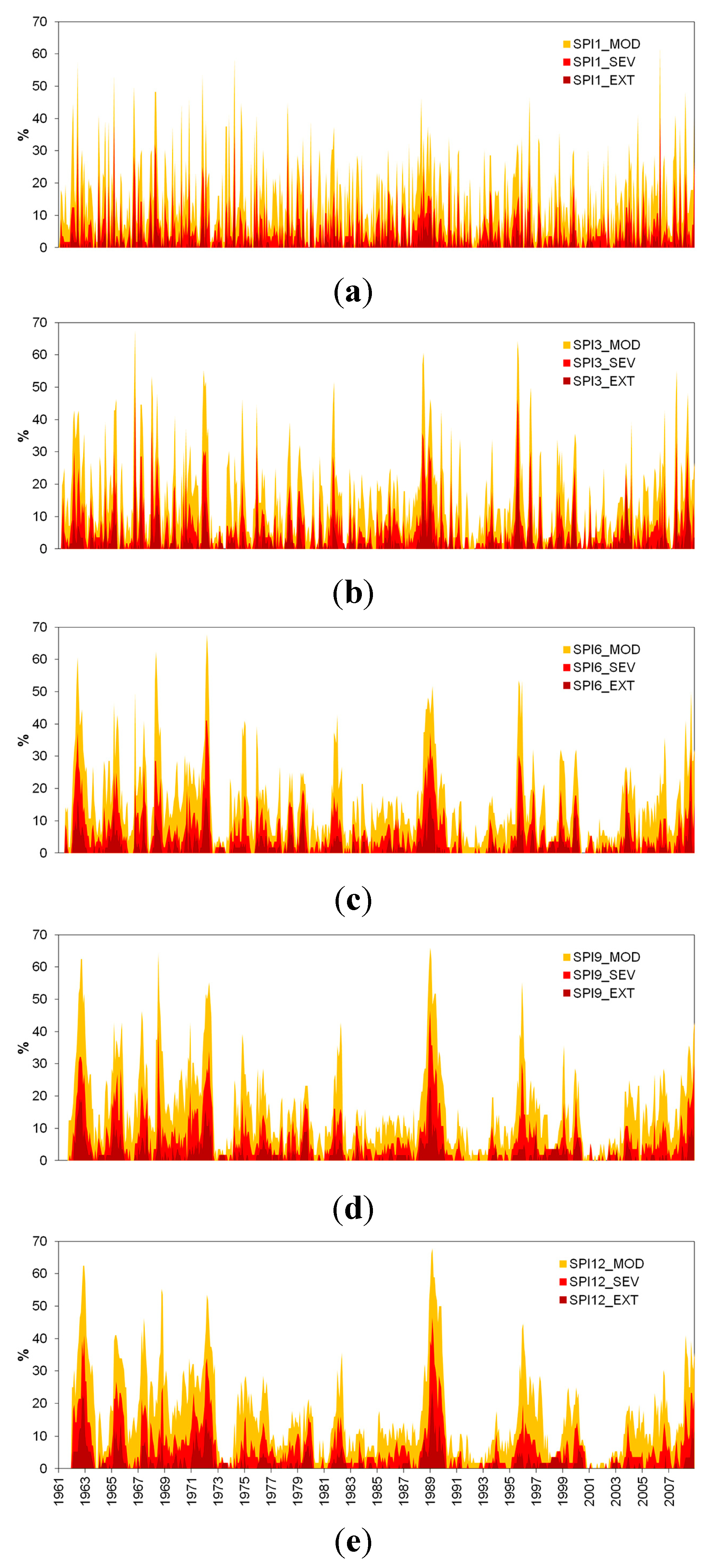
| Category | Moderate | Severe | Extreme | |||
|---|---|---|---|---|---|---|
| Time Scale | Max % | Date | Max % | Date | Max % | Date |
| 1 | 62.50 | May 2006 | 41.07 | May 2006 | 23.21 | March 1965 |
| 3 | 67.86 | October 1966 | 48.21 | October 1966 | 26.79 | October 1966 |
| 6 | 67.86 | March 1972 | 41.07 | February and March 1972 | 17.86 | February 1972 |
| 9 | 66.07 | January 1989 | 46.43 | January 1989 | 23.21 | January 1989 |
| 12 | 67.86 | March 1989 | 46.43 | March 1989 | 25.00 | March 1989 |
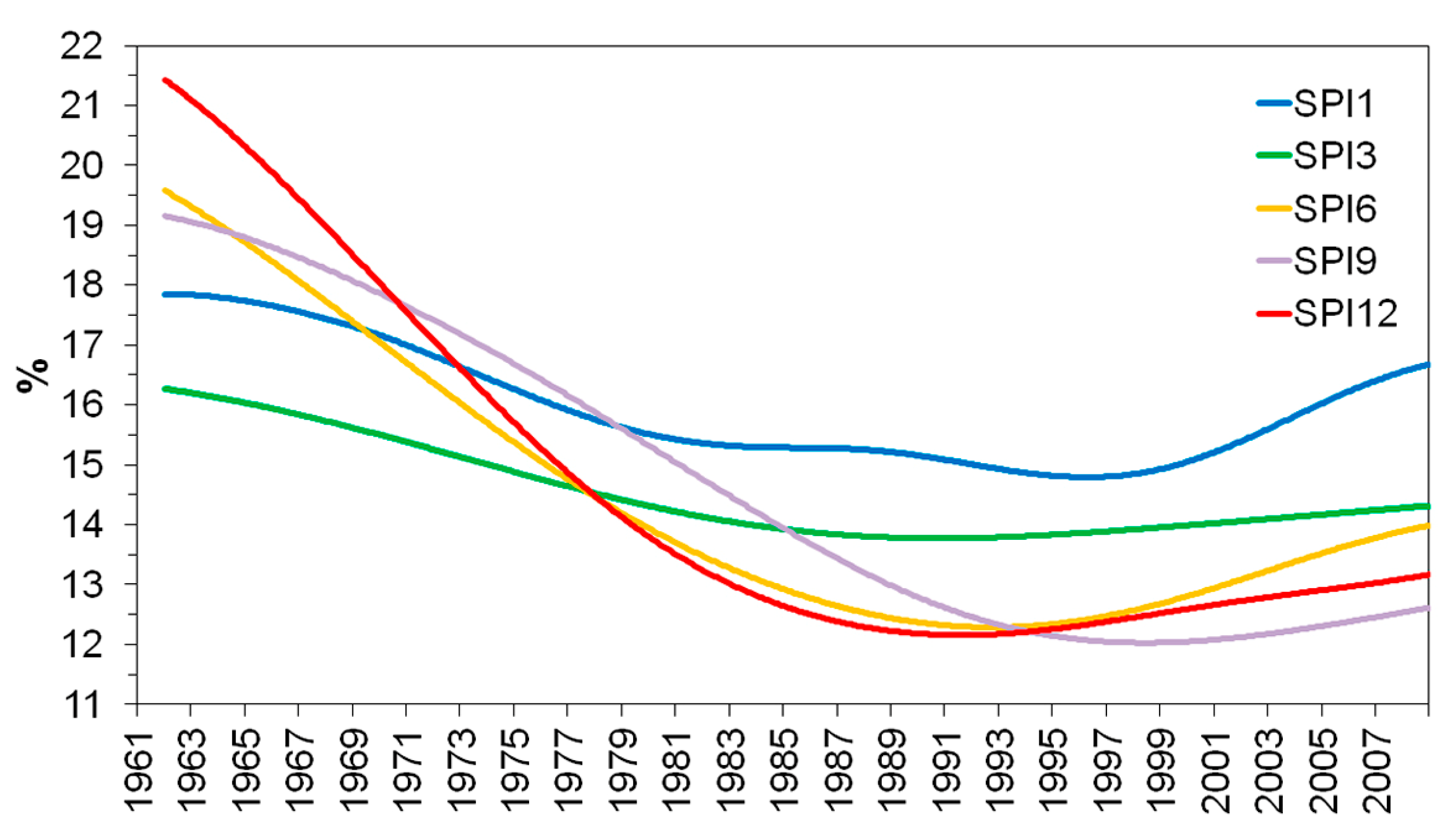
| Category | Moderate | Severe | Extreme | ||
|---|---|---|---|---|---|
| Time Scale | Year of Trend Reversal | Slope/10 Years | Recent Trend | Slope/10 Years | Slope/10 Years |
| 1 | 1996 | −0.38 | 3.40 | −0.21 | −0.11 |
| 3 | 1990 | −0.96 | 0.65 | −0.43 | −0.10 |
| 6 | 1991 | −1.78 | 2.44 | −0.98 | −0.35 |
| 9 | 1998 | −2.38 | 1.09 | −1.18 | −0.56 |
| 12 | 1991 | −2.81 | 1.11 | −1.49 | −0.70 |
3.3. Spatial Evolution of Major Droughts over SSA
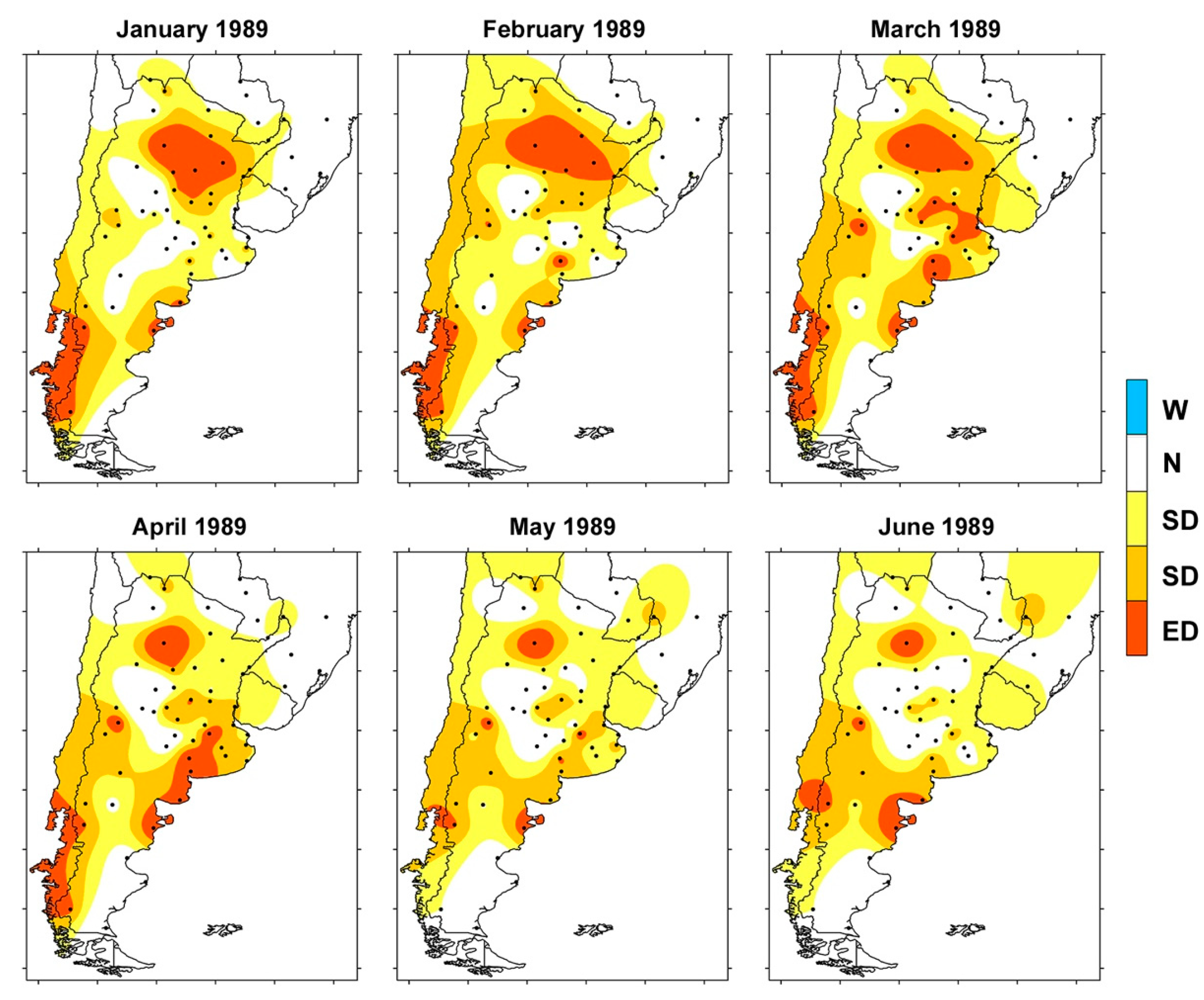
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, T.W.; Valdés, J.B.; Aparicio, J. Frequency and spatial characteristics of droughts in the Conchos river basin, Mexico. Water Int. 2002, 27, 420–430. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. State of the Climate. Available online: http://www.ncdc.noaa.gov/sotc/drought/ (accessed on 18 July 2014).
- Skansi, M.M.; Veiga, H.; Garay, N.G.; Podestá, G. Períodos secos en la región noreste de Argentina descriptos con el índice de precipitación estandarizado. In Proceedings of the XI Argentine Congress of Meteorology (CONGREMET), Mendoza, Argentina, 28 May–1 June 2012.
- Krepper, C.M.; Zucarelli, V. Climatology of water excess and shortages in the La Plata Basin. Theor. Appl. Climatol. 2012, 102, 13–27. [Google Scholar] [CrossRef]
- Barrucand, M.G.; Vargas, W.M.; Rusticucci, M.M. Dry conditions over Argentina and the related monthly circulation patterns. Meteorol. Atmos. Phys. 2007, 98, 99–114. [Google Scholar] [CrossRef]
- Castañeda, M.; Barros, V. Las tendencias de la precipitación en el cono sur de América al este de los Andes. Meteorológica 1994, 19, 23–32. [Google Scholar]
- Penalba, O.C.; Vargas, W.M. Interdecadal and interannual variations of annual and extreme precipitation over Central-Northeastern Argentina. Int. J. Climatol. 2004, 24, 1565–1580. [Google Scholar] [CrossRef]
- Barros, V.R.; Doyle, M.E.; Camilloni, I.A. Precipitation trends in southeastern South America: relationship with ENSO phases and with low-level circulation. Theor. Appl. Climatol. 2008, 93, 19–33. [Google Scholar] [CrossRef]
- Penalba, O.C.; Robledo, F.A. Spatial and temporal variability of the frequency of extreme daily rainfall regime in the La Plata Basin during the 20th century. Clim. Chang. 2010, 98, 531–550. [Google Scholar] [CrossRef]
- Minetti, J.L.; Vargas, W.M.; Poblete, A.G.; Acuña, L.R.; Casagrande, G. Non-linear trends and low frequency oscillations in annual precipitation over Argentina and Chile, 1931–1999. Atmósfera 1931, 16, 119–135. [Google Scholar]
- Rivera, J.A.; Penalba, O.C.; Bettolli, M.L. Inter-annual and inter-decadal variability of dry days in Argentina. Int. J. Climatol. 2013, 33, 834–842. [Google Scholar] [CrossRef]
- Bordi, I.; Fraedrich, K.; Sutera, A. Observed drought and wetness trends in Europe: An update. Hydrol. Earth Syst. Sci. 2009, 13, 1519–1530. [Google Scholar] [CrossRef]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and temporal variability of droughts in Portugal. Water Resour. Res. 2010. [Google Scholar] [CrossRef]
- Rossi, G.; Bonaccorso, B.; Nicolosi, V.; Cancelliere, A. Characterizing drought risk in a Sicilian river basin. In Coping with Drought Risk in Agriculture and Water Supply Systems; Iglesias, A., Garrote, L., Cancelliere, A., Cubillo, F., Wilhite, D., Eds.; Springer: Berlin, Germany, 2009; pp. 187–219. [Google Scholar]
- Di Lena, B.; Vergni, L.; Antenucci, F.; Todisco, F.; Mannocchi, F. Analysis of drought in the region of Abruzzo (Central Italy) by the Standardized Precipitation Index. Theor. Appl. Climatol. 2014, 115, 41–52. [Google Scholar] [CrossRef]
- Lana, X.; Serra, C.; Burgueño, A. Patterns of monthly rainfall shortage and excess in terms of the standardized precipitation index for Catalonia (NE Spain). Int. J. Climatol. 2001, 21, 1669–1691. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim. Dyn. 2008, 31, 79–105. [Google Scholar] [CrossRef]
- Penalba, O.C.; Rivera, J.A.; Pántano, V.C. The CLARIS LPB database: Constructing a long-term daily hydro-meteorological dataset for La Plata Basin, Southern South America. Geosci. Data J. 2014, 1, 20–29. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Pettit, A.N. A non-parametric approach to the change-point detection. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eight Conference on Applied Climatology, Anaheim, CA, USA, 17–23 January 1993; American Meteorological Society: Boston, MA; USA, 1993; pp. 179–184. [Google Scholar]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.I. The influence of atmospheric circulation at different spatial scales on winter drought variability through a semi-arid climatic gradient in northeast Spain. Int. J. Climatol. 2006, 26, 1427–1453. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln Declaration on drought indices: Universal meteorological drought index recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Rivera, J.A.; Penalba, O.C. Comparison of the performance of five indices for drought characterization in La Plata Basin. Perspectives towards a multi-scale monitoring system. In Proceedings of the 2011 WCRP Open Science Conference, Denver, CO, USA, 23–27 October 2011.
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q. An evaluation of the standardized precipitation index, the China-Z index and the statistical Z-score. Int. J. Climatol. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Penalba, O.C.; Rivera, J.A. Future changes in drought characteristics over Southern South America projected by a CMIP5 multi-model ensemble. Am. J. Clim. Chang. 2013, 2, 173–182. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, R.; Wu, M.C.; Shih, E.H.; Zheng, Q.; Tung, C.C.; Liu, H.H. The empirical mode decomposition method and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, Z.; Liu, C. Comparison of the MK test and EMD method for trend identification in hydrological time series. J. Hydrol. 2014, 510, 293–298. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech, 22–27 May 2011; pp. 4144–4147.
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E.; Flandrin, P. Noise-assisted EMD methods in action. Adv. Adapt. Data Anal. 2012. [Google Scholar] [CrossRef]
- Srikanthan, R.; Peel, M.C.; McMahon, T.A.; Karoly, D.J. Ensemble empirical mode decomposition of Australian monthly rainfall and temperature data. In Proceedings of the 19th International Congress on Modelling and Simulation, Pert, WA, Australia, 12–16 December 2011; pp. 3643–3649.
- Peel, M.C.; Srikanthan, T.A.; McMahon, T.A.; Karoly, D.J. Ensemble empirical mode decomposition of monthly climatic indices relevant to Australian hydrolicmatology. In Proceedings of the 19th International Congress on Modelling and Simulation, Pert, WA, Australia, 12–16 December 2011; pp. 3615–3621.
- Iyengar, R.N.; Raghu Kanth, S.T.G. Intrinsic mode functions and a strategy for forecasting Indian monsoon rainfall. Meteorol. Atmos. Phys. 2005, 90, 17–36. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Kumar, D.N. Predictability of nonstationary time series using wavelet and EMD based ARMA models. J. Hydrol. 2013, 502, 103–119. [Google Scholar] [CrossRef]
- Popescu, I.; Brandimarte, L.; Perera, M.S.U.; Peviani, M. Assessing residual hydropower potential of the La Plata Basin accounting for future user demands. Hydrol. Earth Syst. Sci. 2012, 16, 2813–2823. [Google Scholar] [CrossRef]
- Compagnucci, R.H.; Agosta, E.A.; Vargas, W.M. Climatic change and quasi-oscillations in central-west Argentina summer precipitation: Main features and coherent behaviour with southern African region. Clim. Dyn. 2002, 18, 421–435. [Google Scholar] [CrossRef]
- Kogan, F.N. Contribution of remote sensing to drought early warning. In Early Warning Systems for Drought Preparedness and Drought Management, Proceedings of 2000 An Expert Group Meeting in Early Warning Systems for Drought Preparedness and Drought Management, Lisboa, Portugal, 5–7 September 2000; Wilhite, D.A., Sivakumar, W., Wood, D.A., Eds.; World Meteorological Organization: Geneva, Switzerland, 2000; pp. 86–100. [Google Scholar]
- Minetti, J.L.; Vargas, W.M.; Vega, B.; Costa, M.C. Las sequías en la pampa húmeda: Impacto en la productividad del maíz. Rev. Bras. Meteorol. 2007, 22, 218–232. [Google Scholar] [CrossRef]
- Alessandro, A.P. Acciones bloqueantes alrededor de los setenta grados oeste en el sur de Sudamérica. Meteorológica 2005, 30, 3–25. [Google Scholar]
- Junquas, C.; Vera, C.; Li, L.; le Treut, H. Summer precipitation variability over Southeastern South America in a global warming scenario. Clim. Dyn. 2012, 38, 1867–1883. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivera, J.A.; Penalba, O.C. Trends and Spatial Patterns of Drought Affected Area in Southern South America. Climate 2014, 2, 264-278. https://doi.org/10.3390/cli2040264
Rivera JA, Penalba OC. Trends and Spatial Patterns of Drought Affected Area in Southern South America. Climate. 2014; 2(4):264-278. https://doi.org/10.3390/cli2040264
Chicago/Turabian StyleRivera, Juan A., and Olga C. Penalba. 2014. "Trends and Spatial Patterns of Drought Affected Area in Southern South America" Climate 2, no. 4: 264-278. https://doi.org/10.3390/cli2040264
APA StyleRivera, J. A., & Penalba, O. C. (2014). Trends and Spatial Patterns of Drought Affected Area in Southern South America. Climate, 2(4), 264-278. https://doi.org/10.3390/cli2040264





