4.1. Correlations with Climatic Drivers
Links between ENSO and Sri Lankan rainfall are now well established, including the detail of inter-seasonal variation (e.g., [
9]). Analyses presented here add to that knowledge through information on daily rainfall totals, allowing the frequency as well as the amount of rainfall to be considered. This is significant because both amount and reliability of rainfall influence farmers’ decisions on cropping strategies (crop type, variety, cultivation method) and cropping intensities (what area of land to cultivate). This is particularly the case at the start of the
Yala season [
11].
Results in
Table 3c show that number of rain days and the number of days with at least 5 mm rainfall are better correlated with ENSO indices than total seasonal rainfall. It is of course trite to observe that total seasonal rainfall is an accumulation of individual daily totals; the important point is that small totals, those significant to farmers, are well correlated with climatic drivers. There are very poor correlations with very large daily totals and in any case such events are problematic anyway, causing flooding and in extreme cases requiring replanting of crops after the flood-waters have subsided. Rainfall in March and April is crucial in the Wet Zone at the start of the rain-fed
Yala cultivation season. Results in
Table 3a and
Table 4e show how various rainfall indices are correlated with climatic indices, whilst results in
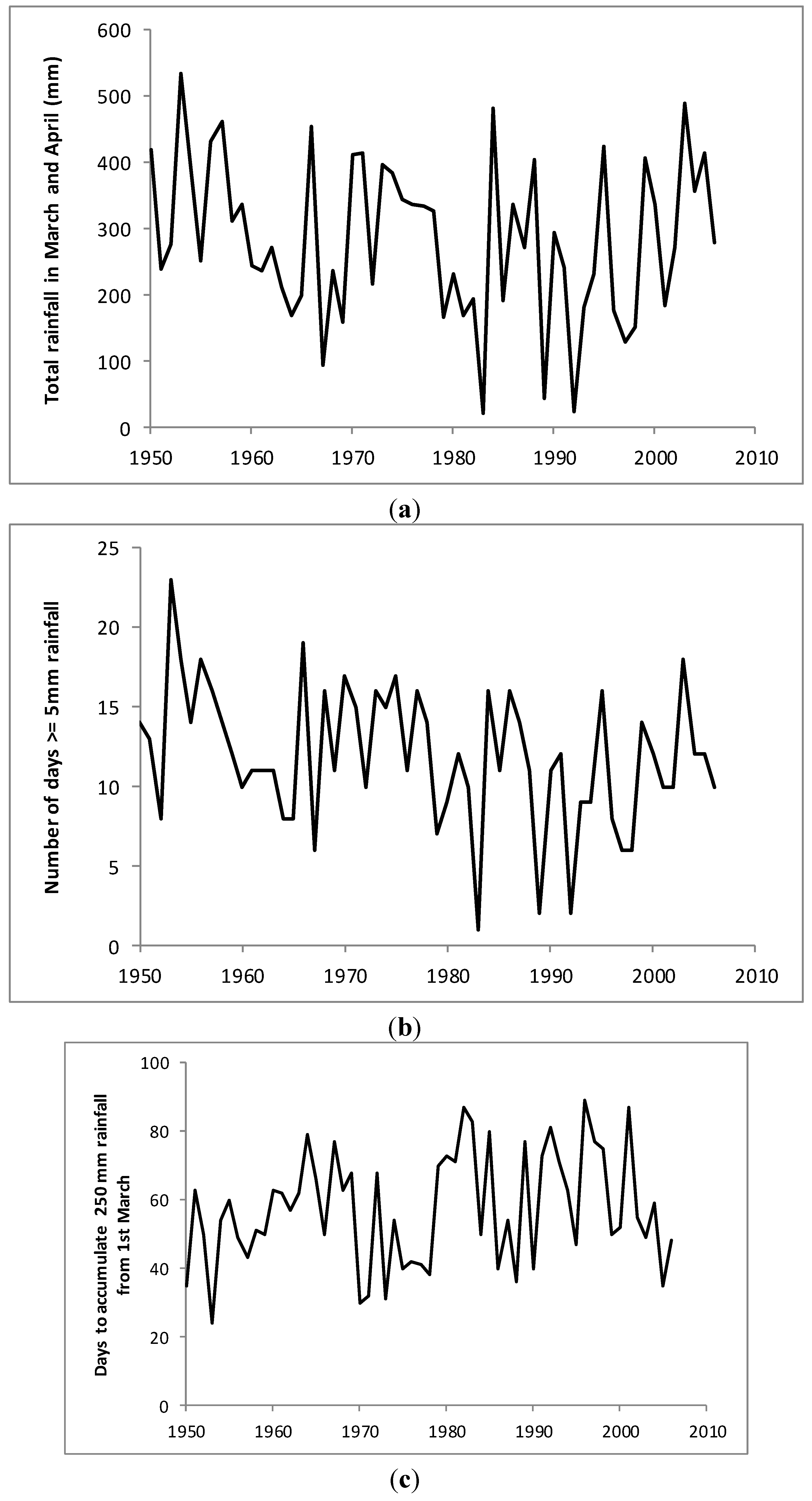
Figure 4 show that there has been a tendency for rainfall totals to decline over time.
Figure 5 shows that occasionally the M+A rainfall total can be very low indeed; such years tend to coincide with strong El Niño conditions, but not exclusively so and further work is needed to understand variations in atmospheric circulation in M+A that can lead to drought at the start of the
Yala cultivation season. For India, authors in [
29] noted that, whilst severe droughts are always associated with El Niño events, not every El Niño produces a severe drought. They showed that El Niño events with the warmest SST anomalies in the central equatorial Pacific were more effective in focusing drought-producing subsidence over India than events with the warmest SSTs in the eastern equatorial Pacific.
Figure 5 also shows that there has been significant variation in M+A rainfall at the decadal time scale; droughts were more likely in the drier 1980s and early 1990s. Clearly more needs to be understood about the onset of the SWM, over Sri Lanka and more generally its progression across the Indian subcontinent [
4,
32].
Authors in [
16] used a
Maha rainfall index (a blend of different station records from 1869 to 2000) to compare with IOD and NINO3. Their results showed the significant role of IOD in modulating
Maha rainfall after removing the NINO3 contribution using partial correlation analysis. For our shorter records from individual stations (from 1976), all the OND correlations are stronger with NINO34 than with IOD. As noted previously, the biennial oscillation associated with the IOD is less apparent in recent years at Mapalana (
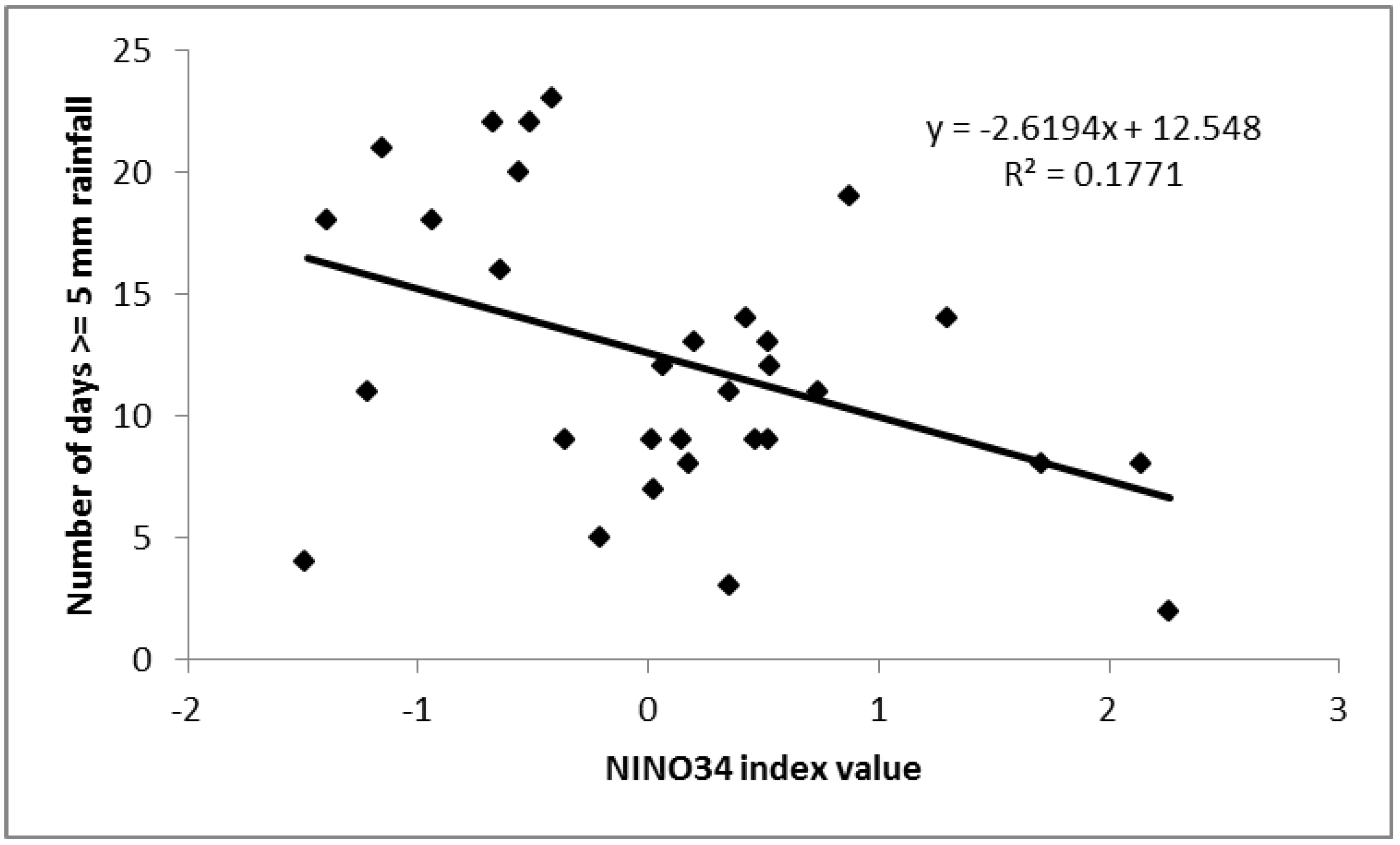
Figure 4) whilst NINO34 is significantly correlated with numbers of days with ≥5 mm rainfall total in JFM (
Figure 6). Our results seem to complement those of [
33] who found modest intensification of the NEM-ENSO relationship since 1980 (in contrast to a weakening of the Indian SWM) which is consistent with the warming of surface temperatures over the Tropical Indian Ocean in recent decades. This is deserving of further attention, to assess the relative importance of climatic drivers on the various seasons of Sri Lanka rainfall under current, warm SST conditions.
4.2. Physical Mechanisms of ENSO Teleconnections
Results show that there are strong teleconnections for Sri Lankan rainfall with SSTs in the Pacific Ocean and, given the relative lack of significant correlations with IOD, these are apparently more important than SSTs in the Indian Ocean. Modulation of Sri Lanka’s climate during El Niño events is related to changes in the Walker circulation, resulting in heightened convection over Sri Lanka in OND and enhanced subsidence during the rest of the year [
34]. During an El Niño event, the convection associated with the rising limb of the Walker circulation, normally located in the Western Pacific, shifts eastwards; there are anomalously warm waters in the Central and Eastern Pacific. Consequently, to the west of the rising limb, there is an anomalous subsidence at low atmospheric levels extending from the Western Pacific to South Asia. This leads to reduction of rainfall over Sri Lanka from January to September. However, in OND the influence of ENSO reverses with anomalous convection extending from Eastern Africa across to Sri Lanka [
9].
We have not investigated links with SSTs in the Bay of Bengal but judging by results in [
27], there is an opposite response during El Niño years in the north and south of the Bay, due no doubt to the location of the ITCZ [
8]. Authors in [
27] note that there is a higher frequency of monsoonal depressions over the northern and adjoining central Bay of Bengal during July and August of El Niño years; this implies higher rainfall in those regions. Authors in [
35] found a significant positive correlation for Bay of Bengal SSTs and All-Bangladesh Monsoon Rainfall for the month of June but not in other summer months. Results for JAS from Sri Lanka, further south, show negative correlations with NINO34, meaning lower rainfall in the El Niño phase. For Sri Lanka, positive correlations with Pacific SSTs occur only in OND when the ITCZ has moved south and the NEM strongly influences all stations except those in the dry southeastern corner of the island. The importance of NEM precipitation is emphasized in
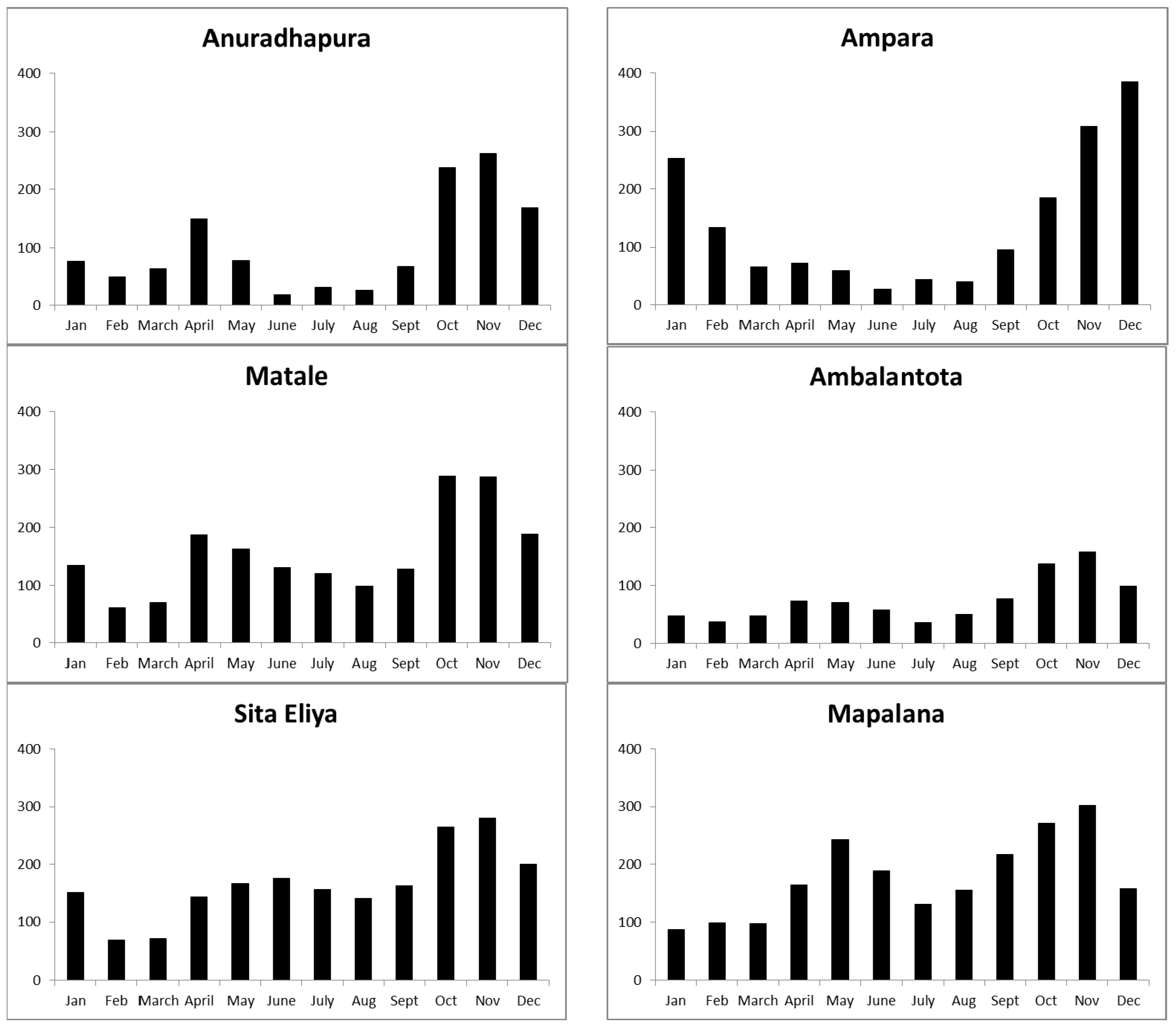
Figure 3, especially for more northern locations like Anuradhapura and Ampara.
Other than OND, significant correlations are almost all negative (JAS, JFM, M+A) or not found at all (AMJ). The inter-seasonal switch in wind direction is thus a crucial element in the link between global-scale tropical circulation and local conditions in Sri Lanka, with the NEM, by definition, the result of a NE circulation pattern, with westerly and south-westerly circulation at other times [
36]. Thus, El Niño tends to reduce rainfall in JFM, M+A (but not AMJ) and JAS; by contrast, El Niño tends to increase rainfall in OND. However, as noted above in relation to
Figure 6, the reverse situation is not entirely consistent, with mostly more rainfall in JFM in La Niña phases but not in during the prolonged La Niña of 1999/2000. The monsoon circulation is fundamentally dependent on surface conditions over both land and ocean and, since sea-surface temperatures in the Indian Ocean are largely controlled by surface winds, the anomalous subsidence during El Niño phases will delay the onset of the SWM because of the relative dryness of the low-level air [
4].
Figure 5c shows that, in terms of rainfall accumulation at Mapalana, the onset of the SWM has tended to become later, by roughly 10 days, since 1950 (but note the trend is not statistically significant); the mean is 57 days from 1 March (
i.e., 26 April) but often this is now delayed until early May. In the worst years, sufficient rainfall may not accumulate until late May and adjustments in cropping are needed. Normally the SWM arrives in Sri Lanka about a week earlier than in southern India but the “onset” date does depend on the method used; our rainfall accumulation index gives an earlier date than either climatological [
32] or hydrological [
30] indices but has been chosen specifically with rice cultivation in mind. Gradual delay in the onset of the SWM and a weaker biennial oscillation in rainfall totals (
Figure 4) may indicate the influence of higher SSTs in the eastern Indian Ocean but further work is needed to explore this issue and to link to what happens in relation to the ENSO. Authors in [
14] show how coupling between atmospheric convection and Indian Ocean SSTs creates the biennial monsoonal oscillation, modulated by lower-frequency ENSO influence from the Pacific. SSTs are the key memory effect in driving biennial variations in cloud formation and thus precipitation.
Building on the work of [
29] and others, further work is needed to improve rainfall forecasts for the onset of the
Yala cultivation season, in particular to anticipate the late arrival of rains in March and April in the wet zone (
Figure 5). Given the strength of some teleconnections and the fact that ENSO is predictable one or two seasons in advance, seasonal rainfall totals in Sri Lanka (and more widely over the Indian subcontinent) should be predictable with some degree of confidence. This cannot assist with forecasting of daily rainfall, of course, but should at least provide some idea of likely timing and amount of rainfall to be expected in the next wet season. We have not attempted, here, to analyze the synoptic situations associated with individual rainfall events. However, we can see that such an analysis could be very valuable in relating large-scale climatological situation to meso-scale precipitation generation. Authors in [
27], working in the Bay of Bengal, showed how such an analysis might proceed.
It seems particularly important to understand ocean-atmosphere conditions at the regional scale associated with both modulation of the NEM by ENSO and the IOD and under which the arrival of SWM rain in March and April is significantly delayed. A good deal of research has been conducted at the scale of the Indian subcontinent, some of it reviewed here, and it is vital to place Sri Lanka in its regional context. For example, in relation to the NEM, authors in [
10] found similar results in Tamil Nadu, Southeast India, to those presented here in terms of ENSO controls on rainfall totals. With regard to the SWM, the findings of [
32] show that being able to place Sri Lanka in its wider regional context could be very worthwhile since this could aid forecasting of the onset of the monsoonal circulation and associated precipitation further north in the Indian subcontinent and hopefully enable monsoon failures to be better anticipated. Finally, it is worthwhile noting that rainfall is important for water resources other than irrigation—drinking water and HEP generation, in particular—so more studies which relate ENSO to river regimes are needed too, for both Sri Lanka (
cf. [
11]) and across South and Southeast Asia more generally [
30].