Frequency Analysis and Trend of Maximum Wind Speed for Different Return Periods in a Cold Diverse Topographical Region of Iran
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Scope and Objective
2. Materials and Methods
2.1. Data Used
2.2. Methodology
2.2.1. Analysis of PDF and CDF of Wind Speed Data
2.2.2. Trend Detection in Wind Speed Data
2.2.3. Probability Distribution Analysis of Wind Speed Data
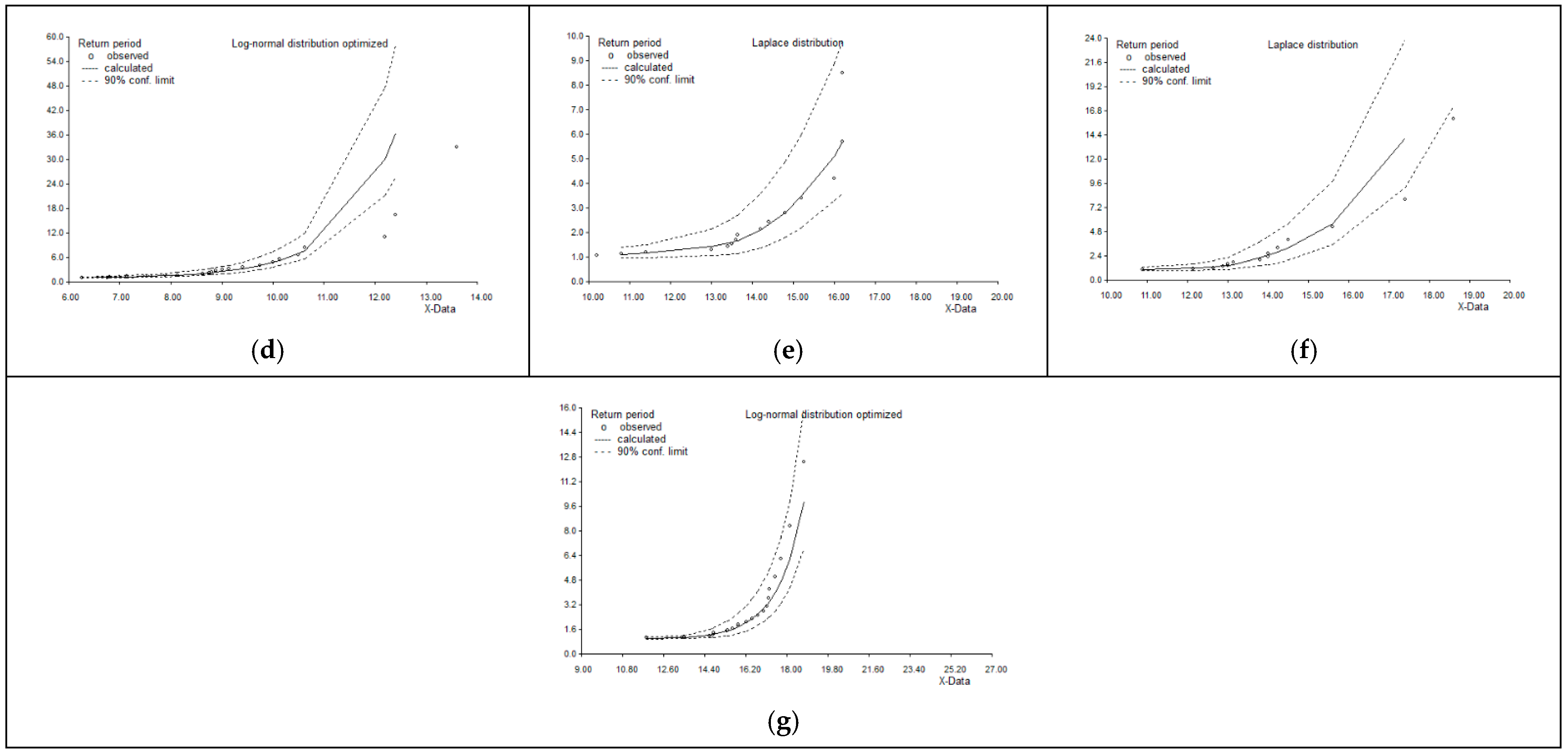
3. Results and Discussion
3.1. PDF and CDF Analysis
3.2. Trend Analysis of Maximum Wind Speed Data
3.3. Probability Distribution Analysis of Maximum Wind Speed Data
3.4. Implications and Future Research Directions
3.5. Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- CAN/CSA-S6-06; Canadian Highway Bridge Design Code. Canadian Standards Association: Toronto, ON, Canada, 2006.
- Mo, H.M.; Hong, H.P.; Li, S.H.; Fan, F. Impact of annual maximum wind speed in mixed wind climates on wind hazard for mainland China. Nat. Hazards Rev. 2022, 23, 04021061. [Google Scholar] [CrossRef]
- Dubina, D.; Dinu, F. Reliability and Durability of Built Environment Under Impact of Climate Natural Hazards. In Proceedings of the 4th International Conference "Coordinating Engineering for Sustainability and Resilience" & Midterm Conference of CircularB “Implementation of Circular Economy in the Built Environment”, Timișoara, Romania, 29–31 May 2024; Springer Nature: Cham, Switzerland, 2024; pp. 20–36. [Google Scholar]
- Landberg, L. Short-term prediction of the power production from wind farms. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 207–220. [Google Scholar] [CrossRef]
- WEPS. Wind Erosion Prediction System, Kansas State University. 1996. Available online: https://www.nrcs.usda.gov/sites/default/files/2023-01/WEPSUserGuide.pdf (accessed on 1 May 2025).
- Cornelis, W.M.; Gabriels, D. Optimal windbreaks design for wind-erosion control. J. Arid. Environ. 2005, 61, 315–332. [Google Scholar] [CrossRef]
- Lee, J.U.; Lee, K.H.; Kim, S.I.; Yook, D.S.; Ahn, S.M. Calculation of Wind Speeds for Return Period Using Weibull Parameter: A Case Study of Hanbit NPP Area. In Proceedings of the Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Republic of Korea, 12–13 May 2016. [Google Scholar]
- De Freitas, N.C.; Silva, M.P.D.S.; Sakamoto, M.S. Wind speed forecasting: A review. Int. J. Eng. Res. Appl. 2018, 8, 4–9. [Google Scholar]
- Zakaria, N.H.; Salleh, S.A.; Asmat, A.; Chan, A.; Isa, N.A.; Hazali, N.A.; Islam, M.A. Analysis of wind speed, humidity and temperature: Variability and trend in 2017. IOP Conf. Ser. Earth Environ. Sci. 2020, 489, 012013. [Google Scholar] [CrossRef]
- Ranjbar, A.; Fattahi, E.; Rahimzadeh, F. Investigation of wind speed homogeneity in Iran meteorology stations. J. Meteorol. Atmos. Sci. 2018, 1, 146–162. [Google Scholar]
- Mazas, F. Extreme events: A framework for assessing natural hazards. Nat. Hazards 2019, 98, 823–848. [Google Scholar] [CrossRef]
- Li, C.Q.; Yang, W. Time-Dependent Reliability Theory and Its Applications; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Dukes, M.D.G.; Palutikof, J.P. Estimation of extreme wind speeds with very long return periods. J. Appl. Meteorol. Climatol. 1995, 34, 1950–1961. [Google Scholar] [CrossRef]
- Morton, I.D.; Bowers, J.; Mould, G. Estimating return period wave heights and wind speeds using a seasonal point process model. Coast. Eng. 1997, 31, 305–326. [Google Scholar] [CrossRef]
- Della-Marta, P.M.; Mathis, H.; Frei, C.; Liniger, M.A.; Kleinn, J.; Appenzeller, C. The return period of wind storms over Europe. Int. J. Climatol. A J. R. Meteorol. Soc. 2009, 29, 437–459. [Google Scholar] [CrossRef]
- Razali, A.M.; Sapuan, M.S.; Ibrahim, K.; Zaharim, A.; Sopian, K. Mapping of annual extreme wind speed analysis from 12 stations in Peninsular Malaysia. In Proceedings of the 9th WSEAS International Conference on System Science and Simulation in Engineering, Iwate, Japan, 4–6 October 2010; pp. 397–403. [Google Scholar]
- Lee, J.K.; Yook, D.; Lee, K.J.; Yun, J.I.; Beeley, P.A. Weibull parameter calculation and estimation of directional and seasonal wind speeds for the return period: A case study in the Barakah NPP area. Ann. Nucl. Energy 2015, 80, 62–69. [Google Scholar] [CrossRef]
- Ekhtesasi, M.R.; Ghaeminia, A.M. Mapping of possible maximum wind speed at different return periods in the central part of Iran. Desert Ecosyst. Eng. 2022, 6, 49–58. [Google Scholar]
- Moradi, M. Investigation of return period annual fastest wind speed in Bushehr stations. J. Clim. Res. 2019, 1397, 31–42. [Google Scholar]
- Deng, T.; Fu, J.; Zheng, Q.; Wu, J.; Pi, Y. Performance-based wind-resistant optimization design for tall building structures. J. Struct. Eng. 2019, 145, 04019103. [Google Scholar] [CrossRef]
- Cao, S. Strong winds and their characteristics. In Advanced Structural Wind Engineering; Springer: Tokyo, Japan, 2013; pp. 1–25. [Google Scholar]
- Palutikof, J.P.; Brabson, B.B.; Lister, D.H.; Adcock, S.T. A review of methods to calculate extreme wind speeds. Meteorol. Appl. 1999, 6, 119–132. [Google Scholar] [CrossRef]
- Ahmadi, M.; Baaghide, M.; Dadashi Roudbari, A.; Asadi, M. Modeling the role of topography on the potential of tourism climate in Iran. Model. Earth Syst. Environ. 2018, 4, 13–25. [Google Scholar] [CrossRef]
- Ghafari, S.; Ghorbani, A.; Moameri, M.; Mostafazadeh, R.; Bidarlord, M. Composition and structure of species along altitude gradient in Moghan-Sabalan rangelands, Iran. J. Mt. Sci. 2018, 15, 1209–1228. [Google Scholar] [CrossRef]
- Mehri, S.; Mostafazadeh, R.; Esmaliouri, A.; Ghorbani, A. Spatial and Temporal Variations of Base Flow Index (BFI) for the Ardabil Province river, Iran. J. Earth Space Phys. 2017, 43, 623–634. [Google Scholar] [CrossRef]
- Gimechi, S.; Mostafazadeh, R.; Alimohamadian, L. Analysis of extreme precipitation trends and probability distributions across return periods in northwest Iran. Geogr. časopis/Geogr. J. 2025, 77, 43–55. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramirez, P.; Velazquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, C.; Zhang, M.; Ji, X.; Shen, Y.; He, J.; Zhang, Z. Statistical modelling of the joint probability density function of air density and wind speed for wind resource assessment: A case study from China. Energy Convers. Manag. 2022, 268, 116054. [Google Scholar] [CrossRef]
- Mostafazadeh, R.; Mehri, S. Trends in variability of flood coefficient in river gauge stations of Ardabil province, Iran. J. Watershed Manag. Res. 2018, 9, 82–95. [Google Scholar] [CrossRef]
- Kisi, O.; Ay, M. Comparison of Mann–Kendall and innovative trend method for water quality parameters of the Kizilirmak River, Turkey. J. Hydrol. 2014, 513, 362–375. [Google Scholar] [CrossRef]
- Barzegari, H.; Gandomkar, A.; Abbasi, A. Correlation between the average temperature of the Abargu-Sirjan Basin and the teleconnection patterns from the Atlantic Ocean. Water Soil Manag. Modell. 2023, 3, 270–285. [Google Scholar]
- Chattopadhyay, G.; Chakraborthy, P.; Chattopadhyay, S. Mann–Kendall trend analysis of tropospheric ozone and its modeling using ARIMA. Theor. Appl. Climatol. 2012, 110, 321–328. [Google Scholar] [CrossRef]
- Esgandari, R.; Esmali Ouri, A.; Mostafazadeh, R.; Choobeh, S. Assessment of temporal and spatial variations of precipition climate extreme indexes in the central part of Ardabil province. J. Environ. Sci. Stud. 2024, 9, 8119–8133. [Google Scholar]
- Atroosh, K.B.; Moustafa, A.T. An estimation of the probability distribution of Wadi Bana flow in the Abyan Delta of Yemen. J. Agric. Sci. 2012, 4, 80. [Google Scholar] [CrossRef]
- Oosterbaan, R.J. Software for generalized and composite probability distributions. Int. J. Math. Comput. Methods 2019, 4, 1–19. [Google Scholar]
- Mostafazadeh, R.; Pourganji, Z.; Esfandiari Darabad, F.; Aghaie, M. Change in flood hydrograph response due to variable precipitation amount during different return periods in Namin watershed. J. Environ. Sci. Stud. 2023, 8, 5869–5882. [Google Scholar]
- Anghel, C.G. Revisiting the use of the Gumbel distribution: A comprehensive statistical analysis regarding modeling extremes and rare events. Mathematics 2024, 12, 2466. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Tsalis, C. Effects of parameter estimation method and sample size in metocean design conditions. Ocean. Eng. 2018, 169, 19–37. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Perrin, O.; Rootzén, H.; Taesler, R. A discussion of statistical methods used to estimate extreme wind speeds. Theor. Appl. Climatol. 2006, 85, 203–215. [Google Scholar] [CrossRef]
- Devis-Morales, A.; Montoya-Sánchez, R.A.; Bernal, G.; Osorio, A.F. Assessment of extreme wind and waves in the Colombian Caribbean Sea for offshore applications. Appl. Ocean. Res. 2017, 69, 10–26. [Google Scholar] [CrossRef]
- Panchang, V.; Zhao, L.; Demirbilek, Z. Estimation of extreme wave heights using GEOSAT measurements. Ocean. Eng. 1998, 26, 205–225. [Google Scholar] [CrossRef]
- Singh, V.P.; Guo, H. Parameter estimation for 2-parameter log-logistic distribution (LLD2) by maximum entropy. Civ. Eng. Syst. 1995, 12, 343–357. [Google Scholar] [CrossRef]


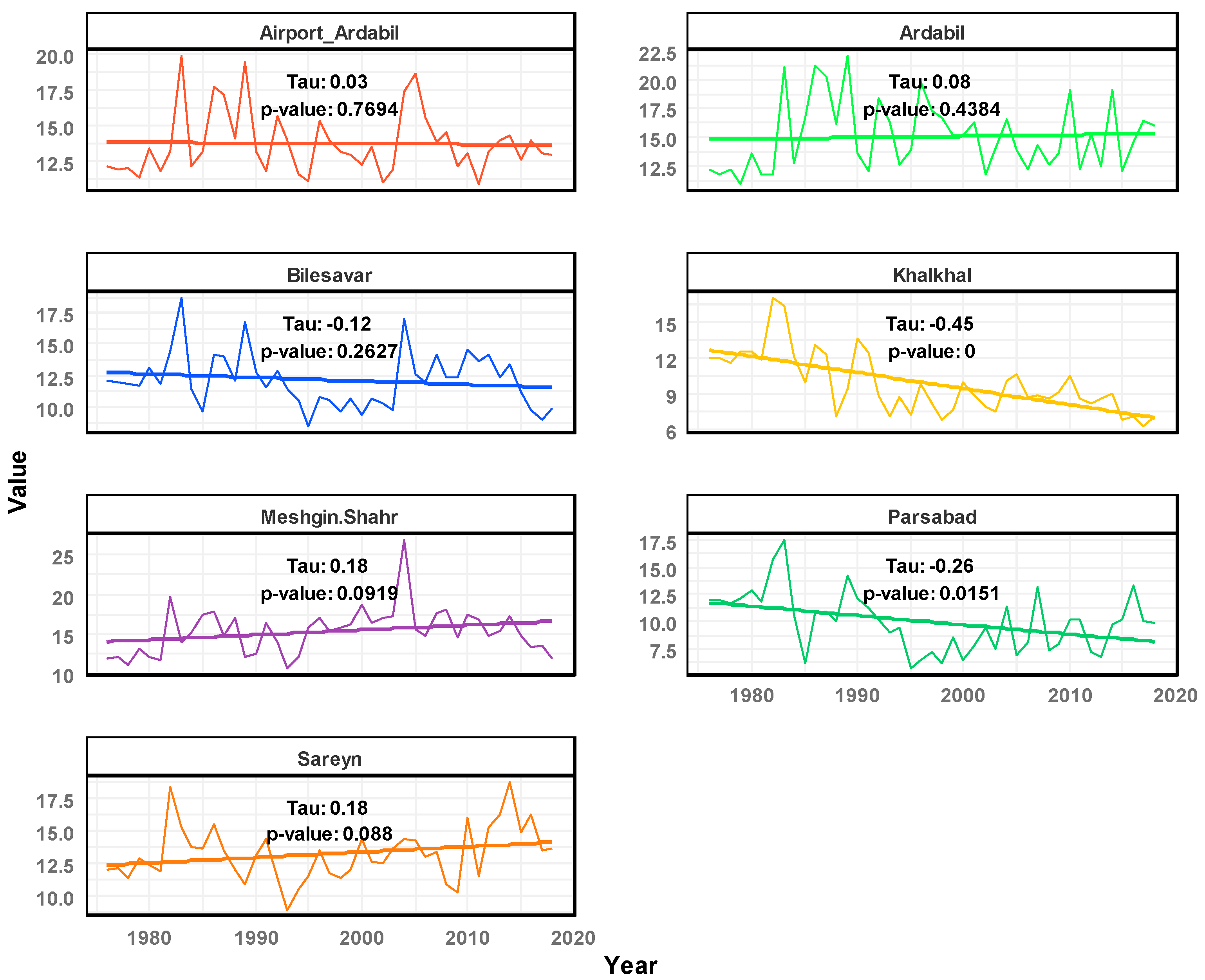
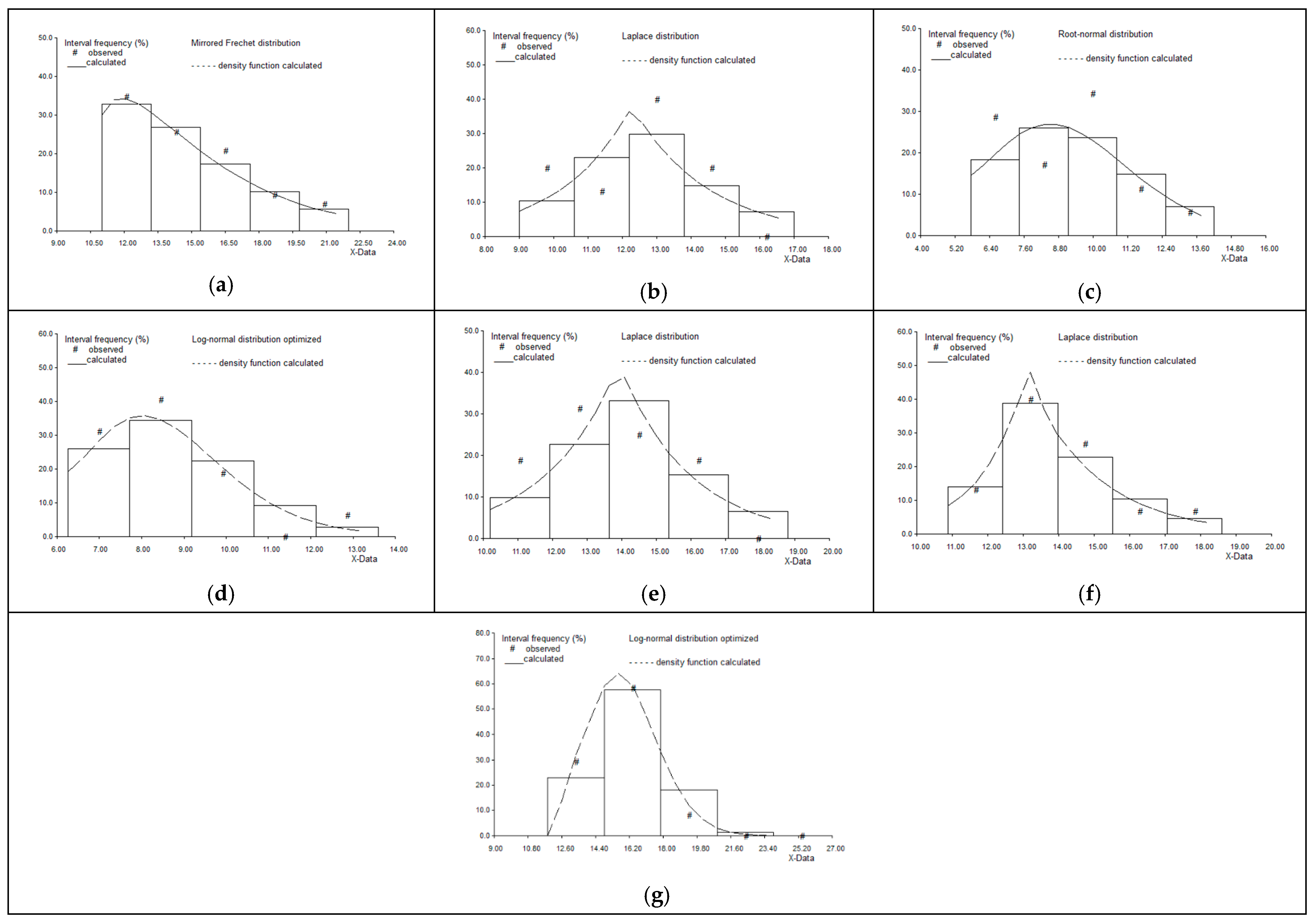
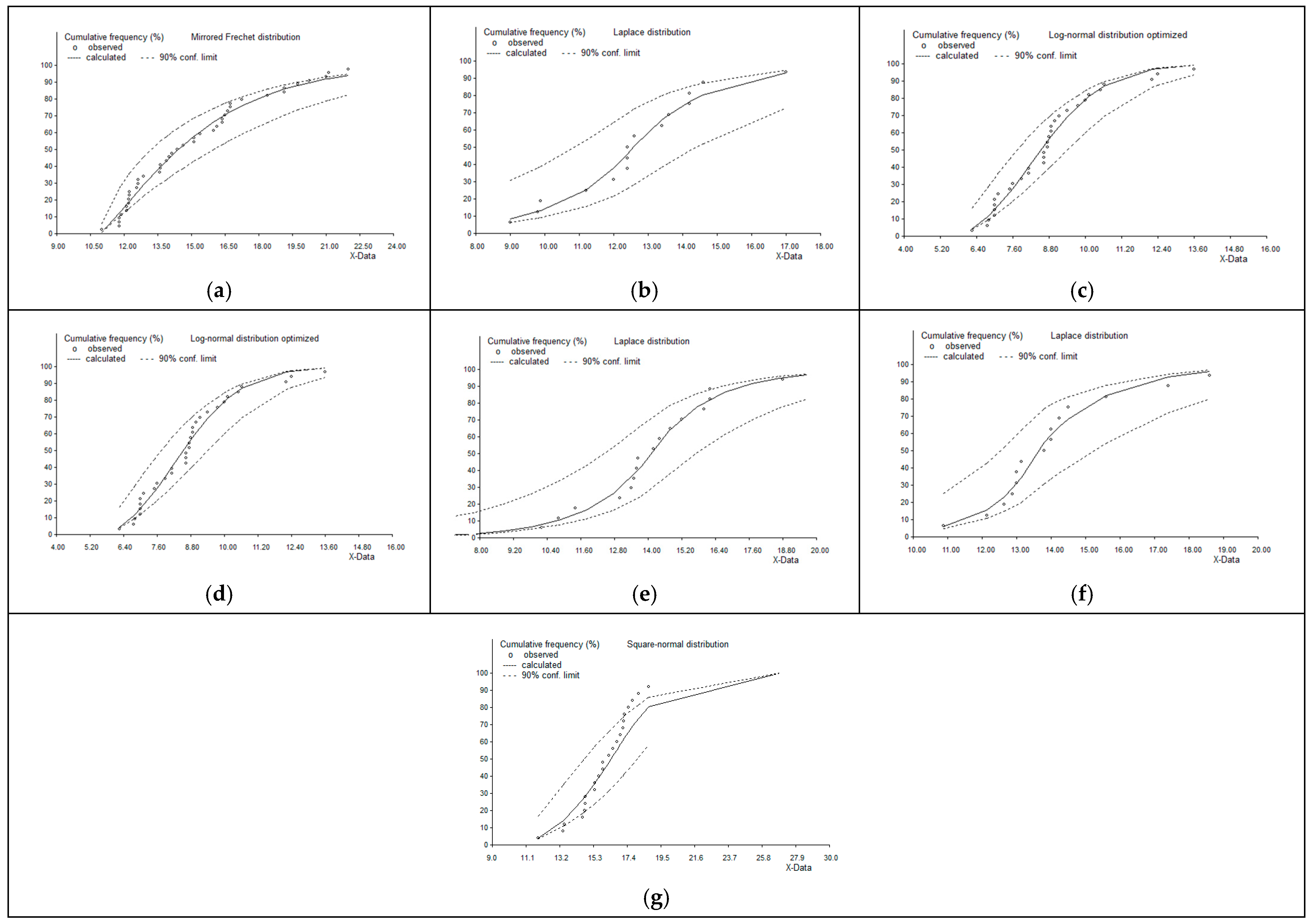
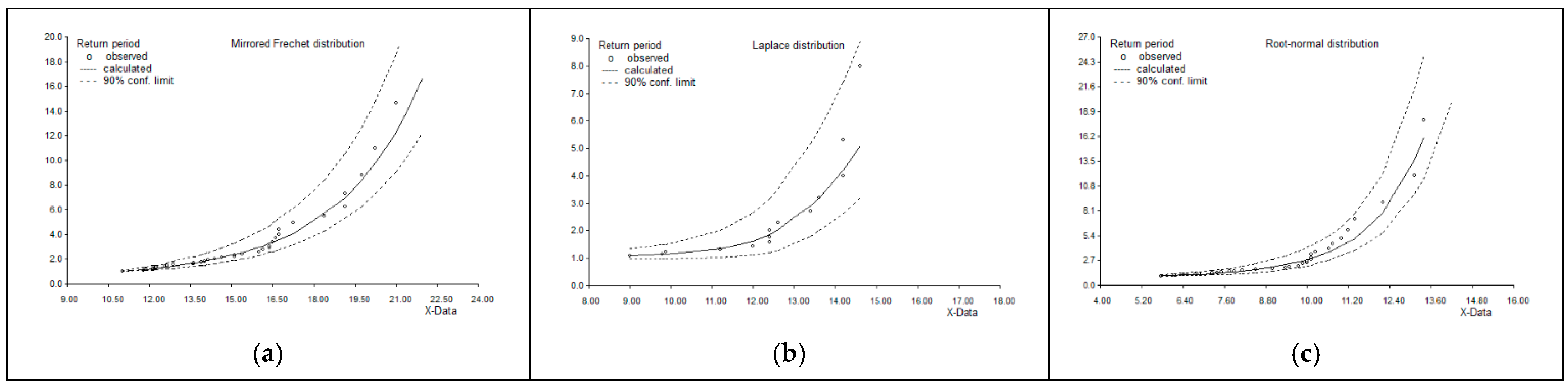

| Stat/Station | Ardabil | Ardabil Airport | Bilesavar | Parsabad | Khalkhal | Sareyn | Meshgin-Shahr |
|---|---|---|---|---|---|---|---|
| Recording Period | 1976–2018 | 2004–2018 | 2004–2018 | 1984–2018 | 1987–2018 | 2003–2018 | 1995–2018 |
| Available period (years) | 43 | 15 | 15 | 35 | 32 | 16 | 24 |
| Mean | 15.10 | 13.99 | 12.58 | 9.20 | 8.78 | 14.08 | 16.37 |
| Standard Error | 0.46 | 0.51 | 0.54 | 0.37 | 0.31 | 0.55 | 0.56 |
| Median | 14.38 | 13.80 | 12.40 | 9.50 | 8.69 | 13.91 | 16.06 |
| Mode | 11.80 | 13.00 | 12.40 | 10.13 | 7.00 | 16.20 | 15.88 |
| Standard Deviation | 2.99 | 1.98 | 2.08 | 2.21 | 1.74 | 2.19 | 2.77 |
| Sample Variance | 8.92 | 3.92 | 4.34 | 4.88 | 3.03 | 4.82 | 7.65 |
| Kurtosis | −0.46 | 1.31 | 0.28 | −0.53 | 0.98 | 0.36 | 8.93 |
| Skewness | 0.71 | 1.06 | 0.14 | 0.34 | 1.00 | 0.13 | 2.29 |
| Minimum | 11.00 | 10.88 | 9.00 | 5.75 | 6.25 | 10.20 | 11.86 |
| Maximum | 22.00 | 18.60 | 17.00 | 14.20 | 13.60 | 18.80 | 26.88 |
| Rank | Ardabil | Abs Diff (%) | Bilesavar | Abs Diff (%) | Parsabad | Abs Diff (%) | Khalkhal | Abs Diff (%) | Sareyn | Abs Diff (%) | Ardabil Airport | Abs Diff (%) | Meshgin-Shahr | Abs Diff (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Fisher– Tippett T2 mirrored | 2.52 | Laplace std | 3.50 | Gamma (Erlang) | 3.29 | Log-normal opt. | 3.20 | Laplace std | 2.78 | Laplace std | 3.83 | Log-normal opt. | 2.98 |
| 2 | Generalized exp. (Poisson type) | 2.62 | Generalized normal | 3.77 | Root-normal opt. | 3.31 | Fisher– Tippett T2 | 3.39 | Logistic | 3.65 | GEV | 3.87 | Generalized logistic | 3.04 |
| 3 | Burr generalized | 2.72 | Logistic | 3.87 | Generalized normal | 3.33 | Gumbel generalized | 3.40 | Generalized logistic | 3.71 | Mirrored Weibull | 4.90 | Laplace std | 3.23 |
| 4 | GEV | 3.01 | Generalized logistic | 3.89 | Fisher–Tippett T3 | 3.34 | Mirrored Weibull | 3.47 | Cauchy | 3.72 | Fisher–Tippett T2 mirrored | 4.92 | Root-normal opt. | 3.44 |
| 5 | Gumbel generalized | 3.24 | Log-logistic | 4.13 | Log-normal opt. | 3.40 | Fisher–Tippett T2 mirrored | 3.49 | Log-logistic | 3.78 | Log-normal opt. | 4.98 | Generalized Cauchy | 4.26 |
| 6 | Mirrored Weibull | 3.25 | Normal opt. | 4.16 | Gompertz generalized | 3.42 | Gumbel | 3.49 | Generalized Cauchy | 3.89 | Gumbel | 5.33 | Log-normal std. | 4.43 |
| 7 | Fisher– Tippett T2 | 3.25 | Fisher–Tippett T2 mirrored | 4.18 | Normal opt. | 3.43 | Fisher– Tippett T3 | 3.49 | Gumbel generalized | 3.90 | Fisher– Tippett T3 | 5.33 | Normal opt. | 4.46 |
| 8 | Gumbel | 3.32 | Weibull | 4.19 | Fisher–Tippett T2 mirrored | 3.44 | Log-normal std. | 3.51 | Normal opt. | 3.90 | Log-normal std. | 5.60 | Cauchy | 4.52 |
| 9 | Fisher– Tippett T3 | 3.32 | Normal std. | 4.25 | Gumbel generalized | 3.45 | Log-normal | 3.55 | Normal std | 3.97 | Log-logistic | 5.74 | GEV | 5.20 |
| 10 | Log-normal opt. | 3.35 | Gompertz generalized | 4.28 | Dagum generalized | 3.48 | GEV | 3.78 | Generalized normal | 4.01 | Root-normal opt. | 6.05 | Log-logistic | 5.67 |
| 11 | Gamma (Erlang) | 4.15 | Gumbel generalized | 4.28 | Logistic | 4.68 | Burr generalized | 3.90 | Fisher–Tippett T3 | 4.03 | Fisher–Tippett T2 mirrored | 6.07 | Fisher–Tippett T2 mirrored | 5.97 |
| 12 | Log-logistic | 4.19 | Generalized Cauchy | 4.37 | Generalized logistic | 3.69 | Root-normal opt. | 3.97 | Root-normal opt. | 4.03 | Cauchy | 6.38 | Normal std. | 6.27 |
| 13 | Root-normal opt. | 4.31 | Fisher–Tippett T3 | 4.38 | Weibull | 3.75 | Generalized logistic | 4.05 | Student 2 d.f. | 4.17 | Generalized exp. (Poisson type) | 6.46 | Fisher- Tippet T2 | 6.62 |
| 14 | Log-normal std. | 4.40 | Root-normal opt. | 4.39 | Log-logistic | 3.88 | Generalized exp. (Poisson type) | 4.11 | Fisher–Tippett T2 mirrored | 4.18 | Burr generalized | 6.53 | Mirrored Weibull | 6.64 |
| 15 | Gompertz generalized | 4.68 | Cauchy | 4.41 | GEV | 3.89 | Laplace std | 4.47 | Gompertz generalized | 4.22 | Normal opt. | 6.59 | Gumbel | 7.70 |
| Station/Return Period | 2 | 5 | 10 | 25 | 50 | 100 |
|---|---|---|---|---|---|---|
| Ardabil | 14.42 | 17.92 | 20.31 | 23.28 | 25.42 | 27.49 |
| Bilesavar | 13.60 | 15.60 | 16.73 | 18.52 | 19.87 | 21.22 |
| Parsabad | 9.07 | 11.33 | 12.60 | 14.04 | 15.01 | 15.91 |
| Khalkhal | 12.56 | 14.57 | 16.09 | 18.10 | 19.62 | 21.15 |
| Sareyn | 14.10 | 15.94 | 17.34 | 19.18 | 20.58 | 21.98 |
| Ardabil Airport | 8.53 | 10.05 | 10.95 | 12 | 12.73 | 13.43 |
| Meshgin-Shahr | 16.17 | 17.65 | 17.37 | 19.11 | 19.58 | 19.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimohamadian, L.; Mostafazadeh, R. Frequency Analysis and Trend of Maximum Wind Speed for Different Return Periods in a Cold Diverse Topographical Region of Iran. Climate 2025, 13, 138. https://doi.org/10.3390/cli13070138
Alimohamadian L, Mostafazadeh R. Frequency Analysis and Trend of Maximum Wind Speed for Different Return Periods in a Cold Diverse Topographical Region of Iran. Climate. 2025; 13(7):138. https://doi.org/10.3390/cli13070138
Chicago/Turabian StyleAlimohamadian, Leila, and Raoof Mostafazadeh. 2025. "Frequency Analysis and Trend of Maximum Wind Speed for Different Return Periods in a Cold Diverse Topographical Region of Iran" Climate 13, no. 7: 138. https://doi.org/10.3390/cli13070138
APA StyleAlimohamadian, L., & Mostafazadeh, R. (2025). Frequency Analysis and Trend of Maximum Wind Speed for Different Return Periods in a Cold Diverse Topographical Region of Iran. Climate, 13(7), 138. https://doi.org/10.3390/cli13070138







