Season-Long Time-Series Analysis of Soil Respiration in Furrow-Irrigated Corn with and Without Cover Crop in the Lower Mississippi River Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description and Field Management
2.2. Gas Sampling and Analyses
2.3. Statistical Analyses
3. Results
3.1. Time Series Analysis
3.1.1. CO2 Ranges and Visual Trends
3.1.2. Stationarity
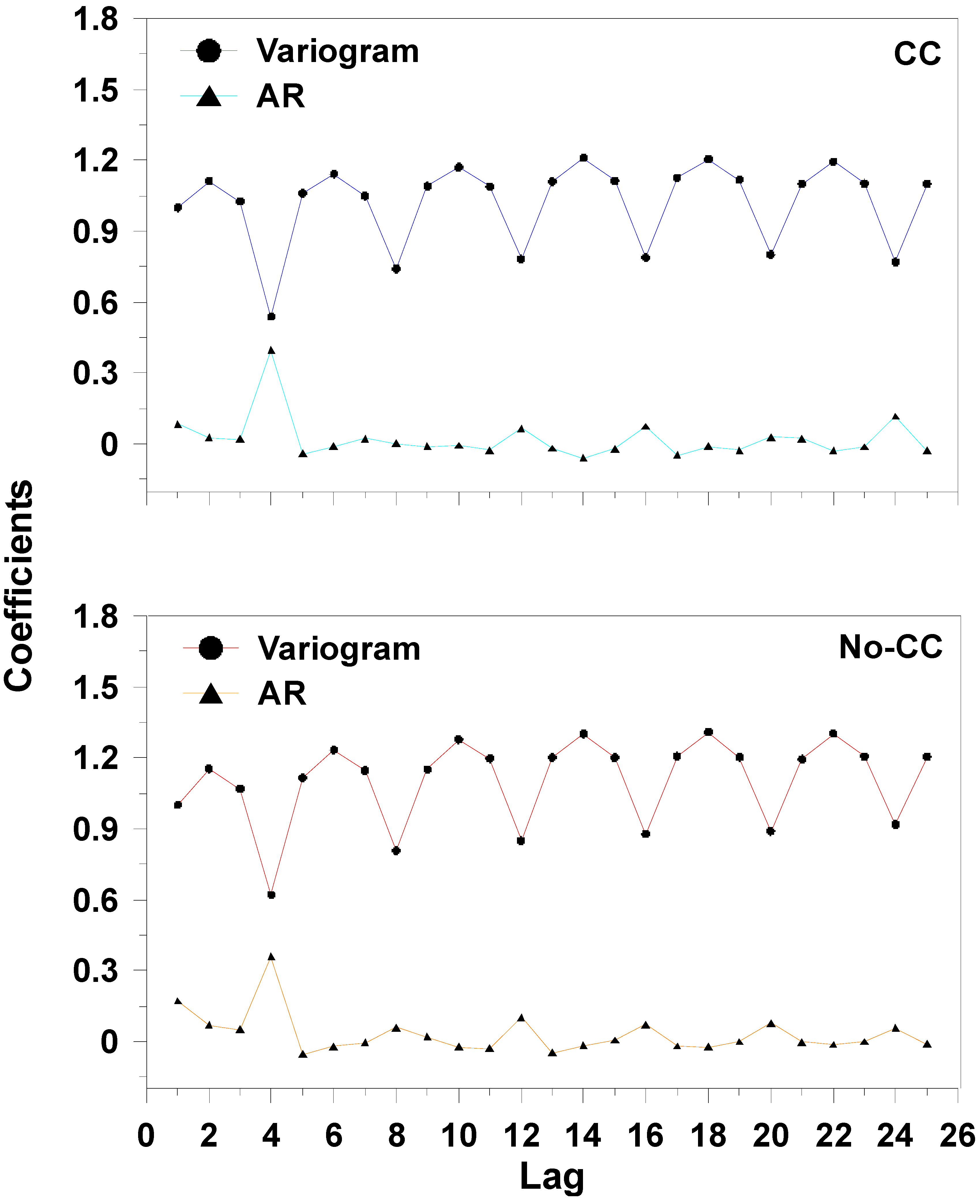
3.1.3. Serial Correlation
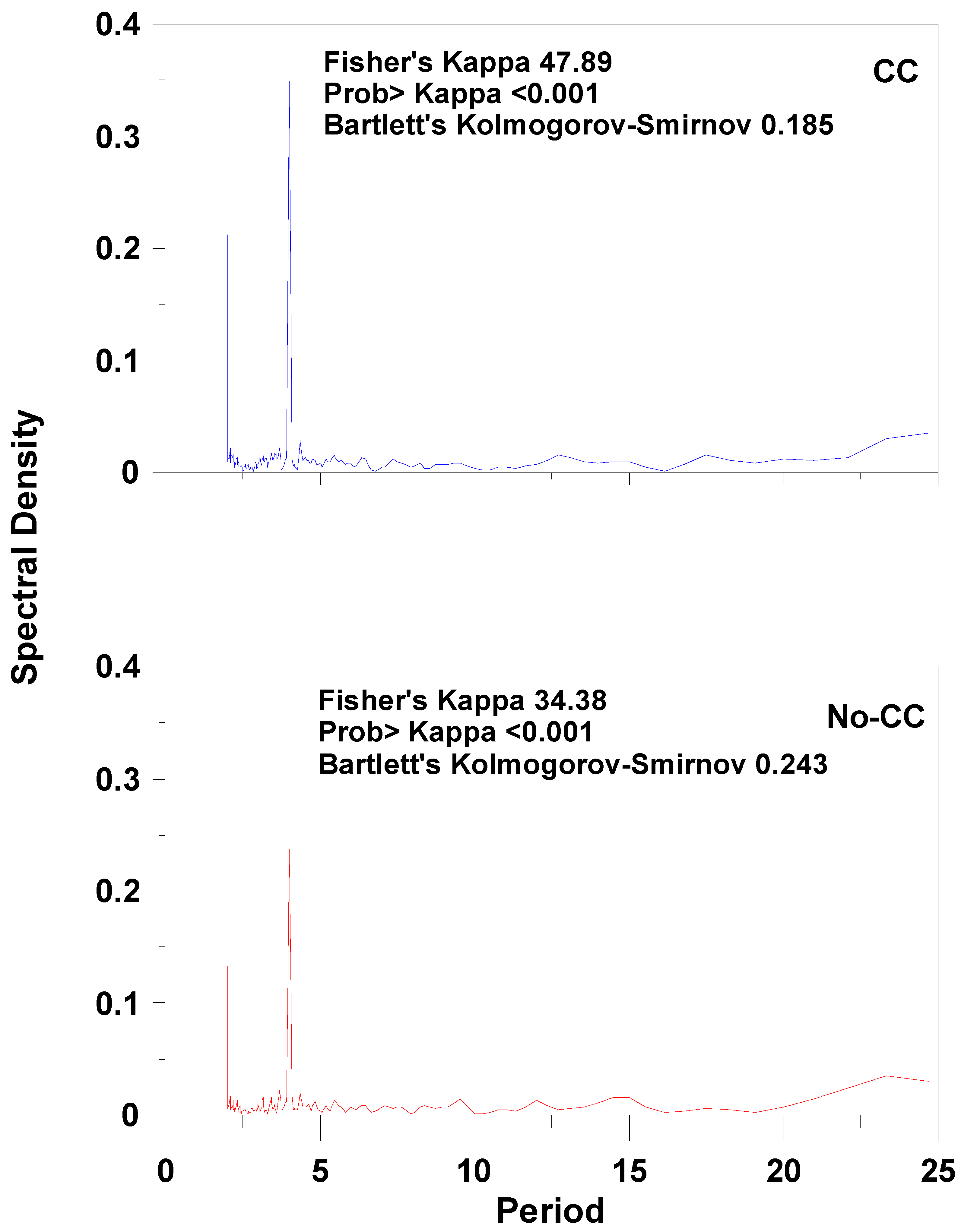
3.1.4. Decomposition
3.1.5. AR and ARMA Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | Autocorrelation function |
| ADF | Augmented Dickey–Fuller |
| AFOLU | Agriculture, Forestry, and Other Land Use |
| AIC | Akaike information criteria |
| ANOVA | Analysis of variance |
| ARMA | Autoregressive-moving-average |
| C | Carbon |
| CC | Cover crop |
| DNDC | Denitrification-Decomposition |
| FAO | Food and Agriculture Organization |
| GHG | Greenhouse gases |
| IAEA | International Atomic Energy Agency |
| LMRB | Lower Mississippi River Basin |
| MAE | Mean absolute error |
| N | Nitrogen |
| No-CC | No-cover crop |
| OF-CEAS | Optical feedback cavity enhanced absorption spectroscopy |
| PACF | Partial autocorrelation function |
| RMSE | Root mean square error |
References
- Intergovernmental Panel on Climate Change (IPCC). Global Carbon and other Biogeochemical Cycles and Feedbacks. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Canadell, J.G., Monteiro, P.M.S., M.H. Costa, M.H., Cotrim da Cunha, L., Cox, P.M., Eliseev, A.V., Henson, S., Ishii, M., Jaccard, S., Koven, C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 673–816. [Google Scholar]
- Bastviken, D.; Wilk, J.; Duc, N.T.; Gålfalk, M.; Karlson, M.; Neset, T.; Opach, T.; Enrich-Past, A.; Sundgren, I. Critical method needs in measuring greenhouse gas fluxes. Environ. Res. Lett. 2022, 17, 104009. [Google Scholar] [CrossRef]
- Chen, R.; Kong, Y. A comprehensive review of greenhouse gas based on subject categories. Sci. Total Environ. 2023, 25, 161314. [Google Scholar] [CrossRef]
- Holmes, C.R.; Woollings, T.; Hawkins, E.; de Vries, H. Robust future changes in temperature variability under greenhouse gas forcing and the relationship with thermal advection. J. Clim. 2016, 29, 2221–2236. [Google Scholar] [CrossRef]
- Smith, K.A.; Ball, T.; Conen, F.; Dobbie, K.E.; Massheder, J.; Rey, A. Exchange of greenhouse gases between soil and atmosphere: Interactions of soil physical factors and biological processes. Eur. J. Soil Sci. 2018, 69, 10–20. [Google Scholar] [CrossRef]
- Lal, R. Global potential of soil carbon sequestration to mitigate the greenhouse effect. Crit. Rev. Plant Sci. 2010, 22, 151–184. [Google Scholar] [CrossRef]
- Aragon, N.U.; Xie, Y.; Bigelow, D.; Lark, T.J.; Eagle, A.J. The realistic potential of soil carbon sequestration in U.S. croplands for climate mitigation. Earth’s Future 2024, 12, e2023EF003866. [Google Scholar] [CrossRef]
- Paustian, K.; Six, J.; Elliot, E.T.; Hunt, H.W. Management options for reducing CO2 emissions from agricultural soils. Biogeochemistry 2000, 48, 147–163. [Google Scholar] [CrossRef]
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Carbon and Other Biogeochemical Cycles. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Luo, Y.; Keenan, T.F.; Smith, M. Predictability of the terrestrial carbon cycle. Glob. Change Biol. 2015, 21, 1737–1751. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cesctti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Shi, P.J.; Hui, D.F.; Luo, Y.Q. Global pattern of temperature sensitivity of soil heterotrophic respiration and its implications for carbon-climate feedback. J. Geophys. Res. Biogeosci. 2009, 114, G02016. [Google Scholar] [CrossRef]
- Le Quéré, C.; Raupach, M.R.; Canadell, J.G.; Marland, G.; Bopp, L.; Ciais, P.; Conway, T.J.; Doney, S.C.; Feely, R.; Foster, P.; et al. Trends in the sources and sinks of carbon dioxide. Nat. Geosci. 2009, 2, 831–836. [Google Scholar] [CrossRef]
- Bond-Lamberti, B.; Pennington, S.C.; Jian, J.; Megonigal, J.P.; Sengupta, A.; Ward, N. Soil respiration variability and correlation across a wide range of temporal scales. Biogeosciences 2019, 124, 3672–3685. [Google Scholar] [CrossRef]
- Courtois, E.A.; Stahl, C.; Van den Berge, J.; Bréchet, L.; Van Langenhove, L.; Richter, A.; Urbina, I.; Soong, J.L.; Peñuelas, J.; Janssens, I.A. Spatial variation of soil CO2, CH4 and N2O fluxes across topographical positions in tropical forests of the Guiana Shield. Ecosystems 2018, 21, 1445–1458. [Google Scholar] [CrossRef]
- Vargas, R.; Baldocchi, D.D.; Bahn, M.; Hanson, P.J.; Hosman, K.P.; Kulmala, L.; Pumpanen, J.; Yang, B. On the multi-temporal correlation between photosynthesis and soil CO2 efflux: Reconciling lags and observations. New Phytol. 2011, 191, 1006–1017. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Robertson, G.P. Statistical challenges in analyses of chamber-based soil CO2 and N2O emissions data. Soil Sci. Soc. Am. J. 2015, 79, 200–211. [Google Scholar] [CrossRef]
- Daelamn, R.; Bauters, M.; Barthel, M.; Bulonza, E.; Leferve, L.; Mbifo, J.; Six, J.; Butterbach-bahl, K.; Wolf, B.; Kiese, R.; et al. Spatiotemporal variability of CO2, N2O and CH4 fluxes from a semi-deciduous tropical forest soil in the Congo Basin. Biogeosciences 2025, 22, 1529–1542. [Google Scholar] [CrossRef]
- Rogers, C.W.; Brye, K.R.; Smartt, A.D.; Norman, R.J.; Gbur, E.E.; Evans-White, M.A. Cultivar and previous crop effects on methane emissions from drill-seeded, delayed-flood rice production on a silt-loam soil. Soil Sci. 2014, 179, 28–36. [Google Scholar] [CrossRef]
- Smartt, A.D.; Brye, K.R.; Rogers, C.W.; Norman, R.J.; Gbur, E.E.; Hardke, J.T.; Roberts, T.L. Previous crop and cultivar effects on methane emissions from drill-seeded, delayed-flood rice grown on a clay soil. Appl. Environ. Soil Sci. 2016, 2016, 9542361. [Google Scholar] [CrossRef]
- Rector, C.; Brye, K.R.; Humphreys, J.; Norman, R.J.; Slaton, N.A.; Gbur, E.E.; Willett, C.; Evans-White, M.A. Tillage and coated-urea effects on nitrous oxide emissions from direct-seeded, delayed-flood rice production in Arkansas. J. Rice Res. Dev. 2018, 1, 25–37. [Google Scholar]
- Wood, J.D.; Gordon, R.J.; Wagner-Riddle, C. Biases in discrete CH4 and N2O sampling protocols associated with temporal variation of gas fluxes from manure storage systems. Agric. For. Meteorol. 2013, 171–172, 295–305. [Google Scholar] [CrossRef]
- Della Lunga, D.; Brye, K.; Mulvaney, M.; Daniels, M.; de Oliveira, T.; Baker, B.; Bradford, T.; Arel, C. Cover crop effects on greenhouse gas emissions and global warming potential in furrow-irrigated corn in the Lower Mississippi River Valley. Atmosphere 2025, 16, 498. [Google Scholar] [CrossRef]
- Silva, J.P.; Lasso, A.; Lubberding, H.J.; Peña, M.R.; Gijzen, H.J. Biases in greenhouse gases static chambers measurements in stabilization ponds: Comparison of flux estimation using linear and non-linear models. Atmos. Environ. 2015, 109, 130–138. [Google Scholar] [CrossRef]
- Savage, K.; Davidson, E.A.; Richardson, A.D.; Hollinger, D.Y. Three scales of temporal resolution from automated soil respiration measurements. Agric. For. Meteorol. 2009, 149, 2012–2021. [Google Scholar] [CrossRef]
- Ludwig, S.A. Comparison of time series approaches applied to greenhouse gas analysis: ANFIS, RNN, and LSTM. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23 June 2019. [Google Scholar]
- Kaufmann, R.S. Fick’s law. In Encyclopedia of Geochemistry; Marshall, C.P., Faribridge, R.W., Eds.; Springer: Dordrecht, The Netherlands, 1998; pp. 245–246. [Google Scholar]
- Healy, R.W.; Striegl, R.G.; Russell, T.F.; Hutchinson, G.L.; Livingston, G.P. Numerical evaluation of static-chamber measurements of soil-atmosphere gas exchange: Identification of physical processes. Soil Sci. Soc. Am. J. 1996, 60, 740–747. [Google Scholar] [CrossRef]
- Bauser, H.H.; Riedel, L.; Berg, D.; Troch, P.A. Challenges with effective representations of heterogeneity in soil hydrology based on local water content measurements. Vadose J. 2020, 19, e20040. [Google Scholar] [CrossRef]
- North, G.R. Time series analysis. Data Anal. 2003, 1, 621–624. [Google Scholar]
- Cui, Z.; Chen, S.; Hu, B.; Wang, N.; Feng, C.; Peng, J. Mapping soil organic carbon by integrating time-series sentinel-2 data, environmental covariates and multiple ensemble models. Sensors 2025, 25, 2184. [Google Scholar] [CrossRef] [PubMed]
- Lucke, M.; Chioua, M.; Thornhill, N.F. From oscillatory to non-oscillatory disturbances: A comparative review of root cause analysis methods. J. Process Control 2022, 113, 42–67. [Google Scholar] [CrossRef]
- Fong, B.N.; Reba, M.L.; Teague, T.G.; Runkle, B.R.K.; Suvočarev, K. Eddy covariance measurements of carbon dioxide and water fluxes in US mid-south cotton production. Agric. Ecosyst. Environ. 2020, 292, 106813. [Google Scholar] [CrossRef]
- Brye, K.R.; Nalley, L.L.; Tack, J.B.; Dixon, B.L.; Barkley, A.P.; Rogers, C.W.; Smartt, A.D.; Norman, R.J.; Jagadish, K. Factors affecting methane emissions from rice production in the Lower Mississippi River Valley, USA. Geoderma Reg. 2016, 7, 223–229. [Google Scholar] [CrossRef]
- Helton, M.; Brye, K.R.; Liechty, H.; Blazier, M.; West, C.; Gbur, E.E.; Savin, M.; Mason, E. Carbon dioxide emissions from switchgrass and cottonwood grown as bioenergy crops in the Lower Mississippi River Alluvial Valley. Biomass Bioenergy 2015, 83, 383–392. [Google Scholar] [CrossRef]
- Smith, S.F.; Brye, K.R. Carbon dioxide emissions as affected by alternative long-term irrigation and tillage management practices in the Lower Mississippi River Valley. Sci. World J. 2014, 2014, 626732. [Google Scholar] [CrossRef] [PubMed]
- McMullen, R.L.; Brye, K.R.; Daigh, A.L.; Miller, D.M.; Gbur, E.E.; Pirani, A.L.; Evans-White, M.A.; Mason, R.A. Long-term leachate water quality trends from a broiler-litter-amended Udult in a karst region. Vadose Zone J. 2014, 13, vzj2014-06. [Google Scholar] [CrossRef]
- Motschenbacher, J.M.; Brye, K.R.; Anders, M.M.; Gbur, E.E.; Slaton, N.A.; Evans-White, M.A. Daily soil surface CO2 flux during non-flooded periods in flood-irrigated rice rotations. Agron. Sustain. Dev. 2015, 35, 771–782. [Google Scholar] [CrossRef]
- Brye, K.R.; Riley, T.L. Soil and plant property differences across a chronosequence of humid-temperate tallgrass prairie restorations. Soil Sci. 2009, 174, 346–357. [Google Scholar] [CrossRef]
- Brye, K.R.; Longer, D.E.; Gbur, E.E. Impact of tillage and reside burning on CO2 flux in a wheat-soybean production system. Soil Sci. Soc. Am. J. 2006, 70, 1145–1154. [Google Scholar] [CrossRef]
- Arnfield, J. Koppen climate classification. In Encyclopedia Brittanica; Encyclopaedia Britannica Inc.: Chicago, IL, USA, 2016. [Google Scholar]
- Oldham, L.; Joes, K. Best Management Practices for Plant Nutrient Management; Mississippi State University Extension Service: Mississippi, MS, USA, 2021; Publication 1622. [Google Scholar]
- Mumu, N.J.; Ferdous, J.; Muller, C.; Ding, W.; Zaman, M.; Mozifur, M.; Jahangir, R. Methodological progress in the measurement of agricultural greenhouse gases. Carbon Manag. 2024, 15, 2366527. [Google Scholar] [CrossRef]
- LI-COR. Capturing and processing soil GHG fluxes using the LI-8100A-Picarro. In Application Note; Licor: Lincoln, NE, USA, 2016. [Google Scholar]
- Sefer, E.; Kleyman, M.; Joseph, Z. Tradeoffs between dense and replicate sampling strategies for high throughput time series experiments. Cell Syst. 2017, 3, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Wigley, T.M.L.; Bruffa, K.R.; Jones, P.D. On the average value of correlated time series, with application in dendroclimatology and hydrometeorology. Am. Meteorol. Soc. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Dickey, D.A.; Hasza, D.P.; Fuller, W.A. Testing for unit roots in seasonal time series. J. Am. Stat. Assoc. 1984, 79, 355–367. [Google Scholar] [CrossRef]
- Fuller, W.A. Introduction to Statistical Time Series; John Wiley & Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Bartlett, M.S. An Introduction to Stochastic Processes; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Della Lunga, D.; Brye, R.K.; Roberts, T.L.; Brye, J.; Evans-White, M.A.; Henry, C.G.; Lessner, D.J.; Arel, C. Struvite-phosphorus effects on greenhouse gas emissions and plant and soil response in a furrow-irrigated rice production system in eastern Arkansas. Front. Clim. 2024, 6, 1342896. [Google Scholar] [CrossRef]
- Karki, S.; Adviento-Borbe, M.A.A.; Massey, J.H.; Reba, M.L. Assessing seasonal methane and nitrous oxide emissions from furrow-irrigated rice with cover crops. Agriculture 2021, 11, 261. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the temperature dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, J.; Wang, J.; Yao, F.; Zhang, S. Quantitative assessment of factors influencing the spatiotemporal variation in carbon dioxide fluxes simulated by multi-source remote sensing data in tropical vegetation. Remote Sens. 2023, 15, 5677. [Google Scholar] [CrossRef]
- Petrica, A.C.; Stancu, S.; Ghitulescu, V. Stationarity-The central conceptin time sereis analysis. Int. J. Emerg. Res. Manag. Technol. 2017, 6, 6–16. [Google Scholar]
- DeJong, D.N.; Nankervis, J.C.; Savin, N.E.; Whiteman, C.H. The power problems of unit root tests in time series with autoregressive errors. J. Econom. 1992, 53, 323–343. [Google Scholar] [CrossRef]
- Brye, J.B.; Della Lunga, D.; Brye, K. Gas-flux-determination-method effects on greenhouse gas emissions and global warming potential from soybean in southeast Arkansas. All Earth 2025, 37, 2569153. [Google Scholar] [CrossRef]
- Seuferling, C.; Brye, K.; Della Lunga, D.; Brye, J.B.; Daniels, M.; Wood, L. Evaluation of greenhouse gas-flux determination-models and calculation in southeast Arkansas cotton production. AgriEngineering 2025, 7, 213. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A. Estimating the persistence and the autocorrelation function of a time series that is measured with error. Econom. Theory 2014, 30, 60–93. [Google Scholar] [CrossRef]
- Davey, A.M.; Flores, B.E. Identification of seasonality in time series: A note. Math. Comput. Model. 1993, 6, 73–81. [Google Scholar] [CrossRef]
- Hamilton, D.C.; Watts, D.G. Interpreting partial autocorrelation functions of seasonal time series models. Biometrika 1978, 65, 135–140. [Google Scholar] [CrossRef]
- Prestly, M. Spectral Analysis and Time Series; John Wiley and Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Stolwijk, A.M.; Straatman, H.; Zielhuis, G.A. Studying seasonality by using sine and cosine functions in regression analysis. J. Epidemiol. Community Health 1999, 53, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Fu, Z. Comparison of methods for extracting annual cycle with changing amplitude in climate series. Clim. Dyn. 2019, 52, 5059–5070. [Google Scholar] [CrossRef]
- Qian, J.; Xin, J.; Shin-Jye, L.; Shaowen, Y. Protein secondary structure prediction: A survey of the state of the art. J. Mol. Graph. Model. 2017, 76, 379–402. [Google Scholar] [CrossRef]
- Hassani, H.; Yeganegi, M.R. Selecting optimal lag order in Ljung-Box test. Phys. A Stat. Mech. Its Appl. 2020, 541, 123700. [Google Scholar] [CrossRef]
- Box, G.E.P.; Pierce, D.A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Cicuéndez, V.; Rodrígruez-Rastrero, M.; Huesca, M.; Uribe, C.; Schmid, T.; Inclán, R.; Litago, J.; Sánchez-Girón, V.; Merino-de-Miguel, S.; Palacios-Orueta, A. Assessment of soil respiration patterns in an irrigated corn field based on spectral information acquired by field spectroscopy. Agric. Ecosyst. Environ. 2015, 212, 158–167. [Google Scholar] [CrossRef]
- Zhang, S.; Hussain, H.A.; Wang, L.; Hussain, S.; Li, B.; Zhou, H.; Luo, H.; Zhang, X.; Ma, Z.; Long, L.; et al. Responses of soil respiration and organic carbon to straw mulching and ridge tillage in maize field of a triple cropping system in the Hilly region of Southwest China. Sustainability 2019, 11, 3068. [Google Scholar] [CrossRef]
- Pennington, S.P.; McDowell, N.M.; Megonical, J.P.; Stegen, J.; Bond-Lamberty, B. Effect of tree proximity on soil respiration dynamics in a coastal temperate decidous forest. Biogeosciences 2019, 218, 1–27. [Google Scholar]
- Kosugi, Y.; Mitani, T.; Itoh, M.; Nogichi, S.; Tani, M.; Matsuo, N. Spatial and temporal variation in soil respiration in a Southeast Asian subtropical rainforest. Agric. For. Meteorol. 2007, 147, 35–47. [Google Scholar] [CrossRef]
- Ryan, O.; Haslbeck, J.M.B.; Waldrop, L.J. Non-stationarity in time series analysis: Modeling stochastic and deterministic trends. Multivar. Behav. Res. 2025, 60, 556–588. [Google Scholar] [CrossRef]
- Hrithik, P.M.; Rehman, M.Z.; Dar, A.A.; Wangmo, T. Forecasting CO2 emissions in India: A time series analysis using ARIMA. Processes 2024, 12, 2699. [Google Scholar] [CrossRef]
- Bence, J.R. Analysis of short time series: Correcting for autocorrelation. Ecology 1995, 76, 628–639. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, M.; Li, T.; Wang, H.; Li, C. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, X.; McLaughlin, N.B.; Liang, A.; Jia, S. Effect of soil temperature and soil moisture on CO2 flux from eroded landscape positions on black soil in Northeast China. Soil Tillage Res. 2014, 144, 119–125. [Google Scholar] [CrossRef]
- Sander, B.O.; Wassmann, R. Common practices for manual greenhouse gas sampling in rice production: A literature study on sampling modalities of the closed chamber method. Greenh. Gas Meas. Manag. 2014, 4, 1–13. [Google Scholar] [CrossRef]
- Hayat, M.J.; Hedlin, H. Modern statistical modeling approaches for analyzing repeated measures data. Nurs. Res. 2012, 61, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, L.M. Repeated Measures. Stat. Primer Cardiovasc. Res. 2008, 117, 1238–1243. [Google Scholar] [CrossRef]
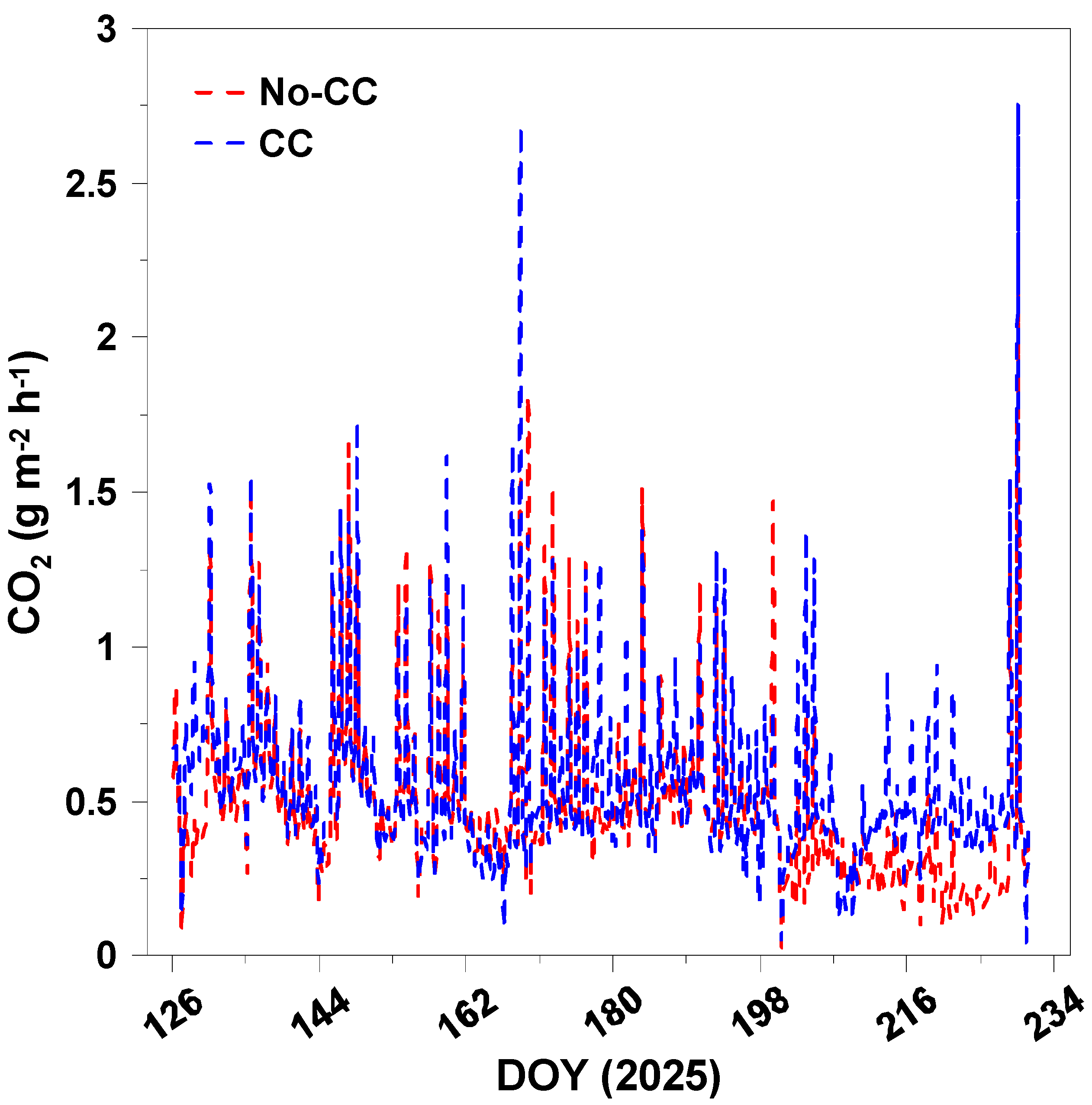

| Measurement Hour | Field Treatment | CO2 (g m−2 h−1) | |
|---|---|---|---|
| Min | Max | ||
| 0300 | CC | 0.06 | 0.87 |
| 0900 | CC | 0.08 | 1.72 |
| 1500 | CC | 0.01 | 2.82 |
| 2100 | CC | 0.03 | 1.01 |
| 0300 | No-CC | 0.01 | 0.70 |
| 0900 | No-CC | 0.01 | 1.09 |
| 1500 | No-CC | 0.01 | 2.40 |
| 2100 | No-CC | 0.01 | 1.17 |
| Statistic | Field Treatment | |
|---|---|---|
| No-CC | CC | |
| Mean (g m−2 h−1) | 0.478 | 0.541 |
| Standard deviation | 0.286 | 0.305 |
| Sample size | 420 | 420 |
| Zero Mean ADF | −6.876 | −7.352 |
| Single Mean ADF | −16.081 | −19.280 |
| Trend ADF | −17.549 | −19.886 |
| Response Variable | Treatment | Model Parameter | Coefficient (Standard Error) | Overall Model p-Value | Overall Model R2 | RMSE † |
|---|---|---|---|---|---|---|
| CO2 | CC | Time | −0.002 (0.0005) | <0.001 | 0.03 | 0.301 |
| No-CC | Time | −0.003 (0.0004) | <0.001 | 0.10 | 0.271 |
| Parameter | CC | No-CC |
|---|---|---|
| Amplitude | 0.20 | 0.16 |
| Units per cycle | 4 | 4 |
| Phase | 0.49 | 0.49 |
| Constant | 0 | 0 |
| Formula | 0.20 x cos † (2 x π † x ((1/4) x t † + 0.49)) | 0.16 x cos(2 x π x ((1/4) ∗ t + 0.49)) |
| Model/Parameter † | CC | No-CC | ||||
|---|---|---|---|---|---|---|
| AIC | R2 | MAE | AIC | R2 | MAE | |
| AR(1 ‡) | 77.55 | <0.01 | 0.16 | 3.87 | 0.03 | 0.16 |
| AR(2) | 65.09 | 0.03 | 0.16 | −14.2 | 0.08 | 0.15 |
| AR(3) | 67.06 | 0.03 | 0.16 | −12.9 | 0.08 | 0.15 |
| AR(4) | 30.19 | 0.12 | 0.14 | −53.4 | 0.17 | 0.13 |
| ARMA(1, 0, 1 §) | 67.56 | 0.03 | 0.16 | −22.6 | 0.09 | 0.15 |
| ARMA(2, 0, 1) | 41.69 | 0.09 | 0.14 | −23.7 | 0.10 | 0.15 |
| ARMA(2, 0, 2) | 32.14 | 0.12 | 0.14 | −50.2 | 0.16 | 0.14 |
| ARMA(3, 0, 1) | 40.44 | 0.10 | 0.14 | −21.7 | 0.10 | 0.15 |
| ARMA(3, 0, 2) | 33.57 | 0.12 | 0.14 | −48.3 | 0.16 | 0.14 |
| ARMA(3, 0, 3) | 29.90 | 0.13 | 0.14 | −48.2 | 0.17 | 0.14 |
| ARMA(4, 0, 1) | 29.79 | 0.13 | 0.14 | −53.7 | 0.17 | 0.13 |
| ARMA(4, 0, 2) | 31.59 | 0.13 | 0.14 | −51.9 | 0.17 | 0.12 |
| ARMA(4, 0, 3) | 28.65 | 0.14 | 0.14 | −53.8 | 0.18 | 0.14 |
| ARMA(4, 0, 4) | 29.97 | 0.14 | 0.14 | −55.7 | 0.19 | 0.13 |
| Lag | CC [ARMA (4, 0, 3 §)] | No-CC [ARMA (4, 0, 4 §)] | ||
|---|---|---|---|---|
| Ljung–Box Q | p-Value | Ljung–Box Q | p-Value | |
| 1 | 0.01 | 0.95 | 0.12 | 0.73 |
| 2 | 0.36 | 0.83 | 0.69 | 0.71 |
| 3 | 2.59 | 0.46 | 1.20 | 0.75 |
| 4 | 6.84 | 0.14 | 3.06 | 0.55 |
| 5 | 8.47 | 0.13 | 3.14 | 0.68 |
| 6 | 8.47 | 0.21 | 3.16 | 0.79 |
| 7 | 9.03 | 0.25 | 3.16 | 0.87 |
| 8 | 9.29 | 0.32 | 3.98 | 0.86 |
| 9 | 9.32 | 0.41 | 4.20 | 0.89 |
| 10 | 9.32 | 0.50 | 4.30 | 0.93 |
| 11 | 9.34 | 0.59 | 4.37 | 0.96 |
| 12 | 10.49 | 0.57 | 4.37 | 0.98 |
| 13 | 10.52 | 0.65 | 4.52 | 0.98 |
| 14 | 11.37 | 0.66 | 4.72 | 0.98 |
| 15 | 11.40 | 0.72 | 4.82 | 0.99 |
| 16 | 12.12 | 0.73 | 4.89 | 0.99 |
| 17 | 12.23 | 0.79 | 4.90 | 0.99 |
| 18 | 12.43 | 0.82 | 5.29 | 0.99 |
| 19 | 12.45 | 0.87 | 5.509 | 0.99 |
| 20 | 13.73 | 0.84 | 5.515 | 0.99 |
| 21 | 13.95 | 0.87 | 5.99 | 0.99 |
| 22 | 14.13 | 0.90 | 6.12 | 0.99 |
| 23 | 14.14 | 0.92 | 6.26 | 0.99 |
| 24 | 14.55 | 0.93 | 7.60 | 0.99 |
| 25 | 14.55 | 0.95 | 7.66 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Della Lunga, D.; Brye, K.; Mulvaney, M.J.; Daniels, M.; de Oliveira, T.; Baker, B.; Bradford, T., Jr.; Arel, C. Season-Long Time-Series Analysis of Soil Respiration in Furrow-Irrigated Corn with and Without Cover Crop in the Lower Mississippi River Basin. Climate 2025, 13, 232. https://doi.org/10.3390/cli13110232
Della Lunga D, Brye K, Mulvaney MJ, Daniels M, de Oliveira T, Baker B, Bradford T Jr., Arel C. Season-Long Time-Series Analysis of Soil Respiration in Furrow-Irrigated Corn with and Without Cover Crop in the Lower Mississippi River Basin. Climate. 2025; 13(11):232. https://doi.org/10.3390/cli13110232
Chicago/Turabian StyleDella Lunga, Diego, Kristofor Brye, Michael J. Mulvaney, Mike Daniels, Tabata de Oliveira, Beth Baker, Timothy Bradford, Jr., and Chandler Arel. 2025. "Season-Long Time-Series Analysis of Soil Respiration in Furrow-Irrigated Corn with and Without Cover Crop in the Lower Mississippi River Basin" Climate 13, no. 11: 232. https://doi.org/10.3390/cli13110232
APA StyleDella Lunga, D., Brye, K., Mulvaney, M. J., Daniels, M., de Oliveira, T., Baker, B., Bradford, T., Jr., & Arel, C. (2025). Season-Long Time-Series Analysis of Soil Respiration in Furrow-Irrigated Corn with and Without Cover Crop in the Lower Mississippi River Basin. Climate, 13(11), 232. https://doi.org/10.3390/cli13110232






