Effect of Temperature on the Spread of Contagious Diseases: Evidence from over 2000 Years of Data

Abstract

The COVID-19 pandemic led to a surge in interest among scholars and public health professionals in identifying the predictors of health shocks and their transmission in the population. With temperature increases becoming a persistent climate stress, our aim is to evaluate how temperature specifically impacts the incidences of contagious disease. Using annual data from 1 AD to 2021 AD on the incidence of contagious disease and temperature anomalies, we apply both parametric and nonparametric modelling techniques and provide estimates of the contemporaneous, as well as lagged, effects of temperature anomalies on the spread of contagious diseases. A nonhomogeneous hidden Markov model is then applied to estimate the time-varying transition probabilities between hidden states where the transition probabilities are governed by covariates. For all empirical specifications, we find consistent evidence that temperature anomalies have a statistically significant effect on the incidence of a contagious disease in any given year covered in the sample period. The best fit model further indicates that the contemporaneous effect of a temperature anomaly on the response variable is the strongest. As temperature predictions continue to become more accurate, our results indicate that such information can be used to implement effective public health responses to limit the spread of contagious diseases. These findings further have implications for designing cost effective infectious disease control policies for different regions of the world.

1. Introduction

The global scale and impact of the COVID-19 pandemic led to heightened interests and efforts among scientists, governments, and academics across different fields to identify ways to minimize the cumulative damage from the spread of infectious diseases to human health and the global economy. Infectious diseases are caused by pathogens, such as viruses and harmful bacteria. They include both noncommunicable and communicable or contagious diseases. These diseases can spread through disease vectors, such as mosquitoes, and other transmission pathways, such as air, water, food, and direct human contact. The macro impact caused by the spread of an infectious disease depends on the number of individuals affected by the disease, the speed at which the disease spreads through a population, and the length of time the disease persists in any population. For example, an epidemic is characterized by an accelerated increase in the number of affected individuals in a given region; whereas an endemic refers to a situation when a disease persists in a region for a long time. A pandemic is a scaled-up epidemic, where a contagious infectious disease spreads at an expedited rate through a larger geographic area. It has an epicenter in a region of the world from where the disease spreads rapidly across multiple countries affecting different populations and causing widespread economic losses. It can happen decades and even centuries after the occurrence of an earlier pandemic, which may have a different epicenter located thousands of miles away.

It is extremely challenging to compare epidemics and pandemics given that a myriad of contextual factors lies behind each occurrence. Given the rarity and uniqueness of such events, identifying a common set of contributory factors that cause these events and influence the transmission rates through space and time can be a demanding task for scholars. For example, each event is characterized by a specific point of origin and shaped by a unique line of historical events leading to the onset of that event. The extent of damage to human lives has also varied greatly among the major disease outbreaks over the last 2000-plus years. For example, the World Health Organization estimates that the total number of deaths from COVID-19 is close to 7 million [1]. In contrast, the estimated number of deaths caused by the Black Death plague of Central Asia between 1347 and 1351 has been estimated to be between 75–200 million [2]. However, in spite of all the challenges inherent in this type of analysis, the effort is always worthwhile, given that epidemics and pandemics are large-scale disruptive events that result in shocks to one or more economies and affect society’s overall wellbeing. The expected damages associated with such events can sometimes affect multiple generations of the population, albeit in different ways. Any lesson learned and applied could potentially lead to scores of human lives being saved during a future occurrence. Unlike earlier pandemics, the 2003 SARS-COVID pandemic and the 2019 COVID-19 happened at a time when ample scientific evidence was available on global warming [3], which has spurred interests among scientists and policymakers alike about the relationship between ambient temperature and the transmission rate of contagious diseases.

The Climate Change 2021 report presented by the Intergovernmental Panel on Climate Change presents some startling changes in the global environment that have happened over the past few decades, which are unprecedented in recent human history. For example, Figure 1 below shows that the global surface temperature increased sharply between 1950 and 2020 when contrasted with the relatively moderate rise in surface temperature between 1850 and 1950. The left panel in the following figure shows the changes in the global surface temperature over the past 2000 years using both reconstructed and observed temperature data [4]. The reconstructed data cover the period from 1 AD until the year 2000; whereas the observed data cover the 1850 to 2020 timeframe. The panel on the right focuses on the 1850–2020 period, showing the changes in global surface temperature. The black line indicates observed temperature data. The brown line shows simulated temperature data accounting for both natural and human-related factors, while the blue line indicates simulated surface temperature data that only account for natural climate-change-related factors. The gap between the brown and the blue lines represents an approximate measure of the rise in global surface temperature that stem from factors related to anthropogenic activities, particularly those following the first industrial revolution.

Between 1970 and 2020, the global surface temperature increased faster than any other 50-year period over at least the past 2000 years. Hot extreme events, such as heatwaves, have become more frequent and intense since 1950; whereas cold extreme events have become less frequent and less severe. Human-induced climate events have led to droughts. While the facts about the changes in the global environment are gravely concerning by themselves, they do not capture the full magnitude of potential adversity that can stem from such changes in the future, such as hastening the spread of infectious diseases in the future [5]. Geographic boundaries of disease ranges are climate sensitive. They can both shift and expand with changes in temperature through the effects of various disease-carrying vectors. For example, valley fever is a fungal disease that is endemic to the southwestern United States [6], with the region’s temperature and precipitation affecting the number of valley fever cases and the extent of the spread of the disease across the region. Using climate projections for the 21st century along with a climate niche model derived from contemporary climate and disease incidence data, [6] predicted that throughout this century the endemic region will spread north reaching up to the Canadian border covering the western U.S. states and resulting in 50% more cases.

Mora et al. [7] systematically analyzed empirical examples of 375 infectious diseases to find that 58% of those diseases have been aggravated by climatic hazards. Their research revealed 1006 unique pathways in which climate hazards, through different transmission types, led to pathogenic diseases. In some situations, climate-related hazards, such as heat waves and droughts, resulted in habitat destruction, which led to shifts in the geographical range of different species that brought pathogens and vectors closer to human populations. Warmer temperatures and precipitation expanded the areas covered by vectors, such as mosquitoes, ticks, and fleas. In their review, Caminade et al. [8] highlighted the impact of climate change on the distributions of vectors and pathogens in peri-Arctic, Arctic, temperate, and high-altitude regions in tropical zones. Malaria is a fatal vector-borne infectious disease caused by a plasmodium species that is transmitted between humans by infected female anopheles mosquitoes. Its incidence is affected by changes in temperature, rainfall, and humidity. Siraj et al. [9] used Ethiopian and Colombian data to demonstrate the impact of temperature on malaria, as warmer temperatures increased the incidence of malaria at higher altitudes. The geographic spread of dengue, a common mosquito-borne viral disease, is also affected by temperature changes and how the vectors respond to such changes [10].

Since contagious diseases often affect the human population through carrier organisms, it is essential to understand the effect of temperature changes on the spread of contagious diseases among wildlife. While the frequency of infectious disease outbreaks among wildlife has increased in recent decades paralleling global climate, the exact mechanisms through which climate change affects the spread of infectious disease largely remains unknown. To address this gap in the knowledge, using both laboratory experiments and field prevalence estimates, refs. [11,12] tested the thermal mismatch hypothesis, which posits that cool-adapted host species are more susceptible to pathogen infection during warm temperature periods; whereas warm-adapted host species are more susceptible to pathogens during periods of cool temperatures. The datasets used in these studies include a large and highly diverse spectrum of wildlife hosts and parasites that vary in ecologically important traits across a worldwide climatic gradient. Their results confirmed the thermal mismatch hypothesis, which suggests that as climate change shifts hosts away from their optimal temperature ranges, hosts can become more susceptible to infectious diseases, though the exact effect will be dependent on the particular host and the direction of the shift in climate patterns. Another example is from [13] who compared the 1918 influenza pandemic with the 2019 COVID pandemic, two disastrous health emergencies caused by different viruses that occurred a century apart from each other. The authors were able to identify similarities in both the clinical, pathological, and epidemiological features of the two pandemics and in the civic, medical, and public health responses to these events.

In this paper, we take a historical perspective to understand the relationship between contagious disease outbreaks and changes in ambient temperature. Using alternative model specifications, both parametric and nonparametric, we first derive estimates for the causal relationship between temperature anomalies and contagious disease outbreaks in any given year, modelled as a binary variable. The time evaluation of the transition probabilities of switching between contiguous disease and noncontiguous disease states or time periods are further studied using a nonhomogeneous hidden Markov model, under the assumption that the data generated follow a Markov process. Bearing the name of Russian mathematician Andrey Markov, the hidden Markov model (HMM) is a stochastic model that is assumed to involve a Markov process in which a sequence of events is characterized by their dependance only on the state that has occurred prior to that event and not on any preceding states. The Markov process is essentially a stochastic process with a memoryless property, implying that if the current state is given, past states do not play any role in its transition from a current state to a future state. Note, the transition process itself remains unobserved and is assumed to follow a Markov process. The probability of the process transitioning from a given state in the present to a future state is referred to as a transition probability. A transition matrix provides the set of transition probabilities that describe the likelihood of transition from any present state to all possible future states. The “hidden” in the term refers to the prior states remaining unobserved. HMM models have wide-ranging applications in finance [14,15], statistics [16,17], cognitive science [18,19], mobile communication [20,21], and climatology [22,23]. The HMM model can be extended to a nonhomogeneous HMM model (NHMM), if we relax the assumption of homogeneity among the transitions and allow them to depend on additional variables.

The analysis presented in this paper contributes to the strand of academic literature that aims to develop our understanding of the determinants of the outbreak and spread of contagious diseases, both contemporarily and temporally. The extent of damages associated with a communicable disease is characterized by a set of environmental and socio-economic factors, some of which are unique to the region, while others are common determinants across space, time, and disease type. For example, disease transmission rates can be affected by precipitation and humidity [24,25], population density [26,27], the rate of urbanization [28], and human migration [29], among others. Social outcomes, such as residential segregation, can impact the spread of contagious diseases [30].

Our interest lies in identifying the role played by a common factor, temperature anomalies, in contagious disease spreads over the past two millennia. We believe that comparing different public health events over time and identifying similar features can offer valuable lessons to help inform and improve public health surveillance systems across regions. Public health surveillance systems are the major defensive mechanisms of nations to prevent and control the spread of diseases. Involving a complex network of government officials, public health practitioners, healthcare providers, and the general population, they systematically collect data and information on the status of public health, identifying disease outbreaks and the transmission of communicable diseases. Epidemiological studies depend on this information to identify risk factors and effective prevention and control measures. Studies involving predictive modelling use this information to anticipate alternative scenarios and identify the likelihood of future events [31].

We demonstrate that temperature changes have always played a fundamental role is the spread of contagious diseases, thereby identifying a common factor in epidemics and pandemics covering the past two millenniums. The insights from these findings provide opportunities to develop region-specific and disease-specific policy recommendations that would account for the role of temperature anomalies in the spread of contagious diseases. In tropical and subtropical regions, such as Sub-Saharan Africa and Southeast Asia, temperature anomalies often exacerbate the conditions favorable to vector-borne diseases, like malaria and dengue fever. High temperatures accelerate vector reproduction and expand habitats into previously unaffected regions [9]. Policy measures should prioritize vector control programs, including insecticide-treated nets, community awareness campaigns, and investments in early warning systems based on real-time temperature and precipitation data [8]. In temperate areas, anomalously warm periods can extend the activity of vectors, such as ticks, increasing the risk of diseases like Lyme disease [32]. Alternatively, low temperature anomalies can displace vectors and wildlife, creating novel interactions that may trigger outbreaks. Public health responses should include enhanced surveillance and biodiversity monitoring to detect emerging zoonotic disease risks promptly [33]. In arid and semi-arid zones, such as the Sahel, rising temperatures combined with unpredictable rainfall can lead to shifts in the distribution of waterborne diseases, such as cholera. Infrastructure development focused on clean water access and improved sanitation should be prioritized in these areas [34]. In Arctic regions and high-altitude locations, warming trends can thaw permafrost, potentially reactivating dormant pathogens like anthrax [35]. Governments and global organizations must invest in pathogen containment measures and disaster preparedness to address the risks associated with environmental changes in these fragile ecosystems. Urban areas with high population densities face compounded risks due to the urban heat island effect. Temperature anomalies can intensify disease outbreaks by creating favorable conditions for diseases like influenza and respiratory infections. Policies should focus on green infrastructure to reduce heat retention and ensure equitable healthcare access during outbreaks [28]. While earlier scholars have provided evidence on region-specific temperature effects on disease spreads, we provide evidence on the role of temperature anomalies in the transmission of contagious diseases using a very long timeseries. Our findings indicate that, while the exact nature of the effects will be region-specific, temperature anomalies can be expected to play a significant role in disease outbreaks and spreads, regardless of location.

The paper is organized as follows: Section 2 provides our data sources and presents a description of the dataset. In Section 3, we present the methodology used in the analysis, which is followed by a discussion of the results in Section 4. In Section 5, we include some reflections and concluding remarks.

2. Data Sources and Description

The data used in this paper were obtained from the data on contagious diseases presented in

Table 1. Contagious disease events and dates included in the sample.

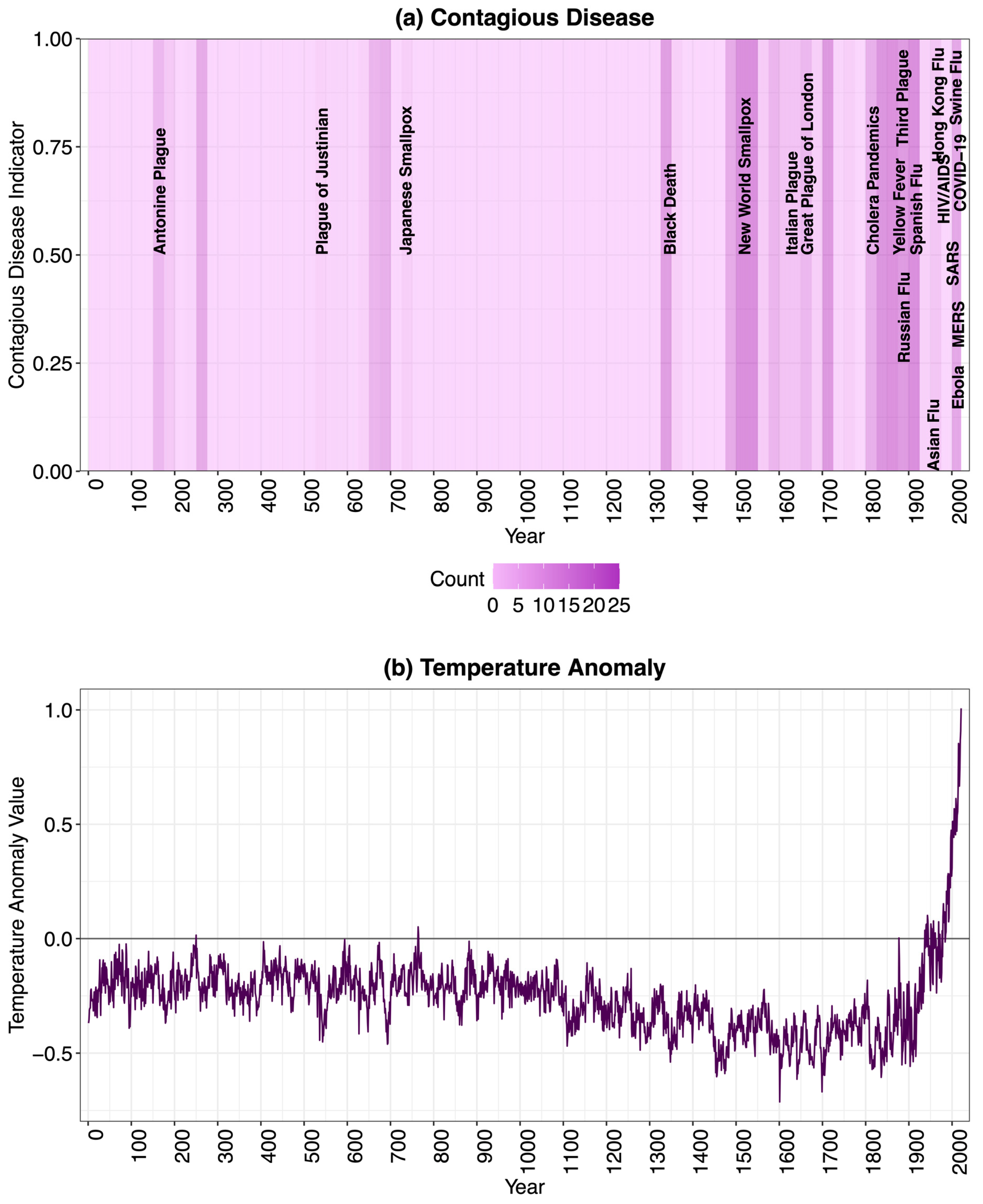
Event	Start Year	End Year	Location	Estimated Deaths
Plague of Athens	−429	−426	Greece, Libya, Egypt, Ethiopia	75,000–100,000
Antonine Plague	165	180	Roman Empire	5–10 million
Plague of Cyprian	250	266	Europe	310,000
Plague of Justinian	541	542	Europe, West Asia	15–100 million
Plague of Amida	562	562	Mesopotamia (modern day Turkey)	30,000
Roman Plague of 590	590	590	Rome, Byzantine Empire	Unknown
Plague of Sheroe	627	628	Bilad al-Sham	25,000+
Plague of the British Isles	664	689	British Isles	Unknown
Plague of Basra	688	689	Basra (southeast Turkey)	200,000
Japanese Smallpox Epidemic	735	737	Japan	2 million
Black Death	1331	1353	Eurasia and North Africa	75–200 million
Sweating Sickness	1485	1551	Britain	10,000+
Smallpox Epidemic in Mexico	1520	1520	Mexico	5–8 million
Cocoliztli Epidemic of 1545–1548	1545	1548	Mexico	5–15 million
1563 London Plague	1562	1564	London, England	20,100
Malta Plague Epidemic	1592	1593	Malta	3000
Plague in Spain	1596	1602	Spain	600,000–700,000
New England Epidemic	1616	1620	New England	Unknown
Italian Plague of 1629–1631	1629	1631	Italy	1 million
Great Plague of Sevilla	1647	1652	Spain	500,000
Plague in Kingdom of Naples	1656	1658	Italy	1,250,000
Plague in the Netherlands	1663	1664	Amsterdam, Netherlands	24,148
Great Plague of London	1665	1666	England	100,000
Plague in France	1668	1668	France	40,000
Malta Plague Epidemic	1675	1676	Malta	11,300
Great Plague of Vienna	1679	1679	Vienna, Austria	76,000
Great Northern War plague Outbreak	1700	1721	Denmark, Sweden, Lithuania	164,000
Great Smallpox Epidemic in Iceland	1707	1709	Iceland	18,000+
Great Plague of Marseille	1720	1722	France	100,000
Great Plague of 1738	1738	1738	Balkans	50,000
Russian Plague of 1770–1772	1770	1772	Russia	50,000
Ottoman Plague Epidemic	1812	1819	Ottoman Empire	300,000+
Caragea’s Plague	1813	1813	Romania	60,000
Malta Plague Epidemic	1813	1814	Malta	4500
First Cholera Pandemic	1816	1826	Asia, Europe	100,000+
Second Cholera Pandemic	1829	1851	Asia, Europe, North America	100,000+
Typhus Epidemic in Canada	1847	1848	Canada	20,000+
Third Cholera Pandemic	1852	1860	Worldwide	1 million+
Cholera Epidemic of Copenhagen	1853	1853	Copenhagen, Denmark	4737
Third Plague Pandemic	1855	1960	Worldwide (India, China)	12–15 million
Smallpox in British Columbia	1862	1863	Pacific Northwest, Canada, US	20,000+
Fourth Cholera Pandemic	1863	1875	Middle East	600,000
Fiji Measles outbreak	1875	1875	Fiji	40,000
Yellow Fever	1880	1900	Mississippi, New Orleans, US	17,000+
Fifth Cholera Pandemic	1881	1896	Asia, Africa, Europe, South America	298,600
Smallpox in Montreal	1885	1885	Montreal, Canada	3164
Russian Flu	1889	1890	Russia, Worldwide	1 million
Sixth Cholera Pandemic	1899	1923	Europe, Asia, Africa	800,000
China Plague	1910	1912	China	40,000
Encephalitis Lethargica Pandemic	1915	1926	Worldwide	500,000
American Polio Epidemic	1916	1916	United States	7130
Spanish Flu	1918	1920	Worldwide	17–100 million
HIV/AIDS Pandemic	1981	2023	Worldwide	42 million
Poliomyelitis in USA	1946	1946	United States	9000
Asian Flu	1957	1958	Worldwide	1–4 million
Hong Kong Flu	1968	1969	Worldwide	1–4 million
London Flu	1972	1973	United States	1027
Smallpox Epidemic of India	1974	1974	India	15,000
Zimbabwean Cholera Outbreak	2008	2009	Zimbabwe	4293
Swine Flu	2009	2009	Worldwide	151,700–575,400
Haiti Cholera Outbreak	2010	2020	Haiti	10,075
Measles in D.R. Congo	2010	2014	Democratic Republic of Congo (DRC)	4500
Ebola in West Africa	2013	2016	Worldwide (Guinea, Liberia, Sierra Leone)	11,323+
Indian Swine Flu Outbreak	2015	2015	India	2035
Yemen Cholera Outbreak	2016	2020	Yemen	3981
2018-2019 Kivu Ebola Epidemic	2018	2020	DRC and Uganda	2280
Measles in D.R. Congo	2019	2020	DRC	7018
Dengue Fever	2019	2020	Asia-Pacific, Latin America	3930
COVID-19 Pandemic	2019	To date	Worldwide	7–29.3 million

in [2], which runs until 2019. We then include the years 2020 and 2021 as periods associated with the COVID-19 pandemic. Table 1 in this paper follows [2] and lists the contagious disease events included in our analysis [2,36,37,38]. The table provides information about the primary regions of the world that were affected and the estimated death tolls.

The temperature anomaly data from 1 AD until 2019 were acquired from [39] and then updated from the National Oceanic and Atmospheric Administration (NOAA) until 2021 AD.

Table 2. Descriptive statistics.

	(1) Temperature Anomaly: Full Sample	(2) Temperature Anomaly: Nondisease Periods	(3) Temperature Anomaly: Disease Periods	(4) Low Temperature Anomaly: Disease Periods	(5) High Temperature Anomaly: Disease Periods	(6) Contagious Disease
Observations	2021	1662	359	342	17	2021
Mean	−0.2565	−0.2439	−0.3148	−0.3630	0.6542	0.1776
S.D.	0.1626	0.1315	0.2544	0.1315	0.1789	0.3823
Min	−0.7128	−0.6688	−0.7128	−0.7128	0.4428	0.0000
Max	1.0071	0.5680	1.0071	0.0774	1.0071	1.0000
Skewness	1.8552	0.6627	2.8153	0.6760	0.4781	1.6856
Kurtosis	10.3064	4.2776	9.2488	0.4030	−1.2498	0.8417
JB	10,128.7200 ***	1394.1920 ***	1776.7710 ***	28.8250 ***	1.5200	1018.6720 ***
Q(1)	1608.9177 ***	1218.9419 ***	291.7578 ***	208.1254 ***	9.8364 ***	1574.3151 ***
Q(4)	5750.1233 ***	4171.6226 ***	981.4622 ***	629.5901 ***	17.7115 ***	4927.1886 ***
ARCH(1)	1844.5608 ***	1297.6202 ***	335.4321 ***	136.2012 ***	4.5872 **	1574.9812 ***
ARCH(4)	1876.8272 ***	1346.6727 ***	337.1974 ***	157.6724 ***	4.6465	1585.6803 ***

Note: The table reports descriptive statistics for the temperature anomaly ($h_t$) and contiguous disease variables ($d_t)$, with annual data covering the period from 1 AD to April 2021 (2021observations). In addition to the full sample (column 1), the descriptive statistics for the temperature anomaly are reported for four additional subsamples: periods of noncontiguous disease ($d_t=0;$ column 2), periods of contiguous disease ($d_t=1;$ column 3), periods of low temperature anomaly and contiguous disease ($d_t=1$ and $h_t\le 0.25$; column 4), and periods of high temperature anomaly and contiguous disease ($d_t=1$ and $h_t>0.25$; column 5). The table reports mean, standard deviation (S.D.), minimum, maximum, skewness, and kurtosis, as well as the Jarque–Bera normality test (JB), the first- [Q(1)] and fifth order [Q(5)] Ljung–Box portmanteau test for serial correlation, and the first- [ARCH(1)] and fifth-order [ARCH(5)] autoregressive conditional heteroskedasticity tests. **, and *** denote rejection at 5%, and 1% level, respectively.

describes the data characteristics for the different variables used in the analysis. The complete dataset including observations on temperature anomalies and contagious disease breakouts contains 2021 observations. It has been divided into two subsamples comprising the “nondisease” and “disease” periods. A temperature anomaly occurs either when the observed temperature is higher than a reference value, such as the long-run average value of the temperature (a positive anomaly) or when it is lower than the reference value (a negative anomaly) [40]. A high temperature anomaly occurs when the standard deviation between the observed temperature, and the reference value is greater than 0.25 points; whereas a low temperature anomaly occurs when the difference is less than 0.25 points.

3. Methodology

Let $t=\mathrm{1,2},\dots , 2021$ denote the year of observation, $d_t$ denote a binary variable taking the value of 1 if a contiguous disease occurred in the year $t$ and zero, otherwise; $h_t$ denote temperature anomaly; and ${\tau }_t$ denote a linear time trend, i.e., ${\tau }_t=t$.

We start with the linear probability model:

$$d_t={\beta }_0+{\beta }_1{h}_t+{\beta }_2{h}_{t-1}+{\beta }_3{h}_{t-2}+{\beta }_4{\tau }_t+{\epsilon }_t$$

(1)

where ${\epsilon }_t$ is an identically and independently distributed error term with zero mean and constant variance ${\sigma }^2$, ${\epsilon }_t~iid(0,{\sigma }^2)$. Defining ${\mathit{x}}_t={\left(1,h_t, h_{t-1}, h_{t-2},{\tau }_t\right)}^{\prime }$ and $\mathit{\beta }={({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4)}^{\prime }$, we can write Equation (1) as

$$d_t={\mathit{\beta }}^{\prime }{\mathit{x}}_t+{\epsilon }_t,t=\mathrm{1,2},\dots ,T$$

(1′)

Defining ${\pi }_t=\pi \left({\mathit{x}}_t\right)=P(d_t=1|{\mathit{x}}_t)$, the linear probability model implies that ${\pi }_t=E\left(d_t=1|{\mathit{x}}_t\right)={\mathit{\beta }}^{\prime }{\mathit{x}}_t$ while $E\left(d_t=0|{\mathit{x}}_t\right)=1-{\pi }_t=1-{\mathit{\beta }}^{\prime }{\mathit{x}}_t$.

We use the linear probability model as one of the benchmark models. The second benchmark model we use is the logistic probability model defined as:

$$d_t={\displaystyle \frac{\exp \left\{g\left({\mathit{x}}_t\right)\right\}}{1+\exp \left\{g\left({\mathit{x}}_t\right)\right\}}}+{\epsilon }_t$$

(2)

where the logistic link function $g\left({\mathit{x}}_t\right)$ is defined as

$$g\left({\mathit{x}}_t\right)=\log \left\{\pi \left({\mathit{x}}_t\right)/\left[1-\pi \left({\mathit{x}}_t\right)\right]\right\}={\mathit{\beta }}^{\prime }{\mathit{x}}_t$$

(3)

Thus, we can write $d_t=\pi \left({\mathit{x}}_t\right)+{\epsilon }_t$, where $\pi \left({\mathit{x}}_t\right)=\exp \left\{g\left({\mathit{x}}_t\right)\right\}/[1+\exp \{g\left({\mathit{x}}_t\right)\left\}\right]$. Here, ${\epsilon }_t$ is distributed with mean zero and variance equal to $\pi \left({\mathit{x}}_t\right)[1-\pi \left({\mathit{x}}_t\right)]$.

A generalized additive model (GAM) replaces the logistic link function in Equation (3) with

$$g\left({\mathit{x}}_t\right)={\beta }_0+s_1\left(h_t\right)+s_2\left(h_{t-1}\right)+s_3\left(h_{t-2}\right)+s_4\left({\tau }_t\right)$$

(4)

where $s_i(\cdot )$, $i=\mathrm{1,2},\dots ,4$, is the univariate smooth function of the arguments. For the GAM model in Equation (4), we specify the smooth terms $s_i(\cdot )$ as nonparametric functions, which are estimated using thin-plate regression splines [41]. We also specify a first order, serially correlated GAM specification, where ${\epsilon }_t$ follows a first-order autoregressive process [AR (1)], i.e., ${\epsilon }_t=\rho {\epsilon }_{t-1}+v_t$ with $v_t~iid(0,{\sigma }_v^2)$.

The time evaluation of the probabilities of switching between contiguous disease and noncontiguous disease states (periods) can be studied using a hidden Markov model (HMM), which is a statistical model that defines a probability distribution over possible sequences of observations in which each observation is a member of a discrete set of outcomes. It is often used to model time-varying processes.

Hidden Markov models are particularly suitable for modeling disease outbreaks due to their ability to capture time-varying processes with latent states, reflecting the episodic nature of disease dynamics. In this study, we leverage HMM to model transitions between “disease” and “nondisease” states, allowing these transitions to depend on external covariates, such as temperature anomalies. This flexibility, extended through nonhomogeneous HMM (NHMM), enables the integration of environmental factors, uncovering how climate fluctuations influence the likelihood of outbreaks. HMM’s memoryless property aligns with the stochastic nature of disease spread, while its ability to incorporate latent states surpasses simpler models in capturing underlying dynamics. This methodology builds on the prior applications of HMM in environmental and epidemiological modeling [17,22,26], making it a robust framework for analyzing complex temporal data and informing predictive models of disease occurrence under changing climatic conditions.

A hidden Markov model is based on the assumption that the underlying process that generates the data is a Markov process, and that the hidden states of the process are unobserved. In our case, the binary variable $d_t$, which indicates the presence or absence of a contiguous disease in year $t$, is a two-state process, with $d_t$ taking values 0 or one. Let these finite states be $\mathsf{\Lambda }=\left\{\mathrm{1,2}\right\}$. The HMM model expresses Markov evolution on the measurable space $\mathsf{\Lambda }$ in terms of a regular Markov chain using the latent variable $S_t\in \left\{\mathrm{1,2}\right\}$, where $S_t=1$ denotes the nondisease stated and $S_t=2$ denotes the disease state. In general, $S_t$ may have $M$ states, $S_t\in \mathsf{\Lambda }=\{\mathrm{1,2},\dots ,M\}$, with the evolution of the state space expressed with the transition probability matrix $\mathit{P}=\left[p_{ij}\right]$, $i,j=\mathrm{1,2},\dots ,M$, and stationary probability distribution $\mathit{\pi }={({\pi }_1,{\pi }_2,\dots ,{\pi }_M)}^{\prime }$. The transition probability of switching from state $i$ in year $t-1$ to state $j$ in year $t$ is defined with the following properties:

$$\begin{array}{l}{p}_{ij}=P\left(S_t=j|S_{t-1}=i\right)\in \left(\mathrm{0,1}\right), \forall i,j\\ {\sum }_{j=1}^M{p}_{ij}=1,\forall i=\mathrm{1,2},\dots ,M\end{array}$$

(5)

In our case, with $M=2$, we have two free transition probabilities, $p_{12}=\left(S_t=2|S_{t-1}=1\right)$ and $p_{21}=\left(S_t=1|S_{t-1}=2\right)$, with $p_{11}=1-p_{12}$ and $p_{22}=1-p_{21}$. The stationary probabilities $={({\pi }_1,{\pi }_2,\dots ,{\pi }_M)}^{\prime }$ are defined with the following properties:

$$\begin{array}{l}{\pi }_i=P(S_t=i)\in \left(\mathrm{0,1}\right), \forall i\\ {\sum }_{i=1}^M{\pi }_i=1, \end{array}$$

(6)

which implies one free state probability ${\pi }_2$, since ${\pi }_1=1-{\pi }_2$ with $M=2$.

If the transition probabilities $p_{ij}$ are independent of time, then the HMM is time invariant or homogenous. However, the homogenous HMM is quite restrictive for many real-world cases where the transition probabilities change over time, likely due to the effects of some underlying factors. We can relax this restrictive assumption by allowing the transition probabilities to be time-varying, which leads to a nonhomogenous HMM model. The time-varying transition probabilities model is an extension of the standard HMM. In the standard Markov model, the transition probabilities between states are constant over time. In the time-varying transition probabilities model, the transition probabilities can vary over time. The time-varying transition probabilities model is a more accurate representation of reality than the standard HMM. It can be used to model processes that change over time, such as the spread of disease, the growth of a population, or the price of a stock. An attractive approach to making transition probabilities time-varying is to allow them to depend on some other covariate. The NHMM model with time-varying transition probabilities and covariates ${\mathit{z}}_t={(z_{1t},z_{1t},\dots ,z_{Kt})}^{\prime }$ can be represented as $p_{ij}\left({\mathit{z}}_t\right)=P\left(S_t=j|S_{t-1}=i,{\mathit{z}}_t\right)$. The transition probabilities between hidden states are allowed to vary over time and are governed by covariates ${\mathit{z}}_t$. In this model, the probability of transitioning from one hidden state to another at any given time $t$ depends on both the value of the covariate at that time and the values of the transition probabilities at previous times.

Given that the observed state variable $d_t$ is binary, we use a NHMM with a logistic link function. The covariates are specified to include the temperature anomaly series $h_t$ and a linear time trend in addition to a constant vector, i.e., ${\mathit{z}}_t={(1,h_t,{\tau }_t)}^{\prime }$. The logistic HMM model specifies the transition probabilities $\{p_{ij},i,j\in \mathsf{\Lambda }\}$ and stationary distribution components $\{{\pi }_i,i\in \mathsf{\Lambda }\}$ with the following logistic models:

$$p_{ij}\left({\mathit{z}}_t\right)={\displaystyle \frac{\exp \left\{{\mathit{\alpha }}_{ij}^{\prime }{\mathit{z}}_t\right\}}{1+\exp \left\{{\mathit{\alpha }}_{ij}^{\prime }{\mathit{z}}_t\right\}}}={\displaystyle \frac{\exp \left\{{\alpha }_{0,i}+{\alpha }_{1,ij}{h}_t+{\alpha }_{2,ij}{\tau }_t\right\}}{1+\exp \left\{{\alpha }_{0,i}+{\alpha }_{1,ij}{h}_t+{\alpha }_{2,ij}{\tau }_t\right\}}}, i,j\in \mathsf{\Lambda }$$

(7)

$${\pi }_i\left({\mathit{z}}_t\right)={\displaystyle \frac{\exp \left\{{\mathit{\gamma }}_i^{\prime }{\mathit{z}}_t\right\}}{1+\exp \left\{{\mathit{\gamma }}_i^{\prime }{\mathit{z}}_t\right\}}}={\displaystyle \frac{\exp \left\{{\gamma }_0+{\gamma }_{1,i}{h}_t+{\gamma }_{2,i}{\tau }_t\right\}}{1+\exp \left\{{\gamma }_0+{\gamma }_{1,i}{h}_t+{\gamma }_{2,i}{\tau }_t\right\}}}, i\in \mathsf{\Lambda }$$

(8)

where ${\mathit{\alpha }}_{ij}={({\alpha }_{0,i},{\alpha }_{1,ij},{\alpha }_{2,ij})}^{\prime }$ and ${\mathit{\gamma }}_i={\left({\gamma }_0,{\gamma }_{1,i},{\gamma }_{2,i}\right)}^{\prime }$ are parameters to be estimated. In reality, only two sets of transition probabilities and one set of stationary state probabilities are estimated for a two-state model, since probabilities sum to one.

There are a number of ways to characterize the statistical properties of a logistic hidden Markov model for binary time series. One common approach is to consider the model’s ability to correctly predict the next time step in the series, given the previous time steps. Another approach is to consider the model’s ability to accurately estimate the underlying probabilities of the time series. Using the later approach, we estimate the parameters of the NHMM model using maximum likelihood (ML) estimation, where the maximization is performed using the expectation maximization (EM) algorithm. Once the NHMM model is estimated, there are a number of methods for decoding the states and obtaining the relevant probabilities. For our purposes, smoothed probabilities are appropriate, as they give us the full sample information for inference in each time point locally.

4. Results and Discussion

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 showcase various attributes of the data. In panel Figure 2a, the dummy variable indicating a contagious disease in a given year is plotted, while Figure 2b shows both the temperature anomalies and years with contagious diseases (shaded bars) between 1 AD and 2021 AD. We use density plots to provide a visualization of the data. In Figure 3, we plot the conditional distributions of the temperature anomaly using kernel density estimates and box plots. The distribution of the temperature anomaly is conditional on the contagious disease periods with high temperature anomaly levels (above 0.25) and low temperature anomaly levels (below 0.25), respectively. Using a Gaussian kernel, the probability densities at each data point are estimated, which are then smoothed to generate continuous curves. In panel Figure 3a, the kernel density estimates are displayed for the conditional probability distribution function of the temperature anomaly series, while, in Figure 3b, the boxplots with overlayed observations conditional on the contagious disease status are presented.

Figure 3 provides a detailed examination of the conditional distribution of temperature anomalies during periods of contagious disease outbreaks. The kernel density plots in Panel (a) reveal that high temperature anomalies ($h_t>0.25$) are more prominently associated with years experiencing disease outbreaks compared to nondisease years. This suggests that elevated temperatures likely exacerbate conditions favorable to the transmission of infectious diseases, such as increased vector activity or accelerated pathogen replication rates. Conversely, the boxplots in Panel (b) show that, during low anomaly periods ($h_t<-0.25$), while less frequent, outbreaks are not negligible. This supports the notion that cooler conditions may indirectly influence disease spread by altering host–pathogen interactions, such as through the thermal mismatch hypothesis, where hosts displaced from their thermal optima become more vulnerable to infections. Both high and low temperature anomalies can have marked effects on disease transmission, but the mechanisms differ significantly. Tian et al. [43] demonstrated that temperature extremes impact both the susceptibility of human populations and the dynamics of disease vectors. High anomalies can increase vector activity and expand the range of diseases like malaria, while low anomalies can displace populations and hosts, creating novel interactions that facilitate outbreaks. These findings underscore the duality of risk posed by temperature extremes, necessitating targeted public health strategies based on regional climatic trends.

The autocorrelation (ACF) and the partial autocorrelation function (PACF) of the contagious disease variable and the temperature anomaly behavior are presented in Figure 4 along with the cross-correlation and partial cross-correlation functions. Together, they provide insights about the time series characteristics of the data. The ACF provides the correlation between the current and the lagged values of a variable; whereas the PACF is used to measure the correlation between the current observation of the variable and an observation from a previous time period, after controlling for the observations at the intermediate lags. In Figure 4, the gradual decline in ACFs and PACFs together helps to define the autoregressive process of the two variables. The cross-correlation and partial cross-correlation plots show the relationship between the two time series used in the model. To provide a visual representation of the assessments of the three models, i.e., the logistic generalized additive model (GAM-Logistic), a logistic model, and the benchmark linear model are presented in Figure 5. We plot the predicted probabilities of the occurrence of a contagious disease against the estimated residuals $(d_t-\widehat{{\pi }_t})$, temperature anomalies, and time, in panels (a), (b), and (c), respectively.

The receiver operating curves (ROC) in panel (d) plot the model sensitivity (true positive rate) against the false positive rate. The true positive rate represents the proportion of observations that are predicted to be positive when the observations are positive; whereas the false positive rate indicates the proportion of observations that are predicted to be positive when they are, in fact, negative. The area under the curve indicates the quality of a model in predicting the observations. The GAM-Logistic model with the highest area under the curve indicates the best fit among three models.

In Figure 6, we plot the quantile–quantile (QQ) plot on the histograms of the residuals of the logistic generalized additive model (GAM-Logistic). The points in the QQ plot fall on a straight line, indicating the residuals of the model approximately follow the normal distribution. The histogram of the residuals indicates that the residuals are centered around zero.

Figure 7, Figure 8 and Figure 9 provide further visualization of various features of the logistic generalized additive model. The smoothed transition and state probabilities estimated using the nonhomogenous hidden Markov model are plotted in Figure 10.

The estimates are obtained using maximum likelihood based on the expectation maximization (EM) algorithm. The estimation results from the alternative parametric and nonparametric model specifications are presented in

Table 3. Linear probability model estimates.

Model:	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Intercept	−0.102 *** (0.019)	−0.101 *** (0.019)	−0.100 *** (0.018)	−0.099 *** (0.018)	−0.098 *** (0.018)	−0.098 *** (0.018)	0.077 *** (0.016)
$h_t$	−0.080 (0.121)		−0.108 (0.115)			−0.185 *** (0.050)	−0.393 *** (0.052)
$h_{t-1}$	−0.034 (0.138)	−0.084 (0.115)	−0.087 (0.117)		−0.186 *** (0.051)
$h_{t-2}$	−0.089 (0.123)	−0.115 (0.117)		−0.192 *** (0.052)
${\tau }_t$	0.00022 *** (0.00001)	0.00022 *** (0.00001)	0.00023 *** (0.00001)	0.00022 *** (0.00001)	0.00023 *** (0.00001)	0.00023 *** (0.00001)
R-squared	0.139	0.139	0.139	0.139	0.139	0.139	0.028
Log L	−772.311	−772.532	−772.573	−773.186	−773.021	−772.851	−895.195
AIC	1556.622	1555.064	1555.146	1554.372	1554.042	1553.703	1796.389
BIC	1590.284	1583.116	1583.198	1584.421	1576.483	1576.144	1813.220

Note: The table reports the estimates for the linear probability model in Equation (1) with various zero restrictions on the parameters. The variable $h_t$ denotes the temperature anomaly in year $t$, $t=\mathrm{1,2},\dots ,2021$, and ${\tau }_t$ denotes a linear time trend for year $t$. The table also reports McFadden’s pseudo-R squared (R-squared), logarithm of likelihood (Log $L$), Akaike information criterion (AIC), and Schwarz’s Bayesian information criterion (BIC). The standard errors of the estimates are given in brackets. Boldface denotes the minimum AIC and BIC values. *** denotes rejection of the null hypothesis of zero effect at the 1% level.

,

Table 4. Logistic model estimates.

Model:	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Intercept	−4.254 *** (0.217)	−4.247 *** (0.217)	−4.247 *** (0.217)	−4.237 *** (0.216)	−4.234 *** (0.216)	−4.237 *** (0.216)	−2.518 *** (0.149)
$h_t$	−0.609 (0.902)		−0.767 (0.859)			−1.237 *** (0.334)	−3.501 *** (0.451)
$h_{t-1}$	−0.191 (1.045)	−0.592 (0.860)	−0.518 (0.875)		−1.240 *** (0.339)
$h_{t-2}$	−0.527 (0.919)	−0.717 (0.875)		−1.271 *** (0.345)
${\tau }_t$	0.002 *** (0.0001)	0.002 *** (0.0001)	0.002 *** (0.0001)	0.002 *** (0.00001)	0.002 *** (0.0001)	0.002 *** (0.000)
R-squared	0.164	0.163	0.164	0.163	0.163	0.163	0.036
Log L	−790.317	−790.545	−790.481	−790.782	−790.881	−790.657	−911.140
AIC	1590.634	1589.090	1588.963	1587.564	1587.763	1587.315	1826.280
BIC	1618.686	1611.532	1611.404	1604.395	1604.594	1604.146	1837.501

Note: The table reports the estimates for the logistic probability model in Equation (2) with various zero restrictions on the parameters. The variable $h_t$ denotes the temperature anomaly in year $t$, $t=\mathrm{1,2},\dots ,2021$, and ${\tau }_t$ denotes a linear time trend for year $t$. The table also reports McFadden’s pseudo-R squared (R-squared), logarithm of likelihood (Log $L$), Akaike information criterion (AIC), and Schwarz’s Bayesian information criterion (BIC). The standard errors of the estimates are given in brackets. *** denotes rejection of the null hypothesis of zero effect at the 1% level. Minimum AIC and BIC values appear in bold.

,

Table 5. Logistic generalized additive model estimates.

Model:	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Intercept	−4.739 *** (0.750)	−4.767 *** (0.755)	−4.753 *** (0.754)	−4.829 *** (0.764)	−4.784 *** (0.760)	−4.791 *** (0.760)	−1.822 *** (0.075)
${s_1(h}_t)$	12.337 ** (3.933)		13.788 ** (3.964)			73.866 *** (5.246)	251.475 *** (6.633)
${s_2(h}_{t-1})$	9.124 (4.186)	29.620 *** (5.257)	10.414 * (4.145)		70.326 *** (5.429)
${s_3(h}_{t-2})$	0.499 (1.243)	3.048 (2.053)		64.645 *** (4.986)
${s_4(\tau }_t)$	207.781 *** (12.176)	208.388 *** (12.188)	208.685 *** (12.182)	209.577 *** (12.214)	210.482 *** (12.196)	209.530 *** (12.199)
R-squared	0.393	0.390	0.393	0.384	0.389	0.388	0.167
Log L	−544.991	−549.450	−545.648	−556.882	−551.469	−550.085	−789.674
AIC	1141.834	1145.625	1138.606	1151.717	1141.915	1138.542	1595.723
BIC	1287.286	1276.693	1271.321	1258.182	1251.255	1246.180	1641.660
UBRE	595.411	598.140	595.064	603.269	598.528	596.767	803.486

Note: The table reports the estimates for the logistic probability model in Equation (4) with various restricted variants. The variable $h_t$ denotes the temperature anomaly in year $t$, $t=\mathrm{1,2},\dots ,2021$, and ${\tau }_t$ denotes a linear time trend for year $t$. The smooth terms $s_i\left(\cdot \right)$ are represented using penalized regression splines with smoothing parameters selected by unbiased risk estimator (UBRE) criterion. The table reports the estimates of the intercept with its standard error in brackets. For the smooth terms $s_i(\cdot )$, the table reports the approximate significance ${\mathsf{\chi }}^2$ statistics with effective degrees of freedom in brackets. The table also reports McFadden’s pseudo-R squared (R-squared), logarithm of likelihood (Log $L$), Akaike information criterion (AIC), and Schwarz’s Bayesian information criterion (BIC), and unbiased risk estimator (UBRE) score. *, **, and *** denote rejection of the null hypothesis of zero effect at the 10%, 5%, and 1% level, respectively. Minimum AIC and BIC values appear in bold.

and

Table 6. Logistic generalized additive model estimates with serial correlation.

Model:	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Intercept	−4.682 *** (0.697)	−4.683 *** (0.697)	−4.695 *** (0.701)	−4.729 *** (0.705)	−4.713 *** (0.705)	−4.719 *** (0.705)	−1.823 *** (0.074)
${s_1(h}_t)$	11.569 ** (3.546)		13.269 *** (3.595)			75.069 *** (4.931)	250.085 *** (6.239)
${s_2(h}_{t-1})$	9.393 ** (3.832)	67.878 *** (5.178)	9.887 ** (3.713)		69.784 *** (5.051)
${s_3(h}_{t-2})$	0.862 (1.000)	2.127 (1.000)		67.738 *** (4.676)
${s_4(\tau }_t)$	192.115 *** (12.023)	192.891 *** (12.029)	193.256 *** (12.030)	195.289 *** (12.056)	195.721 *** (12.043)	195.017 *** (12.045)
$\rho$	0.891	0.858	0.858	0.854	0.858	0.885	0.878
R-squared	0.393	0.389	0.393	0.383	0.388	0.388	0.167
Log L	−599.653	−602.125	−600.074	−607.753	−603.168	−601.435	−802.978
AIC	1217.306	1218.251	1214.148	1225.505	1216.337	1212.870	1611.955
BIC	1267.799	1257.523	1253.421	1253.557	1244.389	1240.922	1628.786

Note: The table reports the estimates for the logistic probability model with AR(1) error structure in Equation (4) with various restricted variants. The variable $h_t$ denotes the temperature anomaly in year $t$, $t=\mathrm{1,2},\dots ,2021$, and ${\tau }_t$ denotes a linear time trend for year $t$. The smooth terms $s_i(\cdot )$ are represented using penalized regression splines with smoothing parameters selected by generalized cross-validation (GCV). The table reports the estimates of the intercept with its standard error in brackets. For the smooth terms $s_i(\cdot )$, the table reports the approximate significance ${\mathsf{\chi }}^2$ statistics with effective degrees of freedom in brackets. The table also reports McFadden’s pseudo-R squared (R-squared), logarithm of likelihood (Log $L$), Akaike information criterion (AIC), and Schwarz’s Bayesian information criterion (BIC). Parameters are estimated using a generalization of the penalized quasi likelihood algorithm. ** and *** denote rejections of the null hypothesis of zero effect at the 5% and 1% levels, respectively. Minimum AIC and BIC values appear in bold.

. The tables indicate when the null hypothesis of zero effect of the temperature anomaly on disease spread can be rejected at the 1% (***), 5% (**), and 1% (*) levels. The R-square, log likelihood function, Akaike information criterion (AIC), and the Schwartz Bayesian information criterion (BIC) values provide measures for the quality of the respective models and help us to compare them. The models with the better fits have lower AIC and BIC values.

In Table 3, the results of the benchmark linear probability model (LPM) are presented, with the first column providing the estimates of the unrestricted model. Columns 2 through 7 represent the restricted versions of the model with estimates of the core model under different zero restrictions on the parameters of the contemporaneous and different lagged terms along with the trend variable. The first column represents the estimated coefficients of the unrestricted model. None of the coefficients that show the relationship between the temperature anomalies and the dependent variable are statistically significant. Column 2 presents the coefficient of the contemporaneous effect (${\beta }_1$), which is restricted to zero. In column (5), the results of a restricted version of the model with both the coefficients of $h_t$ and $h_{t-2}$ set to zero are presented. A comparison of the alternative versions indicates that the restricted models in columns 5 and 6 are closely comparable. However, column 6 with the coefficients of $h_{t-1}$ and $h_{t-2}$ set to zero gives the best results qualitatively in terms of the information requirement, as confirmed by the AIC and BIC scores. The coefficient for the contemporaneous effect is statistically significant at 1%.

While relatively straightforward to specify and estimate, linear probability models are often not a suitable choice, because the predicted probability values can end up being below zero or greater than 1. To counter the standard limitations of the LPM, a logistic model was estimated. The results are presented in Table 4. Qualitatively, the results from the logistic model are in line with our findings from the benchmark model for both the unrestricted and restricted versions. The best results are for the model that includes a contemporaneous effect of temperature anomalies and a trend term.

The results of the nonparametric logistic general additive model (GAM) are presented in Table 5. A GAM is a powerful analytical tool because of its ability to fit many types of nonlinear data. However, because of this flexibility, it can be easy to overfit the data. The goal of the model is to strike a balance between two objectives. First, the model must capture the relationship exhibited in the data as closely as possible. This is indicated by the “likelihood” function, which indicates how well a model captures patterns in the data it is fitted to. Second, we want to avoid overfitting the data, which is captured by the “wiggliness” in the fit. In the model, the smoothing functions, s(.), are represented by penalized regression splines to avoid complex overfitting of the model. A smooth or a spline is essentially a function that can take a wide variety of shapes. The smoothing functions are estimated with thin plate splines, which do not depend on the prior knowledge of the functional form of the data. Thin plate regression splines can be computationally more costly relative to other smoothing options, such as cubic splines. However, they have the advantage of not requiring knots placements that are a feature of conventional regression spine modelling [44].

We estimate Equation (4) with various restrictions imposed on the smooth functions. In column (2), the results presented are conditioned on the smooth function for h_t set to zero. Similarly, the results in column (5) are derived based on the assumption that the two-period lagged effect and the contemporaneous effect of the temperature anomaly of d_t are assumed to be zero. The estimates presented in column (6) indicate that the contemporaneous effect of the temperature anomaly on the incidence of a contagious disease in a given year is statistically significant at the 1% level. This restricted model also provides the lowest AIC and BIC values, indicating a better fit than the alternative versions of the nonparametric model we estimated.

In order to account for the possibility that the error term in Equation (4) might be correlated over time, we also run a version of the GAM specificizing a first-order autoregressive process for the error structure. The results are presented in Table 6, which also includes estimates of $\rho$, the autocorrelation parameter. The estimates from both specifications of the nonparametric model are similar to column 6 (in both tables), indicating the best fit to the data compared to the alternative restricted versions of the core model. In fact, the results from the parametric and nonparametric models are qualitatively consistent. In all specifications, the restricted version of the model that includes the contemporaneous effect of the temperature anomaly and the linear trend term provide the best fit compared to the complete unrestricted specification and the alter zero-restriction variations we imposed.

Table 7. Estimates of the hidden Markov model.

Parameter	Estimate	Probabilities at Zero Values of the Covariates
${\alpha }_{\mathrm{0,2}}$	−6.9516 *** (0.7727)
${\alpha }_{\mathrm{1,12}}$	−0.8445 (0.9618)	$p_{11}$	0.9990
${\alpha }_{\mathrm{2,12}}$	0.0023 *** (0.0004)	$p_{12}$	0.0010
${\alpha }_{\mathrm{0,2}}$	2.3465 *** (0.0016)	$p_{21}$	0.0010
${\alpha }_{\mathrm{1,22}}$	−0.0184 (0.1223)	$p_{22}$	0.9990
${\alpha }_{\mathrm{2,22}}$	0.00002 *** (0.000002)
${\gamma }_0$	−683.0342 (23.2476)
${\gamma }_{\mathrm{1,2}}$	17.7412 (18.0686)
${\gamma }_{\mathrm{2,2}}$	0.4651 *** (0.0155)
Log L	−262.0879
AIC	542.1758
BIC	592.6779

Note: The table reports the estimates for the nonhomogenous hidden Markov model defied in Equations (5)–(8). The variable $h_t$ denotes the temperature anomaly in year $t$, $t=\mathrm{1,2},\dots ,2021$, and ${\tau }_t$ denotes a linear time trend for year $t$. The table also reports the logarithm of likelihood (Log $L$), Akaike information criterion (AIC), and Schwarz’s Bayesian information criterion (BIC) score. *** denotes rejection of the null hypothesis of zero effect at the 1% level.

includes the estimates of the parameters of the transition probability expression in Equation (7) and the parameters in (8) used to derive a set of stationary state probabilities for the logistic HMM model. The transition probabilities are calculated at the zero values of the covariates. The sum of the estimated probabilities of a particular state (disease or nondisease) in any time period evolving into either the same state or the alternative state in the following period adds up to 1. Regardless of the initial state, the estimated transition probabilities imply that the probability of transitioning from a given state in a year to the same year in the following year is significantly higher than the probability of transitioning to the other state (0.999 versus 0.0010).

5. Conclusions

The pace and extent of transmission of any contagious disease depend on many contextual factors, such as the availability of healthcare-related services, governmental efficacy in management of the spread, the nature of the diseases, and local and regional socioeconomic and environmental conditions at the epicenter. In this paper, we used annual data on contagious disease outbreaks and temperature anomalies from 1 AD to 2021 AD and parametric and nonparametric modelling approaches to derive the estimates of contemporaneous and lagged effects of temperature anomalies on the spread of contagious diseases. Our results indicate that temperature anomalies have played an influential role in the spread of transmissible diseases over the last two thousand years, thereby identifying a common cause among different disease spreads over time. These findings can be used to develop public health surveillance systems across different regions of the world, characterized by considerable uncertainty in changes in weather and climate patterns. Region-specific climate forecasting results can be combined with demographic information to develop location-specific, cost-effective disease control policy responses and transmission-based precautionary measures. This is particularly important given that regions across the world vary greatly in available resources that can be dedicated to mitigating the damages associated with the transmission of infectious diseases. Future avenues of research could potentially focus on this line of interdisciplinary work. Our analysis does not include data on covariates other than temperature anomalies. Given the length of the time series, our study did not include other environmental and socioeconomic explanatory variables that have been shown to impact the spread of contagious diseases. Also, while historical data allow us to obtain a long-term perspective of the evolution of relationships and helps us avoid sample selection bias, it comes at the cost of some degree of inaccuracy, as the data might originate from alternative sources. We acknowledge these limitations, but there is no other way of handling the issues in the current context. Future research that focuses on shorter time lengths can address these concerns and also explore the complex dynamics among the contagious diseases mentioned in this study.