Abstract
This study depicts potential climate change impacts on annual rainwater savings from household rainwater harvesting using two different climate projection models; ACCESS 1.0 and CSIRO-Mk3.6. This paper also investigates potential changes in the relationships of ‘water saving efficiency’ and reliability with rainfall ‘seasonality index’ under the mentioned climate change scenarios. The annual water savings were calculated for three weather conditions: dry, average, and wet. Historical daily rainfall amounts provided by the Australian Bureau of Meteorology were used for three locations within the city of Brisbane (Australia). For the same locations, projected future daily rainfall amounts were collected from an online data portal facilitated by the Australian government. Potential annual water savings, water saving efficiency, and reliability values for the selected locations were calculated through a widely used tool, eTank, developed on water balance methodology at a daily scale. It was found that for the coastal location, Manly, the future water savings are not likely to change significantly. However, for the inland location, Sunnybank, the future water savings are expected to decrease under all the weather conditions through both the considered climate projections. For the far inner location, Oxley, the water savings are likely to decrease in the dry year, whereas in wet year, they are likely to increase. Also, it was found that the overall average relationship of SI–water saving efficiency is steeper for ACCESS 1.0 projected data compared to that produced through CSIRO-Mk3.6 data, and that significant differences exist among individual relationships for each location. The overall reliabilities calculated through the model projected data show lower values compared to the reliabilities calculated using historical data.
1. Introduction
The seasonality index (SI), a simple representation of intra-annual monthly variation in hydrological variables within a year, has been mainly used for expressing rainfall variability and the average deviation from an annual mean value. It can be used for any hydrological variable, though it is commonly used for rainfall variability, which is significant for water resource management and/or irrigation scheduling. In rainfall-related research fields, seasonality effects have been widely used [1,2,3]. However, until recently, their uses were limited in the field of rainwater harvesting, which is an important infrastructure for sustainable urban water management, especially with the onslaught of the emerging impacts of climate change. Average monthly rainfall patterns and their shift from the typical average values significantly influence the decision making related to water resource management and prudent water allocations among different users. In many countries, including Australia, the withdrawal of water from a common source for different irrigation projects is restricted by a limited licence amount. Some regions may receive excessive rainfall amounts; however, they may not render fruitful outcomes to the users due to sporadic monthly anomalies in magnitudes. Rather, excessive rainfall may cause flooding and subsequent agricultural damage. Such excessive amounts of water within a few months will render the benefits towards irrigation requirements ineffective, which at times will require uniform, moderate amounts of rainfall to stretch across the year.
As mentioned earlier, the SI, though presented with a simple formula, has wide and significant uses for many hydrological/environmental engineering applications. Sumner [4] originally proposed the formula for the SI, which is described in the following section. Ideally, the values of the SI will vary from 0 to 1.83. The value of the SI will be ‘0’ if each of the twelve months of a year has same amount of rainfall. On the other hand, the value of the SI will be ‘1.83’, if all the rainfall occurs in one month only, leaving the other eleven months without rainfall. However, in reality, both the mentioned extremes are unlikely [5]. Imteaz et al. [6] presented a detailed study on climatic and spatial variabilities in SI values within Australia, using historical monthly rainfall data from six major cities, and revealed wide variations in SI values (0.09~0.78) within Australian cities. Although the study was aimed at exploring a trend in the variation in the SI with weather conditions (dry, average and wet), the existence of a clear trend in weather conditions was not revealed.
Climate scientists unanimously agree that among other hydrological variables, rainfall magnitude and frequency will significantly change due to the impending impacts of climate change, which are already evident and reported in various studies [7,8]. The World Climate Research Programme (WCRP), sponsored by the World Meteorological Organization (WMO), the Intergovernmental Oceanographic Commission (IOC) of UNESCO, and the International Science Council (ISC) through its Coupled Model Intercomparison Project (CMIP), has demonstrated potential future changes in climate variables under different greenhouse gas emission scenarios. The Intergovernmental Panel on Climate Change (IPCC) has been responsible for monitoring, assessing, and deducing polices to overcome the catastrophic disasters of climate change impacts. The IPCC and other international or national climate assessments predominantly depend on data and results produced by CMIPs. From those studies, regarding rainfall, more sporadic rainfall amounts are likely to occur in the future. Also, in addition to a change in the total annual rainfall amount, the intra-annual distribution of rainfall is likely to be altered [9], which is likely to affect the growth of different plants and crops, especially the ones that heavily rely on seasonal rainfall amounts. It is noteworthy that Australian cities have experienced a higher degree of rainfall variabilities, even without the effect of climate change. Climate change impacts are likely to deteriorate the current hydrological anomalies [10]. Some studies have predicted that for several regions in the world, occurrences of typical dry and wet years are likely to be greater in magnitude, as well as having increased frequency [11]. An increase or decrease in usual rainfall amounts associated with the change in patterns will cause additional complexity in efficient water resource management in this continent which frequently experiences drought or flood [12].
It is evident that seasonal rainfall in different parts of Australia is dominated by some large-scale climate drivers that emanate from surrounding oceans. Among those, the Southern Oscillation Index (SOI), Indian Ocean Dipole (IOD), and Southern Annual Mode (SAM) are the ones with significant influence depending on the geographical location. Some studies were conducted on establishing relationships between one or more of these climate indices with the regional rainfall/streamflow [13,14,15]. However, only a few studies were conducted on the relations of localized SI with rainfall and the associated variables [16,17].
Due to continuous increases in water demands, while sources of available water deplete day by day, many water supply authorities around the world are under tremendous pressure to continue providing a smooth supply of potable water. With the aim of reducing potable water demand, many water authorities are emphasizing the implementation of different rainwater harvesting systems, mainly for non-potable purposes. Consequently, several studies have assessed the potential impacts of climate change on different outcomes of domestic rainwater tanks [18,19,20,21]. However, studies on the relationship of the SI with potential rainwater savings using rainwater tanks and its future implications under climate change scenarios are scarce. Even without the consideration of climate change, the study of the relationship between the SI and rainwater harvesting efficiency is limited. Among the studies, the very first one by Jenkins [22] employed a continuous simulation water balance model using historical daily rainfall data for twelve Australian cities and demonstrated that annual water saving efficiency through rainwater tanks linearly decreases with higher SI values, if the SI is calculated with monthly rainfall amounts. Following this, another study [16] utilizing rainfall data from six major Australian cities proposed a generalized relationship between the SI and water saving efficiency through calculating potential water savings using rainwater tanks, which was accomplished via a daily water balance model. Later, some studies [23,24] assessed the adaptability of the generalized relationship under future projected climate change scenarios using future daily rainfall data for different regions of Sydney and Brisbane. The study with the Sydney data [23] reported an overall decrease in the water saving efficiency value, even with the same SI value, whereas the study with Brisbane data [24] reveals a swing; for lower SI values, the future water saving efficiency increases, while for higher SI values, the future water saving efficiency decreases. The latest study [24] was conducted with the projected rainfall data obtained from Australian Community Climate and Earth-System Simulator (ACCESS 1.0) weather model projections. However, it is likely that the projection results from one model will vary from the projections of another model. As such, it is necessary to assess how the results vary with the use of other climate projections and the extent or nature of the variations. If the variations are negligible, the users may confidently use results from any model. However, if the variations are significant, the users need to be cautious in implementing these results and should be aware of the potential extent of variations. Such a study has not been accomplished regarding studies related to rainwater savings under climate change scenarios. As such, this paper presents three aspects of comparisons: (i) comparisons of annual water savings through two different climate models’ (ACCESS 1.0 and CSIRO Mk3.6) projections compared to historical water savings under different weather conditions representing dry, mean and wet weather, (ii) comparisons of relationships between SI and water saving efficiency through projected rainfall data using ACCESS 1.0 and CSIRO-Mk3.6 projections, and (iii) comparisons of relationships between SI and reliability calculated through two climate models’ data.
2. Materials and Methods
2.1. Study Area
Brisbane, the third-largest city of Australia, was selected for this study, mainly due to the availability of uninterrupted, good-quality rainfall data. Also, as an earlier study on a similar theme was conducted for Brisbane, for the sake of comparison, it was necessary to select the same city. Three locations with available daily rainfall data were selected from different directions of the Brisbane metropolitan. The locations were selected based on the availability of data with no/minimal missing records. Details of the selected locations, associated rainfall station numbers (assigned by the Australian Bureau of Meteorology), and geographical locations (with respect to the city centre) are provided in Table 1 below. The physical locations of the selected stations are shown in Figure 1, along with the map of the Brisbane metropolitan area. Figure 2 shows the monthly historical rainfall values of the three selected stations.

Table 1.
Details of the selected rainfall stations within Brisbane metropolitan.
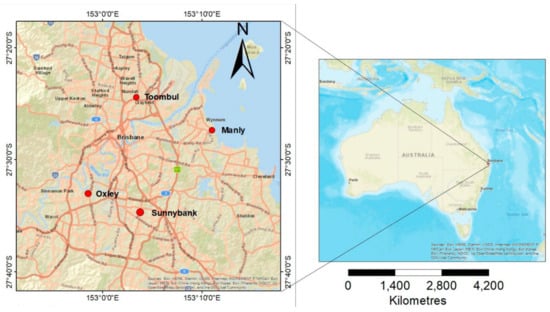
Figure 1.
Map of three tributaries of Goulburn River, Acheron, Rubicon, and Yea River.
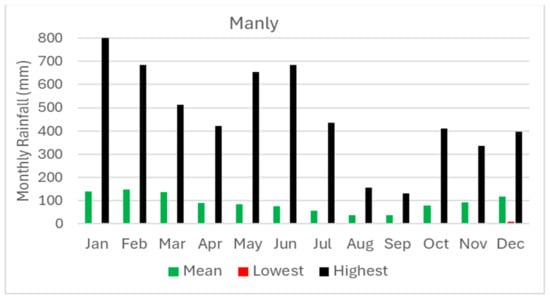
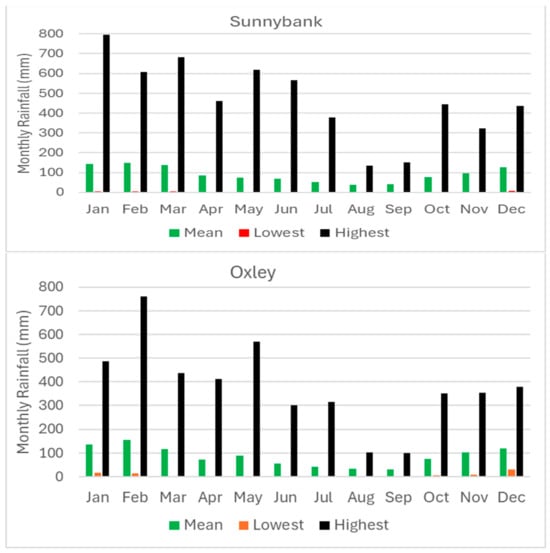
Figure 2.
Historical monthly average rainfall values for the selected stations.
2.2. Climate Model and Data
The earlier study used the ACCESS 1.0 model data and the current study used another significant model’s (CSIRO-Mk3.6) projected data. The CSIRO-Mk3.6 climate model was jointly developed by the Australian government’s Commonwealth Scientific and Industrial Research Organisation (CSIRO) and the Queensland Climate Change Centre of Excellence (QCCCE). The purpose of this modelling task was to prepare a joint submission for “Coupled Model Intercomparison Project (CMIP)”, the details of which are provided in (https://esgf-node.llnl.gov/projects/cmip5/, accessed on 20 March 2024). CSIRO-Mk3.6 was used due to its appropriate model resolution, which meets the specific requirement of the Regional Climate Model version 4.4 (RegCM4) at 25 km horizontal resolution and provides outputs with a 6 h interval. Detailed information on the CSIRO-Mk3 model’s development can be found from Rotstayn et al. [25].
2.3. SI Calculation
The SI equation as proposed by Sumner [5] is given as follows:
In the above equation, the ‘Seasonality Index’ is denoted by ‘SI’. R is the total annual rainfall and Xj is the individual monthly rainfall for the month ‘j’, where the values of ‘j’ vary from 1 (representing January) to 12 (representing December). The SI values for the mentioned stations were calculated using above equation.
Considering a mix of weather conditions, rainfall data were selected from three different weather conditions: dry, average, and wet. To minimize the effect of any unusual year, three years’ data were selected for a specific weather condition. Calculations were performed for each of the three selected years and an average of the three values from the three selected years were presented.
2.4. Calculation of Water Savings and Reliability
eTank, a widely used daily water balance model, was used for the calculations of potential water savings and reliabilities for the selected years. The input data for the used model were daily rainfall, contributing catchment (roof) area, cumulative losses, storage volume, and rainwater demand. In summary, the eTank model considers daily rainfall amounts as prime input data, and a certain portion of the daily incoming rainfall amount is deducted as loss in a daily timescale. The remaining (after loss) amount is multiplied with the roof area to convert it to runoff volume from the roof catchment. This amount is then considered as the input to the rainwater tank with limited volume capacity. At any point in time, the roof-runoff from the current day is added to the accumulated water in the tank from the earlier days (if any). From the accumulated water (if it remains), the assumed rainwater demand amount is deducted on a daily basis. If at any stage the storage tank becomes full, the subsequent runoff amount is considered lost (i.e., overflow) from the water balance. After several day of use without any input, and if no water remains in the tank, it is assumed that the rainwater demand will be fulfilled by the normal town water (potable) supply (as it works in the Australian urban context). Details of the theoretical concepts including operational algorithms and mathematical formulations are presented by Imteaz et al. [26]. Although the tool is capable of higher-level cost analysis, including payback period calculations, calculations were focused only on annual water savings and reliability in the current study.
As defined by many other studies, the ‘reliability’ is the percentage of cumulative days (in a year) the tank is capable of fulfilling the daily rainwater needs. Another parameter used in this study is the ‘Water Saving Efficiency’, which is the ratio of annual water savings (in litres) to annual rainfall amount (in mm). The other input data were assumed to be as follows: roof area = 100 m2, rainwater demand = 200 L/day, tank volume = 5000 L, and rainfall loss = 15% (evaporation and leakage losses). The water demand mentioned here is the non-potable water demand generally attributed to Australian households, which might be partial or full. Also, it is to be noted that the results are likely to vary with variations in these variables; however, these assumed values are very common in the Australian context, as used in the earlier study [24]. The current study’s focus was mainly to compare the different model results with the results of the earlier study, which used data generated from the ACCESS 1.0 model.
The calculations accomplished three aspects: (i) annual water savings for historical and two projected models under three weather conditions; dry, average, and wet, (ii) projected relationships between the SI and water saving efficiency, and (iii) projected relationship between the SI and reliability. For all the mentioned aspects, the calculated outcomes were compared with historical data, ACCESS 1.0 projection data, and CSIRO-Mk3.6 projected data. It is to be noted that dry, average, and wet conditions/years are usually defined as rainfall values of 10, 50, and 90 percentile values of historical annual rainfall values.
3. Results
3.1. Results on Annual Water Savings
Figure 3 shows the calculated annual water saving amounts for all the selected locations for three different sets of rainfall data (historical, ACCESS 1.0 projected, and CSIRO-Mk3.6 projected) under three selected weather conditions: dry, mean, and wet. From the figure, it is evident that the wet years are expected to have highest water savings and the dry years are the least. It was found that for ‘Sunnybank’, both the ACCESS and CSIRO-Mk3.6 models predicted lower water savings compared to the historical water savings. The CSIRO-Mk3.6 model predicts slightly higher water savings compared to the ACCESS model’s predicted water savings, except for in the dry year. For Manly, the ACCESS model data produces slightly lower water savings compared to the historical water savings. However, the CSIRO-Mk3.6 model data produced slightly higher water savings compared to the historical water savings, although the differences among the three calculations are insignificant. This might be because Manly is a coastal location, and any major abruptions in rainfall amounts are buffered by the huge moisture present in the atmosphere above the ocean. The inland location, Oxley, reveals interesting results. While the ACCESS model produces lower water savings compared to the historical water savings, the CSIRO-Mk3.6 model produces a rapid shift; the dry year produces significantly lower water savings, while the wet year produces significantly higher water savings compared to the historical water savings. This finding conforms with the majority of climate scientists’ predictions on future rainfall availability, which mention that climate change is likely to cause future dry years to be drier, while wet years are to be wetter, both in magnitude and frequency.
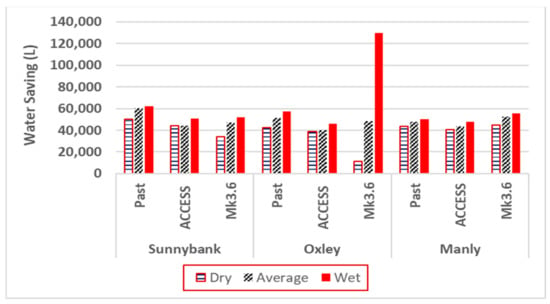
Figure 3.
Annual water savings under different weather conditions.
However, in regard to the potential benefits of rainwater tanks, annual water savings are not the only outcome that should be considered. There are also other factors which govern the rainwater tank size selections. ‘Reliability’ and ‘Water Saving Efficiency’ are two other factors that require significant attention, and these factors can be correlated with the rainfall SI value of a particular locality. The following sections detail such relationships and comparisons of such relationships among two different model projections, as well as using historical rainfall.
3.2. Results on Water Saving Efficiency
Figure 4 shows the relationship between the SI and water saving efficiency, considering data and calculations from all the three selected stations using CSIRO-Mk3.6 data. Figure 4 also shows a similar relationship (solid line) with the ACCESS 1.0 data. For better clarity, the scattered points are omitted (only a solid line is shown) in the figure for calculations produced by ACCESS 1.0, as it was also a part of an earlier study [26]. The figure also shows the trendline equations for both the models’ projected data. From the figure, it is clear that SI–water saving efficiency relationships are likely to swing between the predictions of the CSIRO-Mk3.6 and ACCESS 1.0 data. As per the CSIRO-Mk3.6 data for lower SI values, the water saving efficiency will be lower compared to the ACCESS 1.0 simulation, whereas for higher SI values, the water saving efficiency will be higher compared to the ACCESS 1.0 data.
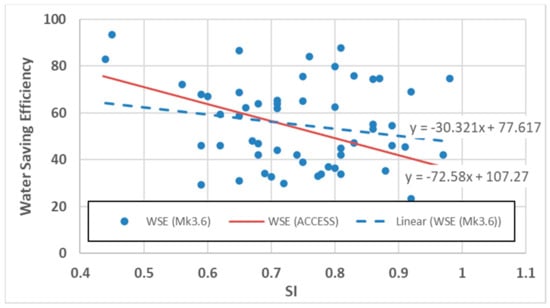
Figure 4.
SI—water saving efficiency relationships for the whole city.
As in the earlier study [26], significant differences were observed among the stations, and, in the current study, calculations for the selected three stations are separated and the results are presented in separate graphs for more clarity. Figure 5, Figure 6 and Figure 7 show the relationship between the SI and water saving efficiency for Sunnybank (Figure 5), Oxley (Figure 6), and Manly (Figure 7) stations. Like the whole city (Figure 4), Figure 5 also shows a similar swing in relationships with the CSIRO-Mk3.6 and ACCESS 1.0 projected data, i.e., with the Mk3.6 projected data, for lower SI values the water saving efficiency becomes lower, and with higher SI values, the water saving efficiency become higher. The figure also shows the same relationship with the past data. It is found that for Sunnybank, compared to the calculations produced by both the models’ projected data, historical water saving efficiencies are lower for the same SI values. The figure also shows the trendline equations from the calculations based on three individual datasets.
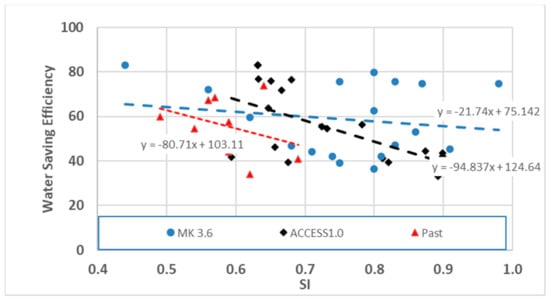
Figure 5.
SI–water saving efficiency relationships for Sunnybank.
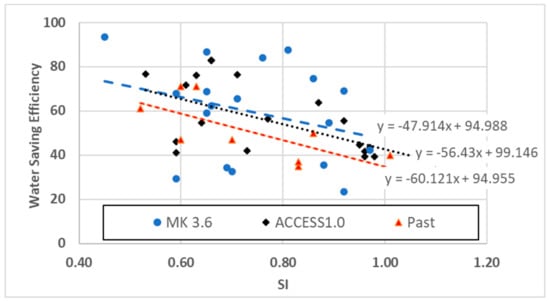
Figure 6.
SI–water saving efficiency relationships for Oxley.
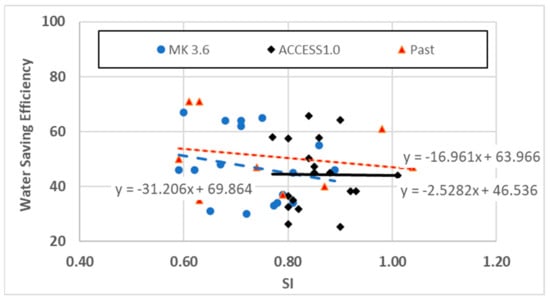
Figure 7.
SI–water saving efficiency relationships for Manly.
Figure 6 shows a similar relationship for the Oxley station. A similar trend (the dotted lines) is observed for the case of Oxley, i.e., with the Mk3.6 data, the water saving efficiency is lower for lower SI values; however, for higher SI values, the water saving efficiency is higher. The only difference is that for the case of Oxley, this swing is more prominent and the trendline rotates anticlockwise, meaning that achievable water savings efficiencies are mostly lower compared to the ACCESS 1.0 data. With the Mk3.6 data, the efficiencies only become higher for very high SI values (>0.9). For both the stations, under the climate change scenario, an overall increase in water saving efficiency is expected with the same SI value, compared to the past climate condition. The figure also shows the trendline equations from the calculations based on three individual datasets.
Figure 7 shows the SI–water saving efficiency relationships (dotted and solid lines) for Manly station. Manly, being a coastal location, exhibits a different trend compared to the two other inland locations mentioned earlier. For Manly, the overall future water saving efficiency is likely to drop compared to the past scenario. However, both the ACCESS 1.9 and Mk3.6 calculations exhibit almost similar trends in regard to the SI–water saving efficiency relationship. Also, as presented in the earlier section, annual water savings through both the models’ calculations produce almost similar magnitudes for all three weather conditions. Like the other two stations, the best fit trendline equations are also shown in the figure for the calculations of all the three datasets used.
3.3. SI–Reliability Relationships
Figure 8 shows the relationships (solid and dotted lines) of the SI with the calculated reliability values for the historical as well as both (ACCESS 1.0 and CSIRO Mk3.6) the climate-projected datasets. The solid line depicts the relationship for historical data, while scattered points with average trend lines represent the individual climate-projected data.
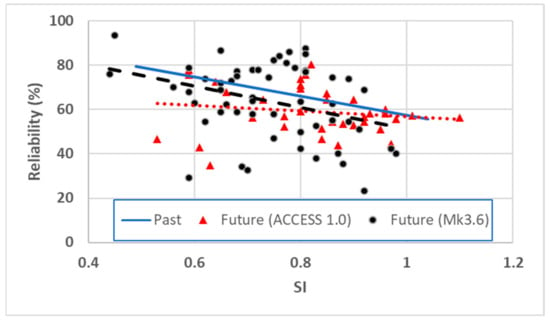
Figure 8.
SI–reliability relationships for the whole city.
From the figure, it is clear that compared to the historical reliability values, the overall reliabilities are likely to be reduced for both the ACCESS 1.0 and CSIRO-Mk3.6 climate projection scenarios for the same SI values. However, under the ACCESS 1.0 scenario, the reliability values are likely to be slightly higher compared to the historical reliability values for very high (>1.0) SI values.
4. Discussions
In general, it is found that the expected annual water savings, reliabilities, and water saving efficiency values are quite scattered in relation to the SI values, which is a similar result to the earlier study as well [23,24]. This is reasonable, as the SI value itself as a ratio of monthly rainfall values can vary even with the same annual rainfall amounts in different years. On the other hand, two different years may have significantly different annual rainfall amounts while having the same SI values. The results were computed for a particular set of values for rainwater demand, roof size, and tanks size. Obviously, the computed results will vary with the variation in these variables. However, the relationship patterns of the SI with other parameters are likely to be similar. The purpose of this study was not to calculate water saving, water saving efficiency, or reliability for any conditions. Rather, the objective was to find the relationships between the SI and the selected parameters and how those are likely to be affected due to climate change. Moreover, we explored how much they can vary with the use of data from different climate projection models. It was found that annual water saving amounts do not significantly vary with the use different projection data, except for in one scenario. However, water saving efficiency values and their relationship with the SI significantly vary with the use of two different projection datasets. Also, the relationships of reliabilities with the SI values do not significantly vary with the use of different projection data.
5. Conclusions
This study presents the probable impacts of emerging climate change on potential rainwater savings, rainwater tank reliability, and the efficiency of water savings through rainwater tanks, employing historical and projected daily rainfall data from the third-largest Australian city, Brisbane. A widely used tool (eTank), which employs water balance methodology at a daily timescale, was used for the computations of the above-mentioned variables. The future projected water saving efficiency of rainwater tank is correlated with the corresponding SI values, which are a measure of intra-annual rainfall variabilities. This study also investigated the impacts of climate change on the earlier established relationship of the seasonality index with potential water saving efficiency, and it compared deviations from the past relationship for two projection models: ACCESS 1.0 and CSIRO-Mk3.6. Three locations spread across greater Brisbane were selected based on the criteria of having high-quality daily rainfall data available. Future rainfall data at a daily timescale were downloaded from the Climate Change in Australia (CCIA) data portal managed by the Australian government. The investigations were conducted for three weather conditions: dry, mean, and wet. For the sake of comparison with previous studies on the same topic, some rainwater tank-related parameters were considered to be the same. They include roof area = 100 m2, rainwater demand = 200 L/day, tank volume = 5000 L, and rainfall loss = 15%.
It was revealed that in most of the cases/scenarios, the future annual water savings with the use of rainwater tanks are likely to decrease for all of the studied locations, except for a few cases. For an inner location, Oxley, and using CSIRO-Mk3.6 projected data, the expected water savings in a wet year will be more compared to the historical wet year annual savings, whereas in a dry year, they will be less compared to the historical dry year. Based on earlier findings, an increase/decrease in accumulated yearly water savings not only depends on the total annual rainfall magnitudes, but also on the SI of incoming rainfall and rainwater tank reliability. For all the selected locations, anomalies in the annual water saving efficiencies can be correlated with the corresponding SI values of the selected locations. Also, the established relationships were compared with similar relationships established using historical rainfall data for the respective locations. It was found that except for Manly, the other two stations’ water saving efficiencies will be higher compared to their water saving efficiency based on historical rainfall data. For Manly, both the ACCESS 1.0 and CSIRO-Mk3.6 data produced lower water saving efficiencies compared to the historical water saving efficiency for the same SI values. Also, it was found that for Sunnybank and Oxley, the seasonality index–water saving efficiency relationship is steepest with the ACCESS 1.0 data, whereas the same relationship is mildest with the CSIRO-Mk3.6 data. In regard to rainwater tank reliability, it was found that reliabilities calculated through both the projection models produced lower reliabilities compared to the reliabilities calculated using historical rainfall data.
It is noteworthy that the current study used ACCESS 1.0 and CSIRO-Mk3.6 climate model-projected data. Nonetheless, there are uncertainties in the models’ projected data, which was out of the scope of this study, as this topic requires a separate intensive study to explore uncertainties in those models’ projected data. The current study provides an insight into how rainwater tank outcomes can be altered by the impacts of climate change. It is recommended that future studies investigate possible uncertainties in those models’ projections. Also, in addition to ACCESS 1.0 and CSIRO-Mk3.6, are other models’ projections are available. It is recommended to investigate how the rainwater tank outcomes and potential climate impacts are likely to vary as per other models’ simulated data.
Author Contributions
Conceptualization, M.A.I.; methodology, A.A. and I.H.; software, M.S.K.; validation, M.S.K.; formal analysis, I.H.; investigation, M.A.I. and I.H.; resources, M.S.K.; data curation, M.S.K.; writing—original draft preparation, I.H.; writing—review and editing, M.A.I. and A.A.; supervision, M.A.I.; project administration, M.A.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are taken from a Ph. D. thesis, which has an embargo of release for 2 years. However, the data used in this study can be obtained by contacting the first author.
Special Note
If one wishes to replicate the results presented in this paper, they will need two rigorous sets of data: (i) historical daily rainfall data available from the Australian Bureau of Meteorology and (ii) projected daily rainfall data from the Climate Change in Australia (CCIA) data portal. Moreover, one will need to use the mentioned daily water balance model, eTank. The model and the associated data will be made available upon request to the first author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Z.; Zhang, J.; Wen, T.; Cheng, J. Uncertainty Quantification of Rainfall-runoff Simulations Using the Copula-based Bayesian Processor: Impacts of Seasonality, Copula Selection and Correlation Coefficient. Water Resour. Manag. 2022, 36, 4981–4993. [Google Scholar] [CrossRef]
- Rachid, G.; Alameddine, I.; El-Fadel, M. Management of Saltwater Intrusion in Data-scarce Coastal Aquifers: Impacts of Seasonality, Water Deficit, and Land Use. Water Resour. Manag. 2021, 35, 5139–5153. [Google Scholar] [CrossRef]
- Serrano, L.; Ribeiro, R.B.; Borges, A.C.; Pruski, F.F. Low-Flow Seasonality and Effects on Water Availability throughout the River Network. Water Resour. Manag. 2020, 34, 1289–1304. [Google Scholar] [CrossRef]
- Sumner, G.N. Precipitation: Process and Analysis; John Wiley & Sons Ltd: Chichester, UK, 1988. [Google Scholar]
- Risbey, J.S.; Pook, M.J.; McIntosh, P.C.; Wheeler, M.C.; Hendon, H.H. On the remote drivers of rainfall variability in Australia. Mon. Weather. Rev. 2009, 137, 3233–3253. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Yilmaz, A.; Ahsan, A. Climatic and spatial variations in seasonality index of rainfall pattern for major Australian cities. Int. J. Hydrol. Sci. Technol. 2021, 14, 14–26. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Mikhaylov, A.; Moiseev, N.; Aleshin, K.; Burkhardt, T. Global climate change and greenhouse effect. Entrep. Sustain. Issues 2020, 7, 2897. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Porporato, A.; Rodriguez-Iturbe, I. Changes in rainfall seasonality in the tropics. Nat. Clim. Chang. 2013, 3, 811–815. [Google Scholar] [CrossRef]
- Chowdhury, R.; Beecham, S. Australian rainfall trends and their relation to the southern oscillation index. Hydrol. Process Int. J. 2010, 24, 504–514. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Beecham, S.; Metcalfe, A. Climatic influences on rainfall and runoff variability in the southeast region of the Murray-Darling Basin. Int. J. Climatol. 2013, 33, 291–311. [Google Scholar] [CrossRef]
- King, A.D.; Pitman, A.J.; Henley, B.J.; Ukkola, A.M.; Brown, J.R. The role of climate variability in Australian drought. Nat. Clim. Chang. 2020, 10, 177–179. [Google Scholar] [CrossRef]
- Holgate, C.; Evans, J.; Taschetto, A.; Gupta, A.; Santoso, A. The Impact of Interacting Climate Modes on East Australian Precipitation Moisture Sources. J. Clim. 2022, 35, 3147–3159. [Google Scholar] [CrossRef]
- Mohamadi, S.; Khozani, Z.; Ehteram, M.; Ahmed, A.N.; El-Shafie, A. Rainfall prediction using multiple inclusive models and large climate indices. Environ. Sci. Pollut. Res. 2022, 29, 85312–85349. [Google Scholar] [CrossRef] [PubMed]
- Ehteram, M.; Afan, H.A.; Dianatikhah, M.; Ahmed, A.N.; Ming Fai, C.; Hossain, M.S.; Allawi, M.F.; Elshafie, A. Assessing the predictability of an improved ANFIS model for monthly streamflow using lagged climate indices as predictors. Water 2019, 11, 1130. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Moniruzzaman, M.; Yilmaz, A. Towards developing generalised equations for calculating potential rainwater savings. In Handbook of Water Harvesting and Conservation; Eslamian, S., Ed.; John Wiley & Sons Inc: Hoboken, NJ, USA, 2021; Chapter 27; ISBN 978–1119478959. [Google Scholar]
- Pascale, S.; Lucarini, V.; Feng, X.; Porporato, A.; Hasson, S.U. Analysis of rainfall seasonality from observations and climate models. Clim. Dyn. 2015, 44, 3281–3301. [Google Scholar] [CrossRef]
- Preeti, P.; Haddad, K.; Rahman, A. Assessing the impacts of climate change on rainwater harvesting: A case study for eight Australian capital cities. Water 2022, 14, 3123. [Google Scholar] [CrossRef]
- Toosi, A.S.; Danesh, S.; Tousi, E.G.; Doulabian, S. Annual and seasonal reliability of urban rainwater harvesting system under climate change. Sustain. Cities Soc. 2020, 63, 102427. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Yue, T.; Jing, X. Impacts of climate change on urban rainwater harvesting systems. Sci. Total Environ. 2019, 665, 262–274. [Google Scholar] [CrossRef] [PubMed]
- Kisakye, V.; Van der Bruggen, B. Effects of climate change on water savings and water security from rainwater harvesting systems. Resour. Conserv. Recycl. 2018, 138, 49–63. [Google Scholar] [CrossRef]
- Jenkins, G. Use of continuous simulation for the selection of an appropriate urban rainwater tank. Australas. J. Water Resour. 2007, 11, 231–246. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Hossain, I. Climate Change Impacts on ‘Seasonality Index’ and its Potential Implications on Rainwater Savings. Water Resour. Manag. 2022, 37, 2593–2606. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Khan, M.S.; Yilmaz, A.G.; Shanableh, A. Climate Change Impacts on Rainwater Tank’s Potential Water Savings, Efficiency and Reliability Presenting Relationship Between ‘Seasonality Index’ and Water Savings Efficiency. Water Resour. Manag. 2023, 37, 2593–2606. [Google Scholar] [CrossRef]
- Rotstayn, L.D.; Jeffrey, S.J.; Collier, M.A.; Dravitzki, S.M.; Hirst, A.C.; Syktus, J.I.; Wong, K.K. Aerosol and greenhouse gas induced changes in summer rainfall and circulation in the Australasian region: A study using single-forcing climate simulations. Atmos. Chem. Phys. 2012, 12, 6377–6404. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Karki, R.; Shamseldin, A.; Matos, C. eTank and contemporary online tools for rainwater tank outcomes analysis. Int. J. Comput. Aided Eng. Technol. 2017, 9, 372–384. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).