Spatiotemporal Rainfall Variability and Trends over the Mahi Basin, India
Abstract
1. Introduction
2. Materials and Methods
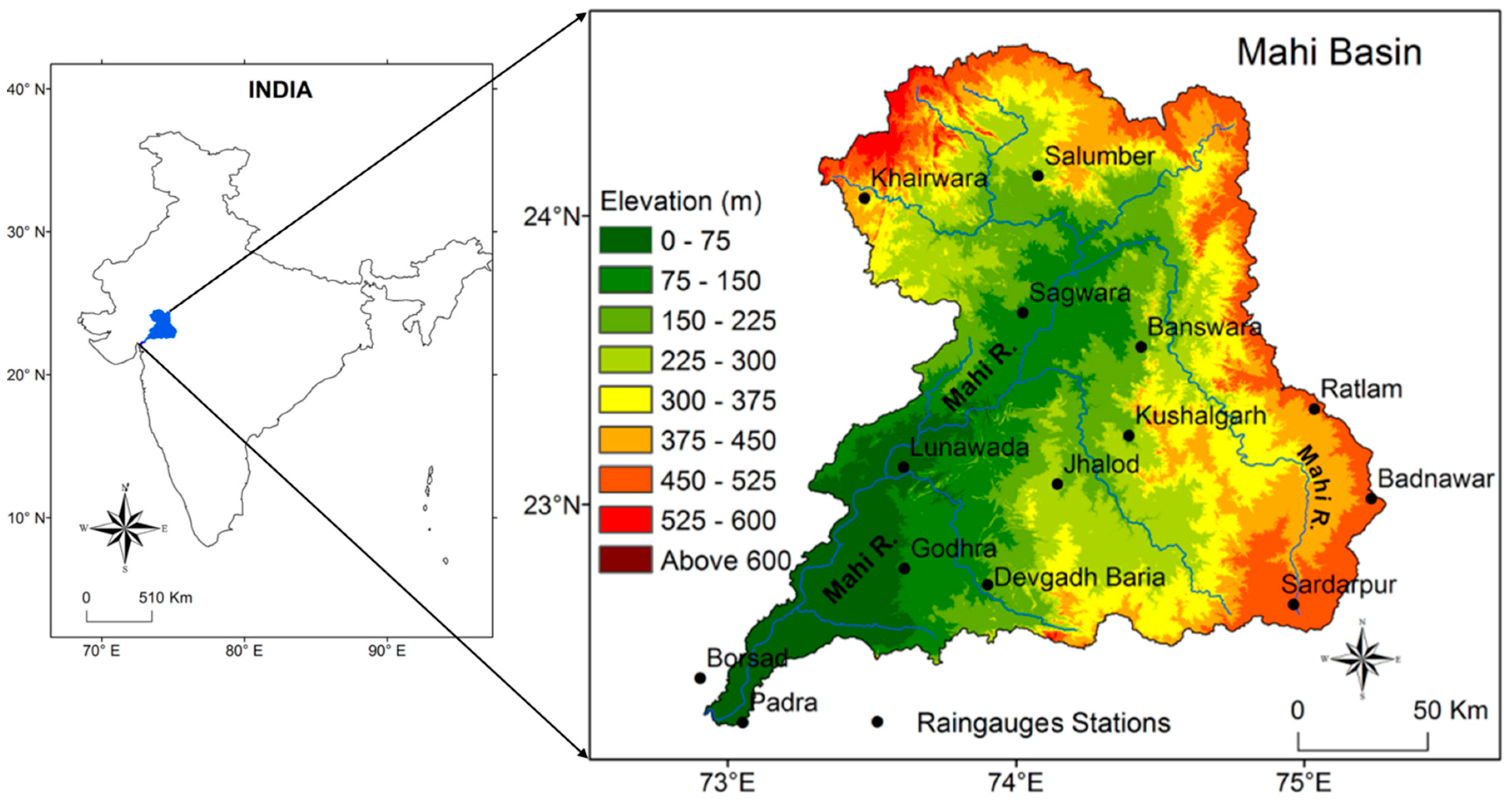
2.1. Study Area
2.2. Data Used
2.3. Methodology
2.3.1. Coefficient of Variation (CV)
2.3.2. Mann–Kendall (MK) Test
2.3.3. Sen’s Slope (SS)
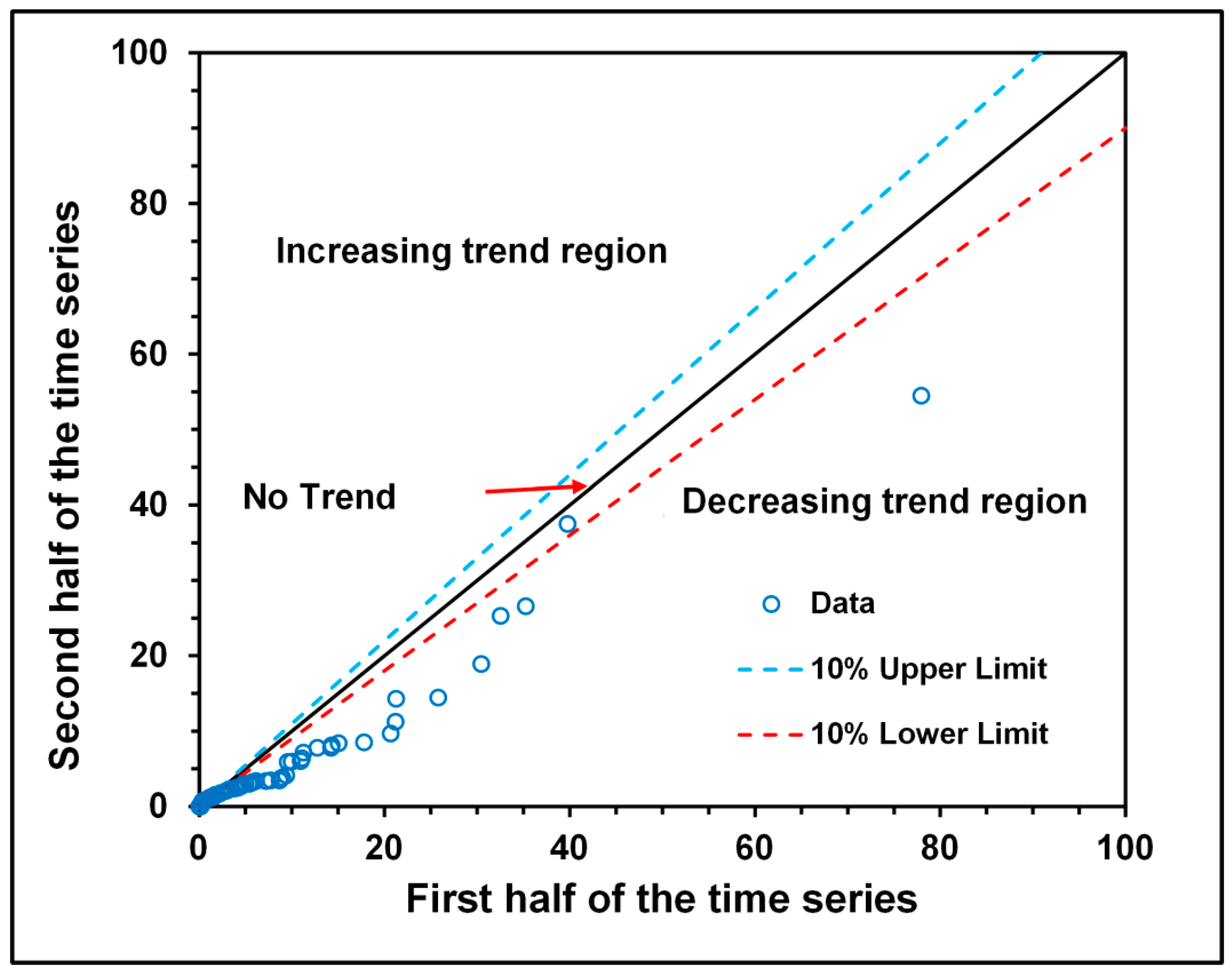
2.3.4. Innovative Trend Analysis (ITA) Method
2.3.5. Pettitt’s Test
3. Results and Discussion
3.1. Serial Autocorrelation Analysis
3.2. Rainfall Characteristics of the Mahi Basin
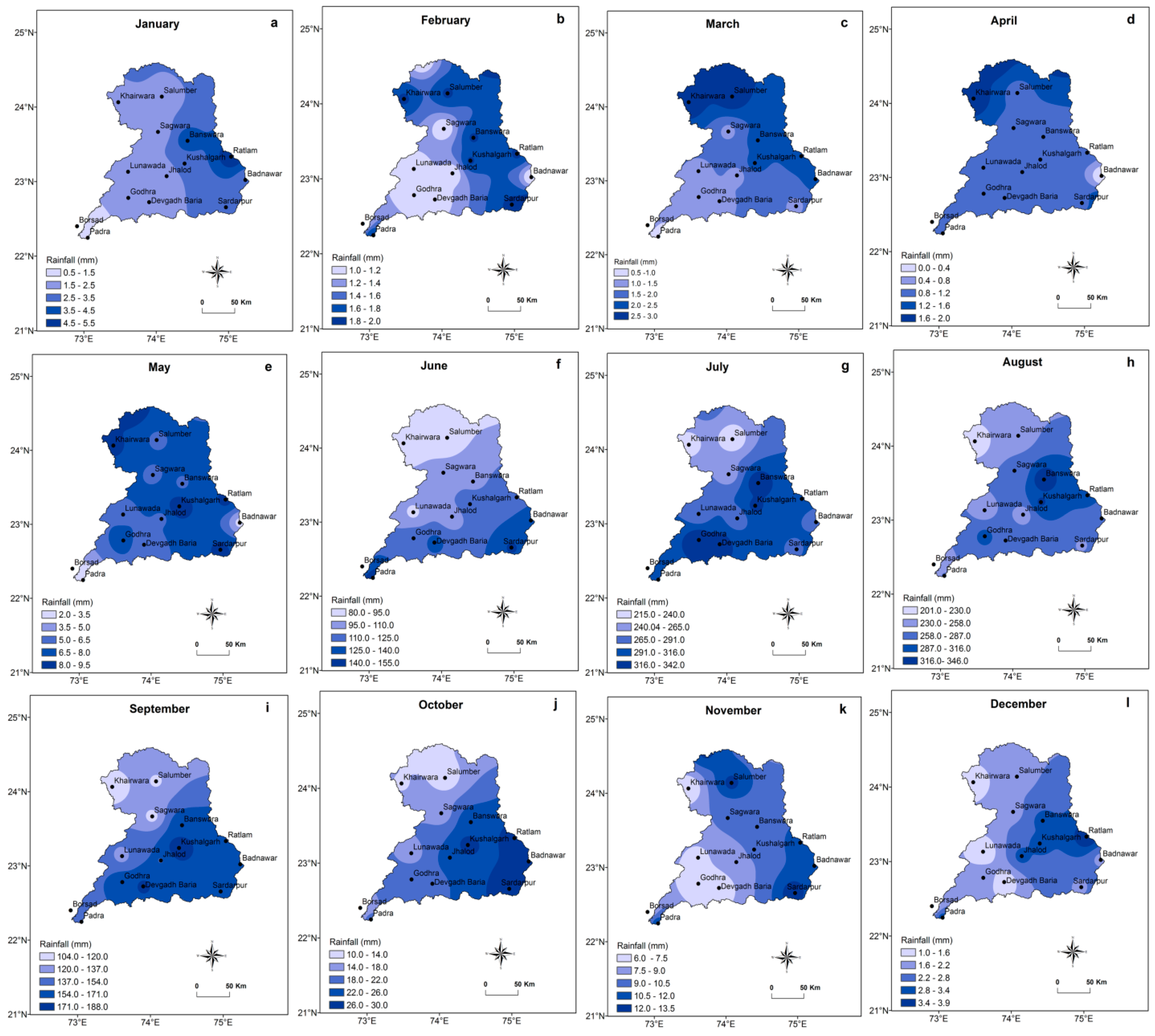
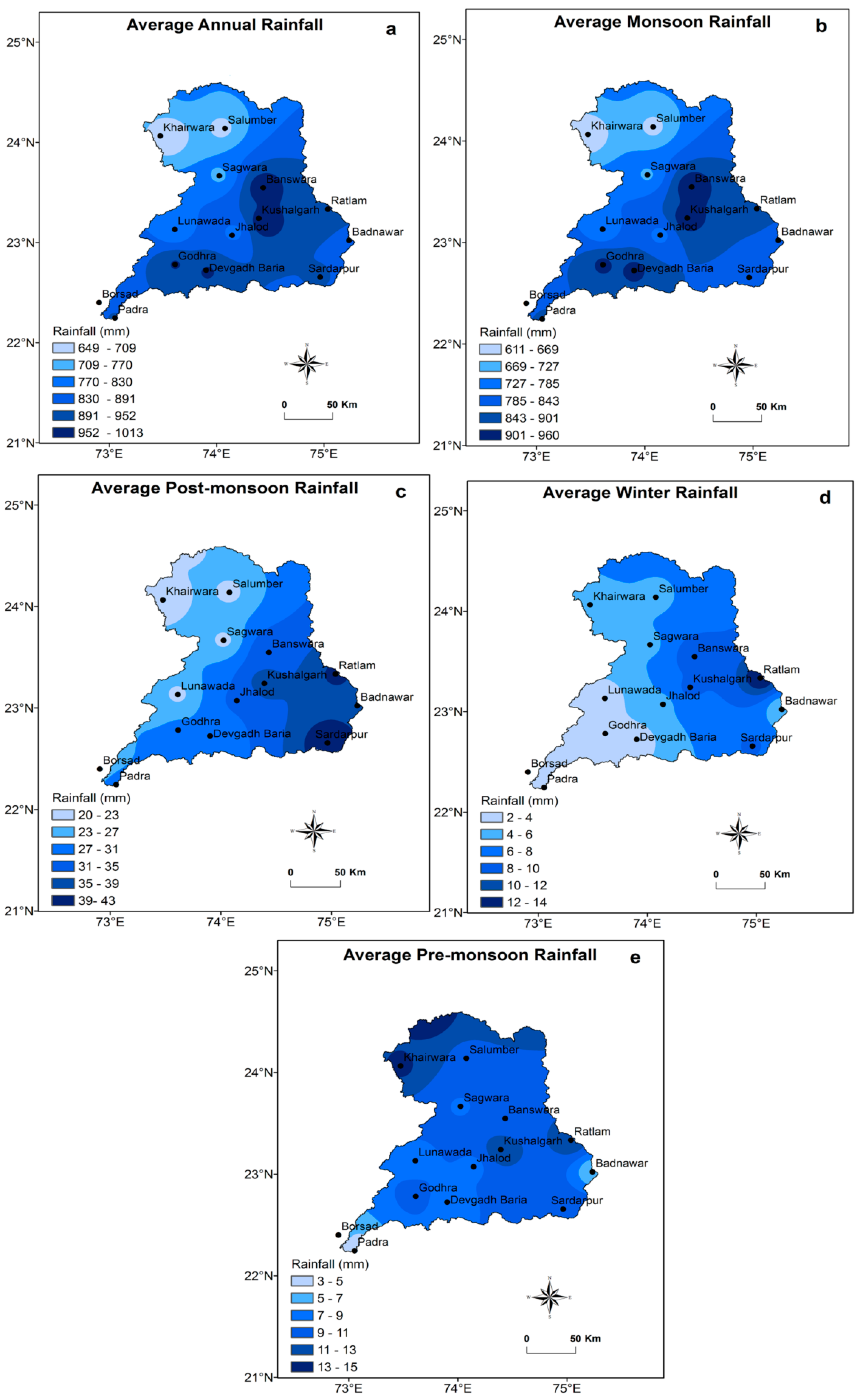
3.3. Rainfall Distribution (Annual and Seasonal) over the Mahi Basin
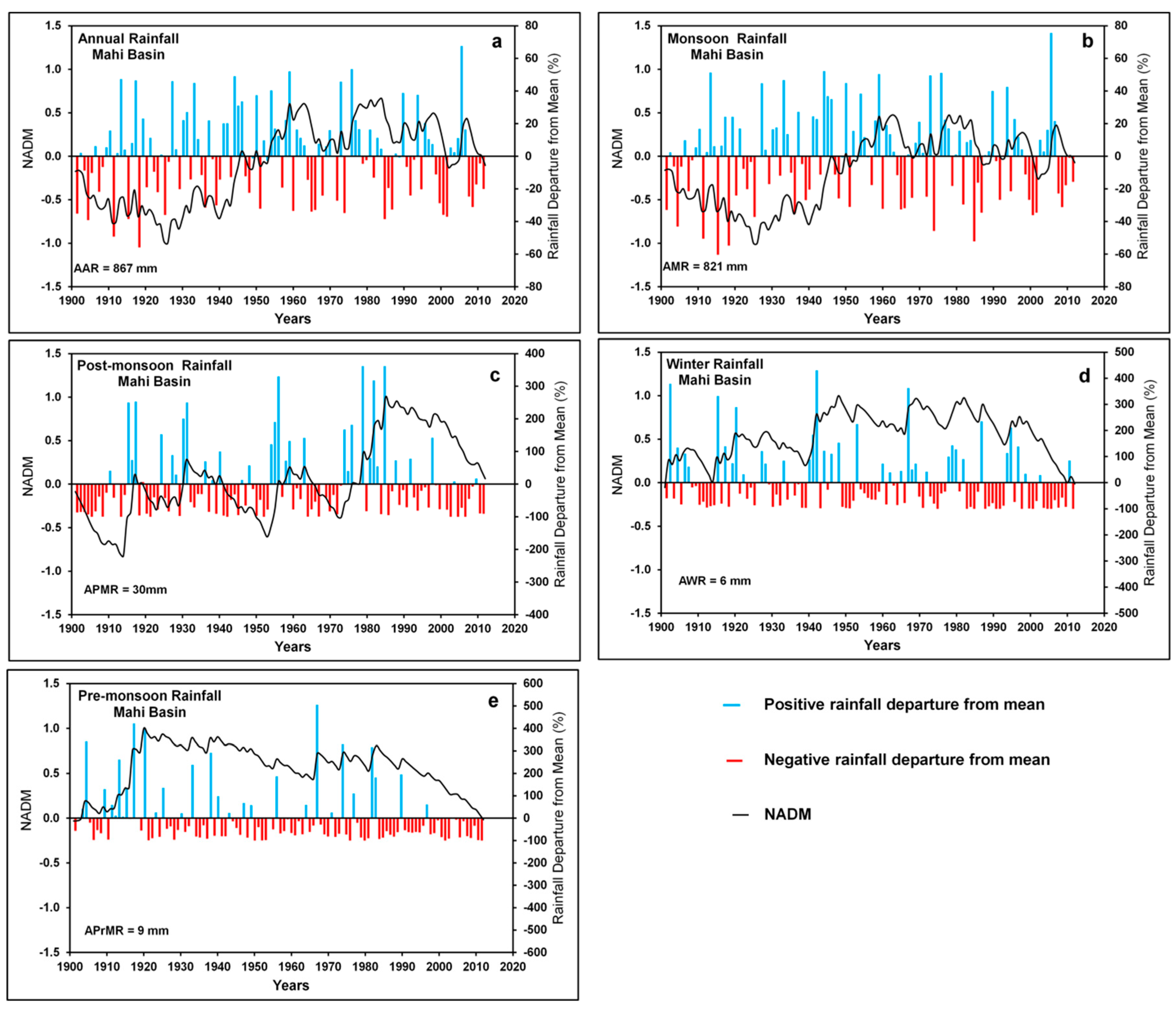
3.4. NADM and Rainfall Departure from the Mean
3.5. Rainfall Varaiation over the Mahi Basin
3.6. Rainfall Trend and Magnitude Change in the Mahi Basin
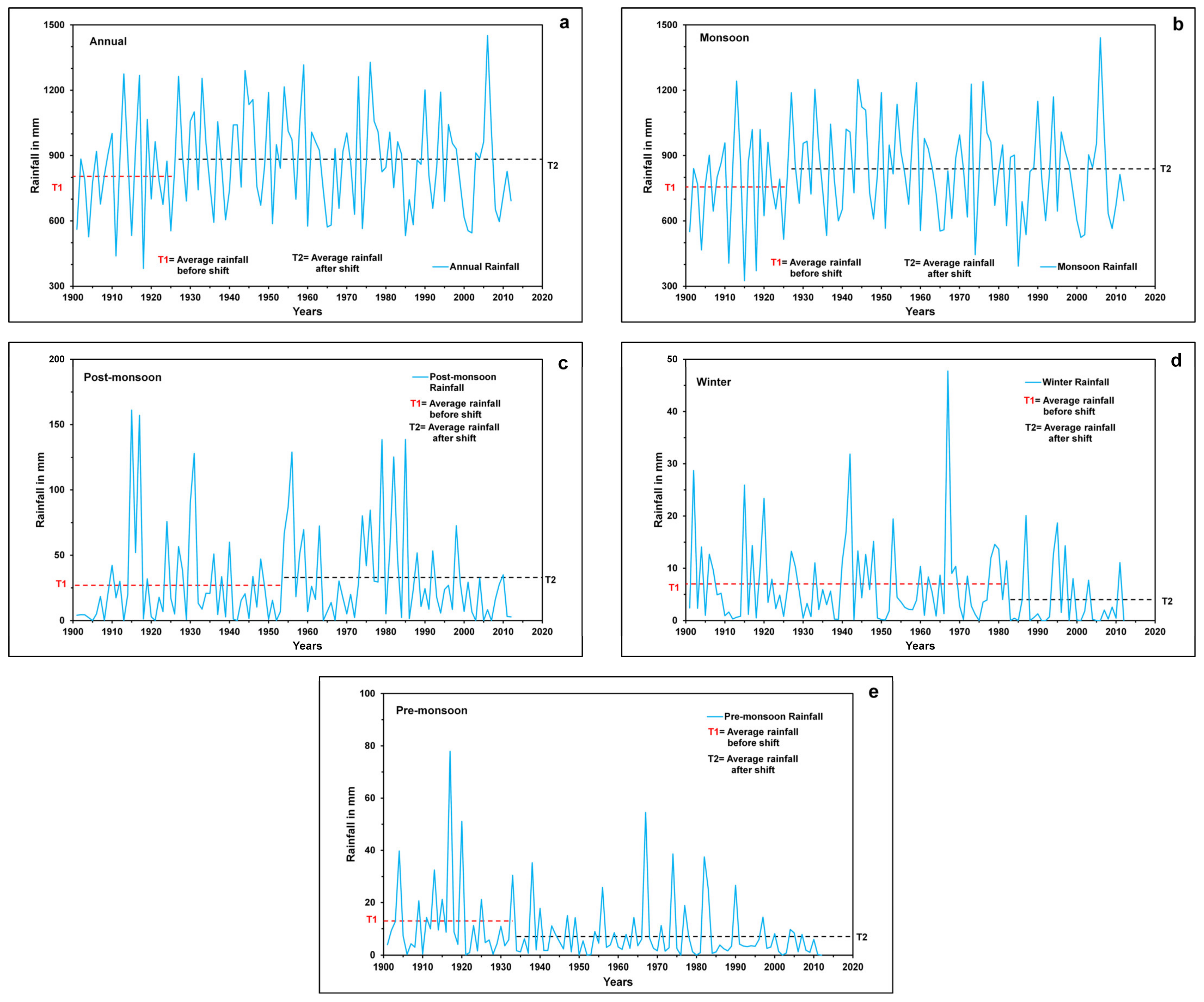
3.7. Analysis of Change-Point Detection Tests of Rainfall
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yue, S.; Wang, C. The Mann-Kendall Test Modified by Effective Sample Size to Detect Trend in Serially Correlated Hydrological Series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Hui-Mean, F.; Yusop, Z.; Yusof, F. Drought analysis and water resource availability using standardised precipitation evapotranspiration index. Atmos. Res. 2018, 201, 102–115. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. Detection of trend or change in annual flow of Australian rivers. Int. J. Climatol. 1993, 13, 643–653. [Google Scholar] [CrossRef]
- Yu, Y.S.; Zou, S.; Whittemore, D. Non-parametric trend analysis of water quality data of rivers in Kansas. J. Hydrol. 1993, 150, 61–80. [Google Scholar] [CrossRef]
- Haigh, M.J. Sustainable management of headwater resources: The Nairobi headwater declaration (2002) and beyond. Asian J. Water Environ. Pollut. 2004, 1, 17–28. [Google Scholar]
- Cannarozzo, M.; Noto, L.V.; Viola, F. Spatial distribution of rainfall trends in Sicily (1921–2000). Phys. Chem. Earth 2006, 31, 1201–1211. [Google Scholar] [CrossRef]
- Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.S.; Xavier, P.K. Increasing Trend of Extreme Rain Events over India in a Warming Environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Gulev, S.; Kollet, S. Changing structure of European precipitation: Longer wet periods leading to more abundant rainfalls. Geophys. Res. Lett. 2010, 37, 460–472. [Google Scholar] [CrossRef]
- Kyoung, M.; Kim, H.; Sivakumar, B.; Singh, V.; Ahn, K. Dynamic characteristics of monthly rainfall in the Korean Peninsula under climate change. Stoch. Environ. Res. Risk Assess. 2011, 25, 613–625. [Google Scholar] [CrossRef]
- World Meteorological Organisation. Detecting trend and other changes in hydrological data. In World Climate Program-Water; Kundzewicz, Z.W., Robson, A., Eds.; WMO/UNESCO, WCDMP-45, WMO/TD-No.1013; World Meteorological Organisation: Geneva, Switzerland, 2000. [Google Scholar]
- Karl, T.R.; Knight, R.W. Secular trends of precipitation amount, frequency, and intensity in the United States. Bull. Am. Meteorol. Soc. 1998, 79, 231–241. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Zin, W.Z.W.; Jamaludin, S.; Deni, S.M.; Jemain, A.A. Recent changes in extreme rainfall events in Peninsular Malaysia: 1971–2005. Theor. Appl. Climatol. 2010, 99, 303–314. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Beecham, S.; Metcalfe, A.V. Estimation of trends in rainfall extremes with mixed effects models. Atmos. Res. 2016, 168, 24–32. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Morais, B.S. Identification of precipitation zones within São Francisco River basin (Brazil) by global wavelet power spectra. Hydrol. Sci. J. 2013, 58, 789–796. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Y.; Wang, Y.; Wu, L.; Li, G.; Song, S. Spatial and temporal trends of reference crop evapotranspiration and its influential variables in Yangtze River Delta, eastern China. Theor. Appl. Climatol. 2016, 130, 945–958. [Google Scholar] [CrossRef]
- Dore, M.H.I. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef]
- Maidment, R.I.; Allan, R.P.; Black, E. Recent observed and simulated changes in precipitation over Africa. Geophys. Res. Lett. 2015, 42, 8155–8164. [Google Scholar] [CrossRef]
- Wang, B.; Bao, Q.; Hoskins, B.; Wu, G.; Liu, Y. Tibetan Plateau warming and precipitation changes in East Asia. Geophys. Res. Lett. 2008, 35, L14702. [Google Scholar] [CrossRef]
- Turner, A.G.; Annamalai, H. Climate change and the South Asian summer monsoon. Nat. Clim. Chang. 2012, 2, 587–595. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z.; Cui, B. Spatial and temporal variability of annual precipitation during 1961–2006 in Yellow River Basin, China. J. Hydrol. 2008, 361, 330–338. [Google Scholar] [CrossRef]
- Perera, A.; Mudannayake, S.D.; Azamathulla, H.M.; Rathnayake, U. Recent climatic trends in Trinidad and Tobago, West Indies. Asia-Pac. J. Sci. Technol. 2020, 25, 1–11. [Google Scholar]
- Thapliyal, V.; Kulshrestha, S.M. Climate changes and trends over India. Mausam 1991, 42, 333–338. [Google Scholar] [CrossRef]
- Ray, K.C.S.; Srivastava, A.K. Is there any change in extreme events like heavy rainfall? Curr. Sci. 2000, 79, 155–158. [Google Scholar]
- Sharma, K.P.; Vorosmarty, C.J.; Moore, I.B. Sensitivity of the Himalayan hydrology to landuse and climatic changes. Clim. Chang. 2000, 47, 117–139. [Google Scholar] [CrossRef]
- Bharath, A.; Maddamsetty, R.; Manjunatha, M.; Ramesh, T.V. Spatiotemporal Rainfall Variability and Trend Analysis of Shimsha River Basin, India. Environ. Sci. Pollut. Res. 2023, 1–20. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, V.; Thomas, T.; Arora, M. Changes in rainfall and relative humidity in different river basins in the north-west and central India. Hydrol. Process. 2008, 22, 2982–2992. [Google Scholar] [CrossRef]
- Mirza, M.Q.; Warrick, R.A.; Ericksen, N.J.; Kenny, G.J. Trends and persistence in precipitation in Ganges, Brahmaputra and Meghna River basins. Hydrol. Sci. J. 1998, 43, 845–858. [Google Scholar] [CrossRef]
- Kumar, V.; Jain, S.K. Trends in rainfall amount and number of rainy days in river basins of India (1951–2004). Hydrol. Res. 2011, 42, 290–306. [Google Scholar] [CrossRef]
- Pandey, B.K.; Khare, D. Identification of trend in long term precipitation and reference evapotranspiration over Narmada River basin (India). Glob. Planet. Chang. 2017, 161, 172–182. [Google Scholar] [CrossRef]
- Sharma, P.J.; Loliyana, V.D.; Resmi, S.R.; Timbadiya, P.V.; Patel, P.L. Spatiotemporal trends in extreme rainfall and temperature indices over Upper Tapi Basin, India. Theor. Appl. Climatol. 2018, 134, 1329–1354. [Google Scholar] [CrossRef]
- Hamilton, J.P.; Whitelaw, G.S.; Fenech, A. Mean annual temperature, and annual precipitation trends at Canadian biosphere reserves. Environ. Monit. Assess. 2001, 67, 239–275. [Google Scholar] [CrossRef] [PubMed]
- Dinpashoh, Y.; Mirabbasi, R.; Jhajharia, D.; Abianeh, H.Z.; Mostafaeipour, A. Effect of short-term and long-term persistence on identification of temporal trends. J. Hydrol. Eng. 2014, 19, 617–625. [Google Scholar] [CrossRef]
- Burn, D.H. Hydrologic effects of climatic change in west-central Canada. J. Hydrol. 1994, 160, 53–70. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Wood, E.F.; Wallis, J.R. Hydro-climatological trends in the continental United States, 1948–1988. J. Clim. 1994, 7, 586–607. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Hire, P.S. Geomorphic and Hydrologic Studies of Floods in the Tapi Basin. Ph.D. Thesis, University of Pune, Pune, India, 2000. [Google Scholar]
- Miller, W.P.; Piechota, T.C. Regional analysis of trend and step changes observed in hydroclimatic variables around the Colorado River Basin. J. Hydrometeorol. 2008, 9, 1020–1034. [Google Scholar] [CrossRef]
- Ngongondo, C.; Xu, C.Y.; Gottschalk, L.; Alemaw, B.F. Evaluation of spatial and temporal characteristics of rainfall in Malawi: A case of data scarce region. Theor. Appl. Climatol. 2011, 106, 79–93. [Google Scholar] [CrossRef]
- Barua, S.; Muttil, N.; Ng, A.W.M.; Perera, B.J.C. Rainfall trend and its implications for water resource management within the Yarra River catchment, Australia. Hydrol. Process. 2013, 27, 1727–1738. [Google Scholar] [CrossRef]
- Taxak, A.K.; Murumkar, A.R.; Arya, D.S. Long term spatial and temporal rainfall trends and homogeneity analysis in Wainganga basin, Central India. Weather Clim. Extrem. 2014, 4, 50–61. [Google Scholar] [CrossRef]
- Prakash, S.; Sathiyamoorthy, V.; Mahesh, C.; Gairola, R.M. An evaluation of high-resolution multi-satellite rainfall products over the Indian monsoon region. Int. J. Remote Sens. 2014, 35, 3018–3035. [Google Scholar] [CrossRef]
- Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalayan region. J. Geophys. Res. Atmos. 2015, 120, 12458–12473. [Google Scholar] [CrossRef]
- Hire, P.S.; Patil, A.D. Detection of variations in the annual rainfall of the Par Basin using non-parametric Mann-Kendall test. Curr. Glob. Rev. 2018, 1, 103–106. [Google Scholar]
- Malik, A.; Kumar, A.; Guhathakurta, P.; Kisi, O. Spatial-temporal trend analysis of seasonal and annual rainfall (1966–2015) using innovative trend analysis method with significance test. Arab. J. Geosci. 2019, 12, 328. [Google Scholar] [CrossRef]
- Pawar, U.; Rathnayake, U. Spatiotemporal rainfall variability and trend analysis over Mahaweli Basin, Sri Lanka. Arab. J. Geosci. 2022, 15, 370. [Google Scholar] [CrossRef]
- Pawar, U. Rainfall distribution and trends over the semi-arid Marathwada region of Maharashtra, India. Arab. J. Geosci. 2022, 15, 1738. [Google Scholar] [CrossRef]
- Kamal, N.; Pachauri, S. Mann-Kendall Test—A Novel Approach for Statistical Trend Analysis. IJCTT 2018, 63, 18–21. [Google Scholar] [CrossRef]
- Davey, C.A.; Sr Pielke, R.A. Microclimate exposures of surface-based weather stations: Implications for the assessment of long-term temperature trends. Bull. Am. Meteorol. Soc. 2005, 86, 497–504. [Google Scholar]
- Maity, R.; Kumar, D.N.; Nanjundiah, R.S. Review of hydroclimatic teleconnection between hydrologic variables and large-scale atmospheric circulation patterns with Indian perspective. ISH J. Hydraul. Eng. 2007, 13, 77–92. [Google Scholar] [CrossRef]
- Varikoden, H.; Revadekar, J.V.; Kuttippurath, J.; Babu, C.A. Contrasting trends in southwest monsoon rainfall over the Western Ghats region of India. Clim. Dyn. 2019, 52, 4557–4566. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Spatio-temporal trend analysis of rainfall using parametric and non-parametric tests: Case study in Uttarakhand, India. Theor. Appl. Climatol. 2020, 140, 183–207. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Sreekesh, S.; King, A. Characteristics of extreme rainfall in different gridded datasets over India during 1983–2015. Atmos. Res. 2022, 267, 105930. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; Muthiah, K.; Sridhar, V. Long-Term homogeneity, trend, and change point analysis of rainfall in the arid district of ananthapuramu, Andhra Pradesh State, India. Water 2020, 12, 211. [Google Scholar] [CrossRef]
- Singh, R.; Sah, S.; Das, B.; Vishnoi, L.; Pathak, H. Spatio-temporal trends and variability of rainfall in Maharashtra, India: Analysis of 118 years. Theor. Appl. Climatol. 2021, 143, 883–900. [Google Scholar] [CrossRef]
- Pawar, U.; Hire, P.; Sarukkalige, R.; Rathnayake, U. Hydro-Meteorological Characteristics of the 1973 Catastrophic Flood in the Mahi Basin, India. Water 2023, 15, 1648. [Google Scholar] [CrossRef]
- Zampieri, M.; Ceglar, A.; Dentener, F.; Toreti, A. Wheat yield loss attributable to heat waves, drought and water excess at the global, national and subnational scales. Environ. Res. Lett. 2017, 12, 64008. [Google Scholar] [CrossRef]
- Pawar, U.V.; Hire, P.S. Long term fluctuations and global teleconnections in the monsoonal rainfall and associated floods of the Mahi Basin: Western India. Int. J. Sci. Res. Sci. Technol. 2018, 5, 237–242. [Google Scholar]
- Sharma, A.; Sharma, D.; Panda, S.K. Assessment of spatiotemporal trend of precipitation indices and meteorological drought characteristics in the Mahi River basin, India. J. Hydrol. 2022, 605, 127314. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Method, 4th ed.; Charles Griffin: London, UK, 1975; p. 202. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Şen, Z. Innovative trend analysis methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z. Innovative trend significance test and applications. Theor. Appl. Climatol. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- O’Brien, N.L.; Burn, D.H.; Annable, W.K.; Thompson, P.J. Trend detection in the presence of positive and negative serial correlation: A comparison of block maxima and peaks-over-threshold data. Water Resour. Res. 2021, 57, e2020WR028886. [Google Scholar] [CrossRef]
- Storch, V.; Navarra, A. Analysis of Climate Variability: Applications of Statistical Techniques; Springer: Berlin, Germany, 1995; pp. 1–26. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the Power of the Mann-Kendall Test for Detecting Monotonic Trends in Hydrometeorological Time Series. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. The importance of pre-whitening in change point analysis under persistence. Stoch. Env. Res. Risk Assess. 2016, 30, 763–777. [Google Scholar] [CrossRef]
- Parthasarathy, B.; Munot, A.A.; Kothawale, D.R. All-India monthly and seasonal rainfall series 1871–1993. Theor. Appl. Climatol. 1994, 49, 217–224. [Google Scholar] [CrossRef]
- Dimri, A.P.; Mohanty, U.C. Simulation of mesoscale features associated with intense western disturbances over western Himalayas. Meteorol. Appl. 2009, 16, 289–308. [Google Scholar] [CrossRef]
- Pawar, U.V. An Analytical Study of Geomorphological, Hydrological, and Meteorological Characteristics of Floods in the Mahi River Basin: Western India. Ph.D. Thesis, Tilak Maharashtra Vidyapeeth, Pune, India, 2019. [Google Scholar]
- Riehl, H.; El-Bakry, M.; Meitin, J. Nile River discharge. Mon. Weather Rev. 1979, 107, 1546–1553. [Google Scholar] [CrossRef]
- Mooley, D.A.; Parthasarthy, B. Fluctuation of all-India summer monsoon rainfall during 1871–1978. Clim. Chang. 1984, 6, 287–301. [Google Scholar] [CrossRef]
- Probst, J.I.; Tardy, Y. Long range stream flow and world continental runoff fluctuations since the beginning of this century. J. Hydrol. 1987, 94, 289–311. [Google Scholar] [CrossRef]
- Kale, V.S. Long-period fluctuations in Monsoon floods in the Deccan Peninsula, India. J. Geol. Soc. India 1999, 53, 5–15. [Google Scholar]
- Patil, A.D.; Hire, P.S. Flood hydrometeorological situations associated with monsoon floods on the Par River in western India. Mausam 2020, 71, 687–698. [Google Scholar]
- Joseph, P.V. Climate change in monsoon and cyclones. In Proceedings of the IIYTM Symposium on Monsoons, Pune, India, 8–10 September 1976; pp. 378–387. [Google Scholar]
- Joseph, P.V. Sub-tropical westerlies in relation to large scale failure of Indian monsoon. Indian J. Meteorol. Hydrol. Geophys. 1978, 29, 412–418. [Google Scholar] [CrossRef]
- Kripalani, R.H.; Kulkarni, A.; Sabade, S.S. Indian Monsoon variability in a global warming scenario. Nat. Hazards 2003, 29, 189–206. [Google Scholar] [CrossRef]
- Gadgil, S.; Rajeevan, M.; Francis, P.A. Monsoon variability: Links to major oscillations over the equatorial Pacific and Indian Ocean. Curr. Sci. 2007, 93, 182–194. [Google Scholar]
- Jhajharia, D.; Yadav, B.K.; Maske, S.; Chattopadhyay, S.; Kar, A.K. Identification of trends in rainfall, rainy days and 24 h maximum rainfall over subtropical Assam in Northeast India. C. R. Geosci. 2012, 344, 1–13. [Google Scholar] [CrossRef]
- Guhathakurta, P.; Saji, E. Detecting changes in rainfall pattern and seasonality index vis-à-vis increasing water scarcity in Maharashtra. J. Earth Syst. Sci. 2013, 122, 639–649. [Google Scholar] [CrossRef]
- Das, M.R.; Mukhopadhyay, R.K.; Dandekar, M.M.; Kshirsagar, S.R. Pre-monsoon western disturbances in relation to monsoon rainfall, its advancement over NW India and their trends. Curr. Sci. 2002, 82, 1320–1321. [Google Scholar]
- Shekhar, M.S.; Chand, H.; Kumar, S.; Srinivasan, K.; Ganju, A. Climate-change studies in the western Himalaya. Ann. Glaciol. 2010, 51, 105–112. [Google Scholar] [CrossRef]
- Serinaldi, F.; Chebana, F.; Kilsby, C.G. Dissecting innovative trend analysis. Stoch. Environ. Res. Risk Assess. 2020, 34, 733–754. [Google Scholar] [CrossRef]







| Time | Rainfall (mm) | SD (mm) | Cv (%) | Contribution to Annual Rainfall (%) |
|---|---|---|---|---|
| January | 2.4 | 1.2 | 51.3 | 0.3 |
| February | 1.4 | 0.8 | 56.1 | 0.2 |
| March | 1.6 | 0.7 | 41.1 | 0.2 |
| April | 1.1 | 0.4 | 38.0 | 0.1 |
| May | 5.9 | 2.2 | 37.5 | 0.7 |
| June | 111.7 | 21.2 | 19.0 | 12.9 |
| July | 288.7 | 40.9 | 14.2 | 33.3 |
| August | 267.4 | 38.1 | 14.3 | 30.8 |
| September | 150.6 | 24.9 | 16.6 | 17.4 |
| October | 21.7 | 6.4 | 29.3 | 2.5 |
| November | 8.9 | 2.3 | 25.3 | 1.0 |
| December | 2.3 | 1.0 | 43.3 | 0.3 |
| Monsoon | 821.0 | 220.4 | 26.8 | 94.8 |
| Post-monsoon | 30.3 | 36.2 | 119.6 | 3.5 |
| Winter | 6.1 | 7.8 | 127.2 | 0.7 |
| Pre-monsoon | 9.0 | 12.6 | 142.1 | 1.0 |
| Annual | 867.0 | 221.4 | 25.5 |
| Stations/Basin | AAR | Monsoon | Post-Monsoon | Winter | Pre-Monsoon | Monsoon | Non-Monsoon |
|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (mm) | % | % | |
| Badnawar | 878.0 | 829.1 | 39.2 | 5.0 | 4.7 | 94.4 | 5.6 |
| Banswara | 1012.8 | 959.6 | 35.2 | 9.1 | 8.9 | 94.7 | 5.3 |
| Borsad | 823.9 | 791.8 | 23.6 | 2.9 | 5.6 | 96.1 | 3.9 |
| Devgadh Baria | 959.0 | 919.5 | 28.2 | 3.7 | 7.5 | 95.9 | 4.1 |
| Godhra | 956.8 | 914.9 | 28.4 | 4.2 | 9.3 | 95.6 | 4.4 |
| Jhalod | 813.8 | 767.6 | 31.8 | 6.4 | 8.0 | 94.3 | 5.7 |
| Khairwara | 649.0 | 610.7 | 20.3 | 5.2 | 12.9 | 94.1 | 5.9 |
| Kushalgarh | 1010.9 | 953.0 | 38.1 | 7.6 | 12.2 | 94.3 | 5.7 |
| Lunawada | 769.8 | 735.4 | 22.7 | 3.9 | 7.9 | 95.5 | 4.5 |
| Padra | 906.5 | 869.2 | 30.4 | 4.1 | 2.8 | 95.8 | 4.2 |
| Ratlam | 943.4 | 879.2 | 39.9 | 12.2 | 12.1 | 93.2 | 6.8 |
| Sagwara | 759.8 | 720.3 | 25.4 | 5.8 | 8.3 | 94.8 | 5.2 |
| Salumber | 691.3 | 652.2 | 22.8 | 6.4 | 10.0 | 94.3 | 5.7 |
| Sardarpur | 904.4 | 842.7 | 43.4 | 7.8 | 10.5 | 93.2 | 6.8 |
| Mahi Basin | 867.0 | 821.0 | 30.3 | 6.1 | 9.0 | 94.8 | 5.2 |
| SN | Stations | Annual | Monsoon | Post-Monsoon | Winter | Pre-Monsoon | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MK z | SS mm/y | MK z | SS mm/y | MK z | SS mm/y | MK z | SS mm/y | MK z | SS mm/y | ||
| 1 | Badnawar | 1.24 | 1.52 | 1.11 | 1.50 | −0.54 | 0.00 | −0.83 | 0.00 | −2.74 | 0.00 |
| 2 | Banswara | 1.68 | 1.77 | 1.34 | 1.6 | 0.61 | 0.00 | −2.10 | 0.00 | −1.54 | 0.00 |
| 3 | Borsad | −0.45 | −0.67 | −0.68 | −0.58 | −0.86 | 0.00 | −3.59 | 0.00 | −3.60 | 0.00 |
| 4 | D. Baria | −1.65 | −1.63 | −1.22 | −1.37 | −0.41 | 0.00 | −4.22 | 0.00 | −4.65 | 0.00 |
| 5 | Godhra | −1.71 | −1.92 | −1.71 | −1.89 | 0.49 | 0.09 | −4.46 | 0.00 | −3.43 | 0.00 |
| 6 | Jhalod | −0.47 | −0.33 | −0.13 | −0.13 | −0.45 | 0.00 | −4.45 | 0.00 | −4.94 | 0.00 |
| 7 | Khairwara | −1.78 | −1.25 | −1.37 | −1.07 | −0.07 | 0.00 | −4.17 | 0.00 | −2.30 | 0.00 |
| 8 | Kushalgarh | 0.5 | 55 | 0.27 | 0.33 | 1.39 | 0.14 | −1.01 | 0.00 | −0.18 | 0.00 |
| 9 | Lunawada | 0.45 | 0.38 | 0.33 | 0.28 | 1.09 | 0.04 | −2.97 | 0.00 | −2.78 | 0.00 |
| 10 | Padra | −1.88 | −6.11 | −1.64 | −5.04 | −1.13 | −0.25 | −0.58 | 0.00 | −1.99 | 0.00 |
| 11 | Ratlam | 1.88 | 1.83 | 1.86 | 1.56 | 1.31 | 0.01 | −2.34 | −0.01 | −1.61 | −0.05 |
| 12 | Sagwara | 1.75 | 1.41 | 1.68 | 1.50 | 0.10 | 0.00 | −1.72 | 0.0 | −1.49 | 0.00 |
| 13 | Salumber | 0.53 | 0.36 | 0.94 | 1.16 | −0.08 | 0.27 | 0.54 | 0.03 | 0.20 | 0.00 |
| 14 | Sardarpur | 0.06 | 0.07 | 0.20 | 0.25 | −0.26 | 0.00 | −1.25 | 0.00 | −1.93 | 0.00 |
| 15 | Mahi Basin | −0.23 | −0.14 | 0.02 | 0.01 | 0.90 | 0.03 | −2.44 | −0.02 | −2.48 | −0.04 |
| Stations/Basin | Annual Rainfall | Monsoon Rainfall | Post-Monsoon Rainfall | Winter Rainfall | Pre-Monsoon Rainfall | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Shift | Year | Shift | Year | Shift | Year | Shift | Year | Shift | Year | |
| Badnawar | Yes | 1957 | Yes | 1957 | Yes | 1953 | Yes | 1957 | Yes | 1938 |
| Banswara | Yes | 1940 | Yes | 1940 | Yes | 1972 | Yes | 1982 | Yes | 1943 |
| Borsad | Yes | 1959 | Yes | 1959 | Yes | 1985 | Yes | 1948 | Yes | 1959 |
| D. Baria | Yes | 1962 | Yes | 1962 | Yes | 1963 | Yes | 1955 | Yes | 1947 |
| Godhra | Yes | 1959 | Yes | 1959 | Yes | 1926 | Yes | 1942 | Yes | 1957 |
| Jhalod | Yes | 1984 | Yes | 1984 | Yes | 1988 | Yes | 1968 | Yes | 1967 |
| Khairwara | Yes | 1963 | Yes | 1963 | Yes | 1973 | Yes | 1948 | Yes | 1933 |
| Kushalgarh | Yes | 1926 | Yes | 1926 | Yes | 1953 | Yes | 1997 | Yes | 1916 |
| Lunawada | Yes | 1940 | Yes | 1940 | Yes | 1953 | Yes | 1944 | Yes | 1947 |
| Padra | Yes | 1929 | Yes | 1929 | Yes | 1931 | Yes | 1943 | Yes | 1928 |
| Ratlam | Yes | 1932 | Yes | 1932 | Yes | 1954 | Yes | 1967 | Yes | 1962 |
| Sagwara | Yes | 1964 | Yes | 1978 | Yes | 1964 | Yes | 1974 | Yes | 1936 |
| Salumber | Yes | 1946 | Yes | 1946 | Yes | 1917 | Yes | 1922 | Yes | 1918 |
| Sardarpur | Yes | 1978 | Yes | 1978 | Yes | 1903 | Yes | 1963 | Yes | 1962 |
| Mahi Basin | Yes | 1926 | Yes | 1926 | Yes | 1953 | Yes | 1982 | Yes | 1933 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawar, U.; Hire, P.; Gunathilake, M.B.; Rathnayake, U. Spatiotemporal Rainfall Variability and Trends over the Mahi Basin, India. Climate 2023, 11, 163. https://doi.org/10.3390/cli11080163
Pawar U, Hire P, Gunathilake MB, Rathnayake U. Spatiotemporal Rainfall Variability and Trends over the Mahi Basin, India. Climate. 2023; 11(8):163. https://doi.org/10.3390/cli11080163
Chicago/Turabian StylePawar, Uttam, Pramodkumar Hire, Miyuru B. Gunathilake, and Upaka Rathnayake. 2023. "Spatiotemporal Rainfall Variability and Trends over the Mahi Basin, India" Climate 11, no. 8: 163. https://doi.org/10.3390/cli11080163
APA StylePawar, U., Hire, P., Gunathilake, M. B., & Rathnayake, U. (2023). Spatiotemporal Rainfall Variability and Trends over the Mahi Basin, India. Climate, 11(8), 163. https://doi.org/10.3390/cli11080163








