Abstract
The climate variability associated with the ENSO phenomenon has a significant impact on wetlands, affecting the total precipitation input and hydrological flows of these ecosystems. The objective of this paper is to study the trophic status variation of an urban tropical wetland under ENSO conditions, through dynamic modeling. The results suggest an increase in precipitation, by 3.32 times, during the La Niña phase compared to the El Niño phase. Wetland input total phosphorus (TP) concentrations are 1.85 times lower during La Niña. This is probably due to a dilution effect exerted by the increase in surface runoff volumes from the basin. The findings suggest a reduction in wetland hydraulic retention time (HRT) during La Niña (1.33 times) compared to El Niño. This trend causes the TP concentration inside the wetland to decrease, possibly due to an increase in the water volume stored (dilution), and by the exit of this nutrient due to a shorter hydraulic renewal (HRT/La Niña < HRT/El Niño). The occurrence of a high input of TP concentration to the wetland does not necessarily indicate a high trophic status index (TSI). This is because the trophic status of the wetland is possibly more associated with HRT rather than input TP concentration. The trophic status of the wetland during the La Niña tends to be eutrophic. Lastly, under ENSO scenarios, the use of Aizaki’s method is suggested, because it considers HRT as a decisive factor for the calculation of wetland trophic status.
1. Introduction
Urban wetlands are biologically productive systems, characterized by a high diversity [1]. By co-existing with human populations, they provide a variety of ecosystem services such as flood mitigation, aquifer supply, regulation of biogeochemical cycles, maintenance of resident and migratory species of flora and fauna, carbon sequestration, and perform recreational and educational and scientific research functions [2,3]. However, various sectors of the economy in developing countries continue to consider urban wetlands unproductive and replaceable by other land uses that generate greater economic benefits. For example, they have been dried by dumping waste, for use as urban development areas [4,5]. The nutrient and sediment transport to aquatic ecosystems increases with the urbanization of watersheds, which is associated with increased impermeable surface coverage [6]. This has caused accelerated rates of deterioration and disappearance of these valuable ecosystems in megacities [7,8].
There are different methods for assessing and classifying trophic status in lentic systems [2]. However, studies on these ecosystems report that the trophic status varies depending on the parameters and classification methods used, and the sampling site location within the ecosystem [9,10]. The trophic status index (TSI) provides information on the nutrient flow regime responsible for the proliferation of primary producers, that reflects the ecological functioning of an aquatic ecosystem [11]. While measuring the eutrophication magnitude, it also suggests the status of biological integrity and human interference [12]. The trophic status classification system was initially developed for temperate environments (e.g., [13,14]). Carlson developed a two-dimensional graphical approach to assess the trophic status of a lake, based on previous calculations of TSI [15]. Freshwater bodies were classified into four potential trophic status (oligotrophic, mesotrophic, eutrophic, and hypereutrophic) according to chlorophyll-a (Chl-a), total phosphorus (TP), and Secchi disk depth [16]. Subsequently, Aizaki et al. [17] evaluated the relationships between TSI values and parameters related to the trophic status of the lake, by examining the possibility of applying Carlson’s index to the lakes of Japan. Vollenweider et al. [18] proposed a new trophic index (TRIX) to categorize the trophic status of inland waters, by focusing on Chl-a, mineral and total nitrogen and phosphorus, and oxygen saturation. Lastly, the most accepted limits for assessing trophic status are those suggested by the Organization for Economic Cooperation and Development—OECD [10].
The relationships between urban ecosystems, people, economy, and government often make them highly complex dynamic systems [19]. Thus, a holistic vision (environmental, social, economic, political, and cultural) must be taken, to collect the information required in the field and to develop dynamic models through specialized programs that simulate the conditions of the ecosystems under study. According to Jiménez et al. [20], to manage the quality and expand the water regulation capacity of a wetland, in order to reduce its eutrophication, it is necessary to use computer-modeling tools that allow one to know and have a certain control over this aquatic ecosystem. For example, Güneralp and Barlas [19] developed a dynamic model of a shallow freshwater lake in Turkey, to study its ecological and economic sustainability. Spieles and Mitsch [21] developed a model of macroinvertebrate trophic structure, detrital cycling, and dissolved oxygen dynamics in shallow freshwater wetlands with variable allochthone subsidies, in Ohio (USA). Ahlgren et al. [22] reported that dynamical theoretical models are better suited for predicting perturbation response rates than empirical steady-state models. This, under the context of the trophic status in lakes and the external load of total phosphorus (TP). Lastly, Beltrán and Rangel [23] also formulated a dynamic ecological simulation model applied to an urban wetland, which included the following four sub-models: hydrological, TP, sedimentation, and phytoplanktonic primary production.
The cycle known as El Niño and La Niña–Southern Oscillation (ENSO), is the cause of the greatest signal of climate variability in the tropical strip of the Pacific Ocean, recurring on an interannual scale. El Niño and its opposite phase (La Niña), are the oceanic components of ENSO, and correspond, in general terms, to the appearance from time to time of relatively warmer (El Niño) or colder (La Niña) surface waters than normal in the central and eastern tropical Pacific [24,25]. The climate variability associated with the ENSO phenomenon has a significant impact on wetlands, affecting the total precipitation and hydrological flows of these ecosystems. Indeed, this generates year-on-year variations in freshwater discharges to wetlands [26]. The trophic status of wetlands may be influenced by this climate oscillation (ENSO), which is associated with periods of increase and decrease in freshwater discharges from drainage basins and surrounding sectors [27]. Brugnoli et al. [28] reported significant differences in the flow of a large estuary in the south of South America (Río de la Plata), between the phases of the ENSO phenomenon. When increasing the flow rate (El Niño phase), negative correlations with Secchi depth and positive correlations with total nutrients were observed. García-Rodríguez et al. [29] reported that warm-phase ENSO (La Niña) events increased the trophic status of sediments in a large estuary in southern South America, which generated episodes of eutrophication. In the literature, there is evidence of the scarcity of studies that analyze the influence of the ENSO phenomenon on urban wetlands in tropical areas (north of South America), and this, in part, also motivated the development of this research.
The objective of this paper is to study the trophic status variation of the Torca wetland (Bogota, Colombia) under ENSO phenomenon conditions, through dynamic modeling. The behavior of the input TP load and variation in TSI of this tropical wetland are analyzed. A dynamic simulation model is also developed, which is validated by a multivariate sensitivity analysis. The study covers the period 2001–2011, in which periods of occurrence of the El Niño and La Niña phases (ENSO) are observed. This paper is relevant in the context of urban wetland management for the following aspects: (i) the analysis of trophic status through dynamic modeling can provide a useful tool for its management and restoration. (ii) Delineating the interrelationship between the trophic status of the tropical wetland and El Niño and La Niña phases of the ENSO phenomenon.
2. Materials and Methods
2.1. Study Site
The Torca wetland is located in the middle of the localities of Suba and Usaquén, belonging to the megacity of Bogotá, Colombia (4°47′05″ N–74°02′23″ W), to the north of South America. The study ecosystem is located on the side of the North Highway with 220th Street (Figure 1). The wetland is shallow (<1.5 m) and high mountain (2553 masl). The wetland has an area of 0.90 ha and is supplied by the Aguas Calientes, Patiño, and San Juan streams. These three streams constitute the main inputs of water and pollution (point sources) to the wetland. The Torca wetland also enables ecological connectivity with the Guaymaral wetland. In addition, because it is located in the Sábana geological formation (layers of sand on the surface), it has a great hydrogeological value, as it is part of primary porosity aquifers and it has become a habitat for aerial fauna in danger of extinction [30]. The urban wetland under study currently faces problems associated with its fragmentation, which has reduced the water body size and its water depth. A significant percentage of wetland area was filled with solid waste, and dried for urban expansion processes and agricultural activities [31]. The sediment and nutrient transport from the watershed and exposed surfaces near the wetland also generated clogging and eutrophication processes. This further decreased its water storage capacity. The wetland also receives a significant volume of urban wastewater [31]. All of the above characteristics are why this urban wetland was selected for our study.
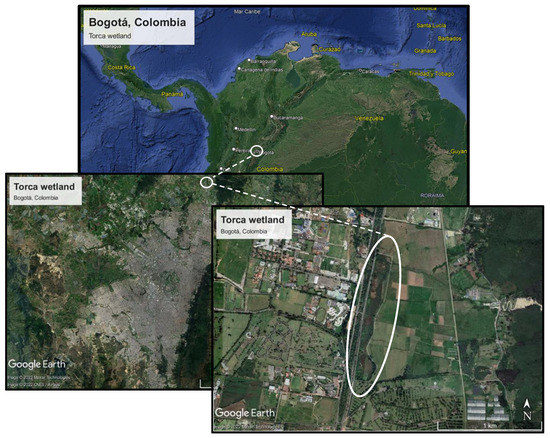
Figure 1.
Location of the tropical wetland under study, in the megacity of Bogotá, Colombia (Google Earth Pro, 2011).
2.2. Dynamic Modeling
The trend in the classification of trophic status was based on the limiting factor, and in most cases, the limiting factor was phosphorus [32]. Phosphorus-rich particles tended to settle at the bottom of the wetland and became a nutrient reserve, which was accessed by aquatic macrophytes. These discharged phosphorus from the sediments to the upper water column, where it was used by phytoplankton, accelerating hypoxia conditions [33]. In addition, the phenomenon of sediment resuspension in the wetland probably removed the phosphorus that was deposited at the bottom, returning it to the water column. This complex interaction between variables that intervened in the eutrophication phenomenon, made it impossible to establish strict limitations between trophic categories and factors that explained them [34]. Thus, in this study, it was assumed that phosphorus was the limiting factor of eutrophication, rather than nitrogen. The Forrester diagram designed for the development of the dynamic wetland trophic status model is shown in Figure 2.
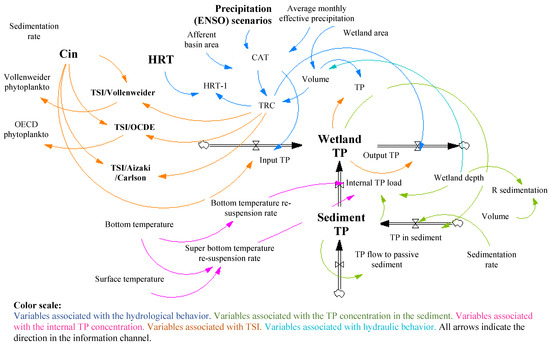
Figure 2.
Forrester diagram for the trophic status dynamic model under ENSO scenarios in the tropical wetland. CAT = wetland basin, Cin = input TP concentration, TSI = trophic status index, TP = total phosphorus, TRC = theoretical retention time of a chemical, HRT = hydraulic retention time, and HRT-1 = TRC*HRT.
The dynamic modeling was carried out with the free software Vensim® [35], which was used as a visual instrument to facilitate the abstraction, registration, simulation, and analysis of the model of the ecosystem under study. This free software has frequently been used for dynamic simulation in wetlands (e.g., [19,36,37]). The validation of the model was carried out by means of a multivariate sensitivity analysis, using the Monte Carlo method [38]. For the purposes of dynamic model development, a random distribution of variables was considered, and the correlation between variables was determined by linear regression analysis [39]. Thus, two input variables (independent) and two output variables (dependent) were selected from the dynamic model for sensitivity analysis. The values of each of the input variables were randomly changed (statistical distribution) during 200 simulations. Subsequently, it was verified by a percentile analysis that the values of the output variables were concentrated around the mean and within the calculated confidence intervals (CI = 95%). All of these analyses were performed using Vensim®. Table 1 shows the variables and information considered for the development of the dynamic model.

Table 1.
Variables, indexes, and information considered for the development of the dynamic model of trophic status under ENSO conditions, in the tropical wetland of study.
2.3. Dynamic Model Systematization
The algorithms used for the development of the trophic status dynamic model of the study wetland, followed the guidelines proposed by Beltrán and Rangel [23], and Hakanson and Boulion [46]. In other words, it was assumed that the eutrophication models proposed by Vollenweider and the OECD had, as a fundamental basis, the mass balance theory, to explain the TP flows in lakes and wetlands. Thus, the charge pattern of input TP was determined using Equation (1) [23], TP was calculated with Equation (2) [46], and HRT was determined by Equation (3) [46]. The theoretical retention time of a chemical or suspended particle (TRC) was calculated with Equation (4) [46], load model for Vollenweider wetlands was determined using Equation (5) [23], OECD empirical model was calculated with Equation (6) [18], and TSI of Aizaki et al. [17] was determined using Equation (7) [23]. The equations used for the systematization of the dynamic model are shown below.
where TPi = TP ingress load pattern (mg/year), Cin = substance concentration in the tributary (mg/m3), and Q = tributary discharge (m3/year).
where V = wetland volume (m3), dC/dt = change in concentration of a substance in the water body (TP) per unit of time (mg/m3/year), Q = tributary discharge (m3/year), Cin = substance concentration in the tributary (mg/m3), C = substance concentration in the water body (mg/m3), and Rsed = sedimentation rate of a substance (L/year).
where HRT = hydraulic retention time (year), V = wetland volume (m3), and Q = tributary discharge (m3/year).
where TRC = theoretical retention time of a chemical or suspended particle (year), V = wetland volume (m3), C = substance concentration in the water body (mg/m3), Q = tributary discharge (m3/year), and Cin = substance concentration in the tributary (mg/m3).
where C = substance concentration in the water body (mg/m3), Cin = substance concentration in the tributary (mg/m3), and TRC = theoretical retention time of a chemical or suspended particle (year).
where C = substance concentration in the water body (mg/m3), Cin = substance concentration in the tributary (mg/m3), and TRC = theoretical retention time of a chemical or suspended particle (year).
where TSI = trophic status index (mg/m3), TP = TP concentration (mg/L), and Ln = natural logarithm. The above equation results from a modification made by Aizaki et al. [17] to the equation proposed by Carlson [13]. Figure 2 shows the Forrester diagram designed for the development of the wetland trophic status dynamic model.
2.4. Dynamic Model Assumptions
The assumptions of the dynamic model developed were the following: (i) The modeling considered the TP concentration from the basin (three point discharges of water), which was corrected by hydraulic renewal [23]. (ii) The model did not consider the TP resuspension phenomenon, nor the effects generated by wind currents, that could influence the nutrient transport and mixing processes. (iii) The possible diffuse contributions by discharge and surface runoff, after the entry of the wetland, were not considered in the input TP concentration (Cin). Lastly, (iv) the model did not include internal TP loads generated by nitrogen fixation by microorganisms, macrophyte decomposition, and those derived from excretions of zooplankton and macroinvertebrates (Figure 2).
2.5. ENSO Scenarios
The dynamic modelling was performed under two ENSO scenarios. The first, under conditions of the El Niño phase in 2001, and the second under conditions of the La Niña phase in 2011. The El Niño Oceanic Index (ONI) in 2001 was between +0.70 and −0.30, which corresponded to the occurrence of a weak El Niño event. This is according to NOAA reports for the north of South America (https://www.cpc.ncep.noaa.gov/ (accessed on 22 March 2022)) [47]. During this period, there were variations in the regime and magnitude of precipitation. The ONI in 2011 was between −1.70 and −0.40, which corresponded to a strong La Niña event. Indeed, during this period there were significant variations in the regime and magnitude of precipitation. In the case of the megacity of Bogotá (Colombia), increases in the precipitation magnitude were observed between 110% and 300%, in relation to the reported historical average [44]. Indeed, precipitation was the main input variable in the dynamic model to simulate the ENSO phenomenon (Figure 2).
3. Results and Discussion
3.1. Dynamic Model Developed
Figure 2 shows the Forrester diagram designed for the development of the wetland trophic status dynamic model under ENSO conditions. The results showed that during the ENSO scenarios considered (El Niño-2001 and La Niña-2011), significant variations in the magnitude of precipitation were observed. The weak El Niño phase (2001) showed a reduction in annual precipitation of 34.7% (573 mm) compared to the historically reported annual average (878 mm) [44]. The results of the dynamic modelling suggested for this period an HRT of 1.47 months in the study wetland. In other words, the wetland renewed its water volume every 44 days. This, for an inflow into the wetland of 760,096 m3/year, which came entirely from the basin. In contrast, the strong La Niña phase (2011) showed an increase in annual precipitation of 53.9% (1904 mm) in relation to the historically reported annual average [44]. Under this scenario, the simulated HRT in the wetland was 1.10 months. During this period, the wetland renewed its volume of water every 33 days. This, for an inflow into the wetland of 2,524,506 m3/year, which came entirely from the basin. The simulation results suggested that HRT in the wetland was increased by 1.33 times during the weak El Niño phase (decreased precipitation) compared to the strong La Niña phase (increased precipitation). Indeed, the precipitation and inflow into the wetland also varied according to the ENSO phases considered. On average, precipitation and inflow were 3.32 times higher during the La Niña phase.
A multivariate sensitivity analysis was performed for the dynamic model developed, using the Monte Carlo method [38]. The independent variables used for the sensitivity analysis were the following: (i) basin area and (ii) wetland area. The values of these variables were changed automatically during 200 simulations (Vensim® software). The results of the sensitivity analysis were analyzed for the following output variables: (i) input TP concentration and (ii) HRT. Sensitivity analysis by percentiles, showed that the results for the output variables were concentrated around the mean (50%), within the confidence intervals (CI = 95%) that were generated when the input variables were randomly modified around the statistical distribution. Therefore, the findings suggested that the sensitivity of the model was optimal, the simulation was accurate in the period evaluated (El Niño and La Niña phases), and the functionality of the model was adequate. Lastly, the results of the model sensitivity analysis showed that variations in input TP concentration significantly affected the trophic status (TSI) behavior of the wetland (p-value < 0.050). This also supported the selection of phosphorus as the limiting factor of eutrophication for the development of the model.
3.2. Simulated Input TP Load
The results of the dynamic simulation showed that input TP concentration (Cin) in the tropical wetland was increased during the El Niño phase compared to the La Niña phase. This behavior was probably associated with the observed precipitation and inflow regimes. During the El Niño phase (2001), the monthly precipitation and TP concentrations simulated were from 20.4–80.6 mm and 1.34–4.58 mg/m3, respectively. In contrast, during the La Niña phase (2011) monthly precipitation and TP concentrations were from 33.9–473.5 mm and 0.52–2.54 mg/m3, respectively (Figure 3). The results suggested that, during the increased precipitation phase (La Niña), and consequently increased surface runoff flow, there was a dilution of the TP that entered the tropical wetland under study. On average, input TP concentrations in the wetland decreased by 1.85 times during the La Niña phase compared to the El Niño phase. Ávila et al. [48] also reported the dilution effect on pollutant concentrations discharged into wetlands during periods of increased precipitation. This dilution effect on the input TP concentrations during the La Niña phase (increased precipitation) was probably related to the type of pollution source on the wetland. In the study wetland, the main pollution sources were associated with point runoff discharges from three streams: Aguas Calientes, Patiño, and San Juan. These streams also received discharges of domestic and agricultural wastewater before their arrival into the wetland (anthropogenic pollution). Li et al. [49] reported that, during strong storms a decrease in input TP concentration (dilution effect) was observed in a wetland subject to point discharges of anthropic pollution. Lastly, Mai et al. [50] reported that shallow wetlands were more susceptible to changes in their water quality during precipitation events, compared to deeper wetlands.
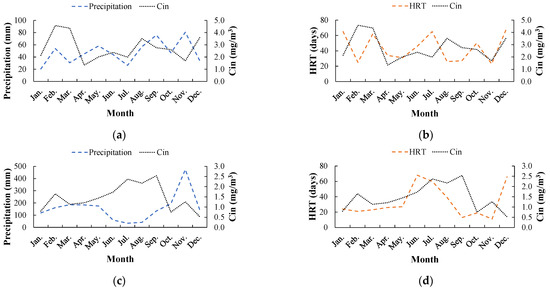
Figure 3.
Monthly modeling of precipitation, input TP concentration (Cin), and HRT, in the study wetland under the ENSO phases of El Niño (a,b) and La Niña (c,d).
The simulation findings showed comparatively that, during the El Niño phase the Cin was possibly related to precipitation and consequently to the input flow into the wetland from the basin. Indeed, during the months in which the higher precipitation was observed (e.g., February, May, August, and September; between 53.9 and 75.9 mm), the input TP concentration also tended to increase (between 2.01 and 4.58 mg/m3). This trend may have been associated with nutrient washing, exerted by surface runoff during precipitation events. Kadlec [51] reported the influence of washing exerted by surface runoff on the pollutant load discharged into water systems. For the La Niña phase, the behavior of Cin was comparatively opposite. In other words, during the months in which high precipitation was observed (e.g., March, April, May, and October; 175–474 mm), input TP concentrations to the wetland tended to decrease (between 0.75 and 1.44 mg/m3). This again suggested that the input TP concentration to the tropical wetland tended to decrease due to dilution generated by high runoff flows (point runoff discharges). In the months of dry weather during the La Niña phase (e.g., June, July, August, and September; 33.9–134.3 mm), input TP concentrations to the wetland tended to increase (1.73–2.54 mg/m3). This behavior was similar to that observed during the El Niño phase (decrease in precipitation frequency and magnitude). Therefore, this trend suggested that the variation pattern in Cin was influenced by factors related to climate dynamics, where precipitation was possibly the main conditioning variable. Certainly, the basin’s morphometric characteristics possibly also influenced the behavior of Cin. According to Childers et al. [52], input nutrient concentrations were mainly influenced by precipitation cycles and surface flow behavior in watercourses in wetland basins. Lastly, some studies have also reported that land use in a basin is a significant variable to consider in the analysis of nutrient input in urban wetlands [53].
The dynamic simulation results showed that, during periods where high precipitation was observed (La Niña), HRT tended to decrease (1.33 times), consequently decreasing the TP concentrations within the tropical wetland under study (1.85 times). Schenone et al. [54] indicated that the above behavior could be associated with a nutrient dilution effect, due to the increase in flow and water level within the wetland. This runoff volume was subsequently discharged from the wetland, becoming an outflow, which possibly allowed the improvement of its trophic status. Fraile [55] reported that, during the months of higher precipitation, the TP concentrations within a wetland tended to decrease, which was attributed to the self-purification of the aquatic system, promoted by the hydraulic renewal that evacuated the TP from it. Indeed, this trend favored the trophic recovery of wetlands. In relation to HRT, there are studies [23] that have reported that this is equivalent to the retention time of a non-reactive substance (TRC), when the second was less than the first (TRC > HRT). Thus, the nutrient was transported from the basin and divided into a series of compartments, with oscillating phosphorus concentrations, which stabilized as they moved away from the pollution source.
The results of the dynamic simulation also suggested that the wetland possibly functioned as a passage channel for water, and in turn for TP, due to the simulated positive relationship between HRT and Cin. Namely, when a larger water volume entered the receiving wetland, the TP concentration tended to decrease, due to a reduction in HRT. The results hinted that the wetland under study did not accumulate phosphorus directly, because the HRT was possibly less than or equal to the retention time of a non-reactive substance (TRC). However, dilution, evacuation, or low TP concentrations were possibly not an indication that the trophic status of the wetland improved significantly.
3.3. TSI Analysis
The results of the TSI dynamic modeling for the ENSO phases of El Niño and La Niña are shown in Figure 4, and Table 2 and Table 3. This is according to the methods developed by the Organization for Economic Cooperation and Development—OECD [56], Vollenweider [18], and Aizaki et al. [17], and in relation to HRT. The method proposed by Aizaki et al. [17] was used to validate the results obtained from the TSI, which corresponded to a modification of Carlson’s proposal [13]. The chromatic scale used to distinguish the different trophic status was assigned according to Lamparelli [57]. Overall, the results of the dynamic modeling showed a similar temporal trend for the three methods of TSI estimation considered (i.e., OECD, Vollenweider, and Aizaki; correlation coefficients > 0.438), during the ENSO phases of El Niño and La Niña under study. A weak to strong negative relationship between TSI and HRT was also observed during the two ENSO phases (El Niño, r-Pearson between −0.233 and −0.873, p-values < 0.050; La Niña, r-Pearson between = −0.384 and −0.699, p-values < 0.050). Aizaki’s method showed the best correlation coefficients. Thus, linear regression models were developed between these two variables for the wetland under study during the El Niño (y = 0.476 × X + 69.7; y = TSI in mg/m3 and X = THR in days; R2 = 0.762) and La Niña (y = −0.930 × X + 109.8; y = TSI in mg/m3 and X = HRT in days; R2 = 0.488) phases.
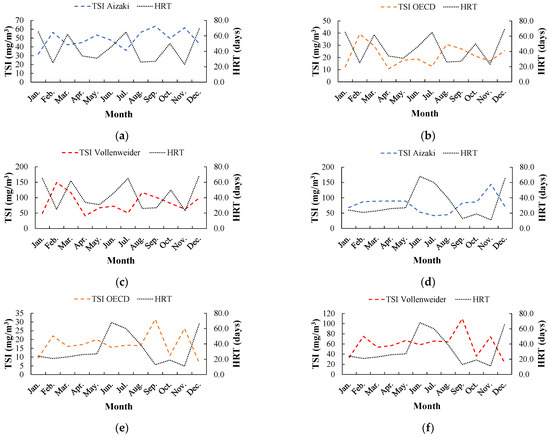
Figure 4.
Dynamic modelling of TSI-OECD, TSI-Vollenweider, TSI-Aizaki, and HRT, in the study wetland, for the ENSO phases of El Niño (a–c) and La Niña (d–f).

Table 2.
Categorization of the trophic status of the tropical wetland under the El Niño phase (Aisaki, OECD, and Vollenweider).

Table 3.
Categorization of the trophic status of the tropical wetland under the La Niña phase (Aisaki, OECD, and Vollenweider).
The simulation findings showed negative correlations between HRT and precipitation (El Niño, r = −0.882, p-value < 0.050; La Niña, r = −0.592, p-value < 0.050; see Figure 3), and between HRT and TSI (El Niño, r = −0.873, p-value < 0.050; La Niña, r = −0.699, p-value < 0.050; see Figure 4). In other words, a positive relationship between precipitation and TSI was observed (El Niño, r = 0.964, p-value < 0.050; La Niña, r = 0.972, p-value < 0.050). These correlations suggested that the lower the precipitation (El Niño phase), the higher the HRT and the lower the TSI, in the study wetland. Indeed, when the rainfall was lower, the residence time of the water in the wetland increased, which possibly allowed a greater self-purification effect, that favored the trophic recovery of this aquatic ecosystem. Gargallo [58], García et al. [59], and Kadlec and Wallace [51] indicated that by increasing flow, vegetation cover, and HRT, it was possible to increase the TP mass removed in wetlands. Alasino et al. [60] also reported that water bodies with high hydrodynamic renewal (i.e., reduced residence times) tended to impede the development or restoration of biogeochemical cycles, which adversely affected the wetland. Zhang and Mitsch [61] reported that wetlands with an HRT greater than 15 days showed a purifying action and restoration of biogeochemical cycles. For example, the findings showed that this condition in the HRT was not met in September (13 days) and November (11 days), during the La Niña phase. This possibly caused the two highest peaks that are observed in the simulated TSI (Figure 4d–f).
In relation to the El Niño phase, the results showed that TSI-OECD classified the wetland under a mesotrophic status, with TP values between 10.7 and 30.7 mg/m3 (Table 2). Except during February, when a eutrophic status was observed (39.2 mg/m3). Vollenweider’s TSI showed that the wetland was under hypereutrophic conditions, with TP values ranging from 81.5–149.4 mg/m3. This trophic status predominated for six non-consecutive months. For the remaining time, the wetland was under eutrophic status. Aizaki’s TSI showed the wetland to be in predominantly mesotrophic conditions, with TP values between 31.9 and 56.5 mg/m3. In September and November, the wetland showed eutrophic conditions (63.4 and 61.7 mg/m3, respectively). In relation to the La Niña phase, the results of the dynamic simulation showed that TSI-OECD classified the wetland under a mesotrophic status from February to November (10.9–31.6 mg/m3). However, oligotrophic status was observed in January and December (6.70–9.50 mg/m3). Vollenweider’s TSI indicated that the wetland was under eutrophic conditions (33.5–75.1 mg/m3), a status that prevailed for much of the year (Table 3), except for in September and December, where the status was hypereutrophic and mesotrophic, respectively. The results of Aizaki’s TSI showed that the wetland was under eutrophic conditions during the La Niña phase (68.1–89.5 mg/m3). Based on the above findings, regarding the different methods for determining TSI, it is suggested in this study that the best method for describing the modeled behavior and status of the tropical wetland is that proposed by Aizaki. This is because Aizaki’s TSI considered the HRT as a decisive factor during the trophic phase of the water body. As mentioned, during the dynamic modeling, a significant negative relationship between the HRT and Aizaki’s TSI was evidenced in the study wetland (El Niño, r = −0.873, p-value < 0.050; La Niña, r = −0.699, p-value < 0.050).
When comparing the results obtained in the ENSO phases (El Niño-2001 and La Niña -2011), the results suggested that the occurrence of high input TP concentrations in the wetland did not necessarily indicate high TSIs. This is because the trophic status of the wetland was possibly more associated with HRT rather than input TP concentration. In this study, higher input TP concentrations were observed during the El Niño phase (2001, Figure 3a) compared to the La Niña phase (2011, Figure 3b), but two of the trophic status indexes analyzed (Aizaki and OECD) hinted that the wetland tended to be under a mesotrophic status (Table 2). The results suggested that this trend in the trophic status of the wetland might be associated with higher HRTs, which were generated by the low precipitation observed during the El Niño phase (−34.7%). During this year (2001) it was classified by other studies as drought, and typical of the El Niño phase (IDEAM, 2004). Conversely, during the La Niña phase (2011), input TP concentrations were lower (1.85 times), but TSI showed a eutrophic status (Aizaki and Vollenweider). This could be associated with a shorter residence time of TP in the wetland, due to the high precipitation levels observed on average (53.9%), which prevented an adequate development of biogeochemical cycles and generated a lower capacity for assimilation of the nutrient by the aquatic ecosystem. Eraso and Trindade [62] suggested that if an aquatic ecosystem did not show stress levels, TSI would have a low value, which implied that the water body had few nutrients, sediments, or pollutants. However, the TSI of the wetland under study showed eutrophic values for the last year of analysis (La Niña-2011), which indicated that it was under conditions of tension and possibly subjected to stress by an abnormal amount of nutrients [1].
4. Conclusions
The results of this study on the dynamic modeling of the trophic status in a tropical wetland under ENSO conditions, allow us to visualize the following conclusions. This is based on a comparison between the La Niña and El Niño phases.
The results suggest an increase in precipitation, by 3.32 times, during the La Niña phase compared to the El Niño phase. This increase in precipitation suggests that input TP concentrations to the wetland tend to decrease, due to a dilution effect exerted by the increase in surface runoff volumes from the basin (point runoff discharges). Wetland input TP concentrations are 1.85 times lower during the La Niña phase. Thus, the results also suggest that the input TP concentration to the tropical wetland is conditioned by the temporal pattern imposed by the ENSO climate variability phenomenon. Indeed, precipitation is the main climate variable that explains the previous trends in the tropical wetland under study. In addition, the findings suggest a reduction in wetland HRT during the La Niña phase (1.33 times) compared to the El Niño phase. The reduction in HRT is probably associated with increased precipitation during the La Niña phase (3.32 times). This trend causes the TP concentration inside the wetland to decrease, possibly due to an increase in the water volume stored in the wetland (dilution) and by the exit of this nutrient due to a shorter hydraulic renewal (HRT-La Niña < HRT-El Niño).
Overall, the results suggest a similar temporal trend in wetland trophic status under ENSO scenarios from the three methods used to calculate TSI in this study (OECD, Vollenweider, and Aizaki). However, under ENSO scenarios, the use of Aizaki’s method is suggested, because it considers HRT as a decisive factor for the calculation of wetland trophic status. In addition, the findings indicate a significant negative correlation between HRT and TSI. As precipitation was the main descriptor variable of the ENSO climate variability phenomenon, the results suggest a significant positive relationship between this variable and TSI. The results also suggest that the occurrence of high input TP concentrations in the wetland did not necessarily indicate a high TSI. This is because the trophic status of the wetland is possibly more associated with HRT rather than input TP concentration. Thus, the trophic status of the wetland during the La Niña and El Niño phases tended to be eutrophic and mesotrophic, respectively. Lastly, this study is relevant because it allows the visualization of the usefulness of the use of dynamic simulation tools for the differentiated management and restoration of tropical wetlands according to existing ENSO scenarios. In fact, these computer simulation tools allow delineation of the interrelationship between the TSI and the La Niña and El Niño phases of ENSO, for better monitoring and restoration of these aquatic ecosystems.
Author Contributions
Conceptualization, L.G.G.-L. and J.E.B.-V.; Methodology, L.G.G.-L. and J.E.B.-V.; Software, L.G.G.-L., J.E.B.-V. and C.A.Z.-M.; Validation, L.G.G.-L.; Formal analysis, L.G.G.-L. and C.A.Z.-M.; Investigation, L.G.G.-L. and C.A.Z.-M.; Resources, J.E.B.-V.; Data curation, L.G.G.-L. and C.A.Z.-M.; Writing – original draft, L.G.G.-L., J.E.B.-V. and C.A.Z.-M.; Writing – review & editing, C.A.Z.-M.; Visualization, L.G.G.-L. and C.A.Z.-M.; Supervision, J.E.B.-V.; Project administration, J.E.B.-V.; Funding acquisition, J.E.B.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors express their gratitude to the Research Groups for Sustainable Development (INDESOS) and Environmental Engineering (GIIAUD) of the Universidad Distrital Francisco José de Caldas, and to the District Secretary of Environment of Bogotá D.C. (Colombia).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Das, S.; Adhikary, P.P.; Shit, P.K.; Bera, B. Assessment of Wetland Health Dynamics: Comparing Fuzzy- AHP and Composite Indexing Methods in an Urban Agglomeration in East India. Geocarto Int. 2022, 1–25. [Google Scholar] [CrossRef]
- Zhao, Q.; Bai, J.; Huang, L.; Gu, B.; Lu, Q.; Gao, Z. A Review of Methodologies and Success Indicators for Coastal Wetland Restoration. Ecol. Indic. 2016, 60, 442–452. [Google Scholar] [CrossRef]
- Izquierdo, A.E.; Blundo, C.; Carilla, J.; Foguet, J.; Navarro, C.J.; Casagranda, E.; Chiappero, M.F.; Vaieretti, M.V. Floristic Types of High-Andean Wetlands from Northwest Argentina and Their Remote-Sensed Characterization at a Regional Scale. Appl. Veg. Sci. 2022, 25, e12658. [Google Scholar] [CrossRef]
- Blettler, M.C.M.; Gauna, L.; Andréault, A.; Abrial, E.; Lorenzón, R.E.; Espinola, L.A.; Wantzen, K.M. The Use of Anthropogenic Debris as Nesting Material by the Greater Thornbird, an Inland–Wetland-Associated Bird of South America. Environ. Sci. Pollut. Res. 2020, 27, 41647–41655. [Google Scholar] [CrossRef]
- Junk, W.J.; Piedade, M.T.F.; Lourival, R.; Wittmann, F.; Kandus, P.; Lacerda, L.D.; Bozelli, R.L.; Esteves, F.A.; Nunes da Cunha, C.; Maltchik, L.; et al. Brazilian Wetlands: Their Definition, Delineation, and Classification for Research, Sustainable Management, and Protection. Aquat. Conserv. Mar. Freshw. Ecosyst. 2014, 24, 5–22. [Google Scholar] [CrossRef]
- Hu, L.; Hu, W.; Deng, J.; Li, Q.; Gao, F.; Zhu, J.; Han, T. Nutrient Removal in Wetlands with Different Macrophyte Structures in Eastern Lake Taihu, China. Ecol. Eng. 2010, 36, 1725–1732. [Google Scholar] [CrossRef]
- Ruíz, A.G.; Hes, E.; Schwartz, K. Shifting Governance Modes in Wetland Management: A Case Study of Two Wetlands in Bogotá, Colombia. Environ. Plann. C Gov. Policy 2011, 29, 990–1003. [Google Scholar] [CrossRef]
- Pinilla, G. An Index of Limnological Conditions for Urban Wetlands of Bogotá City, Colombia. Ecol. Indic. 2010, 10, 848–856. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Zheng, N.; Cao, X. Analysis of Trophic Status and Its Influence Factors of Different Water Body Types in Xixi National Wetland Park, China. Procedia Environ. Sci. 2010, 2, 768–780. [Google Scholar] [CrossRef]
- Dar, S.A.; Rashid, I.; Bhat, S.U. Land System Transformations Govern the Trophic Status of an Urban Wetland Ecosystem: Perspectives from Remote Sensing and Water Quality Analysis. Land Degrad. Dev. 2021, 32, 4087–4104. [Google Scholar] [CrossRef]
- Das Sarkar, S.; Sarkar, U.K.; Lianthuamluaia, L.; Ghosh, B.D.; Roy, K.; Mishal, P.; Das, B.K. Pattern of the State of Eutrophication in the Floodplain Wetlands of Eastern India in Context of Climate Change: A Comparative Evaluation of 27 Wetlands. Environ. Monit. Assess 2020, 192, 183. [Google Scholar] [CrossRef] [PubMed]
- Liou, Y.-T.; Lo, S.-L. A Fuzzy Index Model for Trophic Status Evaluation of Reservoir Waters. Water Res. 2005, 39, 1415–1423. [Google Scholar] [CrossRef] [PubMed]
- Carlson, R.E. A Trophic State Index for Lakes1. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Organisation for Economic Co-Operation and Development. Eutrophication of Waters: Monitoring, Assessment and Control; Organisation for Economic Co-operation and Development; Sold by OECD Publications and Information Center: Paris, France; Washington, DC, USA, 1982; ISBN 978-92-64-12298-7. [Google Scholar]
- Bekteshi, A.; Cupi, A. Use of Trophic State Index (Carlson, 1977) for Assessment of Trophic Status of the Shkodra Lake. J. Environ. Prot. Ecol. 2014, 15, 359–365. [Google Scholar]
- Sruthy, G.S.; Priya, K.L.; Madhu, A.M.; Chellappan, S.; Adarsh, S.; Haddout, S. Fuzzy Logic Approach for the Assessment of Trophic State of Water Bodies. Ecol. Eng. 2021, 169, 106314. [Google Scholar] [CrossRef]
- Aizaki, M.; Otsuki, A.; Fukushima, T.; Hosomi, M.; Muraoka, K. Application of Carlson’s Trophic State Index to Japanese Lakes and Relationships between the Index and Other Parameters. SIL Proc. 1922–2010 1981, 21, 675–681. [Google Scholar] [CrossRef]
- Vollenweider, R.A.; Giovanardi, F.; Montanari, G.; Rinaldi, A. Characterization of the Trophic Conditions of Marine Coastal Waters with Special Reference to the NW Adriatic Sea: Proposal for a Trophic Scale, Turbidity and Generalized Water Quality Index. Environmetrics 1998, 9, 329–357. [Google Scholar] [CrossRef]
- Güneralp, B.; Barlas, Y. Dynamic Modelling of a Shallow Freshwater Lake for Ecological and Economic Sustainability. Ecol. Model. 2003, 167, 115–138. [Google Scholar] [CrossRef]
- Jiménez, P.A.L.; Alberola, M.C.; Solano, F.J.M.; Alemany, V.E. Desarrollo de un modelo matemático de calidad de aguas calibrado para pequeños cauces receptores: Caso práctico. Tecnol. Agua 2002, 22, 56–63. [Google Scholar]
- Spieles, D.J.; Mitsch, W.J. A Model of Macroinvertebrate Trophic Structure and Oxygen Demand in Freshwater Wetlands. Ecol. Model. 2003, 161, 183–194. [Google Scholar] [CrossRef]
- Ahlgren, I.; Frisk, T.; Kamp-Nielsen, L. Empirical and Theoretical Models of Phosphorus Loading, Retention and Concentration Vs. Lake Trophic State. In Phosphorus in Freshwater Ecosystems; Persson, G., Jansson, M., Eds.; Springer: Dordrecht, The Netherlands, 1988; pp. 285–303. [Google Scholar]
- Beltrán Vargas, J.E.; Rangel Churio, J.O. Modelación del Estado Trófico del Humedal De Jaboque, Bogotá D. C., Colombia. Acta Biol. Colomb. 2013, 18, 149–164. [Google Scholar]
- Bustamante-Zapata, A.M.; Zafra-Mejía, C.A.; Rondón-Quintana, H.A. Influence of Vegetation on Outdoor Thermal Comfort in a High-Altitude Tropical Megacity: Climate Change and Variability Scenarios. Buildings 2022, 12, 520. [Google Scholar] [CrossRef]
- Hodson, E.L.; Poulter, B.; Zimmermann, N.E.; Prigent, C.; Kaplan, J.O. The El Niño–Southern Oscillation and Wetland Methane Interannual Variability. Geophys. Res. Lett. 2011, 38, L08810. [Google Scholar] [CrossRef]
- McCarthy, T.S.; Cooper, G.R.J.; Tyson, P.D.; Ellery, W.N. Seasonal Flooding in the Okavango Delta, Botswana—Recent History and Future Prospects. South Afr. J. Sci. 2000, 96, 25–33. [Google Scholar] [CrossRef]
- Ilyas, S.; Xu, X.; Jia, G.; Zhang, A. Interannual Variability of Global Wetlands in Response to El Niño Southern Oscillations (ENSO) and Land-Use. Front. Earth Sci. 2019, 7, 289. [Google Scholar] [CrossRef]
- Brugnoli, E.; Muniz, P.; Venturini, N.; Brena, B.; Rodríguez, A.; García-Rodríguez, F. Assessing Multimetric Trophic State Variability during an ENSO Event in a Large Estuary (Río de La Plata, South America). Reg. Stud. Mar. Sci. 2019, 28, 100565. [Google Scholar] [CrossRef]
- García-Rodríguez, F.; Brugnoli, E.; Muniz, P.; Venturini, N.; Burone, L.; Hutton, M.; Rodríguez, M.; Pita, A.; Kandratavicius, N.; Pérez, L.; et al. Warm-Phase ENSO Events Modulate the Continental Freshwater Input and the Trophic State of Sediments in a Large South American Estuary. Mar. Freshw. Res. 2013, 65, 1–11. [Google Scholar] [CrossRef]
- Díaz-Lozano, A.Y.; Hernández-Bravo, S.M. Análisis Del Plan de Acción Del Humedal Torca, Con Base En La Evaluación Ambiental Estratégica. Rev. Fac. Ing. 2014, 24, 9–19. [Google Scholar] [CrossRef]
- IDEA-Universidad Nacional de Colombia Plan de Manejo Ambiental Del Humedal Torca-Guaymaral—Observatorio Regional Ambiental y de Desarrollo Sostenible Del Río Bogotá. Available online: https://orarbo.gov.co/es/el-observatorio-y-los-municipios/plan-de-manejo-ambiental-del-humedal-torca-guaymaral (accessed on 14 November 2022).
- Moreno Franco, D.P.; Quintero Manzano, J.; López Cuevas, A. Métodos para identificar, diagnosticar y evaluar el grado de eutrofia. Contactos 2010, 78, 25–33. [Google Scholar]
- Ackefors, H.; Enell, M. The Release of Nutrients and Organic Matter from Aquaculture Systems in Nordic Countries. J. Appl. Ichthyol. 1994, 10, 225–241. [Google Scholar] [CrossRef]
- Nicholls, K.H. A Limnological Basis for a Lake Simcoe Phosphorus Loading Objective. Lake Reserv. Manag. 1997, 13, 189–198. [Google Scholar] [CrossRef]
- Peña Escobar, S.; Ramírez Reyes, G.S.; Osorio Gómez, J.C. Evaluación de una estrategia de fidelización de clientes con dinámica de sistemas. Rev. Ing. Univ. Medellín 2015, 14, 87–104. [Google Scholar] [CrossRef]
- Ma, C.; Zhang, G.Y.; Zhang, X.C.; Zhou, B.; Mao, T.Y. Simulation Modeling for Wetland Utilization and Protection Based on System Dynamic Model in a Coastal City, China. Procedia Environ. Sci. 2012, 13, 202–213. [Google Scholar] [CrossRef]
- Wang, C.; Hou, Y.; Xue, Y. Water Resources Carrying Capacity of Wetlands in Beijing: Analysis of Policy Optimization for Urban Wetland Water Resources Management. J. Clean. Prod. 2017, 161, 1180–1191. [Google Scholar] [CrossRef]
- Durga Rao, K.; Gopika, V.; Sanyasi Rao, V.V.S.; Kushwaha, H.S.; Verma, A.K.; Srividya, A. Dynamic Fault Tree Analysis Using Monte Carlo Simulation in Probabilistic Safety Assessment. Reliab. Eng. Syst. Saf. 2009, 94, 872–883. [Google Scholar] [CrossRef]
- Saha, T.K.; Pal, S.; Sarkar, R. Prediction of Wetland Area and Depth Using Linear Regression Model and Artificial Neural Network Based Cellular Automata. Ecol. Inform. 2021, 62, 101272. [Google Scholar] [CrossRef]
- López Barrera, E.A.; Duarte, M.; Moreno Ramírez, R.I.; Gonzalez Calderón, J.; Bejarano, P.; Buitrago Lancheros, D.M.; Caho, C.; Fuentes Cotes, M.M. Humedal Torca-Guaymaral: Iniciativas Para su Conservación; Universidad Sergio Arboleda; Universidad del Bosque; Red Ambiental de Universidades Sostenibles: Bogotá, Colombia, 2015; ISBN 978-958-8866-79-6. [Google Scholar]
- Conservación Internacional Colombia Programas—Convenio de Asociación No 01-201 Del 2013. Available online: https://www.conservation.org.co/Programas/ (accessed on 14 November 2022).
- SDA Red de Calidad Hídrica de Bogotá. Available online: https://www.ambientebogota.gov.co/red-de-calidad-hidrica-de-bogota (accessed on 14 November 2022).
- CAR. Corporación Autónoma de Cundinamarca Centro de Monitoreo Hidrológico y del Clima. Available online: https://www.car.gov.co/monitoreo_hidrometeorologico (accessed on 14 November 2022).
- IDEAM. La Variabilidad Climática y el Cambio Climático en Colombia; Instituto de Hidrología, Meteorología y Estudios Ambientales: Bogotá, Colombia, 2018; ISBN 978-958-8067-97-1. [Google Scholar]
- EAAB Plan de Manejo Ambiental del Humedal Torca—Guaymaral Observatorio Ambiental de Bogotá. Available online: https://oab.ambientebogota.gov.co/?post_type=dlm_download&p=15044 (accessed on 14 November 2022).
- Håkanson, L.; Boulion, V.V. The Lake Foodweb—Modelling Predation and Abiotic/Biotic Interactions; Backhuys Publishers: Leiden, The Netherlands, 2002. [Google Scholar]
- NOAA. NOAA’s Climate Prediction Center. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 22 March 2022).
- Ávila, C.; Salas, J.J.; Martín, I.; Aragón, C.; García, J. Integrated Treatment of Combined Sewer Wastewater and Stormwater in a Hybrid Constructed Wetland System in Southern Spain and Its Further Reuse. Ecol. Eng. 2013, 50, 13–20. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Yang, Z.; Lou, I. Influence of Non-Point Source Pollution on Water Quality of Wetland Baiyangdian, China. Desalination Water Treat. 2011, 32, 291–296. [Google Scholar] [CrossRef]
- Mai, Y.; Zhao, X.; Huang, G. Temporal and Spatial Variability of Water Quality in an Urban Wetland and the Effects of Season and Rainfall: A Case Study in the Daguan Wetland, China. Environ. Monit. Assess 2022, 194, 347. [Google Scholar] [CrossRef]
- Kadlec, R.H. Overview: Surface Flow Constructed Wetlands. Water Sci. Technol. 1995, 32, 1–12. [Google Scholar] [CrossRef]
- Childers, D.L.; Boyer, J.N.; Davis, S.E.; Madden, C.J.; Rudnick, D.T.; Sklar, F.H. Relating Precipitation and Water Management to Nutrient Concentrations in the Oligotrophic “Upside-down” Estuaries of the Florida Everglades. Limnol. Oceanogr. 2006, 51, 602–616. [Google Scholar] [CrossRef]
- Marimón-Bolívar, W.; Jiménez, C.; Toussaint-Jiménez, N.; Domínguez, E. Use of Neural Networks to Estimate a Global Self-Purification Capacity Index for Mountain Rivers: A Case Study in Bogota River Basin. Earth Syst. Environ. 2022, 6, 631–643. [Google Scholar] [CrossRef]
- Schenone, N.; Volpedo, A.; Cirelli, A.F. Estado trófico y variación estacional de nutrientes en los ríos y canales del humedal mixo-halino de Bahía Samborombón (Argentina). Limnetica 2008, 27, 143–150. [Google Scholar] [CrossRef]
- Fraile, H. Evaluación Del Estado Trófico y Comparación de Modelos Relativos al Fósforo En Los Embalses de Cernadilla y Valparaíso (Río Tera, Zamora). Limnetica 1995, 11, 29. [Google Scholar] [CrossRef]
- Casas, J.L.O.; Martínez, R.P. Applicability of the OECD Eutrophication Models to Spanish Reservoirs. SIL Proc. 1922–2010 1984, 22, 1521–1535. [Google Scholar] [CrossRef]
- Lamparelli INDICADORES AMBIENTALES, Índice del Estado Trófico—Cursos de Agua. Available online: https://www.ambiente.gub.uy/indicadores_ambientales/ficha/indice-del-estado-trofico-cursos-de-agua_/ (accessed on 14 November 2022).
- Gargallo, Sara Modelación de La Calidad de Las Aguas En Los Humedales Artificiales de Flujo Superficial (HAFS) Aplicación a Los HAFS Del Tancat de La Pipa En l’Albufera de Valencia. Available online: https://riunet.upv.es/handle/10251/78215 (accessed on 14 November 2022).
- García, J.; Vivar, J.; Aromir, M.; Mujeriego, R. Role of Hydraulic Retention Time and Granular Medium in Microbial Removal in Tertiary Treatment Reed Beds. Water Res. 2003, 37, 2645–2653. [Google Scholar] [CrossRef] [PubMed]
- Alasino, N.; Nadal, F.; Primo, L.; Bollo, P.; Larrosa, N. Comportamiento cinético e hidráulico de un humedal construido a escala real. Tecnol. Cienc. Agua 2015, 6, 93–104. [Google Scholar]
- Zhang, L.; Mitsch, W.J. Modelling Hydrological Processes in Created Freshwater Wetlands: An Integrated System Approach. Environ. Model. Softw. 2005, 20, 935–946. [Google Scholar] [CrossRef]
- Eraso, R.J.M.; Trindade, M. de L.B. Evaluación espacio-temporal del estado trófico de un lago de grandes dimensiones usando imágenes MOD09GA. Cienc. Ing. Neogranadina 2017, 27, 27–42. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).