Abstract
Bottomland hardwood forests (BHFs) offer a wide range of ecosystem services that are of high environmental and socioeconomic value. Yet, nearly 70% of BHFs in the southern United States have been lost during the past 100 years primarily due to land use change including agricultural expansion, calling for restoration efforts. We estimated the statistical relationship of the annual radial growth rate of three red oak species with climatic conditions and tree age using the tree ring data collected from a BHF plantation in the Arkansas Delta region. These species were Cherry bark oak (Quercus pagoda), Shumard oak (Quercus shumardii), and Nuttall oak (Quercus texana). The destructive sampling method was employed to obtain tree growth data and the cross-dating method was used for tree age determination. A log-linear regression model was estimated to uncover the statistical relationship between annual tree ring growth rate and climatic conditions. We identified the most critical time windows of climate variables that affect the growth of these trees. We found that the average temperature in October of the previous year and the minimum temperature between December of the previous year and January of the current year were positively associated with the radial growth rate in the current year although the maximum temperature from January to August and total precipitation from April to July of the current year were negatively correlated with the growth rate. Compared to Cherry bark and Shumard oaks, Nuttall oak was less sensitive to a rise in the minimum temperature between December and January. The projected climate change is likely to create slightly more favorable overall climatic conditions for these oak species in the region. Our findings suggest that these three red oak species are well suited for the study region for restoring BHFs, especially with a changing climate.
1. Introduction
The bottomland hardwood forests (BHFs) in the floodplains of the southeastern United States are critical for the provision of a wide range of ecosystem services such as carbon sequestration, soil and water conservation, timber, wildlife habitat, biodiversity, and recreational resources, among others [1,2,3,4]. These forests once covered over 12 million ha in the region; however, land-use change including agricultural land expansions has resulted in a 70% loss of their area and severe degradation of their quality in the past 100 years [4,5,6,7,8]. This unique type of ecosystems is threatened by human and natural forces, and changes in the BHFs in turn can have environmental and socioeconomic consequences [4,6,8]. This calls for the restoration of BHFs in the region. Yet, guidelines for successfully restoring these forests are lacking. For instance, what tree species will be most suitable for the BHF restoration? How does the growth of different tree species respond to climatic conditions especially climate extremes given the projected climate change? Answers to these questions can enhance the successful establishment and maintenance of BHFs in the region.
Among the most important tree species in BHFs in the Lower Mississippi Alluvial Valley are red oaks [2,9,10], which provide abundant food for wildlife and lumber and veneer for the production of high-quality furniture, flooring, and other products. For instance, acorns of red oaks are a critical food resource for mallards and wood ducks as they contain high levels of saturated fatty acids and other micronutrients [11]. Red oaks are also among the most valuable timber species grown in the region [2,9,10,12,13]. Thus, bottomland red oaks are desired by both wildlife and forest managers for enhancing wildlife habitat and producing high-quality wood.
However, few studies have attempted to quantify the growth/yield of red oaks in BHFs although tremendous efforts have been made in assessing the growth/yield, as well as their response to climate variability, of highly commercialized softwood timber species like loblolly pine in the region [14,15]. Studies that quantify the linkage between tree growth in BHFs and climatic conditions are even rarer. Analyzing annual tree ring growth has been widely employed to investigate the relationship between tree growth and climate variations, which can then be used to disclose and project the impact of climate change on tree growth [16,17,18,19,20]. Global climate change is expected to increase the global aggregate forest productivity largely due to higher CO2 concentration in the atmosphere although the impact will vary across regions, tree species, and forest types [21]. In the United States, forest productivity is projected to decrease in most regions including the southern region due to more frequent and intensive drought [19].
Several studies have probed the effects of climatic conditions on the radial growth of oak species [22,23,24,25,26,27,28]. Most of these studies used monthly average temperature and total precipitation in the previous and current growing seasons to estimate potential correlations between climate variations and annual ring width increment. The growth response to climate climatic conditions was found to vary with tree species and study sites. However, to our knowledge, none of the previous studies has targeted red oaks species of BHFs in the Lower Mississippi Alluvial Valley. There is a lack of understanding about the suitability of red oaks for restoring BHFs in the region in general and the growth response of red oaks in BHFs to changes in precipitation and average and extreme temperatures in particular.
This study aims to assess the impact of climatic conditions including average and extreme temperatures and precipitation in different periods of the year on the annual radial growth rate of three red oak species planted in the Arkansas Delta region. These species are Cherry bark oak (Quercus pagoda), Shumard oak (Quercus shumardii), and Nuttall oak (Quercus texana). We collected and used tree ring data that document annual tree radial growth over 15 years alongside historical weather data to disclose the statistical linkage between the annual radial growth rate of the three oak species and climatic conditions. We incorporated climate factors into tree growth modeling, expanding traditional approaches for modeling tree and forest growth and yield. Additionally, we employed a unique approach for selecting the most appropriate/critical window (time period), rather than a predetermined time period (i.e., daily, monthly, seasonal, annual), for each climate variable based on its influence on tree growth. Our findings derived from the field-based data enrich the literature on the influence of climatic conditions on the growth rate or productivity of individual trees and forest stands while providing guidelines for ensuring the successful restoration of BLFs in the region and beyond with a changing climate.
2. Materials and Methods
2.1. Study Site
The study site is situated at the University of Arkansas’ Division of Agriculture Pine Tree Research Station (AgPTRS) in the Arkansas Delta region (35°07′48″ N, 90°55′45″ W) (Figure 1). The AgPTRS is the largest research station in the state with a total area of 4795 ha (11,850 acres), of which approximately 1416 ha (3500 acres) are tillable and the remaining 3379 ha (8350 acres) are BHFs, pine plantations, and layout areas. This region has rich and fertile soil, with the Calloway, Calhoun, Henry, and Loring soil series being predominant. It is one of the world’s most productive agricultural regions. In addition, the temperate climate makes the region suitable for the growth of many crop and tree species, with a mean January temperature of 2.0 °C, an average July temperature of 27.6 °C, and an average annual precipitation of 1173 mm.
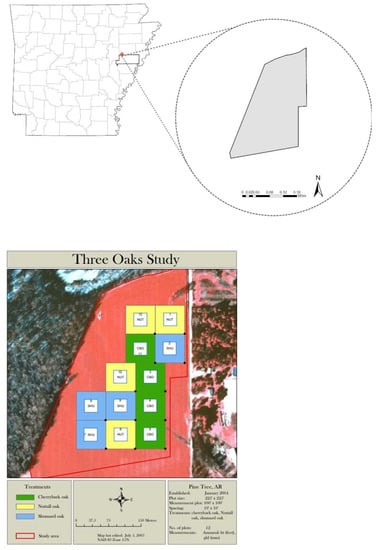
Figure 1.
The plantation area and project site (left) as well as the layout (right) of the measurement plots within the study area with all three oak species (CBO—Cherry bark oak, NUT—Nuttall oak, SHU—Shumard oak) located in the Division of Agriculture Pine Tree Research Station (AgPTRS) in the Arkansas Delta.
A red oak plantation of 12.1 ha (30 acres) was established on an agricultural (soybean) field that was enrolled in the Conservation Reserve Program (CP3A). The dominant soil types on the site are silt loam, Calloway silt loam, and Zachary silt loam. Three red oak species, Cherry bark oak (Quercus pagoda), Shumard oak (Quercus shumardii), and Nuttall oak (Quercus texana) were planted in February 2004 after site preparation using the subsoiling (ripping) process to a depth of 0.91 m (36 inches) in November 2003. The intervening 3 months between ripping and planting allowed the trench to close. The seedlings were hand-planted in 12 plots with four replications for each species with a 3.05 m × 3.05 m (10 feet × 10 feet) spacing between tree rows. Due to space limitations, plot sizes were reduced from 0.81 ha (2 acres) to 0.65 ha (1.6) acres. The 12 plots with a spacing of 30.48 m × 30.48 m (100 feet × 100 feet) were established by randomly assigning one of the three red oak species. A one-tenth-ha (one-fifth-acre) square measurement subplot was established in the center of each experiment plot. The square measurement subplots were accompanied by an 18.29 m (60 feet) buffer zone on all sides of the subplots to minimize the edge effects.
2.2. Data
Sixty (20 trees per species) oak trees were randomly selected from each of the four replications (5 per replication) within the measurement subplots established in the plantation and harvested for tree ring analysis in 2020. Diameter at breast height (DBH) and total height were measured for the sampled trees. DBH was measured in two crossing directions and average DBH was computed for each sample tree. Those trees were felled at ground level by leaving a stump height of approximately 0.3 m (1 foot). The felled stems were then divided into sections of 1.83 m (6 feet), and disks of 2.5–5.1 cm (1–2 inches) in thickness were extracted at the lower and upper ends of each section. These collected disks were marked with species, tree number, and disk number (representing the stem position where it was extracted) and then brought to the laboratory for further analysis. In the laboratory, the disks were sanded prior to measurement. The cross-dating method [29] was used for the determination of tree age (count of rings), and ring width was measured for each growing season with two different directions and then average width was calculated for each.
Daily meteorological data were retrieved from the Applied Climate Information System (ACIS) operated by the National Oceanic and Atmospheric Administration Regional Climate Centers (NOAA RCCs) [30]. The ACIS facilitates the use of complex meteorological data from multiple data collectors and generators under one management system. For the observed historical weather data, we used the gridded weather dataset derived from the Parameter-elevation Regressions on Independent Slopes Model (PRISM) [31]. We retrieved the meteorological data from 2005 to 2018 using the coordinates of the center of the study site. We also downloaded the projected future climate data from the ACIS dataset generated by applying the Localized Constructed Analogs (LOCA) downscaling method to 32 global climate models (GCMs) [30]. We obtained the climate projections for two greenhouse gas (GHG) emission scenarios, Representative Concentration Pathways (RCPs) 4.5 and 8.5, at our study site for the period of 2020–2099. The RCPs are a set of scenarios that depict different potential trajectories of GHG emissions and atmospheric concentrations [32,33]. RCP 4.5 is a moderate emission scenario with global GHG emissions peaking around 2040 whereas RCP 8.5 represents the highest emission scenario with continuously rising GHG emissions throughout the 21st century. Then, bias correction was performed to remove systemic model errors in GCMs. Various methodologies for bias correction have been developed including quantile mapping (QM) and scaled distribution mapping (SDM) [34,35,36,37,38]. These methods calibrate the distributions of modeled climate variables using their corresponding observations. We used the SDM method with a gamma distribution because it can maintain the changes and trends of the raw climate variables projected from the models [35]. The projected future temperatures and precipitation in the study area are shown in Figure 2 and Figure 3, respectively.
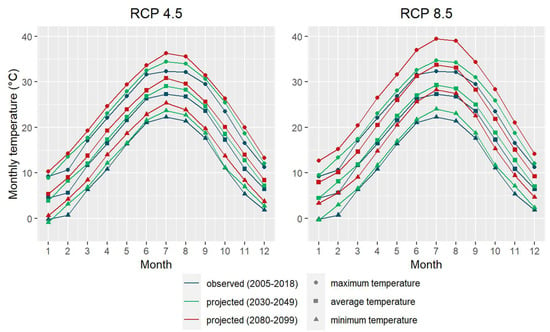
Figure 2.
Monthly temperatures observed between 2005 and 2018 and projected for 2030–2049 and 2080–2099. The projected temperatures represent the averages of temperatures projected by 32 global climate models under Representative Concentration Pathways (RCPs) 4.5 (left) and 8.5 (right). The colors and symbols in the legend denotes the maximum (circle), average (square), and minimum (triangle) temperatures observed between 2005–2018 (blue) and projected for 2030–2049 (green) and 2080–2099 (red).
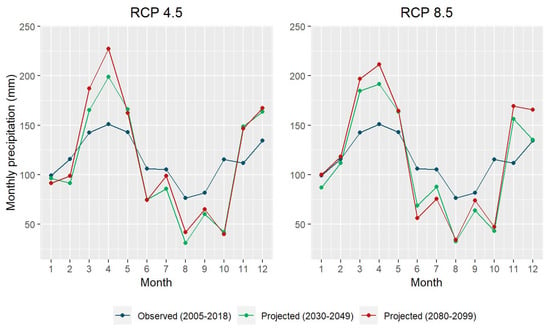
Figure 3.
Monthly precipitation observed between 2005 and 2018 (blue) and projected for 2030–2049 (green) and 2080–2099 (red). The projected precipitation represents the average of precipitation projected by 32 global climate models under Representative Concentration Pathways (RCPs) 4.5 (left) and 8.5 (right).
2.3. Selecting the Most Appropriate Windows for Climate Variables
We attempted to select climate variables that represent the most critical limiting factors such as temperatures and water availability for tree growth for possible inclusion in our regression model. Tree ring growth has been found to depend on the regional pattern of temperature and precipitation [16,39,40,41]. As such, climate drivers considered for inclusion in our model were average temperature (Tavg), maximum temperature (Tmax), minimum temperature (Tmin), and total precipitation (P). We calculated the monthly average, maximum, and minimum from the daily average, maximum, and minimum temperatures, respectively and the monthly total precipitation from the daily precipitation. The monthly temperatures and precipitation were then aggregated over different windows (time periods) for each climate variable.
Different windows of a climate variable can have different impacts on tree growth. Hence, for each climate variable considered in this study we further determined its most appropriate/critical window that had the most statistically significant impact on tree growth. The window was an annually repeating period over which annual tree growth was significantly affected by a climate driver. To reduce the unnecessary large number of inessential windows, we selected the maximum time span of 15 months with several months before and after the growing season. The selection of the maximum time span was based on the aggregate effect of climate drivers on tree growth [16,41,42]. The range and location of the most appropriate/critical window were then identified within the maximum time span.
We used the climwin package [43] in R to determine the most appropriate/critical windows of the climate variables. In this process, we attempted to identify the window in which the climate variable can best explain the variations in the tree ring growth using a nonlinear model that assumes that annual tree ring growth rate varies with tree age and climatic conditions. We prepared all the permutations of the starting and ending months for each climate variable within the maximum time span. Using the climwin package, we identified and estimated the best-fit nonlinear model based on the lowest value of AIC (Akaike Information Criterion corrected for small sample size). We also applied 5-fold cross-validation to calculating AICs to avoid the over-fitting of the model. For each climate variable, we chose a single best window when there was a distinct choice; otherwise, we selected multiple windows that were almost equally appropriate/critical.
2.4. Estimating the Statistical Relationship between Annual Tree Ring Growth Rate and Climatic Conditions
We regressed the annual radial growth rate of tree rings on climate variables, tree age, and tree species. The regression model takes the following form:
where i denotes individual trees, t represents the number of years since the tree was planted; j stands for each of the climate variables included in the model (j = 1, 2, …, J); ln denotes natural logarithm; D is a dummy variable representing the three red oak species; Clim represents the climate variables; * denotes the interaction between the two variables; α, β, γ, and δ are the regression coefficients, and ε is the error term. The annual growth rate of tree rings was calculated using the ratio of the annual radial change in the tree ring to the accumulated tree ring growth (i.e., the radius of the tree ring at the beginning of the year). The climate variables considered include the average, minimum, and maximum temperatures and total precipitation in their respective most appropriate/critical time windows.
The regression model was specified using the bidirectional stepwise variable selection approach. This approach starts with the base model consisting of one constant (foreword selection) or all potential explanatory variables (backward elimination), then attempts to add or delete one variable in each step/iteration to improve the statistical quality of the model. This process continues until adding or deleting one more variable can no longer improve the model. Metrics used for gauging the quality of the model include p-values from extra-sum-of-squares F tests, Bayesian Information Criterion (BIC), and Akaike Information Criterion (AIC) [44]. The AIC values were further adjusted/corrected for the sample size [45]. The corrected AIC (AICc) was then used along with other indicators for detecting multilinearity such as multicollinearity tolerance and the variance inflation factor (VIF). If multilinearity was detected, then the causing variable was dropped from the model, and the variable selection process continued without the eliminated variable. The statistical analysis was conducted using packages in R, primarily the olsrr package [46].
2.5. Estimating the Impact of Climate Change on the Tree Ring Growth
We estimated the impacts of future climate change on the annual radial growth rate of the three red oak species based on the regression results (Equation (1), Table 1) and the projected future climate change (Figure 2 and Figure 3). From Equation (1), we have
where ˆ denotes “estimated” and e is the base of the natural logarithm. Then, at a given future time (t) with a projected climate change (denoted by climjt1 for all j’s) compared to the reference case of no climate change (climjt0), the ratio of change in due to the climate change can be expressed as

Table 1.
The estimated statistical relationship between the annual radial growth rate of three red oak species and climate and other variables. (Year—the number of years since the trees were planted; Tmin(pDec, cJan)—the minimum temperature between December of the previous year and January of the current year; Tavg(pOct, pOct)—the average temperature in October of the previous year; P(cApr, cJul)—the total precipitation between April and July of the current year; Tmax(cJan, cAug)—the maximum temperature between January and August of the current year; Tmin(pDec, cJan):DNUT—the interaction term between the minimum temperature from December of the previous year to January of the current year and the dummy variable indicating Nuttall Oak).
Thus, Equation (3) can be used to estimate the ratio of change in the annual radial growth rate in response to changes in future climatic conditions.
3. Results
3.1. Most Appropriate Time Windows for Climate Variables
From all the possible time windows within the maximum time span, we found the most appropriate/critical window (starting and ending months) for each of the climate variables (Figure 4). It was the month of October of the previous year (Tavg(pOct, pOct)) for average temperature, from January to August of the current year (Tmax(cJan, cAug)) for maximum temperature, from December of the previous year to January of the current year (Tmin(pDec, cJan)) for minimum temperature, and from April to July of the current year (P(cApr, cJul)) for precipitation. These selected windows had distinctive ΔAICc values (change/difference in AICc) when compared to all other windows. In other words, there were no other windows that were nearly as good as these windows for the climate variables considered.
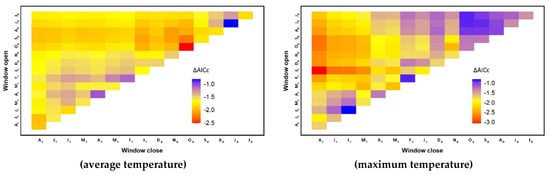
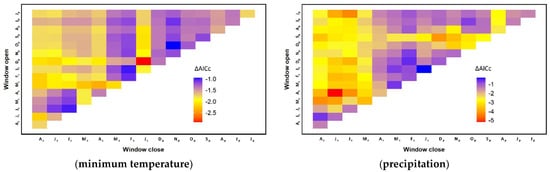
Figure 4.
The most appropriate windows (starting and ending months) of climate variables for explaining tree ring growth. The most appropriate window was selected based on the smallest difference in the corrected Akaike Information Criterion (AICc) value. The vertical axis represents the starting month of the window while the horizontal one expresses the ending month. The capital letters on the axes are the first letters of the months. The subscripts following the capital letters depict the years relative to the growing season with ‘c’ and ‘p’ denoting the current and previous years, respectively.
3.2. Relationships between Annual Radial Growth Rate and Climatic Conditions
The bidirectional stepwise variable selection process led to the inclusion of six independent variables in the final regression model. They were the number of years since the trees were planted, the average temperature in October of the previous year (Tavg(pOct, pOct)), the maximum temperature between January and August of the current year (Tmax(cJan, cAug)), the minimum temperature between December of the previous year and January of the current year (Tmin(pDec, cJan)), the total precipitation between April and July of the current year (P(cApr, cJul)), the interaction term between the minimum temperature from December of the previous year to January of the current year and the dummy variable indicating Nuttall Oak (Tmin(pDec, cJan):DNUT). The model was overall a statistically good fit to the data with R2 = 0.616, F(6,763) = 204.3, and p < 0.001. All the independent variables were significant (p < 0.05), and there was no evidence of multicollinearity (all VIFs < 5). The estimated regression model is shown in Table 1.
The number of years since the trees were planted, the maximum temperature between January and August of the current year (Tmax(cJan, cAug)), the total precipitation between April and July of the current year (P(cApr, cJul)), and the interaction term between the minimum temperature from December of the previous year to January of the current year and the dummy variable indicating Nuttall Oak (Tmin(pDec, cJan):DNUT) had negative impacts on the annual radial growth rate. However, the average temperature in October of the previous year (Tavg(pOct, pOct)) and the minimum temperature between December of the previous year and January of the current year (Tmin(pDec, cJan)) had positive impacts on the tree ring growth rate.
The estimated regression coefficients (Table 1) represent the ratio of change in the growth rate associated with a one-unit increase in each climate variable. For example, a one-unit (1 °C) increase in the average temperature in October of the previous year (Tavg(pOct, pOct)) would lead to a 0.7% increase in the growth rate for all species. A one-unit (1 °C) increase in the minimum temperature between December of the previous year and January of the current year (Tmin(pDec, cJan)) would increase the growth rate by 0.5% for Cherry bark and Shumard oaks and by 0.4% (0.005–0.001) for Nuttall oak, respectively. For all three species, an increase in the maximum temperature between January and August of the current year (Tmax(cJan, cAug)) by 1 °C would reduce the growth rate by 0.7%, and a 1 mm increase the precipitation between April and July of the current year (P(cApr, cJul)) would decrease the growth rate by 1.1%.
3.3. Impacts of Climate Change on the Radial Growth Rate of Red Oaks
Compared to the historical benchmark (2005–2018), the annual radial growth rate of the three red oak species was estimated to rise slightly and gradually with the projected climate change under RCPs 4.5 and 8.5 (Table 2). The increase in the growth rate would become more noticeable from 2030–2043 to 2080–2099 as the average, maximum, and minimum temperatures go up further. The growth rate would increase more from RCP 4.5 to RCP 8.5. Additionally, Cherry bark and Shumard oaks would have a larger increase in the growth rate than Nuttall oak except during 2030–2048 under RCP 4.5.

Table 2.
Estimated average percentage changes in the annual radial growth rate of red oaks under climate change relative to the historical average climatic conditions (2006–2018).
4. Discussion
Our results show that the average temperature in October of the previous year (Tavg(pOct, pOct)) and the minimum temperature from December of the previous year to January of the current year (Tmin(pDec, cJan)) had statistically significant, positive impacts on the annual radial growth rate of all the three red oak species (Table 1). The influence of the average temperature in the previous October on the tree ring growth could be attributed to the carbohydrate reserve of trees prior to the growing season. A warmer October and a rise in the minimum temperature between December and January could lead to the increased accumulation of carbohydrates during the fall and winter seasons [42], which will stimulate radial growth in the following spring [47]. As much as 30% of the annual radial growth of red oaks can be achieved before their bud bursts [48]. Thus, carbohydrate accumulation in the fall and winter seasons can play a vital role in boosting tree ring growth in the coming growing season.
The maximum temperature between January and August, however, was found to be negatively related to the annual radial growth rate of the three red oak species (Table 1). The study site has a very mild climate with ample precipitation except for some summer months. Monthly maximum temperatures on the site can reach above 30 ℃ between June and August and 9 ℃ even in January (Figure 2), and August is the driest month (Figure 3). An increase in the maximum temperature would result in higher plant evapotranspiration and soil moisture evaporation, reducing the radial growth of trees [23,41,49]. Although the average, minimum, and maximum temperatures had different directions and magnitudes of effects on the radial growth of the red oaks, their aggregate impact was positive (Table 1). In other words, an increase in the average, minimum, and maximum temperatures by the same magnitude would increase the annual radial growth rate of the three red oak species.
Likewise, the total precipitation from April to July had a negative impact on the tree ring growth (Table 1). The plantation of this study is located next to the Mississippi River with annual precipitation ranging from 1500 mm to 1750 mm (Figure 3), among the regions with the highest precipitation in the U.S. Excessive rainfalls can raise the water table, reducing oxygen availability to the root system and potentially causing hypoxia, oxygen deficiency of plant tissues [28,50,51,52]. Additionally, increased precipitation is usually associated with more cloudy days, reducing solar radiation available for tree growth. All these may help explain the negative relationship between the annual radial growth rate and the total precipitation from April to July.
The radial growth of the three red oak species responds differently to the minimum temperature between December of the previous year and January of the current year (Table 1). The radial growth of Nuttall oak tends to be less responsive to an increase in the minimum temperature than the other two species (Cherry bark and Shumard oaks). This also indicates that Nuttall oak appears to be more cold-tolerant than the other two species as it can perform better in terms of radial growth than Cherry bark and Shumard oaks in lower minimum temperatures in December and January.
Finally, our results show that the annual radial growth rate diminishes as trees grow older. With a semi-log model used, this indicates a nonlinear trend of diminishing radial growth over time for all three red oak species (Table 1). This result is consistent with the findings of previous studies [53,54,55].
Our findings have useful implications for restoring and managing BHFs in the Arkansas Delta region, especially with a changing climate. All three red oak species seem well suited for the region even with the projected climate change. A warmer climate would in general promote the growth of these red oak species, especially Cherry bark and Shumard oaks (Table 2). However, according to the projected future climate in the region, the average, maximum, and minimum temperatures would increase by different magnitudes (Figure 2). The maximum temperature would rise more than the average temperature, which would increase more than the minimum temperature. Specifically, the maximum temperature between January and August of the current year (Tmax(cJan, cAug)) is projected to increase by 2.1 °C during 2030–2049, which is higher than a 1.5 ℃ increase in the average temperature in October of the previous year (Tavg(pOct, pOct)) and a 0.9 ℃ rise in the minimum temperature between December of the previous year and January of the current year (Tmin(pDec, cJan)) (Figure 2, [30]). With the increase in the minimum temperature under climate change, the advantage of Cherry bark and Shumard oaks over Nuttall oak in terms of diameter growth will become more obvious. Nevertheless, because Nuttall oak can endure lower minimum temperatures in the winter, it seems more suitable for the northern part of the region than Cherry bark and Shumard oaks.
Precipitation in the region is projected to decrease in most months of the year (Figure 3). For instance, precipitation between April and July (P(cApr, cJul)) is expected to decrease by 11.9 mm during 2030–2049. The reduced precipitation in the spring and early summer could promote the diameter growth of the three oak species (Table 1). However, the reduced precipitation in August (the driest month) and October (though outside of the most appropriate/critical precipitation window) coupled with increased temperatures may impose water stress on the trees. This needs to be further monitored and investigated.
5. Conclusions
We estimated the statistical relationship of the annual radial growth rate of three red oak species with climatic conditions and tree age using the tree ring data collected from a BHF plantation in the Arkansas Delta region in the Lower Mississippi Alluvial Valley. We identified the time window of each climate variable that is most critical to the tree growth. We found that the average temperature in October of the previous year and the minimum temperature in December of the previous year and January of the current year were positively associated with the diameter growth of Cherry bark, Shumard, and Nuttall oaks, although the maximum temperature from January to August and the total precipitation from April to July of the current year were negatively correlated with the tree growth. Compared to Cherry bark and Shumard oaks, Nuttall oak was less sensitive to a rise in the minimum temperature between December and January. The projected climate change is likely to create slightly more favorable overall climatic conditions for these oak species in the region. Our findings suggest that these three red oak species are well suited for restoring BHFs in the study region, especially with a changing climate.
This study is based on the data collected from a plantation with 15 growing seasons. Future studies can attempt to obtain and incorporate tree growth data with a longer time series and from both plantations and natural BHFs. This study can also be expanded by exploring the dynamics of total biomass including belowground biomass and other ecosystem services (e.g., carbon, water regulation, wildlife, and biodiversity) of BHFs in response to climate variability.
Author Contributions
Conceptualization, J.G. and N.T.; methodology, J.G., N.T. and J.C.; validation, J.G. and N.T.; formal analysis, J.C., N.T. and J.G.; data curation, O.M., J.C., N.T. and M.P.; writing—original draft preparation, J.C., J.G. and N.T.; writing—review and editing, J.G., N.T. and M.P.; visualization, J.C. and N.T.; supervision and project administration, N.T. and J.G.; funding acquisition, M.P., N.T. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the Arkansas Forest Resources Center, part of the University of Arkansas System Division of Agriculture, and the US Department of Agriculture Climate-smart Program and Arkansas Center for Forest Business.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used in this study were obtained by the authors and from published sources listed in the references.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saikku, M. Down by the riverside: The disappearing bottomland hardwood forest of southeastern North America. Environ. Hist. 1996, 2, 77–95. [Google Scholar] [CrossRef]
- Kellison, R.C.; Young, M.J. The bottomland hardwood forest of the southern United States. For. Ecol. Manag. 1997, 90, 101–115. [Google Scholar] [CrossRef]
- England, J.R.; Paul, K.I.; Cunningham, S.C.; Madhavan, D.B.; Baker, T.G.; Read, Z.; Wilson, B.R.; Cavagnaro, T.R.; Lewis, T.; Perring, M.P. Previous land use and climate influence differences in soil organic carbon following reforestation of agricultural land with mixed-species plantings. Agric. Ecosyst. Environ. 2016, 227, 61–72. [Google Scholar] [CrossRef]
- Schneider, B.; Ehrhart, M.G.; Macey, W.H. Perspectives on organizational climate and culture. In APA Handbook of Industrial and Organizational psychology, Vol. 1. Building and Developing the Organization; American Psychological Association: Washington, DC, USA, 2011. [Google Scholar]
- Franzluebbers, A.J. Achieving soil organic carbon sequestration with conservation agricultural systems in the southeastern United States. Soil Sci. Soc. Am. J. 2010, 74, 347–357. [Google Scholar] [CrossRef]
- Zarfl, C.; Lumsdon, A.E.; Berlekamp, J.; Tydecks, L.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar] [CrossRef]
- EPA. Bottomland Hardwoods. Available online: http://www.epa.gov/wetlands/forms/contact-us-about-wetlands (accessed on 15 November 2022).
- Wohl, E.; Lininger, K.B.; Baron, J. Land before water: The relative temporal sequence of human alteration of freshwater ecosystems in the conterminous United States. Anthropocene 2017, 18, 27–46. [Google Scholar] [CrossRef]
- Allen, J.A. Reforestation of bottomland hardwoods and the issue of woody species diversity. Restor. Ecol. 1997, 5, 125–134. [Google Scholar] [CrossRef]
- Lockhart, B.R.; Tappe, P.A.; Peitz, D.G.; Watt, C.A. Snag recruitment and mortality in a bottomland hardwood forest following partial harvesting: Second-year results. In Proceedings of the 14th Biennial Southern Silvicultural Research Conference, Athens, GA, USA, 26 February–1 March 2007; Stanturf, J.A., Ed.; Gen. Tech. Rep. SRS–121. US Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2010; pp. 505–509. [Google Scholar]
- Heitmeyer, M.E.; Fredrickson, L.H. Fatty acid composition of wintering female mallards in relation to nutrient use. J. Wildl. Manag. 1990, 54, 54–61. [Google Scholar] [CrossRef]
- Smith, D.W.L. The southern hardwood region. In Regional Silviculture of the United State; Barret, J.W., Ed.; John Wiley and Son: New York, NY, USA, 1980; pp. 145–230. [Google Scholar]
- Oliver, C.D.; Burkhardt, E.C.; Skojac, D.A. The increasing scarcity of red oaks in Mississippi River floodplain forests: Influence of the residual overstory. For. Ecol. Manag. 2005, 210, 393–414. [Google Scholar] [CrossRef]
- Huang, J.; Abt, B.; Kindermann, G.; Ghosh, S. Empirical analysis of climate change impact on loblolly pine plantations in the southern United States. Nat. Resour. Model. 2011, 24, 445–476. [Google Scholar] [CrossRef]
- Rauscher, H.M.; Young, M.J.; Webb, C.D.; Robison, D.J. Testing the accuracy of growth and yield models for southern hardwood forests. South. J. Appl. For. 2000, 24, 176–185. [Google Scholar] [CrossRef]
- Fritts, H.C. Growth-Rings of Trees: Their Correlation with Climate. Science 1966, 154, 973–979. [Google Scholar] [CrossRef] [PubMed]
- Stahle, D.W.; Cleaveland, M.K.; Hehr, J.G. North Carolina Climate Changes Reconstructed from Tree Rings: A.D. 372 to 1985. Science 1988, 240, 1517–1519. [Google Scholar] [CrossRef] [PubMed]
- Salzer, M.W.; Hughes, M.K.; Bunn, A.G.; Kipfmueller, K.F. Recent unprecedented tree-ring growth in bristlecone pine at the highest elevations and possible causes. Proc. Natl. Acad. Sci. USA 2009, 106, 20348–20353. [Google Scholar] [CrossRef]
- Williams, A.P.; Michaelsen, J.; Leavitt, S.W.; Still, C.J. Using Tree Rings to Predict the Response of Tree Growth to Climate Change in the Continental United States during the Twenty-First Century. Earth Interact. 2010, 14, 1–20. [Google Scholar] [CrossRef]
- Yang, B.; He, M.; Shishov, V.; Tychkov, I.; Vaganov, E.; Rossi, S.; Ljungqvist, F.C.; Brauning, A.; Griessinger, J. New perspective on spring vegetation phenology and global climate change based on Tibetan Plateau tree-ring data. Proc. Natl. Acad. Sci. USA 2017, 114, 6966–6971. [Google Scholar] [CrossRef]
- Kirilenko, A.P.; Sedjo, R.A. Climate change impacts on forestry. Proc. Natl. Acad. Sci. USA 2007, 104, 19697–19702. [Google Scholar] [CrossRef] [PubMed]
- Cufar, K.; De Luis, M.; Eckstein, D.; Kajfez-Bogataj, L. Reconstructing dry and wet summers in SE Slovenia from oak tree-ring series. Int. J. Biometeorol. 2008, 52, 607–615. [Google Scholar] [CrossRef]
- Cufar, K.; Grabner, M.; Morgós, A.; Martínez del Castillo, E.; Merela, M.; de Luis, M. Common climatic signals affecting oak tree-ring growth in SE Central Europe. Trees 2014, 28, 1267–1277. [Google Scholar] [CrossRef]
- Michelot, A.; Bréda, N.; Damesin, C.; Dufrêne, E. Differing growth responses to climatic variations and soil water deficits of Fagus sylvatica, Quercus petraea and Pinus sylvestris in a temperate forest. For. Ecol. Manag. 2012, 265, 161–171. [Google Scholar] [CrossRef]
- Pilcher, J.R.; Gray, B. The Relationships between Oak Tree Growth and Climate in Britain. J. Ecol. 1982, 70, 297–304. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G.; Uhl, E. Resistance of European tree species to drought stress in mixed versus pure forests: Evidence of stress release by inter-specific facilitation. Plant Biol. 2013, 15, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Rozas, V. Dendrochronology of pedunculate oak (Quercus robur L.) in an old-growth pollarded woodland in northern Spain: Tree-ring growth responses to climate. Ann. For. Sci. 2005, 62, 209–218. [Google Scholar] [CrossRef]
- Rozas, V.; García-González, I. Too wet for oaks? Inter-tree competition and recent persistent wetness predispose oaks to rainfall-induced dieback in Atlantic rainy forest. Glob. Planet. Chang. 2012, 94–95, 62–71. [Google Scholar] [CrossRef]
- Tian, N.; Fan, Z.; Matney, T.G.; Schultz, E.B. Growth and stem profiles of invasive Triadica sebifera in the Mississippi coast of the United States. For. Sci. 2017, 63, 569–576. [Google Scholar]
- NOAA RCCs. Applied Climate Information System. 2022. Available online: https://www.rcc-acis.org/ (accessed on 15 November 2022).
- PRISM Climate Group. PRISM Climate Data. 2014. Available online: https://prism.oregonstate.edu/ (accessed on 15 November 2022).
- Moss, R.H.; Babiker, M.; Brinkman, S.; Calvo, E.; Carter, T.; Edmonds, J.A.; Elgizouli, I.; Emori, S.; Lin, E.; Hibbard, K. Towards New Scenarios for Analysis of Emissions, Climate Change, Impacts, and Response Strategies; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2008. [Google Scholar]
- van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.-F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Switanek, M.B.; Troch, P.A.; Castro, C.L.; Leuprecht, A.; Chang, H.I.; Mukherjee, R.; Demaria, E.M.C. Scaled distribution mapping: A bias correction method that preserves raw climate model projected changes. Hydrol. Earth Syst. Sci. 2017, 21, 2649–2666. [Google Scholar] [CrossRef]
- Bai, K.; Chang, N.-B.; Yu, H.; Gao, W. Statistical bias correction for creating coherent total ozone record from OMI and OMPS observations. Remote Sens. Environ. 2016, 182, 150–168. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching. J. Geophys. Res. 2010, 115, D10101. [Google Scholar] [CrossRef]
- Moghim, S.; McKnight, S.L.; Zhang, K.; Ebtehaj, A.M.; Knox, R.G.; Bras, R.L.; Moorcroft, P.R.; Wang, J. Bias-corrected data sets of climate model outputs at uniform space–time 2 resolution for land surface modelling over Amazonia. Int. J. Climatol. 2017, 37, 621–636. [Google Scholar] [CrossRef]
- Wilmking, M.; van der Maaten-Theunissen, M.; van der Maaten, E.; Scharnweber, T.; Buras, A.; Biermann, C.; Gurskaya, M.; Hallinger, M.; Lange, J.; Shetti, R.; et al. Global assessment of relationships between climate and tree growth. Glob. Chang. Biol. 2020, 26, 3212–3220. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Liu, H.; Li, X.; Ciais, P.; Babst, F.; Guo, W.; Zhang, C.; Magliulo, V.; Pavelka, M.; Liu, S.; et al. Differentiating drought legacy effects on vegetation growth over the temperate Northern Hemisphere. Glob. Chang. Biol. 2018, 24, 504–516. [Google Scholar] [CrossRef]
- Tei, S.; Sugimoto, A.; Yonenobu, H.; Matsuura, Y.; Osawa, A.; Sato, H.; Fujinuma, J.; Maximov, T. Tree-ring analysis and modeling approaches yield contrary response of circumboreal forest productivity to climate change. Glob. Chang. Biol. 2017, 23, 5179–5188. [Google Scholar] [CrossRef] [PubMed]
- Roibu, C.-C.; Sfeclă, V.; Mursa, A.; Ionita, M.; Nagavciuc, V.; Chiriloaei, F.; Leșan, I.; Popa, I. The Climatic Response of Tree Ring Width Components of Ash (Fraxinus excelsior L.) and Common Oak (Quercus robur L.) from Eastern Europe. Forests 2020, 11, 600. [Google Scholar] [CrossRef]
- Pol, M.; Bailey, L.D.; McLean, N.; Rijsdijk, L.; Lawson, C.R.; Brouwer, L.; Gimenez, O. Identifying the best climatic predictors in ecology and evolution. Methods Ecol. Evol. 2016, 7, 1246–1257. [Google Scholar] [CrossRef]
- Murtaugh, P.A. Performance of several variable-selection methods applied to real ecological data. Ecol. Lett. 2009, 12, 1061–1068. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Hebbali, A. olsrr: Tools for Building OLS Regression Models. 2020. Available online: https://cran.r-project.org/web/packages/olsrr/index.html (accessed on 15 November 2022).
- Yang, Z.; Midmore, D.J. Modelling plant resource allocation and growth partitioning in response to environmental heterogeneity. Ecol. Model. 2005, 181, 59–77. [Google Scholar] [CrossRef]
- Barbaroux, C.; Bréda, N. Contrasting distribution and seasonal dynamics of carbohydrate reserves in stem wood of adult ring-porous sessile oak and diffuse-porous beech trees. Tree Physiol. 2002, 22, 1201–1210. [Google Scholar] [CrossRef]
- Peters, R.L.; Steppe, K.; Cuny, H.E.; De Pauw, D.J.W.; Frank, D.C.; Schaub, M.; Rathgeber, C.B.K.; Cabon, A.; Fonti, P. Turgor–A limiting factor for radial growth in mature conifers along an elevational gradient. New Phytol. 2021, 229, 213–229. [Google Scholar] [CrossRef] [PubMed]
- Thomas, F.M.; Hartmann, G. Tree rooting patterns and soil water relations of healthy and damaged stands of mature oak (Quercus robur L. and Quercus petraea [Matt.] Liebl.). Plant Soil 1998, 203, 145–158. [Google Scholar] [CrossRef]
- Vartapetian, B.B.; Jackson, M.B. Plant adaptations to anaerobic stress. Ann. Bot. 1997, 79, 3–20. [Google Scholar] [CrossRef]
- Parelle, J.; Brendel, O.; Bodénès, C.; Berveiller, D.; Dizengremel, P.; Jolivet, Y.; Dreyer, E. Differences in morphological and physiological responses to water-logging between two sympatric oak species (Quercus petraea [Matt.] Liebl., Quercus robur L.). Ann. For. Sci. 2006, 63, 849–859. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Brienen, R.J.W.; Gloor, E.; Phillips, O.L.; Prior, L.D. Detecting trends in tree growth: Not so simple. Trends Plant Sci. 2013, 18, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Matsushita, M.; Takata, K.; Hitsuma, G.; Yagihashi, T.; Noguchi, M.; Shibata, M.; Masaki, T. A novel growth model evaluating age–size effect on long-term trends in tree growth. Funct. Ecol. 2015, 29, 1250–1259. [Google Scholar] [CrossRef]
- Johnson, S.E.; Abrams, M.D. Age class, longevity and growth rate relationships: Protracted growth increases in old trees in the eastern United States. Tree Physiol. 2009, 29, 1317–1328. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).