Brazil Wave Climate from a High-Resolution Wave Hindcast
Abstract
1. Introduction
2. Materials and Methods
2.1. The ECMWF ERA-5 Based Wave Hindcast
2.2. In Situ Wave Observations
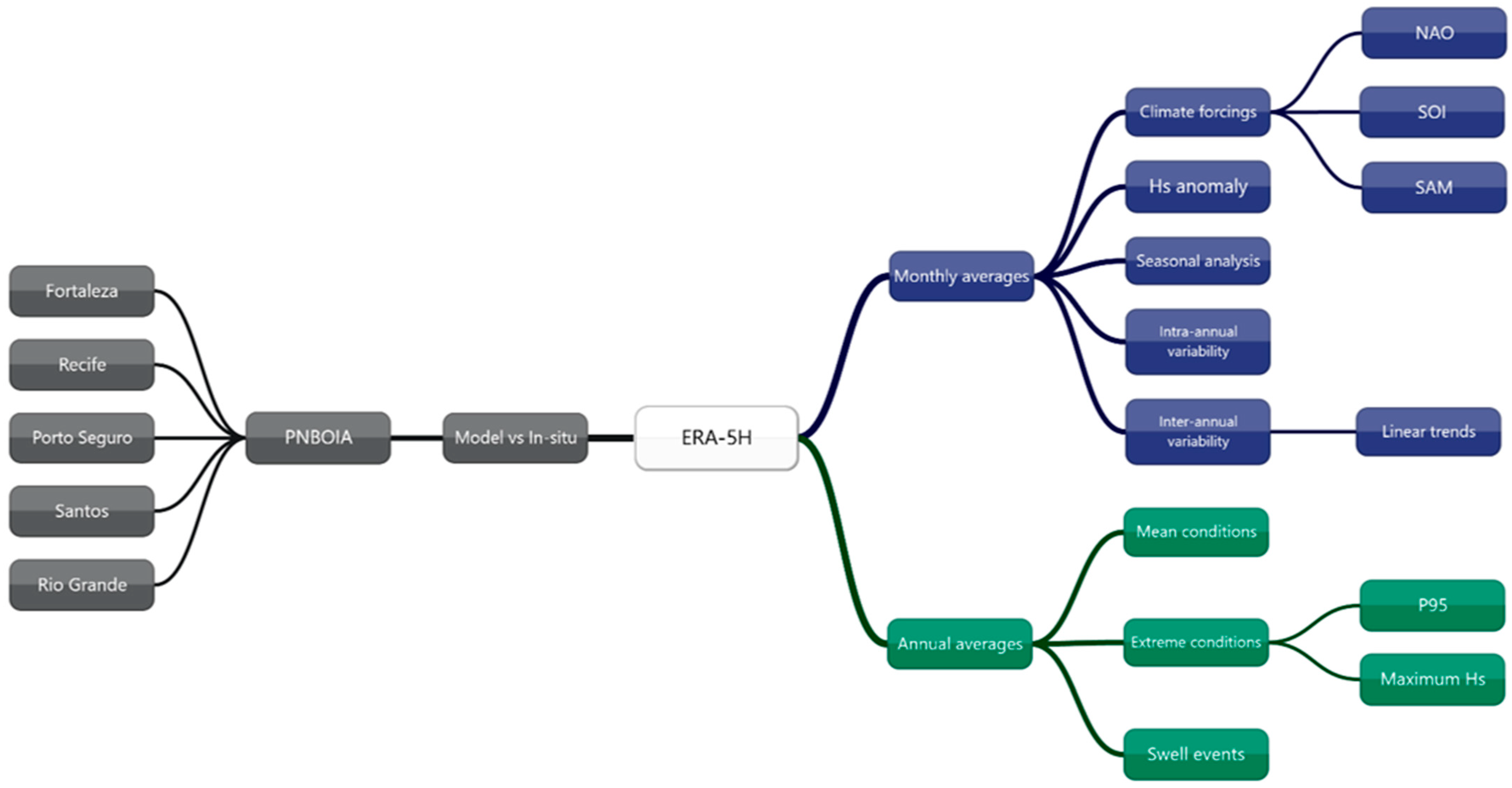
2.3. Methods
3. The Wave Climate of Brazil
3.1. Atlantic Ocean Wind and Wave Climates
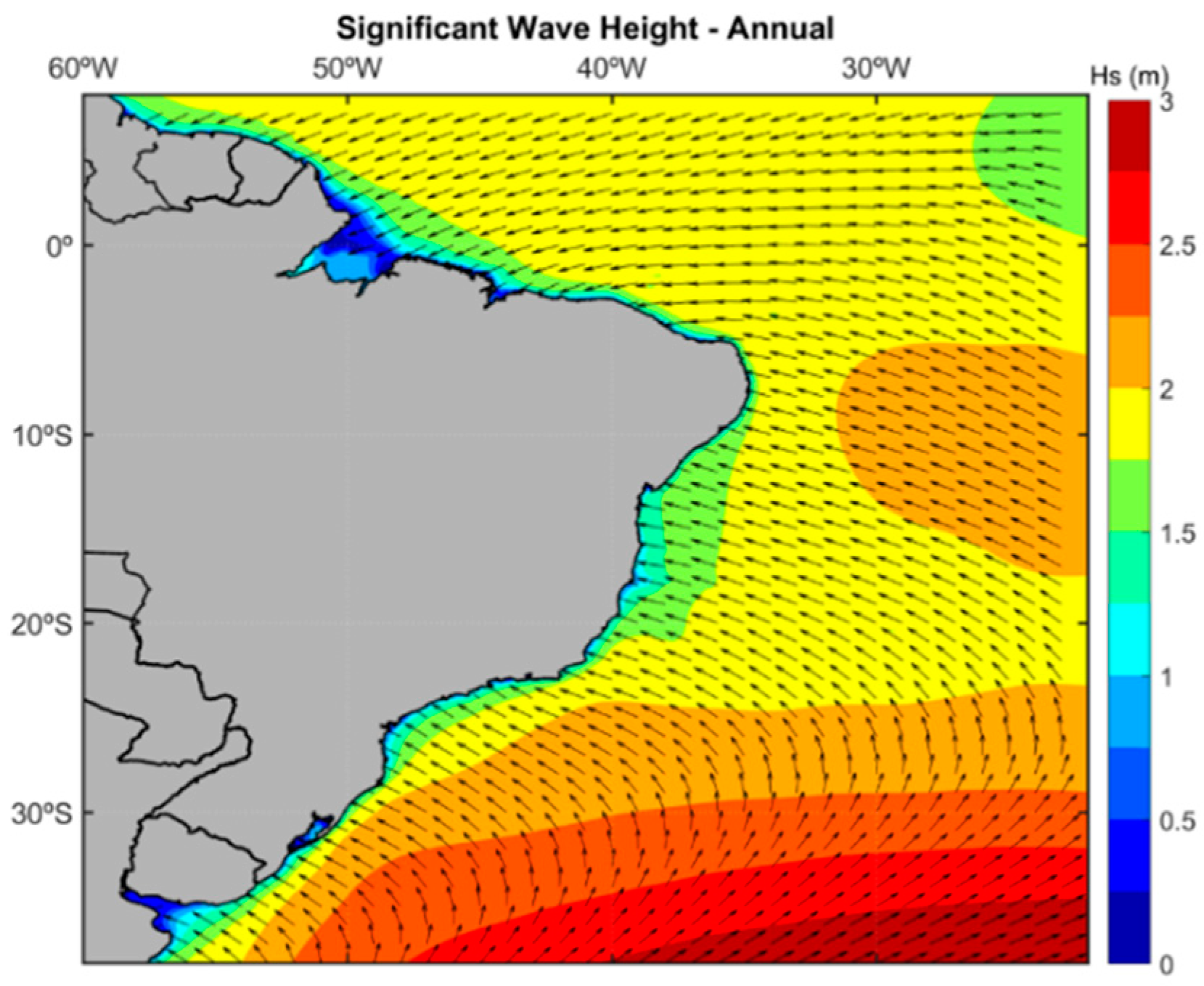
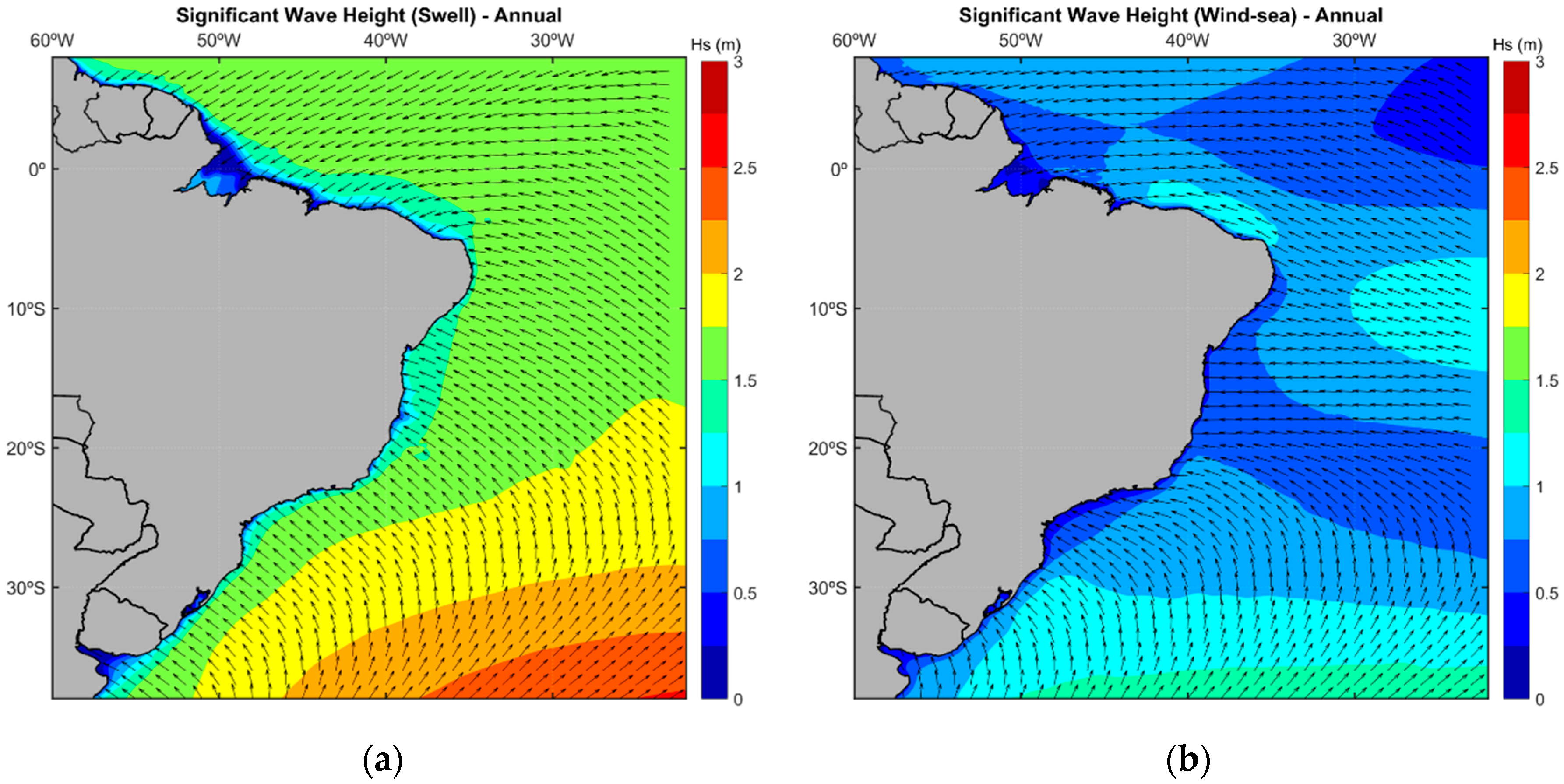
3.2. Brazil’s Mean Wave Heights and Directions (Wind Sea and Swell)
3.3. Extreme Wave Events
3.4. Wave Energy Flux
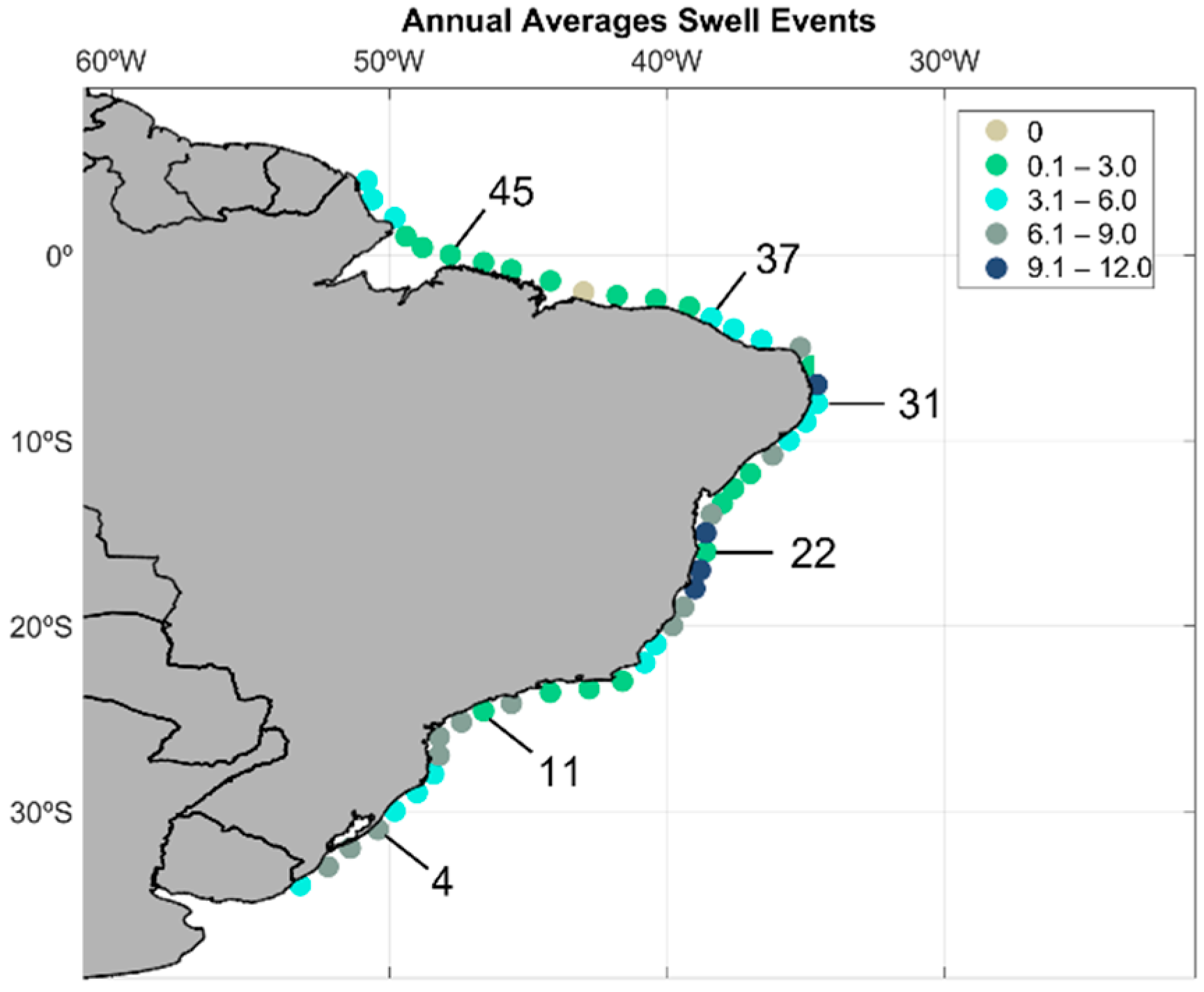
3.5. Swell Events
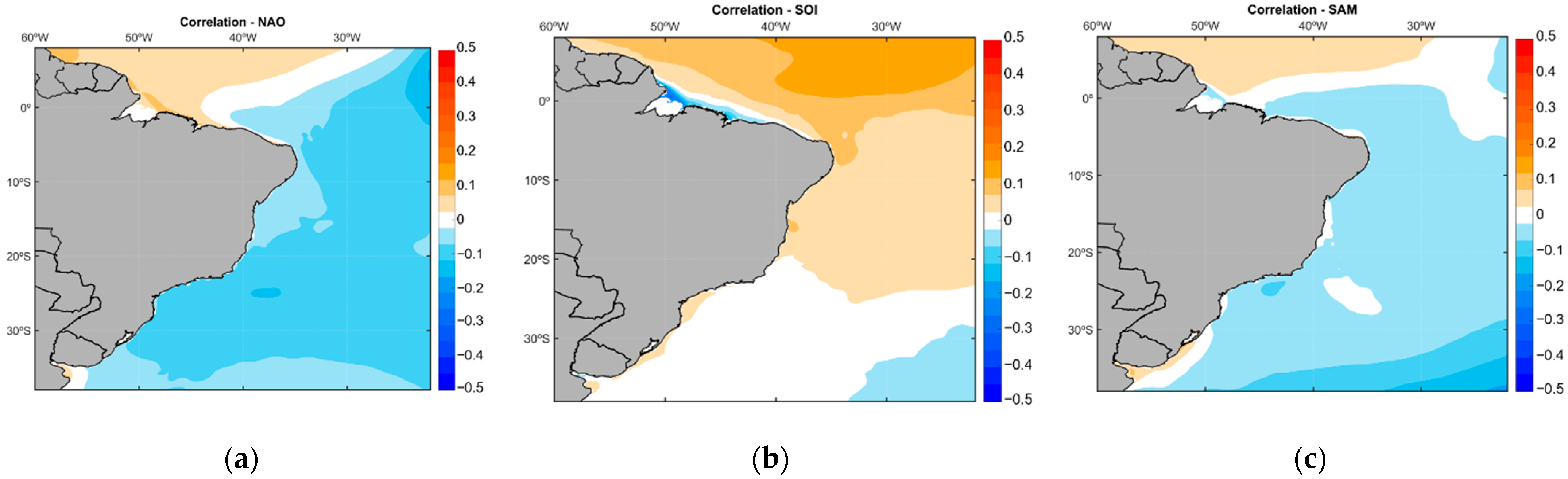
3.6. Large Scale Atmospheric Forcing
4. Key Points Analysis
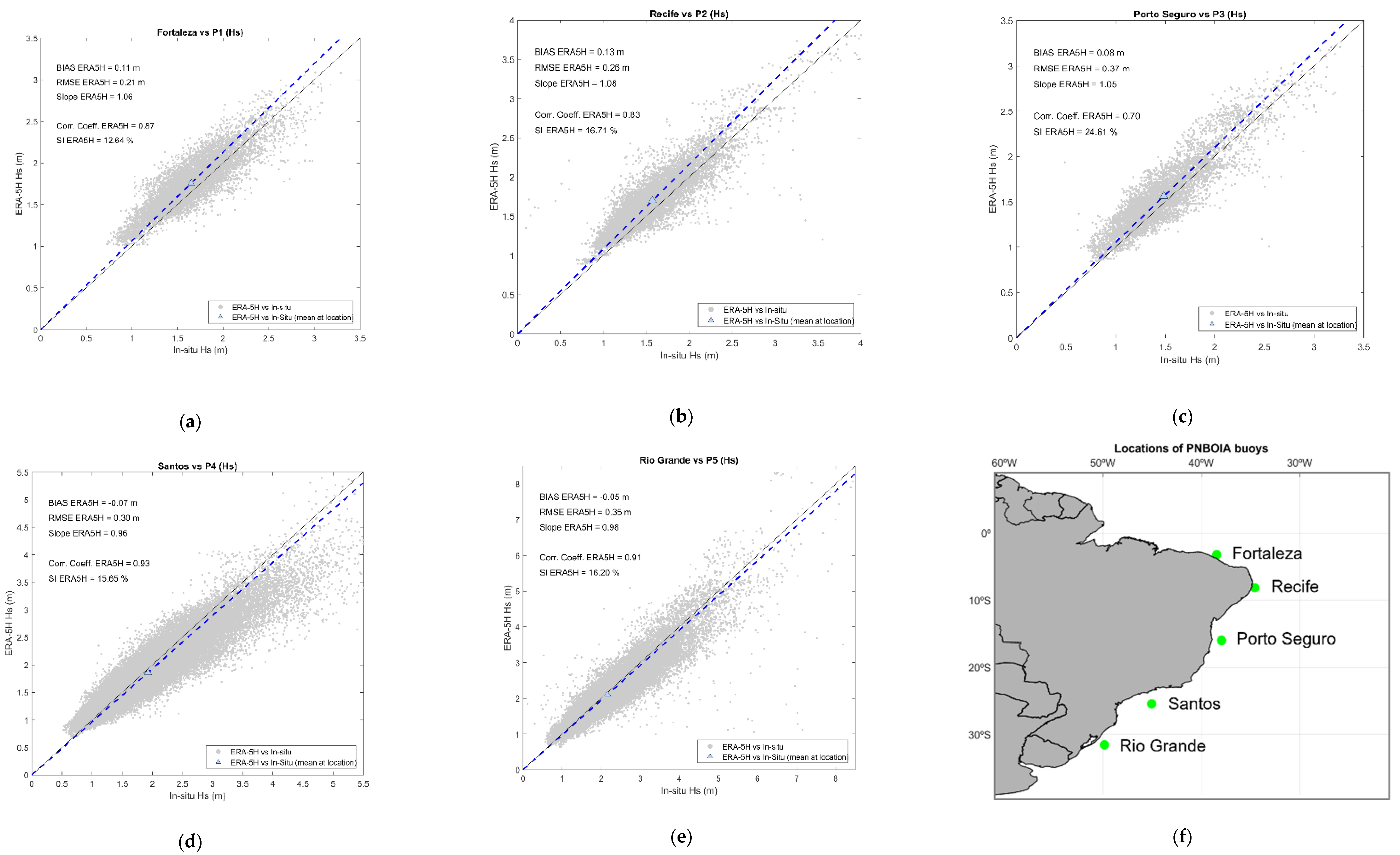
4.1. In Situ vs. ERA-5H Analysis
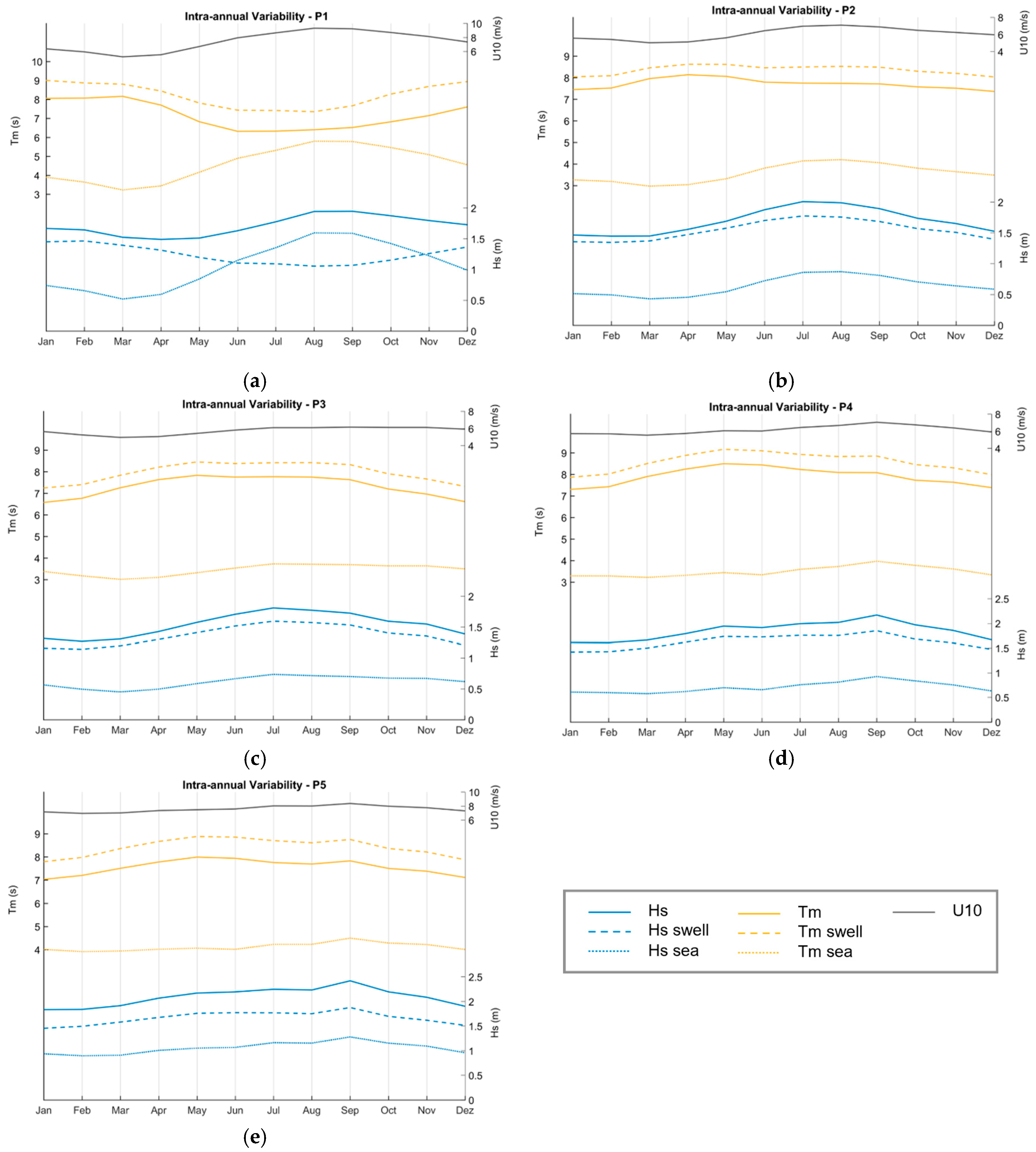
4.2. Intra-Annual Variability
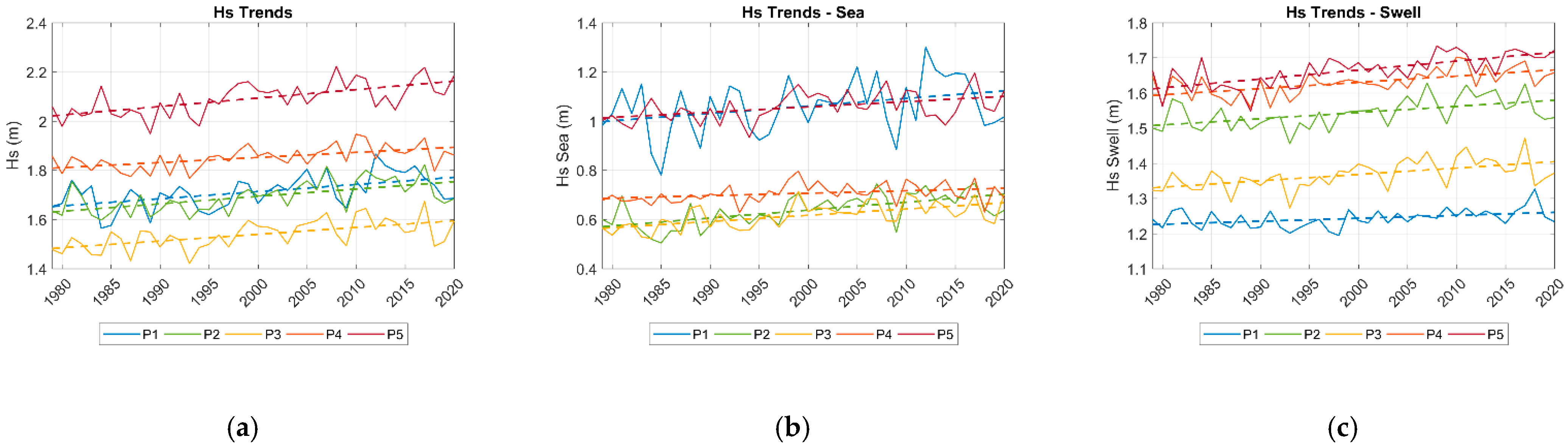
4.3. Inter-Annual Variability and Trends
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Points | Coordinates | Swell Events | Swell Origin Areas (%) | |||||
|---|---|---|---|---|---|---|---|---|
| Latitude | Longitude | Yearly Average | Total | NATL | TAO | SAO | Atlantic Ocean | |
| 1 | −34 | −53.2 | 5.4 | 226 | 0.0 | 0.9 | 81.9 | 82.7 |
| 2 | −33 | −52.2 | 7.0 | 294 | 0.0 | 0.7 | 84.4 | 85.0 |
| 3 | −32 | −51.4 | 7.1 | 299 | 0.0 | 0.7 | 89.0 | 89.6 |
| 4 | −31 | −50.4 | 7.3 | 306 | 0.0 | 0.7 | 89.5 | 90.2 |
| 5 | −30 | −49.8 | 5.7 | 238 | 0.0 | 0.4 | 88.2 | 88.7 |
| 6 | −29 | −49 | 5.0 | 210 | 0.0 | 1.0 | 85.2 | 86.2 |
| 7 | −28 | −48.4 | 5.4 | 228 | 0.0 | 5.3 | 81.6 | 86.8 |
| 8 | −27 | −48.2 | 6.3 | 265 | 0.0 | 6.8 | 78.5 | 85.3 |
| 9 | −26 | −48.2 | 7.4 | 311 | 0.0 | 3.9 | 83.9 | 87.8 |
| 10 | −25.2 | −47.4 | 7.2 | 304 | 0.0 | 4.3 | 79.9 | 84.2 |
| 11 | −24.6 | −46.6 | 2.8 | 116 | 0.0 | 7.4 | 86.8 | 94.1 |
| 12 | −24.2 | −45.6 | 8.5 | 356 | 0.0 | 6.2 | 79.2 | 85.4 |
| 13 | −23.6 | −44.2 | 1.5 | 62 | 0.0 | 25.8 | 45.2 | 71.0 |
| 14 | −23.4 | −42.8 | 1.9 | 81 | 0.0 | 17.3 | 50.6 | 67.9 |
| 15 | −23 | −41.6 | 2.3 | 96 | 0.0 | 19.8 | 54.2 | 74.0 |
| 16 | −22 | −40.8 | 3.1 | 129 | 0.0 | 10.1 | 59.7 | 69.8 |
| 17 | −21 | −40.4 | 4.8 | 200 | 0.0 | 6.0 | 73.0 | 79.0 |
| 18 | −20 | −39.8 | 7.0 | 294 | 0.0 | 4.1 | 68.0 | 72.1 |
| 19 | −19 | −39.4 | 8.0 | 338 | 0.0 | 2.7 | 68.0 | 70.7 |
| 20 | −18 | −39 | 10.7 | 448 | 0.0 | 0.4 | 69.2 | 69.6 |
| 21 | −17 | −38.8 | 11.9 | 501 | 0.0 | 0.6 | 66.7 | 67.3 |
| 22 | −16 | −38.6 | 1.4 | 60 | 0.0 | 13.3 | 71.7 | 85.0 |
| 23 | −15 | −38.6 | 10.0 | 418 | 0.0 | 3.3 | 61.5 | 64.8 |
| 24 | −14 | −38.4 | 6.8 | 285 | 0.0 | 13.0 | 52.6 | 65.6 |
| 25 | −13.4 | −38 | 1.7 | 71 | 0.0 | 12.7 | 43.7 | 56.3 |
| 26 | −12.6 | −37.6 | 0.6 | 26 | 15.4 | 7.7 | 19.2 | 42.3 |
| 27 | −11.8 | −37 | 1.5 | 64 | 71.9 | 10.9 | 0.0 | 82.8 |
| 28 | −10.8 | −36.2 | 6.3 | 264 | 85.2 | 0.8 | 0.0 | 86.0 |
| 29 | −10 | −35.6 | 3.6 | 152 | 88.8 | 0.0 | 0.0 | 88.8 |
| 30 | −9 | −35 | 3.2 | 135 | 90.4 | 0.0 | 0.0 | 90.4 |
| 31 | −8 | −34.6 | 4.1 | 174 | 87.9 | 0.6 | 0.0 | 88.5 |
| 32 | −7 | −34.6 | 9.5 | 399 | 82.5 | 0.5 | 0.0 | 83.0 |
| 33 | −6 | −34.8 | 1.9 | 78 | 0.0 | 6.4 | 76.9 | 83.3 |
| 34 | −5 | −35.2 | 8.8 | 371 | 86.5 | 0.0 | 0.0 | 86.5 |
| 35 | −4.6 | −36.6 | 5.9 | 246 | 87.8 | 0.8 | 0.0 | 88.6 |
| 36 | −4 | −37.6 | 3.4 | 142 | 92.3 | 0.7 | 0.0 | 93.0 |
| 37 | −3.4 | −38.4 | 3.8 | 161 | 89.4 | 2.5 | 0.0 | 91.9 |
| 38 | −2.8 | −39.2 | 2.9 | 121 | 96.7 | 1.7 | 0.0 | 98.3 |
| 39 | −2.4 | −40.4 | 2.4 | 100 | 97.0 | 2.0 | 0.0 | 99.0 |
| 40 | −2.2 | −41.8 | 0.2 | 7 | 100.0 | 0.0 | 0.0 | 100.0 |
| 41 | −2 | −43 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 42 | −1.4 | −44.2 | 2.2 | 91 | 86.8 | 0.0 | 0.0 | 86.8 |
| 43 | −0.8 | −45.6 | 2.1 | 90 | 98.9 | 0.0 | 0.0 | 98.9 |
| 44 | −0.4 | −46.6 | 2.6 | 110 | 0.0 | 5.5 | 83.6 | 89.1 |
| 45 | 0 | −47.8 | 3.0 | 126 | 97.6 | 0.8 | 0.0 | 98.4 |
| 46 | 0.4 | −48.8 | 2.8 | 119 | 0.0 | 5.9 | 76.5 | 82.4 |
| 47 | 1 | −49.4 | 3.0 | 124 | 0.0 | 3.2 | 80.6 | 83.9 |
| 48 | 2 | −49.8 | 3.9 | 164 | 0.0 | 4.9 | 80.5 | 85.4 |
| 49 | 3 | −50.6 | 3.7 | 157 | 0.0 | 5.7 | 80.3 | 86.0 |
| 50 | 4 | −50.8 | 4.5 | 191 | 0.0 | 2.6 | 74.3 | 77.0 |
References
- Cuchiara, D.C.; Fernandes, E.H.; Strauch, J.C.; Calliari, L.J. Modelagem Numérica do Comportamento das Ondas na Costa do Rio Grande do Sul. In Proceedings of the II Seminário e Workshop em Engenharia Oceânica, Rio Grande, Brazil, 23–25 November 2006. [Google Scholar]
- Sempreviva, A.M.; Schiano, M.E.; Pensieri, S.; Semedo, A.; Tomé, R.; Bozzano, R.; Borghini, M.; Grasso, F.; Soerensen, L.L.; Teixeira, J.; et al. Observed development of the vertical structure of the marine boundary layer during the LASIE experiment in the Ligurian Sea. Ann. Geophys. 2010, 28, 17–25. [Google Scholar] [CrossRef]
- Stewart, R.H. Introduction to Physical Oceanography; Department of Oceanography, Texas A&M University: College Station, TX, USA, 2005; p. 353. [Google Scholar] [CrossRef]
- Semedo, A.; Suselj, K.; Rutgersson, A.; Sterl, A. A Global View on the Wind Sea and Swell Climate and Variability from ERA-40. J. Clim. 2011, 24, 1461–1479. [Google Scholar] [CrossRef]
- Rutgersson, A.; Sætra, Ø.; Semedo, A.; Carlsson, B.; Kumar, R. Impact of surface waves in a Regional Climate Model. Meteorol. Z. 2010, 19, 247–257. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: New York, NY, USA, 2007; p. 405. [Google Scholar]
- Carrasco, A.; Semedo, A.; Isachsen, P.E.; Christensen, K.H.; Saetra, Ø. Global surface wave drift climate from ERA-40: The contributions from wind-sea and swell. Ocean Dyn. 2014, 64, 1815–1829. [Google Scholar] [CrossRef]
- Hughes, S.A.; Miller, H.C. Transformation of Significant Wave Heights. J. Waterw. Port Coast. Ocean. Eng. 1987, 113, 588–605. [Google Scholar] [CrossRef]
- Semedo, A. Seasonal Variability of Wind Sea and Swell Waves Climate along the Canary Current: The Local Wind Effect. J. Mar. Sci. Eng. 2018, 6, 28. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy; Springer Open: Aalborg, Denmark, 2017; p. 305. [Google Scholar]
- Cavaleri, L.; Fox-Kemper, B.; Hemer, M. Wind Waves in the Coupled Climate System. Bull. Am. Meteorol. Soc. 2012, 93, 1651–1661. [Google Scholar] [CrossRef]
- WMO. World Meteorological Organization. Guide to Wave Analysis and Forecasting, 2nd ed.; World Meterological Organization WMO: Geneva, Switzerland, 1998; p. 168. [Google Scholar]
- Masselink, G.; Gehrels, R. Coastal Environments & Global Change; American Geophysical Union and John Wiley & Sons, Ltd: New York, NY, USA, 2014; pp. 299–335. Available online: www.wiley.com/go/masselink/coastal (accessed on 23 December 2019).
- Young, I.R. Seasonal variability of the global ocean wind and wave climate. Int. J. Climatol. 1999, 19, 931–950. [Google Scholar] [CrossRef]
- Marcos, M.; Rohmer, J.; Vousdoukas, M.I.; Mentaschi, L.; Le Cozannet, G.; Amores, A. Increased Extreme Coastal Water Levels Due to the Combined Action of Storm Surges and Wind Waves. Geophys. Res. Lett. 2019, 46, 4356–4364. [Google Scholar] [CrossRef]
- Dodet, G.; Bertin, X.; Taborda, R. Wave climate variability in the North-East Atlantic Ocean over the last six decades. Ocean Model. 2010, 31, 120–131. [Google Scholar] [CrossRef]
- Kumar, P.; Min, S.K.; Weller, E.; Lee, H.; Wang, X.L. Influence of climate variability on extreme ocean surface wave heights assessed from ERA-interim and ERA-20C. J. Clim. 2016, 29, 4031–4046. [Google Scholar] [CrossRef]
- Marshall, A.G.; Hemer, M.A.; Hendon, H.H.; McInnes, K.L. Southern annular mode impacts on global ocean surface waves. Ocean Model. 2018, 129, 58–74. [Google Scholar] [CrossRef]
- Lemos, G.; Semedo, A.; Dobrynin, M.; Behrens, A.; Staneva, J.; Bidlot, J.-R.; Miranda, P. Mid-twenty-first century global wave climate projections: Results from a dynamic CMIP5 based ensemble. Glob. Planet. Chang. 2019, 172, 69–87. [Google Scholar] [CrossRef]
- Menéndez, M.; Mendez, F.; Losada, I.; Graham, N.E. Variability of extreme wave heights in the northeast Pacific Ocean based on buoy measurements. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Semedo, A.; Vettor, R.; Breivik, Ø.; Sterl, A.; Reistad, M.; Soares, C.G.; A Lima, D.C. The wind sea and swell waves climate in the Nordic seas. Ocean Dyn. 2014, 65, 223–240. [Google Scholar] [CrossRef]
- Hemer, M.A.; Church, J.A.; Hunter, J.R. Variability and trends in the directional wave climate of the Southern Hemisphere. Int. J. Clim. 2010, 30, 475–491. [Google Scholar] [CrossRef]
- Buizza, R.; Brönnimann, S.; Haimberger, L.; Laloyaux, P.; Martin, M.J.; Fuentes, M.; Alonso-Balmaseda, M.; Becker, A.; Blaschek, M.; Dahlgren, P.; et al. The EU-FP7 ERA-CLIM2 Project Contribution to Advancing Science and Production of Earth System Climate Reanalyses. Bull. Am. Meteorol. Soc. 2018, 99, 1003–1014. [Google Scholar] [CrossRef]
- Dee, D.P.; Balmaseda, M.A.; Balsamo, G.; Engelen, R.; Simmons, A.J.; Thépaut, J.-N. Toward a Consistent Reanalysis of the Climate System. Bull. Am. Meteorol. Soc. 2014, 95, 1235–1248. [Google Scholar] [CrossRef]
- Aarnes, O.J.; Abdalla, S.; Bidlot, J.-R.; Breivik, Ø. Marine Wind and Wave Height Trends at Different ERA-Interim Forecast Ranges. J. Clim. 2015, 28, 819–837. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef]
- Martucci, G.; Carniel, S.; Chiggiato, J.; Sclavo, M.; Lionello, P.; Galati, M.B. Statistical trend analysis and extreme distribution of significant wave height from 1958 to 1999—An application to the Italian Seas. Ocean Sci. 2010, 6, 525–538. [Google Scholar] [CrossRef]
- Wang, X.L.; Feng, Y.; Swail, V.R. North Atlantic wave height trends as reconstructed from the 20th century reanalysis. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Bertin, X.; Prouteau, E.; Letetrel, C. A significant increase in wave height in the North Atlantic Ocean over the 20th century. Glob. Planet. Chang. 2013, 106, 77–83. [Google Scholar] [CrossRef]
- Moura, M.R. Aspectos Climáticos versus Variação Sazonal do Perfil Morfodinâmico das Praias do Litoral Oeste de Aquiraz, Ceará, Brasil. Rev. Bras. Climatol. 2012, 11, 208–222. [Google Scholar] [CrossRef][Green Version]
- Araujo, C.E.S.; Franco, D.; Melo, E.; Pimenta, F. Wave Regime Characteristics of the Southern. In Proceedings of the International Conference on Coastal and Port Engineering in Developing Countries, COPEDEC VI, Colombo, Sri Lanka, 16–20 September 2003; Paper No. 097. p. 15. [Google Scholar]
- Sprovieri, F.C. Clima de Ondas, Potencial Energético e o Transporte de Sedimentos no Litoral Norte do Rio Grande do Sul. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2018. [Google Scholar]
- Silva, P.G.; Klein, A.H.; Gonzalez, M.; Gutiérrez, O.Q.G.; Espejo, A. Performance assessment of the database downscaled ocean waves (DOW) on Santa Catarina coast, South Brazil. An. Acad. Bras. Cienc. 2015, 87, 623–634. [Google Scholar] [CrossRef][Green Version]
- Oliveira, B.A.; Sobral, F.; Fetter, A.; Mendez, F.J. A high-resolution wave hindcast off Santa Catarina (Brazil) for identifying wave climate variability. Reg. Stud. Mar. Sci. 2019, 32, 100834. [Google Scholar] [CrossRef]
- Pereira, N.E.D.S.; Klumb-Oliveira, L.A. Analysis of the influence of ENSO phenomena on wave climate on the central coastal zone of Rio de Janeiro (Brazil). J. Integr. Coast. Zone Manag. 2015, 15, 353–370. [Google Scholar] [CrossRef]
- Pianca, C.; Mazzini, P.L.F.; Siegle, E. Brazilian offshore wave climate based on NWW3 reanalysis. Braz. J. Oceanogr. 2010, 58, 53–70. [Google Scholar] [CrossRef]
- Espindola, R.L.; Araújo, A.M. Wave energy resource of Brazil: An analysis from 35 years of ERA-Interim reanalysis data. PLoS ONE 2017, 12, e0183501. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, J.M.L. The Coastal Zone of Brazil: An Overview. J. Coast. Res. 2013, 39, 16–20. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Portilla, J. Storm-Source-Locating Algorithm Based on the Dispersive Nature of Ocean Swells. Avances 2012, 4, C22–C36. [Google Scholar]
- Amores, A.; Marcos, M. Ocean Swells along the Global Coastlines and Their Climate Projections for the Twenty-First Century. J. Clim. 2020, 33, 185–199. [Google Scholar] [CrossRef]
- Lemos, G.; Semedo, A.; Hemer, M.; Menendez, M.; A Miranda, P.M. Remote climate change propagation across the oceans—The directional swell signature. Environ. Res. Lett. 2021, 16, 064080. [Google Scholar] [CrossRef]
- Chen, G.; Chapron, B.; Ezraty, R.; VanDeMark, D. A Global View of Swell and Wind Sea Climate in the Ocean by Satellite Altimeter and Scatterometer. J. Atmos. Ocean. Technol. 2002, 19, 1849–1859. [Google Scholar] [CrossRef]
- Campos, R.; Alves, J.-H.; Soares, C.G.; Guimaraes, L.; Parente, C.E. Extreme wind-wave modeling and analysis in the south Atlantic ocean. Ocean Model. 2018, 124, 75–93. [Google Scholar] [CrossRef]
- Barbariol, F.; Bidlot, J.; Cavaleri, L.; Sclavo, M.; Thomson, J.; Benetazzo, A. Maximum wave heights from global model reanalysis. Prog. Oceanogr. 2019, 175, 139–160. [Google Scholar] [CrossRef]
- Bacon, S.; Carter, D.J.T. A connection between mean wave height and atmospheric pressure gradient in the North Atlantic. Int. J. Clim. 1993, 13, 423–436. [Google Scholar] [CrossRef]
- Kushnir, Y.; Cardone, V.J.; Greenwood, J.G.; Cane, M.A. The Recent Increase in North Atlantic Wave Heights. J. Clim. 1997, 10, 2107–2113. [Google Scholar] [CrossRef]
- NOAA, National Oceanic and Atmospheric Administration PSD (ESRL). El Niño Southern Oscillation (ENSO). 2019. Available online: https://www.esrl.noaa.gov/psd/enso/ (accessed on 22 March 2021).
- Rodriguez-Fonseca, B.; Polo, I.; García-Serrano, J.; Losada, T.; Mohino, E.; Mechoso, C.R.; Kucharski, F. Are Atlantic Niños enhancing Pacific ENSO events in recent decades? Geophys. Res. Lett. 2009, 36, 1–6. [Google Scholar] [CrossRef]
- Ramos, M.S.; Farina, L.; Faria, S.H.; Li, C. Relationships between large-scale climate modes and the South Atlantic Ocean wave climate. Prog. Oceanogr. 2021, 197, 102660. [Google Scholar] [CrossRef]
- Silva, G.A.M.; Ambrizzi, T.; Marengo, J.A. Observational evidences on the modulation of the South American Low Level Jet east of the Andes according the ENSO variability. Ann. Geophys. 2009, 27, 645–657. [Google Scholar] [CrossRef]
- Limpasuvan, V.; Hartmann, D.L. Wave-maintained annular modes of climate variability. J. Clim. 2000, 13, 4414–4429. [Google Scholar] [CrossRef]
- Castro, B.; Brandini, F.; Pires-Vanin, A.; Miranda, L. Multidisciplinary oceanographic processes on the Western Atlantic continental shelf between 4 N and 34 S. Sea 2006, 14, 259–293. [Google Scholar]
- Tessler, M.G.; Goya, S.C. Processos Costeiros Condicionantes do Litoral Brasileiro. Rev. Dep. Geogr. 2005, 17, 11–23. [Google Scholar] [CrossRef]
- Beserra, E.R.; Mendes, A.L.T.; Estefen, S.F.; Parente, C.E. Wave Climate Analysis for a Wave Energy Conversion Application in Brazil. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, San Diego, CA, USA, 10–15 June 2007; pp. 897–902. [Google Scholar] [CrossRef]
- Bender, M.A.; Knutson, T.R.; Tuleya, R.E.; Sirutis, J.J.; Vecchi, G.A.; Garner, S.T.; Held, I.M. Modeled Impact of Anthropogenic Warming on the Frequency of Intense Atlantic Hurricanes. Science 2010, 327, 454–458. [Google Scholar] [CrossRef]
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Killick, R.; Eckley, I.A.; Ewans, K.; Jonathan, P. Detection of changes in variance of oceanographic time-series using changepoint analysis. Ocean Eng. 2010, 37, 1120–1126. [Google Scholar] [CrossRef]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 10, 205. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, G. A Global View on the Swell and Wind Sea Climate by the Jason-1 Mission: A Revisit. J. Atmos. Ocean. Technol. 2013, 30, 1833–1841. [Google Scholar] [CrossRef]
- Bruno, M.F.; Molfetta, M.G.; Totaro, V.; Mossa, M. Performance Assessment of ERA5 Wave Data in a Swell Dominated Region. J. Mar. Sci. Eng. 2020, 8, 214. [Google Scholar] [CrossRef]
- Semedo, A.; Weisse, R.; Behrens, A.; Sterl, A.; Bengtsson, L.; Günther, H. Projection of Global Wave Climate Change toward the End of the Twenty-First Century. J. Clim. 2013, 26, 8269–8288. [Google Scholar] [CrossRef]




| Parameter | ERA-5 | ERA-5H |
|---|---|---|
| Period covered | 1950–present | 1979–present |
| Data product | Reanalysis | Hindcast |
| Temporal resolution | 1 h | 1 h |
| Spatial resolution (waves) | 40 km | 22 km |
| Spectral resolution | 24 directions, 30 logarithmically spaced frequencies | 36 directions and 36 frequencies |
| Bathymetry | ETOPO2 | ETOPO1 |
| Assimilation scheme | 4D-Var | - |
| IFS 1 model cycle | 41r2 (2016) | 46r1 (2019) |
| Region | Buoy (PNBOIA) | ERA-5H Key Point | Depth (m) | Time Frame | Latitude | Longitude |
|---|---|---|---|---|---|---|
| North | Fortaleza | P1 | 200 | 18/11/2016–20/05/2018 | 03°12.82′ S | 038°25.95′ W |
| Northeast | Recife | P2 | 200 | 21/09/2012–06/04/2016 | 08°09.22′ S | 034°33.57′ W |
| Northeast | Porto Seguro | P3 | 200 | 06/07/2012–19/12/2016 | 16°00.05′ S | 037°56.42′ W |
| Southeast | Santos | P4 | 200 | 12/04/2011–09/12/2018 | 25°26.37′ S | 045°02.17′ W |
| South | Rio Grande | P5 | 200 | 29/04/2009–09/03/2019 | 31°33.74′ S | 049°50.24′ W |
| Point | NATL | TAO | SAO | Atlantic Swells |
|---|---|---|---|---|
| 45 | 97.6 | 0.8 | 0.0 | 98.4 |
| 37 | 89.4 | 2.5 | 0.0 | 91.9 |
| 31 | 87.9 | 0.6 | 0.0 | 88.5 |
| 22 | 0.0 | 13.3 | 71.7 | 85.0 |
| 11 | 0.0 | 7.4 | 86.8 | 94.1 |
| 4 | 0.0 | 0.7 | 89.5 | 90.2 |
| Key Points | |||
|---|---|---|---|
| P1 | 2.9 | 3.0 | 0.8 |
| P2 | 3.0 | 3.2 | 1.8 |
| P3 | 2.7 | 2.5 | 1.8 |
| P4 | 2.1 | 1.0 | 1.8 |
| P5 | 3.4 | 2.1 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cotrim, C.d.S.; Semedo, A.; Lemos, G. Brazil Wave Climate from a High-Resolution Wave Hindcast. Climate 2022, 10, 53. https://doi.org/10.3390/cli10040053
Cotrim CdS, Semedo A, Lemos G. Brazil Wave Climate from a High-Resolution Wave Hindcast. Climate. 2022; 10(4):53. https://doi.org/10.3390/cli10040053
Chicago/Turabian StyleCotrim, Camila de Sa, Alvaro Semedo, and Gil Lemos. 2022. "Brazil Wave Climate from a High-Resolution Wave Hindcast" Climate 10, no. 4: 53. https://doi.org/10.3390/cli10040053
APA StyleCotrim, C. d. S., Semedo, A., & Lemos, G. (2022). Brazil Wave Climate from a High-Resolution Wave Hindcast. Climate, 10(4), 53. https://doi.org/10.3390/cli10040053







